黄金分割法、斐波那契法求极值
黄金分割和Fibonacci法
一、黄金分割法
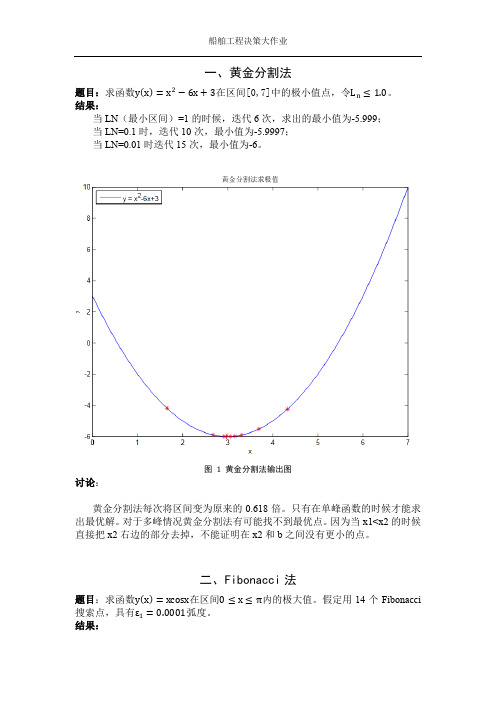
题目:求函数在区间[0,7]中的极小值点,令。
结果:
当LN(最小区间)=1的时候,迭代6次,求出的最小值为-5.999;
当LN=0.1时,迭代10次,最小值为-5.9997;
当LN=0.01时迭代15次,最小值为-6。
图 1 黄金分割法输出图
讨论:
黄金分割法每次将区间变为原来的0.618倍。
只有在单峰函数的时候才能求出最优解。
对于多峰情况黄金分割法有可能找不到最优点。
因为当x1<x2的时候直接把x2右边的部分去掉,不能证明在x2和b之间没有更小的点。
二、Fibonacci法
题目:求函数在区间内的极大值。
假定用14个Fibonacci 搜索点,具有弧度。
结果:
迭代12次,求出最大值为0.5611
图 2 Fibonacci法输出图
讨论:
1、Fibonacci法在布置n个点后的区间长度缩短为原长度L1的1/F n倍。
2、将区间改成10pi,搜索结果如图3,没有达到最大值。
可见fibonacci法同样需
要函数为单峰函数。
图 3 区间为[0 10*pi]时搜索结果。
数学文化之旅------神奇的斐波那契数列与黄金分割

神奇的斐波那契数列与黄金分割石家庄二中南校区孟柳比萨的列奥纳多,又称斐波那契(Leonardo Pisano ,Fibonacci, Leonardo Bigollo,1175年-1250年),中世纪意大利数学家,是西方第一个研究斐波那契数的人,并将现代书写数和乘数的位值表示法系统引入欧洲。
列奥纳多的父亲Guilielmo(威廉),外号Bonacci.因此列奥纳多就得到了外号斐波那契(Fibonacci,意即filius Bonacci,Bonacci之子)。
1202年,他撰写了《算盘全书》(Liber Abacci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,当时仍是小伙子的列奥纳多已经开始协助父亲工作,因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。
于是他就学会了阿拉伯数字。
他是西方第一个研究斐波那契数的人,并将现代书写数和乘数的位值表示法系统引入欧洲。
主要著作有《算盘书》《几何实践》《花朵》《平方数书》斐波那契在《算盘书》中提出了一个有趣的兔子问题:一般而言,兔子在出生两个月后就具有了繁殖能力,一对兔子每个月能生出一对兔子,如果兔子都不死,那么一年后能有多少对兔子?拿新出生的一对兔子研究:第一个月兔子没有繁殖能力,两个月后生下一对小兔总数共有两对;三个月后,老兔子生下又一对,因为上一轮的小兔没有繁殖能力,所以总数是三对;…………..1,1,2,3,5,8,13,21,34,55,89,144……依次类推下去,你会发现,它后一个数等于前面两个数的和。
在这个数列中的数字,就被称为斐波那契数。
2是第3个斐波那契数。
斐波那契数列还满足一下特点:1.任一项的平方数都等于与它相邻的两项乘积相差12.相邻的4个数,内积与外积相差13.前一项与后一项的比大约是0.6184.后一项比前一项大约是1.618经研究发现,相邻两个斐波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。
【交易干货】斐波那契—黄金分割线用法及技巧!

【交易干货】斐波那契—黄金分割线用法及技巧!听过很多交易故事,也见过很多交易者,他们的经历无论多么千奇百怪,有几个共同的词汇频频出现:亏损、扛单、爆仓。
一旦交易出现连亏,大多数交易者离爆仓就不远了。
就小编接触的交易者而言,至少80%的人在连亏之后以爆仓而告终,只有一部分老手能及时找到正确的方向扭转颓势。
那么,老手在连亏的时候是如何及时找到与盘面一致的方向,避免爆仓的呢?大家都知道我们想要预测盘面走势,基本只能靠借助基本面信息或各种各样的指标和理论来分析的。
最常用的就是指标了,因为这个是切切实实可以看到的。
这些指标之中就有一些在预测行情方面有着较高的准确性,学会它你就能在交易中找到方向,防止爆仓了。
而老手最常用的便是斐波那契——黄金分割线!为什么呢?因为它极其简单,你甚至不用知道其背后的复杂逻辑,只需知道如何使用即可,并且它有着神奇的预测作用,学会用它即能轻松找到方向。
下面我们就来详细的了解一下,斐波那契——黄金分割线在交易中的实战应用吧!01斐波那契数列是怎么来的?斐波那契,十二世纪意大利的天才数字研究专家,那时候,罗马数字和阿拉伯数字正好风靡欧洲。
斐波那契醉心数字,因为发明斐波那契数列而闻名全世界。
闲话少说!请看数列:1+1=2 13+21=341+2=3 21+34=552+3=5 34+55=893+5=8 35+89=1445+8=13 89+144=23318+13=21 144+233=377。
直到无穷要知道一个数字天才发现的东西,肯定不是一个简单的东西。
如果你简单一看,你就看明白了,那你也是天才了。
如果如我般看不明白才是真正的蠢才,那是非常正常的。
不可能人人都是天才。
对天才的东西加以利用,至少我们可以从蠢才变成人才、地才。
天才就免了吧。
首先,从上面得出一组数据:1、3、5、8、13、21、34、55、89、144、233、377.......接着,随便取一组数据:34+55=89.做除法得出几个相同且重要的数据:55除以34,结果等于1.618.34除以55,结果等于0.618.34除以89,结果等于0.382.34除以144,结果等于0.236.•无论你把数组中哪一个数字拿出来,都会得到这几个数字,于是这6个数字你是必须记住的:0.236、0.382、0.50、0.618、0.786、1.27、1.618。
最优化方法实验报告(1)

最优化方法实验报告(1)最优化方法实验报告Numerical Linear Algebra And Its Applications学生所在学院:理学院学生所在班级:计算数学10-1学生姓名:甘纯指导教师:单锐教务处2013年5月实验一实验名称:熟悉matlab基本功能实验时间: 2013年05月10日星期三实验成绩:一、实验目的:在本次实验中,通过亲临使用MATLAB,对该软件做一全面了解并掌握重点内容。
二、实验内容:1. 全面了解MATLAB系统2. 实验常用工具的具体操作和功能实验二实验名称:一维搜索方法的MATLAB实现实验时间: 2013年05月10日星期三实验成绩:一、实验目的:通过上机利用Matlab数学软件进行一维搜索,并学会对具体问题进行分析。
并且熟悉Matlab软件的实用方法,并且做到学习与使用并存,增加学习的实际动手性,不再让学习局限于书本和纸上,而是利用计算机学习来增加我们的学习兴趣。
二、实验背景:(一)0.618法(黄金分割法),它是一种基于区间收缩的极小点搜索算法,当用进退法确定搜索区间后,我们只知道极小点包含于搜索区间内,但是具体哪个点,无法得知。
1、算法原理黄金分割法的思想很直接,既然极小点包含于搜索区间内,那么可以不断的缩小搜索区间,就可以使搜索区间的端点逼近到极小点。
2、算法步骤用黄金分割法求无约束问题min (),f x x R ∈的基本步骤如下:(1)选定初始区间11[,]a b 及精度0ε>,计算试探点:11110.382*()a b a λ=+-11110.618*()a b a μ=+-。
(2)若k k b a ε-<,则停止计算。
否则当()()k k f f λμ>时转步骤(3)。
当()()k k f f λμ≤转步骤(4)。
(3)置11111110.382*()k kk k k k k k k k a b b a b a λλμμ+++++++=??=??=??=+-?转步骤(5)(4)置11111110.382*()k k k k k k k k k k a a b a b a μμλλ+++++++=??=??=??=+-?转步骤(5)(5)令1k k =+,转步骤(2)。
斐波那契-黄金分割

斐波那契-黄⾦分割斐波那契数列普通递推F0=0,F1=1,F n=F n−1+F n−2快速倍增递推F2n=F n(2F n+1−F n)F2n=F n(F n+1+F n−1)F2n+1=F2n+1+F2n 矩阵递推1 1 1 0F n−1F n−2=F nF n−1通项公式及其推导令ϕ=1+√52,ˆϕ=1−√52∵F_n = \dfrac{1}{\sqrt{5}}(\phi^n-\hat\phi^n)=\lfloor \dfrac{\phi^i}{\sqrt{5}} + \dfrac{1}{2} \rfloor所以、斐波那契以指数形式增长1.母函数法$ \digamma(x)=\sum\limits_{\infin} F_nx n\ \digamma(x)=x2\digamma(x)+x\digamma(x)+x\ \digamma(x)=\dfrac{1-x-x2} $母函数进⾏展开,⾸先我们要知道⽜顿⼆项式定理、⽜顿⼴义⼆项式定理、⼆项式定理的推⼴⽜顿⼆项式定理(n \in N^{+})(x+y)^n = \sum\limits_{i=0}^{n} C_{n}^{i} x^{n-i}y^{i}**⼆项式定理推⼴⾄(n \in N) **(1+x)^n=\sum\limits_{i=0}^{\infin} C_{n}^{i} x^i~~~~(n>0)(1+x)^{-n} = \sum\limits_{i=0}^{\infin} C_{-n}^{i} x^i=\sum\limits_{i=0}^{\infin}(-1)^i C_{n+i-1}^{i} x^i⽜顿⼴义⼆项式定理(\alpha \in R)(x+y)^{\alpha}=\sum\limits_{i=0}^{\infin}\tbinom{\alpha}{i} x^{\alpha-i}y^k其中\tbinom{\alpha}{i}类似组合数\tbinom{\alpha}{i}=\dfrac{\alpha(\alpha-1)\cdots(\alpha-i+1)}{i!}特殊形式(1+x)^n = (1-x)^{-n} = \sum\limits_{i=0}^{\infin} C_{n}^{i}x^i推导开始:设~\digamma(x)=\frac{x}{1-x-x^2}=\frac{A}{1-\alpha x}+\frac{B}{1-\beta x} \\=\frac{A+B-x(A\beta+B\alpha)}{1-(\alpha+\beta)x+\alpha\beta x^2}\\ \left\{ \begin{matrix} A+B=0\\A\beta+B\alpha=-1\\ \alpha+\beta=1\\ \alpha\beta=-1 \end{matrix} \right. \Rightarrow \left\{ \begin{matrix} A=\frac{1}{\sqrt{5}}\\ B=-\frac{1}{\sqrt{5}}\\ \alpha=\phi\\ \beta=\hat\phi\end{matrix} \right.\\ \therefore \digamma(x)=\frac{1}{\sqrt{5}}(\frac{1}{1-\phi x}-\frac{1}{1-\hat\phi x})\\ \because\frac{1}{1-x}=\sum\limits_{n=0}^{\infin}x^n\\ \digamma(x)=\frac{1}{\sqrt{5}}\sum\limits_{n=0}^{\infin}(\phi^n-\hat\phi^n) x^n2.数列待定系数法类似于求解a_n = pa_{n-1}+q性质1.卡西尼性质F_{n-1}F_{n+1}-F_n^2=(-1)^n证:F_{n-1}F_{n+1}-F_n^2\\ =det \left( \left[ \begin{matrix} F_{n+1}~~F_{n}\\ F_{n}~~F_{n-1} \end{matrix} \right] \right) =det \left( \left[ \begin{matrix} 1~~~~1\\ 1~~~~0 \end{matrix} \right] \right)^n = \left( det \left( \left[ \begin{matrix} 1~~~~1\\ 1~~~~0 \end{matrix} \right] \right) \right)^n=(-1)^n2.附加性质F_{n+m}=F_m F_{n+1}+F_{m-1}F_{n}证:\because \left[ \begin{matrix} F_{n}~~~F_{n-1}\\ F_{n-1}~~~F_{n-2} \end{matrix} \right] = \left[ \begin{matrix} 1~~~~1\\ 1~~~~0 \end{matrix} \right]^{n-1}\\ \therefore \left[ \begin{matrix} F_{n+m}~~~F_{n+m-1}\\ F_{n+m-1}~~~F_{n+m-2} \end{matrix} \right] = \left[ \begin{matrix} 1~~~~1\\ 1~~~~0 \end{matrix} \right]^{n+m-1}=\left[ \begin{matrix} 1~~~~1\\ 1~~~~0\end{matrix} \right]^{n} \left[ \begin{matrix} 1~~~~1\\ 1~~~~0 \end{matrix} \right]^{m-1}= \left[ \begin{matrix} F_{n+1}~~~F_{n}\\ F_{n}~~~F_{n-1} \end{matrix} \right] \left[ \begin{matrix} F_{m}~~~F_{m-1}\\ F_{m-1}~~~F_{m-2} \end{matrix} \right]\\ \therefore F_{n+m}=F_{n+1}F_{m}+F_nF_{m-1}变形:F_{2n} = F_n(F_{n+1}+F_{n-1}) .3.整除与GCD性质\forall a,b \in N,F_a|F_b\Leftrightarrow a|b[][][](F_n,F_m) = F_{(n,m)}证:设~n>m~~则~(F_n,F_m)=(F_{n-km},F_m)\\ 设~r=n-km~,r<m~则~(F_r,F_m)=(F_r,F_{m-kr})\\ 这就类似于欧⼏⾥德算法的过程\\ \therefore~(F_n,F_m)=F_{(n,m)}4.求和公式奇数项:\sum\limits_{i=1}^{2n-1}[2\nmid i] F_{i}= F_{2n}偶数项:\sum\limits_{i=2}^{2n}[2\mid i] F_{i}= F_{2n+1}-1平⽅项:\sum\limits_{i=1}^{n}F_i^2=F_n F_{n+1}证:画图推⼴1.⼴义斐波那契数列当n<0时F_n=F_{n+2}-F_{n+1}F_{-n}=(-1)^{n-1}F_n2 .类斐波那契数列⼜称斐波那契—卢卡斯数列对于数列G,若G_0=a,G_1=b,且数列满⾜递推关系式,则称G是类斐波那契数列G_n =a F_{n-1} + b F_{n}⽤矩阵可证类斐波那契数列也有部分斐波那契数列的性质任意两个或两个以上斐波那契—卢卡斯数列之和或差仍然是斐波那契—卢卡斯数列3. Lucas数列与Fibonacci数列Lucas数列为a=2,b=1的类斐波那契数列,记为LL_n = (\dfrac{1+\sqrt{5}}{2})^n+(\dfrac{1-\sqrt{5}}{2})^n~~~~(n\ge 2)Lucas数列能够辅助写出看似很困难的等式2L_{n+m}=5 F_n F_m+L_n L_m\\ 2F_{n+m}=5 F_n L_m+L_n F_m\\ L_{2n}=L_n^2-2(-1)^n\\ F_{2n}=F_n L_n\\ L_n=F_{n+1}+F_{n-1}4.编码(齐肯多夫定理)齐肯多夫表述法表⽰任何正整数都可以表⽰成若⼲个不连续的斐波那契数之和证:若~m~为斐波那契数,成⽴\\ 否则考虑最⼤~n1~满⾜~F_{n1}< m<F_{n1+1}\\ 继续考虑最⼤~n2~满⾜~F_{n2} < m-F_{n1}<F_{n2+1}\\ 反证:\\ 若~F_{n1}~和~F_{n2}~为连续斐波那契数\\ 则~F_{n1+1}<m~与~F_{n1+1}>m~⽭盾模意义下的循环对于任意整数n , 数列为F_i~(mod~n)周期数列. ⽪萨诺周期\pi(n)记为该数列的周期.例如,模3的斐波那契数列前若⼲项为:0, 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, 2, 2, 1, 0\cdots\therefore \pi(3) = 8.性质:1.~~\pi(n)\le 6 n且只有满⾜n=2*5^k的形式时才取得到等号2.~~\forall a,b\in N~且~(a,b)=1,\pi(a)\pi(b)=\pi(ab)Loading [MathJax]/jax/element/mml/optable/MathOperators.js。
斐波那契数列与黄金分割

两千年前,希腊数学家考虑如下问题:
设线段 AB ,
A
在 AB 上找一点 C , 使得
C
B
令 x AB AC, 于是有 xA C C B 1C B 11,
AC CB
AC AC x
可化为一元二次方程 x2x10.
该方程的根为
1 5 x1 2 ,
x2
1 2
5
.
大自然中数学美---黄金分割 黄金比
A
P
称为黄金分割数.
黄金矩形
a : b = 1 : 1.618…
b
a
2、黄金三角形
A
C
B
底与腰 或腰与底 之比为0.618的三角形,称为黄金
三角形.
黄金梯形:在等腰梯形中, 当上底边长与下底边长之比 为黄金比且上底边长正好与 两条腰长相等 此时下底边 长正好与两条对角线长相等 时,这个梯形就称为黄金梯 形,
a1 a2 1, an1 an an1, n 2, 3, 4,...
斐波那契数列
斐波纳契数列的性质
1 1 2 3 5 8 13 21 34 55 89 144 ・・・
各項分别为前项的多少倍
后一项
前一项 的观察
1 < 1.5 < 1.6 < 1.6153 < 1.6176 < 1.6179 1 2 3 5 8 13 21 34 55 89 144 1 1 2 3 5 8 13 21 34 55 89 1.6180・・・
??
“十秒钟加数”的秘密
• 又例如:
右式的答案是: 610 11 = 6710
34 55 89 144 233 377 610 987 1597 + 2584 ????
斐波那契数列与黄金分割

我们可以在鹦鹉螺的外壳发现这样的螺线
所谓黄金三角形是一个 等腰三角形其底与腰的长 度比为黄金比值。我们若 以底边为一腰作一等腰三 角形则此三角形亦为一黄 金三角形,如下图。图中 三种不同长度的线段,其 中次长的线段(蓝色)与 最长的线段(红色)比是 黄金比例,最短的线段 (绿色)与次长线段(蓝 色)也是黄金比例。
1 5 ,其正根为 x 2
5 1 x 0.6180339 0.618 2 A B
小段 大段
3.黄金矩形
定义:一个矩形,如果从中裁去 一个最大的正方形,剩下的矩形的宽与长 之比,与原矩形的一样(即剩下的矩形与 原矩形相似),则称具有这种宽与长之比 的矩形为黄金矩形。黄金矩形可以用上述 方法无限地分割下去。
Fn Fn1 Fn2 , n 2.
每月大兔对数 Fn 排成数列为: 0,1,1,2,3,5,8,13,21,34,55,89,144,
•••
4
定义:若一个数列,前两项均等于1,而从 第三项起每一项是其前两项之和,则称该数列
为斐波那契数列。即:
1 , 1 , 2 , 3 , 5 , 8 , 13 , … …
(1)人体各部分的比Fra bibliotek肚 脐:
印堂穴:
(头—脚)
(口—头顶)
肘关节: (肩—中指尖) 膝 盖: (髋关节—足尖)
(2)著名建筑物中各部分的比
如埃及的金字塔,高(137米)与底边长 (227米)之比为0.629
雅典的帕德侬神庙 (Parthenon at Athens) 庄严、宏伟,被认为 是古希腊最伟大的建筑之一。有 人认为它之所以显得那么和谐, 是因为这个建筑符合黄金比。
Field daisies have 34 petals
斐波那契数字和黄金分割率

斐波那契数字和黄金分割率
一、斐波那契数字对股市提前预示和警示周期:
斐波那契数字1、1、2、3、5、8、13、21、34、55、89、144......前面两数相加得后面一个数。
1,斐波那契数字在日循环周期中最大上升天数为55天,34天,21天。
2,斐波那契数字在周循环周期中最大上升周数为34周,21周,13周。
3,斐波那契数字在月循环周期中最大上升月数为13月,8月,5月,3月。
涨跌幅度与空间的高低快慢对波段走势时间长短有制约作用。
推测出的变盘日期如果与周的日期重叠,应视为重要的时间之窗。
再与月的相吻合市场就会发生重大转折!
对一个完整小周期:低点---高点---低点;高点---低点---高点。
在分析周期时,只有这两种循环周期与斐波那契数字时间周期相对应。
二、黄金分割位数字的计算是:
1、相邻的两个数互除,得数约等于0.618(记住是相邻的)。
2、相隔的两个数互除,得数约等于0.382和2.618(记住是相隔的)。
3、高位数除相邻的低位数,得数约等于1.618。
4、0.382 X 0.618 = 0.236。
5、通常所用的黄金分割率为:
0.236、0.382、0.5、0.618、0.809、1.236、1.382、1.618、2、2.618、3.236、4.236、5.236、6.854。
黄金分割率的演算同斐波那契数字密不可分。
斐波那契数字同黄金分割位是相互印证的关系。
斐波那契数字表现的是时间的长短,黄金分割位提示的是空间上升下降的幅度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
function y=fx(x)
if nargin==1
y=x+20/x;
end
end
%a为区间下限,b为区间上限,e为精度;
%fx(x)为原方程函数;
function [xj,yj]=huangjin(a,b,e)
a=input('Please enter the value of a:');
b=input('Please enter the value of b:');
e=input('Please enter the value of e:');
while b-a>e
x1=a+*(b-a);
x2=a+*(b-a);
if fx(x1)<fx(x2)
b=x2;
else
a=x1;
end
end
xj=(a+b)/2;
yj=fx(xj);
end
此题中,a=,b=1,e=,程序运行结果为xj=,yj=。
改变方程,将原函数方程改变。
6、用斐波那契法求极值:
()432
31630248 f x x x x x
=-+-+;
%建立原方程函数;
function y=fx(x)
if nargin==1
y=3*x^4-16*x^3+30*x^2-24*x+8; end
end
%建立斐波那契数列函数;
function fn=F(n)
if nargin==1
y=[0];
y(1)=[1];
y(2)=[1];
for k=3:1:n
y(k)=[y(k-1)+y(k-2)];
end
fn=y(n);
end
end
%求解应计算次数的函数;
%s为(b-a)/e的值,其中(a,b)为单峰区间,e为精度;
function n=cishu(s)
if nargin==1
n=1;
while F(n)<s
n=n+1;
end
end
end
%求极值函数;
%a为区间下限,b为区间上限,e为精度;
function [xj,yj]=fib(a,b,e)
a=input('Please enter the value of a:');
b=input('Please enter the value of b:');
e=input('Please enter the valud of e:');
s=(b-a)/e;
n=cishu(s);
x2=a+F(n-1)/F(n)*(b-a);
x1=b-F(n-1)/F(n)*(b-a);
while (b-a)>e
if fx(x2)>=fx(x1)
b=x2;
x2=x1;
x1=a+b-x2;
else
a=x1;
x1=x2;
x2=a+b-x1;
end
end
xj=(a+b)/2;
yj=fx(xj);
end
此题中,a=-10,b=10,e=,程序运行结果为:xj =, yj =,若原方程改变,只需改变原方程函数即可。
