最小二乘法线性详细说明共47页
第五章 最小二乘法

第二节 正规方程
第五章 线性参数的最小二乘法
正规方程:将误差方程按最小二乘法原理转化得到的
有确定解的代数方程组。
一、等精度测量线性参数最小二乘处理的正规方程
v1 l1 (a11 x1 a12 x2 a1 t xt ) v 2 l 2 (a21 x1 a22 x2 a2 t xt ) v l (a x a x a x ) n n1 1 n2 2 nt t n
2
ln (an1 x1 an 2 x2 ant xt )
vi x1
2
2
2a11 l1 (a11 x1 a12 x2 a1t xt ) 2a21 l2 (a21 x1 a22 x2 a2 t xt ) 2an1 ln (an1 x1 an 2 x2 ant xt ) 0
a
i1 i
a
i1
ai 2 x2
a
it
a it x t 0
2 2 vi 2 a i1a i1 0 2 x1
说明存在极小值
正规方程 (t个)
n n n n ai 1 l i ai 1ai 1 x1 ai 1ai 2 x2 ai 1ait x t i 1 i 1 i 1 i 1 n n n n ai 2 l i ai 2 ai 1 x1 ai 2 ai 2 x2 ai 2 ait x t i 1 i 1 i 1 i 1 n n n n ait l i ait ai 1 x1 ait ai 2 x2 ait ait x t i 1 i 1 i 1 i 1
最小二乘法线性详细说明

4
最小二乘法产生的历史
最小二乘法最早称为回归分析法。由著名的英 国生物学家、统计学家道尔顿(F.Gallton)— —达尔文的表弟所创。 早年,道尔顿致力于化学和遗传学领域的研究。 他研究父亲们的身高与儿子们的身高之间的关 系时,建立了回归分析法。
5
父亲的身高与儿子的身高之间关系的研究
1889年F.Gallton和他的朋友K.Pearson收集了 上千个家庭的身高、臂长和腿长的记录 企图寻找出儿子们身高与父亲们身高之间关系 的具体表现形式 下图是根据1078个家庭的调查所作的散点图 (略图)
vi = ∆yi = [ yi − (a + bxi )]
②
12
我们的目的是根据数据点确定回归常数a和b, 并且希望确定的a和b能使数据点尽量靠近直线 能使v尽量的小。由于偏差v大小不一,有正有 负,所以实际上只能希望总的偏差(∑ vi)最小。
2
所谓最小二乘法就是这样一个法则,按照这个 法则,最好地拟合于各数据点的最佳曲线应使 各数据点与曲线偏差的平方和为最小。
解方程,得:
sxy b=
⑥
sxx a = y − bx
⑦
16
公式⑥⑦式中:
sxy
xx
(∑ x ∑ y ) = ∑xy −
i i i i 2 i
2
(∑ x ) s = ∑x − x = ∑x n
i i
n
n
从④不难求出对a, b的二阶偏导数为: a, b
∂ ∑ vi 2 = 2n 2 ∂a ∂ ∑ vi 2 = 2∑ xi 2 2 ∂b ∂ ∑ vi 2 = 2∑ xi ∂a∂b
2
已经确定, 一 是物理量y与x间的函数关系已经确定 已经确定 只有其中的常数未定(及具体形式未定) 时,根据数据点拟合出各常数的最佳值。 未知时,从 二 是在物理量y与x间函数关系未知时 未知时 函数点拟合出y与x函数关系的经验公式以 及求出各个常数的最佳值。
第5章线性参数的最小二乘法处理

最小 1
p1 : p 2 : : p n
有
2 2
x1
2
2
:
n
1
x2
2
::
xn 2
( 55)
p1v1 p 2 v 2 p n v n
pi vi2
i 1
最小
对于等精度测量,有 1 1 n 即
p1 p 2 p n
2 2 n 12 2 2 2 2 最小 1 2 n
当然,由前述给出的结果只是估计量,它们以 最大的可能性接近真值而并非真值,因此上述条件 应以残差的形式表示,即用残差代替绝对误差:
2 v1 2
1 2 n 引入权的符号p,由下面的关系
2 2
2 v2
1
2 vn
2 i
0
2 2 2
0
为测量数据li的权; 为单位权方差;
0 0 2 2 n
i2为测量数据li的方差。
线性参数的不等精度测量可以转化为等精度的 形式(单位权化),从而可以利用等精度测量时 测量数据的最小二乘法处理的全部结果。为此, 应将误差方程化为等权的形式。若不等精度测量 数据li 的权为pi ,将不等精度测量的误差方程式 (5-9)两端同乘以相应权的平方根得:
ˆ V L AX
( -10 5 )
等精度测量时:残差平方和最小这一条件的矩 阵形式为 v1 v v1v2 vn 2 最小 vn 即 T
V V 最小 (5 -11 )
ˆ L AX 最小
T
或
ˆ L AX
(5 - 1 2)
最小二乘法

其中:������������ = ������������ − ������������观测
周期误差的计算
• 测距仪轴向与标准钢卷尺平行,多次移动 棱镜,分别读取测距仪和钢卷尺读数 ������������ , ������0������
• 根据������������ = ������������ − ������0������ 可获得一组 ������������ , ������������ • 根据相位������������ =
最小二乘法
什么是参数估计?
• 最小二乘法是一种参数估计原则 • 参数估计是指从带有误差的观测值中提取我们感兴趣 • 典型的参数估计: 通过测量多条标准基线求得测距仪的加、乘常数 通过三角测量求得被测点的平面坐标 距离交会,求得被测点的坐标
欧式距离最短
• 假设某观测方程为: ������11 ������12 ������1 ������ ������2 = ������21 ������22 ������1 2 ������31 ������32 ������3 • 可写为: ������11 ������12 ������1 ������2 = ������1 ������21 + ������2 ������22 ������31 ������32 ������3
如果我们只知道A有一辆百万级豪车,而不了解 其他任何相关信息,我们更愿意相信,A的年收 入为100万,而不会倾向于相信他的年收入为20 万
• 因此,当我们只有一个观测值x的时候,我 们更愿意相信,真值就等于x,因为此时概 率密度最大
当我们进行了多次观测,得到多个观测值 ( ������1 , ������2 , ⋯ )由于每次观测相互独立,因此 有联合概率分布(似然函数):
第十八讲全面最小二乘法

Y
V H ,其中σ 1 ≥ σ 2 ≥ ≥ σ r > 0 。又设 0 m×n σ 1 Vn (s < r ) 则 U σs 0 m×n
z∈C rankz = s F
min X − Y= X −Z F m×n
H
首先来考虑 F-范数。设 Pm×n = UQV ,U、V 分别为 m 阶、n 阶酉
r
r
n
1 i= r +1 j =
∑ ∑ tij
m
n
2
对任意 Z 矩阵而言,各 tij 之间完全独立,则 X − Z 于零的。但是 rank ( Z )= s < r 。故 X − Z
F
F
是可能等
不可能为零。详细论证
F
可知 tij = 0(i ≠ j ), tii = 0(i > s ), tii = σ i (i = 1, 2,, s ) 时, X − Z 小 下 面 仅 考 虑 在 实 际 应 用 中 非 常 常 见 的 一 种 情 况 : A ∈ Cn
14
= min ∆ F =
显然满足
rank ( C +∆ ) =n
rank ( C +∆ )< n +1
min
C − (C + ∆ )
F
min
= C− ( C + ∆ ) σ n+1
0 H ∆ =U 0 V σ + n 1 O
15
定理 2: 设σ n +1 为 C 的 n-k+1 重奇异值,且 vk +1 , vk + 2 , vn +1 相应的为
第十节最小二乘法

3 6 9 12 15 18 21 24
57.6 41.9 31.0 22.7 16.6 12.2 8.9 6.5
其中 表示从实验开始算起的时间,
y 表示时刻 反应
物的量. 试根据上述数据定出经验公式
解: 由化学反应速度的理论知, 经验公式应取
其中k , m 为待定常数.
对其取对数得
(书中取的是常用对数)
(线性函数)ຫໍສະໝຸດ 因此 a , b 应满足法方程组:
经计算得 解得:
其均方误差为
所求经验公式为
通过计算确定某些经验公式类型的方法:
观测数据:
用最小二乘法确 定a, b
27.125
26.518
25.911
25.303
26.821
26.214 25.607
25.000
-0.125 -0.018
0.189 -0.003
-0.021
0.086
0.093 -0.200
偏差平方和为
称为均方误差,
对本题均方误差
它在一定程度上反映了经验函数的好坏.
例2. 在研究某单分子化学反应速度时, 得到下列数据:
解: 通过在坐标纸上描点可看出它们
大致在一条直线上,
故可设经验公式为
列表计算:
得法方程组 解得
0
0 27.0 0
7
49 24.8 137.6
28 140 208.5 717.0
故所求经验公式为
为衡量上述经验公式的优劣,
计算各点偏差如下:
0123456 7 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8
使
满足:
第五章线性参数的最小二乘法处理01

第五章线性函数的最小二乘处理最小二乘原理应用时的条件是:函数关系确定已知、等精度、误差独立、无偏估计得到满足,在众多的N个测量方程中利用最小二乘原理求得t个(t</N)参数的最佳估计值。
如前所叙,在随机因素作用下,测量次数较多时,计算的结果就会更精密,测量次数往往大于待求未知量的个数,因而出现N>t的现象就成为自然而然的事情了。
众所周知,当N=t时可由线性代数知识求得一组唯一正确解。
当N>t时,代数解法则无能为力了。
也许读者会提出另外一个问题:既然N>t,可由N中取出t个方程来求解,而把(N-t)个方程弃掉,问题不就解决了吗?答案是不行的。
这样求解后的结果不是最佳值,有时会与最佳值离歧很大。
最小二乘法是一种数学原理,高斯于1809年在他的名著《天体沿圆锥截面绕太阳运动的理论》一书中,发表了他发现的最小二乘原理并应用于测量之后,在许多科学领域及技术领域中得到越来越多地应用。
5.1 函数为直接测量值得线性组合5.1.1 测量方程式函数中可能存在着多个待定参数,根据该函数关系可列出多个测量后的方程式,该方程式称作测量方程式。
设含有t个待求参数Xj(j=1,2,…,t)的函数关系已知,表现为线性组合,即Xj是待定系数的真值,aj是在某具体测量条件下获得的直接测量值,经N次测量(N>t)后,理应得到N个函数真关系式。
为了表达更简洁,可将各方程中系数用aij(i=1,2, …,N;j=1,2, …,t)表示,上述方程可简写成量值Y经N次测量后的测量值用Mi表示,则上述方程变为测量方程式,又称测量条件方程,式中,aij及Mi是在某具体测量条件下的直接测量值,Mi含有误差,即Mi≠Yi。
5.1.2 剩余误差方程式若用同直接测量时一样,可将称作剩余误差。
由此便可得到N个剩余误差方程式可以看出,剩余误差是各最可信赖值的函数,即5.1.3 正规方程组现在以三个待求量x1,x2,x3为例,说明建立正规方程组的过程,该计算方法和过程及结论,可推广到t个待求量中去。
线性回归之最小二乘法
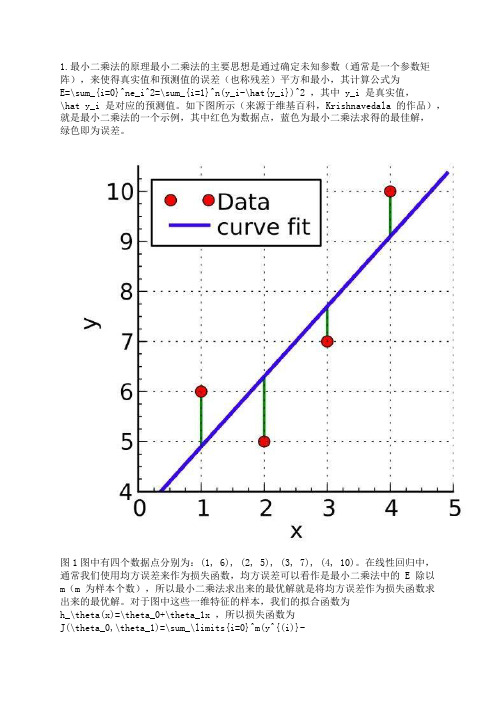
1.最小二乘法的原理最小二乘法的主要思想是通过确定未知参数(通常是一个参数矩阵),来使得真实值和预测值的误差(也称残差)平方和最小,其计算公式为E=\sum_{i=0}^ne_i^2=\sum_{i=1}^n(y_i-\hat{y_i})^2 ,其中 y_i 是真实值,\hat y_i 是对应的预测值。
如下图所示(来源于维基百科,Krishnavedala 的作品),就是最小二乘法的一个示例,其中红色为数据点,蓝色为最小二乘法求得的最佳解,绿色即为误差。
图1图中有四个数据点分别为:(1, 6), (2, 5), (3, 7), (4, 10)。
在线性回归中,通常我们使用均方误差来作为损失函数,均方误差可以看作是最小二乘法中的 E 除以m(m 为样本个数),所以最小二乘法求出来的最优解就是将均方误差作为损失函数求出来的最优解。
对于图中这些一维特征的样本,我们的拟合函数为h_\theta(x)=\theta_0+\theta_1x ,所以损失函数为J(\theta_0,\theta_1)=\sum_\limits{i=0}^m(y^{(i)}-h_\theta(x^{(i)}))^2=\sum_\limits{i=0}^m(y^{(i)}-\theta_0-\theta_1x^{(i)})^2 (这里损失函数使用最小二乘法,并非均方误差),其中上标(i)表示第 i 个样本。
2.最小二乘法求解要使损失函数最小,可以将损失函数当作多元函数来处理,采用多元函数求偏导的方法来计算函数的极小值。
例如对于一维特征的最小二乘法, J(\theta_0,\theta_1) 分别对 \theta_0 , \theta_1 求偏导,令偏导等于 0 ,得:\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)}) =0\tag{2.1}\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}=-2\sum_\limits{i=1}^{m}(y^{(i)}-\theta_0-\theta_1x^{(i)})x^{(i)} = 0\tag{2.2}联立两式,求解可得:\theta_0=\frac{\sum_\limits{i=1}^m(x^{(i)})^2\sum_\limits{i=1}^my^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^mx^{(i)}y^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.3}\theta_1=\frac{m\sum_\limits{i=1}^mx^{(i)}y^{(i)}-\sum_\limits{i=1}^mx^{(i)}\sum_\limits{i=1}^my^{(i)}}{m\sum_\limits{i=1}^m(x^{(i)})^2-(\sum_\limits{i=1}^mx^{(i)})^2} \tag{2.4}对于图 1 中的例子,代入公式进行计算,得: \theta_0 = 3.5, \theta_1=1.4,J(\theta) = 4.2 。
