长方体和正方体解决问题(精品课件)
合集下载
(公开课课件)五年级下册数学《长方体正方体典型例题讲解》(共16张PPT)
注意：单位 练习：用一根铁丝刚好焊成一个棱长8厘米的正方
体框架，如果用这根铁丝焊成一个长10厘米、宽 7厘米的长方体框架，它的高应该是多少厘米？
表面积的应用与考察
1、什么是表面积？物体表面的大小叫做物体的表面积。规 则物体的表面积有规律可循可以用公式来计算，不规则物 体的表面积，可以转化成规则的物体来进行计算。
体积类型题目
▪ 正方体的体积V正=棱长x棱长x棱长=底面积x棱长 ▪ 长方体的体积V长=长x宽x高=底面积x高 ▪ 注意： ▪ 1、底面积和占地面积的概念 ▪ 2、注意底面积求体积的应用 ▪ 正方体的高h=V正÷底面积 ▪ 长方体的高h=V长÷底面积 ▪ 3、注意实际情况的考虑 ▪ 4、注意单位的统一
▪ 3、楼房外壁用于流水的水管是长方体。如果每节长15分 米，横截面是一个长方形，长1分米，宽0.6分米。做一 节水管，至少要用铁皮多少平方分米。
▪ 4、一个游泳池，长25米，宽10米，深2.4米，在游泳池 的四周和池底砌瓷砖，如果瓷砖的边长是2分米的正方形， 那么至少需要这种瓷砖多少块？
▪ 5、做一个长方体的浴缸（无盖），长8分米，宽4分米， 高6分米，至少需要多少平方分米的玻璃？如果每平方分 米玻璃4元钱，至少需要多少钱买玻璃？
例题
▪ 例1：天天游泳池，长25米，宽10米，深1.6米，在游泳 池的四周和池底砌瓷砖，如果瓷砖的边长是1分米的正方 形，那么至少需要这种瓷砖多少块？
▪ 分析：要求多少块需要知道这个用泳池多大的表面积，一 块瓷砖的面积，然后计算总表面积中有几块瓷砖的面积就 可以知道用多少块。
▪ 列式： [ 25x10+（1.6x10+25x1.6）x2 ]÷（0.1x0.1） ▪ 注意：做这种类型的题目要考虑实际情况，用泳池，水塘、
体框架，如果用这根铁丝焊成一个长10厘米、宽 7厘米的长方体框架，它的高应该是多少厘米？
表面积的应用与考察
1、什么是表面积？物体表面的大小叫做物体的表面积。规 则物体的表面积有规律可循可以用公式来计算，不规则物 体的表面积，可以转化成规则的物体来进行计算。
体积类型题目
▪ 正方体的体积V正=棱长x棱长x棱长=底面积x棱长 ▪ 长方体的体积V长=长x宽x高=底面积x高 ▪ 注意： ▪ 1、底面积和占地面积的概念 ▪ 2、注意底面积求体积的应用 ▪ 正方体的高h=V正÷底面积 ▪ 长方体的高h=V长÷底面积 ▪ 3、注意实际情况的考虑 ▪ 4、注意单位的统一
▪ 3、楼房外壁用于流水的水管是长方体。如果每节长15分 米，横截面是一个长方形，长1分米，宽0.6分米。做一 节水管，至少要用铁皮多少平方分米。
▪ 4、一个游泳池，长25米，宽10米，深2.4米，在游泳池 的四周和池底砌瓷砖，如果瓷砖的边长是2分米的正方形， 那么至少需要这种瓷砖多少块？
▪ 5、做一个长方体的浴缸（无盖），长8分米，宽4分米， 高6分米，至少需要多少平方分米的玻璃？如果每平方分 米玻璃4元钱，至少需要多少钱买玻璃？
例题
▪ 例1：天天游泳池，长25米，宽10米，深1.6米，在游泳 池的四周和池底砌瓷砖，如果瓷砖的边长是1分米的正方 形，那么至少需要这种瓷砖多少块？
▪ 分析：要求多少块需要知道这个用泳池多大的表面积，一 块瓷砖的面积，然后计算总表面积中有几块瓷砖的面积就 可以知道用多少块。
▪ 列式： [ 25x10+（1.6x10+25x1.6）x2 ]÷（0.1x0.1） ▪ 注意：做这种类型的题目要考虑实际情况，用泳池，水塘、
《长方体和正方体的体积》ppt课件
06 课堂小结与回顾
关键知识点总结
长方体和正方体的体积公式
长方体的体积V=a×b×c，正方体的体积V=a^3，其中a、 b、c分别为长方体的长、宽、高，a为正方体的棱长。
体积单位的认识与换算
常见的体积单位有立方厘米(cm³)、立方分米(dm³)、立方 米(m³)等，需掌握各单位之间的换算关系。
实际问题的应用
提出改进方案
03
针对可能出现的误差，提出相应的改进方案，如提高测量精度、
使用更精确的计算方法等。
05 拓展延伸：不规则物体体 积估算方法
排水法原理及应用
原理
将不规则物体完全浸没于水中，通过计算物体排开水的体积来估 算物体的体积。
应用
适用于易溶于水或与水发生反应的物体以外的任何不规则物体。 如石块、金属块等。
公式应用注意事项
单位统一
在应用公式计算体积时，需要确 保长度、宽度和高度的单位统一，
避免出现错误结果。
公式适用范围
长方体和正方体的何体需要采用其他方
法进行计算。
公式变形应用
在实际应用中，可以根据需要对 公式进行变形，如已知体积和其
中两个维度求第三个维度等。
体积单位换算
1立方米=1000立方分米，1立 方分米=1000立方厘米。
实物体积感受
常见物体体积
列举生活中常见物体的体积，如 一个苹果的体积约为200立方厘米， 一个电冰箱的体积约为0.5立方米
等。
体积比较
通过比较不同物体的体积大小，让 学生感受体积的概念。
体积估算
通过估算物体的体积，培养学生的 空间想象力和估算能力。
02 长方体和正方体认识
长方体特点与性质
01
02
长方体和正方体PPT课件
公式推导
02
长方体有6个面，每个面的面积分别为ab、bc、ac，因此总表
面积为各面积之和的两倍。
公式应用
03
通过测量长方体的长、宽、高，可以直接套用此公式计算表面
积。
正方体表面积公式推导
正方体表面积公式：S = 6a^2
公式推导：正方体有6个面，每个面的面积均为a^2，因此总表面积为6倍的单面面 积。
REPORTING
切割问题探讨
切割长方体
将长方体按照不同方向进行切割，可以得到不同形状的小长方体 或正方体。
切割正方体
将正方体按照不同方式进行切割，可以得到不同形状的小正方体或 其他多面体。
切割后表面积和体积的变化
探讨切割后各部分的表面积和体积如何变化，以及它们之间的关系 。
拼接问题探讨
相同形状长方体的拼接
数学教育
长方体和正方体是数学教 育中重要的几何图形，有 助于学生理解三维空间的 概念和性质。
工程设计
在工程设计中，长方体和 正方体常被用作设计元素 的基本形状，如机械零件 、电子设备等。
艺术创作
艺术家们常利用长方体和 正方体的形状和质感进行 创作，表现出不同的艺术 风格和视觉效果。
PART 05
长方体和正方体相关数学 问题探讨
包装设计中的应用
包装容器
长方体和正方体常被用作包装容 器的基本形状，如纸盒、塑料盒
等。
空间优化
在包装设计中，通过合理设计长方 体和正方体的尺寸和比例，可以实 现空间的最大化利用，减少浪费。
视觉表现
利用长方体和正方体的形状和图案 设计，可以增加包装的视觉吸引力 ，提高产品的附加值。
其他领域应用举例
复杂几何体的性质研究
五年级下册数学习题课件-3长方体和正方体人教版(共47张PPT)
每个面的面积：_2_×__2_＝__4_(_d_m_2_)_____。 正方体的表面积：__4_×__6_＝__2_4_(_d_m_2)______。
五年级下册数学习题课件-3 长方体和正方体 人教版(共47张PPT)
4. 一个不锈钢花瓶的形状是正方体，棱长和是36 cm，制作这个花瓶至少需要 不锈钢板多少平方厘米？ 36÷12＝3(cm) 3×3×6＝54(cm2)
20×30×2＋8×30×2＋20×8＝1840(cm2)
3. 一个长方体包裹，它的长、宽、高分别是5 dm，4 dm，2 dm。如果实际用纸 是表面积的1.4倍，那么包装这个包裹至少要用多少平方分米的包装纸？ (5×4＋5×2＋4×2)×2×1.4＝106.4(dm2)
4. 小区门前的水池的形状是长方体，它的宽是6 m，长是宽的1.5倍，深1.2 m。 如果把水池的四周和底面贴上瓷砖，那么贴瓷砖的面积是多少平方米？ 长：6×1.5＝9(m) 9×6＋9×1.2×2＋6×1.2×2＝90(m2)
3 长方体和正方体
第1课时 长 方 体
1. 仔细想，认真填。 (1) 同学们正在用一些小棒和橡皮泥拼搭长方体的框架。
① 上图是小明已经拼搭好的部分，他还需要( 5 )个橡皮泥小球、( 1 ) 根9 cm小棒、( 2 )根5 cm小棒、( 3 )根3 cm小棒，就可以拼搭成一个长 ( 9 )cm、宽( 5 )cm、高( 3 )cm的长方体框架。 ② 长方体框架上面是( 长方 )形，长是( 9 )cm，宽是( 5 )cm。 ③ 长方体框架( 左 )面和( 右 )面的长是5 cm，宽是3 cm。 ④ 把长方体框架的所有棱都粘上胶带，至少需要( 68 )cm长的胶带。 (2) 在长、宽、高不全相等的长方体中，最多可以有( 2 )个面是正方形。 在这样的长方体中，有( 4 )个长方形的面相同。
小学五年级奥数举一反三第13讲 长方体和正方体(一)ppt课件
可编辑课件PPT
7
王牌例题3：
一个长方体沿着长的方向切掉一个小正方体，剩下的长方体
的表面积比原来减少24平方厘米，求所切下的正方体的表面
积是多少平方厘米？
【思路导航】当长方体切下一个小正方体后，表面积其实只减
少了周围的4个小正方形的面积，每块正方形的面积是24÷4=6
（平方厘米）。正方体有6个这样的面，所以切下的小正方体的
表面积是6×6=36（平方厘米）。
24÷4×6=36（平方厘可米编辑课）件PPT
8
举一反三3
1. 一个正方体和一个长方体拼成了一个新的长方体，拼成 的长方体的表面积比原来的长方体的表面积增加了60平方 厘米。原正方体的表面积是多少平方厘米？
2.一根长1米，宽和高都是8厘米的长方体钢材，从钢材的一 端锯下一个最大的正方体后，它的表面积减少了多少平方 厘米？
3.把两个完全相同的长方体木块拼成一个正方体，表面积比
原来两个长方体的表面积的和减少了40平方厘米，求原来
每个长方体的面积是多少平方厘米？
可编辑课件PPT
9
王牌例题4： 长方体的不同的三个面的面积分别为10平方厘米、15平方厘 米、6平方厘米。这个长方体的体积是多少立方厘米？
【思路导航】长方体不同的三个面的面积分别是长宽、长高、
五年级奥数 举一反三
第13讲 长方体和正方体（一）
邯郸市峰峰矿区 杨桂林
可编辑课件PPT
1
知识要点
在数学竞赛中，有许多有关长方体、正方体的问题。解答
稍复杂的立体图形问题要注意几点：
1.必须以基本概念和方法为基础，同时把构成几何图形的诸 多条件沟通起来；
2.依赖已经积累的空间观念，观察经过割、补后物体的表面 积或体积所发生的变化；
《长方体和正方体体积解决问题》PPT课件
972000÷216=4500（块） 答：这面墙共用了4500块积木.
做一做
1、 红星村要修一条长1800m，宽 12m的公路，要先铺10cm厚的三合 土，再铺6cm厚的沙石，需要三合 土、沙石各多少立方米？
2、学校道路硬化建设。要在长
4Байду номын сангаас米，宽8米的道路上铺上厚0.25
米的混泥土砂石，需要多少立方米
探究新知例2六一儿童节全市的小学生代表用棱长6cm的正方体塑料积木在广场中央搭起了一面长6m高27m厚6cm的心愿墙算一算这面墙共用了多少块积木
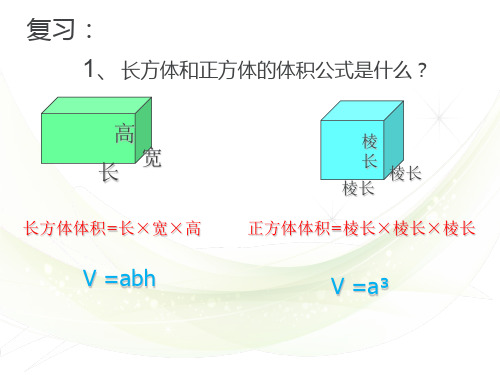
复习： 1、长方体和正方体的体积公式是什么？
高
长 宽
棱 长 棱长
棱长
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
V =abh
V =a³
2、列式解答。
的混泥土砂石？
3、学校要填一个长方体形状的
沙坑，沙坑的长为4米，宽为2米， 深为0.4米，平均每立方米需要45
元，填满这个沙坑需要多少钱？
4、一列火车有容积相同的车厢20 节，每节车厢从里面量长13米，
宽2.5米，装煤的高度是1.2米。
这列火车每次运煤多少立方米？ 每立方米煤重1.4吨,这列火车共运
（1）一个长方体，长7厘米，宽4厘米，高3厘米，它 的体积是多少？ s=abh =7×4×3 =28×3 =84(cm²) 答：它的体积是84平方厘米。 （2）一个正方体的棱长是5厘米，它的体积是多少？ s=a3 =5×5×5 =25 =125(cm²)
答：它的体积是125平方厘米。
人教版五年级数学下册
煤多少吨?
5、一块长方体的钢板长2.5米， 宽1.2米，厚20厘米。这种钢板
每立方分米重7.8千克，这块钢
《长方体和正方体》课件
长方体和正方体的对称性
对称轴
正方体有6个面，每个面都是正方形，每个正方形都有两条对角线作为对称轴。长方体 也有对称轴，但其对称轴数量取决于长方体的形状。
对称性
正方体的6个面都是中心对称的，也就是说，每个面都可以通过中心点旋转180度后与 原面重合。长方体的对称性则取决于其形状，但一般情况下，长方体也有一定的对称性
正方体的表示方法
可以用一个实数来表示正方体的棱长，也可以用三个表示长 、宽、高的实数来表示一个正方体的位置和大小。
02 长方体和正方体的面积与体积
长方体的表面积
总结词
长方体的表面积是指其六个面的总面积。
详细描述
长方体的表面积计算公式为2lw+2lh+2wh，其中l为长度，w为宽度，h为高度 。这个公式可以用来计算长方体的表面积，对于给定的长方体尺寸，可以直接 代入公式进行计算。
长方体和正方体在数学问题中的应用
几何学
长方体和正方体是几何学中基础 且重要的立体图形，常用于研究
空间几何的性质和定理。
面积和体积计算
长方体和正方体的面积和体积计算 是数学中的基础问题，广泛应用于 数学建模和实际问题解决中。
组合图形面积计算
将多个长方体或正方体组合成一个 复杂的图形，需要利用长方体和正 方体的性质来计算组合图形的面积 。
正方体的表面积
总结词
正方体的表面积是指其六个面的总面积。
详细描述
正方体的表面积计算公式为6a²，其中a为正方体的边长。这个公式可以用来计算 正方体的表面积，对于给定的正方体尺寸，可以直接代入公式进行计算。
长方体的体积
总结词
长方体的体积是指其内部所占用的空 间大小。
详细描述
长方体的体积计算公式为lwh，其中l 为长度，w为宽度，h为高度。这个公 式可以用来计算长方体的体积，对于 给定的长方体尺寸，可以直接代入公 式进行计算。
《长方体和正方体的体积》精品PPT课件
课程目标
掌握长方体和正方体 的体积计算公式。
培养学生的空间观念 和几何直觉，提高解 决几何问题的能力。
能够运用公式解决实 际问题，如计算容积、 体积等。
02
长方体的体积
长方体的定义
总结词
长方体的定义
详细描述
长方体是一种三维图形，由六个矩形面组成，相对的两个面完全相同。它的三 个边分别是长度、宽度和高度。
06
总结与回顾
本节课的重点回顾
计算长方体和正方体的体积公式 掌握长方体和正方体的体积计算方法
理解体积的概念和意义 了解体积单位的应用
本节课的难点解析
如何理解体积的概念 如何正确应用长方体和正方体的体积公式进行计算
如何解决与体积相关的实际问题
下节课预告
学习圆柱体的体积计算方法 了解圆锥体的体积计算公式
《长方体和正方体的 体积》精品ppt课件
• 引言 • 长方体的体积 • 正方体的体积 • 体积的单位和换算 • 练习与巩固 • 总结与回顾
目录
01
引言
课程背景
01
长方体和正方体是生活中常见的 几何形状，了解其体积计算方法 对于解决实际问题具有重要意义 。
02
学生已经学习了长方形和正方形 的面积计算，在此基础上进一步 学习长方体和正方体的体积计算 有助于巩固几何知识体系。
学习如何解决与立体几何相关的实际问题
感谢观看
THANKS
体积计算公式
正方体的体积可以通过其 棱长的三次方来计算，即 V = a^3，其中a是正方体 的棱长。
公式推导
正方体的体积可以通过其 底面积和高的乘积来推导， 即 V = a^2 × a = a^3。
单位换算
正方体的体积单位通常是 立方单位，如立方米、立 方厘米等，根据需要可以 进行单位换算。
应用长方体正方体解决问题PPT课件
西师版小学数学五年级下册
《长方体正方体－－ 解决问题》
复习提要
1、说说长方体、正方体的特征。 2、什么是物体的表面积，什么是体积？ 3、怎样求长方体、正方体的表面积、
体积？ 4、说一说，生活中哪些地方要用到长方
体、正方体的表面积、体积计算。
课前练习
1、正方体的表面积÷ 其中一个面的面积=（ 6 ） 2、 一个长方体，长12厘米，宽8厘米，高6厘米，把它平放在桌
（1）3.5×3.5+3.5×5×4=82.25平方分米（2）3.5×3.5×5＝61.25L
12×3×3＋12×7.5＋7.5×3×2=243平方分米
150×5×5×7.8÷1000＝29.25kg
拓展训练
1、一块长方体木块，长20cm，宽15cm，厚2cm。
（1）如果将长方体木块平均分割成相等的正方体，正方体木块 最大体积是多少立方厘米? 2×2×2＝8立方厘米
16
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
讲师：XXXXXX XX年XX月XX日
分析：水的体积没有变化，即V正=V长
典型题例1 一个火柴盒源自如图）：长5cm、宽4cm、高1.5cm。做50个这 样一个火柴盒大约需多少平方分米纸板？（损耗大约0.8dm2）
1、外盒： 上下面：5×4×2＝40(cm2) 前后面：5×1.5×2＝15(cm2) 2、内盒： 下面：5×4＝20(cm2) 前后面：5×1.5×2＝15（cm2） 左右面：4×1.5×2＝12 （cm2） 3、每个盒面积： 40＋15＋20＋15＋12＝102（cm2）＝1.02（dm2） 4、总面积： 1.02×50＋0.8＝51.8（dm2） 答：做50个这样的火柴盒大约需51.8平方分米纸板。
《长方体正方体－－ 解决问题》
复习提要
1、说说长方体、正方体的特征。 2、什么是物体的表面积，什么是体积？ 3、怎样求长方体、正方体的表面积、
体积？ 4、说一说，生活中哪些地方要用到长方
体、正方体的表面积、体积计算。
课前练习
1、正方体的表面积÷ 其中一个面的面积=（ 6 ） 2、 一个长方体，长12厘米，宽8厘米，高6厘米，把它平放在桌
（1）3.5×3.5+3.5×5×4=82.25平方分米（2）3.5×3.5×5＝61.25L
12×3×3＋12×7.5＋7.5×3×2=243平方分米
150×5×5×7.8÷1000＝29.25kg
拓展训练
1、一块长方体木块，长20cm，宽15cm，厚2cm。
（1）如果将长方体木块平均分割成相等的正方体，正方体木块 最大体积是多少立方厘米? 2×2×2＝8立方厘米
16
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
讲师：XXXXXX XX年XX月XX日
分析：水的体积没有变化，即V正=V长
典型题例1 一个火柴盒源自如图）：长5cm、宽4cm、高1.5cm。做50个这 样一个火柴盒大约需多少平方分米纸板？（损耗大约0.8dm2）
1、外盒： 上下面：5×4×2＝40(cm2) 前后面：5×1.5×2＝15(cm2) 2、内盒： 下面：5×4＝20(cm2) 前后面：5×1.5×2＝15（cm2） 左右面：4×1.5×2＝12 （cm2） 3、每个盒面积： 40＋15＋20＋15＋12＝102（cm2）＝1.02（dm2） 4、总面积： 1.02×50＋0.8＝51.8（dm2） 答：做50个这样的火柴盒大约需51.8平方分米纸板。
苏教版六年级上册数学《体积和体积单位》长方体和正方体PPT课件
2.先求总份数，再求各部分占总量 的百分之几或几分之几。最后求各部分量。 例1．六年1班有45人，男生与女生人数的比 是4:5，男生和女生各有多少人？ 例2．学校运进120本儿童读物，按3：4：5分 配给四、五、六年级，三个年级各分多少本？
2、稍复杂的按比例分配应用题 特点：已知一个数的量（部分量或相差量）和各部分 量的比，求总量或其他部分量。 方法：1.（归一法）先求每份数，再求几份数是多少。
7立方厘米 6立方厘米 10立方厘米
9、在括号里填上合适的单位名称：
橡皮的体积大约是 集装箱的体
6( 立方厘米）
积大约是40
（ 立方米 ）
9、在括号里填上合适的单位名称：
水桶的容积大 西瓜的体积大约 约是12（ 升 ） 是4(立方分米）
谢谢观看！
分数、百分数应用题
（归类总结）
分百应用题是六年级上册的重点，也是 一个难点，它涉及了第二，第三，第五以及 第六单元的部分内容，所占比例很大。要想 让学生们准确地掌握好各个类型应用题的特 点，以及解答方法，首先，要对应用题进行 分类，让学生掌握应用题的解题策略。其次， 对于一些平时练习出现的易混易错的典型应 用题进行对比，归类，从而掌握其正确的解 答方法。最后还要对学生进行不同类型应用 题的分组练习，从而进一步提高学生分析解 决应用题的能力。
方法：用单位“1”已知的量×分率=对应量 对应量÷对应分率=所求单位“1”的量。
例：公园里有20颗杨树，柳树的棵树是杨树的3/5， 同时又是柏树的75%，柏树有多少棵？
分数除法应用题的解题策略
1、从分率句入手，找准单位“1” 单位“1”的量未知，可以设为ⅹ。
2、用单位“1”的量(x)×对应分率=对 应的数量。
2.（按比例分配法）先求总份数，再求 部分量占总量的几分之几，最后求出各部分量或总量。
2、稍复杂的按比例分配应用题 特点：已知一个数的量（部分量或相差量）和各部分 量的比，求总量或其他部分量。 方法：1.（归一法）先求每份数，再求几份数是多少。
7立方厘米 6立方厘米 10立方厘米
9、在括号里填上合适的单位名称：
橡皮的体积大约是 集装箱的体
6( 立方厘米）
积大约是40
（ 立方米 ）
9、在括号里填上合适的单位名称：
水桶的容积大 西瓜的体积大约 约是12（ 升 ） 是4(立方分米）
谢谢观看！
分数、百分数应用题
（归类总结）
分百应用题是六年级上册的重点，也是 一个难点，它涉及了第二，第三，第五以及 第六单元的部分内容，所占比例很大。要想 让学生们准确地掌握好各个类型应用题的特 点，以及解答方法，首先，要对应用题进行 分类，让学生掌握应用题的解题策略。其次， 对于一些平时练习出现的易混易错的典型应 用题进行对比，归类，从而掌握其正确的解 答方法。最后还要对学生进行不同类型应用 题的分组练习，从而进一步提高学生分析解 决应用题的能力。
方法：用单位“1”已知的量×分率=对应量 对应量÷对应分率=所求单位“1”的量。
例：公园里有20颗杨树，柳树的棵树是杨树的3/5， 同时又是柏树的75%，柏树有多少棵？
分数除法应用题的解题策略
1、从分率句入手，找准单位“1” 单位“1”的量未知，可以设为ⅹ。
2、用单位“1”的量(x)×对应分率=对 应的数量。
2.（按比例分配法）先求总份数，再求 部分量占总量的几分之几，最后求出各部分量或总量。
人教版《长方体和正方体》完美版课件24(共18张PPT)
那就让我 们开动
脑筋吧！
A
B
C
D
思考：上面的长方体是由体积1立方厘米的小正方体品拼摆出来的，如何快速地数出上图中各长方体中小 正方体的个数？
名称
长方体A 长方体B 长方体C 长方体D
每排个数
4 4
4 4
排数
3 3
3 3
1 2
3
4
层数
小正方体个数 长方体体积（单位 ：cm³）
4×3×1＝12
12
4×3×2＝24
24
4×3×3＝36 36
4×3×4＝48 48
为什么长方体中小正方体的个数和长方体 体积的数量相同呢？
每排个数与长方体的长有什么关系？
排数与长方体的宽有什么关系？
层数与长方体的高有什么关系？
结论：小正方体个数=每排个数 × 排数 × 层数
长方体的体积就是长方体所 含体积单位的数量
猜想：长方体体积 = 长 × 宽 × 高
长方体体 积（单位 ：cm³）
12
12
12
12
观察表格中的数据想一想： 1.比较这些长方体的摆法有什么共同点和不同点？
（这些长方体形状不同，体积相同） 2.为什么这些长方体形状不同而体积相同呢？
（因为它们都含有12个小正方体，也就是说它们含有同样多的体积单 位）
让我们 一起来
揭秘
知识讲解，难点突破
1 、什么是物体的体积？
物体所占空间的大小叫做
物体的体积。
粉笔
以旧引新，复习导入
2、常用的体积单位有（ 立方）厘米 （ 立方分米）和（ ）立方。米
3、体积是 4 立方厘米的长方体里含有 （ 4）个体积是1立方厘米的小正方体。
长方体和正方体的表面积和体积计算题PPT课件
子，如果这个盒子的体积是768立方厘 米，求这块铁皮的面积。
768÷4÷（16-4-4）+4+4=32
（厘米）
32×16=512（平方厘米）
答：这块铁皮的面积为512平方
厘米。
第6页/共22页
8、一个长方体，如果长增加2厘米， 宽和高不变，体积就增加40立方厘米； 如果高增加2厘米，长和宽不变，体积 就增加60立方厘米；如果宽增加2厘米， 长和高不变，体积就增加48立方厘米。 原来长方体的表面积是多少平方厘米？
0.5
第20页/共22页
• 23、一个正方体和一个长方体拼成了 一个新的长方体，拼成的长方体的表 面积比原来的长方体的表面积 增加了 50平方厘米，原正方体的表面积是多 少平方厘米？
第21页/共22页
感谢您的观看！
第22页/共22页
第2页/共22页
4、用一根铁丝刚好焊成一个棱长8厘米的正 方体框架，如果用这根铁丝焊成一个长10厘 米、宽7厘米的长方体框架，它的高应该是多 少厘米？
第3页/共22页
• 5、把两个完全一样的长方体木块粘成一个大长方体，这个大长方体的表面积 比原来两个长方体的表面积的和减少了46平方厘米，而长是原来长方体的2倍。 如果拼成的长方体的长是24厘米，那么一个长方体的体积是多少立方厘米？
2、一个长方体鱼缸，长８０厘米， 宽６０厘米，深４０厘米，把一 块长45厘米，宽32厘米，铁块浸 入在水中，水面上升９厘米,求铁 块的高。
第1页/共22页
3、把80升水倒入底面是正方 形的水箱中，底面的边长是40 厘米，水面的高是多少厘米？
80升=80000毫升 80000÷40÷40=50（厘米） 答：水面的高是50厘米。
20
从一个长方体上截下一个体积是32立方厘米的小 长方体后，剩下的部分正好是一个棱长为4厘米的 正方体。原长方体的表面积是多少平方厘米？
五年级下册数学课件 - 长方体和正方体的认识 人教版(共38张PPT)
8x12=96（厘米）
3、有一根150cm的铁丝，用这根铁丝焊接成一个正方 体框150-6）÷12 =144÷12 =12（厘米）
4、小明用一根铁丝围成一个长30厘米、宽20厘米、高 10厘米的长方体框架。如果把它改围成一个正方体框架， 这个正方体框架的棱长是多少厘米？ (30+20+10)x4
=（长+宽+高）X 4
随堂练习
1、长方体有（ 6 ）个面，它们一般都是（ 长方形 ）， 也有可能有（ 2 ）个相对的面是正方形。 2、长方体的上面和下面、前面和后面、左面和右面都 叫做（ 相对面），他们相对的面积（ 相等 ）。 3、长方体有（ 12）条棱，每相对的（ 4 ）条棱算作一 组，可以分成（ 3 ）组。
正方体棱长=棱长总和÷12
例3 用一根铁丝围成一个长方体，它的长是12分米，
宽是8分米，高是4分米。如果把这根铁丝改围成一个
正方体，这个正方体的棱长是多少？
（12+8+4）x4 =24x4 =96(分米) 96÷12=8(分米)
随堂练习
一个棱长6分米的正方体框架，若把它改成一个长10分
米，宽5分米的长方体框架，这个长方体的高是多少分
100÷4-(8+12) =25-20 =5(厘米) 12x5=60(平方厘米)
例3 有一个礼盒需要用彩带捆扎，捆扎效果如图，打结 部分需要10厘米彩带，一共需要多长的彩带？
（30+20）x2+20x4 =100+80 =180（厘米） 180+10=190（厘米）
例4 用一根长28厘米的铁丝做一个棱长是整厘米数的 长方体框架，这个长方体框架的长、宽、高可能是多少 厘米？想一想，填一填。
4、相较于一个顶点的三条棱的长度，叫做长方体的 （ 长）、（ 宽）、（ 高）。
3、有一根150cm的铁丝，用这根铁丝焊接成一个正方 体框150-6）÷12 =144÷12 =12（厘米）
4、小明用一根铁丝围成一个长30厘米、宽20厘米、高 10厘米的长方体框架。如果把它改围成一个正方体框架， 这个正方体框架的棱长是多少厘米？ (30+20+10)x4
=（长+宽+高）X 4
随堂练习
1、长方体有（ 6 ）个面，它们一般都是（ 长方形 ）， 也有可能有（ 2 ）个相对的面是正方形。 2、长方体的上面和下面、前面和后面、左面和右面都 叫做（ 相对面），他们相对的面积（ 相等 ）。 3、长方体有（ 12）条棱，每相对的（ 4 ）条棱算作一 组，可以分成（ 3 ）组。
正方体棱长=棱长总和÷12
例3 用一根铁丝围成一个长方体，它的长是12分米，
宽是8分米，高是4分米。如果把这根铁丝改围成一个
正方体，这个正方体的棱长是多少？
（12+8+4）x4 =24x4 =96(分米) 96÷12=8(分米)
随堂练习
一个棱长6分米的正方体框架，若把它改成一个长10分
米，宽5分米的长方体框架，这个长方体的高是多少分
100÷4-(8+12) =25-20 =5(厘米) 12x5=60(平方厘米)
例3 有一个礼盒需要用彩带捆扎，捆扎效果如图，打结 部分需要10厘米彩带，一共需要多长的彩带？
（30+20）x2+20x4 =100+80 =180（厘米） 180+10=190（厘米）
例4 用一根长28厘米的铁丝做一个棱长是整厘米数的 长方体框架，这个长方体框架的长、宽、高可能是多少 厘米？想一想，填一填。
4、相较于一个顶点的三条棱的长度，叫做长方体的 （ 长）、（ 宽）、（ 高）。
五年级下册数学课件长方体和正方体中的切割问题(13页PPT)人教版
六、 一个长方体形木料，长是20厘米，宽 是15厘米，高是30厘米，从木料上截取一个 高 2 dm的长方体，表面积减少多少？
长方体的表面积=长 方形的面积—四个正 方形的面积
一、成功之处 本节教学最大的成功在于教师把主要精力放在积极引导学生探索发现问题之上。利用复习准备、导入两个环节,为学生探索比例的基 本性质搭建了桥梁,新知构建部分,有教师引导的思路设计,学生通过阅读教材、分析、计算,总结出比例的基本性质,教学自然流畅。随 堂练习,让学生展示自己发现的成果,在获得成功的同时也收获了解决问题的方法。 二、不足之处 在例1的教学时教师放手还是有些不够,问的太多,学生自主学习成分略显不足。 三、再教设计 再教这个内容时,我应该在引导学生发现问题时,真正让学生自主阅读,自主发现,培养学生探究发现新知的本领。
五年级下册数学课件长方体和正方体 中的切 割问题 （13页 PPT） 人教版
长方体和正方体中的切割 问题
数学—王老师
五年级下册数学课件长方体和正方体 中的切 割问题 （13页 PPT） 人教版
一、 把三个棱长相等的正方体拼成一个长方体，
表面积减少100平方厘米。原来每个正方体的表面积 和体积是多少？
拼接一次少两个面，成一个长方体，
表面积减少144平方厘米。原来每个正方体的表面积 和体积是多少？
二、 一根3米长的方木，截成3段后，表 面积增加了3.6平方米，这根方木的体积 是多少立方米？
练习、 一根3米长的方木，截成2段后， 表面积增加了3.6平方米，这根方木的体 积是多少立方米？
三、 把一个底面为正方形且边长是3分 米，高是5分米的长方体石料加工为体积 最大的正方体，那么正方体的体积是多少 立方分米？ 以长方体中最短边为棱长
截正方体
人教部编版五年级数学下册《3长方体和正方体【全单元】》精品PPT优质课件
最多能看到3个面
1.一个长方体的长是7厘米，宽是6厘米， 高是5厘米，它的棱长和是多少？
（7+6+5）×4=72（厘米） 2.一个长方体的长是15厘米，宽是12厘米， 棱长总和是148厘米，它的高是多少？
148-15×4-12×4=40（厘米） 40÷4=10（厘米）
课后作业
1.从教材课后习题中选取； 2.从练习册中选取。
长方体和正方体
1.长方体和正方体的认识
第 1 课时 长方体
R·五年级下册
平 面 图 形 立 体 图 形
我们周围许多物体的形状都是长方体或 正方体（正方体也叫立方体）。
长 方 体
认识长方体的面、棱、顶点 顶点：棱和棱的交点
面
棱：面与面相 交的线段
拿几个长方体的物品来观察，并说 一说你发现了什么？
1.一个正方体的棱长是8cm，它的棱长 总和是多少厘米？
8×12＝96（cm）
2.用一根长48cm的铁丝围成一个长方 体，这个长方体的长是5cm，宽是4cm， 它的高是多少厘米？
48÷4－5－4＝3（cm）
3.小红为妈妈准备了一件生日礼物，下图是 这件礼物的包装盒，长、宽、高分别是15cm、 15 cm、8 cm。现在用彩带把这个包装盒捆上， 接头处长18 cm。一共需要多少厘米彩带？
面 6个面，都是正方形，6个面完全相同 棱 12条棱，长度相等 顶点 8个顶点
剪下本书附页中下面的图样做一个正 方体，再量出它的棱长是多少厘米。
棱长
想一想
长方体和正方体有哪些 相同点，有哪些不同点?
长方体和正方体都 有 6 个面、 8 个
顶点……
正方体的棱长度 都 相等，长方体相 对 的棱长度 相等。
（6）长方体有__8__个顶点。
1.一个长方体的长是7厘米，宽是6厘米， 高是5厘米，它的棱长和是多少？
（7+6+5）×4=72（厘米） 2.一个长方体的长是15厘米，宽是12厘米， 棱长总和是148厘米，它的高是多少？
148-15×4-12×4=40（厘米） 40÷4=10（厘米）
课后作业
1.从教材课后习题中选取； 2.从练习册中选取。
长方体和正方体
1.长方体和正方体的认识
第 1 课时 长方体
R·五年级下册
平 面 图 形 立 体 图 形
我们周围许多物体的形状都是长方体或 正方体（正方体也叫立方体）。
长 方 体
认识长方体的面、棱、顶点 顶点：棱和棱的交点
面
棱：面与面相 交的线段
拿几个长方体的物品来观察，并说 一说你发现了什么？
1.一个正方体的棱长是8cm，它的棱长 总和是多少厘米？
8×12＝96（cm）
2.用一根长48cm的铁丝围成一个长方 体，这个长方体的长是5cm，宽是4cm， 它的高是多少厘米？
48÷4－5－4＝3（cm）
3.小红为妈妈准备了一件生日礼物，下图是 这件礼物的包装盒，长、宽、高分别是15cm、 15 cm、8 cm。现在用彩带把这个包装盒捆上， 接头处长18 cm。一共需要多少厘米彩带？
面 6个面，都是正方形，6个面完全相同 棱 12条棱，长度相等 顶点 8个顶点
剪下本书附页中下面的图样做一个正 方体，再量出它的棱长是多少厘米。
棱长
想一想
长方体和正方体有哪些 相同点，有哪些不同点?
长方体和正方体都 有 6 个面、 8 个
顶点……
正方体的棱长度 都 相等，长方体相 对 的棱长度 相等。
（6）长方体有__8__个顶点。
《长方体正方体》课件
长方体和正方体的性质
总结词
长方体和正方体的性质包括空间位置、大小和形状。
详细描述
空间位置是指长方体和正方体的相对位置关系，如平移、旋转等。大小是指长 方体和正方体的尺寸，如长度、宽度、高度等。形状是指长方体和正方体的外 观特征，如面数、棱数、顶点数等。
02
长方体和正方体的面 积与体积
长方体和正方体的表面积
图形组合
通过将长方体和正方体进行组合，可以形成各种不同的几何图形，用于解决几何 问题。
长方体和正方体在日常生活中的应用
建筑结构
长方体和正方体的结构在建筑设计中广泛应用，如墙、柱、 门窗等。
包装和存储
长方体和正方体的形状适合用于包装和存储物品，如纸箱、 盒子等。
长方体和正方体在科学实验中的应用
物理实验
在建筑设计、艺术和工程领域中，对 称性被广泛运用，以实现美观和功能 性的平衡。
性质
长方体和正方体都具有对称性，可以 通过对称轴或对称中心进行对称变换 。
04
长方体和正方体的应 用
长方体和正方体在几何图形中的应用
几何图形建模
长方体和正方体是基本的几何图形，可以作为建模的基础，用于构建更复杂的几 何形状和物体。
详细描述
在计算长方体和正方体的容积时，需要先统一单 位，然后根据实际应用场景选择合适的数据进行 计算，如液体容器需要考虑到液体的密度和高度 等因素。
03
长方体和正方体的关 系与变换
长方体和正方体的相似性
01
02
03
定义
长方体和正方体都是三维 几何图形，具有六个面、 十二条边和八个顶点。
性质
长方体的三组对面分别相 等，正方体的六个面都相 等。
详细描述
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6分米
？分米 ？分米
10分米
1分米
1分米
？分米
？分米
14
有A、B两种型号的卡车，它们车厢里 面的长、宽、高分别为3m,1.7m,0.5m 和3.2m,2m,0.6m。一堆碎石全部用A 型卡车运载，车厢内碎石的平均高度 为0.4m。如果将这堆碎石全部用B型 卡车运载，车厢内碎石的平均高度有 多少米？（的数保留两位小数）
50×30×10 ＝15000(立方厘米)
15000÷(30×20) ＝25(厘米)
18
4、长方体、正方体的体积怎么算？
长方体体积=长×宽×高
（底面积）
底面积×高
正方体体积=棱长×棱长×棱长
（底面积）
2
5、填空：
5.4L=( 5400 )mL
=﹙5.4 ﹚dm³
6.08m³=﹙6080 ﹚dm³
=﹙6080 ﹚L 0.85m²=﹙85 ﹚dm²
=﹙ 8500 ﹚cm²
1250cm³=﹙1250 ﹚mL
8
即时练习2：
一块长方体钢件，长6cm，宽5cm， 高4cm。如果每立方厘米重7.8克，那么 这块钢件重多少克？
先算钢件的体积： 6X5X4=120(立方厘米)
再算钢件的重量： 120X7.8=936（克） 答：这块钢件重936克。 9
20x20x20=8000（立方厘米） 8000÷( 25x16)= 20(厘米）
答：这时水深18cm。
11
2．在一个棱长为50厘米有水的正 方体观赏鱼缸中，放入一块宽25厘 米、高10厘米的长方体铅块，使铅
块完全浸入水中容器中的水面高度 由32厘米上升到36厘米，放入鱼缸 的长方体铅块长多少厘米？
50×50×(36－32) 10000÷(25×10) ＝10000(立方厘 ＝40(厘米)
答：这是的水位是20厘米。 10
即时练习3：在棱长为30cm的正方体
玻璃缸里装满水，然后将这些水倒入长 60cm，宽25cm的长方体玻璃缸里，这 时水深多少？（玻璃厚度忽略不计）
分析：水的体积没有变化。正方体中水的 体积和长方体中水的体积相等。
30×30×30
=27000 ( cm3)
27000÷(60×25) =18(cm)
分析:先算粉刷的面积是多少平方米？
8×6＋（8×4 ＋6×4 ）×2 =160（㎡）
160－20=140（㎡） 2×140 =280（元）
答：粉刷这间教室共需材料费280元。 6
解决问题： 先求油箱的容积
再算内装柴油的价钱
7
10 X 5 X 4.5 =225（d㎡）=225（L） 7.2 X 225 =1620（元）
米)
答：放入鱼缸的长方体铅块长40厘米。
12
在一个长25cm，宽12cm，高 20cm的长方体玻璃缸中装入一个棱长 8cm的正方体铅块，然后往缸中放一些 水，使它完全淹没这个正方体铅块，当 铅块从缸中取出时，缸中的水会下降多 少厘米？
13
用一块长10分米，宽6分米的铝板铝 板，在它的四个角分别剪去一个边长 为1分米的小正方形（如图），焊接 成一个无盖的长方体水槽，这个水槽 的容积是多少升
=﹙1.25 ﹚dm³
3
4
8×6＋（6×3 ＋8×3 ）×2 =132（㎡）
132－26 =106（㎡）
答：粉刷的面积是106平方米. 5
即时练习1：
一间教室长8米，宽6米，高4米，现在 要粉刷屋顶和四壁，除去门窗和黑板面积 20平方米。如果每平方米需材，料费2元粉刷 这间教室共需材料费多少元?
15
1．一根96厘米长的铁丝做成一个正 方体框架，做成后在它的表面糊纸， 至少要用多少平方厘米的纸？
(96÷12)×(96÷12)×6 ＝384（平方厘米）
2．如右图，在一个长方体的表 面挖去一个小长方体后，求剩余 部分的表面积。（单位：厘米）
(5×2＋5×3＋2×3)×2 ＝62(平方厘米)
2
3
西师大版五年级数学下册
解决问题
1
1、什么是表面积？ 一个物体表面所有面的面积之和叫做它的表面积。
2、长方体、正方体的表面积怎么算？ 长方体表面积=长×宽×2＋长×高×2＋宽×高×2
=（长×宽＋长×高＋宽×高）×2 正方体表面积=棱长×棱长×6
3、什么是体积？ 一个物体所占空间的大小，叫做这个物体的体积。
5
16
5cm 3cm
3．有一个形状如右图的
零件。(1)它的表面积是 2cm
多少？ (2)它的体积是多
6cm
少？
(1)(6×2＋6×3＋2×3)×2＋2×5×4 ＝112(平方厘米)
(2) 2×2×5＋2×3×6 ＝56(立方厘米)
17
4 ．一个密封的长方体玻璃缸，长50 厘米、宽30厘米、高20厘米,水深10 厘米,如果把玻璃缸向右竖立后，这 时水深多少厘米？