齿轮机构汇总PPT教学课件
合集下载
齿轮培训教材ppt课件.ppt

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
3.铣齿的工艺特点和应用 篮球比赛是根据运动队在规定的比赛时间里得分多少来决定胜负的,因此,篮球比赛的计时计分系统是一种得分类型的系统 (1)生产成本低。 (2)加工精度低。 (3)生产率低。
465
0.6
1.86
0.8
五轮轮片 (15片)
1260
0.3
1.5
0.6
六轮轮片
900
(8片)
0.3
2
0.8
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
齿形加工
一、
概述
齿轮类型
应用
直齿轮、斜齿轮、人字齿轮 平行轴间传动
❖ ㈡、抛光去毛刺作业要求:
1、按下表参数比例将工件与磨料放入抛光桶中,并加入适量的水,盖上桶盖并拧 紧螺丝;(注意:水平面至少应高出磨料2-5mm,低于桶顶至少10mm) 2、将抛光机机盖打开,将刹车杆卡入刹车槽,确认转盘不能转动后将抛光桶装入 并拧紧螺丝;
3、确认所有的抛光桶已安装牢固后,合上机盖,按表一参数设置抛光时间; 4、打开电源,进行抛光,抛光结束后取下抛光桶,有相应的筛子分离工件与磨料, 如工件为钢件应放入脱水油中浸,时间至少3分钟; 5、抛光后的工件应检查切削毛刺是否已被去除; 6、本工序采用湖牌XGP30型卧式行星滚抛光机。
㈡、机床的主要工作运动
⑴主运动 即滚刀的旋转运动。根据合理的切削速度和滚刀直径,即
可确定滚
刀的转速。
⑵展成运动 即滚刀与工件之间的啮合运动。没滚刀头数为k,工件齿 数为z,则每当滚刀转1转时,工件应转k/z
机械原理齿轮机构及其设计PPT

α
5、基圆 rb
s = e = p/2
6、齿顶高 ha
O
7、齿根高 hf
8、全齿高 h h = ha + hf
9、压力角 α
一、齿轮各部分名称
ακ
1、齿数 z
2、模数 m (非常主要旳概念) 以齿轮分度圆为计算各部分尺寸基准
齿数 z ×齿距 p = 分度圆周长 πd
分度圆直径d = z × p / π
一对齿轮作无侧隙啮合传动时,共存在四个基本原因:
两个几何原因,即一对共轭旳渐开线齿廓 给定其中任何三个原因, 两个运动原因,即两轮旳角速度 ω0 和ω 就能取得第四个原因
刀具齿廓拟定,强制刀具与轮坯以定传动比 i = ω0/ω运动
刀具旳齿廓(一种几何原因)就必然在轮坯上切削(包络)出轮 坯旳齿廓(另一种几何素)。
连续传动旳条件为:B1B2 ≥ Pb
可表达为:重叠度ε a = B1B2 / Pb≥ 1
ε a 分析:重叠度旳大小表白同步参加啮合轮齿啮合对数旳平均值
ε a = 1 时,一直只有一对轮齿啮合,确保最低连续传动; ε a < 1 时,齿轮传动部分时间不连续; ε a > 1 时,部分时间单齿啮合,部分时间双齿啮合。
pb
2
B1B2
B1P + PB2
ω2
ε = pb = πmcosα
ε=
1 (z1(tan α a1 – tanα ’) + z2(tan α a2 – tanα ’))
2π
由上式可知,重叠度 ε 与齿数 z 正有关,z 越大ε 越高;
啮合角 α’ 越大,重叠度 ε 越小。与模数m无关。
四、原则中心距 a 与实际中心距 a’
齿轮传动设计PPT课件

一、渐开线的形成和特性 二、渐开线齿廓满足定角速比要求
17
一、渐开线的形成和特性
发生线
K
1、渐开线的形成:
一直线在一个圆周上做 纯滚动时,直线上任意一点 的轨迹称为渐开线。
AK曲线称为渐开线。 BK直线称为发生线。 这个圆称为基圆。
k 称渐开线A K的展角
B
rb
基圆
A
k
O
18
2、渐开线特性:
(1)BK = A B 发生线沿基圆滚
标准齿轮
分度圆上齿厚与齿槽宽相等,且模数、压力 角、齿顶高系数及顶隙系数均为标准值的齿轮称 为标准齿轮。
33
三、齿条的基本参数:
齿条的主要特点是:
1.齿条同侧齿廓为平行的直 线,齿廓上各点具有相同的 压力角,即为其齿形角,它 等于齿轮分度圆压力角。
2.齿廓在不同高度上,具有 相同的齿距。但齿厚和槽宽各不相同.
为使前后两轮齿能同时 在啮合线上接触,必须使法 向齿距K1K'1 = K2K'2,否 则 若K1K'1 > K2K'2 ,传动中断。
若K1K'1 < K2K'2 ,两轮可能卡住。
38
Pn1 Pn2
Pn1 Pn2
Pn1 Pn2
39
pb
db
z
d
z
db d
p cos
m cos
pb1 m1 cos 1 ; pb2 m2 cos 2
5
外啮合 内啮合
齿轮齿条
6
斜齿轮
人字 齿轮
直齿 圆锥 齿轮
海拔
齿轮
7
蜗轮蜗杆
交错轴斜齿轮 (旧称螺旋齿轮)
8
17
一、渐开线的形成和特性
发生线
K
1、渐开线的形成:
一直线在一个圆周上做 纯滚动时,直线上任意一点 的轨迹称为渐开线。
AK曲线称为渐开线。 BK直线称为发生线。 这个圆称为基圆。
k 称渐开线A K的展角
B
rb
基圆
A
k
O
18
2、渐开线特性:
(1)BK = A B 发生线沿基圆滚
标准齿轮
分度圆上齿厚与齿槽宽相等,且模数、压力 角、齿顶高系数及顶隙系数均为标准值的齿轮称 为标准齿轮。
33
三、齿条的基本参数:
齿条的主要特点是:
1.齿条同侧齿廓为平行的直 线,齿廓上各点具有相同的 压力角,即为其齿形角,它 等于齿轮分度圆压力角。
2.齿廓在不同高度上,具有 相同的齿距。但齿厚和槽宽各不相同.
为使前后两轮齿能同时 在啮合线上接触,必须使法 向齿距K1K'1 = K2K'2,否 则 若K1K'1 > K2K'2 ,传动中断。
若K1K'1 < K2K'2 ,两轮可能卡住。
38
Pn1 Pn2
Pn1 Pn2
Pn1 Pn2
39
pb
db
z
d
z
db d
p cos
m cos
pb1 m1 cos 1 ; pb2 m2 cos 2
5
外啮合 内啮合
齿轮齿条
6
斜齿轮
人字 齿轮
直齿 圆锥 齿轮
海拔
齿轮
7
蜗轮蜗杆
交错轴斜齿轮 (旧称螺旋齿轮)
8
齿轮机构全解.pptx
刀具外移χ · m→正变位
因刀具不变,故变位齿轮的齿距.模数 和压力角均不变,分度圆和基圆也保持 不变。 变位→齿廓形状不相同。 刀具外移(正变位)→齿轮的齿根变宽,齿顶变窄。 刀具内移(负变位)→齿轮的齿根变窄,齿顶变宽。 ∵齿廓取同一渐开线的不同部位,不同部位的渐开线其曲率半径不相同
刀具中线
第16页/共25页
└tgαn=tgαt·cosβ
4,p.68) ┌d=mnZ/cosβ ( ha*=1 ,C*=0.25) │da=d+2ha=d+2mn │df=d-2hf=d-2.5mn └a=(d1+d2)/2=mn(Z1+Z2)/(2cosβ)
3. 斜齿的重合度:由于螺旋角的影响,斜齿传动的啮合弧增长了,故重合
装和强度。
第8页/共25页
n K
(P12)
C
2
(P23)O2 图4-2
§4-3渐开线齿廓
(二)渐开线齿廓满足定角速比要求
p.56
→i 瞬 =常数 (齿廓公法线通过节点P) 证明:渐开线齿廓E1和E2在任一点K接触,过K点作两齿廓的
公法线nn与两轮连心线交于P点。根据渐开线的性质,nn必同时 与两基圆相切 →两齿廓公法线nn即为两基圆内公切线,齿轮传 动时基圆位置变,同一方向的内公切线只有一条 → nn与连心线 O1O2交点P 为定点→故渐开线满足定角速比的条件。
和啮合角是两个齿轮啮合时才出现的。
第11页/共25页
三、重合度及连续传动条件
开始啮合点: 主动论齿根与从动轮齿顶接触点与N1N2交于A点。
退出啮合点:主动轮齿顶与从动轮齿顶根接触点与N1N2交于E点
ω1 da1
∴AE为实际啮合线段。 当两轮齿顶加大时,A和E驱
因刀具不变,故变位齿轮的齿距.模数 和压力角均不变,分度圆和基圆也保持 不变。 变位→齿廓形状不相同。 刀具外移(正变位)→齿轮的齿根变宽,齿顶变窄。 刀具内移(负变位)→齿轮的齿根变窄,齿顶变宽。 ∵齿廓取同一渐开线的不同部位,不同部位的渐开线其曲率半径不相同
刀具中线
第16页/共25页
└tgαn=tgαt·cosβ
4,p.68) ┌d=mnZ/cosβ ( ha*=1 ,C*=0.25) │da=d+2ha=d+2mn │df=d-2hf=d-2.5mn └a=(d1+d2)/2=mn(Z1+Z2)/(2cosβ)
3. 斜齿的重合度:由于螺旋角的影响,斜齿传动的啮合弧增长了,故重合
装和强度。
第8页/共25页
n K
(P12)
C
2
(P23)O2 图4-2
§4-3渐开线齿廓
(二)渐开线齿廓满足定角速比要求
p.56
→i 瞬 =常数 (齿廓公法线通过节点P) 证明:渐开线齿廓E1和E2在任一点K接触,过K点作两齿廓的
公法线nn与两轮连心线交于P点。根据渐开线的性质,nn必同时 与两基圆相切 →两齿廓公法线nn即为两基圆内公切线,齿轮传 动时基圆位置变,同一方向的内公切线只有一条 → nn与连心线 O1O2交点P 为定点→故渐开线满足定角速比的条件。
和啮合角是两个齿轮啮合时才出现的。
第11页/共25页
三、重合度及连续传动条件
开始啮合点: 主动论齿根与从动轮齿顶接触点与N1N2交于A点。
退出啮合点:主动轮齿顶与从动轮齿顶根接触点与N1N2交于E点
ω1 da1
∴AE为实际啮合线段。 当两轮齿顶加大时,A和E驱
齿轮机构及其设计教学课件PPT

2. 渐开线函数 由渐开线性质,有:AN = NK
ak
vk
Fn
K
t
t
A
k
rk ak
N
rbΒιβλιοθήκη Orb (ak + k ) = AN = NK = rbtanak
k = tanak -ak
展角K称为压力角aK的渐开线函数,工程上常用invaK表示。即
invak = tanak -ak
18
3.渐开线的极坐标参数方程
1
【教学目标】
了解齿轮机构的类型和应用; 理解齿廓啮合基本定律及有关共轭齿廓的基本知识; 掌握渐开线直齿圆柱齿轮的啮合特性及渐开线齿轮传动的正确啮合条件
和连续传动条件; 掌握渐开线齿轮各部分的名称、基本参数及各部分几何尺寸的计算; 了解渐开线齿廓的展成切齿原理及根切现象; 了解渐开线标准齿轮的最少齿数及渐开线齿轮的变位修正; 了解斜齿圆柱齿轮齿廓曲面的形成、啮合特点,并能计算标准斜齿圆柱
§5-1 齿轮机构的应用和分类 §5-2 齿廓啮合基本定律 §5-3 渐开线和渐开线齿廓的啮合特性 §5-4 渐开线齿轮的各部分名称及标准齿轮的尺寸 §5-5 渐开线直齿圆柱齿轮的啮合传动 §5-6 渐开线齿廓的切制及根切现象 §5-7 变位齿轮及最小变位系数 §5-8 平行轴斜齿圆柱齿轮机构 §5-9 圆锥齿轮机构
rk= rb/cosak k = invak= tanak -ak
ak
Fn
t
vk
K
t
A
k
rk ak
N
rb
O
19
4.渐开线的直角坐标方程
x =OC-DN=rbsinu- rbucosu y =NC+DK =rbcosu+ rbusinu 式中u称为滚动角:
ak
vk
Fn
K
t
t
A
k
rk ak
N
rbΒιβλιοθήκη Orb (ak + k ) = AN = NK = rbtanak
k = tanak -ak
展角K称为压力角aK的渐开线函数,工程上常用invaK表示。即
invak = tanak -ak
18
3.渐开线的极坐标参数方程
1
【教学目标】
了解齿轮机构的类型和应用; 理解齿廓啮合基本定律及有关共轭齿廓的基本知识; 掌握渐开线直齿圆柱齿轮的啮合特性及渐开线齿轮传动的正确啮合条件
和连续传动条件; 掌握渐开线齿轮各部分的名称、基本参数及各部分几何尺寸的计算; 了解渐开线齿廓的展成切齿原理及根切现象; 了解渐开线标准齿轮的最少齿数及渐开线齿轮的变位修正; 了解斜齿圆柱齿轮齿廓曲面的形成、啮合特点,并能计算标准斜齿圆柱
§5-1 齿轮机构的应用和分类 §5-2 齿廓啮合基本定律 §5-3 渐开线和渐开线齿廓的啮合特性 §5-4 渐开线齿轮的各部分名称及标准齿轮的尺寸 §5-5 渐开线直齿圆柱齿轮的啮合传动 §5-6 渐开线齿廓的切制及根切现象 §5-7 变位齿轮及最小变位系数 §5-8 平行轴斜齿圆柱齿轮机构 §5-9 圆锥齿轮机构
rk= rb/cosak k = invak= tanak -ak
ak
Fn
t
vk
K
t
A
k
rk ak
N
rb
O
19
4.渐开线的直角坐标方程
x =OC-DN=rbsinu- rbucosu y =NC+DK =rbcosu+ rbusinu 式中u称为滚动角:
《平行轴斜齿轮机构》课件

可维护性
斜齿轮机构的零部件易 于更换,维护成本较低
。
斜齿轮机构的应用场景
工业传动
斜齿轮机构广泛应用于各种工 业传动设备中,如减速器、变
速器等。
汽车传动
汽车变速器和传动轴等关键部 件中广泛应用斜齿轮机构。
航空航天
在航空航天领域,斜齿轮机构 因其高效、可靠的性能而被广 泛应用于各种飞行器中。
船舶工业
在船舶工业中,斜齿轮机构因 其适应性强、稳定性高的特点 而被广泛应用于船舶的传动系
平行轴斜齿轮机构的优化目标
提高齿轮传动效率
通过减小齿轮摩擦和传动误差,提高齿轮传 动的效率。
增强齿轮承载能力
通过合理设计齿轮参数和材料,提高齿轮的 承载能力。
降低齿轮噪音
通过优化齿轮参数和齿形,降低齿轮传动过 程中的噪音。
延长齿轮使用寿命
通过改善齿轮制造工艺和使用条件,延长齿 轮的使用寿命。
平行轴斜齿轮机构的优化方法
遗传算法优化
利用遗传算法对齿轮参数进行优化, 以获得最佳的传动性能。
有限元分析
通过建立齿轮传动的有限元模型,分 析齿轮应力分布和变形情况,优化齿 轮参数。
多目标优化
采用多目标优化方法,综合考虑多个 性能指标,优化齿轮参数。
实验设计
通过实验设计方法,对不同参数组合 进行实验,找到最优的齿轮参数组合 。
05
平行轴斜齿轮机构的发展趋势与 展望
平行轴斜齿轮机构的研究现状
国内外研究概况
介绍了国内外对平行轴斜齿轮机构的研究现状,包括研究团队、研究成果和研 究方向等。
实际应用情况
概述了平行轴斜齿轮机构在工业、交通、能源等领域的应用现状,以及其在实 际应用中存在的问题和挑战。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
2
2
O2
2.节点、节圆
节点:公法线与连心线的交点C 节圆:过节点所作的两圆(d1’、d2’)
意义:一对齿轮的传动可以看成两 节圆件的纯滚动(∵节点C是瞬心) 若两轮传动为定传动比则:
i12 1 2 O O1 2C Crr2’ 1’con. st
n
则节点C应为定点!
什么样的齿廓可以做到?
O1
1
K
1n
节圆
C
节圆
2
2
O2
3.齿廓曲线的确定
❖什么样的齿廓满足定传动比?
理论上很多! (包络线法)
❖常用曲线: 渐开线、摆线、圆弧线、抛物线等。
❖实际中的选用:应考虑
设计、制造、安装、使用、维护等因素。 本章主要研究
渐开线齿廓
O1
1
1 K
2
2
O2
4.3 渐开线齿廓及啮合特性
4.3.1 渐开线的形成和特性 1.圆的渐开线的形成及方程
N2 rb2
З
1
t r2'
a
o2
∵基园半径rb、节圆半径r’均为定值, 即啮合角也是一常数(正压力方向不变)
2020/10/16
З
2
15
4.4 渐开线标准直齿圆柱齿轮 的几何尺寸
一、外齿轮√ 二、内齿轮
1 各部分名称和符号 2 基本参数 3 几何尺寸的计算 4 例题
三、齿条
4.4.1齿轮各部分名称
(直线是渐开线的特例)。
B1
渐开线的形状取决基圆大小!
B2
5)基圆内没有渐开线!
rb1 O1
A1
i
A2
i
rb2
O2
O3
8
推论
❖1.同一基圆上渐开线形状相同
❖ 2.同一基圆所生成的同向渐开线 其法向等距
A2
B1K1B2K2
A1
❖3.两反向渐开线公法线处处相等
(等于两渐开线间的基圆弧长)
A1B1A2B2
(注意:在分度圆上不注下标,如:p=s+e)
齿顶高 ha:分度圆到齿顶距离 齿根高 hf:分度圆到齿根距离 齿全高 h=ha+hf:齿顶与齿根间的距离 齿宽 B:齿轮的宽度
B
eei
s si
p pi
O
4.4.2 齿轮的基本参数
p
1.模数m:
由 d=zp 得 d=zp/ 令p/=m
则 d=zm
称m 为模数,单位:mm。
基圆(db, rb):产生渐开线的圆 齿顶圆da(ra):连接齿轮各齿顶的圆 齿根圆df(rf):齿槽底部连接的圆 分度圆d (r):
计算齿轮的基准圆(无下标)
齿厚(si) :
在di圆周上, 一个轮齿左右两 侧齿廓间的弧线长
齿槽宽(ei ):
在di圆周上, 齿间的弧线长(齿间)
齿距pi:相邻两齿同侧间的弧长,pi=si+ei
K
ak
KB(切线)=KB(法线) 3)压力角ak和曲率半径rKB
渐开线上各点aK不同!
B
ak A
rk
r ∴
K↓
coask
OBrb OK rk
aK ↓ 当rK=rb时,aK=0
rb
O
曲率和曲率半径:ρ=1/r,rBK
渐开线上各点rKB也不同!
C3
C2
4)渐开线的形状取决于基圆半径 C1
K
基圆半径越大,渐开线越平直
2020/10/16
C1
N1 N2
C2
B1 K1
B2
B
K2
K O
12
4.3.3 渐开线齿廓啮合特性
1.传动比恒定
(运动方面)
由齿廓啮合基本定律
i1 212
O2C O1C
渐开线齿廓:
内公切线N1N2为定直线
(∵二基圆为定圆 )
连心线O1O2也为定直线
N2
O1
1 rb1
N1 K
E1 C
K’
E2
2
(∵ O1、O2 固定)
渐开线:一直线在圆上作纯滚动时,该直线任一点的轨迹
F
vK
渐开线
压力角 αK
K
rK 向径
基圆
发生线 基圆
αK
rb
θK 展角
基圆半径 rb
渐开线函数 rk=rb/cosak
θk= tanak-ak = invak
极坐标方程
2.渐开线的特性
1)发生线滚过基圆的长度等于基圆上被滚过的弧长?
KBAB
2)渐开线上任一点法线一定切于基圆 (或基圆的切线必为渐开线上某点的法线)
3
2)空间齿轮机构(了解)
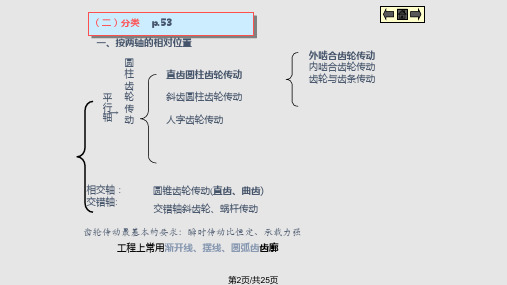
圆锥齿轮传动(直齿、斜齿、曲线齿) 交错轴斜齿轮传动 蜗杆传动.意两轴(平行、相交、交错)的旋转运动,
或转动转换为移动。
应用举例: 机床
汽车变速箱
4.2 齿廓啮合基本定律
1.齿廓啮合的一般规律
工作对齿廓曲线的要求(∵齿廓形状影响传动性能)
标准模数系列(GB/T 1357—2008)
O
第一系列 1 1.25 1.5 2 2.5 3 4 5 6 8 10 12 16 20 25 32 40 50 第二系列 1.75 2.25 2.75 (3.25) 3.5 (3.75) 4.5 5.5 (6.5) 7 9 (11) 14 18 22 28 36
N2rb2 o2
З
2
a a'
可分性: 基圆半径由齿轮加工时确定,
o'2
2
使用时即使中心距(a或a’)有微变,其传动比也不会改变。
3.啮合角不变
(动力方面)
啮合角 ’:啮合线(N1N2) 与节圆公切线(tt)所夹的锐角
(等于节圆上的压力角)
coasrb1rb2 r1 r2
r1' o1 rb1
N1
t a' C
第4章
齿轮机构及其设计
2020/10/16
1
你的手表 如何保证准确性?
4.1 齿轮机构的类型及特点
1.类型
按两轴的相对位置分:平面齿轮机构、空间齿轮机构
1)平面齿轮机构
外啮合齿轮传动 直齿圆柱齿轮传动 内啮合齿轮传动 斜齿圆柱齿轮传动 齿轮与齿条传动
人字齿轮传动
曲齿圆柱齿轮传动
2020/10/16
不同模数的齿轮比较
模数: 轮齿大小和抗弯能力的标志 模数m↑—— 齿厚↑、抗弯能力↑
m=4 z=16 m=2 z=16
m=1 z=16
2.压力角a (分度圆上的压力角) 不同圆上的压力角ak:
coask
OBrb OK rk
压力角与rk有关(最大αa、最小αb),
标准压力角(分度圆上):a=20º
传动质量?
——惯性力、振动、噪音?
——转速是否均匀? ——传动比是否变化?
vC1
由瞬心定理:C为齿廓1、2 的瞬心
vC2
VC1 = VC2 即: ω1O1C = ω2O2C
n
i1212
O2C O1C
齿廓啮合基本定律:
一对传动齿轮在任一位置的传动比等于连 心线被齿廓接触点公法线所分线段的反比
O1
1
K
1n
则节点C必为定点
rb2
i 2020/10/16 12
1O 2Cr2'rb2co.n 2 O 1C r1' rb1
s
t
O2
13
З
2.传动的可分性
(制造、使用方面)
i12
1o2Crb2 2 o1C rb1
i1 2 1 2 o o1 2 C C''rrb b1 2
1
o1
rb1
N1
N1'
C
C' N2 rb2
