过程控制系统解耦控制系统页
过程控制及仪表_解耦控制共39页文档

1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
过程控制及仪表_解耦控制
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
工业过程先进控制及应用--6.解耦控制系统.
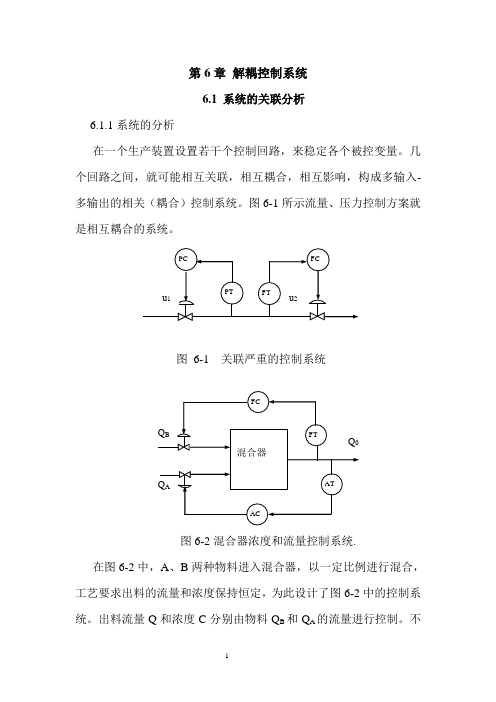
第6章解耦控制系统6.1 系统的关联分析6.1.1系统的分析在一个生产装置设置若干个控制回路,来稳定各个被控变量。
几个回路之间,就可能相互关联,相互耦合,相互影响,构成多输入-多输出的相关(耦合)控制系统。
图6-1所示流量、压力控制方案就是相互耦合的系统。
图6-1 关联严重的控制系统图6-2混合器浓度和流量控制系统.在图6-2中,A、B两种物料进入混合器,以一定比例进行混合,工艺要求出料的流量和浓度保持恒定,为此设计了图6-2中的控制系统。
出料流量Q和浓度C分别由物料Q B和Q A的流量进行控制。
不难看出,这两个控制回路是相互关联的,而关联程度与工艺操作数据有关。
系统间的关联程度是不一样的。
那么如何来表征系统的关联程度呢?可以采用“相对增益”的方法来分析 6.1.2相对增益令某一通道y i u j →在其它系统均为开环时的放大系数与该一通道在其它系统均为闭环时的放大系数之比为λij ,称为相对增益,则yu y uu y λij j i j i ∂∂∂∂=(6-1)上式中分子项外的下标u 表示除了u j 以外,其它都保持不变,即都为开环;分母项外的下标y 表示除了y i 以外,其它y 都保持不变,即其它系统都为闭环系统。
现以图6-1所示双输入双输出系统为例。
该系统被控变量与操纵变量关系如图6-4所示。
图6-4 双输入双输出对象静态特性框图由图6-4可得该系统静态方程为u k u k y u k u k y 22212122121111+=+= (6-2)式中k ij 表示第j 个输入变量作用于第i 个输出变量的放大系数。
求λ11,首先求取λ11的分子项u u y 11∂,除u 1外,其它u 不变,则有11211k u u y ==∂∂常数(6-3)再求λ11的分母项y u y 11∂∂,除y 1外,其它y 不变,由式(6-2)可得u k u k 0u k u k y 2221212121111+=+=由上两式可得2211211222112221121111122211211112k k k k k k k k k k u y u k k k u k y y -=-=∂∂∴-==常数(6-4)在求得λ11的分子项与分母项可得λ11yu y u u y j i j i ∂∂∂∂=11λk k k k k k 211222112211-=(6-5) 同样可推导出 k k k k k k 2112221122111122-==λλ (6-6) k k k k k k 2112221121122112--==λλ (6-7)如果排成数阵形式λ22λ21λ12λ11u u y 2y 121 (6-8)上式称为布里斯托尔阵列(Briistol 阵列),或相对增益阵列。
解耦控制所谓解耦控制系统PPT33页

▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪ቤተ መጻሕፍቲ ባይዱ
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
33
解耦控制所谓解耦控制系统
61、辍学如磨刀之石,不见其损,日 有所亏 。 62、奇文共欣赞,疑义相与析。
63、暧暧远人村,依依墟里烟,狗吠 深巷中 ,鸡鸣 桑树颠 。 64、一生复能几,倏如流电惊。 65、少无适俗韵,性本爱丘山。
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
解耦控制系统PPT课件

• 在两个回路都闭合的情况下, 控制系统的输入y1,sp、 y2,sp 和输出y1、 y2间的关系为
(1 G11Gc1) y1 (G12Gc2 ) y2 (G11Gc1) y1,sp (G12Gc2 ) y2,sp (G21Gc1) y1 (1 G22Gc2 ) y2 (G21Gc1) y1,sp (G22Gc2 ) y2,sp
第七章 解耦控制系统
• 7.1系统的关联分析
• 在过程控制系统设计中, 常常会遇到多输出-多输入对象, 如何正确选择输出(被控变量)和输入(控制变量)的合理搭配关 系, 是制定良好的控制方案的关键。 Bristol(1966年)提出的 相对增益矩阵的概念, 为我们的方案选择提供了一个定量的判 定标准。 设计好控制系统后, 常常会发现控制器回路之间还存在关 联, 要通过设计补偿装置来消除或减少回路之间关联的作用, 使系统平稳运行, 就要采用多变量解耦控制(Multivariable Decoupling Control)技术。
传回来, 反过来又影响回路2的输出, 并且通过回路2反馈通道
返回至y2,sp输入端, 形成第三个闭合回路, 这便是两控制回路 间关联的实质。 如果处于闭环状态的两个控制器的输出u1、 u2不断地相互影响, 就会严重影响控制系统的品质。 在大多数
场合中, 控制系统的关联都是不好的, 应予避免或削弱。
8
k11
k12k21 k22
k11k22
k11k22 k12k21
(7-9)
25
• 同理可从式(7-8)中求出
12
k12k21 k11k22 k12k21
21
k12k21 k11k22 k12k21
22
k11k22 k11k22 k12k21
过程控制系统[李国勇][电子教案]第9章解耦控制系统
![过程控制系统[李国勇][电子教案]第9章解耦控制系统](https://img.taocdn.com/s3/m/b013dd3f5a8102d276a22f84.png)
Yk const
17
pij与qij之比定义为相对增益或相对放大系数ij, ij可表示为 pij Y Y i i ij (9-8) qij U j U j U k const Yk const 即 由相对增益ij元素构成的矩阵称为相对增益矩阵。
3
4
图9-1所示是化工生产中的精馏塔温度控制方案。 ul的改变不仅仅影响y1,同时还会影响y2;同样 地,u2的改变不仅仅影响y2,同时还会影响y1。因此, 这两个控制回路之间存在着相互关联、相互耦合。这 种相关与耦合关系如图9-2所示。 耦合是过程控制系统普遍存在的一种现象。耦合 结构的复杂程度主要取决于实际的被控对象以及对控 制系统的品质要求。因此如果对工艺生产不了解,那 么设计的控制方案不可能是完善的和有效的。
Y1 q11 U 1
Y2 const
K 12 K 21 K 11 K 22 K 12 K 21 K 11 K 22 K 22
25
类似地可求得
q 21 K 11 K 22 K12 K 21 K K K 21 K 12 K K K12 K 21 ; q12 11 22 ; q 22 11 22 K 12 K 21 K 22
pij
U j
U k const
16
然后,在所有其它回路均闭合,即保持其它被控 变量都不变的情况下,找出各通道的开环增益,记作 矩阵Q。它的元素qij的静态值称为Uj与Yi通道的第二放 大系数。它是指利用闭合回路固定其它被控变量时, Uj与Yi的开环增益。qij可以表为 (9-7)
Yi qij U j
13
U 1 R1 Y1 Y1 3U 1 4U 2 ; U 2 R2 Y2 Y2 5U 1 U 2
高等过程控制-第6章解耦控制

解耦控制系统
第一节、概 述 第二节、系统的耦合 第三节、解耦控制方法
第一节 概 述
耦合:控制量与被控量之间是互相影
响的,一个控制量的变化同时引起几 个被控制量变化的现象。
解耦:消除系统之间的相互耦合,使
各系统成为独立的互不相关的控制回 路。
解耦方法:
被控量和控制量之间的适当匹配; 重新整定调节器参数; 附加解耦装置
yi 可表示为 qij j
yr
yi ij j
r
yi j
yr
上式即为μj到yi这个通道的相对增益; 由各通道相对增益构成的矩阵∧则称为相对增益 矩阵。
1 y1 11 y2 21 y i i1 yn n1 2 12 22 i2 n2 j 1i 2 j ij nj n 11n 2n in nn
令
Y1' s Y1 s K 2Y2 s
' s K1Y1 s Y2 s Y2
则
Y ' s W11 K 2W21 1' Y2 s W21 K1W11
W12 K 2W22 T 1 s W22 K1W12 T 2 s
2. 三角矩阵法
三、前补偿法
前面所述的解耦方法是加入补偿装置,将对象传递矩 阵变为对角阵、三角矩阵等,从而实现解耦控制。而前补 偿法是不加任何补偿装置,将对象传递矩阵经变换后变成 对角矩阵、三角矩阵等,达到解耦的目的。
r1
WT1(s)
T 1
W11(s)
W21(s) W12(s)
Y1
解耦控制 ppt课件

ppt课件
9
实现对角解耦后的等效系统框图
U1(S)
GP(S)
Uc1(S)
G (S)
U2(S)
Uc2(S)
根据解耦要求,解耦后的等效传递函数矩阵为对角阵。即:
Y Y1 2((S S)) G 0.1.1 (G S .).2.2 .(S .0 ). .U U .1 2((S S))
耦合对象的传函矩阵为 G(S)G G1211((SS))....G G ..1..22..2((SS)) 解耦环节的传函矩阵为 GP(S)Gቤተ መጻሕፍቲ ባይዱGP P121(1(SS))....G G ..P P..12..2(2(SS))
U U C C 1 2 ((S S)) G G P P 1 2((1 1 S S))..G G ..P P .1 .2(.2 .(2 S S ..)) U U 1 2((S S))
第一章 解耦控制系统
被控过程的耦合现象及对控制过程的影响 解耦控制系统 ※解耦控制系统设计 解耦控制中的问题 相对增益(自学)
ppt课件
1
1.1被控过程的耦合现象及对控制过程的影响 图1-1为某精馏塔温度控制系统
在石油化工生产中,使用的原料和反 应后的产物多是由若干组分组成的混合 物,常需要进行分离得到比较纯的组分 作为中间产品或最终产品。要进行蒸馏 处理。精馏塔是由精馏塔身、冷凝器和 再沸器等基本部件构成。 被控参数:塔顶温度T1和塔底温度T2, 控制变量:塔顶回流量QL和加热蒸汽流 量QS T1C:塔顶温度控制器,其输出u1控制 回流调节阀,调节塔顶回流量QL,实现 塔顶温度T1控制。 T2C:塔底温度控制器,其输出u2控制 再沸器加热蒸汽调节阀,调节加热蒸汽 量QS,实现塔底温度T2控制。
过程控制系统解耦控制系统

K 21 K12K21
Y1
K11 K11K22 K12 K21
Y2
(8.16)
15
2. 相对增益与相对增益矩阵
引入H矩阵,则(8-16)式可写成矩阵形式, 即
U1(s) U1(s)
h11 h21
h12 Y1(s)
相对增益与相对增益矩阵
令某一通道在其它系统均为开环时的放大系 数与该一通道在其它系统均为闭环时的放大 系数之比为λij,称为相对增益;
相对增益λij是Uj相对于过程中其他调节量对
该被控量Yi而言的增益( Uj → Yi );
λij定义为
p
ij
q ij ij
pij 第一放大系数(开环增益) qij 第二放大系数(闭环增益)
40
3. 解耦控制系统设计
三 单位矩阵解耦法
单位阵解耦设计是对角阵解耦设计的一种特殊 情况。它要求被控对象特性矩阵与解耦环节矩 阵的乘积等于单位阵。即
G p11 ( s) G p 21 ( s)
Gp12 (s) N11(s)
G
p 22
(
s)
N
21
(
s)
N12 N 22
(s) (s)
p
22
(s)
G
p12
(
s)G
p
21
(s)
Gp11(s)Gp22 (s)
G
p11
(
s)G
p
22
(s)
G
p12
(
s)G
p
21
(s)
(8.51)
39
