GPS网平差系列之求误差椭圆代码
误差椭圆

2 E[∆x ] = E[( x− x)2 ] = E[( x − E(x)) 2 ] = σ x 2 2 E[∆y ] = E[( y− y)2 ] = E[( y − E( y)) 2 ] = σ y 2 ~
~
σ = σ +σ
p
ϕ
p′′
p′′′
∆ϕ
y
由广义误差传播律: 由广义误差传播律
Qϕϕ = Qxx cos2 ϕ + Qyy sin2 ϕ + Qxy sin 2ϕ
2 2 2 σϕ = σ 0 Qϕϕ = σ 0 (Qxx cos2 ϕ + Qyy sin2 ϕ + Qxy sin(2ϕ)
三、位差的极大值 E和极小值 F
上
E = σ QEE =
2 2 0
σ02
2
(Qxx + Qyy + K),
∆ψ = cosψ∆E + sinψ∆F Q = QEE cos2 ψ + QFF sin2 ψ + QEF sin 2 ψ ψψ
QEF = 0
Qψψ = QEE cos2 ψ + QFF sin 2 ψ
2 2 2 σψ = σ 0 Qψψ = σ 0 (QEE cos2 ψ + QFF sin 2 ψ ),
∧
Q∧ Q∧ Q∧ Q∧ Q∧ Q∧
∧
X1 X i
∧
X1Y i
∧
L Q∧ L Q∧ L
∧
X1 X u
∧
Y1 Y1
Y1 X i
Y1 Y i
Y1 X u
误差椭圆

Qxx Qxx
Qyy Qyy
K
其中 K Qxx Qyy 2 4Q2xy
22
7.5 点位落入误差椭圆内的概率
二维正态分布的联合概率密度函数:
f
x,
y
2
1
x y
1
2
exp
1
21 2
PP PP PP
x cos y sin cos
sin
x y
6
Q cos
s
in
Qxx Qxy
Qxy Qyy
c s
os in
Qxx cos2 Qyy sin 2 Qxy sin 2
• 误差椭圆反映的是待定点的点位分布情况,是一 个概率形象。当坐标轴旋转E角后,可得标准椭 圆方程。
17
• 在误差椭圆上量取任意方向的位差
X´
P
• 方法:过椭圆作方向的正交切线PF
F
• P-切点,F-垂足,则
OF
O Y´
• 中误差曲线在测量中的应用举例
18
•误差椭圆绘制: • 1) E角无负值; • 2) E>F; • 3) 测量坐标系绘制;
用求
特征
向量
的方
法求极
大值
和极
小值
的方
向
E、
。
F
Qxx Qxy
1
Qxy Qyy
1
c s
osE in E
0
,
得
tan E
QEE Qxx Qxy
误差椭圆

第十章——误差椭圆
2 令: K (Qxx Q yy ) 2 4Qxy K为算术平方根,恒大于零。 1 则有: Q Q xx Q yy K 2 用E表示位差的极大值,F表示位差的极小值,则有: 1 2 2 2 E 0 Q E E 0 Q xx Q yy K 2 (5) 1 2 2 2 F 0 Q F F 0 Q xx Q yy K 2 (5)式就是计算位差极大值与极小值的实用公式。
第十章——误差椭圆
(7)式和(8)式就是用极值E、F计算纵横坐标中误差 的公式。 若规定任何方向都由E 轴起算,则纵坐标轴X相对于E轴 的方位角为 360 E (如图)。故(7)式可写为:
2 x E 2 cos2 (360 E ) F 2 sin 2 (360 E )
第十章——误差椭圆
GPS 网 三 维 无 约 束 平 差 误 差 椭 圆
第十章——误差椭圆
GPS 网 三 维 无 约 束 平 差 误 差 椭 圆
第十章——误差椭圆
§10-5 相对误差椭圆
在平面控制网中,绘出各待定点的位误差椭圆后,就可应用点位误 差椭圆图解各待定点与已知点之间的边长中误差与方位角中误差。 但不能用同样的方法图解待定点与待定点之间的边长中误差与方位 角中误差。而在实际工作中,重要的却是任意两个待定点之间的相 对精度。为此,有必要研究任意两个待定点之间的相对精度问题。 设有任意两个待定点 为:
第十章——误差椭圆
极值方向
当
当
tan 2 0
2Qxy Qxx Q yy
Qxy 0 时,极大值在一、三象限;
Qxy
极小值在二、四象限。 时,极大值在二、四象限; 0 极小值在一、三象限。
测量平差基础课件——误差椭圆

tg2 0
2Q xy (Qxx Q yy )
2020/6/11
确定极值方 向的公式
两个根:2 0 和 20 180 即,使Q 取得极值的方 向值为 0 和 0 90 ,其 中一个为极大值方向, 另一个为极小值方向。 那么,哪个是极大值方 向?哪个是极小值方向 呢?下面作进一步的推 证:
9
§6-2 点位ห้องสมุดไป่ตู้差
三、位差的极大值 E 和极小值 F
1.极值方向的确定
总之:
tg2 0
2Q xy (Qxx Q yy )
两个根: 2 0
20 180
两个极值方向:0 0 90
当 当Qxy 0 : 极大值方向 E 在一、
三象限,极小值在二、四象限。
当 当Qxy 0 : 极大值方向 F 在一、
三象限,极小值在二、四象限。
2 P
02(Qxx
Qyy)
02(
1 Px
1 )
Py
P 0
Qxx Qyy 0
11 Px Py
Qx1 y1
Qx1 x2
Qx1 y2
Qx1 xk
Q x1
yk
Q y1 y1 Qx2 y1 Q y2 y1
Q y1 x2 Qx2 x2 Q y2 x2
Q y1 y2 Qx2 y2 Q y2 y2
三、位差的极大值 E 和极小值 F
1.极值方向的确定
cos2
0
1
cos 20
2
,
sin2
0
1
cos 20
2
或
Q
(Qxx
1 cos 20 2
Qyy
1 cos 20 2
Qxy sin20 )
误差理论与平差基础_第10章_误差椭圆

一.点位中误差 二.点位误差的计算 三.误差曲线 四.误差椭圆
一、点位中误差
控制点的平面位置是用一对平 面直角坐标来确定的。坐标是 由观测值的平差值计算所得的, 因此不可避免地带有误差。
x
A
O
Dy P¢(x, y) Du
Dx DP Ds
P(x, y)
y
在平面控制网的平差计算中,往往要评定待定点的点位精度; 待定点的点位精度通常用点位中误差简称“点位误差”的大 小来评定; 经过平差后的坐标(坐标的平差值)是估值,而不是真值!
Qxy Qyy
c s
os in
Qxx cos2 Qyy sin 2 Qxy sin 2
Dx
j
P
P¢¢ Dj
s
2 j
=
s
2 0
éëQxx
cos2
j
+
Qyy
sin2
j
+
Qxy
sin
2jùû
坐标方位角
P¢
P¢¢¢
y
二、点位任意方向的位差
x
与 j 垂直方向的位差如何求?
Q
=
æ èç
2 0.5
0.5 3
öø÷(dm2 / ('')2 )
单位权方差 0 0.5''
待定点P点到已知点A的距离为6.45km,方位角为45°,求P 点在AP方向的纵向误差和横向误差及AP边的边长相对中误 差。
s
2 j
=
s
2 0
éëQxx
cos2
j
+
Qyy
sin2
j
误差椭圆

Qmin 0
QFF 0
1 2
Qxx Qyy K
或写成
E2
1 2
2 x
2 y
2 x
2 y
2
4
2 xy
F 2
1 2
2 x
2 y
2 x
2 y
2
4
2 xy
其中:E 2
F2
2 x
2 y
2 P
11
第七章 误差椭圆
1
• 7.1 概述 • 一、点位误差 • A--已知点 • P--待放样点P的真位置 • P´--P点平差后的平差值点位
P点在x、y方向的真误差:X
x y
~xP ~yP
xˆP yˆ P
x
P点点位真误差: A
y P´ u
s P
P x2 y2
QXX I C 0
就是QXX的两个特征根。
9
由特征方程:
QXX
I
Qxx
Qxy
Qxy 0
Qyy
,
得
1 2
Qxx Qyy
1 2
Qxx Qyy 2 4 QxxQyy Qx2y
即
1
Qmax QEE
• 4)误差椭圆绘制的比例尺比地形图的比例尺要 大,一般为1:10或1:1等。
19
• 7.4 相对误差椭圆
• 点位误差椭圆-待定点对已知点的点位精度情况
科傻GPS平差软件说明书

科傻系统(COSA)系列软件GPS工程测量网通用平差软件包(CosaGPS V5.1)使用说明书2007年11月CosaGPS版权所有不得翻录Tel: 131******** 136******** 133******** 133******** Email: **************************CosaGPS目录目录 (1)1.简介 (3)1.1 功能全面 (3)1.2 整体性好 (3)1.3 解算容量大,运算速度快 (3)1.4 操作简明,使用方便 (4)2.“文件”下拉菜单 (6)2.1 工程与文件 (6)2.2 “文件”菜单项 (8)2.2.1新建 (8)2.2.2打开 (9)2.2.3关闭 (9)2.2.4保存 (9)2.2.5另存为 (9)2.2.6新建工程 (9)2.2.7 打开工程 (15)2.2.8 打印 (16)2.2.9 打印预览 (16)2.2.10 打印设置 (16)2.2.11 退出 (16)3.“GPS数据处理”下拉菜单 (17)3.1 已知数据 (17)3.1.1 三维已知坐标 (18)3.1.2 二维已知坐标 (19)3.1.3 一维高程点 (19)3.1.4 输入地面边长 (19)3.1.5 输入地面方位 (20)3.2 基线数据 (20)3.3 GPS三维向量网平差(无约束平差或约束平差) (21)3.4 二维网联合/约束平差 (22)CosaGPS 13.4.1 联合/约束平差 (22)3.4.2 输出用户自定义任意两点相对精度 (23)3.5 椭球面上三维平差 (23)3.6 工程网(一点一方向)平差 (24)3.7 GPS高程拟合 (25)3.8 GPS三维秩亏自由网平差 (26)3.9 稳定性分析 (27)3.10 设置 (28)4.“查看”下拉菜单 (28)5.“工具”下拉菜单 (29)5.1 闭合差计算 (30)5.2 重复基线差 (30)5.3 网图显绘 (31)5.4 贯通误差影响值计算 (31)5.5 GPS网设计 (32)5.6 输出AutoCAD格式的GPS网图 (33)6.“坐标转换”下拉菜单 (34)6.1 XYZ-〉BLH (34)6.2 BLH->XYZ (35)6.3 BL->XY (36)6.4 XY->BL (36)6.5 XY1->XY2 (37)6.6 XYZ1->XYZ2 (39)6.7 高程面坐标变换 (41)7.“帮助”下拉菜单 (42)附录1. 功能菜单框图 (43)附录2. 算例及说明 (44)附录3. 基线解文件格式说明 (46)附录4. 方向及经纬度的角度格式说明 (54)附录5. 简要操作步骤 (55)CosaGPS 21.简介基于全球卫星定位系统(GPS)的现代测量理论和技术改变了传统的测量模式,使工程测量行业发生了革命性变化,测量外业工作自动化程度大大提高,测量内业软件的作用更加重要。
二维网约束平差报告.doc
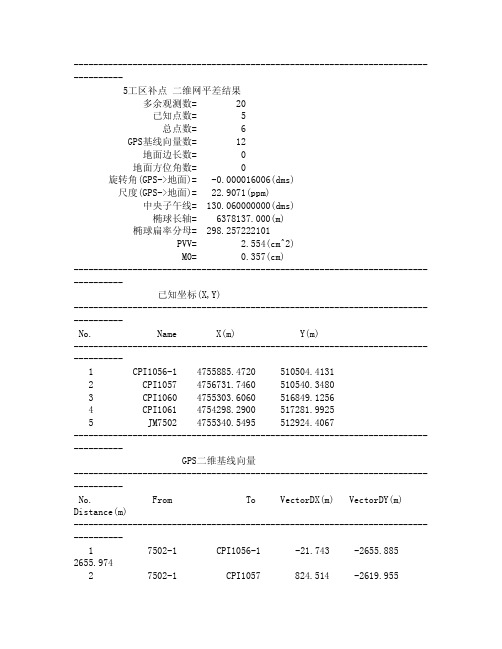
----------------------------------------------------------------------------------5工区补点二维网平差结果多余观测数= 20已知点数= 5总点数= 6GPS基线向量数= 12地面边长数= 0地面方位角数= 0旋转角(GPS->地面)= -0.000016006(dms)尺度(GPS->地面)= 22.9071(ppm)中央子午线= 130.060000000(dms)椭球长轴= 6378137.000(m)椭球扁率分母= 298.257222101PVV= 2.554(cm^2)M0= 0.357(cm)----------------------------------------------------------------------------------已知坐标(X,Y)----------------------------------------------------------------------------------No. Name X(m) Y(m)----------------------------------------------------------------------------------1 CPI1056-1 4755885.4720 510504.41312 CPI1057 4756731.7460 510540.34803 CPI1060 4755303.6060 516849.12564 CPI1061 4754298.2900 517281.99255 JM7502 4755340.5495 512924.4067----------------------------------------------------------------------------------GPS二维基线向量----------------------------------------------------------------------------------No. From To VectorDX(m) VectorDY(m) Distance(m)----------------------------------------------------------------------------------1 7502-1 CPI1056-1 -21.743 -2655.885 2655.9742 7502-1 CPI1057 824.514 -2619.9552746.6323 7502-1 JM7502 -566.646 -235.947 613.8064 7502-1 JM7502 -566.644 -235.945 613.8055 CPI1057 CPI1056-1 -846.255 -35.930 847.0186 CPI1060 7502-1 603.591 -3688.679 3737.7377 CPI1060 JM7502 36.945 -3924.627 3924.8018 CPI1061 7502-1 1608.884 -4121.537 4424.4309 CPI1061 CPI1060 1005.291 -432.859 1094.52210 CPI1061 JM7502 1042.238 -4357.483 4480.39311 JM7502 CPI1056-1 544.904 -2419.940 2480.53012 JM7502 CPI1057 1391.159 -2384.010 2760.222--------------------------------------------------------------------------------------平差坐标(X,Y)--------------------------------------------------------------------------------------No. Name X(m) Y(m) Mx(cm) My(cm) Mp(cm) --------------------------------------------------------------------------------------1 CPI1056-1 4755885.4720 510504.41312 CPI1057 4756731.7460 510540.34803 CPI1060 4755303.6060 516849.12564 CPI1061 4754298.2900 517281.99255 JM7502 4755340.5495 512924.40676 7502-1 4755907.2116 513160.3612 0.14 0.14 0.20 --------------------------------------------------------------------------------------最弱点--------------------------------------------------------------------------------------No. Name MX(cm) MY(cm) MP(cm)--------------------------------------------------------------------------------------6 7502-1 0.14 0.14 0.20--------------------------------------------------------------------------------------误差椭圆参数(E,F,T)--------------------------------------------------------------------------------------No. Name E(cm) F(cm) T(dms)--------------------------------------------------------------------------------------1 CPI1056-1 0.00 0.00 0.00002 CPI1057 0.00 0.00 0.00003 CPI1060 0.00 0.00 0.00004 CPI1061 0.00 0.00 0.00005 JM7502 0.00 0.00 0.00006 7502-1 0.15 0.13 46.3509--------------------------------------------------------------------------------------二维基线向量残差--------------------------------------------------------------------------------------No. From To V_DX(cm) V_DY(cm)--------------------------------------------------------------------------------------1 7502-1 CPI1056-1 0.19 -0.222 7502-1 CPI1057 -0.02 0.103 7502-1 JM7502 -0.36 -0.154 7502-1 JM7502 -0.48 -0.365 CPI1057 CPI1056-1 0.07 -0.386 CPI1060 7502-1 -0.18 -0.147 CPI1060 JM7502 -0.58 -0.218 CPI1061 7502-1 -0.28 -0.099 CPI1061 CPI1060 0.12 0.0910 CPI1061 JM7502 -0.62 -0.3611 JM7502 CPI1056-1 0.39 0.1212 JM7502 CPI1057 0.42 0.46--------------------------------------------------------------------------------------二维基线向量可靠性--------------------------------------------------------------------------------------No. From To 内部可靠性DX DY--------------------------------------------------------------------------------------1 7502-1 CPI1056-1 0.77 0.722 7502-1 CPI1057 0.81 0.743 7502-1 JM7502 0.81 0.794 7502-1 JM7502 0.81 0.895 CPI1057 CPI1056-1 0.99 0.996 CPI1060 7502-1 0.68 0.627 CPI1060 JM7502 0.86 0.918 CPI1061 7502-1 0.70 0.679 CPI1061 CPI1060 0.97 0.9410 CPI1061 JM7502 0.85 0.8811 JM7502 CPI1056-1 0.90 0.8712 JM7502 CPI1057 0.92 0.90累计内部可靠性 10.08 9.92平均内部可靠性 0.84 0.83内部可靠性总和 20.00内部可靠性均值 0.83--------------------------------------------------------------------------------------------------平差后方位角、边长及精度--------------------------------------------------------------------------------------------------No. FROM TO A(dms) MA(s) S(m) MS(cm) MS:S ppm--------------------------------------------------------------------------------------------------1 7502-1 CPI1056-1 269.31517 0.11 2656.0371 0.14 1/1887000 0.532 7502-1 CPI1057 287.28088 0.11 2746.6937 0.13 1/2036000 0.493 7502-1 JM7502 202.36235 0.45 613.8244 0.15 1/419000 2.384 7502-1 JM7502 202.36235 0.45 613.8244 0.15 1/419000 2.385 CPI1057 CPI1056-1 182.25533 0.00 847.0366 0.00 0 0.006 CPI1060 7502-1 279.17353 0.08 3737.82320.14 1/2719000 0.377 CPI1060 JM7502 270.32215 0.00 3924.89280.00 0 0.008 CPI1061 7502-1 291.19253 0.07 4424.53090.13 1/3308000 0.309 CPI1061 CPI1060 336.42157 0.00 1094.54740.00 0 0.0010 CPI1061 JM7502 283.27052 0.00 4480.49760.00 0 0.0011 JM7502 CPI1056-1 282.41238 0.00 2480.58650.00 0 0.0012 JM7502 CPI1057 300.15552 0.00 2760.28320.00 0 0.00--------------------------------------------------------------------------------------------------最弱边--------------------------------------------------------------------------------------------------No. FROM TO A(dms) MA(s) S(m)MS(cm) MS:S ppm--------------------------------------------------------------------------------------------------3 7502-1 JM7502 202.36235 0.45 613.82440.15 1/419000 2.38--------------------------------------------------------------------------------------------------相邻点坐标分量及其相对中误差--------------------------------------------------------------------------------------------------No. FROM TO dX(m) dY(m) mdX(cm) mdY(cm)--------------------------------------------------------------------------------------------------1 7502-1 CPI1056-1 -21.7396 -2655.9481 0.14 0.14 合格2 7502-1 CPI1057 824.5344 -2620.0132 0.14 0.14 合格3 7502-1 JM7502 -566.6621 -235.9545 0.14 0.14 合格4 7502-1 JM7502 -566.6621 -235.9545 0.14 0.14 合格5 CPI1057 CPI1056-1 -846.2740 -35.9349 0.00 0.00 合格6 CPI1060 7502-1 603.6056 -3688.7644 0.14 0.14 合格7 CPI1060 JM7502 36.9435 -3924.7189 0.00 0.00 合格8 CPI1061 7502-1 1608.9216 -4121.6313 0.14 0.14 合格9 CPI1061 CPI1060 1005.3160 -432.8669 0.00 0.00 合格10 CPI1061 JM7502 1042.2595 -4357.5858 0.00 0.00 合格11 JM7502 CPI1056-1 544.9225 -2419.9936 0.00 0.00 合格12 JM7502 CPI1057 1391.1965 -2384.0587 0.00 0.00 合格--------------------------------------------------------------------------------------------------。
