第一章 微积分学的理论基础__第五节 连续函数
微积分课件2.7连续函数

解 由于
lim f ( x) lim(x2 1) 1
x0
x0
且
lim f (x) lim(2x b) b
x0
x0
又因为f(x)在点 x = 0处连续,故
lim f (x) lim f (x)
x0
x0
即 b 1
若函数 ƒ(x)在开区间 (a , b) 内的每一点都连续, 则称函
数ƒ(x)在开区间 (a , b) 内连续; 若函数ƒ(x)在开区间 (a , b) 内连续, 且在左端点 a 右连
lim
x x0
f ( x) 不存在;
(3)
ƒ(x)在 x0 处虽有定义,
且
lim f ( x) 存在, 但
x x0
lim
x x0
f (x)
f ( x0 )
依据函数在间断点处的左、右极限是否都存在,通常
把函数的间断点划分为两类. 设点 x0是函数 ƒ(x)的间断点.
第一类间断点:左右极限都存在的间断点;
f (1)
1 e1 arctan 1
4 (1 e)
例10
xn 1
lim
x 1
xm
;(m, n 1
N)
解 因为 an bn (a b)(an1 an2b
abn2 bn1 )
故
xn 1
lim
x1
xm
1
n个
( x 1) ( xn1 xn2 1)
lim
x 1
(x
1) ( xm1
y f (x0 x) f (x0 )
为函数对应的增量(或改变量).
定义2.7.2 设函数 ƒ(x) 在 x0 的某邻域内有定义, 如果
lim y
《微积分》(上下册) 教学课件 01.第1章 函数、极限、连续 高等数学第一章第9-10节
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
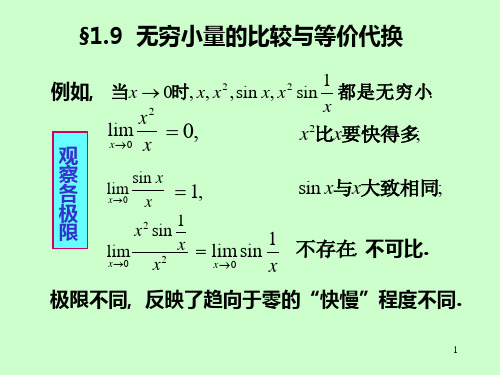
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
一元微积分(第一章 函数、极限、连续)

第一章 函数、极限、连续重点:1、求函数的极限(最重要的方法是L ’P 法则)2、无穷小的比较3、考察分段函数在分段点的连续性4、间断点的判定及分类5、介值定理 一、函数1、函数的定义及表示法【理解函数的概念,掌握函数的表示法,会建立简单应用问题的函数关系式】 函数概念 ()y f x =函数的两要素 ⎧⎨⎩定义域对应规则函数的表示方法① 显函数: ()y f x =② 隐函数:由方程(,)0F x y =确定的函数()y y x =.例:1y y xe +=确定了()y y x =⇒01x y==.③ 参数方程表示的函数:由方程()()x x t y y t =⎧⎨=⎩确定的函数()y y x =.例:2ln(1)arctan x t y t⎧=+⎨=⎩ 确定了()y f x =.④ 积分上限函数: ()()xax f t dt Φ=⎰.例:2311()(1)3xx t dt x Φ==-⎰⑤ 概率表示的函数:()()F x P X x =≤, 其中X 为随机变量,x 为实数.⑥ 分段函数:自变量不同范围内用不同式子表示的一个函数.【例】 ,0()sin ,0a x x f x x x x +≥⎧⎪=⎨<⎪⎩ ; 1sin ,0()0,0x x f x x x ⎧≠⎪=⎨⎪=⎩ .如 A. 绝对值表示的函数 11111x x y x xx -≥⎧=-=⎨-<⎩ ; B. 极限表示的函数 2211()lim111nnn x x x f x x x x x x →∞⎧<-⎪=⋅==⎨+⎪->⎩; C. 其他形式 2022101()max{1,}12x x f x x xx ≤≤≤≤⎧==⎨<≤⎩ .10sgn()0010x y x x x >⎧⎪===⎨⎪-<⎩-------符号函数[]y x =--取整函数.2、函数的性质 【了解函数的有界性,单调性,周期性,奇偶性】①.有界性:()f x 在某区间I 内有定义,若存在0M >,对任意x I ∈,总有()f x M ≤, 则称()f x 在某区间I 内有界.否则称()f x 在某区间I 内无界.例:2111sin1,(0);arctan ,();,1,()2121xx x x x R x R xx e π≤≠≤∈≤<∈++. ②.单调性:()f x 在某区间I 内有定义,若12,x x I ∀∈,当12x x <时12()()f x f x ≤,就称()f x 单调上升;当12x x <时,12()()f x f x ≥,就称()f x 单调下降. 不含等号时称严格单增(或单减).③.奇偶性:若()()f x f x -=, 则称()f x 为偶函数,偶函数的图形关于y 轴对称; 若()()f x f x -=-,则称()f x 为奇函数,奇函数的图形关于原点对称.④.周期性:()()(0)f x T f x T +=≠. (主要是三角函数)【例1】讨论()ln(f x x =+的奇偶性. 【奇函数】 【例2】 设sin ()tan xf x x x e=⋅⋅,则()f x 是( ).A. 偶函数B. 无界函数C. 周期函数D. 单调函数. 【解】 因为 2x k ππ→+时, ()f x →∞,所以()f x 非有界即为无界函数.3、 基本初等函数 【掌握基本初等函数的性质及图形】 (反、对、幂、三、指)① 常数函数---y C =② 幂函数---y x μ= (μ为常数)例:21,y x y y x===③ 指数函数---x y a = (0,1a a >≠) ,x y e =④ 对数函数---log a y x = (0,1a a >≠) , ln y x =, lg y x = ⑤ 三角函数---sin ,cos ,tan y x y x y x===⑥ 反三角函数---arcsin ,arctan y x y x==4、 复合函数、反函数、初等函数 【了解反函数和隐函数的概念,理解复合函数及分段函数的概 念,了解初等函数的概念】① 复合函数 (),()[()y f u u x y f x ϕϕ==⇒=;f 为外层函数,ϕ称为内层函数.② 反函数 ()y y x =的反函数为1()x fy -=或1()y fx -=.【例】3y x x y =⇒=⇒=3y x =的反函数.【例】 sin xy e= 看作是由 ,sin uy e u x == 复合而成的复合函数.③ 初等函数:由六类基本初等函数经过有限次四则运算及有限次复合运算而得的用一个数学式子 表示的函数. 注意:分段函数一般不是初等函数。
微积分知识点总结(期末考研笔记)

微积分知识点总结(期末考研笔记)一、第一章:极限与连续第一节:函数1.什么是函数?未知变量x通过某种固定的对应关系确定唯一变量y,称y是x的函数2.什么是复合函数?内层变量导出中间函数的值域,中间函数的值域满足外层函数的定义域,则外层变量是内层变量的复合函数。
3.什么是反函数?能“反”的函数,正函数能由x确定唯一的y与之对应,反函数则要求由y能确定唯一的x与之对应!4.什么是基本初等函数?幂函数,指数函数,对数函数,三角函数,反三角函数通过四则运算把基本初等函数组合构成初等函数5.特殊函数特殊定义的函数:高斯函数,符号函数,狄利克雷函数第二节:极限1.极限定义是什么?●数列极限定义(ε--N),函数极限定义(ε--δ)、(ε--X)\large \epsilon:任意小的正数,可以是是函数值与极限值之差;也可以是数列项与极限值之差。
\large δ:是邻域半径。
2.极限的性质是什么?●唯一性极限存在必唯一。
从左从右逼近相同值。
●保号性极限两侧正负相同●有界性数列极限收敛,必有界,反之不成立;连续函数闭区间有界。
●列与子列同极限数列有极限,子列也存在相同极限;反之不成立。
●极限运算性质1、满足四则运算。
2、满足复合函数嵌套极限。
3、极限存在则左右极限相等。
●极限存在性质迫(夹)敛(逼)定理。
●两个重要极限x\to0 时,\frac{sinx}{x}=1;(1+x)^{1/x} 的1/x次方极限为e●几个特殊关系式●[0,\frac {\pi}{2} ] 时,sinx <x <tanx●x>0 时,\frac{x}{(x+1)} <ln(1+x) <x3.无穷小●什么是无穷小1、定义:自变量趋向某个边界时,f(x)\to 02、无穷小是函数变化极限值,而非确定具体值,即要多小,有多小,但不是0! 3、高阶、同阶、等价无穷小●常用的等价无穷小第三节:连续与间隔1.连续的定义1、该点有定义,且该点极限值等于函数值,则该处连续2、闭区间连续,左边界函数值等于右极限,区间内各点连续,右边界函数值等于左极限2.间断定义第一类间断点:可去间断点,跳跃间断点。
微积分的基础知识与运算

微积分的发展历程
微积分作为现代数学中重要的分支,在牛顿、莱 布尼茨等数学家的努力下逐渐发展成熟。它的应 用领域广泛,是解决现实问题的重要工具之一。
● 05
第五章 链式法则与微分中 值定理
链式法则的概念
链式法则描述了复合 函数的导数计算规则, 对于求解复杂函数的 导数具有重要作用。 通过链式法则,我们 可以更有效地计算复 合函数的导数,提高 求导的效率。
物理学
近似计算物理现象 解决实际问题
工程学
估算工程参数 优化设计方案
微分方程
是求解微分方程的重要工 具
积分中值定理的 概念
积分中值定理描述函 数在某一区间上的平 均值性质,其中有柯 西中值定理、勒贝格 积分中值定理等,为 理解函数性质提供重 要依据。
积分中值定理的应用
性质证明
用于证明函数的 性质
学习微积分的建议
坚持练习
掌握基本概念和 方法
理解应用场 景
将理论知识应用 到实践中
多练习计算
熟练运用微积分 技巧
多与他人交 流
加深理解
拓展学习
学习高阶微积分
掌握不定积分、定积分等 高级概念 深入理解微积分的推导和 应用
探索多元微积分
理解多元函数概念 学习多元微分、多元积分 等内容
应用微积分解决问题
计算复杂图形的面积
03 速度与加速度
通过微积分求解物体的运动特性
微积分的数值计算
复化梯形法
求定积分的数值 近似
牛顿-拉夫逊 插值
曲线的插值与逼 近
预处理法
提高数值解的精 度
龙贝格积分 法
加速定积分的收 敛速度
感谢观看
THANKS
微分中值定理的应用
微积分中的函数极限与连续性

微积分中的函数极限与连续性在微积分这门学科中,函数极限与连续性是两个极为重要的概念。
它们不仅是微积分理论的基础,也在解决各种实际问题中发挥着关键作用。
让我们先从函数极限说起。
想象一下,有一个函数 f(x),当 x 趋近于某个特定的值 a 时,函数 f(x) 的值会越来越接近一个确定的数 L ,那么我们就说函数 f(x) 在 x 趋近于 a 时的极限是 L 。
这里的“趋近”可以是从左边趋近,也可以是从右边趋近。
举个简单的例子,比如函数 f(x) =(x 1) /(x 1) ,当 x 趋近于1 时,分母和分子都趋近于 0 。
但是,如果我们直接把 x = 1 代入函数,会得到 0/0 这种不确定的形式。
然而,当 x 非常接近但不等于 1 时,比如 10001 或者 09999 ,我们会发现函数的值非常接近 1 。
所以,我们就说这个函数在 x 趋近于 1 时的极限是 1 。
函数极限的定义是非常严谨和精确的。
用数学语言来表述,就是对于任意给定的一个很小的正数ε ,都存在一个正数δ ,使得当 0 <|x a| <δ 时,|f(x) L| <ε 成立。
这个定义虽然看起来有点复杂,但它的核心思想就是说,只要 x 与 a 足够接近(但不等于 a ),那么 f(x) 与 L 的差距就可以任意小。
了解了函数极限,接下来谈谈函数的连续性。
一个函数在某一点处连续,直观地说,就是当自变量在这一点处有一个很小的变化时,函数值也会有一个相应的很小的变化,而且函数在这一点没有“跳跃”或者“断裂”。
比如说,常见的一次函数 y = x + 1 ,在其定义域内的每一点都是连续的。
因为无论 x 怎么变化,只要变化量很小,函数值 y 的变化也会很小,而且图像是一条连续不断的直线。
再看一个稍微复杂点的例子,函数 f(x) =|x| 。
在 x = 0 处,当 x从负数趋近于 0 时,f(x) 的值趋近于 0 ;当 x 从正数趋近于 0 时,f(x)的值也趋近于 0 ,并且 f(0) = 0 。
微积分第一章
高等数学教案、第一章 函数、极限与与连续本章将在分别研究数列的极限与函数的极限的基础上,讨论极限的一些重要性质以及运算法则,函数的连续性,闭区间上连续函数的性质。
具体的要求如下:1. 理解极限的概念(理解极限的描述性定义,对极限的N -ε、δε-定义可在学习过程中逐步加深理解,对于给出ε求N 或δ不作过高要求)。
2. 掌握极限四则运算法则。
3. 了解极限存在准则(夹逼准则和单调有界准则),会用两个重要极限求极限。
4. 了解无穷小、无穷大及无穷小的阶的概念.能够正确运用等价无穷小求极限。
5。
理解函数在一点连续的概念,理解区间内(上)连续函数的概念。
6. 了解间断点的概念,会求函数的间断点并判别间断点的类型。
7. 了解初等函数的连续性和闭区间上连续函数的性质(最大、最小值定理、零点定理、介值定理)。
第一章共12学时,课时安排如下绪论 §1.1、函数 §1.2初等函数 2课时 §1。
4数列极限及其运算法则 2课时 §1.4函数极限及其运算法则 2课时 §1。
4两个重要极限 无穷小与无穷大 2课时 §1.4函数的连续性 2课时 第一章 习题课 2课时绪论数学:数学是研究空间形式和数量关系的一门学科,数学是研究抽象结构及其规律、特性的学科.数学具有高度的抽象性、严密的逻辑性和应用的广泛性。
关于数学应用和关于微积分的评价:恩格斯:在一切理论成就中,未必再有像17世纪下叶微积分的微积分的发现那样被看作人类精神的最高胜利了。
如果在某个地方我们看到人类精神的纯粹的和唯一的功绩,那就正是这里.华罗庚:宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之迷,日用之繁,无处不用数学。
张顺燕:微积分是人类的伟大结晶,它给出了一整套科学方法,开创了科学的新纪元,并因此加强和加深了数学的作用。
……有了微积分,人类才有能力把握运动和过程;有了微积分,就有了工业革命,有了大工业生产,也就有了现代的社会。
一元微积分(第一章 函数、极限、连续)
第一章 函数、极限、连续重点:1、求函数的极限(最重要的方法是L ’P 法则)2、无穷小的比较3、考察分段函数在分段点的连续性4、间断点的判定及分类5、介值定理 一、函数1、函数的定义及表示法【理解函数的概念,掌握函数的表示法,会建立简单应用问题的函数关系式】 函数概念 ()y f x =函数的两要素 ⎧⎨⎩定义域对应规则函数的表示方法① 显函数: ()y f x =② 隐函数:由方程(,)0F x y =确定的函数()y y x =.例:1yy xe +=确定了()y y x =⇒01x y==.③ 参数方程表示的函数:由方程()()x x t y y t =⎧⎨=⎩确定的函数()y y x =.例:2ln(1)arctan x t y t⎧=+⎨=⎩ 确定了()y f x =.④ 积分上限函数: ()()xax f t dt Φ=⎰.例:2311()(1)3xx t dt x Φ==-⎰⑤ 概率表示的函数:()()F x P X x =≤, 其中X 为随机变量,x 为实数.⑥ 分段函数:自变量不同范围内用不同式子表示的一个函数.【例】 ,0()sin ,0a x x f x x x x +≥⎧⎪=⎨<⎪⎩ ; 1sin ,0()0,0x x f x x x ⎧≠⎪=⎨⎪=⎩ .如 A. 绝对值表示的函数 11111x x y x xx -≥⎧=-=⎨-<⎩ ;B. 极限表示的函数 2211()lim111nnn x x x f x x x x x x →∞⎧<-⎪=⋅==⎨+⎪->⎩; C. 其他形式 2022101()max{1,}12x x f x x xx ≤≤≤≤⎧==⎨<≤⎩ .10sgn()0010x y x x x >⎧⎪===⎨⎪-<⎩-------符号函数[]y x =--取整函数.2、函数的性质 【了解函数的有界性,单调性,周期性,奇偶性】①.有界性:()f x 在某区间I 内有定义,若存在0M >,对任意x I ∈,总有()f x M ≤, 则称()f x 在某区间I 内有界.否则称()f x 在某区间I 内无界.例:2111sin1,(0);arctan ,();,1,()2121xx x x x R x R xx e π≤≠≤∈≤<∈++. ②.单调性:()f x 在某区间I 内有定义,若12,x x I ∀∈,当12x x <时12()()f x f x ≤,就称()f x 单调上升;当12x x <时,12()()f x f x ≥,就称()f x 单调下降. 不含等号时称严格单增(或单减).③.奇偶性:若()()f x f x -=, 则称()f x 为偶函数,偶函数的图形关于y 轴对称; 若()()f x f x -=-,则称()f x 为奇函数,奇函数的图形关于原点对称.④.周期性:()()(0)f x T f x T +=≠. (主要是三角函数)【例1】讨论()ln(f x x =的奇偶性. 【奇函数】 【例2】 设sin ()tan xf x x x e=⋅⋅,则()f x 是( ).A. 偶函数B. 无界函数C. 周期函数D. 单调函数. 【解】 因为 2x k ππ→+时, ()f x →∞,所以()f x 非有界即为无界函数.3、 基本初等函数 【掌握基本初等函数的性质及图形】 (反、对、幂、三、指)① 常数函数---y C =② 幂函数---y x μ= (μ为常数)例:21,y x y y x===③ 指数函数---xy a = (0,1a a >≠) ,xy e =④ 对数函数---log a y x = (0,1a a >≠) , ln y x =, lg y x = ⑤ 三角函数---sin ,cos ,tan y x y x y x===⑥ 反三角函数---arcsin ,arctan y x y x==4、 复合函数、反函数、初等函数 【了解反函数和隐函数的概念,理解复合函数及分段函数的概 念,了解初等函数的概念】① 复合函数 (),()[()y f uu x y f x ϕϕ==⇒=;f 为外层函数,ϕ称为内层函数.② 反函数 ()y y x =的反函数为1()x fy -=或1()y fx -=.【例】3y x x y =⇒=⇒3y x =的反函数.【例】 sin xy e= 看作是由 ,sin uy e u x == 复合而成的复合函数.③ 初等函数:由六类基本初等函数经过有限次四则运算及有限次复合运算而得的用一个数学式子 表示的函数. 注意:分段函数一般不是初等函数。
大学数学-微积分-连续
详细描述
不定积分是微积分中的一个基本概念,它表示原函数在 某区间上的积分值。不定积分的结果是一个函数集合, 这些函数之间相差一个常数。不定积分具有线性性质, 即两个函数的和或差的积分等于它们各自积分的和或差 。此外,不定积分还具有积分常数性质,即在对函数进 行积分时,可以在积分结果中添加或减去任意常数。最 后,不定积分具有微分性质,即函数的微分与函数的积 分互为逆运算。
定积分的应用
总结词
定积分在解决实际问题中有着广泛的应 用,如求平面图形的面积、求曲线的长 度、计算变力沿直线所做的功等。
VS
详细描述
定积分在实际问题中有着广泛的应用。例 如,求平面图形的面积时,可以将图形分 成若干个小矩形,然后计算每个小矩形的 面积和,最后取极限得到整个图形的面积 。此外,定积分还可以用于求曲线的长度 、计算变力沿直线所做的功等问题。这些 应用都表明了定积分的实用性和重要性。
连续性在数学与其他学科中的应用
在物理学中,连续性的概念广泛应用于解决力学、热学、电磁学等问题,如物体运动轨迹的连续性、 温度变化的连续性等。
在经济学中,连续性被用于描述经济变量的变化规律和趋势,如价格、需求和供给等函数的连续性分析。
在计算机科学中,连续性的概念对于理解数据结构和算法设计具有重要意义,如连续存储和离散存储的 区别。
函数在点$x_0$处的左极限是指当$x to x_0$且$x < x_0$时,函数值的趋势;右极限 是指当$x to x_0$且$x > x_0$时,函数值的趋势。
连续函数极限的性质
唯一性
若函数在某点的极限存在,则 该极限值是唯一的。
有界性
若函数在某点的极限存在,则 该点的函数值是有限的。
局部有界性
一元微积分(第一章 函数、极限、连续)共13页文档
第一章 函数、极限、连续重点:1、求函数的极限(最重要的方法是L ’P 法则)2、无穷小的比较3、考察分段函数在分段点的连续性4、间断点的判定及分类5、介值定理 一、函数1、函数的定义及表示法【理解函数的概念,掌握函数的表示法,会建立简单应用问题的函数关系式】 函数概念 ()y f x =函数的两要素 ⎧⎨⎩定义域对应规则函数的表示方法 ① 显函数: ()y f x =② 隐函数:由方程(,)0F x y =确定的函数()y y x =.例:1yy xe +=确定了()y y x =⇒01x y==.③ 参数方程表示的函数:由方程()()x x t y y t =⎧⎨=⎩确定的函数()y y x =.例:2ln(1)arctan x t y t ⎧=+⎨=⎩确定了()y f x =.④ 积分上限函数: ()()xax f t dt Φ=⎰.例:2311()(1)3xx t dt x Φ==-⎰⑤ 概率表示的函数:()()F x P X x =≤, 其中X 为随机变量,x 为实数.⑥ 分段函数:自变量不同范围内用不同式子表示的一个函数.【例】 ,0()sin ,0a x x f x x x x +≥⎧⎪=⎨<⎪⎩ ; 1sin ,0()0,0x x f x x x ⎧≠⎪=⎨⎪=⎩ . 如 A. 绝对值表示的函数 11111x x y x xx -≥⎧=-=⎨-<⎩ ;B. 极限表示的函数 2211()lim 0111n nn xx x f x x x x x x →∞⎧<-⎪=⋅==⎨+⎪->⎩; C. 其他形式 2022101()max{1,}12x x f x x xx ≤≤≤≤⎧==⎨<≤⎩ .10sgn()0010x y x x x >⎧⎪===⎨⎪-<⎩-------符号函数[]y x =--取整函数.2、函数的性质 【了解函数的有界性,单调性,周期性,奇偶性】①.有界性:()f x 在某区间I 内有定义,若存在0M >,对任意x I ∈,总有()f x M ≤, 则称()f x 在某区间I 内有界.否则称()f x 在某区间I 内无界.例:2111sin1,(0);arctan ,();,1,()2121xx x x x R x R xx eπ≤≠≤∈≤<∈++. ②.单调性:()f x 在某区间I 内有定义,若12,x x I ∀∈,当12x x <时12()()f x f x ≤,就称()f x 单调上升;当12x x <时,12()()f x f x ≥,就称()f x 单调下降. 不含等号时称严格单增(或单减).③.奇偶性:若()()f x f x -=, 则称()f x 为偶函数,偶函数的图形关于y 轴对称; 若()()f x f x -=-,则称()f x 为奇函数,奇函数的图形关于原点对称.④.周期性:()()(0)f x T f x T +=≠. (主要是三角函数)【例1】讨论()ln(f x x =的奇偶性. 【奇函数】 【例2】 设sin ()tan xf x x x e=⋅⋅,则()f x 是( ).A. 偶函数B. 无界函数C. 周期函数D. 单调函数. 【解】 因为 2x k ππ→+时, ()f x →∞,所以()f x 非有界即为无界函数.3、 基本初等函数 【掌握基本初等函数的性质及图形】 (反、对、幂、三、指)① 常数函数---y C =② 幂函数---y x μ= (μ为常数)例:21,y x y y x===③ 指数函数---x y a = (0,1a a >≠) ,xy e =④ 对数函数---log a y x = (0,1a a >≠) , ln y x =, lg y x = ⑤ 三角函数---sin ,cos ,tan y x y x y x===⑥ 反三角函数---arcsin ,arctan y x y x==4、 复合函数、反函数、初等函数 【了解反函数和隐函数的概念,理解复合函数及分段函数的概 念,了解初等函数的概念】① 复合函数 (),()[()y f uu x y f x ϕϕ==⇒=;f 为外层函数,ϕ称为内层函数.② 反函数 ()y y x =的反函数为1()x fy -=或1()y fx -=.【例】3y x x y =⇒=⇒3y x =的反函数.【例】 sin xy e= 看作是由 ,sin uy e u x == 复合而成的复合函数.③ 初等函数:由六类基本初等函数经过有限次四则运算及有限次复合运算而得的用一个数学式子 表示的函数. 注意:分段函数一般不是初等函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x cos( x ) 1, 2
对任意的, 当 0时,
有 sin ,
x 当x 0时, y 0. 故 y 2 sin x , 2 即函数 y sin x对任意 x (,)都是连续的.
10
二、函数的间断点
函数 f ( x )在点 x0处连续必须满足的三个条件 :
x x0
意义 1.极限符号可以与函数符号互换;
2.变量代换( u ( x ))的理论依据 .
ln(1 x ) . 例9 求 lim x 0 x
解 原式 lim ln(1 x )
x 0 1 x
ln[lim(1 x ) ] ln e 1. x 0
1 x
24
ex 1 . 例10 求 lim x 0 x
20
第二部分 连续函数的运算性质 与初等函数的连续性 一、四则运算的连续性
定理1
若函数 f ( x ), g ( x )在点 x0处连续, f ( x) 则 f ( x ) g ( x ), f ( x ) g ( x ), ( g ( x0 ) 0 ) g( x ) 在点 x0处也连续.
x 0 x 0
lim f ( x ) lim( x 2) 2 f (0),
x 0 x 0
右连续但不左连续 ,
故函数 f ( x )在点 x 0处不连续.
8
4.连续函数与连续区间
在区间上每一点都连续的函数,叫做在该区间上 的连续函数,或者说函数在该区间上连续.
如果函数在开区间 (a , b)内连续, 并且在左端点 x a处右连续, 在右端点 x b处左连续, 则称 函数 f ( x )在闭区间 [a , b]上连续.
解
令 e x 1 y,
则 x ln(1 y ),
当x 0时, y 0.
y lim 原式 lim y0 y 0 ln(1 y )
同理可得
25
1 ln(1 y )
1 y
1.
ax 1 lim ln a . x 0 x
三、初等函数的连续性
★ 三角函数及反三角函数在它们的定义域内是
解 f (0 0) 0,
f (0 0) ,
o x
x 0为函数的第二类间断点 .
这种情况称为无穷间 断点.
16
1 例7 讨论函数 f ( x ) sin 在 x 0处的连续性. x 解 在x 0处没有定义,
1 且 lim sin 不存在. x0 x
y sin 1 x
则有 lim f [( x )] f (a ) f [ lim ( x )].
证
f (u)在点 u a连续, 0, 0, 使当 u a 时,
恒有 f (u) f (a ) 成立.
又 lim ( x ) a, x x0 对于 0, 0, 使当 0 x x0 时,
又 f (0) 0,
lim f ( x ) f (0), x 0
由定义2知
函数 f ( x )在 x 0处连续.
6
3.单侧连续
若函数f ( x )在(a , x 0 ]内有定义, 且f ( x 0 0) f ( x 0 ), 则称f ( x )在点x 0处左连续; 若函数f ( x )在[ x 0 , b)内有定义, 且f ( x 0 0) f ( x 0 ), 则称f ( x )在点x 0处右连续.
连续函数的图形是一条连续而不间断的曲线. 例如,
9
多项式函数在区间, )内是连续的 ( .
例3 证明函数 y sin x在区间( ,)内连续. 证
任取 x (,),
x x cos( x ) 2 2 x 则 y 2 sin . 2
y sin( x x ) sin x 2 sin
一元函数微积分与 Mathematics Laboratory 无穷级数
阮小娥博士 阮小娥
Sept. 2008
第一章 微积分的理论基础
第五节 连续函数(3课时)
• 函数的连续性概念与间断点的分类 • 连续函数的运算性质与 初等函数的连续性 • 闭区间上连续函数的性质 • 小结与思考题
作业: Page66. 6,7,8,10(2)(3), 11(1)(2)
0, 0, 使当 x x0 时, 恒有 f ( x ) f ( x0 ) .
5
1 x sin , x 0, 例1 试证函数 f ( x ) 在x 0 x 0, x 0, 处连续. 1 证 lim x sin 0, x0 x
y
解
f (0 0) 0,
f (0 0) 1,
f (0 0) f (0 0),
x 0为函数的跳跃间断点 .
12
o
x
2.可去间断点如果 f ( x )在点 x0处的极限存在 ,
但 lim f ( x ) A f ( x0 ), 或 f ( x )在点 x0处无定 x x
定理
函数 f ( x)在 x0 处连续
函数 f ( x)在 x0处既左连续又右连续.
7
x 2 , x 0, 例2 讨论函数 f ( x ) 在 x 0处的 x 2, x 0, 连续性.
解 lim f ( x ) lim( x 2) 2 f (0),
0
义则称点 x0为函数 f ( x )的可去间断点 .
例5 讨论函数
2 x , 0 x 1, f ( x ) 1, x 1 1 x , x 1, 在x 1处的连续性 .
y
2 1
y 1 x
y2 x
1
o
x
13
y
解
f (1) 1,
2
f (1 0) 2,
仅在x=0处连续, 其余各点处处间断.
18
★
1, 当x是有理数时, f ( x) 1, 当x是无理数时,
在定义域 R内每一点处都间断, 但其绝对值处 处连续. 判断下列间断点类型:
y
y f x
x1
o
x2
x3
x
19
例8 当a取何值时,
cos x , x 0, 函数 f ( x ) 在 x 0处连续. a x , x 0, 解 f ( 0) a ,
1
第一部分 函数的连续性概念 与间断点的分类
y y
o y
x0
x
o y
x0
x
o o 2
x0
x
x
一、函数的连续性
1.函数的增量
设函数 f ( x)在U ( x 0 )内有定义, x U ( x 0 ), x x x 0 , 称为自变量在点 x 0的增量.
y f ( x ) f ( x0 ), 称为函数 f ( x )相应于x的增量.
讨论不同值,
(均在其定义域内连续 )
连续的.
★ 指数函数 y a x
(a 0, a 1)
在(,)内单调且连续 ;
★ 对数函数 y loga x
(a 0, a 1)
在(0,)内单调且连续;
26
★
y x a log
ax
y a , u loga x.
u
在(0, )内连续,
恒有 ( x ) a u a 成立. 即 0, 0, 使当0 x x 时, 0
f ( u) f (a ) f [ ( x )] f (a ) 成立.
23
lim f [ ( x )] f (a ) f [ lim ( x)]. x x0
4
定义 2
设函数 f ( x ) 在U ( x 0 ) 内有定义,如果函
数 f ( x ) 当 x x0 时的极限存在,且等于它在点
x 0 处的函数值 f ( x 0 ) ,即
lim f ( x ) f ( x0 ) x x
0
那末就称函数 f ( x ) 在点x 0 连续.
" " 定义 :
x 0
lim [ f ( x 0 x ) f ( x 0 )] 0 ,那末就称函数
f ( x ) 在点 x 0 连续, x 0 称为 f ( x ) 的连续点.
设 x x0 x,
y f ( x ) f ( x0 ),
x 0 就是 x x0 , y 0 就是 f ( x ) f ( x0 ).
(1) f ( x )在点x0处有定义;
( 2) lim f ( x )存在;
x x 0
( 3) lim f ( x ) f ( x 0 ).
x x0
如果上述三个条件中只 要有一个不满足 则称 , 函数 f ( x )在点 x0处不连续(或间断), 并称点 x0为 f ( x )的不连续点(或间断点).
y
2 1
o
1
x
跳跃间断点与可去间断点统称为第一类间断点.
特点 函数在点x0处的左、右极限都存在 .
15
3.第二类间断点 如果 f ( x )在点 x0处的左、
右极限至少有一个不存在, 则称点 x0为函数 f ( x )的第二类间断点 . 1 例6 讨论函数 f ( x ) x , x 0,在x 0处的连续性. x , x 0, y
x 0为第二类间断点 .
这种情况称为的振荡间 断点.
注意 不要以为函数的间断点只是个别的几个点.
17
★ 狄利克雷函数
1, 当x是有理数时, y D( x ) 0, 当x是无理数时,
