四、 材料力学正应力分析
材料力学应力

材料力学应力材料力学是研究材料内部受力和变形的科学,其中应力是一个非常重要的概念。
应力是单位面积上的力,是描述材料内部受力状态的物理量。
在材料力学中,应力可以分为正应力、剪切应力等不同类型,它们在材料的力学性能和应用中起着至关重要的作用。
首先,正应力是指垂直于材料截面的力对单位面积的作用。
正应力可以分为拉伸应力和压缩应力两种类型。
拉伸应力是指材料受到拉力作用时产生的应力,而压缩应力则是指材料受到压力作用时产生的应力。
正应力的大小可以通过应力=力/面积来计算,单位通常为帕ascal(Pa)或兆帕(MPa)。
正应力的大小和方向决定了材料的变形和破坏性能,因此在工程设计和材料选择中需要进行合理的评估和分析。
其次,剪切应力是指平行于材料截面的力对单位面积的作用。
剪切应力是材料内部的相对位移所引起的应力,它可以导致材料的剪切变形和破坏。
剪切应力的大小和方向也是影响材料性能的重要因素,通常可以通过应力=剪切力/截面积来计算,单位同样为帕ascal(Pa)或兆帕(MPa)。
在材料的加工和使用过程中,剪切应力会对材料的强度和韧性产生重要影响,因此需要进行有效控制和管理。
在实际工程中,材料力学应力的研究和应用是非常广泛的。
例如,在建筑结构设计中,需要考虑材料的正应力和剪切应力对结构的影响,以确保结构的安全和稳定;在机械制造中,需要对材料的应力进行分析和计算,以保证零部件的可靠性和耐久性。
因此,深入理解材料力学应力的概念和特性,对于工程领域具有重要的意义。
综上所述,材料力学应力是描述材料内部受力状态的重要物理量,包括正应力和剪切应力两种类型。
正应力和剪切应力的大小和方向对材料的性能和应用具有重要影响,在工程设计和材料选择中需要进行合理的评估和分析。
通过对材料力学应力的深入研究和应用,可以推动工程技术的发展和进步,为社会经济的发展做出贡献。
材料力学应力状态分析

材料力学应力状态分析材料力学是研究物质内部力学性质和行为的学科,其中应力状态分析是材料力学中的重要内容之一。
应力状态分析是指对材料内部受力情况进行分析和研究,以揭示材料在外力作用下的应力分布规律和应力状态特征,为工程设计和材料选用提供依据。
本文将从应力状态的基本概念、分类和分析方法等方面展开讨论。
首先,我们来介绍一下应力状态的基本概念。
应力是指单位面积上的力,是描述物体内部受力情况的物理量。
在材料力学中,通常将应力分为正应力和剪应力两种基本类型。
正应力是指垂直于截面的应力,而剪应力是指平行于截面的应力。
在实际工程中,材料往往同时受到多种应力的作用,因此需要对应力状态进行综合分析。
其次,我们将对应力状态进行分类。
根据应力的作用方向和大小,可以将应力状态分为拉应力状态、压应力状态和剪应力状态三种基本类型。
拉应力状态是指材料内部受到拉力作用的状态,压应力状态是指材料内部受到压力作用的状态,而剪应力状态是指材料内部受到剪切力作用的状态。
这三种应力状态在工程实践中都具有重要的意义,需要我们进行深入的分析和研究。
接下来,我们将介绍应力状态分析的方法。
应力状态分析的方法有很多种,常用的有应力分析法、应变分析法和能量方法等。
应力分析法是通过应力分布的计算和分析来揭示应力状态的特征,应变分析法则是通过应变分布的计算和分析来揭示应力状态的特征,而能量方法则是通过能量原理和平衡条件来揭示应力状态的特征。
这些方法各有特点,可以根据具体情况选择合适的方法进行分析。
最后,我们需要注意的是,在进行应力状态分析时,需要考虑材料的本构关系、边界条件和载荷情况等因素,以确保分析结果的准确性和可靠性。
同时,还需要注意应力状态分析的结果对工程实践的指导意义,以便更好地指导工程设计和材料选用。
总之,材料力学应力状态分析是一个复杂而重要的课题,需要我们进行深入的研究和分析。
只有深入理解应力状态的特征和规律,才能更好地指导工程实践,为实际工程问题的解决提供科学依据。
实验四:弯曲正应力电测实验

实验四:弯曲正应力电测实验一、实验目的和要求1.学习使用应变片和电阻应变仪测定静态应力的基本原理和方法。
2.用电测法测定纯弯曲钢梁横截面不同位置的正应力。
3.绘制正应力沿其横截面高度的的分布图,观察正应变(正应力)分布规律,验证纯弯曲梁的正应力计算公式。
二、实验设备、仪器和试件1.CLDS-2000型材料力学多功能实验台。
2.YJZ —8型智能数字静态电阻应变仪。
3.LY —5型拉力传感器。
4.直尺和游标卡尺。
三、实验原理和方法(1)理论公式:本实验的测试对象为低碳钢制矩形截面简支梁,实验台如图4-1所示,加载方式如图4-2所示。
图4-1 图4-2由材料力学可知,钢梁中段将产生纯弯曲,其弯矩大小为c PM 2∆=(1) 横截面上弯曲正应力公式为ZI My=σ (2) 式中y 为被测点到中性轴z 的距离,I z 为梁截面对z 轴的惯性矩。
123bh I Z =(3)横截面上各点正应力沿截面高度按线性规律变化,沿截面宽度均匀分布,中性轴上各点的正应力为零。
截面的上、下边缘上各点正应力为最大,最大值为WM =max σ。
(2)实测公式:实验采用螺旋推进和机械加载方法,可以连续加载,荷载大小可由电子测力仪读出。
当增加压力P ∆时,梁的四个点受力分别增加作用力2/P ∆,如图4-2所示。
为了测量梁纯弯曲时横截面上应变分布规律,在梁的纯弯曲段侧面布置了5片应变片,如4-2所示,各应变片的粘贴高度见梁上各点标注。
此外,在梁的上表面沿横向粘贴了第6片应变片,用以测定材料的泊松比μ;在梁的端部上表面零应力处粘贴了第7片温度补偿应变片,可对以上各应变片进行温度补偿。
在弹性范围内,如果测得纯弯曲梁在纯弯曲时沿横截面高度上的轴向应变,则由单向应力状态的胡克定律,即:σε=E (4) 由上式可求出各点处的应力实验值。
将应力实验值σε=E 与理论值ZI My=σ进行比较,以验证弯曲正应力公式。
如果测得应变片4和6的应变满足μεε=46/则证明梁弯曲时近似为单向应力状态,即梁的纵向纤维间无挤压的假设成立。
材料力学-应力分析、强度理论

点的研究常采用分析单元体的方法
Down Up
σy y
空间一般应力状态
y
σy
A
σx x
τxy
平面一般应力状态
τyz
τxz
σx
τxy
x
z σz
7
Down Up
主平面:若单元体上某个平面上的切应力为零,
则该平面称为主平面。
而主平面上的正应力称为主应力。
主单元体:所有面均为主平面的单元体。
σ3 σ2
σ1 σ2
例如:拉(压)杆横截面上各点的应力状态
P
P
k
σ
k
P
FN =σA
σ= FN/A
10
分析薄壁圆筒受内压时的应力状态
σ’’ m n
n
σ’
k σ’ p
Dp
p
σ’’ l
πD
2
m
(D
)
n
4
pD
4
n
2
plD (2l
)
dq
Oq
p
D
t
pD
2
直径平面
pD
2
1
3 p 0 11
例7.2 圆球形薄壁容器,壁厚为δ,内径为D,
切应力2个下标的意义:
第1个下标表示切应力所 τyx
< 0 σy
在的面;
σx
第2个下标表示切应力实际 沿那个坐标轴的方向。
x
τxy > 0
18
7.3 二向应力状态分析----解析法
若图示单元体上的应力
y
σx、 σy 、τxy
ττyxxy
均为已知,
则由平衡方程可求得 σx 斜角为α的斜截面上
正应力测定实验报告

正应力测定实验报告正应力测定实验报告一、引言正应力测定是材料力学中的重要实验之一,通过测定材料在受力状态下的正应力变化,可以了解材料的力学性能及其变化规律。
本实验旨在通过实验方法测定不同材料在不同受力状态下的正应力,并分析其结果。
二、实验原理正应力是指在材料内部某一点处,垂直于该点处截面的力的作用,通常用σ表示。
正应力的单位为帕斯卡(Pa)。
正应力测定实验中常用的方法有拉伸试验、压缩试验和剪切试验等。
三、实验步骤1. 准备不同材料的试样,如金属材料、塑料材料等。
2. 将试样放置在拉伸试验机或压缩试验机中,并调整好试样的位置和夹持方式。
3. 施加适当的拉伸或压缩力,开始实验。
4. 在实验过程中,记录下试样的变形情况和施力情况。
5. 根据实验数据计算出试样在不同受力状态下的正应力。
四、实验结果与分析通过实验测得的数据,我们可以计算出试样在不同受力状态下的正应力。
通过对不同材料的实验结果进行比较分析,可以得出以下结论:1. 材料的强度差异:不同材料在相同受力状态下的正应力会有所不同,这是由于材料的强度不同所致。
例如,金属材料的强度通常较高,其正应力也会相应较大。
2. 受力方式对正应力的影响:不同受力方式下的正应力也会有所差异。
例如,在拉伸试验中,试样的正应力主要集中在试样的中心位置,而在压缩试验中,试样的正应力主要集中在试样的表面。
3. 应力-应变曲线的特征:通过实验数据可以绘制出应力-应变曲线,该曲线反映了材料在受力状态下的变形规律。
根据曲线的形状可以判断材料的强度、韧性等力学性能。
五、实验误差分析在实验过程中,由于各种因素的影响,可能会产生一定的误差。
例如,试样的准备不均匀、试验设备的精度限制以及操作人员的技术水平等。
因此,在进行实验结果分析时,需要考虑这些误差对结果的影响,并进行相应的修正和讨论。
六、实验的意义与应用正应力测定实验是材料力学研究中的重要实验之一,其结果可以为材料的设计、制造和使用提供重要的参考依据。
材料力学中正应力和切应力方向

材料力学中正应力和切应力方向In materials mechanics, stress is a fundamental concept that helps us understand how materials deform and fail under various conditions. Stress can be divided into two main components: normal stress (or normal force) and shear stress (or tangential force). Normal stress acts perpendicular to the surface of a material, while shear stress acts parallel to the surface. Understanding the direction of normal and shear stresses is crucial for predicting the behavior of materials in different situations.在材料力学中,应力是一个基本的概念,帮助我们了解材料在不同条件下是如何变形和破坏的。
应力可以分为两个主要组成部分:正应力(或法向力)和切应力(或切向力)。
正应力作用垂直于材料表面,而切应力作用平行于表面。
了解正应力和切应力的方向对于预测材料在不同情况下的行为至关重要。
Normal stress, also known as tensile or compressive stress, is caused by forces acting perpendicular to the surface of a material. When a force is applied in a direction parallel to the surface, it results in shear stress. Normal stress causes a material to elongate or compressalong the direction of the applied force, while shear stress leads to deformation in the form of slipping or sliding between layers of material. The direction of normal and shear stresses can have a significant impact on how materials behave under different loadsand environmental conditions.正应力,也称为拉伸或压缩应力,是由作用在材料表面垂直方向的力引起的。
应力与应变分析材料力学

(
20)sin
60
o
单位:sM" Pa
t
a
30
2
40
sin
60
o
(
20
)cos60o
20.3MPa
2)ss'''
30 2
40
30 40 2
2
202
35.3MPa 45.3MPa
s1 s' 35.3MPa ,s 2 0,s 3 s'' 45.3MPa
tg2a
0
20 30 40
a0 14.9o,主单元体如上
第一节 应力状态的概念
应力与应变分析
一、一点的应力状态
1.一点的应力状态:通过受力构件一点处各个不同截面
上的应力情况。
2.研究应力状态的目的:找出该点的最大正应力和剪应力
数值及所在截面的方位,以便研究构件破坏原因并进行失效分 析。
二、研究应力状态的方法—单元体法
1.单元体:围绕构件内一所截取的微小正六面体。
t—使微元产生顺时针转动趋势者为正,反之为负
3.主应力及其方位:
①由主平面定义,令t
=0,得:
tan 2a0
2t xy sx sy
可求出两个相差90o的a0值,对应两个互相垂直主平面。
②令
ds a da
0
得: tan 2a0
2t xy sx s
y
即主平面上的正应力取得所有方向上的极值。
③主应力大小:
sy z
Z sz
应力与应变分析
tzy tzx
txy
tyx
tyz
txz
O
txy
sx
工程力学(静力学与材料力学)习题及答案 )-正应力分析
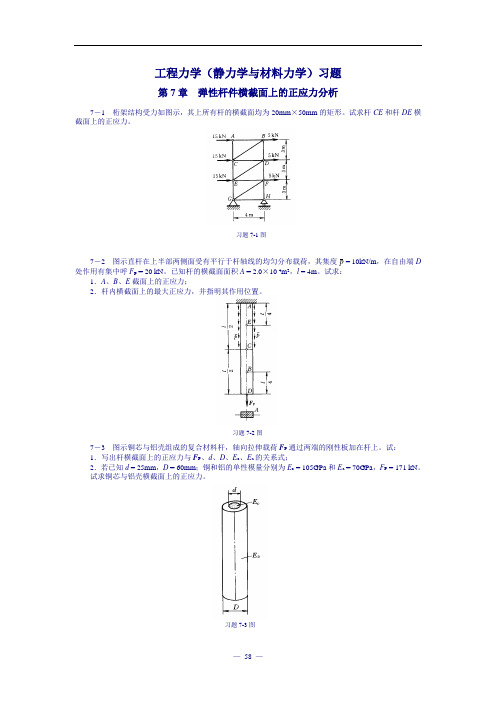
习题7-1图习题7-2图 习题7-3图工程力学(静力学与材料力学)习题第7章 弹性杆件横截面上的正应力分析7-1 桁架结构受力如图示,其上所有杆的横截面均为20mm ×50mm 的矩形。
试求杆CE 和杆DE 横截面上的正应力。
7-2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷,其集度p = 10kN/m ,在自由端D 处作用有集中呼F P = 20 kN 。
已知杆的横截面面积A = 2.0×10-4m 2,l = 4m 。
试求:1.A 、B 、E 截面上的正应力;2.杆内横截面上的最大正应力,并指明其作用位置。
7-3 图示铜芯与铝壳组成的复合材料杆,轴向拉伸载荷F P 通过两端的刚性板加在杆上。
试:1.写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式;2.若已知d = 25mm ,D = 60mm ;铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ,F P = 171 kN 。
试求铜芯与铝壳横截面上的正应力。
习题7-4图 习题7-5图 习题7-6图习题7-7图 7-4 图示由铝板钢板组成的复合材料柱,纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。
试:1.导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式;2.已知F P = 385kN ;E a = 70GPa ,E s = 200GPa ;b 0 = 30mm ,b 1 = 20mm ,h = 50mm 。
求铝板与钢板横截面上的最大正应力。
7-5 从圆木中锯成的矩形截面梁,受力及尺寸如图所示。
试求下列两种情形下h 与b 的比值:1.横截面上的最大正应力尽可能小;2.曲率半径尽可能大。
7-6 梁的截面形状为正方形去掉上、下角,如图所示。
梁在两端力偶M z 作用下发生弯曲。
设正方形截面时,梁内最大正应力为0σ;去掉上、下角后,最大正应力变为0max σσk =,试求:1.k 值与h 值之间的关系;2.max σ为尽可能小的h 值,以及这种情形下的k 值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
h
H
b
与应力分析相关的截面图形几何性质
小鸟
与 应 力 分 析 相 关 的 截 面 图 形 几 何 性 质
平面弯曲时梁横截面上的正应力
1、平面弯曲的概念 梁的对称面:梁的横截面具有 对称轴,所有相 同的对称轴组成 的平面。 形心主轴平面:所有相同的形 心主轴组成的平 面。 平面弯曲:所有外力都作用在梁 的同一主轴平面内, 梁的轴线在该平面中 弯曲成曲线。
第4章
弹性杆件横截面上的 正应力分析
第4章 弹性杆件横截面上的正应力分析
1、与应力分析相关的截面图形几何性质 2、平面弯曲时梁横截面上的正应力 3、斜弯曲时梁横截面上的正应力 4、弯矩与轴力同时作用时杆件横截面上的正应力
5、基于最大正应力的强度计算
与应力分析相关的截面图形几何性质
1、横截面面积 常见的横截面有: 矩形—— A = h×b ; 圆形—— A = πR² ; 2、静矩、形心 截面面积对轴的矩称为静矩:S Y
平面弯曲时梁横截面上的正应力
例题4-2 受均布荷载简支梁如图,已知梁的截面为矩形 b=20mm;h=30mm;q=10kN/m;l=450mm.试求最大弯矩截 面B上1、2两点的正应力。
q A l/2 C B l/2 z 1 h/4 b y
2 h
平面弯曲时梁横截面上的正应力
解:1、作梁的内力图,确定最大弯矩及位置 MZB = q l² / 8; 2、计算正应力 1点的正应力:
max
σmax+
c
σmax ˉ
弯矩和轴力同时作用时杆件横截面上的正应力 2、计算闭口链环直段部分横截面上最大 应力,受力如图:横截面上只有拉应力。
FN 4 FN 3 .5 7 M P a ; 2 A d
800N
800N 400N 400N
比较两种形式链环的正应力大小相差近 22倍。
ΔA
z
y
σx
x
M y 得正应力公式: z Iz
z
正应力与截面上弯矩、中性轴距离成正比;
与截面的惯性矩成反比。应力分布如图:
平面弯曲时梁横截面上的正应力
d、中性轴在横截面上的位置 中性轴通过横截面的形心,并且垂直于形心主轴。 e、最大正应力公式与弯曲截面模量 对于横截面上正应力最大值
max
c、应用静力方程确定正应力公式 由
y
dA y M
A x
z
( A
E E ydA ) y
A
y 2 dA M z
z ΔA
y
σx
x
由 E y 2 dA M z A
E
z
Mz Iz
平面弯曲时梁横截面上的正应力
y
E E Mz y 将 带人公式 Iz
96.4
x
位置在梁的上边缘处。
思考:对于脆性材料,极限拉伸应力小于极限压缩应力,
设置上下非对称的横截面并且如此放置,是否最大限 度地发挥了材料的强度潜力?
1
50
σmax +
150
斜弯曲时梁横截面上的正应力
1、产生斜弯曲的加载条件 当梁的外力平面与梁的轴线变形平面不共面时,这种弯曲 称斜弯曲。如图:
800N 800N
21mm
800N
800N
弯矩和轴力同时作用时杆件横截面上的正应力 解:1、计算开口链环直段部分横截面上
最大应力,受力如图;横截面上弯矩:
800N 800N
M
z
8 0 0 1 5 1 0 3 1 2 ( N m );
800N
Mz
800N
横截面上正应力(如图所示)
M FN W A 32 12 4 800 77.8 MPa; 3 -6 2 -6 12 10 12 10 M FN max W A 32 12 4 800 63.6 MPa; 3 6 2 6 12 10 12 10
Wz
D3
32
(1 4 );
d ; D
平面弯曲时梁横截面上的正应力
f、梁平面弯曲后轴线曲率的计算公式
1
Mz EI z
公式表明梁的轴线弯曲后的曲率与弯矩成正比,与弯曲刚度 成反比。 3、弯曲正应力公式的应用与推广
max
M z y max Mz Iz Wz
a、梁上最大正应力位置的判定 需要考虑弯矩分布;横截面形状等因素; b、纯弯曲正应力公式可以推广到横向弯曲 纯弯曲正应力公式在横向弯曲也是近似适用的。
1
h/4
b
为压缩正应力
平面弯曲时梁横截面上的正应力
例题4-3 丁字截面简支梁受力如图,已知梁的参数:
FP 32kN; l 2m; 形心坐标 yc 96.4mm ; I z 1.02108 mm4
试求最大弯矩截面上的最大拉应力和最大压应力。
y
50
A
l/2
FP B
l/2
C
z
200
96.4
3
y
z b
y
h
b、圆形截面的惯性矩
IY I Z
d
4
z
;
y
d
64
C、圆环截面的惯性矩
d Iy Iz (1 4 ); ; 64 D
D 4
z
d
D
与应力分析相关的截面图形几何性质
d、圆形截面的极惯性矩
IP
d 4
32
;
e、圆环截面的极惯性矩
IP
d 4
32
(1 4 );
FP2
z
FP1
变形平面
y
合力作用平面
斜弯曲时梁横截面上的正应力
2、叠加法确定斜弯曲时横截面上的正应力 当梁的受到外力作用在竖直平面和水平面同时弯曲,梁横 截面上的正应力可以应用叠加法确定。如图:
y y
σmax +
C C
z
z
σmax ˉ
My My M M _ 其最大正应力: max z ; max ( z ); Wz Wy Wz Wy
M z y max M z Iz Wz
σmax
σmax
其中 Wz = Iz / ymax 称为弯曲截面系数;
平面弯曲时梁横截面上的正应力
弯曲截面系数: Wz = Iz /ymax ;
*矩形截面的弯曲截面系数:
Wz = b h² /6;
*圆形截面的弯曲截面系数:
*圆环截面的弯曲截面系数
Wz = π d³ / 32 ;
其中轴力和弯矩将使梁横截面产生正应力:
max
FP
Mz Mz
M FN M FN ; max ( ) ; W A W A
FP
弯矩和轴力同时作用时杆件横截面上的正应力 例4-5 图示开口链环由直径d=12mm的园钢制作而成。 试求: 1)、链环直段部分横截面上最大拉应力和最大压应力; 2)、当链环焊接成闭口状态应力如何?
A
FP
l/2
C B
l/2
Fq
+ x
-
M
Fpl/4 + x
位置在梁的下边缘处 最大压缩正应力:
max M z ymax 16103 96.4 103 6 15 . 12 10 Pa 8 3 4 Iz 1.0210 (10 )
50
y z
200
σmax ˉ
MZ
2、纯弯曲时梁的正应力分析 纯弯曲梁的正应力分析需要三个步骤: 应 应 应 变 平面假定 物性关系 静力方程 力 力 变 公 分 分 形 式 布 布
平面弯曲时梁横截面上的正应力
a、应用平面假设确定应变分布 1) 弯曲梁变形后,梁表面的纵向线弯曲,截面上面缩短、 下面伸长、中间长度未变化。根据外表面线条可以确定横截 面上面受到压应力;下面受到拉应力;而中间没有应力。我
SZ
b h
R
zdA A z ; ydA A y ;
A i Ci A i Ci
图形几何形状的中心称形心:YC
ZC
S Z A S Y A
A
ydA A
A y
i
Ci
Ai
i Ci
; ;
zdA A Z
A
A
Ai
与应力分析相关的截面图形几何性质
3、惯性矩、极惯性矩、惯性半径 惯性矩---IY IZ
y
MAy FA1 z FQ My 2FP!l y MAz z FQ Mz FP2l FA2 FP2
FP1 x x
x
M y max Wy Wy
⊕ ⊕ ⊕ ⊕ ⊕
M 6 2 FP1l 6 FP 2l z max 9.98MPa; 2 2 Wz hb bh M z max ) 9.98MPa; Wz
们把中间未伸长的一层称为中性层,中性层与横截面的交线
称为中性轴。
M M
中性轴
平面弯曲时梁横截面上的正应力
2)梁弯曲时的平面假设 梁变形后周边表面的横向线仍然是直 线,且垂直于纵向线。我们假定梁的横截 面在变形前后仍然保持为平面,只是相对 转过一个角度 dθ 。 3)沿梁横截面高度方向正应力表达式:
⊕ ⊕ ⊕
x
_ max
(
M y max
A
A
σmax +
x
⊖ ⊖ ⊖ ⊖ ⊖
Mz
⊖ ⊖
x
My
⊖
B
B
