062三维各向异性稳态渗流
悬挂式止水帷幕对基坑降水的影响(1)

第20卷第4期2006年8月土 工 基 础Soil Eng.and FoundationVol.20No.4Aug.2006悬挂式止水帷幕对基坑降水的影响冯晓腊1,谢武军1,卢智强23,王超峰(1.中国地质大学工程学院,湖北武汉430074;2.中铁隧道集团,河南洛阳)摘 要:在广泛分析目前深基坑降水的设计计算理论和施工的基础上,建立了三维渗流的有限元模型,编制了三维有限元计算程序,并以武汉长江隧道武昌盾构井深基坑降水工程为例进行计算。
通过将有无悬挂式帷幕两种工况的水头降深计算结果与实际存在悬挂式止水帷幕的实际监测值进行对比,定量说明悬挂式止水帷幕对基坑降水的影响。
关键词:悬挂式帷幕,基坑降水,三维有限元法中图分类号:TU46 文献标识码:B 文章编号:100423152(2006)04200332041 引言长江中下游沿岸大都位于长江一级阶地之上,地基土呈典型的二元结构。
上部由透水性弱、强度低的粘性土层组成;下部由强度高、透水性强的砂、砾、卵石层组成,富水性好,在两层结构之间,间或出现厚度不一的粉砂过渡层,抗渗强度低[1,2]。
这样更增加了地下工程支护与施工的难度,开挖深基坑时必须进行降水。
目前,对于深基坑井群降水渗流场的分析计算主要是采用解析方法[3],对基坑渗流场的分析大多是二维的,这是对实际情况的简化,而利用三维有限元对复杂基坑进行模拟,也多停留在稳定渗流的水平[4]。
文[5]采用二维有限元法对某水坝悬挂式帷幕周围的渗流场进行了模拟。
本文以里兹有限单元法为基础,建立地下水流动的三维渗流模型进行计算,预测有无止水帷幕工况下基坑各处水头降深,并与实际工程中存在悬挂式止水帷幕的降水监测数据进行对比,并阐明悬挂式止水帷幕在基坑降水中的影响。
2 渗流模型的建立及求解基坑降水中各向异性承压含水层中地下水三维不稳定流问题,若考虑x、y和z轴的取向与含水层介质各向异性的主方向一致,则该状况的地下水流动规律可用以下三维模型表达[6]:99x(K xx9H9x)+99y(K yy9H9y)+99z(K zz9H9z) =μs9H9t (x、y<Ω)H|t=0=H0(x,y,z)H|B1=H b[K xx9H9x co s(n,x)+K yy9H9y cos(n,y)+ K zz9H9z cos(n,z)]B2=ν(1)式中:Ω为渗流区域,B1为研究区的第一类边界(定水头边界),B2为研究区的第二类边界(定流量边界),ν为第二类边界B2处的渗流速度,K xx、K yy、K zz分别为x、y、z方向上的渗透系数。
稳态渗流

谢谢观看
概念引入
中流动的欧姆定律十分相似,在解决地下水渗流问题时,
我们可以运用电流流动模型。在两个例子中,势能是引
起物体克服阻碍发生流动趋势的原因,因此物体的导电 性和土体的渗流性是相似的。
Tips
水力梯度的定义
contrast
流网的引入和相关计算
基本定义
实际水滴流速
contrast
第四节简化流网中的流动
第二节地下水流动的实际问题
如图 (a) 所示是岩土工程中一个典型的渗流问题,水沿着流线ABC从水 位高的区域流向水位低的区域:注意在图 (a)中,水从B向上流到C。由 于最上面的流线PQRS是被不透水的混凝土大坝限制着,所以图 (a)所示 的是承压流。水向上流到C点,此时流线在下游地面流出。如果渗流速率 很大,土颗粒会被冲走。
图14.2(b)所示的是非承压流,并存在着浸润线,此浸润线同时也是 最上面的流线TU,如果下游排水沟的位置不正确的话,那么流线TU就
会从大坝的表面流出,此时大坝会受到破坏。在发生漫坝的之后,这种 情况是最常见的由小孩造成的溃坝原因。
第三节稳态渗流基本特征
描述水在土体中流动的达西定律和描述电流在导电体
稳态渗流 Steady state seepage
第一节 地下水状态
(b)稳态渗流 如图(b)所示,浸润线不是水平的,水将会沿着流线ABC流动, 图(b)中水从A点流向B点是升高的,C点的静水压力比B点的静水 压力要高。 需要注意的是:测压管水头并没有真实反映浸润线(在第五 节中详细讲解
029二维稳态渗流
(1)启动 SciFEA,选择“项目”—>“新建项目”菜单或选择新建项目按钮 弹出如图 7-1-2 所示的对话框。
图 7-1-2
选择项目类型对话框
(2)点击“问题类型”栏中的“二维稳态渗流”选项。如图 7-1-2 所示。 (3)点击“OK”按钮完成项目类型的选择。
1.1.2.b 设置材料参数和边界条件
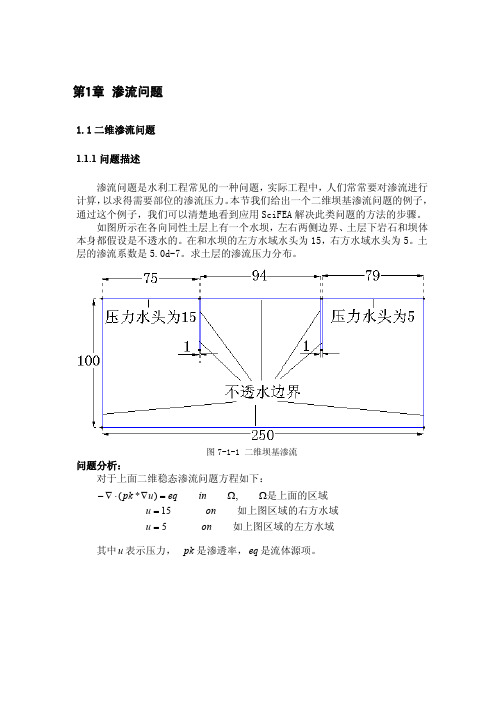
图 7-1-1 二维坝基渗流
问题分析: 对于上面二维稳态渗流问题方程如下:
( pk * u ) eq u 15 u5 in on on , 是上面的区域 如上图区域的右方水域 如上图区域的左方水域
其中 u 表示压力, pk 是渗透率, eq 是流体源项。
1.1.2 求解步骤
第1章 渗流问题
1.1 二维渗流问题 1.1.1 问题描述 渗流问题是水利工程常见的一种问题,实际工程中,人们常常要对渗流进行 计算, 以求得需要部位的渗流压力。 本节我们给出一个二维坝基渗流问题的例子, 通过这个例子,我们可以清楚地看到应用 SciFEA 解决此类问题的方法的步骤。 如图所示在各向同性土层上有一个水坝,左右两侧边界、土层下岩石和坝体 本身都假设是不透水的。在和水坝的左方水域水头为 15,右方水域水头为 5。土 层的渗流系数是 5.0d-7。求土层的渗流压力分布。
图 7-1-29 进入后处理结果分析
(2)点击菜单【View results】-【Contour fill】-【unoda0】 ,如图 7-1-30 所示, 显示得到渗流场云图分布,如图 7-1-31 所示。
图 7-1-30 选择渗流压力水头云图
图 7-1-31 渗流场云图分布
(3)点击菜单【View results】-【Display Vectors】-【unoda0】-【|unodb0|】 , 如图 7-1-32 所示,显示得到渗流速度场云图分布,如图 7-1-33 所示。
康-第一章 渗流基本理论

河间地块流网的应用
比较: HA与HB? JA与JB? VA与 VB?
A
B
河间地块流网图
层状非均质介质中的流网
典型流网特征
各向异性介质中的流网
1.1.3
渗流分类
1. 按运动要素(v,p,H)是否随时间变化,分:稳定流与非稳定流 2. 按地下水质点运动状态的混杂程度,分: 层流、紊流与过渡区流态 3. 按地下水有无自由表面,分为: 承压流、无压流、承压—无压流
z 4.按渗流速度在空间上变化的特点,分 一维流、二维流、三维流 a. 一维流:仅沿一个方向存在流速 b. 二维流:沿两个方向存在分流速 分:平面二维流、剖面二维流)
图1-2-8a 一维流
y
x
c. 三维流: 三个方向均存在分流速
图1-2-8b1 平面二维流
图1-2-8b2 剖面二维流
三维流图示
图1-2-8c 三维流
同一点各方向上渗透性相同的介质称为各向同性介质; 同一点各方向上渗透性不同的介质称为各向异性介质 。 均质、非均质:指K于空间坐标的关系,即不同位置K是否相同; 各向同性、各向异性: 指同一点不同方向的K是否相同。
这两对概念可任意组合
z
四种介质
均质各向同性 均质各向异性 非均质各向同性 非均质各向异性
V——I 曲线
V
1
砂样
2
O
I
V = K · I ——(3)
达西定律讨论
1 渗流速度(V)与过水断面(ω) Q = K ω I = ω V
过水断面与水力学中的水流过断面是否一致?否 过水断面——ω,假想的断面
实际孔隙断面——ω n
实际水流断面——ω n 有效孔隙度 过水断面比较 Q/ω =V 比照水力学,实际流速 Q/ω’= u
渗透各向异性土层中考虑挡墙厚度的基坑稳态渗流解析解

渗透各向异性土层中考虑挡墙厚度的基坑稳态渗流解析解余俊;李东凯;和振;张志中;张鑫全
【期刊名称】《铁道学报》
【年(卷),期】2024(46)5
【摘要】本文对考虑厚度挡墙支护下渗透各向异性土层中基坑的二维稳态渗流进行了解析研究。
根据对称性取基坑半截面,将周围土层划分为5个规则区域,采用坐标变换将渗透各向异性土层转换成等效各向同性土层,对各区域利用叠加法和分离变量法推导得到二维稳态渗流场、挡墙上水压力以及坑底出逸比降的显式解析解。
对比保角变换和积分变换方法,本文解渗流场计算结果连续且无奇异点,且基坑水头和挡墙两侧水压力分布情况与数值软件分析一致性较好,说明本文解析解的正确性和优越性。
本文解与不同计算方法得到的挡墙水压力结果对比分析发现,挡墙厚度d、竖直与水平向渗透系数比α对挡墙上水压力的影响不可忽略。
分析α、d对挡墙底部水压力及出逸比降的影响,随着α和d的增大,基坑外侧挡墙底部水压力增大,基坑内侧挡墙底部水压力减小;随着α和d的逐渐减小,坑底出逸比降不断增大;当α和d较小时,考虑一维渗流情况得到的出逸比降安全性较低,且随着α和d的减小与本文解析解差距越来越大。
【总页数】10页(P142-151)
【作者】余俊;李东凯;和振;张志中;张鑫全
【作者单位】中南大学土木工程学院;中铁城建集团有限公司总承包分公司
【正文语种】中文
【中图分类】U21
【相关文献】
1.渗透各向异性土层中基坑二维稳定渗流半解析解
2.深埋圆形隧洞围岩各向异性稳态渗流场解析解
3.考虑挡墙厚度基坑稳态渗流场的解析解
4.成层土中基坑二维稳态渗流场解析解研究
5.考虑潜水面的基坑二维稳态渗流场解析解
因版权原因,仅展示原文概要,查看原文内容请购买。
大学课件 稳态渗流理论

第三章 稳态渗流理论用Euler 方法描述流体渗流时可以把渗流分为两大类稳态渗流和不稳态渗流两大类。
稳态渗流是一种特殊的渗流阶段,指的是渗流运动要素(P 、v 、T )只是空间坐标的函数,与时间无关,反之则是不稳定渗流。
当渗流系统有稳定的能量补给存在时,便可以发生稳态渗流。
对于渗流场,流线和等压线可以直观描绘了流体的流向和能量损失规律,而刻画流场图时规定:相邻流线间的流量差必须相等,相邻等势线间的势差相等。
本章讨论三种经典系统稳态渗流理论旨在阐明渗流方式及其渗流场特征,并给出稳态渗流平均地层压力和流量计算公式。
另外,简要阐述了直线边界系统、等值渗流阻力法以及底水锥进等典型的稳态渗流问题。
3-1典型渗流系统·平均地层压力典型渗流系统包括线性渗流系统、径向渗流系统及球形渗流系统。
线性系统:流体在狭长的介质中发生渗流,流线在平面上是相互平行的,则称这样一种流动为平面线性渗流,这样的渗流系统为线性渗流系统。
选取直角坐标来建立数学模型是有利的,其渗流控制方程为:tPc x P k t∂∂=∂∂φμ22 (3-1-1)径向系统:流体在具有对称泄流面积的等厚均质地层中发生渗流,流线在平面上向一个汇点聚集,称这样一种流动为平面径向渗流,这样的渗流系统为平面径向渗流系统。
选择极坐标系来建立数学模型显然是有利的,其渗流控制方程为:t Pc r P r r P k t ∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂φμ122 (3-1-2)球形系统:流体在厚层、部分出流情形下发生渗流,流线在空间上向一个汇点聚集,称这样一种流动为空间球形渗流。
选取球坐标来建立数学模型是有利的,其渗流控制方程为:tPc r P r r P k t ∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂φμ222 (3-1-3)在稳定渗流条件下,方程(1~3)的右端为零,通过直接积分可以得到地层压力分布通解,由此能够查明流场特征。
若给出相应的边界条件,可得到平均压力公式和流量公式。
渗流的基本定律(达西定律)
彼此连通的网络,几何形态及连通情况异常复杂, 难以用精确的方法来描述。 由固体骨架和孔隙组成,孔隙通道是不连续的。
因此,无论是固体骨架,还是空隙空间,微观上讲都不是连续函数
普通水流与渗流
共同点: 1.总体流向取决于水头差 2.流量取决于水头差及沿程损耗 区别:水在管道中运动取决于 管道大小、形状及粗糙度;渗流运动取决于空隙大小、形状、 连通性。
是否适用:非均匀介质,二维或三维流动, 非稳定流,层流条件?
三、变水头达西实验 非稳定流达西实验(实验一): 水自上部加入,用溢水管保持稳定水位,下部用管口出流,可 通过它测定渗流量,用两根测压管来测量水头值。 达西定理:
实验结果: 在非稳定流条件下,地下水运动仍满足 线性渗流定律
达西定律适用条件 1.临界雷诺数Re(J. Bear):
L——渗透途径(上下游过水断面的距 离) ;
I ——水力梯度(相当于h / L,即水头 差除以渗透途径) ;
K——渗透系数。 此即达西公式。
二、达西实验条件
稳定达西实验:得出渗透流速与水力坡度成 正比即线性渗流定律,说明此时地下水的流 动状态呈层流。
实验条件:均匀介质,一维流动,稳定流, 层流。
1. 几点讨论: (1) 当K1≠K2,α1≠0,流线才会折射 (2)当K1=K2,α1= α2 (3) 只有在0< α1<90,才会折射 (4)在层界面上发生的流线折射并不改变地下水流总方向,总体 流向仍受边界条件和源汇等控制。
典型流网特征
各向异性介质中的流网
小结
– 上述分类标准不同,无从属系,可以 组合
– 均质与非均质,各向同性与各向异性概 念容易混淆
地下水渗流基本方程及数学模型总结
方程右端项:
( nz ) z H H [ (1 e) e ] t 1 e t t H z ( n ) t
§5 描述地下水运动的数学模型及解算方法
第三步:方程的左端项=方程的右端项
H H H (K xx ) (K yy ) (K zz ) xyz x x y y z z H z( n ) xy t
(二)含水层的状态方程
根据Terzaghi有效应力公式:水压力p减少,将引起含 水层状态发生哪些变化? p减少 p减少 地下水体积膨胀,从而释放出一部分地下水; 地下水对上覆岩土体浮力降低,为维持平衡,
这部分力将转嫁到多孔介质固体骨架上,有效应力增大 ,压缩多孔介质(固体+空隙),结果使含水层空隙度 n变小、介质挤密、厚度变薄,从孔隙中(挤压)释放 一部分地下水;
(二)含水层的状态方程 含水层的弹性存储
取一典型处于平衡状态的饱和地层柱体来研究,这里只考虑垂直一维 变形,忽略侧面上粒间力(包括内聚力和摩擦力)的作用。 含水层上覆(岩土体、地表建筑物和大气压力等)荷载形成的总压应 力由固体颗粒粒间应力的垂向分量s和孔隙水压力p两者来平衡。
测压水头
p hp
§5 描述地下水运动的数学模型及解算方法
第二步:化简方程右端项:
e e e p H 根据 (1 e)和dp dH , 得 (1 e) p t p t t d p H 根据 和dp dH , 得 dp t p t t
§5 描述地下水运动的数学模型及解算方法
第一步:化简方程左端项: 由于在一般情况下,水的密度变化很小,可视 ρ 近似不变:
( v x ) H ( K xx ) x x x H H K xx K xx x x x x H H [ K xx (K xx )] x x x x
土力学地基基础课件第三章渗流固结理论
渗流固结理论的重要性
渗流固结理论在土木工程、水利工程 、地质工程等领域具有广泛的应用价 值。
它对于理解土体的力学行为、预测土 体的变形和稳定性、优化工程设计和 施工具有重要意义。
渗流固结理论的应用领域
01
02
03
水利工程
水库、堤防、水电站等水 利设施的设计和安全评估。
土木工程
高层建筑、高速公路、桥 梁等基础设施的建设和安 全评估。
渗透试验
通过测量土体的渗透系数、 渗透速度等参数,研究土 体的渗透特性。
现场试验方法
现场观测
通过在土体中埋设传感器和监测 仪器,实时监测土体的渗流和固
结过程。
触探试验
通过触探设备对土体进行触探,测 量土体的物理性质和强度特性。
旁压试验
通过旁压设备对土体施加压力,测 量土体的变形和强度特性。
数值模拟方法
三维固结理论通过求解偏微分方程组, 得到土体在固结过程中任意时刻的孔隙
水压力分布、土层沉降和位移场。
04
渗流固结理论的实验研究
室内试验方法
室内模型试验
通过模拟实际土体中的渗 流和固结过程,研究土体 的变形和强度特性。
土工离心机试验
利用离心加速度模拟土体 应力状态,研究土体在复 杂应力状态下的渗流和固 结行为。
06
结论
渗流固结理论的发展趋势
数值模拟与实验研究的结 合
随着计算机技术的进步,数值 模拟方法在渗流固结理论的研 究中越来越受到重视。通过与 实验研究相结合,可以更准确 地模拟复杂条件下的土体渗流 和固结过程。
多场耦合分析
考虑土体的应力、应变、渗流 和温度等多场耦合效应,对土 体的复杂行为进行更全面的分 析。
渗流固结理论可以用于分析地 下水的流动规律和土体的渗透 性能,为地下水控制提供理论 支持。
大学课件 稳态渗流理论
(3-2-2)
今有一水平地层,固定厚度为h,宽度为w,由n个区域构成,长度分别为l1,l2……ln,区域间连续,渗透率分别为k1,k2……kn,孔隙度为φ1,φ2……φn,不可压缩流体发生平面线性流动,供给边界压力为Pe,排液道压力为Pwf,讨论稳态渗流问题。
解法:用数学语言描述地层物性为:
(3-1-3)
在稳定渗流条件下,方程(1~3)的右端为零,通过直接积分可以得到地层压力分布通解,由此能够查明流场特征。若给出相应的边界条件,可得到平均压力公式和流量公式。
平均地层压力:在渗流系统中,平均地层压力是指定泄流体积内压力分布的算术平均值:
(3-1-4)
平均地层压力标志着泄流体积内的能量水平,对不同的渗流方式,这一公式有更具体的表达形式。
,
首先利用边界条件确定压力分布通式中的积分常数,得到压力分布公式:
平均压力公式:
根据物性方程,具体有:
,
平均渗透率等效关系:
, (3-2-2)
如果仅考虑二区油藏,则平均压力:
以上是非均质线性渗流的主要问题,当然也可以详细给出压力梯度、渗流速度等公式。
3-3-3
多层复合稳态渗流问题的描述参见3-2-1节,平面径向稳态渗流控制方程组为:
直接积分可以得到压力分布方程通式
由压力分布通式可以看出,空间球形渗流流场的特点:
等压线方程:
等压线为球面,在井底附近密集。
流线方程:
球坐标系如图1-13所示,流线为空间一簇射线,在井底附近密集,指向生产井或由注入井发散开去。
如果给定供给边界压力为Pe,井的流量为Q,内边界条件方程依律写为:
(3-1-14)
流量方程:若已知井底压力为Pwf,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1求解步骤
1.1模块挂载
(1)启动SciFEA,选择“工具”—>“模块挂载”菜单弹出如图1-1所
示的对话框,在对话框当中选择“三维各向异性稳态渗流。
图1-1 选择项目类型对话框
(2)点击“SciFEA模块挂载”栏中的“三维各向异性稳态渗流”选项。
如图1-1所示。
(3)点击“确定”按钮完成项目类型的选择。
(4)单击工具条中的按钮弹出如图1-2所示,找到SciFEA下的tempudm 目录,并且选择打开udm.pro文件。
图1-2
(5)点击“打开”按钮之后,弹出如图1-3:
图1-3
(6)最后点击“OK”按钮。
1.2设置材料参数和边界条件
(1)单击工具条中的按钮弹出如图1-4所示材料参数数据输入表格。
图1-4 材料参数输入
(2)单击工具条中的按钮弹数据输入表格。
按照问题描述中的参数依次
填入边界条件数据表格。
填写完成后如图1-5所示。
图1-5填写完成扩散边界
2建模、设置材料属性和施加边界条件
(1)启动GID以创建模型。
单击工具条中的按钮弹出如图1-6所示前
处理初始化窗口。
图1-6前处理初始化窗口
2.1建模。
a. 点击菜单【Geometry】-【Create】-【Line】,在命令栏依次输入点坐标,最后得到模型图如1-7所示:
图1-7建成的模型图
b.定义材料特性、施加载荷约束。
点击菜单【Data】-【Conditions】弹出“Conditions”对话框。
①施加载荷。
点击线单元按钮,选中下拉菜单中的“surface-anip3da”,最后得到如图1-8所示。
图1-8 施加载荷
②施加载荷。
点击线单元按钮,选中下拉菜单中的“V olume-ace8”,最后得到如图1-9所示。
图1-9
需要说明的是,这几步定义材料,施加载荷的操作没有先后顺序要求,但必须保证不能遗漏某个条件的定义。
2.2划分网格和导出数据
(1).划分网格。
点击菜单【Meshing】-【Generate】,要求定义单元尺寸大小,
点击“OK”按钮,此时弹出“Progress in meshing”进度条,网格划分完毕后弹出消息框显示总的单元数和节点数,如图1-10所示。
图1-10划分网格得到的单元节点信息
点击“OK”按钮后即可得到划分完的网格模型,如图1-11
图1-11网格图
(2)把前处理数据转化为SciFEA所需计算格式。
点击【Files】-【Save】菜单,
保存为GID文件。
点击菜单【Calculate】-【Calculate】,弹出“process info”
消息框,如图1-12所示,点击“ok”按钮,然后退出Gid,至此前处理工作
结束。
图1-12 转化数据消息框
3有限元计算
(1) 单击工具条中的按钮弹出如图1-13所示计算模拟窗口。
图1-13 计算模拟窗口
4结果分析
对计算结果进行分析属于后处理,GID提供了丰富的后处理操作,可以从不同角度,不同方式来输出计算结果。
(1)点击工具菜单中的进入后处理,如图1-14所示。
图1-14 进入后处理结果分析
(2)点击菜单【Files】-【Postprocess】进入后处理程序。
(3)点击菜单【View results】-【Contour fill】-【unoda0】显示沿y方向的位
移云图,如图1-15所示。
图1-15。
