061二维各向异性稳态渗流
每天一点土力学(17):二维渗流及应用

每天一点土力学(17):二维渗流及应用拉普拉斯对于边界条件简单的一维渗流问题,可直接利用达西定律进行渗流计算。
但工程中遇到的渗流问题,常常属于边界条件复杂一些的二维或三维渗流问题。
例如闸坝下透水地基的渗流以及土坝坝身的渗流等(图a),其流线都是弯曲的,不能再视为一维渗流。
为了求解和评价渗流在地基或坝体中是否造成有害的影响,需要知道整个渗流场中各处的测管水头、渗流坡降和渗流速度。
著名的拉普拉斯(Laplace)方程。
它与水力学中的平面势流的拉普拉斯方程一样,该方程描述了渗流场内部的测压管水头h 的分布,是平面稳定渗流的基本方程式。
通过求解一定边界条件下的拉普拉斯方程,即可求得该条件下的渗流场。
流网的特征与绘制上述拉普拉斯方程表明,渗流场内任一点水头是其坐标的函数,知道了水头分布,即可确定渗流场的其他特征。
求解拉普拉斯方程一般有4类方法,即数学解析法、数值解法、电模拟法、图解法。
其中图解法简便、快速,在工程中实用性强,因此,这里简要介绍图解法。
所谓图解法即用绘制流网的方法求解拉普拉斯方程的近似解。
1)流网的特征流网是由流线和等势线所组成的曲线正交网格。
在稳定渗流场中,流线表示水质点的流动路线,流线上任一点的切线方向就是流速矢量的方向。
等势线是渗流场中势能或水头的等值线。
流网的绘制如图所示为板桩墙围堰的流网图。
图中实线为流线,虚线为等势线。
对于各向同性渗流介质,由水力学可知,流网具有下列特征:①流线与等势线互相正交;②流线与等势线构成的各个网格的长宽比为常数,当长宽比为1时,网格为曲线正方形,这也是最常见的一种流网;③相邻等势线之间的水头损失相等;④各个流槽的渗流量相等。
由这些特征可进一步知道,流网中等势线越密的部位,水力梯度越大,流线越密的部位流速越大。
流网的工程应用根据流网,就可以直观地获得渗流特性的总体轮廓,并可定量求得渗流场中各点的测管水头、水力坡降、渗流速度和渗流量。
1)测管水头根据流网的特征可知,任意两相邻等势线间的势能差相等,即水头损失相等,从而相邻两条等势线之间的水头损失Δh 为:2)孔隙水压力渗流场中各点的孔隙水压力,等于该点以上测压管中的水柱高度h u乘以水的容重γ w,故 a点的孔隙水压力为:3)水力坡降流网中任意网格的平均水力坡降,Δl 为该网格处流线的平均长度,可从图中量出。
高等土力学(李广信)4.4_二维渗流与流网课件

3)坝和土堤的渗流
图4-37 不同的情况土坝上游面的流线
(a)图的浸润线应垂直于坝面,这是因为坝的 上游面为一等势线,流线与之垂直。 ( b )与( c )图表示上游面有粗粒料堆体,浸 润线应与水平线相切。
图4-38 不同情况下土坝下游的流线
(a)为水平排水垫褥(等势线) (b)为排水棱体(等势线)
不同土层界面处流线 的折射角 图4-36
2) 交界面两边流槽的宽度△s 随偏转角发生变化 △s1 AB cos1 △s2 AB cos 2
s1 cos 1 s2 cos 2
k1 tg 1 k2 tg 2
图4-36
3) 交界面两边网格的形状随渗透系数发生变化
3. 各向异性土与分层土中的流网
流入=流出:不可压缩流体的连续性原理
vx vz vx dz vz dx (vx dx)dz (vz dz )dx (1) x z
vx vz 0 x x
(2)
2h 2h k x 2 k y 2 0 (4) x y
h q1 k1 s1 l1
=
h q2 k 2 s2 l2
h h k1 s1 k2 s2 l1 l2
s1 s2 k1 k2 l1 l2
s1=l1
k1 s2 非正方形 k2 l2 l2
图4-36
流网的应用
1)计算渗流量、孔隙水压力和水力坡降
流入=流出:不可压缩流体的连续性原理
(1)
x h v y k y y 2h 2h kx 2 k y 2 0 x y
(3)
(4)
2h 2h 2 0 2 x y
图4-31 二维土单元的渗流
029二维稳态渗流
(1)启动 SciFEA,选择“项目”—>“新建项目”菜单或选择新建项目按钮 弹出如图 7-1-2 所示的对话框。
图 7-1-2
选择项目类型对话框
(2)点击“问题类型”栏中的“二维稳态渗流”选项。如图 7-1-2 所示。 (3)点击“OK”按钮完成项目类型的选择。
1.1.2.b 设置材料参数和边界条件
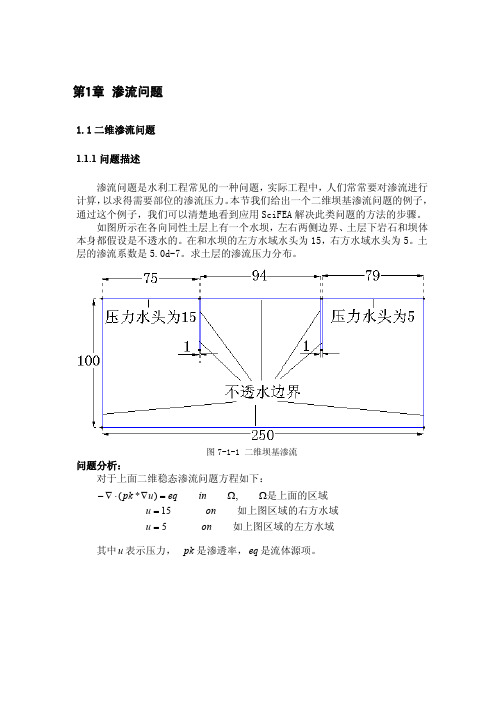
图 7-1-1 二维坝基渗流
问题分析: 对于上面二维稳态渗流问题方程如下:
( pk * u ) eq u 15 u5 in on on , 是上面的区域 如上图区域的右方水域 如上图区域的左方水域
其中 u 表示压力, pk 是渗透率, eq 是流体源项。
1.1.2 求解步骤
第1章 渗流问题
1.1 二维渗流问题 1.1.1 问题描述 渗流问题是水利工程常见的一种问题,实际工程中,人们常常要对渗流进行 计算, 以求得需要部位的渗流压力。 本节我们给出一个二维坝基渗流问题的例子, 通过这个例子,我们可以清楚地看到应用 SciFEA 解决此类问题的方法的步骤。 如图所示在各向同性土层上有一个水坝,左右两侧边界、土层下岩石和坝体 本身都假设是不透水的。在和水坝的左方水域水头为 15,右方水域水头为 5。土 层的渗流系数是 5.0d-7。求土层的渗流压力分布。
图 7-1-29 进入后处理结果分析
(2)点击菜单【View results】-【Contour fill】-【unoda0】 ,如图 7-1-30 所示, 显示得到渗流场云图分布,如图 7-1-31 所示。
图 7-1-30 选择渗流压力水头云图
图 7-1-31 渗流场云图分布
(3)点击菜单【View results】-【Display Vectors】-【unoda0】-【|unodb0|】 , 如图 7-1-32 所示,显示得到渗流速度场云图分布,如图 7-1-33 所示。
地下水动力学习题及答案(1)

18.在同一条流线上其流函数等于_常数_,单宽流量等于_零_,流函数的量纲为__ __。
19.在流场中,二元流函数对坐标的导数与渗流分速度的关系式为_ _。
20.在各向同性的含水层中流线与等水头线_除奇点外处处正交_,故网格为_正交网格_。
3.在多孔介质中,不连通的或一端封闭的孔隙对地下水运动来说是无效的,但对贮水来说却是有效的。
4.地下水过水断面包括_空隙_和_固体颗粒_所占据的面积.渗透流速是_过水断面_上的平均速度,而实际速度是_空隙面积上__的平均速度。
在渗流中,水头一般是指测压管水头,不同数值的等水头面(线)永远不会相交。
5.在渗流场中,把大小等于_水头梯度值_,方向沿着_等水头面_的法线,并指向水头_降低_方向的矢量,称为水力坡度。水力坡度在空间直角坐标系中的三个分量分别为_ _、 _和_ _。
31.在均质各向同性的介质中,任何部位的流线和等水头线都正交。(×)
32.地下水连续方程和基本微分方程实际上都是反映质量守恒定律。(√)
33.潜水和承压水含水层的平面二维流基本微分方程都是反映单位面积含水层的水量均方程。(√)
34.在潜水含水层中当忽略其弹性释放水量时,则所有描述潜水的非稳定流方程都与其稳定流方程相同。(×)
27.沿流线的方向势函数逐渐减小,而同一条等势线上各处的流函数都相等。(×)
28.根据流函数和势函数的定义知,二者只是空间坐标的函数,因此可以说流函数和势函数只适用于稳定流场。(×)
29.在渗流场中,一般认为流线能起隔水边界作用,而等水头线能起透水边界的作用。(√)
30.在同一渗流场中,流线在某一特定点上有时候也可以相交。(√)
渗流的基本定律(达西定律)(稻谷书苑)

教学运用
2
多孔介质概念与特性
我们把孔隙岩层称为多孔介质(porous media). •多孔介质特性:
彼此连通的网络,几何形态及连通情况异常复杂, 难以用精确的方法来描述。 由固体骨架和孔隙组成,孔隙通道是不连续的。
因此,无论是固体骨架,还是空隙空间,微观上讲都不是连续函数
教学运用
3普通水流与渗流共同点 1.总体流向取决于水头差2.流量取决于水头差及沿程损耗 区别:水在管道中运动取决于
管道大小、形状及粗糙度;渗流运动取决于空隙大小、形状、
连通性。
教学运用
4
渗流特点
– 通道是曲折的,质点运动轨迹弯曲; – 流速是缓慢的,多数为层流; – 水流仅在空隙中运动,在整个多孔介质中不连续; – 通常是非稳定的; – 通常为缓变流。
2.1912年克拉斯诺波里斯基提出紊流公式:
教学运用
21
四、达西定律的微分形式 微分形式:
教学运用
22
渗透系数K
从达西定律V = KI可以看出。水力梯度I 是无因次的,故渗 透系数K的因次与渗透流速V 相同。一般采用 m/d 或 cm/s 为单位。令 I = 1 ,则V =K 。意即渗透系数为水力梯度等 于 1 时的渗透流速。水力梯度为定值时,渗透系数愈大。 渗透流速就愈大;渗透流速为一定值时,渗透系数愈大, 水力梯度愈小。由此可见,渗透系数可定量说明岩石的渗 透性能。渗透系数愈大,岩石的透水能力愈强。
教学运用
5
一、典型体元
(Representative elementary volume)
在水力学中引进质点的概念,把水看成连续介质, 则可用连续函数描述运动要素。 为了把渗流场概化为多孔介质连续体,用连续函数 描述,引进典型体元的概念。
渗透各向异性土层中考虑挡墙厚度的基坑稳态渗流解析解

渗透各向异性土层中考虑挡墙厚度的基坑稳态渗流解析解余俊;李东凯;和振;张志中;张鑫全
【期刊名称】《铁道学报》
【年(卷),期】2024(46)5
【摘要】本文对考虑厚度挡墙支护下渗透各向异性土层中基坑的二维稳态渗流进行了解析研究。
根据对称性取基坑半截面,将周围土层划分为5个规则区域,采用坐标变换将渗透各向异性土层转换成等效各向同性土层,对各区域利用叠加法和分离变量法推导得到二维稳态渗流场、挡墙上水压力以及坑底出逸比降的显式解析解。
对比保角变换和积分变换方法,本文解渗流场计算结果连续且无奇异点,且基坑水头和挡墙两侧水压力分布情况与数值软件分析一致性较好,说明本文解析解的正确性和优越性。
本文解与不同计算方法得到的挡墙水压力结果对比分析发现,挡墙厚度d、竖直与水平向渗透系数比α对挡墙上水压力的影响不可忽略。
分析α、d对挡墙底部水压力及出逸比降的影响,随着α和d的增大,基坑外侧挡墙底部水压力增大,基坑内侧挡墙底部水压力减小;随着α和d的逐渐减小,坑底出逸比降不断增大;当α和d较小时,考虑一维渗流情况得到的出逸比降安全性较低,且随着α和d的减小与本文解析解差距越来越大。
【总页数】10页(P142-151)
【作者】余俊;李东凯;和振;张志中;张鑫全
【作者单位】中南大学土木工程学院;中铁城建集团有限公司总承包分公司
【正文语种】中文
【中图分类】U21
【相关文献】
1.渗透各向异性土层中基坑二维稳定渗流半解析解
2.深埋圆形隧洞围岩各向异性稳态渗流场解析解
3.考虑挡墙厚度基坑稳态渗流场的解析解
4.成层土中基坑二维稳态渗流场解析解研究
5.考虑潜水面的基坑二维稳态渗流场解析解
因版权原因,仅展示原文概要,查看原文内容请购买。
大学课件 稳态渗流理论
第三章 稳态渗流理论用Euler 方法描述流体渗流时可以把渗流分为两大类稳态渗流和不稳态渗流两大类。
稳态渗流是一种特殊的渗流阶段,指的是渗流运动要素(P 、v 、T )只是空间坐标的函数,与时间无关,反之则是不稳定渗流。
当渗流系统有稳定的能量补给存在时,便可以发生稳态渗流。
对于渗流场,流线和等压线可以直观描绘了流体的流向和能量损失规律,而刻画流场图时规定:相邻流线间的流量差必须相等,相邻等势线间的势差相等。
本章讨论三种经典系统稳态渗流理论旨在阐明渗流方式及其渗流场特征,并给出稳态渗流平均地层压力和流量计算公式。
另外,简要阐述了直线边界系统、等值渗流阻力法以及底水锥进等典型的稳态渗流问题。
3-1典型渗流系统·平均地层压力典型渗流系统包括线性渗流系统、径向渗流系统及球形渗流系统。
线性系统:流体在狭长的介质中发生渗流,流线在平面上是相互平行的,则称这样一种流动为平面线性渗流,这样的渗流系统为线性渗流系统。
选取直角坐标来建立数学模型是有利的,其渗流控制方程为:tPc x P k t∂∂=∂∂φμ22 (3-1-1)径向系统:流体在具有对称泄流面积的等厚均质地层中发生渗流,流线在平面上向一个汇点聚集,称这样一种流动为平面径向渗流,这样的渗流系统为平面径向渗流系统。
选择极坐标系来建立数学模型显然是有利的,其渗流控制方程为:t Pc r P r r P k t ∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂φμ122 (3-1-2)球形系统:流体在厚层、部分出流情形下发生渗流,流线在空间上向一个汇点聚集,称这样一种流动为空间球形渗流。
选取球坐标来建立数学模型是有利的,其渗流控制方程为:tPc r P r r P k t ∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂φμ222 (3-1-3)在稳定渗流条件下,方程(1~3)的右端为零,通过直接积分可以得到地层压力分布通解,由此能够查明流场特征。
若给出相应的边界条件,可得到平均压力公式和流量公式。
稳定渗流作用下出逸坡降的随机分析
稳定渗流作用下出逸坡降的随机分析罗显枫;李昕【摘要】利用局部平均(local average)法和协方差分解法生成的各向异性随机场来模拟单隔水板桩下的透水型地基土层的渗透系数的空间变异分布,并结合有限元法绘制出随机流网图,从而刻画出稳定渗流作用下的出逸坡降的统计特征,为实际工程风险评价提供科学依据.【期刊名称】《湖北理工学院学报》【年(卷),期】2016(032)004【总页数】4页(P31-34)【关键词】局部平均法;各向异性随机场;稳定渗流;出逸坡降【作者】罗显枫;李昕【作者单位】湖北理工学院土木建筑工程学院,湖北黄石435003;大连理工大学建设工程学部,辽宁大连116023【正文语种】中文【中图分类】TV223.4闸坝下游渗流出逸处,最容易发生流土、管涌之类的渗透破坏。
造成这类事故的主要原因是渗流出逸坡降大于该处土料的临界坡降,因此设计人员必须严格控制渗流出逸坡降。
国内学者也对此类问题展开了研究。
沙金煊[1]推导了简单地下轮廓布置的出逸坡降计算公式。
吴世余[2]提出了奇点附近渗透出逸坡降的测定方法。
毛海涛[3]推导了无限深透水地基上土石坝坝基垂直防渗的出逸坡降计算公式。
这些基于确定性土体的渗透系数计算工作有一定的理论价值。
但是在实际工程中,由于土的渗透系数具有较大的空间变异性,采用传统的确定性方法计算得到的渗流出逸坡降不能为工程决策提供更精确的科学依据,因此本研究采用随机有限元方法进行渗流出逸坡降的仿真。
具体做法为:利用局部平均法生成的各向异性随机场模拟单隔水板桩下的透水型地基土层的渗透系数的空间变异分布,并结合有限元法绘制出随机流网图,从而刻画出稳定渗流作用下的出逸坡降的统计特征,为实际工程风险评价提供依据。
1.1 二维随机场的局部平均土的工程特性依赖于空间土体的平均特性而非某一特定点的性质指标,所以考虑用随机场的局部平均进行随机有限元计算。
随机场的单元A和单元A' 的相对位置图如图1所示,T1和T2分别为面积A水平和竖直方向尺寸。
二维平面有限单元法在坝体渗流稳定评价中的应用——以赤泥堆场4#坝北坝段渗流稳定分析评价为例
二维平面有限单元法在坝体渗流稳定评价中的应用——以赤泥堆场4#坝北坝段渗流稳定分析评价为例王跃;伍锡举;安源远【摘要】中铝贵州分公司赤泥堆场4#坝为库中坝,坝为赤泥堆砌而成,其北坝段位于二叠系茅口组、龙潭组交接地段附近,随着该坝的不断加高使用,对该坝北段的渗流稳定进行了分析,其间用到的一些计算方法值得借鉴.【期刊名称】《矿产勘查》【年(卷),期】2010(001)006【总页数】3页(P516-518)【关键词】二维平面有限单元法;渗流;出逸坡降;赤泥堆场【作者】王跃;伍锡举;安源远【作者单位】贵州省有色金属和核工业地质勘查局地质勘测设计院,贵阳,550005;贵州省有色金属和核工业地质勘查局地质勘测设计院,贵阳,550005;贵州省有色金属和核工业地质勘查局地质勘测设计院,贵阳,550005【正文语种】中文【中图分类】P641.2;TV6411 概况中铝贵州分公司赤泥堆场4#坝为库中坝(坝前为5#库、坝后为3#库),坝为赤泥堆砌而成,2004年9月坝顶高程为1348.50 m,库水位高程为1344 m,其北坝段位于二叠系茅口组、龙潭组交接地段附近。
为预测当5#库水位使用到1355m后,4#坝坝后渗流能否威胁4#坝的正常安全使用,故对4#坝北段进行渗流稳定分析评价。
2 赤泥、黏土、灰岩渗透系数的确定现场布置6个勘探孔(图1),根据钻探揭露,该坝岩土构成从上而下为赤泥、耕植土、黏土、二叠系茅口组灰岩。
以钻孔ZK4作抽水孔,其余孔作观测孔进行抽水试验;采用固定薄皮取土器取赤泥样、土样作含水量及渗透性测试;对灰岩作压水试验。
通过整理分析后认为:(1)对ZK4钻孔进行抽水试验,其余5孔为观测孔。
其中最大降深Sw=16.83m的抽水试验,为混合抽水,不能代表各层的渗透性;在赤泥层的2次抽水试验,降深分别为Sw=7.50 m和Sw=6.02 m,在抽水过程中,观测孔ZK2水位变化明显,采用具有1个观测孔的潜水完整井公式以及利用ZK4钻孔水位恢复观测资料求渗透系数k,计算结果见表1。
大学课件 稳态渗流理论
(3-2-2)
今有一水平地层,固定厚度为h,宽度为w,由n个区域构成,长度分别为l1,l2……ln,区域间连续,渗透率分别为k1,k2……kn,孔隙度为φ1,φ2……φn,不可压缩流体发生平面线性流动,供给边界压力为Pe,排液道压力为Pwf,讨论稳态渗流问题。
解法:用数学语言描述地层物性为:
(3-1-3)
在稳定渗流条件下,方程(1~3)的右端为零,通过直接积分可以得到地层压力分布通解,由此能够查明流场特征。若给出相应的边界条件,可得到平均压力公式和流量公式。
平均地层压力:在渗流系统中,平均地层压力是指定泄流体积内压力分布的算术平均值:
(3-1-4)
平均地层压力标志着泄流体积内的能量水平,对不同的渗流方式,这一公式有更具体的表达形式。
,
首先利用边界条件确定压力分布通式中的积分常数,得到压力分布公式:
平均压力公式:
根据物性方程,具体有:
,
平均渗透率等效关系:
, (3-2-2)
如果仅考虑二区油藏,则平均压力:
以上是非均质线性渗流的主要问题,当然也可以详细给出压力梯度、渗流速度等公式。
3-3-3
多层复合稳态渗流问题的描述参见3-2-1节,平面径向稳态渗流控制方程组为:
直接积分可以得到压力分布方程通式
由压力分布通式可以看出,空间球形渗流流场的特点:
等压线方程:
等压线为球面,在井底附近密集。
流线方程:
球坐标系如图1-13所示,流线为空间一簇射线,在井底附近密集,指向生产井或由注入井发散开去。
如果给定供给边界压力为Pe,井的流量为Q,内边界条件方程依律写为:
(3-1-14)
流量方程:若已知井底压力为Pwf,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1求解步骤
1.1模块挂载
(1)启动SciFEA,选择“工具”—>“模块挂载”菜单弹出如图1-1所
示的对话框,在对话框当中选择“二维各向异性稳态渗流。
图1-1 选择项目类型对话框
(2)点击“SciFEA模块挂载”栏中的“二维各向异性稳态渗流”选项。
如图1-1所示。
(3)点击“确定”按钮完成项目类型的选择。
(4)单击工具条中的按钮弹出如图1-2所示,找到SciFEA下的tempudm 目录,并且选择打开udm.pro文件。
图1-2
(5)点击“打开”按钮之后,弹出如图1-3:
图1-3
(6)最后点击“OK”按钮。
1.2设置材料参数和边界条件
(1)单击工具条中的按钮弹出如图1-4所示材料参数数据输入表格。
依次
输入参数。
图1-4 材料参数输入
(2)单击工具条中的按钮弹数据输入表格。
按照问题描述中的参数依次
填入边界条件数据表格。
填写完成后如图1-5所示。
图1-5填写完成边界
2建模、设置材料属性和施加边界条件
(1)启动GID以创建模型。
单击工具条中的按钮进入前处理界面如图
1-6所示。
图1-6前处理界面
2.1建模。
a. 点击菜单【Geometry】—【Create】—【point】,在命令栏依次输入点坐标:0,0,按ENTER键,输入24.4,0,按ENTER,输入0,49.4,按ENTER 键,输入24.4,49.4,按ENTER键,接着按Esc键。
点击【Geometry】—【Create】—【staight line】,点击右键contextual-join ctrl-a,依次拾取各点,形成线条,按esa退出。
选择【Geometry】—【Create】—【NURBS surface】—【By contour】,拾取线条,形成面。
如图1-7.
图1-7
依次重复上面的操作命令得到如图1-8所示的模型。
图1-8建成的模型图
b.选择问题类型。
如图1-9所示,点击菜单【Data】-【Problem Type】-【SCI】,将弹出如图1-10所示对话框,点击“确定”按钮即可。
图1-9 选SCI
图1-10 Dialog Window
c.定义材料特性、施加载荷约束。
点击菜单【Data】-【Conditions】弹出“Conditions”对话框。
①施加线单元初始条件。
点击线单元按钮,选中下拉菜单中的“line-anip2da”,
在u-1中输入-1,在u-D中输入20e6,点击图中绿色的线,在u-1中输入-1,在u-D中输入15e6,点击图中黄色的线,如图1-11所示。
图1-11
②施加面单元条件。
点击线单元按钮,选中下拉菜单中的“surface-aeq4”,
设置mate Num栏材料代号为1,单击Assign,选择面单击Finish,如图1-12所示。
图1-12
需要说明的是,这几步定义材料,施加载荷的操作没有先后顺序要求,但必须保证不能遗漏某个条件的定义。
2.2划分网格和导出数据
(1).划分网格。
点击菜单【Meshing】-【structured】-【surface】,选择图中四个小的面,加密网格,点击菜单【Meshing】-【Generate】,要求定义单元尺寸大小,点击“OK”按钮,此时弹出“Progress in meshing”进度条,网格划分完毕后弹出消息框显示总的单元数和节点数,如图1-13所示。
图1-13划分网格得到的单元节点信息
点击“OK”按钮后即可得到划分完的网格模型,如图1-14
图1-14网格图
(2)把前处理数据转化为SciFEA所需计算格式。
点击【Files】-【Save】菜单,
保存为GID文件。
点击菜单【Calculate】-【Calculate】,弹出“process info”
消息框,如图1-15所示,点击“ok”按钮,然后退出Gid,至此前处理工作结束。
图1-15 转化数据消息框
3有限元计算
(1) 单击工具条中的按钮弹出如图1-16所示计算模拟窗口。
图1-16 计算模拟窗口
4结果分析
对计算结果进行分析属于后处理,GID提供了丰富的后处理操作,可以从不同角度,不同方式来输出计算结果。
(1)点击工具菜单中的进入后处理,如图1-17所示。
图1-17 进入后处理结果分析
(2)点击菜单【Files】-【Postprocess】进入后处理程序。
(3)点击菜单【View results】-【Contour fill】-【unoda0】显示沿x方向的位
移云图,如图1-18所示。
图1-18
(4)点击菜单【View results】-【Contour fill】-【unodb0】-【ux】显示结果云图,如图1-18所示。
图1-19。
