非参数统计讲义六--多个样本的检验
合集下载
第11讲 独立样本(多样本)非参数检验ppt课件
你会解释吗？
26
本例中，T=？
把T标准化，就得到统计量：
其中，
K
T * T T 服从标准正态分布 T
N 2 nk2
T
k 1
4
K
N (N 1)(2N 5) nk (nk 1)(2nk 5) 2A2 5A1
2 T
k 1
72
K
K
[ nk (nk 1)(nk 2)]( A2 2A1) [ nk (nk 1)]A1
P小于0.05，拒绝原假设，认为分
布不同。
21
R操作： x=matrix(c(2,3,1,4,7,0),ncol=3) chisq.test(x)
22
独立样本（多样本）非参数检验3： Jonckheere-Terpstra 检验
案例4（来源：陈希孺《非参数统计教程》P158
从三个总体中分别抽出大小为5，5，7的样本，如下：
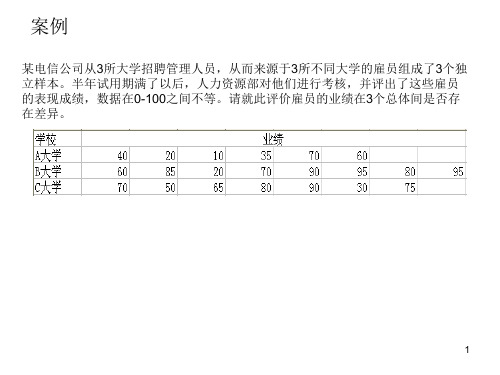
某电信公司从3所大学招聘管理人员，从而来源于3所不同大学的雇员组成了3个独 立样本。半年试用期满了以后，人力资源部对他们进行考核，并评出了这些雇员 的表现成绩，数据在0-100之间不等。请就此评价雇员的业绩在3个总体间是否存 在差异。
14
独立样本（多样本）非参数检验2： Median 检验(中位数检验）
8
9
SPSS操作
10
点击“定义范围”，如下，再 继续，确定！
11
可看出差异较大
拒绝原假设，认为分布 不同
12
R操作
• X1=c( • X2=c( • X3=c( • X4=c( • X=list(x1,x2,x3,x4) • Kruskal.test(x)
13
案例2
文件，npara3.sav，来自张文彤《SPSS统计分析基础教程》 P290
多样本尺度参数的非参数检验
多样本尺度参数的非参数检验
非参数统计方法是一种不基于数据分布假设的统计推断方法，因此适用于各种类型和
尺度的数据。
在研究中，我们经常需要对多个样本进行比较，这时就需要用到多样本尺度
参数的非参数检验方法。
本文将介绍多样本尺度参数的非参数检验方法，包括
Kruskal-Wallis检验、Friedman检验和Page趋势检验。
Kruskal-Wallis检验是一种用于比较三个或更多个独立样本的方法，它是一种秩和检验统计方法，基本思想是将数据合并为一个总体，然后根据秩次进行比较。
Kruskal-Wallis检验的零假设是各样本总体的位置参数相等，即它们来自相同的总体分布。
计算Kruskal-Wallis检验统计量的步骤如下：
1. 对所有样本的数据合并，并按照大小排序；
2. 计算每个样本的秩次和；
3. 计算秩次和的平方和；
4. 根据样本量和秩次和的平方和计算Kruskal-Wallis检验的统计量。
以上三种非参数检验方法都是基于秩和的统计方法，它们都不需要对数据的分布做出
假设，适用于各种类型和尺度的数据。
在研究中，我们需要根据具体情况选择合适的非参
数检验方法，以便对多个样本进行比较，并得出统计显著性结论。
非参数统计讲义六--多个样本的检验
a
Sh apiro-Wil k Statistic df .882 6
Si g. .278
*. Th is is a lower bound of the true significa nce .
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .178 6 .200* a. Lillie fors Significance Correction b. G = 3.00
H c H / C 8.9163 / 0.9925 8.9839
P=CHIDIST(8.9839,2)＝ 0.011199
EXCEL函数可知道，自由度为卡方分布， 在显著水平下0.05，分布的上尾临界值 为5.99，由于8.98>5.99，所以拒绝原 假设。因此秩和最低的B组至少与秩和 最高的A组是不同的。 xx=CHIINV(0.05,2)=5.99
检验是否几个独立样本来自相同总体 （Tests whether several independent samples are from the same population.） 零假设：样本来自的多个独立总体的分布 无显著差异。
方差分析过程关注三个或更多总体的均值 是否相等的问题，数据是被假设成具有正 态分布和相等的方差，此时F检验才能奏效。 F检验对正数据的正态性非常敏感。 当采集的数据常常不能满足正态的条件时 需要用非参数统计。
药 秩
10 11 13 14 15 63 5 16.0 20.5 22.5 29.0 36.0 — —
乙 死亡率
药 秩
4 6 7 9 12 38 5
丙 死亡率
6.5 9.0 12.5 18.0 24.0 — —
统计学非参数检验
c2拟合优度检验
➢ 对定类变量用c2统计量进行统计显著性检验
K-S拟合优度检验
检验分布
中位数的符号检验
单样本K-S检验
➢ 检验总体分布是否为理论分布（正态、Possion、 均匀、指数）
➢ 是以两位苏联数学家Kolmogorov 和 Smirnov 命 名的，全称为Kolmogorov- Smirnov检验。
软件操作：结果分析（2）
卡方 df 渐近显著性 精确显著性 点概率
材料
11.250 2
.004 .003 .000
结果分析（3）
结论：计算出的c2统计量的值为11.250，自由 度为2，相应的p值（渐近显著性）为0.004， 小于a=0.05。所以检验的结论是拒绝总体中消 费者对3种材料的偏好程度无差异的零假设。
根据检验统计量的精确分布或渐进分布，可以 计算出假设检验的p值，从而得出检验的结论。
SPSS K-S检验中检验统计量Z的计算
SPSS K-S检验中p值的计算
有100名儿童每周看电视时间的数据（数据文件：电 视时间.sav）。检验能否认为总体中儿童每周看电视 的时间服从正态分布（显著性水平a=0.05）。
软件操作：数据录入
软件操作：方法设定
选择“分析”“非参数检验”“卡方”，在弹出的对话框中 将“材料”设定为检验变量；单击对话框中的“精确…”，选中 弹出对话框中的“精确”，单击“继续”、“确定”
软件操作：结果分析（1）
观察数 期望数 残差 1.00 55 40.0 15.0 2.00 25 40.0 -15.0 3.00 40 40.0 .0 总数 120
1912年4月15日，豪华巨轮泰坦尼克号与冰山 相撞沉没。当时船上共有2208人，其中男性 1738人，女性470人。
多样本尺度参数的非参数检验
多样本尺度参数的非参数检验
多样本尺度参数的非参数检验是统计学中一种用于比较多个样本组之间差异的方法。
传统的参数检验方法假设数据符合特定的分布，而非参数检验方法不对数据的分布进行任
何假设，因此更适用于一些不满足正态分布的情况。
在进行多样本尺度参数的非参数检验之前，首先需要明确要比较的多个样本组的数量
和特征。
可以比较的多个样本组可以是两个以上，每个样本组内的数据可以是有序（连续），也可以是无序（离散）。
一种常见的多样本非参数检验方法是Kruskal-Wallis检验，也称为多样本方差分析的非参数版本。
Kruskal-Wallis检验的基本思想是比较多个样本组之间的中位数是否存在差异。
该检验的原假设是多个样本组的中位数相等，备择假设是多个样本组的中位数至少有
一个不相等。
Kruskal-Wallis检验的统计量是计算每个样本组的秩之和，然后与期望值进行比较。
如果计算得到的统计量值远大于期望值，则可以拒绝原假设，即认为多个样本组
之间存在差异。
需要注意的是，多样本尺度参数的非参数检验虽然不对数据的分布作出假设，但是仍
然对数据的独立性和随机性有一定的要求。
在进行检验之前，需要检查样本数据是否满足
这些要求。
多样本尺度参数的非参数检验是一种用于比较多个样本组之间差异的方法，常用的方
法有Kruskal-Wallis检验和Friedman检验。
在进行检验之前，需要明确要比较的多个样
本组的数量和特征，并对样本数据的独立性和随机性进行检查。
非参数检验综合概述PPT(30张)
•
9、别再去抱怨身边人善变，多懂一些道理，明白一些事理，毕竟每个人都是越活越现实。
•
10、山有封顶，还有彼岸，慢慢长途，终有回转，余味苦涩，终有回甘。
•
11、人生就像是一个马尔可夫链，你的未来取决于你当下正在做的事，而无关于过去做完的事。
•
12、女人，要么有美貌，要么有智慧，如果两者你都不占绝对优势，那你就选择善良。
多个独立样本的非参数检验
例3 14名新生儿出生体重按其母亲的吸烟习惯分组（A组： 每日吸烟多于20支；B组：每日吸烟少于20支；C组：过去 吸烟而现已戒烟；D组：从不吸烟），具体如下。试问四个 吸烟组出生体重分布是否相同？数据见npc.sav：
A组： 2.7 2.4 2.2 3.4 B组： 2.9 3.2 3.2 C组： 3.3 3.6 3.4 3.4 D组： 3.5 3.6 3.7
两独立样本的非参数检验 （2） 检验统计量
分析结果
给 出 Mann-Whitney U 、 Wilcoxon W 统 计 量 和 Z 值 ， 近 似 值 概 率 （Asymp.Sig）和精确概率值（Exact.sig）均小于0.05，结论一致，表明 猫、兔在缺氧条件下的生存时间的差异具有统计学意义，由平均秩次猫 （15.7）、兔（7.96）来看，可以认为缺氧条件下猫的生存时间长于兔。
•
3、命运给你一个比别人低的起点是想告诉你，让你用你的一生去奋斗出一个绝地反击的故事，所以有什么理由不努力!
•
4、心中没有过分的贪求，自然苦就少。口里不说多余的话，自然祸就少。腹内的食物能减少，自然病就少。思绪中没有过分欲，自然忧就少。大悲是无泪的，同样大悟无言。缘来尽量要惜，缘尽就放。人生本来就空，对人家笑笑，对自己笑笑，笑着看天下，看日出日落，花谢花开，岂不自在，哪里来的尘埃!
多样本的非参数检验课件
它基于等级变量之间的相对大小，通过计算等级相关系数来评估两个变量之间的关 联程度。
弗里德曼等级相关检验在处理有序分类数据时具有较高的实用价值，尤其适用于无 法进行参数检验的情况。
柯尔莫哥洛夫-斯米尔诺夫检验
柯尔莫哥洛夫-斯米尔诺夫检验 是一种非参数统计方法，用于检 验两个独立样本是否来自同一总
体。
缺点
对数据要求高
非参数检验要求数据之间具有相 互独立性，如果数据之间存在相 关性，则检验结果可能不准确。
检验效力较低
相对于参数检验，非参数检验的 检验效力较低，尤其是在样本量 较小的情况下，其检验效力更低。
解释性较差
非参数检验的结果通常只能给出 数据之间的关系是否显著，而不 能给出具体的参数估计或置信区
案例一：不同处理对植物生长的影响
总结词
关联性分析
详细描述
非参数检验还可以用于分析不同处理与植物生长指标之间的关联性。例如，通过Spearman秩相关分析可以确定 植物生长与土壤养分之间的关联程度，为农业生产提供指导。
案例二：不同药物对动物行为的影响
总结词：行为变化
详细描述：在药物研究中，非参数检验可用于分析不同药物对动物行为的影响。例如，可以使用非参 数检验比较不同药物处理组之间动物探索行为、运动能力等指标的差异，以评估药物的安全性和有效 性。
PART 04
非参数检验的优缺点
优点
适用范围广
非参数检验适用于各种类型的数 据，包括定序、定类和定距数据，
甚至对于一些不符合正态分布的 连续数据也可以使用。
稳健性高
非参数检验对数据的分布假设较少， 因此在面对异常值或非正态分布的 数据时，其结果相对稳定。
直观易懂
非参数检验的原理相对简单，其结 果易于解释，不需要复杂的数学背 景也能理解。
弗里德曼等级相关检验在处理有序分类数据时具有较高的实用价值，尤其适用于无 法进行参数检验的情况。
柯尔莫哥洛夫-斯米尔诺夫检验
柯尔莫哥洛夫-斯米尔诺夫检验 是一种非参数统计方法，用于检 验两个独立样本是否来自同一总
体。
缺点
对数据要求高
非参数检验要求数据之间具有相 互独立性，如果数据之间存在相 关性，则检验结果可能不准确。
检验效力较低
相对于参数检验，非参数检验的 检验效力较低，尤其是在样本量 较小的情况下，其检验效力更低。
解释性较差
非参数检验的结果通常只能给出 数据之间的关系是否显著，而不 能给出具体的参数估计或置信区
案例一：不同处理对植物生长的影响
总结词
关联性分析
详细描述
非参数检验还可以用于分析不同处理与植物生长指标之间的关联性。例如，通过Spearman秩相关分析可以确定 植物生长与土壤养分之间的关联程度，为农业生产提供指导。
案例二：不同药物对动物行为的影响
总结词：行为变化
详细描述：在药物研究中，非参数检验可用于分析不同药物对动物行为的影响。例如，可以使用非参 数检验比较不同药物处理组之间动物探索行为、运动能力等指标的差异，以评估药物的安全性和有效 性。
PART 04
非参数检验的优缺点
优点
适用范围广
非参数检验适用于各种类型的数 据，包括定序、定类和定距数据，
甚至对于一些不符合正态分布的 连续数据也可以使用。
稳健性高
非参数检验对数据的分布假设较少， 因此在面对异常值或非正态分布的 数据时，其结果相对稳定。
直观易懂
非参数检验的原理相对简单，其结 果易于解释，不需要复杂的数学背 景也能理解。
多样本尺度参数的非参数检验
多样本尺度参数的非参数检验
多样本尺度参数的非参数检验是数据分析的重要方法之一。
在科学研究和实际应用中，我们常常需要对多个样本的尺度参数进行比较和分析，例如比较多个组的方差是否相等、
多个组的位置参数是否相似等等。
传统的参数检验方法在某些情况下不适用，因此需要使
用非参数检验来解决这些问题。
非参数检验是指不依赖于总体分布形式的统计推断方法，这种方法不对总体分布做出
任何假设，只利用已经观测到的样本数据进行统计推断。
常用的非参数检验方法包括秩和
检验、秩和差检验、克鲁斯卡尔-沃利斯检验等。
秩和检验是一种用来比较两个独立样本的尺度参数的非参数检验方法。
该方法是基于
样本数据的秩次而不是具体的观测值进行统计检验的。
秩和检验的基本思想是将两个样本
合并起来，然后计算秩次总和，最后通过比较秩次总和与预期理论值的差异来判断两个样
本的尺度参数是否有显著差异。
秩和检验的具体计算步骤如下：将两个样本的观测值按照大小顺序进行排列，并为每
个观测值分配一个秩次。
然后计算两个样本的秩次总和，得到统计量。
通过查表或计算得
到的统计量与临界值进行比较，从而判断两个样本的尺度参数是否有显著差异。
通过使用这些非参数检验方法，我们可以比较多个样本的尺度参数，从而得到一些有
关样本总体的重要信息。
这些方法的优点是不对总体分布形式做出任何假设，适用于各种
类型的数据。
非参数检验方法可能缺乏一些参数检验的敏感性，尤其在样本量较小时。
在
选择使用非参数检验方法时，需要权衡各种因素并且谨慎使用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a,b Test S tatistics
Ra nks X G 1.00 2.00 3.00 To tal N 6 6 6 18 Mean Rank 15.00 9.33 4.17
Ch i-Squa re df Asymp. S ig.
X 12.36 3 2 .002
a. Kruska l Wallis Test b. Grouping Variab le: G
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .182 6 .200* a. Lillie fors Significance Correction b. G = 1.00
a
Statistic .964
Sh apiro-Wil k df 6
9D 存活日数 2 2 2 3 4 4 4 5 7 7 Ri ni
i
11C 秩 2 2 2 4.5 7 7 7 10.5 21 21 84 10 8.40 存活日数 5 5 6 6 6 7 8 10 12 秩 10.5 10.5 15.5 15.5 15.5 21 24 26.5 30
R
— — —
169 9 18.78
组间平方和 H 全体样本的秩方差
n(n 1) 全体样本的秩方差 ＝ 12
为做出精确的判断，我们计算K-W统计 量H，以反映平均秩间的差异。
k 12 H＝ ni ( Ri R ) 2 N N +1 i 1 （ ）
R 12 n 3( N 1) N ( N 1) i 1 i
H c H / C 8.9163 / 0.9925 8.9839
P=CHIDIST(8.9839,2)＝ 0.011199
EXCEL函数可知道，自由度为卡方分布， 在显著水平下0.05，分布的上尾临界值 为5.99，由于8.98>5.99，所以拒绝原 假设。因此秩和最低的B组至少与秩和 最高的A组是不同的。 xx=CHIINV(0.05,2)=5.99
5 6 7
95 90 80
40 35
90 70 75
25
70
1
1 1 1
检验假设 H0：三所大学的学生成绩相等 H1：并非三所大学的学生成绩都相等
60 85
95
90 80 60 20 30 15 40 35
1
1 1 2 2 2 2 2 2
50
70 60 80 90 70 75
3
3 3 3 3 3 3
N 1.00 2.00 3.00 To tal 6 6 6 18
Mean St d. Deviatio n St d. Error 51.83 33 10.18 659 4.158 66 34.83 33 8.109 67 3.310 76 21.83 33 6.145 46 2.508 87 36.16 67 14.85 716 3.501 87
X G
45 38 56 1 1 1
60
47 65 30
1
1 1 2
40
28 44 25
2
2 2 2
42
22 19 15 31 27
2
3 3 3 3 3
软件一 软件二 软件三 45 30 22 38 40 19 56 28 15 60 44 31 47 25 27 65 42 17
Si g. .851
*. Th is is a lower bound of the true significa nce .
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .238 6 .200* a. Lillie fors Significance Correction b. G = 2.00
雇员
1
大学A
25
统一编 秩
3
大学B
60
统一编 秩
9
大学C
50
统一编 秩
7
2 3
4 5 6
70 60
85 95 90
12 9
17 20 18.5
20 30
15 40 35
2 4
1 6 5
70 60
80 90 70
12 9
15.5 18.5 12
7
秩和
80
组A秩 和
15.5
95 组B秩 和 27
75
组C秩 和
Minim um 38.00 25.00 15.00 15.00
Maximum 65.00 44.00 31.00 65.00
分组数据的正态性检验
SORT CASES BY G . SPLIT FILE SEPARATE BY G . EXAMINE VARIABLES=X /PLOT BOXPLOT STEMLEAF NPPLOT /COMPARE GROUP /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
14
88
12 (95) (27 ) (88) H 3(20 1) 8.9163 20(21) 7 6 7
2 2 2
计算校正系数C
(33 3 33 3 2 3 2 2 3 2) C 1 0.9925 3 20 20
例1：某制造商雇用了来自三个本地大学的雇员作
为管理人员。最近，公司的人事部门已经收集信息并 考核了年度工作成绩。从三个大学来的雇员中随机地 抽取了三个独立样本，见表所示。制造商想知道是否 来自这三个不同的大学的雇员在管理岗位上的表现有 所不同。
雇员 1 2 3 4 大学A 25 70 60 85 大学B 60 20 30 15 大学C 50 70 60 80
检验是否几个独立样本来自相同总体 （Tests whether several independent samples are from the same population.） 零假设：样本来自的多个独立总体的分布 无显著差异。
方差分析过程关注三个或更多总体的均值 是否相等的问题，数据是被假设成具有正 态分布和相等的方差，此时F检验才能奏效。 F检验对正数据的正态性非常敏感。 当采集的数据常常不能满足正态的条件时 需要用非参数统计。
k
2 i
给出显著性水平，若K-W统计量H的显著 性小于该显著性水平，则拒绝零假设，认 为样本来自的多个独立总体的分布存在显 著性差异。近似服从df=K-1的卡方分布
每组样本小于5时为小样本，查表 大于等于≥5时为大样本。近似卡方分布
例：某公司需要购买一套文字软件， 有三个产品，选择18个员工分成三组 学习，比较三个软件学习时间最短。
a
Sh apiro-Wil k Statistic df .882 6
Si g. .278
*. Th is is a lower bound of the true significa nce .
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .178 6 .200* a. Lillie fors Significance Correction b. G = 3.00
K个样本检验
K个独立样本检验
K个相关样本检验
一、多个独立样本检验
概述：多样本检验推断样本来自的多个 独立总体的分布是否存在显著性差异。 其方法是：通过检验样本的均值或中位 数是否存在显著性差异，以推断样本来 自的多个独立总体的分布是否存在显著 性差异。多样本检验提供了常用的三种 检验方法:克拉夏尔-瓦里斯检验法 （Kruskal-wallis H）、JonchheereTerpstra和中位数(Median)检验法。
DSC1 存活日数 秩 3 4.5 5 10.5 6 15.5 6 15.5 6 15.5 7 21 7 21 9 25 10 26.5 11 28.5 11 28.5 212 — 11 — — 19.27
克拉夏尔-瓦里斯检验法
基本思想： 如果样本来自的总体分布相同，每个独立样本应 均匀地分布于在该总体之中。我们可以将这些独 立样本混合按升序排序，求出每个观察值的秩， 然后对多组样本的秩求平均数，每组的平均秩应 大致相同。
因为秩统计量的分布与总体分布无关， 可以摆脱总体分布的束缚。
将数据样本转换成秩样本后，再对这个 秩样本进行方差分析。
Kruskal-Wallis检验
K-W法将多个样本数混合并按升序排序, 求出其秩对多个样本的秩分别求平均秩 序如果各样本的平均秩大致相等,则认为 多个总体分布无显著差异
有结点（tie)需修正！
表 8–9 三种药物杀灭钉螺的死亡率%比较
甲 死亡率
32.5 35.5 40.5 46.0 49.0 Ri ni
药 秩
10 11 13 14 15 63 5 16.0 20.5 22.5 29.0 36.0 — —
乙 死亡率
药 秩
4 6 7 9 12 38 5
丙 死亡率
6.5 9.0 12.5 18.0 24.0 — —
药 秩
1 2 3 5 8 19 5
表 8–10 小白鼠接种三种不同菌型伤寒杆菌的存活日数比较
proc print data=rankings; run;
proc npar1way data=tj08; class g; var x; run;
H0:三种软件学习时间相等
H1：并非所有软件学习时间都相同
NPAR TESTS /K-W=X BY G(1 3) /MISSING ANALYSIS.
Ra nks X G 1.00 2.00 3.00 To tal N 6 6 6 18 Mean Rank 15.00 9.33 4.17
Ch i-Squa re df Asymp. S ig.
X 12.36 3 2 .002
a. Kruska l Wallis Test b. Grouping Variab le: G
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .182 6 .200* a. Lillie fors Significance Correction b. G = 1.00
a
Statistic .964
Sh apiro-Wil k df 6
9D 存活日数 2 2 2 3 4 4 4 5 7 7 Ri ni
i
11C 秩 2 2 2 4.5 7 7 7 10.5 21 21 84 10 8.40 存活日数 5 5 6 6 6 7 8 10 12 秩 10.5 10.5 15.5 15.5 15.5 21 24 26.5 30
R
— — —
169 9 18.78
组间平方和 H 全体样本的秩方差
n(n 1) 全体样本的秩方差 ＝ 12
为做出精确的判断，我们计算K-W统计 量H，以反映平均秩间的差异。
k 12 H＝ ni ( Ri R ) 2 N N +1 i 1 （ ）
R 12 n 3( N 1) N ( N 1) i 1 i
H c H / C 8.9163 / 0.9925 8.9839
P=CHIDIST(8.9839,2)＝ 0.011199
EXCEL函数可知道，自由度为卡方分布， 在显著水平下0.05，分布的上尾临界值 为5.99，由于8.98>5.99，所以拒绝原 假设。因此秩和最低的B组至少与秩和 最高的A组是不同的。 xx=CHIINV(0.05,2)=5.99
5 6 7
95 90 80
40 35
90 70 75
25
70
1
1 1 1
检验假设 H0：三所大学的学生成绩相等 H1：并非三所大学的学生成绩都相等
60 85
95
90 80 60 20 30 15 40 35
1
1 1 2 2 2 2 2 2
50
70 60 80 90 70 75
3
3 3 3 3 3 3
N 1.00 2.00 3.00 To tal 6 6 6 18
Mean St d. Deviatio n St d. Error 51.83 33 10.18 659 4.158 66 34.83 33 8.109 67 3.310 76 21.83 33 6.145 46 2.508 87 36.16 67 14.85 716 3.501 87
X G
45 38 56 1 1 1
60
47 65 30
1
1 1 2
40
28 44 25
2
2 2 2
42
22 19 15 31 27
2
3 3 3 3 3
软件一 软件二 软件三 45 30 22 38 40 19 56 28 15 60 44 31 47 25 27 65 42 17
Si g. .851
*. Th is is a lower bound of the true significa nce .
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .238 6 .200* a. Lillie fors Significance Correction b. G = 2.00
雇员
1
大学A
25
统一编 秩
3
大学B
60
统一编 秩
9
大学C
50
统一编 秩
7
2 3
4 5 6
70 60
85 95 90
12 9
17 20 18.5
20 30
15 40 35
2 4
1 6 5
70 60
80 90 70
12 9
15.5 18.5 12
7
秩和
80
组A秩 和
15.5
95 组B秩 和 27
75
组C秩 和
Minim um 38.00 25.00 15.00 15.00
Maximum 65.00 44.00 31.00 65.00
分组数据的正态性检验
SORT CASES BY G . SPLIT FILE SEPARATE BY G . EXAMINE VARIABLES=X /PLOT BOXPLOT STEMLEAF NPPLOT /COMPARE GROUP /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
14
88
12 (95) (27 ) (88) H 3(20 1) 8.9163 20(21) 7 6 7
2 2 2
计算校正系数C
(33 3 33 3 2 3 2 2 3 2) C 1 0.9925 3 20 20
例1：某制造商雇用了来自三个本地大学的雇员作
为管理人员。最近，公司的人事部门已经收集信息并 考核了年度工作成绩。从三个大学来的雇员中随机地 抽取了三个独立样本，见表所示。制造商想知道是否 来自这三个不同的大学的雇员在管理岗位上的表现有 所不同。
雇员 1 2 3 4 大学A 25 70 60 85 大学B 60 20 30 15 大学C 50 70 60 80
检验是否几个独立样本来自相同总体 （Tests whether several independent samples are from the same population.） 零假设：样本来自的多个独立总体的分布 无显著差异。
方差分析过程关注三个或更多总体的均值 是否相等的问题，数据是被假设成具有正 态分布和相等的方差，此时F检验才能奏效。 F检验对正数据的正态性非常敏感。 当采集的数据常常不能满足正态的条件时 需要用非参数统计。
k
2 i
给出显著性水平，若K-W统计量H的显著 性小于该显著性水平，则拒绝零假设，认 为样本来自的多个独立总体的分布存在显 著性差异。近似服从df=K-1的卡方分布
每组样本小于5时为小样本，查表 大于等于≥5时为大样本。近似卡方分布
例：某公司需要购买一套文字软件， 有三个产品，选择18个员工分成三组 学习，比较三个软件学习时间最短。
a
Sh apiro-Wil k Statistic df .882 6
Si g. .278
*. Th is is a lower bound of the true significa nce .
b Tests of Normality
X
Ko lmogorov-Smirnov Statistic df Si g. .178 6 .200* a. Lillie fors Significance Correction b. G = 3.00
K个样本检验
K个独立样本检验
K个相关样本检验
一、多个独立样本检验
概述：多样本检验推断样本来自的多个 独立总体的分布是否存在显著性差异。 其方法是：通过检验样本的均值或中位 数是否存在显著性差异，以推断样本来 自的多个独立总体的分布是否存在显著 性差异。多样本检验提供了常用的三种 检验方法:克拉夏尔-瓦里斯检验法 （Kruskal-wallis H）、JonchheereTerpstra和中位数(Median)检验法。
DSC1 存活日数 秩 3 4.5 5 10.5 6 15.5 6 15.5 6 15.5 7 21 7 21 9 25 10 26.5 11 28.5 11 28.5 212 — 11 — — 19.27
克拉夏尔-瓦里斯检验法
基本思想： 如果样本来自的总体分布相同，每个独立样本应 均匀地分布于在该总体之中。我们可以将这些独 立样本混合按升序排序，求出每个观察值的秩， 然后对多组样本的秩求平均数，每组的平均秩应 大致相同。
因为秩统计量的分布与总体分布无关， 可以摆脱总体分布的束缚。
将数据样本转换成秩样本后，再对这个 秩样本进行方差分析。
Kruskal-Wallis检验
K-W法将多个样本数混合并按升序排序, 求出其秩对多个样本的秩分别求平均秩 序如果各样本的平均秩大致相等,则认为 多个总体分布无显著差异
有结点（tie)需修正！
表 8–9 三种药物杀灭钉螺的死亡率%比较
甲 死亡率
32.5 35.5 40.5 46.0 49.0 Ri ni
药 秩
10 11 13 14 15 63 5 16.0 20.5 22.5 29.0 36.0 — —
乙 死亡率
药 秩
4 6 7 9 12 38 5
丙 死亡率
6.5 9.0 12.5 18.0 24.0 — —
药 秩
1 2 3 5 8 19 5
表 8–10 小白鼠接种三种不同菌型伤寒杆菌的存活日数比较
proc print data=rankings; run;
proc npar1way data=tj08; class g; var x; run;
H0:三种软件学习时间相等
H1：并非所有软件学习时间都相同
NPAR TESTS /K-W=X BY G(1 3) /MISSING ANALYSIS.