工程光学习题解答--第二章-理想光学系统
2理想光学系统2
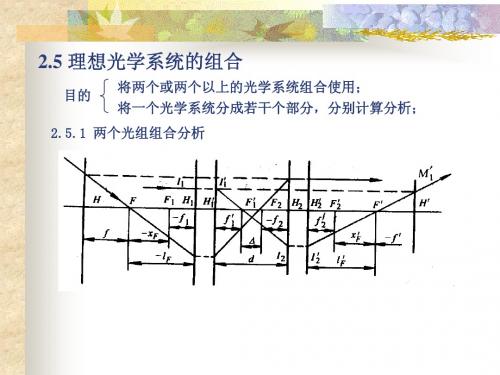
h2 175 tgu 2 ' = tgu 2 + = −0.25 + = 0.1 f2 ' 500 h2 175 100 lF = = = 1750mm ∴ f '= = 1000mm tgu 2 ' 0.1 0. 1
物方焦点位于第一面左1750mm处 而焦距为1000mm, 物方焦点位于第一面左1750mm处,而焦距为1000mm,所以主面位 1750mm 1000mm 于第一面左750mm 750mm处 于第一面左750mm处。
xF
f1 f1 ' xF = ∆
注意: 注意: x F 为F1与 F之间距离
x F < 0 则F在F1左侧
组合光组的 焦距
H'F' M'H' = 像方焦距: ⊿M’F H ∽⊿I H F 像方焦距: ⊿M F’H’∽⊿I2’H2’F’ → F'H2 ' H2 'I2 '
I 1 ' H 1 ' H 1 ' F1 ' = ⊿I2H2F1’∽⊿I1’H1’F1 → ∽⊿I H F H2I2 F1 ' H 2
n −1 dρ1 透镜组像方主面到第二面主面的距离 主面位置: 主面位置: l H ' = − f '⋅ n n −1 lH = − f ' dρ 2 透镜组物方主面到第一面主面的距离 n
结论: 透镜结构参数r 结论: 透镜结构参数r1,r2,d,n决定光学性能 f(焦距) 焦距) 物像方主面位置) l H , l H ' (物像方主面位置)
H ' F ' H 1 ' F1 ' = 所以 F ' H 2 ' F1 ' H 2
工程光学2-2

第四节 里想光学系统的放大率
一、垂轴放大率
第二章 理想光学系统
y′ f x′ l ′f β = =− =− =− y x f′ lf ′
1.微小位移时的 α
f =− f ′
l′ = l
二、轴向放大率
xx ' = ff '
⇒ xdx ' + x ' dx = 0
dx ' dl ' α = = dx dl
若物空间与像空间的介质折射率相等 n=n'
f =−f′
β =
l' l
四 理想光学系统两焦距之间的关系
第二章
理想光学系统
∵ (−l )tg (−u ) = ltgu = l ′tgu ′ = h ∵ −( x + f )tg (−u ) = ( x + f )tgu = ( x′ + f ′)tgu ′…… (1) ′ y′ f x′ fy f y′ ∵ β = = − = − ⇒ x = − ; ; x′ = − 带入(1 )式得: y x f′ y′ y ′ ′ fytgu = − f y′tgu ′ ∵ tgu ≈ u ⇒ fyu = − f y′u ′ ∵ nyu = n′y′u ′ f′ n′ ∴ = − ; 当n = n ′ ⇒ f ′ = − f f n
解:这是个两次成像的问题,设对L1的物距、像距分别为l1和l1′ ′ 对L 2为l2 和l2 , 注意l2 = (l1′ − d ), 则由高斯公式: 1 1 1 1 1 1 − = ⇒ − = l1′ l1 f1′ l1′ −10 5 1 1 1 1 1 1 1 1 1 − = ⇒ − = ⇒ − = ′ ′ ′ l 2 l2 f 2′ l2 (l1′ − d ) f 2′ l2 (l1′ − 5) −10 ′ ⇒ l1′ = 10.00cm; l2 = −5.00cm; l2 = 10.00cm ′ l1′ l2 10 10 β1 = − = − = −1.00; β 2 = − = − = 2.00 l1 10 −5.0 l2
工程光学第二章练习参考答案

(5)
n sinU NA sinU 0.1
U 5.73917 D 2( ltgU ) 2(45 tg 5.73917 ) 9.045mm
(5)
lz 160 D D' 1.667 9.00mm lz ' 29.63
(6)
-l (6)
l’ 180 -lz
h3 h2 d 2 tgu2 ' 12 10 0.04 11.6 tgu3 ' tgu3 h3 11.6 0.04 0.156 f3' 100
第二章 17
F’ 求物方参数。反向算。 h1=10
H’
u3’
f’
h1 10 f ' 64.102564 tgu3 ' 0.156 h3 11.6 lF ' 74.35897 tgu3 ' 0.156
第二章 17
求物方参数。反向算。
h1=10
H’
u3’
F’
f1 ' 50, f 2 ' 50, f 3 ' 100 d1 d 2 10
f’
lF’
tgu1 ' tgu2
h1
f1 '
10
50
0.2
h2 h1 d1tgu1 ' 10 10 ( 0.2) 12 tgu2 ' tgu3 tgu2 h2 f2' 0.2 12 50 0.04
第二章 3
y H -f d 1140mm 7200mm H’ f’ y’
l ' l 10
l d l ' 7200 2 f ' d 1140 1 1 1 l' l f'
工程光学习题参考答案第二章理想光学系统
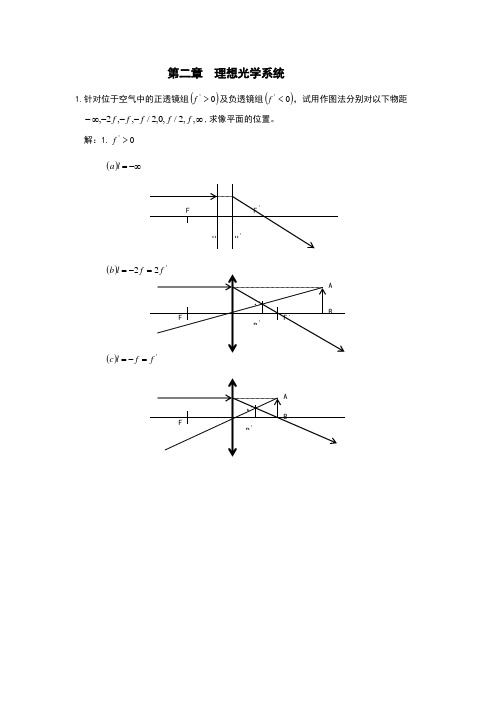
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′= (3)x ′= (4)x ′= (5)x ′=(6)x ′=3.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
工程光学基础教程-习题答案(完整)

第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s , 当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学第02章

(3) 一个共轴理想光学系统,如果已知两对共轭面的位置和放大率, 或者一对共轭面的位置和放大率,以及轴上两对共轭点的位置,则 其它一切物点的共轭像点都可以根据这些已知的共轭面和共轭点来 表示。
(2)实例
① 轴外点 ② 轴上点:(方法一,方法二) ③ 轴上点经两个光组
B’
A
H’
F
H
F’
A’
B
① 过物方焦点的光线,经系统后平行于光轴; ② 平行于光轴的入射光线,经系统后过像方焦点。
(2)实例
① 轴外点 ② 轴上点:(方法一,方法二) ③ 轴上点经两个光组
A
H’
A’
A
F
H F’
xx' f f' (牛顿公式)
(2)高斯公式 以主点为坐标原点,来规定物(像)位置: • 主点→物(像)与光传播方向一致,为(+) • 物距用 l 表示,像距用 l ’ 表示
f f' l l' 1
(高斯公式)
※① 牛顿公式推导:
M
M’
B’
y’
A
H’
-y
F
H
F’
A’
B
N
N’
-x
-f
f’
x’
-l
l’
• 平均轴向放大率: 定义—— x' x2' x1'
x x2 x1
x'f'ff'ff'fx2x1
x2 x1
x1x2
x f 1 x '2 f f f' x f 1 x f 2 f f' 12 n n ' 12
工程光学习题解答--第二章-理想光学系统
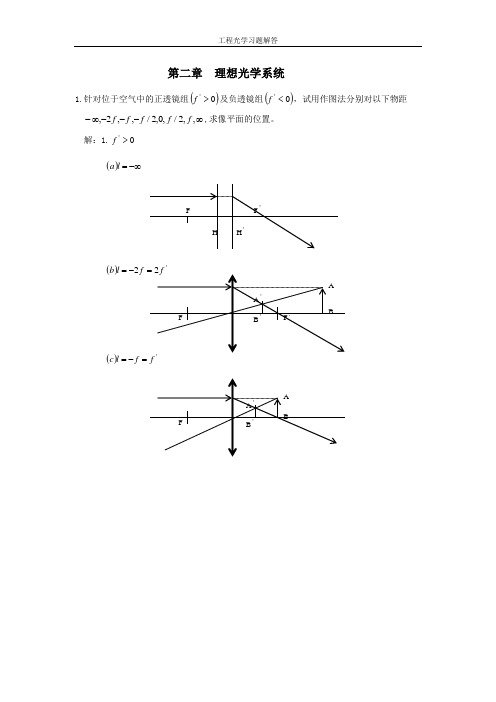
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c=-=()/f l d -=()0=l e()/f lf =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′=0.5625 (3)x ′=0.703 (4)x ′=0.937 (5)x ′=1.4(6)x ′=2.813.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少? 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
理想光学系统

第三节 理想光学系统的物像关系
几何光学的基本内容之一是求像,即对于确定的 光学系统,给定物体的位置、大小、方向,求像的位 置、大小、正倒及虚实。常用的用以求取物象位置关 系的方法有二种:一为图解法,一为解析法。 一、图解法求像
图解法求像的定义
已知一个光学系统的主点(主面)和焦点的位置, 利用光线通过这些基点后表现的性质,对物空间给 定的点、线和面,通过画图追踪典型光线的方法求 像。
工程光学
石家庄铁道大学
机械工程学院
总第三讲
第二章 理想光学系统
Perfect Optical System
光学系统的具体结构(r、d、n) 实际光学系统与高斯(近轴)光学系统 研究光学系统成像的目的在于将高斯光学 完善成像的理论推广到任意大的空间,本 章的主要内容即介绍建立在高斯光学之上 的所谓理想光学系统,并研究理想光学系 统的主要光学参数、成像关系、放大率以 及光组组合和透镜。
可选择的典型光线和可利用的性质: ①平行于光轴入射的光线,经系统后过像方焦点; ②过物方焦点的光线,经过系统后平行于光轴; ③倾斜于光轴入射的平行光束经过系统后会交于像 方焦平面上的一点; ④自物方焦平面上一点发出的光束经系统后成倾斜 于光轴的平行光束; ⑤共轭光线在主面上的投射高度相等。 欲在理想光学系统条件下确定像点位置,只需 求出其对应物点发出的两条特定光线在像空间的共 轭光线,其交点即为所求像点。
总第三讲
3、主点与主平面
Q
Q'
h
f
'
h tanU '
F
U
H
H'
U
'
h'
F'
f
h tan U
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程光学习题解答--第二章-理想光学系统
第二章 理想光学系统
1.针对位于空气中的正透镜组()0
'
>f
及负透镜组
()0
'
<f
,试用作图法分别对以下物距
∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'
>f ()-∞=l a
()'
l b
()'
f f l c
=-=
()
d
()l e ()2/'2/f
f l f -==
')(f f l g -==
l
h-
=
=
'
f
2 (f
2
)
+∞
l i)(
= Array
2.0'<f
c(
(
l g )(
+∞
=l i )(
2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F点为坐标原点)=x,2,4,6,8,
-
-
∝
-处,
-
-
m
10
,m
m
m
m-
试求照相底片应分别放在离物镜的像方焦面多
远的地方。
解:(1)x= -∝,xx′=ff′得到:x′=0
(2)x′=0.5625
(3)x′=0.703
(4)x′=0.937
(5)x′=1.4
(6)x′=2.81
3.设一系统位于空气中,垂轴放大率*
β,由
=10
-
物面到像面的距离(共轭距离)为7200mm,物镜两焦点间距离为1140mm。
求该物镜焦距,
并绘出基点位置图。
解:
∵ 系统位于空气中,f
f
-='
10'
'-===
l
l y y β
由已知条件:1140)('
=+-+x f f
7200)('
=+-+x l l
解得:mm
f
600'
= mm x 60-=
4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:
3
1
'
11-==l l β
⇒
()
183321'1--=-=l l l ①
4
2
'2
2-==l l β ⇒ 2
'2
4l l -=
②
18
21+-=-l l ⇒ 18
21
-=l l
③
'
/1/1/11'1f l l =- '
/1/1/12'2f l l =- 将①②③代入④中得 mm
l
2702
-= mm
l
1080'2
-=
∴ mm f 216'=
方法二: 31
1
-=-
=x f
β
42
2
-=-
=x f
β
⇒
mm
f 216-=
18
12
=-x x
方法三: 12
)4)(3(21''=--==∆∆=ββαn
n x x
2161812'
-=⨯=∆x
'
'
f
x -=βΘ
143''
'
'2
'121
=+-=∆=+-=
-∴f
x f
x x ββ
mm
x f
216''
=∆=∴
5.一个薄透镜对某一物体成实像,放大率为⨯
-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少? 解:
⇒ 2
'2
1
'
1
/1/1/1/1l l l l -=- ④
6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
解:由已知得:
2
1
1'11-
==l l β
1
2
'2
2-==l l β 100
21
+-=-l l
由高斯公式:2
'2
1
'1
1111l l l l -=-
解得:mm l
f 10022
'=-=
7.希望得到一个对无限远成像的长焦距物镜,焦距mm
f
1200'
=,由物镜顶点到像面的距离L=mm 700,
由系统最后一面到像平面的距离(工作距)为
,按最简单结构的薄透镜系统考虑,求系
统结构,并画出光路图。
解:
-
l '
1
100-l 2
l '2
8. 一短焦距物镜,已知其焦距为mm 35,筒长L=mm 65,工作距mm
l
k
50'=,按最简单结构的薄透镜系
统考虑,求系统结构。
解:
9.已知一透镜5
.1,50,300,2002
1
==-=-=n mm d mm r
mm r ,求其焦
距,光焦度,基点位置。
解:已知5
.1,50,300,2002
1
==-=-=n mm d mm r
mm r 求:,'
f ϕ,基点位置。
1
2
1
2
2
1
69.0)
1())(1('/1--=-+--==m d n
n n f ρ
ρρρϕ
mm
f 1440'
-=
mm d n n f l F
1560)1
1('1'-=--
=ρ mm
d n n f l F 1360)1
1('2=-+-=ρ
mm
d n n f l H 120)1('1'
-=--=ρ
mm d n
n f l
H
80)1
(
'2-=-=ρ
10. 一薄透镜组焦距为mm 100,和另一焦距为mm 50的薄透镜组合,其组合焦距仍为mm 100,问两薄透镜的相对位置,并求基点位置,以图解法校核之。
解:
11. 长mm 60,折射率为1.5的玻璃棒,在其两端磨成曲率半径为mm 10的凸球面,试求其焦距及基点位置。
解:
12. 一束平行光垂直入射到平凸透镜上,会聚于透镜后mm
480处,如在此透镜凸面上镀银,则平
行光会聚于透镜前mm
80处,求透镜折射率和凸面曲率半径。
解:
13.一块厚透镜,,
30,320,120,6.12
1
mm d mm r
mm r n =-===试求该
透镜焦距和基点位置。
如果物距m
l
51
-=时,问像
在何处?如果平行光入射时,使透镜绕一和光轴垂直的轴转动,而要求像点位置不变,问该轴应装在何处? 解:
⑴[]
mm d n r r n n r
nr f 27.149)1()()1('12
21=-+--= mm d n n f l F 28.135)1
1(1''
=--
=ρ
mm
d n n f l F 02.144)1
1(2'-=-+-=ρ
mm
d n n f l H 99.1311''
-=--=ρ
mm
d n
n f l H 25.51
2'=--=ρ
⑵mm
l l
l H 25.500525.550001
-=--=-=
'
'
1
11f
l l =
-Θ mm
l 86.153'
=∴
mm l l l H
89.13999.1386.153'''2=-=+=
⑶绕过像方节点位置轴旋转,'
H 点处。
14 思考题:
1、同一物体经针孔或平面镜所成的像有何不同?
答:由反射定律可知,平面镜的物和像是关于镜面对称的。
坐标由右旋坐标
系变为像的左旋坐标系,因此像和物左右互易上下并不颠倒。
即物体经平面镜生 成等大、正立的虚像。
物体经针孔成像时,物点和像点之间相对于针孔对称。
右旋坐标系惊针孔所
成的像仍为右旋坐标系,因此像和物上下左右都是互易的,而且像的大小与针孔
到接收屏的距离有关。
即物体经针孔生成倒立的实像。
2、一束在空气中波长为589.3nm 的钠黄光,从
空气进入水中时,它的波长将变
为多少?在水中观察这束光时,其颜色会改变吗?
3、凹透镜可否单独用作放大镜?
答:因凹透镜对实物只能生成缩小的虚像,当人眼通过凹透镜观察物体时,
人眼对缩小的虚像的视角总是小于(最多等于)不用凹透镜时直接观察物体的视
角(这是人眼须紧贴凹透镜),故凹透镜的视角放大率不可能大于1。
所以凹透
镜不能单独用作放大镜。
4、薄透镜的焦距与它所在介质是否有关?凸透镜一定是会聚透镜吗?凹透镜一
定是发散透镜吗?。
