线性规划解决实际问题专项练习
线性规划题及答案
线性规划题及答案线性规划是一种数学优化方法，用于在给定的约束条件下，寻找一个线性目标函数的最优解。
在实际应用中，线性规划可以用于解决各种决策问题，如生产计划、资源分配、投资组合等。
以下是一个线性规划问题的示例：问题描述：某工厂生产两种产品A和B，每天的生产时间为8小时。
产品A每件需要2小时的加工时间，产品B每件需要3小时的加工时间。
每天的加工时间总共有16个小时。
产品A的利润为100元/件，产品B的利润为150元/件。
工厂的目标是最大化每天的总利润。
解决步骤：1. 定义变量：设产品A的生产数量为x，产品B的生产数量为y。
2. 建立目标函数：目标函数是每天的总利润，即：Z = 100x + 150y。
3. 建立约束条件：a) 加工时间约束：2x + 3y ≤ 16，表示每天的加工时间不能超过16小时。
b) 非负约束：x ≥ 0，y ≥ 0，表示产品的生产数量不能为负数。
4. 求解最优解：将目标函数和约束条件带入线性规划模型，使用线性规划算法求解最优解。
最优解及分析：经过计算，得到最优解为x = 4，y = 4，此时总利润最大为100 * 4 + 150 * 4 = 1000元。
通过最优解的分析可知，工厂每天应生产4件产品A和4件产品B，才能达到每天最大利润1000元。
同时，由于加工时间约束，每天的加工时间不能超过16小时，这也是生产数量的限制条件。
此外，也可以通过灵敏度分析来了解生产数量的变化对最优解的影响。
例如，如果产品A的利润提高到120元/件，而产品B的利润保持不变，那么最优解会发生变化。
在这种情况下，最优解为x = 6，y = 2，总利润为120 * 6 + 150 * 2 = 960元。
这表明，产品A的利润提高会促使工厂增加产品A的生产数量，减少产品B 的生产数量，以获得更高的总利润。
总结：线性规划是一种重要的数学优化方法，可以用于解决各种实际问题。
通过建立目标函数和约束条件，可以将实际问题转化为数学模型，并通过线性规划算法求解最优解。
线性规划的应用习题
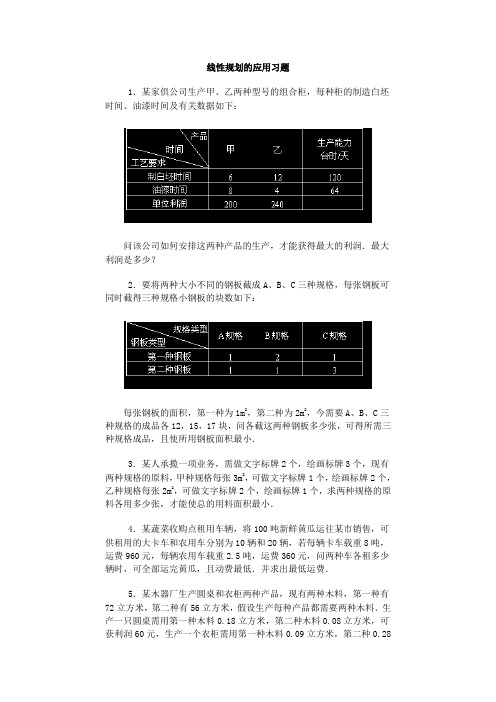
线性规划的应用习题1．某家俱公司生产甲、乙两种型号的组合柜，每种柜的制造白坯时间、油漆时间及有关数据如下：问该公司如何安排这两种产品的生产，才能获得最大的利润．最大利润是多少？2．要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格小钢板的块数如下：每张钢板的面积，第一种为1m2，第二种为2m2，今需要A、B、C三种规格的成品各12，15，17块，问各截这两种钢板多少张，可得所需三种规格成品，且使所用钢板面积最小．3．某人承揽一项业务，需做文字标牌2个，绘画标牌3个，现有两种规格的原料，甲种规格每张3m2，可做文字标牌1个，绘画标牌2个，乙种规格每张2m2，可做文字标牌2个，绘画标牌1个，求两种规格的原料各用多少张，才能使总的用料面积最小．4．某蔬菜收购点租用车辆，将100吨新鲜黄瓜运往某市销售，可供租用的大卡车和农用车分别为10辆和20辆，若每辆卡车载重8吨，运费960元，每辆农用车载重2.5吨，运费360元，问两种车各租多少辆时，可全部运完黄瓜，且动费最低．并求出最低运费．5．某木器厂生产圆桌和衣柜两种产品，现有两种木料，第一种有72立方米，第二种有56立方米，假设生产每种产品都需要两种木料．生产一只圆桌需用第一种木料0.18立方米，第二种木料0.08立方米，可获利润60元，生产一个衣柜需用第一种木料0.09立方米，第二种0.28立方米，可获利润100元，木器厂在现有木料情况下，圆桌和衣柜应各生产多少，才能使所获利润最多．线性规划的应用习题答案1．设x，y分别为甲、乙两种柜的日产量，目标函数z=200x＋240y，线性约束条件：作出可行域．z最大=200×4＋240×8=2720答：该公司安排甲、乙两种柜的日产量分别为4台和8台，可获最大利润2720元．2．设需截第一种钢板x张，第二种钢板y张，所用钢板面积zm2．目标函数z=x＋2y，线性约束条件：作出可行域．作一组平行直线x＋2y=t．的整点中，点(4，8)使z取得最小值．答：应截第一种钢板4张，第二种钢板8张，能得所需三种规格的钢板，且使所用钢板的面积最小．3．设用甲种规格原料x张，乙种规格原料y张，所用原料的总面积是zm2，目标函数z=3x＋2y，线性约束条件，作出可行域．作一组平等直线3x＋2y=t．A不是整点，A不是最优解．在可行域内的整点中，点B(1，1)使z取得最小值．z最小=3×1＋2×1=5，答：用甲种规格的原料1张，乙种原料的原料1张，可使所用原料的总面积最小为5m2．4．设租用大卡车x辆，农用车y辆，最低运费为z元．z=960x＋360y．线性约束条件是：作出可行域．作直线960x＋360y=0．即8x＋3y=0，向上平移至过点B(10，8)时，z=960x＋360y取到最小值．z最小=960×10＋360×8=12480答：大卡车租10辆，农用车租8辆时运费最低，最低运费为12480元．5．设圆桌和衣柜的生产件数分别为x、y，所获利润为z，则z=6x ＋10y．作出可行域．即M(350，100)．当直线6x＋10y=0即3x＋5y=0平移到经过点M(350，100)时，z=6x ＋10y最大．答：圆桌和衣柜应分别生产350件、100件时，才能获得最大利润．。
线性规划解决实际问题专项练习
学科：数学教学内容：研究性课题与实习作业：线性规划的实际应用【自学导引】1．线性规划问题的数学模型是已知(这里“≤”也可以是“≥”或“＝”号)，其中a ij (i ＝1，2，…，n ，j ＝1，2，…，m )，b i (i ＝1，2，…，m )都是常量，x j (j ＝1，2，…，m )是非负变量，求z ＝c 1x 1＋c 2x 2＋…＋c m x m 的最大值或最小值，这里c j (j ＝1，2，…，m )是常量．2．线性规划常见的具体问题有物质调运问题、产品安排问题、下料问题．【思考导学】1．应用线性规划解决实际问题的一般步骤是什么？答：一般步骤是①设出变量，列出线性约束条件和线性目标函数；②利用图解法求出最优解，进而求得目标函数的最大(或最小)值．2．线性规划的理论和方法主要在哪两类问题中得到应用？答：一是在人力、物力、资金等资源一定的条件下，如何使用它们来完成最多的任务；二是给定一项任务，如何合理安排和规划，能以最少的人力、物力、资金等资源来完成该项任务．【典例剖析】［例1］ 已知甲、乙两煤矿每年的产量分别为200万吨和260万吨，需经过东车站和西车站两个车站运往外地．东车站每年最多能运280万吨煤，西车站每年最多能运360万吨煤，甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨，乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨．煤矿应怎样编制调运方案，能使总运费最少?解：设甲煤矿向东车站运x 万吨煤，乙煤矿向东车站运y 万吨煤，那么总运费z ＝x ＋1.5(200－x )＋0.8y ＋1.6(260－y )(万元)即z ＝716－0.5x －0.8y ．x、y应满足作出上面的不等式组所表示的平面区域，如图7—22．设直线x＋y＝280与y＝260的交点为M，则M(20，260)．把直线l：0.5x＋0.8y＝0向上平移至经过平面区域上的点M时，z的值最小．∵点M的坐标为(20，260)，∴甲煤矿生产的煤向东车站运20万吨，向西车站运180万吨，乙煤矿生产的煤全部运往东车站时，总运费最少．［例2］制造甲、乙两种烟花，甲种烟花每枚含A药品3ｇ、B药品4ｇ、C药品4ｇ，乙种烟花每枚含A药品2ｇ、B药品11ｇ、C药品6ｇ．已知每天原料的使用限额为A药品120ｇ、B药品400ｇ、C药品240ｇ．甲烟花每枚可获利2美元，乙种烟花每枚可获利1美元，问每天应生产甲、乙两种烟花各多少枚才能获利最大．解：设每天生产甲种烟花x枚，乙种烟花y枚，获利为z元，则作出可行域，如图7—23所示．目标函数为：z＝2x＋y．作直线l：2x＋y＝0，将直线l向右上方平移至l1的位置时，直线经过可行域上的点A且与原点的距离最大．此时z＝2x＋y取最大值．解方程组得答：每天生产甲种烟花24枚、乙种烟花24枚，能使利润总额达到最大．点评：把实际问题抽象为线性规划问题是解线性规划应用问题的关键．即根据实际问题找出约束条件和目标函数是解应用问题的关键．例1可用图示法找约束条件和目标函数，如例2可用列表去找，如：【随堂训练】1．图中阴影部分的点满足不等式组，在这些点中，使目标函数k＝6x＋8y取得最大值的点的坐标是_____．解析：当x∈［0，1］时，x＋y≤5，即y≤5－x，代入k＝6x＋8y得：k≤40－2x，当x＝0，y＝5时，k最大为40．当x∈［1，3］时，2x＋y≤6，即y≤6－2x代入k＝6x＋8y得：k≤48－10x，当x＝1，y＝4时，k最大为38．综上所述，使k取得最大值的坐标为(0，5)．答案：(0，5)2．某厂生产A与B两种产品，每公斤的产值分别为600元与400元．又知每生产1公斤A产品需要电力2千瓦、煤4吨；而生产1公斤B产品需要电力3千瓦、煤2吨．但该厂的电力供应不得超过100千瓦，煤最多只有120吨．问如何安排生产计划以取得最大产值?解：设生产A、B两种产品分别为x公斤、y公斤，总产值z元，则z＝600x＋400y．作出不等式组表示的平面区域由得取点M(20，20)作直线3x＋2y＝0的平行线l1，当l1经过点M时，z的值最大，最大值为20000元．答：安排生产A产品20公斤、B产品20公斤能取得最大产值．3．某工厂有甲、乙两种产品，计划每天各生产不少于15 t．已知生产甲产品1t需煤5t、电力4千瓦、劳力3个；生产乙产品1t需煤6t、电力5千瓦、劳力10个；甲产品每1t利润7万元，乙产品每1t利润12万元，但每天用煤不超过300t，电力不超过200千瓦，劳力只有300个，问每天各生产甲、乙两种产品多少，能使利润总额达到最大?解：设每天生产甲、乙两种产品各x t、y t，利润总额为z万元，则z＝7x＋12y．且作出不等式组的可行域．由即P(20，24)．当直线l：7x＋12y＝0向上平移到过P点，即生产甲、乙两种产品各20 t、24 t时，利润总额最大为428万元．【强化训练】1．某工厂生产甲、乙两种产品，已知生产甲种产品1 t需耗A种矿石8 t、B种矿石8 t、煤5 t；生产乙种产品1 t需耗A种矿石4t、B种矿石8 t、煤10 t．每1t甲种产品的利润是500元，每1 t乙种产品的利润是400元．工厂在生产这两种产品的计划中要求消耗A种矿石不超过320 t、B种矿石不超过400 t、煤不超过450 t．甲、乙两种产品应各生产多少能使利润总额达到最大?解：设生产甲、乙两种产品分别为x t、y t，利润总额为z元，那么作出以上不等式组所表示的平面区域，即可行域．令z＝500x＋400y作直线l：5x＋4y＝0，把直线l向右上方平移至l1的位置时，直线经过可行域上的点M，且与原点距离最大，此时，z＝500x＋400y取最大值．解方程组得M的坐标为(30，20)．答：应生产甲产品30 t、乙产品20 t，能使利润总额最大．2．某人需要补充维生素，现有甲、乙两种维生素胶囊，这两种胶囊都含有维生素A、C、D、E和最新发现的Z．甲种胶囊每粒含有维生素A、C、D、E、Z分别是1 mｇ、1 mｇ、4 m ｇ、4 mｇ、5 mｇ；乙种胶囊每粒含有维生素A、C、D、E、Z分别是3 mｇ、2 mｇ、1 mｇ、3 mｇ、2 mｇ．如果此人每天摄入维生素A至多19 mｇ，维生素C至多13 mｇ，维生素D 至多24 mｇ，维生素E至少12 mｇ，那么他每天应服用两种胶囊各多少粒才能满足维生素的需要量，并能得到最大量的维生素Z．解：设该人每天服用甲种胶囊x粒，乙种胶囊y粒，则z＝5x＋2y．作出以上不等式组所表示的平面区域，即可行域．作直线l：5x＋2y＝0，把直线向右上方平移，直线经过可行域上的点M时，与原点距离最大，此时z＝5x＋2y取得最大值，解方程组得M点坐标为(5，4)此时z＝5×5＋2×4＝33(mｇ)．答：每天应服用5粒甲种胶囊，4粒乙种胶囊满足维生素的需要量，且能得到最大量的维生素Z为33mｇ．3．张明同学到某汽车运输队调查，得知此运输队有8辆载重量为6 t的A型卡车与6辆载重量为10 t的B型卡车，有10名驾驶员．此车队承包了每天至少搬运720 t沥青的任务．已知每辆卡车每天往返的次数为A型卡车16次，B型卡车12次．每辆卡车每天往返的成本费为A型车240元，B型车378元．根据张明同学的调查写出实习报告，并回答每天派出A型车与B型车各多少辆运输队所花的成本最低?解：设每天出动A型车x辆、B型车y辆，运输队所花的成本为z元，则且x，y为整数，z＝240x＋378y．以上约束条件可简化成作出可行域如图：在可行域内的整点中，点(8，0)使z＝240x＋378y取最小值．最小值是z＝240×8＋378×0＝1920．实习报告2002年5月6日答：每天派出A型车8辆，B型车不派，运输队所花的成本最低．【学后反思】把调查的数据列成表格有利于写出约束条件(不等式组)．在画可行域时，画图准确是十分重要的．。
线性规划习题及答案
线性规划习题及答案线性规划是运筹学中的一个重要分支，它主要用于解决资源分配问题，以达到最大化或最小化目标函数。
下面是一个线性规划的习题及答案：习题：某工厂生产两种产品A和B，每种产品都需要使用机器时间和劳动力。
产品A每件需要3小时的机器时间和2小时的劳动力，产品B每件需要2小时的机器时间和3小时的劳动力。
工厂每天有24小时的机器时间和18小时的劳动力。
设生产产品A的数量为x，生产产品B的数量为y。
1. 建立目标函数和约束条件。
2. 求解线性规划问题，找出最优生产计划。
答案：1. 目标函数：设目标是最大化利润，产品A的利润为40元/件，产品B的利润为30元/件。
因此，目标函数为：\[ \text{Maximize } P = 40x + 30y \]2. 约束条件：- 机器时间约束：\[ 3x + 2y \leq 24 \]- 劳动力时间约束：\[ 2x + 3y \leq 18 \]- 非负约束：\[ x \geq 0, y \geq 0 \]3. 图解法求解：- 首先在坐标系中画出约束条件所形成的可行域。
- 可行域的顶点坐标为：(0,0), (0,6), (4,2), (8,0)。
- 将这些点代入目标函数计算利润：- P(0,0) = 40*0 + 30*0 = 0- P(0,6) = 40*0 + 30*6 = 180- P(4,2) = 40*4 + 30*2 = 200- P(8,0) = 40*8 + 30*0 = 3204. 最优解：- 通过比较各点的利润，发现当生产8件产品A和0件产品B时，利润最大，为320元。
5. 结论：- 工厂应该生产8件产品A和0件产品B，以实现最大利润320元。
注意：本题答案仅为示例，实际解题时需要根据具体题目条件进行分析和计算。
线性规划练习题
线性规划练习题线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法。
通过线性规划，我们可以在有限的资源条件下，实现最优的决策和资源分配。
下面让我们一起来看看一些线性规划练习题。
例题 1：某工厂生产甲、乙两种产品，已知生产甲产品 1 件需要 A原料 3 千克，B 原料 2 千克；生产乙产品 1 件需要 A 原料 2 千克，B原料 4 千克。
现有 A 原料 120 千克，B 原料 100 千克。
甲产品每件利润为 20 元，乙产品每件利润为 30 元。
问工厂应如何安排生产，才能使利润最大？首先，设生产甲产品 x 件，生产乙产品 y 件。
根据题目条件，可以列出以下不等式组：3x ＋2y ≤ 120 （A 原料限制）2x ＋4y ≤ 100 （B 原料限制）x ≥ 0 ，y ≥ 0 （产品数量非负）目标函数为：Z ＝ 20x ＋ 30y （总利润）接下来，我们通过画图来找到可行域。
将不等式组转化为等式方程，画出直线，然后根据不等式确定可行域的范围。
然后，在可行域内找到目标函数的最优解。
通常可以通过顶点法，计算可行域顶点处的目标函数值，比较得出最大值。
经过计算，当 x ＝ 20，y ＝ 20 时，利润最大，最大利润为 1000 元。
例题 2：某运输公司有 A、B 两种型号的货车，A 型货车每辆可载货 5 吨，B 型货车每辆可载货 8 吨。
现要运输 100 吨货物，且 A 型货车的数量不少于 B 型货车数量的 2 倍。
已知 A 型货车每辆运费 500 元，B 型货车每辆运费 800 元。
问如何安排车辆，能使运费最少？设安排 A 型货车 x 辆，B 型货车 y 辆。
则有：5x ＋ 8y ＝ 100 （货物总量）x ≥ 2y （车辆数量限制）x ≥ 0 ，y ≥ 0 （车辆数量非负）目标函数为：C ＝ 500x ＋ 800y （总运费）同样地，通过画图找到可行域，再计算顶点处的运费，找到最小值。
线性规划题及答案
线性规划题及答案引言概述：线性规划是运筹学中的一种数学方法，用于寻觅最优解决方案。
在实际生活和工作中，线性规划问题时常浮现，通过对问题进行建模和求解，可以得到最优的决策方案。
本文将介绍一些常见的线性规划题目，并给出详细的答案解析。
一、生产规划问题1.1 生产规划问题描述：某工厂生产两种产品A和B，产品A每单位利润为100元，产品B每单位利润为150元。
每天工厂有8小时的生产时间，产品A每单位需要2小时，产品B每单位需要3小时。
问工厂每天应该生产多少单位的产品A 和产品B，才干使利润最大化？1.2 生产规划问题答案：设产品A的生产单位为x，产品B的生产单位为y，则目标函数为Max Z=100x+150y，约束条件为2x+3y≤8，x≥0，y≥0。
通过线性规划方法求解，得出最优解为x=2，y=2，最大利润为400元。
二、资源分配问题2.1 资源分配问题描述：某公司有两个项目需要投资，项目A每万元投资可获得利润2万元，项目B每万元投资可获得利润3万元。
公司总共有100万元的投资额度，问如何分配投资额度才干使利润最大化？2.2 资源分配问题答案：设投资项目A的金额为x万元，投资项目B的金额为y万元，则目标函数为Max Z=2x+3y，约束条件为x+y≤100，x≥0，y≥0。
通过线性规划方法求解，得出最优解为x=40，y=60，最大利润为240万元。
三、运输问题3.1 运输问题描述：某公司有两个仓库和三个销售点，每一个销售点的需求量分别为100、150、200，每一个仓库的库存量分别为80、120。
仓库到销售点的运输成本如下表所示，问如何安排运输方案使得总成本最小？3.2 运输问题答案：设从仓库i到销售点j的运输量为xij，则目标函数为Min Z=∑(i,j) cij*xij，约束条件为每一个销售点的需求量得到满足，每一个仓库的库存量不超出。
通过线性规划方法求解，得出最优的运输方案，使得总成本最小。
四、投资组合问题4.1 投资组合问题描述：某投资者有三种投资标的可选择，预期收益率和风险如下表所示。
习题范例解决实际问题的线性规划
习题范例解决实际问题的线性规划线性规划是一种用于求解实际问题的数学模型，它通过建立一个数学方程系统来描述问题，并利用线性规划的方法求解最优解。
本文将通过提供一个习题范例，来介绍如何使用线性规划解决实际问题。
假设一个工厂生产A、B两种产品，每个产品的单位利润分别为10元和15元。
工厂有两个车间，车间1每天可生产A产品100个，B产品50个；车间2每天可生产A产品80个，B产品120个。
现在工厂需要确定每个车间应该生产多少个A产品和B产品，以最大化总利润。
为了解决这个问题，我们需要确定以下几个要素：决策变量、目标函数和约束条件。
首先，我们设定决策变量。
假设车间1每天生产的A产品数量为x1，B产品数量为y1；车间2每天生产的A产品数量为x2，B产品数量为y2。
其次，我们需要建立目标函数。
目标函数是我们要最大化或最小化的目标。
在这个问题中，我们的目标是最大化总利润。
由于A产品的单位利润为10元，B产品的单位利润为15元，所以总利润可以表示为10x1 + 15y1 + 10x2 + 15y2。
最后，我们需要确定约束条件。
约束条件是问题的限制条件。
根据题目中给出的信息，我们可以得到以下约束条件：车间1每天生产的A产品数量不能超过100个：x1 ≤ 100车间1每天生产的B产品数量不能超过50个：y1 ≤ 50车间2每天生产的A产品数量不能超过80个：x2 ≤ 80车间2每天生产的B产品数量不能超过120个：y2 ≤ 120我们还需要添加非负约束条件，即决策变量的值必须为非负数：x1 ≥ 0, y1 ≥ 0, x2 ≥ 0, y2 ≥ 0综上所述，我们得到了一个线性规划模型，可以表示为：最大化目标函数：10x1 + 15y1 + 10x2 + 15y2约束条件：x1 ≤ 100y1 ≤ 50x2 ≤ 80y2 ≤ 120x1, y1, x2, y2 ≥ 0我们使用线性规划的方法来求解这个模型。
一般来说，可以使用各种数学软件或在线工具来求解线性规划模型。
线性规划经典例题
线性规划经典例题1. 问题描述假设我们有一个农场，种植两种作物：小麦和大豆。
农场有一定的土地和资源限制，我们需要确定如何分配这些资源，以最大化农场的利润。
我们知道每亩小麦的利润为1000元，每亩大豆的利润为2000元。
同时，我们还知道种植每亩小麦需要2个单位的肥料和3个单位的水，而种植每亩大豆需要4个单位的肥料和2个单位的水。
农场总共有100个单位的肥料和90个单位的水可用。
我们需要确定种植多少亩小麦和多少亩大豆，以最大化利润。
2. 数学建模为了解决这个问题，我们可以使用线性规划来建立数学模型。
假设我们种植x 亩小麦和y亩大豆，则我们的目标是最大化利润，即最大化目标函数Z = 1000x + 2000y。
同时，我们需要满足资源限制，即种植小麦和大豆所需的肥料和水不能超过总量。
因此，我们有以下约束条件：2x + 4y ≤ 100（肥料限制）3x + 2y ≤ 90（水限制）x ≥ 0，y ≥ 0（非负性约束）3. 求解方法我们可以使用线性规划的求解方法来找到最优解。
常见的方法有图形法、单纯形法和内点法等。
在这个例题中，我们使用单纯形法求解。
4. 求解过程首先，我们将约束条件转化为标准形式。
将不等式约束转化为等式，并引入松弛变量，得到以下等式约束：2x + 4y + s1 = 1003x + 2y + s2 = 90其中，s1和s2为松弛变量。
接下来，我们构建初始单纯形表格：基变量 | x | y | s1 | s2 | b |--------------------------------------s1 | 2 | 4 | 1 | 0 | 100 |s2 | 3 | 2 | 0 | 1 | 90 |--------------------------------------Z | -1000| -2000| 0 | 0 | 0 |其中，Z表示目标函数的系数，初始解为0。
我们选择最负的目标函数系数对应的列作为进入变量，即选择-2000对应的y列。
线性规划题及答案
线性规划题及答案线性规划（Linear Programming）是一种数学优化方法，用于在一组线性约束条件下，寻找目标函数的最优解。
在实际应用中，线性规划常用于资源分配、生产计划、物流运输等领域。
下面我将为您提供一道线性规划题及其答案，以帮助您更好地理解和应用线性规划方法。
题目：某工厂生产两种产品A和B，每单位产品A的利润为10元，每单位产品B的利润为8元。
工厂有两个车间可供生产，分别称为车间1和车间2。
车间1每天可生产产品A 4个单位或产品B 6个单位，车间2每天可生产产品A 3个单位或产品B 5个单位。
每天工厂总共有8个工时可供分配。
假设工厂每天至少需要生产10个单位的产品A和15个单位的产品B。
请问应如何安排生产，以使得工厂的利润最大化？解答：首先，我们需要定义决策变量。
设x为工厂生产的产品A的单位数，y为工厂生产的产品B的单位数。
其次，我们需要建立目标函数和约束条件。
目标函数：最大化利润：Z = 10x + 8y约束条件：1. 车间1每天可生产产品A 4个单位或产品B 6个单位：4x + 6y ≤ 82. 车间2每天可生产产品A 3个单位或产品B 5个单位：3x + 5y ≤ 83. 每天工厂总共有8个工时可供分配：4x + 3y ≤ 84. 工厂每天至少需要生产10个单位的产品A和15个单位的产品B：x ≥ 10y ≥ 15接下来，我们可以使用线性规划求解器来求解该问题。
求解结果如下：最优解：x = 10y = 15Z = 10x + 8y = 10(10) + 8(15) = 100 + 120 = 220因此，当工厂每天生产10个单位的产品A和15个单位的产品B时，可以获得最大利润为220元。
需要注意的是，这只是一个简单的线性规划问题示例，实际应用中可能会涉及更多的约束条件和决策变量。
在解决实际问题时，需要根据具体情况进行建模和求解。
希望以上内容能够帮助您理解和应用线性规划方法。
如有任何疑问，请随时向我提问。
高中数学线性规划练习题及讲解
高中数学线性规划练习题及讲解线性规划是高中数学中的一个重要概念，它涉及到资源的最优分配问题。
以下是一些线性规划的练习题，以及对这些题目的简要讲解。
### 练习题1：资源分配问题某工厂生产两种产品A和B，每生产一件产品A需要3小时的机器时间和2小时的人工时间，每生产一件产品B需要2小时的机器时间和4小时的人工时间。
工厂每天有机器时间100小时和人工时间80小时。
如果产品A的利润是每件50元，产品B的利润是每件80元，工厂应该如何安排生产以获得最大利润？### 解题思路：1. 首先，确定目标函数，即利润最大化。
设生产产品A的数量为x，产品B的数量为y。
2. 目标函数为：\( P = 50x + 80y \)。
3. 根据资源限制，列出约束条件：- 机器时间：\( 3x + 2y \leq 100 \)- 人工时间：\( 2x + 4y \leq 80 \)- 非负条件：\( x \geq 0, y \geq 0 \)4. 画出可行域，找到可行域的顶点。
5. 计算每个顶点的目标函数值，选择最大的一个。
### 练习题2：成本最小化问题一家公司需要生产两种产品，产品1和产品2。
产品1的原材料成本是每单位10元，产品2的原材料成本是每单位15元。
公司每月有原材料预算3000元。
如果公司希望生产的产品总价值达到最大，应该如何分配生产？### 解题思路：1. 设产品1生产x单位，产品2生产y单位。
2. 目标函数为产品总价值最大化，但题目要求成本最小化，所以实际上是求成本最小化条件下的产品组合。
3. 约束条件为原材料成本：\( 10x + 15y \leq 3000 \)4. 非负条件：\( x \geq 0, y \geq 0 \)5. 画出可行域，找到顶点。
6. 根据实际情况，可能需要考虑产品1和产品2的市场价格，以确定最大价值。
### 练习题3：运输问题一个农场有三种作物A、B和C，需要运输到三个市场X、Y和Z。
线性规划问题的求解练习题
线性规划问题的求解练习题在数学和运筹学领域中，线性规划是一种常见的数学优化问题。
它的目标是在满足一系列线性约束条件的前提下，寻找一个线性模型的最优解。
线性规划可以应用于许多实际问题，如生产计划、资源分配、投资组合等。
本文将通过一些求解练习题来介绍线性规划问题的求解方法。
练习题一：某工厂生产两种产品A和B，每天的生产时间为8小时。
已知生产一单位产品A和B所需的时间分别为3小时和2小时。
产品A的单位利润为10元，产品B的单位利润为8元。
工厂的目标是最大化利润。
请问应该如何安排生产时间以达到最优解？解答：设工厂生产产品A的数量为x，产品B的数量为y。
由题目可知，生产一单位产品A需3小时，生产一单位产品B需2小时，生产时间为8小时。
因此，我们可以得到以下约束条件：3x + 2y ≤ 8目标是最大化利润，单位利润分别为10元和8元。
我们可以通过构建目标函数来表示利润：目标函数：Z = 10x + 8y综合约束条件和目标函数，我们可以列出线性规划模型：最大化 Z = 10x + 8y约束条件：3x + 2y ≤ 8非负约束条件：x ≥ 0，y ≥ 0根据上述模型，我们可以使用线性规划方法求解最优解。
线性规划方法可以通过图形法、单纯形法等来求解，这里我们使用单纯形法。
通过单纯形法求解得到最优解为x = 2，y = 1，最大利润为28元。
练习题二：某公司在生产两种产品X和Y，其中产品X的生产需要30天，产品Y的生产需要50天。
公司计划生产的总天数为120天。
已知产品X 的利润为3000元，产品Y的利润为5000元，公司的目标是最大化利润。
请问应该如何安排产品的生产数量以达到最优解？解答：设公司生产产品X的数量为x，产品Y的数量为y。
由题目可知，生产一单位产品X需要30天，生产一单位产品Y需要50天，共有120天的生产时间。
因此，我们可以得到以下约束条件：30x + 50y ≤ 120目标是最大化利润，单位利润分别为3000元和5000元。
线性规划练习题及解答
线性规划练习题及解答线性规划是数学中一种常见的优化方法，它广泛应用于实际问题的解决中。
本文将提供一些线性规划的练习题及解答，以帮助读者更好地理解和运用线性规划。
练习题1：某公司生产两种产品：甲品和乙品。
每天可用于生产的原料数量分别为A和B。
已知每单位甲品所需的原料A和B的消耗量分别为a1和b1，每单位乙品所需的原料A和B的消耗量分别为a2和b2。
假设甲品和乙品的利润分别为p1和p2，求解出该公司在给定原料限制下能获得的最大利润。
解答：设甲品的生产量为x，乙品的生产量为y，则目标函数为最大化利润，即maximize p1 * x + p2 * y。
受限条件为原料A的消耗量限制 a1 * x + a2 * y <= A，原料B的消耗量限制 b1 * x + b2 * y <= B。
另外，x和y的取值范围为非负数（x >= 0，y >= 0）。
这样，我们可以得出完整的线性规划模型如下：maximize p1 * x + p2 * ysubject to:a1 * x + a2 * y <= Ab1 * x + b2 * y <= Bx >= 0y >= 0练习题2：某工厂生产三种产品：甲、乙、丙。
已知每单位甲、乙、丙产品的利润分别为p1、p2、p3，每天需要的原材料A、B的数量为a和b，每单位甲、乙、丙产品消耗的原材料A、B的数量分别为a1、b1和a2、b2以及a3、b3。
现在要求在给定的原材料数量限制下，求解出最大化利润的生产方案。
解答：设甲、乙、丙产品的生产量分别为x、y、z，则目标函数为最大化利润，即maximize p1 * x + p2 * y + p3 * z。
受限条件为原材料A和B的数量限制，分别为 a1 * x + a2 * y + a3 * z <= a 和 b1 * x + b2 * y + b3 * z <= b。
另外，x、y、z的取值范围为非负数（x >= 0，y >= 0，z >= 0）。
线性规划经典例题
线性规划经典例题引言概述：线性规划是一种数学优化方法，用于求解线性约束条件下的最优解。
它在实际问题中有着广泛的应用，如生产计划、资源分配、运输问题等。
本文将介绍几个经典的线性规划例题，并详细阐述每个例题的解题思路和步骤。
一、最大化利润问题1.1 目标函数的建立首先，我们需要确定目标函数。
假设有两种产品A和B，每个单位的利润分别为x和y。
令x表示产品A的产量，y表示产品B的产量，我们的目标是最大化总利润。
1.2 约束条件的建立其次，我们需要确定约束条件。
假设产品A和B的生产所需的资源有限，分别为资源1和资源2。
我们需要考虑资源的限制以及产品的需求量。
1.3 求解最优解根据目标函数和约束条件，我们可以建立线性规划模型。
通过线性规划求解器，我们可以得到最优解，即产量x和y的数值，以及最大化的利润。
二、最小化成本问题2.1 目标函数的建立假设有n种原材料，每种原材料的价格为c1、c2、...、cn。
我们需要确定购买每种原材料的数量，以最小化总成本。
2.2 约束条件的建立每种原材料的数量要满足一定的约束条件，如总量限制、质量要求等。
此外，我们还需要考虑生产过程中的限制条件，如生产能力、工时等。
2.3 求解最优解根据目标函数和约束条件，我们可以建立线性规划模型。
通过线性规划求解器，我们可以得到最优解，即每种原材料的购买数量，以及最小化的成本。
三、资源分配问题3.1 目标函数的建立假设有m个任务需要分配给n个人员，每个人员的效率不同。
我们需要确定每个任务分配给哪个人员，以最大化总效率。
3.2 约束条件的建立每个任务只能由一个人员完成，每个人员只能执行一个任务。
此外，我们还需要考虑人员的可用时间、技能匹配等约束条件。
3.3 求解最优解根据目标函数和约束条件，我们可以建立线性规划模型。
通过线性规划求解器，我们可以得到最优解，即每个任务分配给哪个人员，以及最大化的总效率。
四、运输问题4.1 目标函数的建立假设有m个供应地和n个需求地，每个供应地的供应量和每个需求地的需求量已知。
线性规划练习(文科)
线性规划练习(文科)线性规划是运筹学中的一种重要方法，它在文科领域也有着广泛的应用。
通过线性规划，我们可以有效地解决一些文科领域中的优化问题，例如资源分配、课程安排等。
本文将介绍线性规划在文科领域的应用，并提供一些练习题供读者练习。
一、资源分配问题1.1 制定一个学校的食堂菜单，使得在保证营养均衡的前提下，最大化学生的满意度。
1.2 设计一个广告投放方案，使得在有限的广告预算下，最大化广告效果。
1.3 制定一个图书馆的书籍采购计划，使得在有限的经费下，最大化读者的阅读需求满足。
二、课程安排问题2.1 安排学生的课程时间表，使得在满足学分要求的前提下，最大化学生的学习效率。
2.2 设计一个会议议程，使得在有限的时间内，最大化会议的效率和成果。
2.3 制定一个考试安排计划，使得在有限的考场和监考人员资源下，最大化考试的顺利进行。
三、人员调配问题3.1 安排员工的工作时间表，使得在保证工作效率的前提下，最大化员工的满意度。
3.2 设计一个志愿者分配方案，使得在有限的志愿者资源下，最大化志愿者的参预度和效率。
3.3 制定一个团队项目分工计划，使得在有限的团队成员和时间下，最大化项目的完成度和质量。
四、成本控制问题4.1 制定一个活动预算方案，使得在有限的经费下，最大化活动的效果和参预度。
4.2 设计一个旅行路线规划，使得在有限的预算下，最大化旅行的体验和收获。
4.3 制定一个研究项目经费分配计划，使得在有限的经费下，最大化研究的成果和影响力。
五、决策支持问题5.1 制定一个招聘计划，使得在有限的招聘资源下，最大化招聘的成功率和员工质量。
5.2 设计一个学生活动安排方案，使得在有限的活动资源下，最大化学生的参预度和活动效果。
5.3 制定一个政策实施计划，使得在有限的政策资源下，最大化政策的实施效果和社会影响力。
通过以上练习题，读者可以更好地理解线性规划在文科领域的应用，提升解决问题的能力和效率。
希翼读者能够认真思量每一个问题，灵便运用线性规划方法，找到最优解决方案。
线性规划题及答案
线性规划题及答案线性规划是一种数学优化方法，用于在给定的一组约束条件下，寻找目标函数的最大值或最小值。
它常被应用于经济学、工程学、运筹学等领域，用于解决资源分配、生产计划、物流优化等实际问题。
下面我将为你提供一道线性规划题目及其答案，以帮助你更好地理解和应用线性规划方法。
题目：某工厂生产两种产品，分别为A和B。
产品A每单位利润为5元，产品B每单位利润为4元。
工厂有两个车间，分别为车间1和车间2。
车间1每天最多可以生产100个A产品或80个B产品；车间2每天最多可以生产80个A产品或60个B产品。
每天工厂的总生产时间为8小时。
生产一个A产品需要1小时，生产一个B产品需要1.5小时。
工厂希望通过合理的生产安排，最大化每天的总利润。
请问，应该如何安排每个车间的生产数量，才能使得每天的总利润最大化？答案：为了解决这个问题，我们可以使用线性规划方法。
首先，我们定义决策变量：x1：车间1生产的A产品数量x2：车间1生产的B产品数量x3：车间2生产的A产品数量x4：车间2生产的B产品数量其次，我们需要建立目标函数和约束条件。
目标函数：总利润 = 5x1 + 4x2 + 5x3 + 4x4约束条件：车间1生产时间约束：x1 + 1.5x2 ≤ 8车间2生产时间约束：x3 + 1.5x4 ≤ 8车间1产量约束：x1 ≤ 100, x2 ≤ 80车间2产量约束：x3 ≤ 80, x4 ≤ 60非负约束：x1, x2, x3, x4 ≥ 0现在，我们可以使用线性规划求解器来求解这个问题。
求解结果如下：车间1生产的A产品数量（x1）= 80车间1生产的B产品数量（x2）= 0车间2生产的A产品数量（x3）= 20车间2生产的B产品数量（x4）= 60总利润 = 5(80) + 4(0) + 5(20) + 4(60) = 400 + 0 + 100 + 240 = 740 元因此，为了使每天的总利润最大化，工厂应该安排车间1生产80个A产品，车间2生产20个A产品和60个B产品。
线性规划题及答案
线性规划题及答案引言概述：线性规划是一种数学优化方法，用于在一组线性约束条件下寻觅使目标函数取得最大（最小）值的变量值。
在实际生活和工作中，线性规划往往被用于资源分配、生产计划、运输问题等方面。
本文将介绍一些常见的线性规划题目，并给出相应的答案。
一、资源分配问题1.1 问题描述：某公司有两个生产部门A和B，每天生产产品X和Y。
部门A 每天生产产品X需要消耗3个单位的资源，生产产品Y需要消耗2个单位的资源；部门B每天生产产品X需要消耗2个单位的资源，生产产品Y需要消耗4个单位的资源。
公司每天有20个单位的资源可供分配，如何分配资源才干使得产出最大化？1.2 解答：设部门A每天生产产品X的数量为x，生产产品Y的数量为y；部门B每天生产产品X的数量为u，生产产品Y的数量为v。
根据题目描述，可以建立如下线性规划模型：Maximize Z = 3x + 2y + 2u + 4vSubject to:3x + 2y + 2u + 4v <= 20x, y, u, v >= 0通过线性规划求解器可以得到最优解。
二、生产计划问题2.1 问题描述：某工厂有两个生产车间，每天生产产品P和Q。
车间1每天生产产品P需要花费5个单位的时间，生产产品Q需要花费3个单位的时间；车间2每天生产产品P需要花费4个单位的时间，生产产品Q需要花费6个单位的时间。
工厂每天有40个单位的时间可供分配，如何安排生产计划才干使得产量最大化？2.2 解答：设车间1每天生产产品P的数量为x，生产产品Q的数量为y；车间2每天生产产品P的数量为u，生产产品Q的数量为v。
根据题目描述，可以建立如下线性规划模型：Maximize Z = 5x + 3y + 4u + 6vSubject to:5x + 3y + 4u + 6v <= 40x, y, u, v >= 0通过线性规划求解器可以得到最优解。
三、运输问题3.1 问题描述：某公司有两个仓库和三个销售点，每一个仓库有一定数量的产品可供销售点购买。
线性规划问题解决练习题
线性规划问题解决练习题线性规划是数学规划中的一种重要方法，广泛应用于实际问题的求解中。
本文将通过一些练习题来展示线性规划问题的解决过程，帮助读者更好地理解和掌握这一方法。
问题一：某企业生产A、B、C三种产品，已知每天可用的原材料总量为M 吨。
设每生产一吨A、B、C产品所需的原材料分别为a、b、c吨，并设每天生产的产品A、B、C分别为x、y、z吨。
已知产品A、B、C 的售价分别为p、q、r元/吨。
企业的目标是使每天的总收入最大化。
如何制定最佳生产计划？解决方案：首先，我们需要建立数学模型来描述该问题。
由于企业的目标是使总收入最大化，因此我们需要最大化目标函数Z，即：Z = px + qy + rz同时，我们需要满足以下约束条件：1. 原材料约束条件：ax + by + cz ≤ M2. 非负约束条件：x ≥ 0, y ≥ 0, z ≥ 0接下来，我们使用单纯形法来求解该线性规划问题。
单纯形法是一种常用的线性规划求解算法。
步骤一：将原问题转化为标准型为了使用单纯形法求解，我们需要将原问题转化为标准型。
标准型要求目标函数为最小化问题，并且所有的约束条件均为等式形式。
为了实现这一目标，我们引入了三个松弛变量s1、s2、s3，并对约束条件进行变形，得到以下等价的问题：最小化Z = -px - qy - rz约束条件：ax + by + cz + s1 = Mx ≥ 0, y ≥ 0, z ≥ 0, s1 ≥ 0步骤二：初始化单纯形表将约束条件和目标函数写成表格形式，得到如下的单纯形表（初始表）：基变量 x y z s1 b-------------------------------s1 a b c 1 M注意：b表示约束条件右侧的值。
步骤三：判断是否达到最优解检查目标函数最后一行（即表格中最后一行）的系数，如果系数均大于或等于0，则得到最优解；否则，继续进行下一步。
步骤四：确定入基变量和出基变量在初始表中选择一个入基变量和一个出基变量。
线性规划题及答案
线性规划题及答案引言概述：线性规划是一种数学优化方法，用于在给定约束条件下寻找使目标函数最大或最小的变量值。
在实际生活和工作中，线性规划经常被应用于资源分配、生产计划、运输问题等方面。
本文将介绍一些常见的线性规划题目，并给出相应的答案。
一、资源分配问题1.1 约束条件：某公司有两种产品A和B，生产一单位产品A需要耗费2个单位的资源X和1个单位的资源Y，生产一单位产品B需要耗费1个单位的资源X和3个单位的资源Y。
公司每天可用资源X和资源Y分别为10个单位和12个单位。
假设产品A的利润为3万元，产品B的利润为4万元，问如何分配资源才能使公司利润最大化？1.2 目标函数：设生产产品A的单位数为x，生产产品B的单位数为y，则目标函数为Maximize 3x + 4y。
1.3 答案：通过线性规划计算，最优解为生产产品A 4个单位，生产产品B 2个单位，公司利润最大化为20万元。
二、生产计划问题2.1 约束条件：某工厂生产两种产品C和D，生产一单位产品C需耗费2个单位的资源M和3个单位的资源N，生产一单位产品D需耗费4个单位的资源M和2个单位的资源N。
工厂每天可用资源M和资源N分别为8个单位和10个单位。
产品C的利润为5万元，产品D的利润为6万元，问如何安排生产计划以最大化利润？2.2 目标函数：设生产产品C的单位数为x，生产产品D的单位数为y，则目标函数为Maximize 5x + 6y。
2.3 答案：经过线性规划计算，最佳生产计划为生产产品C 2个单位，生产产品D 2个单位，工厂利润最大化为22万元。
三、运输问题3.1 约束条件：某公司有三个仓库分别存储产品E、F和G，每个仓库的存储容量分别为100、150和200个单位。
产品E、F和G的单位运输成本分别为2元、3元和4元，需求量分别为80、120和150个单位。
问如何安排运输计划以最小化总成本？3.2 目标函数：设从仓库i运输产品j的单位数为xij，则目标函数为Minimize2x11 + 3x12 + 4x13 + 2x21 + 3x22 + 4x23 + 2x31 + 3x32 + 4x33。
线性规划经典例题
线性规划经典例题一、问题描述某公司生产两种产品A和B，每个单位产品A的利润为100元，每个单位产品B的利润为150元。
公司有两个车间可用于生产这两种产品，每个车间每天的工作时间为8小时。
产品A在车间1生产需要1小时，产品B在车间1生产需要2小时；产品A在车间2生产需要2小时，产品B在车间2生产需要1小时。
每天车间1的生产能力为400个单位产品A或200个单位产品B，车间2的生产能力为300个单位产品A或150个单位产品B。
公司的目标是在满足车间生产能力的前提下，最大化利润。
二、数学建模设x1为在车间1生产的产品A的数量，x2为在车间1生产的产品B的数量，x3为在车间2生产的产品A的数量，x4为在车间2生产的产品B的数量。
目标函数：max Z = 100x1 + 150x2 + 100x3 + 150x4约束条件：车间1的生产能力：x1 + x2 ≤ 4002x1 + x2 ≤ 800车间2的生产能力：x3 + x4 ≤ 300x3 + 2x4 ≤ 300非负约束：x1, x2, x3, x4 ≥ 0三、求解过程使用线性规划的求解方法，可以得到最优解。
1. 将目标函数和约束条件转化为标准形式：目标函数：max Z = 100x1 + 150x2 + 100x3 + 150x4约束条件：x1 + x2 + 0x3 + 0x4 ≤ 4002x1 + x2 + 0x3 + 0x4 ≤ 8000x1 + 0x2 + x3 + x4 ≤ 3000x1 + 0x2 + x3 + 2x4 ≤ 300x1, x2, x3, x4 ≥ 02. 使用线性规划求解器求解得到最优解：最优解为：x1 = 200, x2 = 200, x3 = 0, x4 = 100最大利润为：Z = 100(200) + 150(200) + 100(0) + 150(100) = 50000元四、结果分析根据求解结果，最优解是在车间1生产200个单位产品A，200个单位产品B，在车间2生产100个单位产品B，不需要在车间2生产产品A。
线性规划应用题.
线性规划应用题1.某企业生产甲、乙两种产品，已知生产每吨甲产品要用A 原料3吨、B 原料２吨;生产每吨乙产品要用Ａ原料1吨、B 原料３吨。
销售每吨甲产品可获得利润５万元，每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A 原料不超过１3吨，B 原料不超过1８吨，求该企业可获得最大利润。
解析:设甲、乙种两种产品各需生产x 、y 吨，可使利润z 最大,故本题即已知约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+001832133y x y x y x ，求目标函数y x z 35+=的最大值,可求出最优解为⎩⎨⎧==43y x ，故271215max =+=z ．2。
某公司租赁甲、乙两种设备生产Ａ,B 两类产品,甲种设备每天能生产A 类产品５件和B 类产品10件,乙种设备每天能生产Ａ类产品6件和B 类产品20件。
已知设备甲每天的租赁费为2０0元，设备乙每天的租赁费为300元,现该公司至少要生产Ａ类产品50件,Ｂ类产品140件,求所需租赁费的最少值.【解析】：设甲种设备需要生产x 天，乙种设备需要生产y 天，该公司所需租赁费为z 元，则200300z x y =+,甲、乙两种设备生产A,Ｂ两类产品的情况为下表所示: 产品 设备 A 类产品 （件)（≥50)B 类产品 （件)(≥140) 租赁费 (元)甲设备 5 1020０ 乙设备６20 30０则满足的关系为565010201400,0x y x y x y +≥⎧⎪+≥⎨⎪≥≥⎩即：61052140,0x y x y x y ⎧+≥⎪⎪⎨+≥⎪⎪≥≥⎩,作出不等式表示的平面区域,当200300z x y =+对应的直线过两直线6105214x y x y ⎧+=⎪⎨⎪+=⎩的交点（4,5）时,目标函数200300z x y =+取得最低为２300元. 答案:23０0３． 某人上午7时,乘摩托艇以匀速v n mi l e/h(4≤ｖ≤20）从A 港出发到距50 ｎ ｍi l ｅ的B 港去，然后乘汽车以匀速w km/h （30≤w ≤1０0）自B 港向距３00 km 的C 市驶去应该在同一天下午4至9点到达Ｃ市设乘汽车、摩托艇去所需要的时间分别是x h 、y h(1）作图表示满足上述条件的x 、y 范围;（2）如果已知所需的经费ｐ＝10０+３×（5-ｘ)＋2×（8－y )(元）, 那么v 、w 分别是多少时走得最经济?此时需花费多少元？分析：由p ＝10０+3×(５-x )+2×(8－y ）可知影响花费的是3ｘ+2y 的取值范围解：(1)依题意得v ＝y 50，w =x300,4≤v ≤20,30≤w ≤1０0 ∴3≤x ≤１0,25≤y ≤225①由于乘汽车、摩托艇所需的时间和x +y 应在9至14个小时之间，即９≤x +y ≤14 ② 因此,满足①②的点(x ,y )的存在范围是图中阴影部分(包括边界) （2)∵ｐ=１00+3·（5－x ）+2·(8－ｙ）， ∴3x ＋2y ＝131-p设１3１-ｐ=k ，那么当k 最大时,p 最小在通过图中的阴影部分区域(包括边界）且斜率为－23的直线3x +２y =k 中，使k 值最大的直线必通过点(1０，4)，即当ｘ＝10，ｙ=4时，p 最小 此时，v ＝125，w ＝30，ｐ的最小值为9３元点评：线性规划问题首先要根据实际问题列出表达约束条件的不等式然后分析要求量的几何意义4． 某公司计划在今年内同时出售变频空调机和智能洗衣机，由于这两种产品的市场需求量非常大,有多少就能销售多少，因此该公司要根据实际情况（如资金、劳动力)确定产品的月供应量，以使得总利润达到最大已知对这两种产品有直接限制的因素是资金和劳动力，通过调查，得到关于这两种产品的有关数据如下表：(表中单位：百元）资金 单位产品所需资金 月资金供应量空调机 洗衣机 成本 3０ 20 300 劳动力:工资 5 10 1１0 单位利润68试问:怎样确定两种货物的月供应量,才能使总利润达到最大，最大利润是多少？ 解:设空调机、洗衣机的月供应量分别是x 、y 台,总利润是P ,则P =６x +8y ，由题意有30x ＋20y ≤30０,5x +１0y ≤1１0,x ≥0,y ≥0,x 、y 均为整数由图知直线y =－43x +81P 过M (4，9）时,纵截距最大这时P 也取最大值P m ａx ＝6×4＋8×9=9６（百元）3 9 10 14 xO 2.5 9 14y故当月供应量为空调机4台,洗衣机９台时，可获得最大利润960０元5。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学科：数学
教学内容：研究性课题与实习作业：线性规划的实际应用
【自学导引】
1
．线性规划问题的数学模型是已知(这里“≤”也可以是“≥”或“＝”号)，其中a ij (i ＝1，2，…，n ，j ＝1，2，…，m )，b i (i ＝1，2，…，m )都是常量，x j (j ＝1，2，…，m )是非负变量，求z ＝c 1x 1＋c 2x 2＋…＋c m x m 的最大值或最小值，这里c j (j ＝1，2，…，m )是常量．
2．线性规划常见的具体问题有物质调运问题、产品安排问题、下料问题．
【思考导学】
1．应用线性规划解决实际问题的一般步骤是什么？
答：一般步骤是①设出变量，列出线性约束条件和线性目标函数；②利用图解法求出最
优解，进而求得目标函数的最大(或最小)值．
2．线性规划的理论和方法主要在哪两类问题中得到应用？
答：一是在人力、物力、资金等资源一定的条件下，如何使用它们来完成最多的任务；二是给定一项任务，如何合理安排和规划，能以最少的人力、物力、资金等资源来完成该项任务．
【典例剖析】
［例1］ 已知甲、乙两煤矿每年的产量分别为200万吨和260万吨，需经过东车站和西
车站两个车站运往外地．东车站每年最多能运280万吨煤，西车站每年最多能运360万吨煤，甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨，乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨．煤矿应怎样编制调运方案，能使总运费最少?
解：设甲煤矿向东车站运x 万吨煤，乙煤矿向东车站运y 万吨煤，那么总运费z ＝x ＋
1.5(200－x )＋0.8y ＋1.6(260－y )(万元)
即z ＝716－0.5x －0.8y ．
x、y应满足
作出上面的不等式组所表示的平面区域，如图7—22．
设直线x＋y＝280与y＝260的交点为M，则M(20，260)．
把直线l：0.5x＋0.8y＝0向上平移至经过平面区域上的点M时，z的值最小．
∵点M的坐标为(20，260)，
∴甲煤矿生产的煤向东车站运20万吨，向西车站运180万吨，乙煤矿生产的煤全部运往东车站时，总运费最少．
［例2］制造甲、乙两种烟花，甲种烟花每枚含A药品3ｇ、B药品4ｇ、C药品4ｇ，乙种烟花每枚含A药品2ｇ、B药品11ｇ、C药品6ｇ．已知每天原料的使用限额为A药品120ｇ、B药品400ｇ、C药品240ｇ．甲烟花每枚可获利2美元，乙种烟花每枚可获利1美元，问每天应生产甲、乙两种烟花各多少枚才能获利最大．
解：设每天生产甲种烟花x枚，乙种烟花y枚，获利为z元，则
作出可行域，如图7—23所示．
目标函数为：z＝2x＋y．
作直线l：2x＋y＝0，将直线l向右上方平移至l1的位置时，直线经过可行域上的点A
且与原点的距离最大．此时z＝2x＋y取最大值．解方程组得答：每天生产甲种烟花24枚、乙种烟花24枚，能使利润总额达到最大．
点评：把实际问题抽象为线性规划问题是解线性规划应用问题的关键．即根据实际问题找出约束条件和目标函数是解应用问题的关键．
例1可用图示法找约束条件和目标函数，如
例2可用列表去找，如：
【随堂训练】
1．图中阴影部分的点满足不等式组，在这些点中，使目标函数k＝6x＋8y取得最大值的点的坐标是_____．
解析：当x∈［0，1］时，x＋y≤5，
即y≤5－x，
代入k＝6x＋8y
得：k≤40－2x，
当x＝0，y＝5时，k最大为40．
当x∈［1，3］时，2x＋y≤6，
即y≤6－2x代入k＝6x＋8y得：k≤48－10x，
当x＝1，y＝4时，k最大为38．
综上所述，使k取得最大值的坐标为(0，5)．
答案：(0，5)
2．某厂生产A与B两种产品，每公斤的产值分别为600元与400元．又知每生产1公斤A产品需要电力2千瓦、煤4吨；而生产1公斤B产品需要电力3千瓦、煤2吨．但该厂的电力供应不得超过100千瓦，煤最多只有120吨．问如何安排生产计划以取得最大产值?
解：设生产A、B两种产品分别为x公斤、y公斤，总产值z元，则
z＝600x＋400y．
作出不等式组表示的平面区域
由得
取点M(20，20)
作直线3x＋2y＝0的平行线l1，当l1经过点M时，z的值最大，最大值为20000元．
答：安排生产A产品20公斤、B产品20公斤能取得最大产值．
3．某工厂有甲、乙两种产品，计划每天各生产不少于15 t．已知生产甲产品1t需煤5t、电力4千瓦、劳力3个；生产乙产品1t需煤6t、电力5千瓦、劳力10个；甲产品每1t利润7万元，乙产品每1t利润12万元，但每天用煤不超过300t，电力不超过200千瓦，劳力只有300个，问每天各生产甲、乙两种产品多少，能使利润总额达到最大?
解：设每天生产甲、乙两种产品各x t、y t，利润总额为z万元，
则z＝7x＋12y．
且作出不等式组的可行域．
由
即P(20，24)．当直线l：7x＋12y＝0向上平移到过P点，即生产甲、乙两种产品各20 t、24 t时，利润总额最大为428万元．
【强化训练】
1．某工厂生产甲、乙两种产品，已知生产甲种产品1 t需耗A种矿石8 t、B种矿石8 t、煤5 t；生产乙种产品1 t需耗A种矿石4t、B种矿石8 t、煤10 t．每1t甲种产品的利润是500元，每1 t乙种产品的利润是400元．工厂在生产这两种产品的计划中要求消耗A种矿石不超过320 t、B种矿石不超过400 t、煤不超过450 t．甲、乙两种产品应各生产多少能使利润总额达到最大?
解：设生产甲、乙两种产品分别为x t、y t，利润总额为z元，
那么
作出以上不等式组所表示的平面区域，即可行域．
令z＝500x＋400y作直线l：5x＋4y＝0，把直线l向右上方平移至l1的位置时，直线经过可行域上的点M，且与原点距离最大，此时，z＝500x＋400y取最大值．
解方程组
得M的坐标为(30，20)．
答：应生产甲产品30 t、乙产品20 t，能使利润总额最大．
2．某人需要补充维生素，现有甲、乙两种维生素胶囊，这两种胶囊都含有维生素A、C、D、E和最新发现的Z．甲种胶囊每粒含有维生素A、C、D、E、Z分别是1 mｇ、1 mｇ、4 m ｇ、4 mｇ、5 mｇ；乙种胶囊每粒含有维生素A、C、D、E、Z分别是3 mｇ、2 mｇ、1 mｇ、3 mｇ、2 mｇ．如果此人每天摄入维生素A至多19 mｇ，维生素C至多13 mｇ，维生素D 至多24 mｇ，维生素E至少12 mｇ，那么他每天应服用两种胶囊各多少粒才能满足维生素的需要量，并能得到最大量的维生素Z．
解：设该人每天服用甲种胶囊x粒，乙种胶囊y粒，则z＝5x＋2y．作出以上不等式组所表示的平面区域，即可行域．作直线l：5x＋2y＝0，把直线向右上方平移，直线经过可行域上的点M时，与原点距离最大，
此时z＝5x＋2y取得最大值，解方程组得M点坐标为(5，4)此时z＝5×5＋2×4＝33(mｇ)．
答：每天应服用5粒甲种胶囊，4粒乙种胶囊满足维生素的需要量，且能得到最大量的维生素Z为33mｇ．
3．张明同学到某汽车运输队调查，得知此运输队有8辆载重量为6 t的A型卡车与6辆载重量为10 t的B型卡车，有10名驾驶员．此车队承包了每天至少搬运720 t沥青的任务．已知每辆卡车每天往返的次数为A型卡车16次，B型卡车12次．每辆卡车每天往返的成本费为A型车240元，B型车378元．根据张明同学的调查写出实习报告，并回答每天派出A型车与B型车各多少辆运输队所花的成本最低?
解：设每天出动A型车x辆、B型车y辆，运输队所花的成本为z元，则
且x，y为整数，z＝240x＋378y．
以上约束条件可简化成
作出可行域如图：
在可行域内的整点中，点(8，0)使z＝240x＋378y取最小值．
最小值是z＝240×8＋378×0＝1920．
实习报告2002年5月6日
答：每天派出A型车8辆，B型车不派，运输队所花的成本最低．
【学后反思】
把调查的数据列成表格有利于写出约束条件(不等式组)．在画可行域时，画图准确是十分重要的．。