2003年中考数学精品模拟试题一
湖北省荆州市2003年中考数学试题

湖北省荆州市2003年中考数学试题注意事项:1.本试卷共8页,三大题,满分150分,考试时间120分钟.2.答卷前将密封线内和答题卡上的姓名、准考证号填写清楚,答题卡上的准考证号和作本考试科目代号的矩形框。
用2B 铅笔涂黑.3.第5页右侧的座位号填写准考证号最末两位数.4.第Ⅰ卷(选择题)在答题卡上答题.用2B 铅笔把答题卡上对应题号下正确答案的代号涂黑,在试卷上答题无效;第Ⅱ卷(非选择题)的答案用钢笔或圆珠笔直接写在试卷相应的位置上.第Ⅰ卷(选择题,共40分) 一、选择题:(本大题共10个小题,每小题4分,共40分) 1.12化成最简二次根式是( )A. 62B. 32 C .23 D .262.地球上的海洋面积约为361000000千米2,用科学记数法表示为( )A .3.61×106千米2B .3.61×107千米2C .3.61×108千米2D .3.61×109千米2 3.点P(1,―2)关于y 轴对称的点的坐标是( )A (―1,―2)B (1, 2)C (―1,2)D (―2,1) 4.下列计算中,正确的是( )A. a a a =-222 B 、326a a a =÷ C 532)(a a =- D. 3222a a a -=⋅-5.如图,□ABCD 的周长为16cm ,AC 、BD 相交于点O , OE ⊥AC 交AD 于E ,则△DCE 的周长为( ) A .4 cm B .6cm C .8cm D .10cm6.如图,已知⊙O 的两弦AB 、CD 相交于点P ,PA=4 cm ,PB=5 cm ,CP :PD=1:4,则CD 的长是( ) A . 54 cm B .55cm C .56cm D .58cm7.小宁买了20个练习本,店主给他八折(即标价的80%),优惠,结果便宜了1.60元,则每个练习本的标价是( )A. 0.20元 B .0.40元 C.0.60元 D .0.80元8、某车间为了改变管理松散的状况,准备采取每天任务定额,超产有奖的措施来提高工作效率,下面是该车间15名工人过去一天中各自装备机器的数量(单位:台),6,7,7,8,8,8,8,9,10,10,13,14,16,16,17,为了促进生产,又能保证大多数工人的积极性,那么管理者应确定每人每天装备机器的定额最好为( ) A.10台 B .9台 C .8台 D .7台 9、如图:在△ABC 中,∠A=30°,tanB=23,AC=32,则AB 的长是( )A 、3+3B 、2+23C 、5D 、29 10、下列命题:①顺次连结四边形四条边的中点,所得的四边形是平行四边形; ②等边三角形既是轴对称图形,又是中心对称图形; ③若直角三角形的两边是3和4,则第三边是5;④若半径分别是1和3的两圆相交,则公共弦的最大值是2 其中正确命题的个数是( )(A )4个 (B )3个 (C )2个 (D )1个第Ⅱ卷(非选择题,共110分)二、填空题:(本大题共8小题,每小题4分,共32分)ABCA BCOEDA BCO DP ·11、在函数12-=x y 中自变量x 的取值范围是12、方程组⎩⎨⎧=+=++224)2(2y x y x x 的解是13、若反比例函数xky =的图象过点M (2,-3),那么k= 14、如图,在边长为4的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是 15、抛物线342-+=x x y 的顶点坐标是 16、观察下面一列有规律的数,486,355,244,153,82,31, 根据这个规律可知第n 个数是 (n 是正整数) 17、已知△ABC 中,E 、F 分别是AB 、AC 上的点,且EF ∥BC ,在BC 边上取一点D ,连结DF ,要使以C 、F 、D 为顶点的三角形与△AEF 相似,还需添加一个条件,这个条件可以是 18、为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若测得PA=5cm ,则铁环的半径是cm 三、解答题:(本大题共7个小题,共78分) 19、(本题满分8分)当121+=x 时,求代数式222)131(-+÷--+x x x x 的值20(本题满分10分)在菱形ABCD 中,E 、F 分别在CD 、BC 上,且CE=CF ,求证:AE=AF21(本题满分10分)已知二次函数12)14(222-++-=k x k x y 的图象与x 轴交于两点,设这两点的坐标分别为x 1,x 2;(1)求实数k 的取值范围; (2)当x 1+x 2<67,且k 为整数时,求二次函数的解析式;22、(本题满分12分)一自行车队进行训练,训练的路程是55千米,出发后所有队员都保持相同的速度前进,行进一段路程后,1号队员将速度提高10千米超出队伍,当其余队员又前进20千米后,2号队员的速度也提高了10千米,结果2号队员比1号队员晚101小时到达终点,问车队从出发至最后的队员到达终点所花的时间是多少?B AC DE F P A23、(本题满分12分)已知,如图,在直角梯形COAB 中,CB ∥OA ,以O 为原点建立平面直角坐标系,A 、B 、C 的坐标分别为A (10,0)、B (4,8)、C (0,8),D 为OA 的中点,动点P 自A 点出发沿A →B →C →O 的路线移动,速度为每秒1个单位,移动时间记为t 秒,(1)动点P 在从A 到B 的移动过程中,设△APD 的面积为S ,试写出S 与t 的函数关系式,指出自变量的取值范围,并求出S 的最大值(2)动点P 从出发,几秒钟后线段PD 将梯形COAB 的面积分成1:3两部分?求出此时P 点的坐标24、(本题满分12分)如图,AB 是⊙O 的直径,以B 为圆心的圆交OB 于C ,交⊙O 于E 、F ,交AB 的延长线于D ,连结EC 并延长交⊙O 于M ,(1) 求证:AE 是⊙O 的切线 (2) 求证:EM 平分∠AEF(3) 连结OM ,N 为AO 上一点,且MN=MO ,求证:MN ∥BEOBACDMNEF25、(本题满分14分)如图,在直角坐标系xoy 中,半径为2的⊙O 与x 轴交于A 、B 两点,与y 轴交于点P ,T 是OB 上一点,OT= a (0<a <2),过 A 作AC ⊥AB ,且AC=AT ,连结CP 并延长交半圆于另一点Q ,且Q 恰为 弧PB 的中点(1)求出点Q 的坐标(2)求直线CP 的解析式及a 的值;(3)由点P 发出的光线,经过T 点处反射后,反射光线是否通过点Q ?请说明理由。
2003年江西省中考数学试题(WORD版含扫描答案)

机密★2003年6月19日江西省2003年初中毕业暨中等学校招生考试数学试题卷说明:1.本卷共有六个大题,28个小题,全卷满分120分,考试时间120分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.一、填空题(本大题共12题,每题3分,满分36分) 1、计算:(-100)×(-20)-(-3)= ; 2、如图,一个矩形推拉窗,窗高1.5米,则活动窗扇的通风面积A (平方米)与拉开长度b (米)的关系式是: ;30O O30第6题图OOEDCB A∙30第7题图O OP TBOA3、分解因式:x x -3= ;4、一件夹克标价为a 元,现按标价的7折出售,则售价用代数式表示为: 元。
5、函数66--=x x y 中,自变量x 的取值范围是: ; 6、如图,在△ABC 中,DE ∥BC ,AD =3,AB =5,则DE ∶BC 的值是: ;7、如图PT 切⊙O 于点T ,经过圆心的割线PAB 交⊙O 于点A 和B ,PT =4,PA =2,则⊙O 的半径是: ;8、写出一个分母至少含有两项、且能够约分的分式: ; 9、图中,∠1+∠2+∠3+∠4= 度。
30第9题图O O4321∙ ∙ 30第11题图O OBA10、完成下列配方过程:122++px x =()[]()________________22+++px x =()()____________2++x ;11、已知右边方格纸中的每个小方格是边长为1的正方形,A 、B 两点在小方格的顶点上,位置如图所示.请在小方格的顶点上确定一点C ,连结AB 、AC 、BC ,使△ABC 的面积为2个平方单位。
12、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:第一个第二个 第三个 ……30OO⑴ 第4个图案中有白色地面砖 块; ⑵ 第n 个图案中有白色地面砖 块。
二、选择题(本大题共8题,每题3分,满分24分)各题中的选项只有一个是正确的。
2003年重庆中考数学试题和详细答案

重庆市2003年普通高中招生统一考试数 学 试 卷(本卷共四大题,满分150分,考试时间120分钟)一、选择题:(本大题12个小题,每小题4分,共48分) 1、下列各组数中,互为相反数的是( )A 、2与21B 、2)1(-与1C 、-1与2)1(- D 、2与∣-2∣2、下列一元二次方程中,没有实数根的是( )A 、0122=-+x x B 、02222=++x xC 、0122=++x x D 、022=++-x x3、如图,⊙O 中弦AB 、CD 相交于点F ,AB =10,AF =2。
若CF ∶DF =1∶4,则CF 的长等于( ) A 、2 B 、2 C 、3 D 、224、三峡大坝从6月1日开始下闸蓄水,如果平均每天流入库区的水量为a 立方米,平均每天流出的水量控制为b 立方米。
当蓄水位低于135米时,b <a ;当蓄水位达到135米时,b =a ;设库区的蓄水量y (立方米)是时间t (天)的函数,那么这个函数的大致图象是( )5、随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费标准按原标准每分钟降低了a 元后,再次下调了25%,现在的收费标准是每分钟b 元,则原收费标准每分钟为( )A 、⎪⎪⎭⎫ ⎝⎛-a b 45元 B 、⎪⎭⎫ ⎝⎛+a b 45元 C 、⎪⎭⎫ ⎝⎛+a b 43元 D 、⎪⎭⎫ ⎝⎛+a b 34元 6、如下图,在△ABC 中,若∠AED =∠B ,DE =6,AB =10,AE =8,则BC 的长为( )A 、415B 、7C 、215D 、5247、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:CAA 、618B 、638C 、658D 、678第6题图EDCBA450 1200第8题图DCB A 第10题图PDCBA8、已知:如图,梯形ABCD 中,AD ∥BC ,∠B =450,∠C =1200,AB =8,则CD 的长为( )A 、638B 、64C 、238 D 、249一位同学可能获得的奖励为( )A 、3项B 、4项C 、5项D 、6项10、如图:△ABP 与△CDP 是两个全等的等边三角形,且PA ⊥PD 。
2003年广东省深圳市中考数学试卷+答案

2003年广东省深圳市中考数学试卷一、选择题(共10小题,每小题5分,满分50分)1.(5分)将695600保留两个有效数字的近似数是()A.690000 B.700000 C.6.9×105D.7.0×1052.(5分)实数227,sin30°,√2+1,2π,(√3)0,|﹣3|中,有理数的个数是()A.2个 B.3个 C.4个 D.5个3.(5分)已知三角形的两边a=3,b=7,第三边是c,且a<b<c,则c的取值范围是()A.4<c<7 B.7<c<10 C.4<c<10 D.7<c<134.(5分)某班5位同学的身高分别为155,160,160,161,169(单位:厘米),这组数据中,下列说法错误的是()A.众数是160 B.中位数是160 C.平均数是161 D.标准差是2√5 5.(5分)下列命题正确的是()A.3x﹣7>0的解集为x>37B.关于x的方程ax=b的解是x=bb aaC.9的平方根是3D.(√2+1)与(√2−1)互为倒数6.(5分)计算:cccccc45°−cccccc60°cccccc30°⋅tt tt tt60°的结果是()A.1 B.13C.2√3﹣3 D.2√33−17.(5分)一个等腰梯形的高恰好等于这个梯形的中位线,若分别以这个梯形的上底和下底为直径作圆,则这两个圆的位置关系是()A.相离B.相交C.外切D.内切8.(5分)已知一元二次方程2x2﹣3x﹣6=0有两个实数根x1、x2,直线l经过点A(x1+x2,0)、B(0,x1•x2),则直线l的解析式为()A.y=2x﹣3 B.y=2x+3 C.y=﹣2x﹣3 D.y=﹣2x+39.(5分)如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3,下列命题错误的是()A.△AED∽△BEC B.∠AEB=90°C.∠BDA=45° D.图中全等的三角形共有2对10.(5分)如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是()A.5:2 B.4:1 C.2:1 D.3:2二、解答题(共4小题,满分50分)11.(10分)先化简再求值:xx2+xxxx−2xx2xx−2xxxx+xx−(1−xxyy2)(1+xxyy2)−xx2÷1xx,其中x=√3+√2,y=√3−√2.12.(10分)某工人要制造180个相同零件,在制造完40个零件后,他改进技术每天多制造15个零件,恰好共用6天全部完成,问该工人改进技术后每天制造多少个零件?13.(12分)如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.(1)求证:△ACF∽△BEC;(2)设△ABC的面积为S,求证:AF•BE=2S;(3)试判断以线段AE、EF、FB为边的三角形的形状并给出证明.14.(18分)如图,已知A(5,﹣4),⊙A与x轴分别相交于点B、C,⊙A与y 轴相且于点D,(1)求证过D、B、C三点的抛物线的解析式;(2)连接BD,求tan∠BDC的值;(3)点P是抛物线顶点,线段DE是直径,直线PC与直线DE相交于点F,∠PFD的平分线FG交DC于G,求sin∠CGF的值.2003年广东省深圳市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)将695600保留两个有效数字的近似数是()A.690000 B.700000 C.6.9×105D.7.0×105【分析】一个近似数的有效数字:从左边第一个不是0的数字起,后面所有的数字都是这个数的有效数字.精确到十位或十位以前的数位时,要先用科学记数法表示出这个数,再进行四舍五入.【解答】解:695600保留两个有效数字的近似数是7.0×105.故选D.【点评】对于用科学记表示的数,有效数字的计算方法,与精确到哪一位是需要识记的内容,经常会出错.2.(5分)实数227,sin30°,√2+1,2π,(√3)0,|﹣3|中,有理数的个数是()A.2个 B.3个 C.4个 D.5个【分析】根据有理数的概念判断.【解答】解:227是有理数;sin30°=12是有理数;√2+1是无理数;2π是无理数;(√3)0=1是有理数;|﹣3|=3是有理数.有理数有227,sin30°,(√3)0,|﹣3|,共四个.故选C.【点评】解答此题要明确有理数和无理数的概念和分类.有理数包括正整数,负整数,正分数,负分数.无理数是无限不循环小数.3.(5分)已知三角形的两边a=3,b=7,第三边是c,且a<b<c,则c的取值范围是()A.4<c<7 B.7<c<10 C.4<c<10 D.7<c<13【分析】首先根据三角形的三边关系:第三边>两边之差4,而<两边之和10,根据a<b<c即可得c的取值范围.【解答】解:根据三角形三边关系可得4<c<10,∵a<b<c,∴7<c<10.故选B.【点评】已知三角形的两边,则第三边的范围是:>已知的两边的差,而<两边的和.需注意本题的第三边要比其余两边较大的边要大.4.(5分)某班5位同学的身高分别为155,160,160,161,169(单位:厘米),这组数据中,下列说法错误的是()A.众数是160 B.中位数是160 C.平均数是161 D.标准差是2√5【分析】利用众数是出现频数最高的数据即可判断A是对的;利用中位数的求法,可知B是对的;利用平均数的求法可知C是对的;利用方差的公式可求出方差,和标准差=方差的算术平方根,从而对D作出判断.【解答】解:因为众数是出现频数最高的数据即160厘米,所以A是对的;对于中位数,因题中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可,本题是最中间的一个数即160厘米,所以B是对的;根据平均数的公式得平均数为15(155+160+160+161+169)=161厘米,故C是对的;这组数据的方差为:15[(155﹣161)2+(160﹣161)2+(160﹣161)2+(161﹣161)2+(169﹣161)2]=1025,标准差=方差的算术平方根,所以标准差是√5105,所以D是错误的.综上,故选D.【点评】本题考查的是平均数、众数、中位数及标准差.要注意,当所给数据有单位时,所求得的平均数、众数和中位数与原数据的单位相同,不要漏单位.5.(5分)下列命题正确的是()A.3x﹣7>0的解集为x>37B.关于x的方程ax=b的解是x=bb aaC.9的平方根是3D.(√2+1)与(√2−1)互为倒数【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.【解答】解:A、3x﹣7>0的解集为x>73,错误;B、关于x的方程ax=b的解是x=bb aa需加条件a≠0,错误;C、9的平方根是±3,错误;D、正确;故选D.【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.6.(5分)计算:cccccc45°−cccccc60°cccccc30°⋅tt tt tt60°的结果是()A.1 B.13C.2√3﹣3 D.2√33−1【分析】根据特殊角的三角函数值计算.【解答】解:∵cot45°=1,cos60°=12,cos30°=√32,tan60°=√3,∴原式1−12√32•√3=1.故选A.【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,要熟练掌握.7.(5分)一个等腰梯形的高恰好等于这个梯形的中位线,若分别以这个梯形的上底和下底为直径作圆,则这两个圆的位置关系是()A.相离B.相交C.外切D.内切【分析】本题可根据等腰梯形的中位线=上下底边和的一半,得出高的长,再解出两个圆的半径和,与高的长比较;若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d<R+r则两圆相交.【解答】解:设AD=x,BC=y,则高=中位线=12(x+y),两圆半径和为:12x+12y=12(x+y)=高,所以两圆外切.故选C.【点评】本题主要考查两圆的位置关系和等腰梯形的性质.两圆的位置关系有:外离(d>R+r)、内含(d<R﹣r)、相切(外切:d=R+r或内切:d=R﹣r)、相交(R﹣r<d<R+r).等腰梯形的中位线=上下底边和的一半.8.(5分)已知一元二次方程2x2﹣3x﹣6=0有两个实数根x1、x2,直线l经过点A(x1+x2,0)、B(0,x1•x2),则直线l的解析式为()A.y=2x﹣3 B.y=2x+3 C.y=﹣2x﹣3 D.y=﹣2x+3【分析】根据一元二次方程的根与系数的关系,求出A,B的坐标,代入直线的解析式,求出k,b的值,从而确定直线的解析式.【解答】解:由题意知,x1+x2=32,x1•x2=﹣3,∴A(32,0),B(0,﹣3),设直线l的解析式为:y=kx+b,把点A,点B的坐标代入,解得,k=2,b=﹣3,∴直线l的解析式为:y=2x﹣3.故选A.【点评】本题主要考查了两个内容:1、一元二次方程的根与系数的关系,若方程ax2+bx+c=0(a≠0,且a、b、c都是常数),有两个实数根x1和x2,则x1+x2=−bb tt,x1•x2=cc aa;②利用待定系数法求函数的解析式.9.(5分)如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3,下列命题错误的是()A.△AED∽△BEC B.∠AEB=90°C.∠BDA=45° D.图中全等的三角形共有2对【分析】由圆周角的推论可以知道,∠ABE=∠DCE,∠BAE=∠CDE,而AB=DC,可求出△ABE≌△DCE,由此可得出三对全等三角形,也可得出BE=CE,AE=DE,那么AE=4,根据勾股定理的逆定理,可知△ABE为直角三角形,即∠AEB=90°.由此可得出其他正确的结论.【解答】解:A、根据圆周角的推论,可得到:∠ADE=∠BCE,∠DAE=∠CBE,∴△AED∽△BED,正确;B、由上面的分析可知,BE=CE=3,AB=5,AE=AC﹣CE=4,根据勾股定理的逆定理,△ABE为直角三角形,即∠AEB=90°,正确;C、AE=DE,∴∠EAD=∠EDA=45°,正确;D、从已知条件不难得到△ABE≌△DCE、△ABC≌△DCB、△ABD≌△DCA共3对,错误.故选D.【点评】此题运用了圆周角定理的推论和相似三角形的判定、性质的有关知识.还用到了勾股定理的逆定理.10.(5分)如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是()A.5:2 B.4:1 C.2:1 D.3:2【分析】为了便于计算,可设AF=2x,BF=3x,BC=2y,CD=y,利用AG∥BD,可得△AGF∽△BDF,从而可求出AG,那么就可求出AE:EC的值.【解答】解:如图所示,∵AF:FB=2:3,BC:CD=2:1∴设AF=2x,BF=3x,BC=2y,CD=y在△AGF和△BDF中,AAAA BBBB=AAAA BBAA∴AAAA3xx=23∴AG=2y在△AGE和△CDE中,AE:EC=AG:CD=2y:y=2:1故选C.【点评】根据三角形相似,找到各对相似三角形的共公边,建立起不同三角形之间的联系,是解答此题的关键.二、解答题(共4小题,满分50分)11.(10分)先化简再求值:xx2+xxxx−2xx2xx−2xxxx+xx−(1−xxyy2)(1+xxyy2)−xx2÷1xx,其中x=√3+√2,y=√3−√2.【分析】本题可先把分式化简,然后将x、y的值代入化简后的式子求值即可.【解答】解:原式=(xx+2xx)(xx−xx)(xx−xx)﹣(1﹣x2y4)﹣x2y4=3xx xx−xx;当x=√3+√2,y=√3−√2时,原式3×(√3−√2)√3+√2−√3+√2=34√6−32.【点评】本题考查了分式先化简再求值的问题,注意分式混合运算的顺序.12.(10分)某工人要制造180个相同零件,在制造完40个零件后,他改进技术每天多制造15个零件,恰好共用6天全部完成,问该工人改进技术后每天制造多少个零件?【分析】根据题目中的“恰好共用6天全部完成”可得出相等关系,从而只要表示出原来与现在所需的时间即可列出方程.【解答】解:设该工人改进技术后每天制造x个零件.由题意可得:40xx−15+140xx=6.解之得:x=35或10(不合题意,舍去)经检验:x=35是原方程的解.答:该工人改进技术后每天制造35个零件.【点评】找到合适的等量关系是解决问题的关键.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.13.(12分)如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.(1)求证:△ACF∽△BEC;(2)设△ABC的面积为S,求证:AF•BE=2S;(3)试判断以线段AE、EF、FB为边的三角形的形状并给出证明.【分析】(1)对应角相等,两三角形相似;(2)根据相似三角形的性质证明AF•BE=AC•BC=2S;(3)将△ACE绕O顺时针旋转90°到△CBG,边角边证明三角形全等,得出FG=EF,在证明△FBG为直角三角形,得出三边构成三角形的形状.【解答】证明:(1)∵AC=BC,∠ECF=45°,∠ACB=90°,∴∠A=∠B=45°,∠AFC=45°+∠BCF=∠ECB=45°+∠BCF.∴∠AFC=∠ECB.∴△ACF∽△BEC.(2)∵△ACF∽△BEC,∴AAAA BBBB=AAAA BBAA,∴AF•BE=AC•BC.∵SS△AAAAAA=12AAAA⋅AAAA,∴AF•BE=2S.(3)直角三角形.提示:方法1:将△ACE绕点C顺时针旋转90°到△BCG,使得AC与BC重合,连接FG.可以证明△FBG是直角三角形.方法2:将△ACE和△BCF分别以CE、CF所在直线为轴折叠,则AC、BC的对应边正好重合与一条线段CG,连接GE、GF,则△FEG是直角三角形.方法3:由(2)可知AF•BE=AC•BC=AAAA2=12AAAA2.设AE=a,BF=b,EF=c.则(a+b)(b+c)=12(a+b+c)2,化简即得a2+b2=c2,所以以线段AE、EF、FB为边的三角形是以线段EF为斜边的直角三角形.【点评】综合运用了相似三角形的判定和性质,旋转的方法将AE、EF、FB巧妙地转化为三角形.14.(18分)如图,已知A(5,﹣4),⊙A与x轴分别相交于点B、C,⊙A与y 轴相且于点D,(1)求证过D、B、C三点的抛物线的解析式;(2)连接BD,求tan∠BDC的值;(3)点P是抛物线顶点,线段DE是直径,直线PC与直线DE相交于点F,∠PFD的平分线FG交DC于G,求sin∠CGF的值.【分析】(1)已知了A点坐标,即可得出圆的半径和OD的长,连接AB,过A 作BC的垂线不难求出B、C的坐标.然后可用待定系数法求出抛物线的解析式.(2)可取弧BC的中点H,连接AH、AB,那么根据垂径定理和圆周角定理不难得出∠BDC=12∠BAC=∠BAH,由此可求出∠BDC的正切值.(也可通过求弦切角∠PCO的正切值来得出∠BDC的正切值)(3)由于∠CGF=∠CDF+∠GFD=∠CDF+12∠CFD,而∠PCO=∠PFD=∠BDC,那么∠CGF=∠CDF+12∠BDC=∠HDF,在直角三角形ADH中,DA=AH,因此∠HDF=45°,即∠CGF=45°,据此可求出其正弦值.【解答】解:(1)D(0,﹣4),B(2,0),C(8,0);∴抛物线的解析式为y=﹣14x2+52x﹣4∴y=﹣14(x﹣5)2+94.(2)由垂径定理,作弧BC的中点H,连接AH、AB,则∠BDC=∠BAH=12∠BAC,∴tan∠BDC=tan∠BAH=34.(3)由(1)可知:P(5,94),可求得直线PC的解析式为y=﹣34x+6.设M为直线PC与y轴的交点,则M的坐标为(0,6).∴MD=MC=10,∴∠MCD=∠MDC,∴∠MCA=∠MDA=∠MDC+∠CDA=90°,∴∠MCO=∠BDC=∠PFD,∴∠CGF=∠GDF+12∠PFD=∠GDF+12∠BDC=∠HDF=45°,∵DA=AH=半径,∴sin∠CGF=sin45°=√22.【点评】本题主要考查了二次函数解析式的确定、切线的性质、弦切角定理和垂径定理等知识.。
河南省2003年中考数学试题
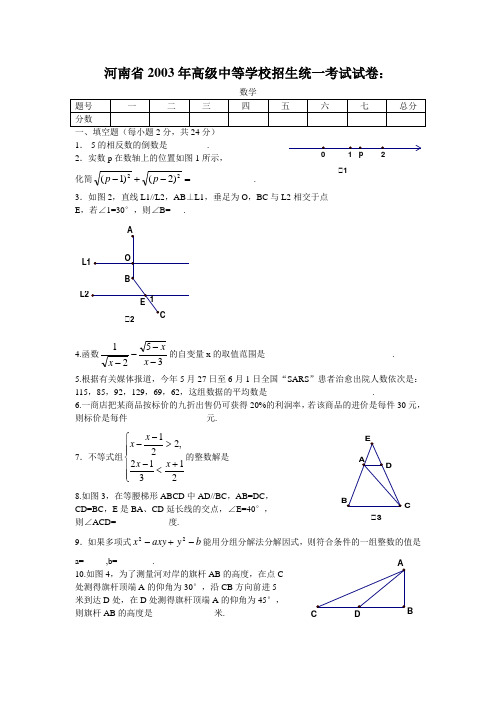
河南省2003年高级中等学校招生统一考试试卷:一、填空题(每小题2分,共24分) 1.-5的相反数的倒数是_________.2.实数p 在数轴上的位置如图1所示,化简=-+-22)2()1(p p ______________.3.如图2,直线L1//L2,AB ⊥L1,垂足为O ,BC 与L2相交于点E ,若∠1=30°,则∠B=___.ͼ2L24.函数3521----x xx 的自变量x 的取值范围是_____________________________. 5.根据有关媒体报道,今年5月27日至6月1日全国“SARS ”患者治愈出院人数依次是:115,85,92,129,69,62,这组数据的平均数是________________________. 6.一商店把某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件__________________元.7.不等式组⎪⎪⎩⎪⎪⎨⎧+<->--21312,221x x x x 的整数解是8.如图3,在等腰梯形ABCD 中AD//BC ,AB=DC ,CD=BC ,E 是BA 、CD 延长线的交点,∠E=40°, 则∠ACD=____________度.9.如果多项式b y axy x -+-22a=_____,b=________.10.如图4,为了测量河对岸的旗杆AB 的高度,在点C 处测得旗杆顶端A 的仰角为30°,沿CB 方向前进5 米到达D 处,在D 处测得旗杆顶端A 的仰角为45°, 则旗杆AB 的高度是______________米.11.点P (m ,n )既在反比例函数)0(2>-=x xy 的图象上,又在一次函数2--=x y 的图象上,则以m 、n 为根的一元一次方程为___________________. 12.如图5,某燃料公司的院内堆放着10个外 径为1米的空油桶,为了防雨需搭建简易防 雨蓬,这个防雨棚的高度最低应为___________ (3取1.73,结果精确到0.1米).二、选择题(每小题3分,只有一个正确答案,共15分) 13.若单项式752222b a b am n nm 与+-+是同类项,则m n 的值是( )(A )-3 (B )-1 (C )1/3 (D )314.某专卖店在统计2003年第一季度的销售额时发现,二月份比一月份增加10%,三月份比二月份减少10%,那么三月份比一月份 ( ) (A) 增加10% (B )减少10% (C )不增不减 (D )减少1% 15.用两块完全重合的等腰三角形纸片拼下列图形:(1)平行四边形(不包含菱形、矩形、正方形);(2)矩形;(3)正方形;(4)等边三角形;(5)等腰直角三角形,一定能拼成的图形是( ) (A )(1)(2)(3) (B )(1)(3)(5) (C )(2)(3)(5) (D )(1)(3)(4)(5) 16.在学校对学生进行的晨检体温测量中,学生甲连续10天的体温与36°C ,的上下波动数据为0.2,0.3,0.1,0.1,0,0.2,0.1,0.1,0,0.1,在这十天中该学生的体温波动数据中不正确的是( )(A )平均数为0.12 (B )众数为0.1 (C )中位数为0.1 (D )方差为0.02 17.已知如图6,ABCD 是⊙O 内接正方形,AB=4,F 是BC 的中点,AF 的延长线交⊙O 于点E ,则AE的长是( )(A )5512 (B )554 (C )55 (D )556 三、(第18、19小题各5分,第20、21小题各6分,共22分) 18.已知2231-=x ,2231+=y ,求4-+xyy x 的值.19.已知,如图7是两个同心圆被两条半径截得的一个扇形图,请你画出一个以O 为对称中心的扇形的对称图(保留作图痕迹,写出画法)ͼ7B20.已知关于x 的方程012)14(2=-+++k x k x . (1)求证:该方程一定有两个不相等的实数根;(2)若x 1、x 2是两个实数根,且32)2)(2(21-=--k x x ,求k 的值.21.已知:如图8,在Rt △ABC 中,∠ACB=90°,AC=BC ,点D 是BC 的中点,CE ⊥AD ,垂足为点E ,BF//AC 交CE 的延长线于点F. 求证:AB 垂直平分DF.ͼ8B四、(每小题7分,共14分) 22.解方程31234222=----x x x x .23.已知:如图9,在直角梯形ABCD 中AB//CD ,AD ⊥AB ,以腰BC 为直径的半圆O 切AD 于点E ,连结点BE ,若BC=6,∠EBC=30°. 求梯形ABCD 的面积.ͼ9E A五、(8分)24.在防治“SARS ”的战役中,为防止疫情扩散,某制药厂接到了生产240箱过氧乙酸消毒液的任务.在生产了60箱后,需要加快生产,每天比原来多生产15箱,结果6天就完成了任务.求加快速度后每天生产多少箱消毒液.六、(8分)25.已知:如图10,⊙O 1与⊙O 2相交,⊙O 1的弦AB 交⊙O 2于点C 、D ,O 1O 2⊥AB 于点F ,过点B 作⊙O 2切线BE ,切点为E ,连结EC 、DE.若BE=DE ,∠BED=30°,AC 、CE 的长是方程016102=+-x x 的两个根,(AC<CE ). (1)求证:BC=EC ;(2)求⊙O 2的半径.(该题是一个错题)ͼ10七、(9分)26.已知:如图11,在平面直角坐标系中,以BC 为直径的圆M 交x 轴于正半轴于点A 、B ,交y 轴于点E 、F ,过点C 作CD 垂直y 轴于点D ,连结AM 并延长交⊙M 于点P ,连结PE.(1)求证:∠FAO=∠EAM ;(2)若二次函数q px x y ++-=2的图象经过B 、C 、E 三点,且以点C 为顶点,当点B 的横坐标等于2时,四边形OECB 的面积是411,求这个二次函数的解析式.。
近十年(2003-2012年)上海中考数学试题及答案

上海市2003年中考数学试卷一、填空题(本大题共14题,每题2分,满分28分) 1.8的平方根是________. 2.在6,8,21,4中,是最简二次根式的是________. 3.已知函数xx x f 1)(+=,那么)12(-f ________. 4.分解因式:1222+--a b a ________. 5.函数xxy -=1的定义域是________. 6.方程x x =-++22的根是________.7.上海浦东磁悬浮铁路全长30千米,单程运行时间约8分钟,那么磁悬浮列车的平均速度用科学记数法表示约________米/分钟.8.在平面直角坐标系内,从反比例函数)0(>=k xk y 的图象上的一点分别作x 、y 轴的垂线段,与x 、y 轴所围成的矩形面积是12,那么该函数解析式是________.9.某公司今年5月份的纯利润是a 万元,如果每个月份纯利润的增长率都是x ,那么预计7月份的纯利润将达到________万元(用代数式表示).10.已知圆O 的弦AB =8,相应的弦心距OC =3,那么圆O 的半径长等于________. 11.在△ABC 中,点D 、E 分别在边AB 、AC 上,CD 平分∠ACB ,DE ∥B C .如果AC =10,AE =4,那么BC =________.12.如图,矩形内有两个相邻的正方形,面积分别为4和2,那么阴影部分的面积为________.13.正方形ABCD 的边长为1.如果将线段BD 绕着点B 旋转后,点D 落在BC 延长线上的点D ′处,那么tan ∠BAD ′=________.14.矩形ABCD 中,AB =5,BC =12.如果分别以A 、C 为圆心的两圆相切,点D 在圆C 内,点B 在圆C 外,那么圆A 的半径r 的取值范围是________.二、多项选择题(本大题共4题,每题3分,满分12分.每题列出的四个答案中,至少有一个是正确的,把所有正确答案的代号填入括号内,错选或不选得0分,否则每漏选一个扣1分,直至扣完为止)15.下列命题中正确的是( ). A .有限小数是有理数 B .无限小数是无理数C .数轴上的点与有理数一一对应D .数轴上的点与实数一一对应16.已知0<b <a ,那么下列不等式组中无解的是( ). A .⎩⎨⎧b x a x <>, B .⎩⎨⎧bx a x <->-,C .⎩⎨⎧b x a x <->,D .⎩⎨⎧b x a x <>-,17.下列命题中正确的是( ).A .三点确定一个圆B .两个等圆不可能内切C .一个三角形有且只有一个内切圆D .一个圆有且只有一个外切三角形18.如图,已知AC 平分∠P AQ ,点B 、B ′分别在边AP 、AQ 上.如果添加一个条件,即可推出AB =AB ′,那么该条件可以是( ).A .BB '⊥AC B .BC =B 'CC .∠ACB =∠ACB 'D .∠ABC =∠AB 'C三、(本大题共4题,每题7分,满分28分)19.已知222=-x x ,将下式先化简,再求值:1)3)((3)3)((1)(2--+-++-x x x x x .20.解方程组21.将两块三角板如图放置,其中∠C =∠EDB =90°,∠A =45°,∠E =30°,AB =DE =6.求重叠部分四边形DBCF 的面积.22.某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:(1)这32名学生培训前考分的中位数所在的等级是________,培训后考分的中位数所在的等级是________;(2)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;(3)估计该校整个初二年级中,培训后考分等级为“合格”与“优秀”的学生共有________名;(4)你认为上述估计合理吗?理由是什么?答:________,理由:_________________________.四、(本大题共4题,每题10分,满分40分)23.已知:如图,一条直线经过点A(0,4)、点B(2,0),将这条直线向左平移与x 轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC.求以直线CD为图象的函数解析式.24.已知:如图,△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE,G是垂足.求证:(1)G是CE的中点;(2)∠B=2∠BCE.25.卢浦大桥拱形可以近似看作抛物线的一部分.在大桥截面1∶11000的比例图上,跨度AB=5 cm,拱高OC=0.9 cm,线段DE表示大桥拱内桥长,DE∥AB,如图(1).在比例图上,以直线AB为x轴,抛物线的对称轴为y轴,以1 cm作为数轴的单位长度,建立平面直角坐标系,如图(2).(1)求出图(2)上以这一部分抛物线为图象的函数解析式,写出函数定义域;(2)如果DE 与AB 的距离OM =0.45 cm ,求卢浦大桥拱内实际桥长(备用数据:4.12≈,计算结果精确到1米).26.已知在平面直角坐标系内,O 为坐标原点,A 、B 是x 轴正半轴上的两点,点A 在点B 的左侧,如图.二次函数c bx ax y ++=2(a ≠0)的图象经过点A 、B ,与y 轴相交于点C .(1)a 、c 的符号之间有何关系?(2)如果线段OC 的长度是线段OA 、OB 长度的比例中项,试证a 、c 互为倒数; (3)在(2)的条件下,如果b =-4,34=AB ,求a 、c 的值.五、(本大题只有1题,满分12分,(1)、(2)、(3)题满分均为4分) 27.如图(1),在正方形ABCD 中,AB =1,是以点B 为圆心,AB 长为半径的圆的一段弧,点E 是边AD 上的任意一点(点E 与点A 、D 不重合),过E 作所在圆的切线,交边DC 于点F ,G 为切点.(1)当∠DEF =45°时,求证点G 为线段EF 的中点;(2)设AE =x ,FC =y ,求y 关于x 的函数解析式,并写出函数的定义域;(3)将DEF 沿直线EF 翻折后得EF D 1∆,如图(2),当65=EF 时,讨论D AD 1∆与F ED 1∆是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.(1) (2) (3)(备用图)参考答案一、填空题(本大题共14题,每题2分,满分28分)1.22± 2.6 3.22+ 4.(a -b -1)(a +b -1) 5.x ≤1且x ≠0 6.x =-2 7.31075.3⨯ 8.xy 12=9.2)1(x a + 10.5 11.15 12.222- 13.2 14.1<r <8或18<r <25二、多项选择题(本大题共4题,每题3分,满分12分.错选或不选得0分,否则每漏选一个扣1分,直至扣完为止)15.A 、D 16.A 、C 17.B 、C 18.A 、C 、D 三、(本大题共4题,每题7分,满分28分)19.解:原式=34912222+-++-x x x x x -+……………………………………3分 5632--=x x …………………………………………………………………………………1分解法一:5)2(32--=x x .………………………………………………………2分 ∵ 222=-x x ,∴ 原式=3×2-5=1.………………………………………1分解法二:从222=-x x 中解得31±=x ,1分 分别代入,答案正确. (1)20.解:由①,得(2x +y )(2x -y )=0, ∴ 2x +y =0,2x -y =0.…………1分,1分它们与方程②分别组成两个方程组:⎩⎨⎧;04,022=+-=+xy x y x (*)……………………………………………………………………1分⎩⎨⎧-.04,022=+-=xy x y x (**)…………………………………………………………………1分分别解这两个方程组,可知方程组(*)无解;………………………………………1分 方程组(**)的解是⎩⎨⎧==;4,211y x ⎩⎨⎧-=-=.4,222y x ………………………………………1分,1分 所以原方程组的解是⎩⎨⎧==;4,211y x ⎩⎨⎧-=-=.4,222y x 21.解:在△EDB 中,∵ ∠EDB =90°,∠E =30°,DE =6, ∴ 3233630tan ==⨯=︒⋅DE DB .……………………………………………1分 ∴ 326--==DB AB AD .又∵ ∠A =45°,∴ ∠AFD =45°,得FD =AD .∴ 31224)326(212122-=-=⨯=∆AD S ADF .…………………………………2分 在等腰直角三角形ABC 中,斜边AB =6,所以9412=∆AB S ABC =.…………… 2分∴ )31224(9--==四边形ADF ABC DBCF S S S ∆∆-=15312-……………………2分 22.解:(1)不合格,合格;(2)75%,25%;(3)240;(4)合理,该样本是随机样本(或该样本具有代表性).………………………………………………………每个空格1分 四、(本大题共4题,每题10分,满分40分)23.解:设以直线AB 为图象的一次函数解析式为y =kx +b . 因为直线AB 经过点(0,4)、点(2,0),所以得方程组⎩⎨⎧=.20,4b k b +=……………………………………………………………………………1分解得⎩⎨⎧-=.4,2=b k …………………………………………………………………………2分所以以直线AB 为图象的一次函数解析式为y =-2x +4.由于CD ∥AB ,设以直线CD 为图象的一次函数解析式为y =-2x +b '.………2分 解法一:由于DB =DC ,DO ⊥CB ,∴ OC OB =.………………………… 2分 所以点C 的坐标是(-2,0),得b '=-4.…………………………………1分,1分所以以直线CD 为图象的一次函数解析式为y =-2x -4.………………………1分解法二:由题意,得点D 的坐标是(0,b '),点C 的坐标是(2b ',0). ∵ DB =DC ,∴2222)2()()(2b b b '''+=+.………………………………………………………2分 解得4±'=b .……………………………………………………………………………1分因为点D '与点A 不重合,所以4=b '舍去.…………………………………………1分 因此以直线CD 为图象的一次函数解析式为y =-2x -4.……………………………1分 24.证明:(1)如图,连结DE .………………………………………………………1分 ∵ ∠ADB =90°,E 是AB 的中点,∴ DE =AE =BE .………………………………………………………………………2分 又∵ DC =BE ,∴ DC =DE .………………………………………………………1分 又因为DG ⊥CE ,所以G 是CE 中点.…………………………………………………2分 (2)∵DE =DC ,∴ ∠DCE =∠DEC .……………………………………………1分 ∴ ∠EDB =∠DEC +∠DCE =2∠BCE .……………………………………………1分 又∵ DE =BE ,∴ ∠B =∠EDB .………………………………………………… 1分∴ ∠B =2∠BCE .………………………………………………………………………1分25.解:(1)由于顶点C 在y 轴上,所以设以这部分抛物线为图象的函数解析式为1092+=ax y .……………………………………………………………………………1分 因为点A (25-,0)(或B (25,0))在抛物线上,所以109)25(02+=-⋅a ,得12518=-a .……………………………………………1分因此所求函数解析式为)2525(109125182≤≤-x x y +=-.……………………………………………1分,1分 (2)因为点D 、E 的纵坐标为209,……………………………………………………1分所以109125182092+-x =,得245±=x ……………………………………………2分所以点D 的坐标为(245-,209),点E 的坐标为(245,209). 所以225)245(245=-=-DE .…………………………………………………1分 因此卢浦大桥拱内实际桥长为385227501.011000225≈⨯⨯=(米).…………………………………………2分 26.(1)解:a 、c 同号.………………………………………………………………2分 或当a >0时,c >0;……………………………………………………………………1分 当a <0时,c <0.……………………………………………………………………1分 (2)证明:设点A 的坐标为(1x ,0),点B 的坐标为(2x ,0),则210x x <<. ∴ 1x OA =,2x OB =,c OC =.…………………………………………………1分据题意,1x 、2x 是方程)0(02≠=a c bx ax ++的两个根.…………………………1分∴ acx x =⋅21.…………………………………………………………………………1分 由题意,得2OC OB OA =⋅,即22c c ac ==.………………………………………1分所以当线段OC 长是线段OA 、OB 长的比例中项时,a 、c 互为倒数.(3)解:当4-=b 时,由(2)知,0421>==-+aa b x x ,∴ a >0.…………1分 解法一:AB =OB -OA =21221124)(x x x x x x -+=-, ∴ aa ac a c a AB 32416)(4)4(22=-==-.……………………………………1分 ∵ 34=AB ,∴3432=a .得21=a .∴ c =2. ……………………………………………1分 解法二:由求根公式,aa a ac x 322416424164±-±-±===,∴ ax 321-=,a x 322+=.∴ aa a x x OA OB AB 32323212=--=-=-=+.………………………1分 ∵ 34=AB ,∴ 3432=a ,得21=a .∴ c =2…………………………………………………………………………………1分五、(本大题只有1题,满分12分) 27.(1)证明:∵ ∠DEF =45°,得∠DFE =90°-∠DEF =45°,∴ ∠DFE =∠DEF . ∴ DE =DF .又∵ AD =DC ,∴ AE =FC .…………1分 因为AB 是圆B 的半径,AD ⊥AB ,所以AD 切圆B 于点A ;………………………1分 同理,CD 切圆B 于点C .又因为EF 切圆B 于点G ,所以AE =EG ,FC =FG .………………………………1分因此EG =FG ,即点G 为线段EF 的中点.……………………………………………1分(2)解:∵ EG =AE =x ,FG =CF =y ,∴ ED =1-x ,FD =1-y . 在R t △DEF 中,由222EF FD ED =+,得222)()1()1(y x y x +-+-= .…………………………………………………………2分 ∴ )10(11<<+-=x xxy .………………………………………………………1分,1分 (3)解:当65=EF 时,由(2)得6511=+-+x x x FC AE FG EG EF =+=+=.得311=x 或212=x ,即31=AE 或21=AE .①当21=AE 时,D AD 1∆∽F ED 1∆.………………………………………………1分证明如下:设直线EF 交线段1DD 于点H ,如图. 据题意,△EDF ≌F ED 1∆;1DD EF ⊥且H D DH 1=. ∴ 21=AE ,AD =1,得AE =ED ,∴ EH ∥1AD .∴ 11FED FED AD D ∠∠∠==,……………………………………………………1分 ︒∠∠901==EHD D AD . 又∵ ︒=∠=∠901EDF F ED ,∴ D AD F ED 11∠=∠.………………………………………………………………1分 ∴ D AD 1∆∽F ED 1∆.②当31=AE 时,D AD 1∆与F ED 1∆不相似.…………………………………………1分G图12004年上海市中等学校高中阶段招生文化考试数学试卷(满分120分,考试时间120分钟)一、填空题:(本大题共14题,每题2分,共28分)1.计算:(2)(2)__________a b a b -+=.2.不等式组230320x x -<⎧⎨+>⎩的整数解是______________.3.函数y =的定义域是__________________. 41x =-的根是________________. 5.用换元法解22114x x x x +++=,可设1y x x=+,则原方程可化为关于y 的方程是______________.6.一个射箭运动员连续射靶5次,所得的环数分别是8,6,10,7,9,则这个运动员所得环数的标准差为__________.7.已知0a b <<,则点A (,)a b b -在第________象限.8.正六边形是轴对称图形,它有_______条对称轴.9.在△ABC 中,点D 、E 分别在边AB 、AC 上,DE ∥BC ,AD=1,BD =2,则:ADE ABC S S ∆∆=__________.10.在△ABC 中,∠A =90°,设∠B =θ,AC =b ,则AB =________(用b 和θ的三角比表示).11.某山路坡面坡度i =沿此山路向上前进200米,升高了__________米.12.在△ABC 中,点G 是重心,若BC 边上的高为6,则点G 到BC 的距离为______________. 13.直角三角形的两条边长分别为6和8,那么这个三角形的外接圆的半径等于_______________. 14.如图1,边长为3的正方形ABCD 绕点C 按顺时针方向旋转30°后得到的正方形EFCG ,EF 交AD 与点H ,那么DH 的长为___________.二、 多项选择题:(本大题共4题,每题3分,共12分)【每题列出的四个答案中,至少有一个是正确的,把所有正确答案的代号填入括号内,错选或不选得0分,否则每漏选一个扣一分,直至扣完为止】C图215.下列运算,计算结果正确的是……………………………………………( )(A ) 437a a a =; (B ) 632a a a ÷=; (C ) 325()a a =; (D ) 333()a b a b =.16.如图2,在△ABC 中,AB=AC ,∠A =36°,BD 平分∠ABC ,DE ∥BC 那么在下列三角形中,与相似的三角形是……………………( (A ) △DBE ; (B ) △ADE ; (C ) △ABD ; (D ) △BDC . 17.下列命题中,正确的是…………………………( )(A )一个点到圆心的距离大于这个圆的半径,这个点在圆外; (B )一条直线垂直于圆的半径,这条直线一定是圆的切线;(C )两个圆的圆心距等于它们的半径之和,这两个圆有三条公切线; (D )圆心到一条直线的距离小于这个圆的半径,这条直线与圆有两个交点. 18.在函数(0)ky k x=>的图像上有三点111(,)A x y 、222(,)A x y 、333(,)A x y ,已知1230x x x <<<,则下列各式中,正确的是…………………………( )(A ) 130y y <<; (B ) 310y y <<; (C ) 213y y y <<; (D ) 312y y y <<.三、(本大题共4题,每题7分,共28分)19-20.关于x 的一元二次方程2(31)210mx m x m --+-=,其根的判别式的值为1,求m 的值及该方程的根.21.如图3,等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于点D ,折痕分别交AB 、BC 于点F 、E .若AD=2,BC =8, 求:(1)BE 的长; (2)∠CDE 的正切值.22.某区从参加数学质量检测的8000名学生中,随机抽取了部分学生的成绩作为样本,为了节省时间,先将样本分成甲、乙两组,分别进行分析,得表一;随后汇总成样本数据,得到部分结果,如表二.(1)样本中,学生的数学成绩的平均分数约为_________分(结果精确到0.1分); (2)样本中,数学成绩在[)84,96分数段的频数________,等第为A 的人数占抽样学生总数的百分比为_________,中位数所在的分数段为______________;(3)估计这8000名学生成绩的平均分数约为__________分(结果精确到0.1分).四、(本大题共4题,每题10分,共40分)23.在平面直角坐标系中,点O 是坐标原点,二次函数)4()5(2+--+=k x k x y 的图像交x 轴于A )0,(1x 、B )0,(2x ,且8)1)(1(21-=++x x .图4 (1)求二次函数的解析式;(2)将上述二次函数的图像沿x 轴向右平移2个单位,设平移后的图像与y 轴的交点为C ,顶点为P ,求△POC 的面积.24.如图4,在△ABC 中,∠BAC =90°,延长BA 到点D ,使AD =21AB ,点E 、F 分别为边BC 、AC 的中点. (1)求证:DF=BE ;(2)过点A 作AG ∥BC ,交DF 于点G ,求证:AG=DG25.为加强防汛工作,市工程队准备对苏州河一段长为2240米的河堤进行加固.由于采用新的加固模式,现在计划每天加固的长度比原计划增加了20米,因而完成此段加固工程所需天数将比原计划缩短2天.为进一步缩短该段加固工程的时间,如果要求每天加固224米,那么在现在计划的基础上,每天加固的长度还要再增加多少米?A BCO图5如图6,在平面直角坐标系中,O 为坐标原点,A 点的坐标为(1,0),点B 在x 轴上,且在点A 的右侧,AB=OA ,过点A 和B 作x 轴的垂线,分别交二次函数2x y =的图像于点C和D ,直线OC 交BD 于点M ,直线CD 交y 轴于点H ,记点C 、D 的的横坐标分别为C x 、D x ,点H 的纵坐标为H y .26.在△ABC 中,∠BAC =90°,AB=AC=22,⊙A 的半径为1,如图5所示.若点O 在BC 上运动(与点B 、C 不重合),设BO =x ,△AOC 的面积为y(1)求关于的函数解析式,并写出函数的定义域;(2)以点O 为圆心,BO 长为半径作⊙O ,求当⊙O 与⊙A 相切时,△AOC 的面积.五、(本大题只有1题,满分12分,(1)小题满分6分,(2)(3)小题满分均为3分)27.数学课上,老师出示图6和下面框中的条件.同学发现两个结论:①3:2:ABMC =梯形S S CMD ∆ ②数值相等关系:H D C y x x -=∙ (1)请你验证结论①和结论②成立;(2)请你研究:如果上述框中的条件“A 的坐标(1,0)”改为“A 的坐标(t ,0) (t>0)”,其他条件不变,结论①是否仍成立?(请说明理由)(3)进一步研究:如果上述框中的条件“A 的坐标(1,0)”改为“A 的坐标(t ,0) (t>0)”,又将条件“2x y =”改为“)0(2>=a ax y ”, 其他条件不变,那么C x 、D x 与H y 有怎样的数值关系?写出结果并说明由)12005年上海市初中毕业生统一学业考试数学试卷一、填空题(本大题共14题,满分42分) 1、 计算:()22x=2、 分解因式:22a a -= 3、计算:)11=4、函数y =的定义域是5、 如果函数()1f x x =+,那么()1f =6、 点A(2,4)在正比例函数的图象上,这个正比例函数的解析式是7、 如果将二次函数22y x =的图象沿y 轴向上平移1个单位,那么所得图象的函数解析式是8、 已知一元二次方程有一个根为1,那么这个方程可以是 (只需写出一个方程) 9、 如果关于x 的方程240x x a ++=有两个相等的实数根,那么a = 10、 一个梯形的两底长分别为6和8,这个梯形的中位线长为 11、 在△ABC 中,点D 、E 分别在边AB 和AC 上,且DE ∥BC ,如果AD =2,DB =4,AE =3,那么EC = 12、 如图1,自动扶梯AB 段的长度为20米,倾斜角A 为α,高度BC 为 米(结果用含α的三角比表示).13、 如果半径分别为2和3的两个圆外切,那么这两个圆的圆心距是 14、 在三角形纸片ABC 中,∠C =90°,∠A =30°,AC =3,折叠该纸片,使点A 与点B 重合,折痕与AB 、AC 分别相交于点D 和点E (如图2),折痕DE 的长为二选择题:(本大题共4题,满分12分) 15、 在下列实数中,是无理数的为 ( ) A 、0 B 、-3.5 C D 16、 六个学生进行投篮比赛,投进的个数分别为2、3、3、5、10、13,这六个数的中位数为 ( )A 、3B 、4C 、5D 、6图117、 已知Rt △ABC 中,∠C =90°,AC =2,BC =3,那么下列各式中,正确的是( )A 、2sin 3B =B 、2cos 3B =C 、23tgB =D 、23ctgB = 18、 在下列命题中,真命题是 ( )A 、两个钝角三角形一定相似B 、两个等腰三角形一定相似C 、两个直角三角形一定相似D 、两个等边三角形一定相似 三、(本大题共3题,满分24分) 19、 (本题满分8分) 解不等式组:()315216x xx x +>-⎧⎨+-<⎩,并把解集在数轴上表示出来.20、(本题满分8分)解方程:228124x x x x x +-=+--21、 (本题满分8分,每小题满分各为4分)(1)在图3所示编号为①、②、③、④的四个三角形中,关于y 轴对称的两个三角形的编号为 ;关于坐标原点O 对称的两个三角形的编号为 ; (2)在图4中,画出与△ABC 关于x 轴对称的△A 1B 1C 1x-5-4-3-2-15432O1四、(本大题共4题,满分42分) 22、 (本题满分10分,每小题满分各为5分)在直角坐标平面中,O 为坐标原点,二次函数2y x bx c =++的图象与x 轴的负半轴相交于点C (如图5),点C 的坐标为(0,-3),且BO =CO (1) 求这个二次函数的解析式; (2) 设这个二次函数的图象的顶点为M ,求AM 的长.23、 (本题满分10分)已知:如图6,圆O 是△ABC 的外接圆,圆心O 在这个三角形的高CD 上,E 、F 分别是边AC 和BC 的中点,求证:四边形CEDF 是菱形.24、 (本题满分10分,第(1)、(2)、(3)小题满分各为2分,第(4)小题满分4分) 小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图7),同时将前4个月的用电量和相应电费制成表格(如表1) 根据上述信息,解答下列问题:(1) 计算5月份的用电量和相应电费,将所得结果填入表1中; (2) 小明家这5个月的月平均用电量为 度;(3) 小明家这5个月的月平均用电量呈 趋势(选择“上升”或“下降”);这5个月每月电费呈 趋势(选择“上升”或“下降”);(4) 小明预计7月份家中用电量很大,估计7月份用电量可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.25、 (本题满分12分,每小题满分各为4分)在△ABC 中,∠ABC =90°,AB =4,BC =3,O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D ,交线段OC 于点E ,作EP ⊥ED ,交射线AB 于点P ,交射线CB 于点F 。
2003年浙江省杭州市中考数学试卷

2003年浙江省杭州市中考数学试卷一、选择题(共15小题,每小题3分,满分45分)1.(3分)直线y=x﹣1不经过()A.第一象限B.第二象限C.第三象限D.第四象限2.(3分)如图所示立方体中,过棱BB1和平面CD1垂直的平面有()A.1个B.2个C.3个D.0个3.(3分)某商店举办有奖销售活动,办法如下:凡购货满100元者得奖券1张,多购多得.每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率应该是()A.B.C.D.4.(3分)计算(0.04)2003×[(﹣5)2003]2得()A.1B.﹣1C.D.5.(3分)天安门广场的面积约为44万平方米,请你估计一下,它的百万分之一大约相当于()A.教室地面的面积B.黑板面的面积C.课桌面的面积D.铅笔盒盒面的面积6.(3分)一个圆柱的侧面展开图是一个面积为4平方单位的矩形,那么这个圆柱的母线长L和底面半径r之间的函数关系是()A.反比例函数B.正比例函数C.一次函数D.二次函数7.(3分)已知,则的值为()A.5B.6C.3D.48.(3分)如图,要判断△ABC的面积是△DBC的面积的几倍,只有一把仅有刻度的直尺,需要度量的次数最少是()A.3次以上B.3次C.2次D.1次9.(3分)有一块长为a,宽为b的长方形铝片,四个角上剪去一个边长为x的相同的正方形后,折成一个无盖的盒子,则此盒子的容积V的表达式是()A.V=x2(a﹣x)b(b﹣x)B.V=x(a﹣x)(x﹣b)C.V=x(a﹣2x)(b﹣2x)D.V=x(a﹣2x)(b﹣2x)10.(3分)如图,点C为⊙O的弦AB上一点,点P为⊙O上一点,且OC⊥CP,则有()A.OC2=CA•CB B.OC2=PA•PB C.PC2=PA•PB D.PC2=CA•CB 11.(3分)把抛物线y=x2+bx+c的图象向左平移3个单位,再向下平移2个单位,所得图象的关系式为y=x2﹣3x+5,则有()A.b=3,c=7B.b=﹣9,c=25C.b=3,c=3D.b=﹣9,c=21 12.(3分)设x1,x2是关于x的方程x2+px+q=0的两根,x1+1,x2+1是关于x的方程x2+qx+p=0的两根,则p,q的值分别等于()A.1,﹣3B.1,3C.﹣1,﹣3D.﹣1,3 13.(3分)某种型号的空调器经过3次降价,价格比原来下降了30%,则其平均每次下降的百分比(精确到1%)应该是()A.26.0%B.33.1%C.8.5%D.11.2% 14.(3分)在高速公路上,一辆长4米,速度为110千米/小时的轿车准备超越一辆长12米,速度为100千米/小时的卡车,则轿车从开始追及到超越卡车,需要花费的时间约是()A.1.6秒B.4.32秒C.5.76秒D.345.6秒15.(3分)对于以下四个命题:①若直角三角形的两条边长为3与4,则第三边的长是5;②()2=a;③若点P(a,b)在第三象限,则点Q(﹣a,﹣b)在第一象限;④两边及其第三边上的中线对应相等的两个三角形全等,正确的说法是()A.只有①错误,其他正确B.①②错误,③④正确C.①④错误,②③正确D.只有④错误,其他正确二、填空题(共5小题,每小题4分,满分20分)16.(4分)据信息产业部2003年4月公布的数字显示,我国固定电话和移动电话用户近年来都有大幅度增加,移动电话用户已接近固定电话用户,根据下图所示,我国固定电话从年至年的年增加量最大;移动电话从年至年的年增加量最大.17.(4分)如图,锐角三角形ABC的边AB,AC上的高线CE和BF相交于点D,请写出图中的两对相似三角形:(用相似符号连接).18.(4分)中国CBA篮球赛中,八一队某主力队员在一场比赛中22投14中,得了28分,除了3个三分球全中外,他还投中了个2分球和个罚球.19.(4分)根据指令[s,A](s≥0,0°<A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,现机器人在直角坐标系的坐标原点,且面对x轴正方向.(1)若给机器人下了一个指令[4,60°],则机器人应移动到点;(2)请你给机器人下一个指令,使其移动到点(﹣5,5).20.(4分)求函数的最小值,较合适的数学方法应该是法,当然还可以用法等方法来解决.三、解答题(共6小题,满分55分)21.(7分)创新设计题:如图所示的集合中有5个实数,请计算其中的有理数的和与无理数的积的差.22.(8分)如图,EF为梯形ABCD的中位线,AH平分∠DAB交EF于M,延长DM交AB于N.求证:△ADN是等腰三角形.23.(8分)如图,⊙C经过原点且与两坐标轴分别交于A、B两点,点A的坐标是(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标.24.(10分)解方程组:25.(10分)转炉炼钢产生的棕红色烟尘会污染大气,某装置可通过回收棕红色烟尘中的氧化铁从而降低污染.该装置的氧化铁回收率与其通过的电流有关,现经过试验得到下列数据:如图建立直角坐标系,用横坐标表示通过的电流强度,纵坐标表示氧化铁回收率.(1)将试验所得数据在上图所给的直角坐标系中用点表示;(注:该图中坐标轴的交点代表点(1,70))(2)用线段将题(1)所画的点从左到右顺次连接,若用此图象来模拟氧化铁回收率y 关于通过电流x 的函数关系,试写出该函数在1.7≤x ≤2.4时的表达式;(3)利用题(2)所得函数关系,求氧化铁回收率大于85%时,该装置通过的电流应该控制的范围.(精确到0.1A )26.(12分)如图,在矩形ABCD 中,BD=20,AD >AB ,设∠ABD=α,已知sinα是方程25x 2﹣35x +12=0的一个实根,点E ,F 分别是BC ,DC 上的点,EC +CF=8,设BE=x ,△AEF 的面积等于y .(1)求出y 与x 之间的函数关系式;(2)当E ,F 两点在什么位置时,y 有最小值并求出这个最小值.2003年浙江省杭州市中考数学试卷参考答案与试题解析一、选择题(共15小题,每小题3分,满分45分)1.(3分)直线y=x﹣1不经过()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵y=x﹣1∴k>0,b<0∴y=x﹣1的图象经过第一、三、四象限,不经过第二象限故选:B.2.(3分)如图所示立方体中,过棱BB1和平面CD1垂直的平面有()A.1个B.2个C.3个D.0个【解答】解:过棱BB1和平面CD1垂直的平面有CBB1C1,所以只有1个.故选:A.3.(3分)某商店举办有奖销售活动,办法如下:凡购货满100元者得奖券1张,多购多得.每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率应该是()A.B.C.D.【解答】解:P(买100元商品的中奖)=.故选:D.4.(3分)计算(0.04)2003×[(﹣5)2003]2得()A.1B.﹣1C.D.【解答】解:(0.04)2003×[(﹣5)2003]2,=(0.04)2003×[(﹣5)2]2003,=(0.04)2003×(25)2003,=(0.04×25)2003,=1.故选:A.5.(3分)天安门广场的面积约为44万平方米,请你估计一下,它的百万分之一大约相当于()A.教室地面的面积B.黑板面的面积C.课桌面的面积D.铅笔盒盒面的面积【解答】解:44万平方米=440 000平方米,440 000×=0.44平方米,不足半平方米,应是课桌面的面积.故选:C.6.(3分)一个圆柱的侧面展开图是一个面积为4平方单位的矩形,那么这个圆柱的母线长L和底面半径r之间的函数关系是()A.反比例函数B.正比例函数C.一次函数D.二次函数【解答】解:根据题意,得2πrL=4,则L=.所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数.故选:A.7.(3分)已知,则的值为()A.5B.6C.3D.4【解答】解:∵a==,b==,∴==5.故选:A.8.(3分)如图,要判断△ABC的面积是△DBC的面积的几倍,只有一把仅有刻度的直尺,需要度量的次数最少是()A.3次以上B.3次C.2次D.1次【解答】解:连接AD并延长交BC于M,作DF∥BC交AP于点F.一次测量AM(AD)即可得AD,AM长,即可算出DM长,由=,即可求出△ABC的面积是△DBC的面积的几倍.所以只量一次.故选:D.9.(3分)有一块长为a,宽为b的长方形铝片,四个角上剪去一个边长为x的相同的正方形后,折成一个无盖的盒子,则此盒子的容积V的表达式是()A.V=x2(a﹣x)b(b﹣x)B.V=x(a﹣x)(x﹣b)C.V=x(a﹣2x)(b﹣2x)D.V=x(a﹣2x)(b﹣2x)【解答】解:根据题意得V=x(a﹣2x)(b﹣2x)故选:D.10.(3分)如图,点C为⊙O的弦AB上一点,点P为⊙O上一点,且OC⊥CP,则有()A.OC2=CA•CB B.OC2=PA•PB C.PC2=PA•PB D.PC2=CA•CB 【解答】解:延长PC交圆于D,连接OP,OD根据相交弦定理,得CP•CD=CA•CB∵OP=OD,OC⊥PC∴PC=CD则PC2=CA•CB故选:D.11.(3分)把抛物线y=x2+bx+c的图象向左平移3个单位,再向下平移2个单位,所得图象的关系式为y=x2﹣3x+5,则有()A.b=3,c=7B.b=﹣9,c=25C.b=3,c=3D.b=﹣9,c=21【解答】解:根据题意y=x2﹣3x+5=(x﹣)2+,向右平移3个单位,再向上平移2个单位得y=(x﹣)2+=x2﹣9x+25.所以b=﹣9,c=25.故选:B.12.(3分)设x1,x2是关于x的方程x2+px+q=0的两根,x1+1,x2+1是关于x的方程x2+qx+p=0的两根,则p,q的值分别等于()A.1,﹣3B.1,3C.﹣1,﹣3D.﹣1,3【解答】解:由根与系数的关系可知:x1+x2=﹣p,x1•x2=q;x1+1+x2+1=﹣q,(x1+1)(x2+1)=p,即x1+x2+x1•x2+1=p.将x1+x2=﹣p,x1•x2=q代入整理,得解得.故选C13.(3分)某种型号的空调器经过3次降价,价格比原来下降了30%,则其平均每次下降的百分比(精确到1%)应该是()A.26.0%B.33.1%C.8.5%D.11.2%【解答】解:设平均每次下降的百分比为x,则(1﹣x)3=1﹣30%,解得x=11.2%.故选D.14.(3分)在高速公路上,一辆长4米,速度为110千米/小时的轿车准备超越一辆长12米,速度为100千米/小时的卡车,则轿车从开始追及到超越卡车,需要花费的时间约是()A.1.6秒B.4.32秒C.5.76秒D.345.6秒【解答】解:设需要的时间为x秒,110千米/小时=米/秒,100千米/小时=米/秒,根据轿车走的路程等于超越卡车的路程加上两车的车身长,得出:解得:x=5.76故选:C.15.(3分)对于以下四个命题:①若直角三角形的两条边长为3与4,则第三边的长是5;②()2=a;③若点P(a,b)在第三象限,则点Q(﹣a,﹣b)在第一象限;④两边及其第三边上的中线对应相等的两个三角形全等,正确的说法是()A.只有①错误,其他正确B.①②错误,③④正确C.①④错误,②③正确D.只有④错误,其他正确【解答】解:①错误,应强调为直角三角形的两条直角边长为3与4,则第三边的长是5;②正确,隐含条件a≥0,根据二次根式的意义,等式成立;③正确,若点P(a,b)在第三象限,则a<0,b<0;则﹣a>0,﹣b>0,点Q(﹣a,﹣b)在第一象限;④正确,作辅助线,倍长中线,可证明两个三角形全等.故选:A.二、填空题(共5小题,每小题4分,满分20分)16.(4分)据信息产业部2003年4月公布的数字显示,我国固定电话和移动电话用户近年来都有大幅度增加,移动电话用户已接近固定电话用户,根据下图所示,我国固定电话从1999年至2000年的年增加量最大;移动电话从2001年至2002年的年增加量最大.【解答】解:由图可知,我国固定电话从1999年至2000年的年增加量最大;移动电话从2001年至2002年的年增加量最大.故依次填:1999~2000,2001~2002.17.(4分)如图,锐角三角形ABC的边AB,AC上的高线CE和BF相交于点D,请写出图中的两对相似三角形:△BDE∽△CDF,△ABF∽△ACE(用相似符号连接).【解答】解:(1)在△BDE和△CDF中∠BDE=∠CDF∠BED=∠CFD=90°∴△BDE∽△CDF(2)在△ABF和△ACE中∵∠A=∠A,∠AFB=∠AEC=90°∴△ABF∽△ACE18.(4分)中国CBA篮球赛中,八一队某主力队员在一场比赛中22投14中,得了28分,除了3个三分球全中外,他还投中了8个2分球和3个罚球.【解答】解:设2分球投中了x个,罚球罚进y个.则可列方程组为,解得:x=8,y=3.故投中了8个2分球和3个罚球.19.(4分)根据指令[s,A](s≥0,0°<A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,现机器人在直角坐标系的坐标原点,且面对x轴正方向.(1)若给机器人下了一个指令[4,60°],则机器人应移动到点(2,2);(2)请你给机器人下一个指令[5,135°] ,使其移动到点(﹣5,5).【解答】解:(1)此点为A,做AB⊥x轴于点B,则OA=4,∠AOB=60°,∴OB=AO×cos60°=2,AB=AO×sin60°=2,机器人应移动到点(2,2);(2)此点为C,属于第二象限的点,做CD⊥x轴于点D,那么OD=DC=5,∴OC=OD÷sin45°=5,∠COD=45°则∠AOC=180﹣45=135°,那么指令为[5,135°](2,2);[5,135°].20.(4分)求函数的最小值,较合适的数学方法应该是配方法,当然还可以用图象法等方法来解决.【解答】解:要求该函数的最小值,可以运用配方法:即y=(x﹣)2+2≥2,则当x=±1时,有最小值是2;或者通过正确画出图象,观察图象发现函数的最小值.三、解答题(共6小题,满分55分)21.(7分)创新设计题:如图所示的集合中有5个实数,请计算其中的有理数的和与无理数的积的差.【解答】解:有理数是32,﹣23,它们的和为32+(﹣23)=9﹣8=1;无理数是,π,,它们的积为•π•=2π.所以有理数的和与无理数的积的差等于1﹣2π.22.(8分)如图,EF为梯形ABCD的中位线,AH平分∠DAB交EF于M,延长DM交AB于N.求证:△ADN是等腰三角形.【解答】证明:∵EF为梯形ABCD的中位线,∴EF∥AB,∴∠EMA=∠NAM,∵AH平分∠DAB,∴∠EAM=∠NAM,∴∠EAM=∠EMA=∠NAM,∴EA=EM,可得AD=2AE,又EM∥AB,E为AD的中点,∴M为DN的中点,∴EM为△DAN的中位线,∴AN=2EM=2AE,则可得AD=AN.∴△ADN是等腰三角形.23.(8分)如图,⊙C经过原点且与两坐标轴分别交于A、B两点,点A的坐标是(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标.【解答】解:(1)连接AB,AM,则由∠AOB=90°,故AB是直径,由∠BAM+∠OAM=∠BOM+∠OBM=180°﹣120°=60°,得∠BAO=60°,又AO=4,故cos∠BAO=,AB==8,从而⊙C的半径为4.(2)由(1)得,BO==4,过C作CE⊥OA于E,CF⊥OB于F,则EC=OF=BO==2,CF=OE=OA=2.故C点坐标为(﹣,2).24.(10分)解方程组:【解答】解:令,,则等价于解方程组,解得或.继而解得或.经检验它们都是原方程组的解.25.(10分)转炉炼钢产生的棕红色烟尘会污染大气,某装置可通过回收棕红色烟尘中的氧化铁从而降低污染.该装置的氧化铁回收率与其通过的电流有关,现经过试验得到下列数据:如图建立直角坐标系,用横坐标表示通过的电流强度,纵坐标表示氧化铁回收率.(1)将试验所得数据在上图所给的直角坐标系中用点表示;(注:该图中坐标轴的交点代表点(1,70))(2)用线段将题(1)所画的点从左到右顺次连接,若用此图象来模拟氧化铁回收率y关于通过电流x的函数关系,试写出该函数在1.7≤x≤2.4时的表达式;(3)利用题(2)所得函数关系,求氧化铁回收率大于85%时,该装置通过的电流应该控制的范围.(精确到0.1A)【解答】解:(1)如下图:(2)图象正确,<<(3)当1.7≤x<1.9时,由45x+2.5>85得1.8<x<1.9;当2.1≤x≤2.4时,由﹣30x+150>85得2.1≤x<2.2;又当1.9≤x<2.1时,恒有﹣5x+97.5>85.综合上述可知:满足要求时,该装置的电流应控制在1.8A至2.2A之间26.(12分)如图,在矩形ABCD中,BD=20,AD>AB,设∠ABD=α,已知sinα是方程25x2﹣35x+12=0的一个实根,点E,F分别是BC,DC上的点,EC+CF=8,设BE=x,△AEF的面积等于y.(1)求出y与x之间的函数关系式;(2)当E,F两点在什么位置时,y有最小值并求出这个最小值.【解答】解:(1)解方程可得sinα1=或sinα2=,∵AD>AB,∴sinα=,舍去取sinα=,则有AD=16,AB=12∵BE=x,∴EC=16﹣x,FC=8﹣EC=x﹣8,DF=12﹣FC=20﹣x.则△AEF的面积y=16×12﹣×12x﹣×16(20﹣x)﹣(16﹣x)(x﹣8)=x2﹣10x+96(8<x<16).(2)y=x2﹣10x+96=(x﹣10)2+46,所以当x=10,即BE=10,CF=2时,y有最小值为46.。
2003年绍兴市中考数学试卷和参考答案

2003年绍兴市中考数学试卷和参考答案(共150分,考试时间120分钟>【目录】一、选择题<本题有12小题,每小题4分,共48分)下列各题所附地四个选项中,有且只有一个是正确地,请把正确选项前面地字母填在题后地括号内1二、填空题<本题有6小题,每小题5分,共30分)3三、解答题<本题有7小题,共72分)下列各小题都必须写出解答过程32002年中考数学试卷参考答案6一、选择题<本题有12小题,每小题4分,共48分)下列各题所附地四个选项中,有且只有一个是正确地,请把正确选项前面地字母填在题后地括号内1.地倒数是< )A.2 B.-2 C.D.-2.化简:等于< )A.2B.C.D.3.一元二次方程地两根为,,则+地值是< )A.3B.-3 C.-1 D.14.2003年3月末,我国城乡居民储蓄存款余额达94600亿元,用科学记数法表示为< )A.94.6×102亿元B.9.46×103亿元C.9.46×104亿元D.0.946×105亿元5.若点(-1,2>是反比例函数图象上一点,则k 地值是< ) A .-B .C .-2D .26.如果梯形一底边长为6,中位线长为8,那么另一底边长为< ) A .4B .7C .10D .147.圆锥地母线长为13cm,底面半径为5cm,则此圆锥地高线长为< ) A .6 cm B .8 cmC .10 cmD .12 cm8.小明测得一周地体温并登记在下表(单位:℃>星期 日一二三四 五六周平均体温体温 36.6 36.7 37.0 37.336.9 37.1 36.9A .36.7:℃B .36.8:℃C .36.9:℃D .37.0:℃9.已知,则代数式地值为< )A .-B .C .3D .410.已知点G 是△ABC 地重心,GP ∥BC 交AB 边于点P,BC=,则GP 等于< )A .B .C .D .11.身高相等地三名同学甲、乙、丙参加风筝比赛,三人放出风筝线长、线与地面交角如右表<假设风筝线是拉直地),则三人所放地风筝中< ) A .甲地最高B .丙地最高C .乙地最低D .丙地最低12.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将△AED 以DE 为折痕向右折叠,AE 与BC 交于点F ,则△CEF 地面积为< )A .4B .6C .8D .10同学 甲 乙 丙放出风筝线长 100m 100m 90m 线与地面交角 40°45°60°二、填空题<本题有6小题,每小题5分,共30分)13.如果节约16度水记作+16度,那么浪费6度水记作度.14.若正六边形地边长为2㎝,则此正六边形地外接圆半径为㎝.15写出和为6地两个无理数<只需写出一对).16.若半径不相等地两个圆有唯一公共点,则此两圆地公切线有条.17.若某人沿坡度ⅰ=3:4地斜坡前进10m,则他所在地位置比原来地位置升高m.18.抛物线与x轴地正半轴交于A,B两点,与y轴交于C点,且线段AB地长为1,△ABC地面积为1,则b地值是.三、解答题<本题有7小题,共72分)下列各小题都必须写出解答过程19.<本题8分)计算:.20. <本题8分)已知关于x地方程有两个不相等地实数根,求k地取值范围.21. <本题10分)如图,在正方形网络上有一个△ABC.(1) 作△ABC 关于直线MN 地对称图形<不写作法);(2) 若网络上地最小正方形地边长为1,求△ABC 地面积.22. <本题10分)已知二次函数地图象地顶点坐标为<-2,-3),且图象过点<-3,-2).(1) 求此二次函数地解读式;(2) 设此二次函数地图象与x 轴交于A ,B 两点,O 为坐标原点,求线段OA ,OB 地长度之和.23. <本题10分)改革开放以来,我国国民经济保持良好发展势头,国内生产总值持速较快增长,下图是1998年-2002年国内生产总值统计图:根据图中信息,解答下列问题:A BC M N第21题<1)1999年国内生产总值是;<2)已知2002年国内生产总值比2000年增加12956亿元,2001年比2000年增加6491亿元,求2002年国内生产总值比2001年增长地百分率<结果保留两个有效数字)24. <本题12分)如图,BC是半圆地直径,O是圆心,P是BC延长线上一点,PA切半圆于点A,AD⊥BC于点D.(1)若∠B=30°,问:AB与AP是否相等请说明理由;(2)求证:PD·PO=PC·PB;(3)若BD:DC=4:1,且BC=10,求PC地长.25. <本题14分)已知∠AOB=90°,OM是∠AOB地平分线,按以下要求解答问题:(1)将三角板地直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.①在图甲中,证明:PC=PD;②在图乙中,点G是CD与OP地交点,且PG=PD,求△POD与△PDG地面积之比.将三角板地直角顶点P在射线OM上移动,一直角边与边OB交于点D,OD=1,另一直角边与直线OA,直线OB分别交于点C,E,使以P,D,E为顶点地三角形与△OCD相似,在图丙中作出图形,试求OP地长.G2002年中考数学试卷参考答案一、选择题<本题有12小题,每小题4分,共48分)1.A 2.B 3.A 4.C 5.C6.C 7.D 8.A 9.B 10.B11.B 12.C二、填空题<本题有6小题,每小题5分,共30分)13.-6 14.2 15.略 16.1或3 17.6 18.-3三、解答题<本题有7小题,共72分)19. <本题8分)原式=2-1+3=4.20. <本题8分)△=4-4<k-1)=8-4k,令△>0,得8-4k>0,解得 k<2,∴所求k地取值范围是k<2.21. <本题10分)(1)作图略.(2)此三角形面积为:.22. <本题10分)<1)∵函数图象地顶点坐标为<-2,-3)∴设此二次函数地解读式为.又∵图象过点<-3,-2),∴,∴ a=1.∴此二次函数地解读式为.(3)设点A,B地横坐标分别为,,则,是方程地两根,∴+=-4,·=1,∴<0,<0,∴ OA+OB=<+)=4.23. <本题10分)(1)82067亿元.(2)设2000年国内生产总值为x亿元,则2001年,2002年分别为<x+6491)亿元,<x+12956)亿元.由题意得:,解得,则 x+6491=95933,∴增长率=.答:2002年国内生产总值比2001年增长.24. <本题12分)(1)相等.连结AO,∵PA是半圆地切线,∴∠OAP=90°.∵OA=OB,∴∠B=∠OAB,∴∠AOD=2∠B=60°,∴∠APO=30°,∴∠B=∠APO,∴AB=AP.(2)在Rt△OAP中,∵AD⊥OP,∴PA2=PD·PO.∵PA是半圆地切线,∴PA2=PC·PB,∴PD·PO= PC·PB.<3)∵BD:DC=4:1,且BC=10,∴BD=8,CD=2,∴OD=3.∵OA2=OD·OP,∴25=3×OP,∴OP=,∴PC=-5=.25. <本题14分)(1)①过P作PH⊥OA,PN⊥OB,垂足分别为H,N,得∠HPN=90°,∴∠HPC+∠CPN=90°.而∠CPN+∠NPD=90°,∴∠HPC=∠NPD.∵OM是∠AOB地平分线,G ∴PH=PN,又∵∠PHC=∠PND=90°,∴△PCH≌△PDN,∴PC=PD.②∵PC=PD,∴∠PDG=45°,而∠POD=45°,∴∠PDG=∠POD.又∵∠GPD=∠DPO,∴△POD~△PDG.∴.<2)若PC与边OA相交,∵∠PDE>∠CDO,∴△PDE~△OCD,∴∠CDO=∠PED,∴CE=CD,而CO⊥ED,∴OE=OD,∴OP=ED=OD=1.若PC与边OA地反向延长线相交,过P作PH⊥OA,PN⊥OB,垂足分别为H,N,∵∠PDE>∠EDC,∴△PDE~△ODC,∴∠PDE=∠ODC.∵∠OEC>∠PED,∴∠PDE=∠HCP.而PH=PN,∴Rt△PHC≌Rt△PND,∴HC=ND,PC=PD,∴∠PDC=45°,∴∠PDO=∠PCH=22.5°,∴OP=OC.设OP=x,则OH=ON=,∴HC=DN=OD-ON=1-,而HC=HO+OC=+x,∴1-=+x,∴x=,即OP=申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2003年中考数学精品模拟试题一
(满分130分,时间120分钟)
姓名; 学号: 成绩:
一、填空题(1-10每小题2分,11-12每题3分共26分)
1、1)2
1(-= ; 2、5-的相反数是 ;
3、16的平方根是 ;
4、
6
6
312
---x x = 。
5、分解因式:ab bx b ax -+-2
= 。
6、如图,若圆周角∠ABC =35°,则劣弧AC 的度数是 。
7、若等腰三角形一边的长是5,另一边的长是11,则此等腰三角形的周长是 。
•
第6题图
O C
B A
•
第8题图 P
O
B
A
D ' B '
A '
第11题图 D
C
B
A
8、如图,PA 、PB 分别切⊙O 于点A 、B ,且∠APB =62°,若C 是⊙O 上异于A 、B 的
任一点,则∠ACB = 。
9、请写出三个自变量的取值范围都是x ≠2的函数,这三个函数分别是 。
10、2002年5月份,在某市市区某一周的空气质量报告中,某项污染指数的数据是: 21 25 21 24 20 22 21
这组数据的众数和中位数分别是 。
11、如图,一块边长为6cm 的等边三角形木板ABC ,在水平桌面上绕C 点按顺时针方向
旋转到△A ′B ′C 的位置,则边AB 的中点D 运动路径的长是 。
12、若三角形内有54个点,四边形内有72个点,五边形内有90个点,……,按这样的
规律,二十五边形内有 个点。
二、选择题(每小题3分,共24分)
13、在直角坐标系中,点P ()3,2-位于( )
A 、第一象限
B 、第二象限
C 、第三象限
D 、第四象限 14、下列运算中,正确的是( )
A 、632x x x =⋅
B 、3
26x x x =÷ C 、4
2224)2(y
x xy =- D 、
44)2(22++=-x x x
15、若方程0242
=+-m x x 有两个实数根,则m 的取值范围是( )
A 、m >2
B 、m ≥2
C 、m <2
D 、m ≤2
16、不等式组⎩
⎨⎧-≤-<x x x 3936
3的最大整数解是( )
A 、1
B 、3
C 、2
D 、0
17、使分式654
22+--x x x 有意义的x 值是( )
A 、x ≠2
B 、x ≠2或x ≠3
C 、x ≠3
D 、x ≠2且x ≠3
18、在下列函数中,y 随着x 的增大而增大的是( )
A 、x
y 1= B 、22
+=x y C 、2+-=x y D 、12+=x y
19、若一个多边形的内角和与外角和的比是2∶1,则这个多边形的边数是( ) A 、4 B 、5 C 、6 D 、7
20、如图,在平行四边形ABCD 中,AB =4,BC =6,E 是AB 的中点,F 是BC 上一点,
F 是BC 上一点,FC =1,
G 是CD 上的动点,若C 、F 、G 三点所确定的三角形与△ADE 相似,则CG 的长为( )
A 、3
B 、31
C 、3或3
1
D 、2 三、解答题(共80分) 21、(6分)计算:()(
)()(
)
2
00
1260tan 1133--
-+--π
22、(6分)求代数式2
23
2232b a ab b a b a -++的值,其中13+=a ,13-=b 。
23、(8分)用换元法解方程:5336
22
-=-+x x
x x 。
第20题图
G
F E
D
C
B A
24、(8分)如图,在梯形ABCD 中,AD ∥BC ,AB =8cm ,AD =6cm ,BC =14cm ,∠B
=∠C ,求梯形ABCD 的面积
第24题图
D
C
B
A
25、(8分)如图,DE 是⊙O 的弦,A 是优弧DE 的中点,分别延长ED 、DE 到B 、C ,使
BD =CE ,连结AB 、AC 。
求证:∠B =∠C 。
• 第25题图
E O
D
C
B A
26、(12分)已知抛物线m x x y +-=42
与x 轴交于A (1x ,0)、B (2x ,0)两点(A
点在B 点的左边),且262
22
1=+x x 。
(1)求m 的值;
(2)设此抛物线的顶点为C ,交y 轴于D ,求直线CD 的解析式; (3)求四边形ABCD 的面积
27、(14分)某批发商要将一批海产品从A 地运到B 地,运输路程为180千米,可采用汽
车运输或火车运输,汽车和火车的速度分别为60千米/时和100千米/时,两运输公司的收费项目和收费标准如下表所示:
用分别为1y (元)和2y (元),求1y 、2y 与x 之间的函数关系式;
(2)若该批发商待运的海产品不少于40吨,则他应选择哪一个运输方式。
28、如图,在Rt △ABC 中,CD 是斜边AB 上的高,AC =20,BD =9。
(1)求AB 的长;
(2)在此图形中,要求经过A 、B 、C 三点的抛物线的解析式,应该怎样建立直角坐标系?并求出此抛物线的解析式;
(3)在此抛物线上是否存在一点P ,使A 、B 、P 三点所确定的三角形与△ABC 全等?若存在,请求出P 点的坐标,若不存在,请说明理由。
第28题图
D C
B
A。
