一维射影对应
第二章 射影变换-第四节 一维射影变换课件ppt课件
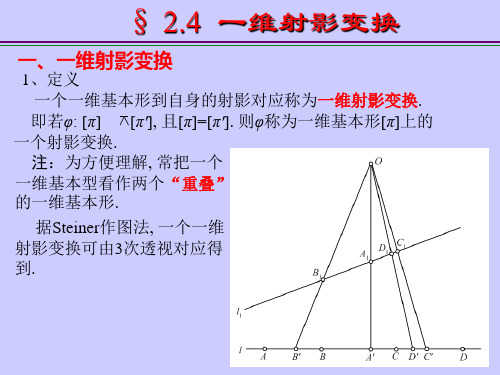
一、一维射影变换
1、定义 一个一维基本形到自身的射影对应称为一维射影变换. [π'], 且[π]=[π']. 则φ称为一维基本形[π]上的 即若φ: [π] 一个射影变换. 注:为方便理解, 常把一个 一维基本型看作两个“重叠” 的一维基本形. 据Steiner作图法, 一个一维 射影变换可由3次透视对应得 到.
a11 a12 0,
a21 a22
0
(2.10)
其中对应点的坐标是关于一维基本形[π]上的同一坐标系取得的.
(ad bc 0)
§ 2.4 一维射影变换
一、一维射影变换
1、定义 2、代数表示 (1). 坐标表示 (2). 参数表示 定理2.16 一维基本形上的一个变换为射影变换其对应元素 的参数λ,λ' 满足一个双线性方程 a 'b c 'd 0 (ad bc 0) (2.13) 证 “=>”. 见教材, 略. “<=”. 设一维基本形(P)上的一个变换φ使得任一对对应元素的 参数λ,λ' 满足双线性方程(2.13). 显然φ是一个双射,只要证φ保交比. 设λi ,λi' (i=1,2,3,4)为任意四对对应元素的参数. 则 b1 d b3 d (ad bc)(1 3 ) 1 '3 ' . a1 c a3 c (a1 c)(a3 c) 同法可以求出λ2'–λ4', λ2'–λ3', λ1'–λ4', 得到 (1 '3 ' )(2 '4 ' ) (1 3 )(2 4 ) . (2 '3 ' )(1 '4 ' ) (2 3 )(1 4 )
几何学引论答案

几何学引论答案【篇一:数学文化作业答案(全正确答案)】3 1870-1950是现代数学的形成阶段。
正确答案:√4集合论是哪位科学家提出的a、康托5庞加莱创立了拓扑学正确答案:√6现代数学时期的成果称为高等数学,力学,物理学等科学教学的内容,并被科技工作者应用。
正确答案:√ 7抓三堆问题可以抽象成三维向量正确答案:√8现代数学时期从什么时间开始b、19世纪20年代9数学起源于四个“河谷文明”地域,以下不是的是:c、亚马逊河 10现代数学繁荣阶段是从1950年至今。
正确答案:√11现代数学时期分为几个阶段:b、3个12数学发展史可以分为几个阶段:d、四个13“现代微分几何”是哪位学者创建的:d、黎曼14现代数学从()开始。
a、19世纪20年代16拓扑学是()创立的d、庞加莱17爱因斯坦何时提出广义相对论c、1915年18周长和直径之比是一个常数。
正确答案:√20平面图形中对称性最强的是a、圆21爱因斯坦何时提出狭义相对论c、1905年1目前我们采用十进制和()有关。
a、人的十指3国际数学家大会每四年举办一次正确答案:√4中国的甲骨文出现在c、公元前1600年5十进制和人的十个手指有关正确答案:√6称为中国古代数学第一人的是b、刘徽7狼骨上的刻痕计数考古发现在3万年前左右。
正确答案:√8古埃及的象形文字在()出现。
b、公元前3400年10直角三角形两条直角边的平方和等于斜边的平方,这是勾股定理。
正确答案:√11中国的甲骨数字出现在:d、公元前1600年12以下不是初等数学的主要分支的是:b、函数13在古希腊数学家中,阿基米德的主要贡献是:c、面积和体积14人类现在主要采用十进制,与人的手指共有十个有关。
正确答案:√16考古发现最早的计数是()。
c、狼骨上刻痕17“数学”这词是谁创的a、毕达哥拉斯18发现的第一个无理数是a、根号219“万物皆数”是谁提出d、毕达哥拉斯1阿拉伯数字是()发明的。
d、印度人2属于印度波罗摩笈多时期的成就的是c、代数3《阿耶波多历数书》出现在公元()年。
高等几何讲义(第3章)

a12 a22
12,det(aij)
0.
反之,也可证明(3.1)必为射影对应.
在 (3.1) 中令 1/2,/ /1//2,a a21,b
a11,c a22,d a12,则可得
高 等 几 何 ( Higher Geometry )
δ/ d/
§1 一维射影变换
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
例4 已知两射影点列的三对对应点
{a, b, c} /{a/, b/, c/}, 求作 上任意点 d 在 /上的对应点.
作法见下图:
a
bc
dδ
a/
b/
c/
高 等 几 何 ( Higher Geometry )
的线性变换:
T:
//12 aa1211
a12 a22
12,det(aij)
0.
(3.1)
证明:不妨设两个一维基本形 I 与 II 均为点列.
在 I 上取定三点 u、v、t,使其在 II 上的对应点依
次为 II 的坐标系 / [u/, v/; t/] 中的基点和单位点.
21.
解法三:(交比法) 设 上任意点 x( )对应于 / 上
的点 x/(/ ),则
(0,1; 2, ) (1,0; 2, / ),即
(02)(1)/(0)(12) (12)(0/)/(1 /)(02),
故所求射影对应为 3/ 4 4/ 4 0.
由以上三式联立求解,得
a: b: c: d 3 : 4 : 4: 4,
故所求射影对应为 3/ 4 4/ 4 0.
高等几何习题集[1]2
![高等几何习题集[1]2](https://img.taocdn.com/s3/m/946569ff846a561252d380eb6294dd88d0d23d08.png)
高等几何习题集习题1.11.证明:任一三角形都有一个内切椭圆,其切点为三边的中点,中心为三角形的重心;同时有一个外接椭圆以三角形的重心为中心。
2.平行于平行四边形ABCD 对角线AC 作一直线与AB 、BC 交于点E 、F ,证明:三角形AED 和CDF 的面积相等。
3.在椭圆的内接三角形的顶点作切线构成外切三角形,证明:如果这两上三角形有两对边平行,则第三对边也平行。
4.过三角形ABC 内任一点P 作DE//BC ,交AB 、AC 于E 、E ,作FG//CA 交BC 、BA 于F 、G ,作HK//AB 交BC 、CA 于H 、K ,证明:=++ABHK CA FG BC DE 常数。
5.设X 、Y 是三角形ABC 的边AB 、CA 上的动点,满足BX :XA=CY :Y A 。
证明:BY 与CX 的交点在一条定直线上。
6.设D 、E 、F 各是三角形ABC 的边BC 、CA 、AB 上的点,且DE//AB ,DF//CA ,证明:CD E BFD AEF S S S ∆∆∆⋅=2。
7.将三角形的每边三等分,将每个分点与三角形的对顶点相连,这六条直线构成一个六边形,证明:此六边形的三双对顶点的连线共点。
8.在三角形ABC 的边BC 、CA 、AB 上取点D 、E 、F 使BD :DC = CE :EA = AF :FB = 1 :n 。
设AD 交BE 于L ,BE 交CF 于K ,CF 交AD 于M ,证明:1122++-=n n n S S ABC LKM )(∆∆ 。
9.设点D 、E 、F 分别位于三角形ABC 的边BC 、CA 、AB 上,且BD :DC=CE :EA=AF :FB ,三线AD 、BE 、CF 构成三角形PQR ,证明:三角形ABC 、DEF 和PQR 具有共同的重心。
10.过椭圆的弦AB 的中点C 任作二弦PQ 和ST ,PS 、QT 分别交AB 于M 、N ,证明:MC=CN 。
高等几何讲义 第三章 射影变换____§1 一维射影变换

高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 例1 设 abcd 为平行四边形,过顶点 a 作直线
ae 与对角线 bd 平行.证明:直线 ab、ad
与直线 ac、ae 成调和共轭.
证明:因 ae 与 bd 平行,故 a
设二者交点为无穷远点 p.
o
p e
d
记(ac)(bd) o.则
的线性变换:
T:
//12 aa1211
a12 a22
12,det(aij)
0.
(3.1)
证明:不妨设两个一维基本形 I 与 II 均为点列.
在 I 上取定三点 u、v、t,使其在 II 上的对应点依
Hale Waihona Puke 次为 II 的坐标系 / [u/, v/; t/] 中的基点和单位点.
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
高 等 几 何 ( Higher Geometry )
§1 一维射影变换
➢ 同类一维基本形间的透视:
若两个点列是同一线束的 若两个线束是同一点列的
截影,则称这两个点列是 投影,则称这两个线束是
透视的.
透视的.
线束的心称为透视中心. 点列的底称为透视轴.
§1 一维射影变换
且设 I 上的动点 x 对应 II 上
的点 x/,则 (u/v/; t/x/) (uv; tx).
u
t
设各点射影坐标分别为 u(u1,
u2)、v(v1, v2)、t(t1, t2)、 x(1,
u/
t/
2)、x/(/1, /2),则得
11 0 0 11
关于二阶曲线,二级曲线

1.预备知识一维基本形指点列和线束,一维基本形之间的关系有两种;透视对应和射影对应。
1.1一维基本形的透视对应和射影对应1.1.1一维基本形的透视对应 定义1:如果两个点列与同一线束成透视对应,则这两个点列叫做透视点列,点S 叫透视中心,记以()()(),,,...,,,...S s A B C s A B C ∧''''= 如图(1),(2)对偶地,有定义2:如果两个线束与同一点列成透视对应,则这两个线束透视线束,点列的底s 叫做透视轴,记以()()(),,,...,,,...s S a b c S a b c ∧''''= 如图(3),(4)bcdD ' C 'B 'BsA A 'aD SCs '图(1)SAA 'B ' D 'B CDC ' ab cdss '图(2)由此可知,两个成透视对应的点列,其对应点之连线共点。
两个成透视对应的线束,其对应之交点共线。
1.1.2一维基本形的射影对应定义3:(Poncelet 定义)设有两个一维基本形(点列或线束)[]π与[]π', 如果存在n 个一维基本形[][][]12,,...,n πππ,使得 [][][][][]12...n πππππ'∧∧∧∧∧则把[]π与[]π'之间的对应叫做射影对应,记以[][]ππ'∧,这1n +次透视对应形成透视链,既有限个透视对应乘积是射影对应,()()()()(),,,...,,,...,,,...S S s A B C s A B C s A B C ''∧∧''''''''''''==()(),,,...,,,...s A B C s A B C ''''''''''''∧ 如图(5)由此可以得到射影对应有以下性质: (1)保持一一对应关系; (2)[][]ππ∧;(3)如果[][]ππ'∧,则[][]ππ'∧;Db ca ' d 'b ' sdc ' aB CAS 'S图(3)CBa 'd 'b 'c 'db c aDSAsS ' 图(4)(4)如果[][]ππ'∧,[][]ππ'''∧,则[][]ππ''∧; (5)如果[][]ππ'∧,则[][]ππ'∧,但反之不成立。
第三章一维射影几何学
O
a s, b s, c s a s 1 b s d s a s 2 b s
1 2 B,C D 1 A 2
A a
A
C
D
C B
B D b d a 2b
所以,点列上任意一点M的坐标可表为:
(a1 ub1 , a 2 b2 , a3 b3 )
的形式,当时,
0 可表为
(a1 b1 , a 2 b2 , a3 b3 )
的形式.为
M 1 , M 2 点列的基点
u
AC BD 定义:设A、B、C、D为共线的四点,把 定义为这四点 AD BC
sin Q3 cos Q1 sin Q1 cos Q3 sin Q4 cos Q2 sin Q2 cos Q4 sin Q4 cos Q1 sin Q1 cos Q4 sin Q3 cos Q2 cos Q3 sin Q2 sin Q3 Q1 sin Q4 Q2 sin Q4 Q1 sin Q3 Q2
第三章 一维射影几何学
§3.1 点列与线束
维的概念:平面内的点与直线都有两个坐标,平面内的点几 何学和线几何学都是二维的。 定义1 点列:动点在一条直线上移动产生的图形称为点列。那 条定直线称为点列的底,设 M 1 a1 a2 a2 ,M 2 b1 b2 b2
M 为定直线上二点, x1 , x2 , x3 为点列的动点,则:
1, ,0
四点中也只当某两点重合时,六个交比值才能有等于
第二种情况
1
AC AD BC BD
第三章射影变换
第三章 射影变换与射影坐标本章首先引入射影不变量——交比。
然后在此基础上,讨论了一维基本形之间的射影对应与射影变换,以及二维射影对应和射影变换,还定义了一维和二维射影坐标。
§1 交比与调和比点列中四点的交比与调和比定义1.1 共线的四个不同点A ,B ,C ,D 的交比等于单比(ABC )与单比(ABD )的比,记作:(AB ,CD ),即(AB ,CD )=)()(ABD ABC其中A ,B 叫基点偶,C ,D 叫分点偶。
交比又称交叉比和复比。
由交比和单比的定义,我们可AD BC BDAC BDAD BC ACABD ABC CD AB ⋅⋅===)()()(, 其中AC ,BC ,AD ,BD 是有向线段的数量。
我们不难得出:(1) 点偶C ,D 不分离点偶A ,B 时,交比(AB ,CD )﹥0; (2) 点偶C ,D 分离点偶A ,B 时,交比(AB ,CD )﹤0; (3) 当C ,D 重合时,(AB ,CD )=1; (4) 当A ,C 重合时,(AB ,CD )=0。
定理1.1 基点偶与分点偶交换,交比值不改变,即 (AB ,CD )=(CD ,AB ) 证明 由定义1.1,(CD ,AB )=),(CD AB BCAD BDAC CB DA DB CA =⋅⋅=⋅⋅ 定理1.2 基点偶的两个字母交换或分点偶的两个字母交换,交比的值变成原来的交比值的倒数,即(BA ,CD )=(AB ,DC )=),(1CD AB证明(AB ,DC )=),(1)()(1)()(CD AB ABD ABC ABC ABD == 又(BA ,CD )=(CD ,BA )=),(1),(1CD AB AB CD =推论 同时交换每个点偶里的字母,交比的值不改变,即 (AB ,CD )=(BA ,DC ) 定理1.3 交换中间的两个字母或两端的两个字母,交比的值等于1减去原来的交比值,即(AC ,BD )=(DB ,CA )=1-(AB ,CD )证明(AC ,BD )AD CB CD AB ⋅⋅=AD CB BD CB BC AC ⋅++=))(( AD CB BDAC CB BD CB AC ⋅⋅+++=)(AD CB BD AC ⋅⋅+=1=1+)(ADBC BDAC ⋅⋅-=1-(AB ,CD )共线四点1,2,3,4一共有4!=24中不种的排列,所以有24个交比,根据交比的运算性质,它们只有6个不同的交比值,即(12,34)=(34,12)=(21,43)=(43,21)=m(21,34)=(34,21)=(12,43)=(43,12)=m1(13,24)=(24,13)=(31,42)=(42,31)=1-m(13,42)=(42,13)=(31,24)=(24,31)=m-11(14,23)=(23,14)=(41,32)=(32,41)=1-m 1(14,32)=(32,14)=(41,23)=(23,41)=1-m m例1 已知(P 1P 2,P 3P 4)=3,求(P 4P 3,P 2P 1)和(P 1P 3,P 2P 4)的值解 (P 4P 3,P 2P 1)= (P 2P 1 ,P 4P 3)=(P 1P 2,P 3P 4)=3 (P 1P 3,P 2P 4)=1-(P 1P 2,P 3P 4)=1-3=-2下面研究交比的代数表示定理1.4 一直线上的无穷远点分其上任何两点的单比等于1。
几何学概论期末试题及答案
《几何学概论》试题(1)1. 试确定仿射变换,使y 轴,x 轴的象分别为直线01=++y x ,01=--y x ,且点(1,1)的象为原点.(51')2. 利用仿射变换求椭圆的面积.(01')3. 写出直线12x +23x -3x =0,x 轴,y 轴,无穷远直线的齐次线坐标.(01')4. 叙述笛沙格定理,并用代数法证之.(51')5. 已知A (1,2,3),B (5,-1,2),C (11,0,7),D (6,1,5),验证它们共线,并求(CD AB ,)的值.(8')6. 设1P (1,1,1),2P (1,-1,1),4P (1,0,1)为共线三点,且(4321,P P P P )=2,求3P 的坐标.(21')7. 叙述并证明帕普斯(Pappus)定理.(01')8.一维射影对应使直线l 上三点P (-1),Q (0),R (1)顺次对应直线l '上三点P '(0),Q '(1),R '(3),求这个对应的代数表达式.(01')9.试比较射影几何、仿射几何、欧氏几何的关系.(01')《高等几何》试题(2)1.求仿射变换424,17++='+-='y x y y x x 的不变点和不变直线. (51')2. 叙述笛沙格定理,并用代数法证之.(51')3.求证a (1,2,-1) ,b (-1,1,2),c (3,0,-5)共线,并求l 的值,使).3,2,1(=+=i mb la c i i i (01')4.已知直线421,,l l l 的方程分别为02321=-+x x x ,0321=+-x x x ,01=x ,且=),(4321l l l l 32-,求2l 的方程.(51') 5.试比较欧氏、罗氏、黎氏几何的关系. (01')6.试证两个点列间的射影对应是透视对应的充要条件是它们底的交点自对应. (01')7.求两对对应元素,其参数为121→,0→2,所确定对合的参数方 程. (01')8.两个重叠一维基本形B A B A λλ'++,成为对合的充要条件是对应点的参数λ与λ'满足以下方程:)0(0)(2≠-=+'++'b ad d b a λλλλ (51')《高等几何》试题(3)1. 求仿射变换424,17++='+-='y x y y x x 的不变点和不变直线. (51')2. 求椭圆的面积.(01')3. 写出直线12x +23x -3x =0,x 轴,y 轴,无穷远直线的齐次线坐标.(01')4. 叙述笛沙格定理,并用代数法证之.(51')5. 已知直线421,,l l l 的方程分别为02321=-+x x x ,0321=+-x x x ,01=x ,且=),(4321l l l l 32-,求2l 的方程.(51') 6. 在一维射影变换中,若有一对对应元素符合对合条件,则这个射影变换一定是对合. (51') 7. 试比较射影几何、仿射几何、欧氏几何的关系, 试比较欧氏、罗氏、黎氏几何的关系. (02')[2005—2006第二学期期末考试试题] 《高等几何》试题(A ) 一、 填空题(每题3分共15分)1、 是仿射不变量, 是射影不变量2、 直线30x y +=上的无穷远点坐标为3、 过点(1,i,0)的实直线方程为4、 二重元素参数为2与3的对合方程为5、 二次曲线22611240x y y -+-=过点(1,2)P 的切线方程 二、 判断题(每题2分共10分)1、两全等三角形经仿射对应后得两全等三角形 ( )2、射影对应保持交比不变,也保持单比不变 ( )3、一个角的内外角平分线调和分离角的两边 ( )4、欧氏几何是射影几何的子几何,所以对应内容是射影几何对应内容的子集 ( )5、共线点的极线必共点,共点线的极点必共线 ( )三、(7分)求一仿射变换,它使直线210x y +-=上的每个点都不变,且使点(1,-1)变为(-1,2)四、(8分)求证:点 (1,2,1),(1,1,2),(3,0,5)A B C --三点共线,并求,t s使,(1,2,3)i i i c ta sb i =+=五、(10分)设一直线上的点的射影变换是/324x x x +=+证明变换有两个自对应点,且这两自对应点与任一对对应点的交比为常数。
一维射影变换
一维基本形的射影变换
2、一维射影变换的性质
(1). 双曲型、椭圆型射影变换
定理. 对于双曲、椭圆型射影变换,任一对相异的对应元 素与两个不变元素的交比为定值,该定值称为双曲、椭圆型射 影变换的特征不变量.
证明 设X, Y为两个不变元素, PP'为任一对相异的对应元 素. 设X, Y, P, P'的坐标依次为x, y, x+y, x+y. 则这四元素的参 数依次为0, , 1, . 于是 0 0 a ' b c ' d 0 d 0. 1 1 1 ab c d 0 a 0. ' ' b 1 b c 0 . c 1 c ( XY , PP ') 常数。 从而, b
a a
( ) ( ) 2 0, a a
1 c 于是 k a 是常数。
c c
一维基本形的射影变换
例1 设A, B, C为相异的共线点且有 (A, B, C, P, Q, R) (B, C, A, Q, R, X). 求证:X=P. 证明. 因为 A B 所以 (AB, CP) = (BC, AQ) =(CA, BR) = (AB, CX) . 从而有X=P. B C C A P Q Q R R X
1、一维射影变换的分类 设有射影变换 a ' b c ' d 0 (ad bc 0) (*) 若存在 0 R, 使a02+(b+c)0+d=0, 则称A+0B为的一个不变元素. 定理. 在实-复射影平面上, 任一个一维射影变换至少有一个 不变元素. 非恒同的一维射影变换至多有两个相异的不变元素.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4. 设两直线l1, l2交于点O, 两定点S1, S2与O共线, 动直线l经 过另一定点M, 分别交l1, l2于点A1, A2. 证明:直线S1A1, S2A2的交 点轨迹为一条直线.
一维基本形的射影对应
例5:设两相异定直线ll'=O, 不经过O的定直线m分别交l, l'于 点U, V'. X为m上异于U, V'的一点, 过X异于m的两直线与l, l'的交 点依次为A , B' ; B, A'. 求证:l(O, U, A, B) l'(V', O, A', B'). 证明 因为UV', AB', BA'共点于X, 于是由此确定了l(P)到l'(P')的以X为透 视中心的透视对应, O为自对应的公共 元素. 所以 (OU, AB)=(OV', B'A') 从而有 (OU, AB)=(V'O, A'B'). 所以有 l(O, U, A, B)
一维基本形的射影对应 一、一维透视对应(中心射影)
定义 以下三种对应称为一维基本形之间的透视对应: 透视中心
(1). 点列与线束. 如果一点列与一 线束的对应元素是结合的,就称 该点列与线束成透视对应,记为: s( A, B, C ,...) S (a, b, c,...)
(2). 点列与点列. 如果两点列对应 点连线共点,或者说这两点列与 同一线束成透视对应,则称这两 点列成透视对应,记为: s( A, B, C ,...) (S) s '( A ', B ', C ',...)
一维基本形的射影对应
连P0'P1, P0'P2; P0P1', P0P2'. 设P0'P1P0P1'=Q1, P0'P2P0P2'=Q2. 连Q1Q2=m, 连P0'P交m于Q, 连P0Q交l于P'', 设P0P'0交m于Q0, 则
l ( P , P , P2 , P) 0 1
(P0')
连
(P0)
将已知三对对应点的坐标分别代入, 得
(**)
xi (1, 0) (2, 1)
(4, 1)
xi' (1, 0) (–1, 1 0 a21 2 2a11 a12 2 2a21 a22 3 4a11 a12 3 4a21 a22
一维基本形的射影对应 三、射影对应成为透视对应的条件
定理3. 两个同类的一维基本形之间的射影 对应成为透视对应公共元素自对应. 证明 由对偶原则, 只要考虑点列. “” 设点列l(P)与l'(P')透视对应, S为透视中心, l l'=X. 由于 直线SX交l, l'于同一点X, 所以X自对应. “” 设f: l(P)→ l'(P')为射影对应, 使得f(X)=X. 设f(P)=P'. 在l(P)上取异于X的两相异点A, B. 设f(A)=A', f(B)=B'. 则A', B' 相异且不同于X. 设AA' BB'=S, 并设SP l'=P''. 设是以S为透视中心l(P), l'(P')间的透视对应. 则因为射影对 应与f有相异的三双对应点重合, 即A, A'; B, B'; X, X, 从而=f. 于是P'=P''. 即f是透视对应.
基础解系
一维基本形的射影对应
一维射影对应 (1) 直观的定义 Poncelet定义 (2) 利用几何特征性质的定义 Steiner定义 (3) 代数(解析)的定义 非奇异线性对应
因为P0, P1, P2互异, 故P0', P1', P2'互异. 从而P'=P''. 即Pl(P)均有 P'=P''=(P). 可以通过两次透视对应得到, 满足Poncelet定义.
一维基本形的射影对应
注:利用截的方法, 可证两个线束的情 况. 也可证明一个点列与一个线束的情况. 推论 两个相异的同类一维基本形之间 的任一射影对应都可表为不超过两个透视对 应的积.
定理 代数定义Steiner定义. 证明. (不作要求). 注. 相差一个非零比例常数的二阶非异矩阵为同一个一维射 影对应的矩阵.
一维基本形的射影对应
x1 ' a11 x1 a12 x2 x2 ' a21 x1 a22 x2 注. 由(*)理解定理.
a11
a12
a21 a22
0,
0
(*)
一维基本形的射影对应
例8. 求射影对应式, 使l上的点(1, 0), (2, 1), (4, 1)依次对应于l' 上的点(1, 0), (–1, 1), (1, 1). 解. 设所求对应式为 x1 ' a11 x1 a12 x2 x2 ' a21 x1 a22 x2
m(Q0 , Q1 , Q2 , Q)
l '( P ', P ', P2 ', P '') 0 1
l ( P , P , P2 , P) 0 1
l '( P ', P ', P2 ', P '') 0 1
于是有
( P P , P2 P) ( P ' P ', P2 ' P '') ( P ' P ', P2 ' P '). 0 1 0 1 0 1
(P)
(C,C1,C2,…)
于是有 R(B,B1,B2,…) Q(C,C1,C2,…) A,A1,A2恰为上述两射影点列对应直线的 交点. 下面只需证明上述射影对应为透 视对应,为此只需证明QR是自对应直 线。设QR与BB1和CC1的交点分别是 B'C', 则 R(B,B1,B2,B'…) Q(C,C1,C2,C'…) 注记. 可用Desargues透视定理证明.
a21 0
代入
2 2a11 a12 2 a22 3 4a11 a12 3 a22
2a11 a12 a22 0 4a11 a12 a22 0
解得 a11 : a12 : a21 : a22 1: 3: 0 :1 于是, 所求对应式为 x1 ' x1 3 x2 x2 x2 '
一维基本形的射影对应
定理1. Poncelet定义Steiner定义. 证明. “”. 显然. “”. 只证明点列对应点列的情况. 设: l(P)→l'(P')为满足Steiner定义的射 影对应. 只要证可以表示为有限次透视对应 的积. 设P0, P1, P2为l(P)上相异三点, P为l(P)上任意一点, 且 ( Pi ) Pi (i 0,1, 2), ( P) P. 则有 ( P0 P , P2 P ) ( P0 P , P2 P). 1 1 连P0'P1, P0'P2; P0P1', P0P2'. 设P0'P1P0P1'=Q1, P0'P2P0P2'=Q2. 连Q1Q2=m,连P0'P交m于Q, 连P0Q交l于P'', 设P0P'0交m于Q0, 则
透视轴
(3). 线束与线束. 如果两线束对应直线交点共线,或者说这两线 束与同一点列成透视对应,则称这两线束成透视对应,记为: S (a, b, c,...) (s) S '(a ', b ', c ',...) 注记 透视对应保交比;两透视对应的复合不必是透视对应。
一维基本形的射影对应 二、一维射影对应
推论 任何两个一维基本形之间的射影对应都可表为不超过 三个透视对应的积. 思考:已知两点列间射影对应的三双相异的对应元素, 求作 任一元素的对应元素. 定理2. 两个一维基本形间的射影对应可由已知相异的三双 对应元素唯一确定. l ( P , P , P2 , P) l '( P ', P ', P2 ', P ') 0 1 0 1
(B2, D, N, A1)
(A2)
(O, C1, B1, A1)
(C2)
(B2, C1, L, E)
注:直线LN叫Pappus线
一维基本形的射影对应
例2. 如图, Pappus线p分别交l1,l2于P1,P2, 且l1,l2交于点O. 求证: 在由A1A2, B1B2, C1C2所确定的射影对应下, OP2, P1O.
证明 设C1C2p=T.
l1(A1,B1,C1,O) (C2) p(M,L,T,P2)(C1) l2(A2,B2,C2,P2)
OP2.
l1(A1,B1,C1,P1)(C2) p(M,L,T,P1)(C1) l2(A2,B2,C2,O) P1O.
