工程力学习题答案 高斌版工程力学
《工程力学》课后习题解答

4日1-1试画出以下各题中圆柱或圆盘的受力争.与其它物体接触处的摩擦力均略去.12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N =⨯+-==⨯--=∴==∑∑AC 与BC 两杆均受拉.2-3 程度力F 感化在刚架的B 点,如图所示.如不计刚架重量,试求支座A 和D 处的束缚力.解:(1) 取整体(2) 22D A F2-4 在简支梁AB 的中点C 感化一个竖直45o 的力F,力的大小等于20KN,如图所示.若梁的自重不计,试求两支座的束缚力.解:(1) 研讨AB ,(2)类似关系:B A F F FCDE cde CD CE ED ∆≈∆∴==几何尺寸:11 222CE BD CD ED =====FFF AF D求出束缚反力:12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kNCDCECD α=⨯=⨯==⨯===-= 2-6 如图所示构造由两弯杆ABC 和DE 构成.构件重量不计,图中的长度单位为cm.已知F =200N,试求支座A 和E 的束缚力.解:(1)取 (2) 取3-1已知梁,支座A和B解:(a) A B M F F l∴==(b) 受力剖析,画受力争;A.B 处的束缚力构成一个力偶;0 0 B B A B M M Fl M F lM F F l=⨯-==∴==∑(c)受力剖析,画受力争;A.B 处的束缚力构成一个力偶;列均衡方程:cos cos A B MM l M F F l θθ==∴==∑3-3 齿轮箱的两个轴上感化的力偶如题图所示,它们的力偶矩的大小分离为M 1=500Nm,M 2=125Nm.求两螺栓处的铅垂束缚力.图中长度单位为cm.解:(1);(2) 500125750 50750 A B M N F F N-===∴==∑3-5 四连杆机构在图示地位均衡.已知OA=60cm,BC=40cm,感化BC 上的力偶的力偶矩大小为M 2=1N.m,试求感化在OA 上力偶的力偶矩大小M 1和AB 所受的力F AB .各杆重量不计.解:(1) 研讨BC 杆,列均衡方程:22015 0.4sin 30sin 30BB o oM M F N BC ====⨯BF F B(2) 研讨AB (二力杆),受力如图:可知:'' 5 A B B F F F N===(3) 研讨OA 杆,受力剖析,画受力争:列均衡方程:113 M M M Nm==∴=∑4-1 试求题4-1图所示各梁支座的束缚力.设力的单位为kN,力偶矩的单位为kN ⋅m,长度单位为m,散布载荷集度为kN/m.(提醒:盘算非均布载荷的投影和与力矩和时需应用积分). 解:(b):(1) 整体受力剖析,(2) 选坐标系Axy ,(20AB B MF +⨯=∑0B =(c):(1) 研讨AB 杆,受力剖析,画出受力争(平面随意率性力系); (2) 选坐标系Axy ,0A B AF (e)F x F20: 2cos3004.24 kNo y Ay B B F F dx F F =-⨯+==∑⎰0: sin 3002.12 kNo xAx B Ax FF F F =-==∑束缚力的偏向如图所示.(e):(1) 研讨C ABD 杆,受力剖析,画出受力争(平面随意率性力系);(2) 选坐标系Axy ,(021 kNAB B MF F ==∑0.80: 2020015 kNyAy B Ay Fdx F F F =-⨯++-==∑⎰束缚力的偏向如图所示.4-13 运动梯子置于滑腻程度面上,并在铅垂面内,梯子两部分AC 和A B 各重为Q ,重心在A 点,彼此用搭钮A 和绳索DE 衔接.一人重为P 立于F 处,试求绳索DE 的拉力和B .C 两点的束缚力.解:(1):研讨整体,受力剖析,(2) 选坐标系Bxy ,)()0: -2cos 2cos 0B C C M F Q l a F l F αα=-+⨯=∑0: 202yB C B FF F Q P a F Q P l=+--==+∑(3) 研讨AB ,受力剖析,画出受力争(平面随意率性力系);xq x(4) 选A 点为矩心,()0:0A D M F F h α=+⨯=∑4-16 由AC 和CD 4-16图所示.已知均布载荷集度q =10 kN/m,力偶M =40 kN ⋅m,a =2 m,不计梁重,试求支座A .B .D 的束缚力和搭钮C 所受的力.解:(1) 研讨CD 杆,(2) 选坐标系Cxy ,20D a ⨯=∑0: 025 kNy C D C F F q dx F F =-⨯-==∑⎰(3) 研讨ABC 杆,受力剖析,画出受力争(平面平行力系);(4) 选坐标系Bxy ,'()0B C M F x F a -⨯=∑'080 kNyB C B FF F =-==∑束缚力的偏向如图所示.4-17 刚架ABC 和刚架CD 经由过程搭钮C 衔接,并与地面经由过程搭钮A .B .D 衔接,如题4-17图所示,载荷如图,试求刚架的支座束缚力(尺寸单位为m,力的单位为 kN,载荷集度单x(a):(1) 研讨CD 杆,它是二力杆,又依据D 点的束缚性质,可知:F C =F D =0;(2) 研讨整体,受力剖析,画出受力争(平面随意率性力系);(3) 选坐标系Axy ,60B F ⨯=∑180 kNy Ay B Ay F ==束缚力的偏向如图所示.(b):(1) 研讨CD 杆,受力剖析,画出受力争(平面随意率性力系);(2) 选C 点为矩心,3015 kN D q dx x F ⨯⨯+⨯=(3) 研讨整体,);(4) 选坐标系35030AyM⨯+⨯=∑300: 010 kNyAy B D B FF q dx F F F =-⨯-+==∑⎰束缚力的偏向如图所示.=50x5-5 感化于半径为120 mm 的齿轮上的啮合力F 推进皮带绕程度轴AB 作匀速迁移转变.已知皮带紧边拉力为200 N,松边拉力为100 N,尺寸如题5-5图所示.试求力F 的大小以及轴承A .B 的束缚力.(尺寸单位mm).解: (1) 研讨整体,8-2 试画出8-1解:(a) (b)(c) (d) 8-14 图示桁架,杆与d 2=20mm,两杆材料雷同,F =80kN 感化,试校解:(1) 对节点A(2) 列均衡方程0 sin 0 cos30x AB yAB FF FF =-=∑∑解得:41.4 58.6AC AB F kN F kN ====(2)分离对两杆进行强度盘算;[][]1282.9131.8ABAB ACAC F MPa A F MPa A σσσσ====所以桁架的强度足够.8-15 图示桁架,杆1为圆截面钢杆,杆2为方截面木杆,在节点A 处推却铅直偏向的载荷F 感化,试肯定钢杆的直径d 与木杆截面的边宽b .已知载荷F =50kN,钢的许用应力[σS ] =160MPa,木的许用应力[σW ] =10MPa.解:(1) 对节点A;50AB F kN ==(2) []322 20.070.71010 84.1ABAC ACW d mm F MPa b mm A b σσσ≥⨯==≤=≥所以可以肯定钢杆的直径为20mm,木杆的边宽为84mm. 8-16 题8-14所述桁架,试定载荷F 的许用值[F ].解:(1) 由8-14得到AB.AC 两杆所受的力与载荷F 的关系;AC AB F F ==(2) 应用强度前提,分离对两杆进行强度盘算;[]211160 154.54ABAB F MPa F kN A d σσπ==≤=≤[]222160 97.14ACAC F MPa F kN A d σσπ==≤=≤取[F ]=97.1kN.8-18图示阶梯形杆AC ,F =10kN,l 1= l 2=400mm,A 1=2A 2=100mm 2,E =200GPa,试盘算杆AC 的轴FFF ABF AC向变形△l .解:(1)(2) 分段盘算个杆的轴向变形;33112212331210104001010400200101002001050 02 N N F l F l l l l EA EA .mm⨯⨯⨯⨯∆=∆+∆=+=-⨯⨯⨯⨯=-AC 杆缩短.8-26 图示两头固定等截面直杆,横截面的面积为A ,推却轴向载荷F 感化,试盘算杆内横截面上的最大拉应力与最大压应力.解:(1)xA B(2) 用截面法求出AB .BC .CD 段的轴力;123 N A N A N BF F F F F F F =-=-+=-(3) 用变形调和前提,列出补充方程;AB BC CD l l l ∆+∆+∆=代入胡克定律;231 /3()/3/3 0N BC N CDN ABAB BC CD A A B F l F l F l l l l EA EA EA F l F F l F l EA EA EA ∆=∆=∆=-+-+-=求出束缚反力:/3A B F F F ==FACB(b)(4) 最大拉应力和最大压应力;21,max ,max 2 33N N l y F F F FA A A A σσ====-8-27 图示构造,梁BD 为刚体,杆1与杆2用统一种材料制成,横截面面积均为A =300mm 2,许用应力[σ]=160MPa,载荷F =50kN,试校核杆的强度.解:(1) 对BD=(2) 由变形调和关系,代之胡克定理,可得;21212 2N N N N F l F lF F EA EA ==解联立方程得:122455N N F F F F ==(3) 强度盘算;[][]3113222501066.7 160 530045010133.3 160 5300N N F MPa MPaA F MPa MPaA σσσσ⨯⨯====⨯⨯⨯====⨯所以杆的强度足够.8-33 图示接头,推却轴向载荷F 感化,试校核接头的强度.已知:载荷F =80kN,板宽b =80mm,板厚δ=10mm,铆钉直径d =16mm,许用应力[σ]=160MPa,许用切应力[τ] =120MPa,许用挤压应力[σbs ] =340MPa.板件与铆钉的材料相等.解:(1)[]21499.5 120 14QSF F MPa MPaA d ττπ===≤=(2) 校核铆钉的挤压强度;[]14125 340 b bs bs b FF MPa MPaA d σσδ===≤=(3) 斟酌板件的拉伸强度; 对板件受力剖析,画板件的轴力争;校核1-1160 MPa校核2-2] 160 MPa =所以,接头的强度足够.10-2. 解:(c)(1) (2) 11111 (0/2) (0/2)S F F x l M Fx x l =-=-≤≤ ()21221 (/2) (/2)S F F l x l M F l x l x l ==--≤≤(3) 画剪力争与弯矩图 F xq(d)(1) )S F l 21 (0)42M x x x l =-≤(2) 画剪力争与弯矩图10-5(b)(1) 求束缚力;(2) 画剪力争和弯矩图 (c)(1) 求束缚力; q AxF xM A xF S(2) 画剪力争和弯矩图; (d)(1) 求束缚力;(2) 画剪力争和弯矩图;(e)(1) 求束缚力;(2) 画剪力争和弯矩图 (f)(1) 求束缚力;(2) 11-6图示悬臂梁,折正应力,解:(1)(2) (3) 盘算应力: 最大应力:F SM xFzK 点的应力:11-7图示梁,由No22槽钢制成,弯矩M =80N.m,并位于纵向对称面(即x-y 平面)内.试求梁内的最大曲折拉应力与最大曲折压应力.解:(1)79 b mm =(2) 最大曲折拉应力(产生鄙人边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPaI σ-+-⋅-⨯-⨯===⨯(3) 最大曲折压应力(产生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯6max max max227.510176 408066ZM M MPabh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯MMz。
工程力学习题答案高等教育出版社
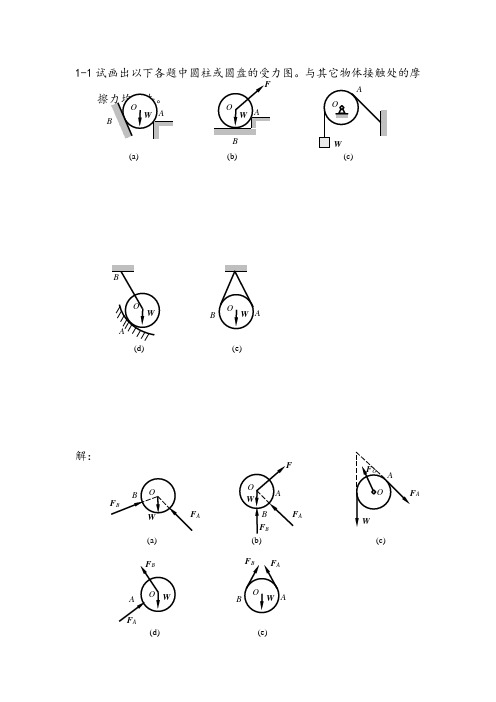
A W FOx
O B FB FOy FC C
8
《工程力学》习题选解
2-2 杆 AC、BC 在 C 处铰接,另一端均与墙面铰接,如图所示,F1 和
F2 作用在销钉 C 上,F1=445 N,F2=535 N,不计杆重,试求两杆
所受的力。
A
30o
F1
4 3
B
C c
F2
解:(1) 取节点 C 为研究对象,画受力图,注意 AC、BC 都为二力杆,
z
FAD 2F 1.2 kN
FAC FAB
6 FAD 0.735 kN 4
AB、AC 杆受拉,AD 杆受压。
15
《工程力学》习题选解
3-1 已知梁 AB 上作用一力偶,力偶矩为 M,梁长为 l,梁重不计。求 在图 a,b,c 三种情况下,支座 A 和 B 的约束力
l/2
M
l/3
AB 的约束力:
21
《工程力学》习题选解
FA
及整体。
B W
A B P (a) (b) P
A
5
《工程力学》习题选解
A F B W2 C (c) D F
W1 A
E
F (d)
C
B
A
O B G C’ C W (e)
D
解:(a)
FAT
A FAB
FBT
B W
FBA
6
《工程力学》习题选解
FA
(b)
C A FC C P FB B P FB F’C A B P FN P FA
B F’B M
2
FA
A
2 ' FB 3a a M 0 2 M FA FC 0.354 a
工程力学高斌第九章答案

15kN . m
5kN . m
15kN . m
-
Q qa/2 +
-
qa/2 + x
qa/2
M q a 2/8 +
-
x
q a 2/8
5. 设梁的剪力图如图所示,试作弯矩图及载荷图。已知梁上设有作用集中力偶。 (a)
4kN q=1kN/m
3kN
Q
3kN
2kN
3kN
1kN
A
B
1kN
C
D
x
5
3kN 2m 2m 4m
3
2
⎡ 50 × 2003 ⎤ 150 × 503 Iz = ⎢ + 50 × 200 × 53.62 + + 50 × 150 × 71.4 2 ⎥ mm 4 12 ⎣ 12 ⎦ = 10180 cm 4
根据弯曲正应力强度条件
M
0.8p
σ max
M = ymax ≤ [σ ] , M≤[σ].Iz/ymax Iz
解:梁的弯矩图如图, 弯矩的两个极值分别为
µ1 = 0.8P , MA =2P×1.4 - P×2= 0.8P µ2 = 0.6 P , MC = -0.6 P
截面对形心轴的惯性矩为
8
(Iz =bh /12 + Ah1 , h1 腹 = 153.6–100=53.6mm ,h1 翼 =200-153.6+25 =71.4mm )
实心圆截面梁的最大应力
σ max =
空心圆截面最大应力
′ = σ max
空心圆截面梁比实心圆截面梁的最大正应力减少了
′ σ max − σ max 159 − 93.6 = = 41.1% σ max 159
工程力学习题答案 高斌版工程力学
工程力学习题答案第一章 静力学基础知识思考题:1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1.根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在A 、B 、C 三处受力作用。
由于力p 和B R的作用线交于点O 。
如图(a )所示,根据三力平衡汇交定理,可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
(b )同上。
由于力p 和B R的作用线交于O 点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
2.不计杆重,画出下列各图中AB 解:(a )取杆AB 为研究对象,杆除受力p外,在处受绳索作用的拉力B T ,在A和E 两处还受光滑接触面约束。
约束力A N 和E N 的方向分别沿其接触表面的公法线,并指向杆。
其中力E N 与杆垂直,力A N 通过半圆槽的圆心O 。
AB 杆受力图见下图(a )。
(b)由于不计杆重,曲杆BC 只在两端受铰销B 和C 对它作用的约束力B N 和C N ,故曲杆BC 是二力构件或二力体,此两力的作用线必须通过B 、C 两点的连线,且B N =C N 。
研究杆两点受到约束反力A N 和B N,以及力偶m 的作用而平衡。
根据力偶的性质,A N 和B N(d)由于不计杆重,杆AB 在A 、C 两处受绳索作用的拉力A T 和C T ,在B 点受到支座反力B N 。
A T 和C T 相交于O 点,根据三力平衡汇交定理,可以判断B N必沿通过B 、O 两点的连线第二章力系的简化与平衡思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1. 平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm ,求此力系向O 点简化的结果,并确定其合力位置。
《工程力学》课后习题解答

解:(1) 取整体为研究对象,受力分析,A、B 处 x 方向和 y 方向的约束力分别组成力偶, 画 受力图。 (2) 列平衡方程:
M
FBz
x
0
FBz AB F2 2r 0
2rF2 2 20 5 2.5 N FAz FBz 2.5 N 80 AB M z 0 FBx AB F1 2r 0 FBx
W (c)
W
B
W A
FB
A FA
B
W A
(d)
(e)
1-2 试画出以下各题中 AB 杆的受力图。 A E C W D (a) B (b) W C D C B W (c) B A A
《工程力学》习题选解
A C
F A B (d) (e) A E C FA C W D B FB (a) A F C B (d) FB FA C W (e) (b) FD D B FB W (c) B FB C W B
10
《工程力学》习题选解
A FA
M1 M2 B
50
FB
解:(1) 取整体为研究对象,受力分析,A、B 的约束力组成一个力偶,画受力图; (2) 列平衡方程:
M 0
FB l M1 M 2 0
FB
M1 M 2 500 125 750 N l 50
FA FB 750 N
2-7 在四连杆机构 ABCD 的铰链 B 和 C 上分别作用有力 F1 和 F2,机构在图示位置平衡。 试 求平衡时力 F1 和 F2 的大小之间的关系。 C B
45o 90o F1 30o 60o
F2
A
D
解: (1)取铰链 B 为研究对象,AB、BC 均为二力杆,画受力图和封闭力三角形; FBC B FAB
工程力学练习册习题答案1共3份(完整资料).doc

第一章静力学基础7 【最新整理,下载后即可编辑】第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)8 第一章静力学基础(d)(e)(f)(g)第一章静力学基础71-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)8 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础7(b)(c)(d)8 第一章静力学基础第一章静力学基础7(e)(f)8 第一章静力学基础(g)附录Ⅰ平面图形的几何性质25第二章平面力2-1 电动机重P=5000N,放在水平梁AC的中央,如图所示。
梁的A端以铰链固定,另一端以撑杆BC支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A、B处的约束反力。
题2-1图24 附录Ⅰ 平面图形的几何性质∑∑=︒+︒==︒-︒=P F F F F F FB A y A B x 30sin 30sin ,0030cos 30cos ,0解得: N P F FB A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F F P F F F BC y BC AB x解得:PFPFBCAB732.2732.3=-=2-3 如图所示,输电线ACB架在两电线杆之间,形成一下垂线,下垂距离CD=f=1m,两电线杆间距离AB=40m。
电线ACB 段重P=400N,可近视认为沿AB直线均匀分布,求电线的中点和两端的拉力。
(完整版)工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
《工程力学》课后习题与答案全集
工程力学习题答案第一章静力学基础知识思考题:1. X ;2. V ;3. V ;4. V ;5. K 6. K 7. V ;8. V习题一1•根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在 A B 、C 三处受力作用。
u由于力p和uuv R B 的作用线交于点Q 如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 0两点的连线。
uP 3uvB 处受绳索作用的拉力uuv R B (b )同上。
由于力交于0点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
的作用线 2.不计杆重,画出下列各图中 AB 杆的受力图。
uP 解:(a )取杆AB 和E 两处还受光滑接触面约束。
约束力UJVN E uuvuuN A 和 N E,在A的方向分别沿其接触表面的公法线, 外,在 并指向杆。
其中力uuvN A 与杆垂直,通过半圆槽的圆心 Q力 AB 杆受力图见下图(a )。
和C 对它作用的约束力 NBo------- r -------- —y —uuv N C铰销此两力的作用线必须通过(b )由于不计杆重,曲杆 BC 只在两端受 故曲杆BC 是二力构件或二力体,和 B 、C 两点的连线,且B O两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. V ;2.>;3. X ;4. K 5. V ;6.$7.>;8. x ;9. V .1.平面力系由三个力和两个力偶组成, 它们的大小和作用位置如图示,长度单位为cm 求此力系向O 点简化的结果,并确定其合力位置。
uvR R 解:设该力系主矢为 R ,其在两坐标轴上的投影分别为Rx、y。
由合力投影定理有:。
4.梁AB 的支承和荷载如图, 小为多少?解:梁受力如图所示:2. 位置:d M o /R 25000.232 火箭沿与水平面成F ,100 0.6100 80 2000 0.5 580m 23.2cm,位于O 点的右侧。
《工程力学》课后习题解答
BC
FBC
BC
FAB
F1
F1
7
《工程力学》习题选解
FBC 2 F1
(2) 取铰链 C 为研究对象,BC、CD 均为二力杆,画受力图和封闭力三角形; FCB C FCD F2 FCD FCB F2
FCB F2 cos 30o
由前二式可得:
3 F2 2
FBC FCB F1
l/3
A FA 列平衡方程:
FB
M 0
FA FB
FB l M 0 M l
M
FB
M l
(c) 受力分析,画受力图;A、B 处的约束力组成一个力偶; FA A
l l/2
B
θ
FB
9
《工程力学》习题选解
列平衡方程:
M 0
FA FB
FB l cos M 0 M l cos
(c)
W1 A FAy FAx
(d)
A F FC
A D D F
C
E B FB FE
F FF
C
F ’C
E FE
F FF
C
B FB
(e) FB A W FOx FOy O B FB FC C W FC’ B G D A FOx FOy C’ C O B G D
4
《工程力学》习题选解
2-2 杆 AC、BC 在 C 处铰接,另一端均与墙面铰接,如图所示,F1 和 F2 作用在销钉 C 上, F1=445 N,F2=535 N,不计杆重,试求两杆所受的力。 A
11
《工程力学》习题选解
A
FA
M1 FO 列平衡方程: O
M 0
《工程力学》详细版习题参考答案
∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此,该力系的简化结果为一个力偶矩 M = 3Fl / 2 ,逆时针方向。
题 2-2 如图 2-19(a)所示,在钢架的 B 点作用有水平力 F,钢架重力忽 略不计。试求支座 A,D 的约束反力。
(a)
(b)
图 2-18
解:(1)如图 2-18(b)所示,建立直角坐标系 xBy。 (2)分别求出 A,B,C 各点处受力在 x,y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ,FAy
= − 3 F 2
= FBx F= ,FBy 0
FCx
= − 12 F ,FCy
= 3 F 2
(3)求出各分力在 B 点处的合力和合力偶
(3)根据力偶系平衡条件列出方程,并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正,说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 ( a ) 所 示 , 水 平 梁 上 作 用 有 两 个 力 偶 , 分 别 为
3-4 什么是超静定问题?如何判断问题是静定还是超静定?请说明图 3-12 中哪些是静定问题,哪些是超静定问题?
(a)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程力学习题答案第一章 静力学基础知识思考题:1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1.根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在A 、B 、C 三处受力作用。
由于力p 和B R的作用线交于点O 。
如图(a )所示,根据三力平衡汇交定理,可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
(b )同上。
由于力p 和B R的作用线交于O 点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
2.不计杆重,画出下列各图中AB 解:(a )取杆AB 为研究对象,杆除受力p外,在处受绳索作用的拉力B T ,在A和E 两处还受光滑接触面约束。
约束力A N 和E N 的方向分别沿其接触表面的公法线,并指向杆。
其中力E N 与杆垂直,力A N 通过半圆槽的圆心O 。
AB 杆受力图见下图(a )。
(b)由于不计杆重,曲杆BC 只在两端受铰销B 和C 对它作用的约束力B N 和C N ,故曲杆BC 是二力构件或二力体,此两力的作用线必须通过B 、C 两点的连线,且B N =C N 。
研究杆两点受到约束反力A N 和B N,以及力偶m 的作用而平衡。
根据力偶的性质,A N 和B N(d)由于不计杆重,杆AB 在A 、C 两处受绳索作用的拉力A T 和C T ,在B 点受到支座反力B N 。
A T 和C T 相交于O 点,根据三力平衡汇交定理,可以判断B N必沿通过B 、O 两点的连线第二章力系的简化与平衡思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1. 平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm ,求此力系向O 点简化的结果,并确定其合力位置。
解:设该力系主矢为R ' ,其在两坐标轴上的投影分别为x R 、y R 。
由合力投影定理有:x i R x =∑ 1.53=-=-1.5kN2y i R y ==-∑ kNsin /i y R α'=∑0.8=-;cos /i x R α'=∑0.6=-233α≈由合力矩定理可求出主矩:300()30.31015000.21008020000.5580i M M F ==⨯⨯-⨯---⨯=-∑m N合力大小为:' 2.5R R ==kN ,方向233α≈m 23.2=cm ,位于O 点的右侧。
2.1100F =kN 与运动方向成5θ= 角。
如火箭重200P =kN ,求空气动力2F 和它与飞行方向的交角γ。
解:火箭在空中飞行时,若只研究它的运行轨道问题,可将火箭作为质点处理。
这时画出其受力和坐标轴x 、如下图所示,可列出平衡方程。
∑4. 梁AB 的支承和荷载如图,CB AB ⊥,梁的自重不计。
则其支座B 的反力BR 大小为多少?解:梁受力如图所示:由()0A M F =∑得:5.起重机构架如图示,尺寸单位为cm ,滑轮直径为20d =cm ,钢丝绳的倾斜部分平行于BE 杆,吊起的荷载10Q =kN ,其它重量不计。
求固定铰链支座A 、B 的反力。
由()0A M F =∑,800sin (800)0D Y Q CD α+-=0Y =∑,sin 0AD YQ Y α++=解得: 5.875DY =-kN ,0.125A Y =-kN再研究整体,受力如图(b ),由0Y =∑,0AB Y Y Q +-= 0X =∑,0ABX X +=()0AM F =∑,()600800300100BX Q -++=解得:10.125B Y =kN ,18.5A X =-kN ,18.5B X =kN6. 平面桁架的支座和荷载如图所示,求杆1,2和3的内力。
由0X =∑,30F-=再研究接点C ,受力如图() 8.图示夹钳夹住钢管,已知钳口张角为20,1F F =。
问钢管与夹钳间的静摩擦因数至少应为多少才夹得住而不至滑落?解:取钢管为研究对象,受力如图.列出平衡方程:0X =∑,''1111cos10cos10cos80cos800F F N N +--=①根据结构的对称性及'F F =知:'11F F =,'11N N = ②③ 联立可解得既钢管与夹钳的静摩擦因数至少应为0.176才夹得住而不至滑落。
10.杆子的一端A 用球铰链固定在地面上,杆子受到30kN 的水平力的作用,用两根钢索拉住,使杆保持在铅直位置,求钢索的拉力1T F 、2T F 和A 点的约束力。
解:研究竖直杆子,受力如图示。
由()0X i M F =∑ ,23049cos sin 0T F αβ⨯-= ①()0Y i M F =∑,126cos cos 0T T F F αβ-+= ②将245.8T F =kN 代入②可得:126.7T F =kN 将1T F ,2T F 分别代入③、④、⑤可得:8.90A X =kN ,16.67A Y =kN ,40.00A Z =kN既8.9016.6740.00NAF i j k =++(kN ) 14.已知木材与钢的静滑动摩擦因数为0.6s f =,动滑轮摩擦因数为0.4d f =,求自卸货车车厢提升多大角度时,才能使重的木箱开始发生滑动?解:取木材为研究对象,受力如图所示由0X =∑,sin 0SF p θ-= (1) 0Y =∑,cos 0N p θ-= (2)式中 S S F F N= (3)联立(1)、(2)、(3)可得:tan0.6S f θ==,arctan 0.631θ== 第三章 点的合成运动判断题:1.√;2.×;3.√习题三1. 指出下述情况中绝对运动、相对运动和牵连运动为何种运动?画出在图示的牵连速度。
定系固结于地面;(1).图(a )中动点是车1, 动系固结于车2; (2).图(b )中动点是小环M ,动系固结于杆OA ;(3).图(c )中动点是L 形状的端点A ,动系固结于矩形滑块M ; (4).图(d )中动点是脚蹬M ,动系固系于自行车车架;(5).图(e )中动点是滑块上的销钉(a)(c)(d)解:(1)绝对运动:向左做直线运动;相对运动:斜相上方的直线运动;牵连运动:向下直线运动。
牵连速度e v如图(a )。
(2)绝对运动;圆周运动;相对运动:沿OA 的直线运动;牵连运动:绕O 的定轴转动。
牵连速度e v如图(b )。
(3)绝对运动:以O 为圆心,OA 为半径的圆周运动;相对速度:沿BC 的直线运动;牵连运动:竖直方向的直线运动;牵连运动e v 如图(c )(4)绝对运动:曲线运动(旋轮线);相对速度:绕O 的圆周运动;牵连运动:水平向右的直线运动。
牵连速度e v如图(d )。
(5)绝对运动:竖直方向的直线运动;相对运动:沿AB 的直线运动;牵连运动:绕O 的圆周运动。
牵连速度e v如图(e )。
(e)4.牛头刨床急回机构如图示,轮O 5ω=水平支承面往复运动。
已知OA =r OA 水平时1O B 角速度和刨床速度。
解:(1)先求1O B的角速度。
取滑块A 为动点,动系与摇杆1O B 相固连。
定系与机架相固连。
因而有:绝对运动:滑块A 相对与机架的圆周运动; 相对运动:滑块A 沿槽作直线运动;牵连运动:随摇杆1O B相对于机架作定轴转动。
根据速度合成定理,动点A 的绝对速度a A e A rV V V =+ 式中各参数为:cos eA aA V V α=10cos O A ωα=故摇杆1O B 的角速度:(2)求刨枕速度,即滑块E 的速度O B绝对运动:滑块E 沿滑道作水平直线运动; 相对运动:滑块E 沿斜滑槽作直线运动;牵连运动:随摇杆1O B 相对于机架作定轴转动。
根据速度合成定理:aEeE rE V V V =+方向水平相左。
6.L 形直OAB 以角速度ω绕O 轴转动,OA l =,OA 垂直于AB ;通过滑套C 推动杆CD 沿铅直导槽运动。
在图示位置时,∠AOC =ϕ,试求杆CD 的速度。
解:取DC 杆上的C 为动点,OAB 为动系,定系固结在支座上。
由ae r V V V =+,作出速度平行四边形,如图示:7.图示平行连杆机构中,11100O A O B ==mm,12O O AB =。
曲柄1O A 以匀角速度ω=2rad/s 绕1O 轴转动,通过连杆AB 上的套筒C 带动杆CD 沿垂直于12O O 的导轨运动。
试示当60ϕ=时杆CD 的速度和加速度。
解:取CD 杆上的点C 为动点,AB 杆为动系。
对动点作速度分析和加速度分析,如图(a )、(b )所示。
图中:ae r V V V =+则e a V V =1O A w = 200(/)mm s =cos 100a e V V ϕ== (mm/s )故CD a V V ==100(mm/s )又有:21eA a a O A ω==2400(/)mm s =,因a e r a a a =+即:CDa a a =2346.4(/)mm s =第四章 刚体的平面运动思考题1.×;2.√; 3.√;4.√;5.×. 习题四1.图示自行车的车速 1.83v =m/s,此瞬时后轮角速度3w =rad/s,车轮接触点A 打滑,试求点A 的速度。
解:如图示,车轮在A 点打滑,0 1.83v v ==m/s,3ω==rad/s,车轮作平面运动,以O 为基点。
A O AO v v v =+故A 点速度为:A O v v R ω=- 1.830.66043=-⨯0.15=-m/s(方向向左)2. 图示平面机构中,滑块B 沿水平轨道向右滑动,速度 1.5Bv =cm/s,求图示曲柄OA 和连杆AB 的角速度。
/sin 1.625AB B v v a ==cm/s3. 瓦特行星传动机构如图所示。
齿轮Ⅱ与连杆AB 固结。
长r =75cm,AB 长l =150cm 。
试求60ϕ= 、90θ= 、06ω=rad/s 时,曲柄1O B 及齿轮Ⅰ的角速度。
P 是AB 杆和轮Ⅱ的速度瞬心,故:杆1O B的角速度为:两轮齿合点Mm AB v PM ω= ,6.在图所示星齿轮结构中,齿轮半径均为12r =cm 。
试求当杆OA 的角速度2ω=rad/s 、角加速度28/rad s α=时,齿轮Ⅰ上B 和C 两点的加速度。
解:(1)B 为轮Ⅰ的速度瞬心,0B v =2A v r ω=.设轮工角速度为1ω则12r r ωω=,12ωω=取A 为基点,对B 点作加速度分析如图(b ),有n n n BB A A BA BA a a a a a a τττ+=+++ 大小:??2r α,22r ω,2r α,方向皆如图所示:向AB 方向投影得:n n n B A BA a a a =+22r ω=296(/)cm s =向AB 故;B (2)以A 为基点,对C 点作加速度分析如图(c ),有n n n CC A A CA CA a a a a a a τττ+=+++大小 ?? 2r α,22r ω,2r α,24r ω 方向皆如图所示,222()()480(/)n a a a cm s τ=+=0.1m,EB 在铅直位置。
