动态规划(二)
《信息学奥赛一本通》：第9章 第2节 动态规划背包问题(C++版)
【参考程序】
#include<cstdio> using namespace std;
const int maxm = 201, maxn = 31;
int m, n;
int w[maxn], c[maxn];
int f[maxn][maxm];
int main()
{
scanf("%d%d",&m, &n);
for (int i=1; i <= n; i++)
//设f(v)表示重量不超过v公斤的最大价值
for (int v = m; v >= w[i]; v--)
if (f[v-w[i]]+c[i]>f[v])
f[v] = f[v-w[i]]+c[i];
printf("%d",f[m]);
// f(m)为最优解
【例9-12】、完全背包问题 【问题描述】
设有n种物品，每种物品有一个重量及一个价值。但每种物品的数量是无限 的，同时有一个背包，最大载重量为M，今从n种物品中选取若干件(同一种物品 可以多次选取)，使其重量的和小于等于M，而价值的和为最大。
【输入格式】
第一行：两个整数，M(背包容量，M<=200)和N(物品数量，N<=30)； 第2..N+1行：每行二个整数Wi,Ci，表示每个物品的重量和价值。 【输出格式】
第九章 动态规划
第二节 背包问题
第二节 背包问题
一、01背包问题 问题：
有N件物品和一个容量为V的背包。第i件物品的费用（即体积，下同）是w[i]， 价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量， 且价值总和最大。 基本思路：
《算法与数据结构(2) 》期末考试卷
班号 学号 姓名 成绩《算法与数据结构(2) 》期末考试卷注意事项：1、关闭手机、将考试用文具以外的物品放于讲台上 2、严格遵守学校的考场纪律，违纪者请出考场 题目：一、 判断题（20分）请在正确的陈述前面括号中打√，在错误的陈述前面括号中打×。
1. （ × ）如果一个问题不是NP 问题，那么它有可能是P 问题。
2. （ × ）回溯法用深度优先或广度优先法搜索状态空间树。
3. （ × ）)(n n O 221=+且)(n n O 222=4． （ × ）贪心算法通过增加空间复杂性来减少时间复杂性。
5． （ × ）快速排序算法的平均时间复杂度是O(nlogn),使用随机化快速排序算法可以将平均时间复杂度降得更低。
6． （ √ ）基于比较的寻找数组A[1...n ]中最大值元素问题的下界是)3/(n Ω。
7． （ √ ）直观地讲，P 类问题是易解的问题；而NP 问题是易被验证的问题。
8． （ × ）下列问题是一个判定问题：给定一个合取范式，对其中的所有逻辑变量求一组真值赋值，使得给定的合取范式在该组真值赋值下为真。
9． （ √ ）max(f(n),g(n))= Θ(f(n)+g(n))10．（ √ ）若 ))(()(n g O n f =，则 ))(()(n f n g Ω=二、 简答题（30分）：1．简述拉斯维加斯（Las Vegas ）算法和蒙特卡洛（Monte Carlo ）算法的主要区别前者不一定总能给出解，但给出的解一定是正确的； 后者总能给出解，但是给出的解可能是错误的。
2．按照增长率上升的顺序排列以下函数，即，若在你的排序结果中，函数f(n) 跟在 g(n)的后面，则说明应该满足g(n)是O （f(n)）：4/31)(n n f = n n f 2)(2= n n f log )(3= !)(4n n f = 22)(5n n f = nn n f log )(6= )(3n f , )(1n f , )(6n f , )(2n f , )(4n f , )(5n f3．推导以下递推式的解：T(n)=2 当n = 1时T(n)=2T(n/3)+2n 当n ≥2时T(n)=2T(n/3)+2n=2[2T(n/32)+2(n/3)]+2n=4T(n/32)+4(n/3)+2n=4[2T(n/33)+2(n/32)]+ 4(n/3)+2n=8T(n/33)+8(n/32)+ 4(n/3)+2n=…设n=3k=2k T(n/3k )+ 2k (n/3k-1)+ 2k-1 (n/3k-2)+…+ 4(n/3)+2n =2k 2+2n[(2/3)k-1 +(2/3)k-2 +…+2/3+1]=2k 2+6n[1-(2/3)k]=2k 2+6n-6.2k=6n-4.2k=6n-4.2=n n3log246⋅-4．请给出基于比较的对数组A[1…n]进行排序问题的最紧的下界，并写出两个平均时间复杂度为该下界的排序算法的名称。
动态规划-最优二叉搜索树
动态规划-最优⼆叉搜索树摘要： 本章介绍了⼆叉查找树的概念及操作。
主要内容包括⼆叉查找树的性质，如何在⼆叉查找树中查找最⼤值、最⼩值和给定的值，如何找出某⼀个元素的前驱和后继，如何在⼆叉查找树中进⾏插⼊和删除操作。
在⼆叉查找树上执⾏这些基本操作的时间与树的⾼度成正⽐，⼀棵随机构造的⼆叉查找树的期望⾼度为O(lgn)，从⽽基本动态集合的操作平均时间为θ(lgn)。
1、⼆叉查找树 ⼆叉查找树是按照⼆叉树结构来组织的，因此可以⽤⼆叉链表结构表⽰。
⼆叉查找树中的关键字的存储⽅式满⾜的特征是：设x为⼆叉查找树中的⼀个结点。
如果y是x的左⼦树中的⼀个结点，则key[y]≤key[x]。
如果y是x的右⼦树中的⼀个结点，则key[x]≤key[y]。
根据⼆叉查找树的特征可知，采⽤中根遍历⼀棵⼆叉查找树，可以得到树中关键字有⼩到⼤的序列。
介绍了⼆叉树概念及其遍历。
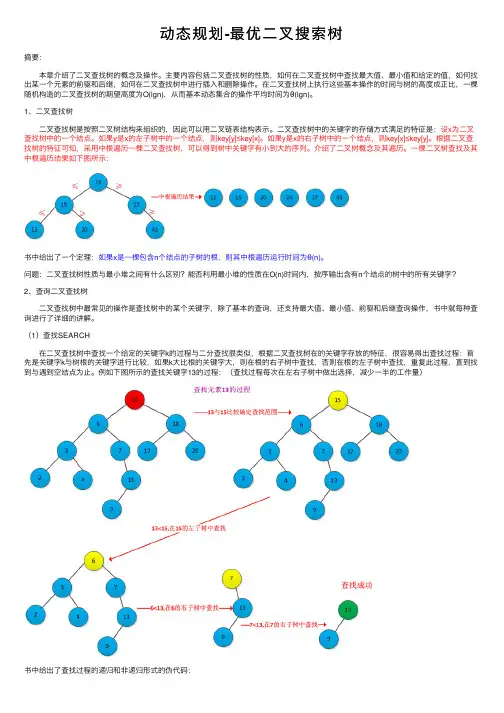
⼀棵⼆叉树查找及其中根遍历结果如下图所⽰：书中给出了⼀个定理：如果x是⼀棵包含n个结点的⼦树的根，则其中根遍历运⾏时间为θ(n)。
问题：⼆叉查找树性质与最⼩堆之间有什么区别？能否利⽤最⼩堆的性质在O(n)时间内，按序输出含有n个结点的树中的所有关键字？2、查询⼆叉查找树 ⼆叉查找树中最常见的操作是查找树中的某个关键字，除了基本的查询，还⽀持最⼤值、最⼩值、前驱和后继查询操作，书中就每种查询进⾏了详细的讲解。
（1）查找SEARCH 在⼆叉查找树中查找⼀个给定的关键字k的过程与⼆分查找很类似，根据⼆叉查找树在的关键字存放的特征，很容易得出查找过程：⾸先是关键字k与树根的关键字进⾏⽐较，如果k⼤⽐根的关键字⼤，则在根的右⼦树中查找，否则在根的左⼦树中查找，重复此过程，直到找到与遇到空结点为⽌。
例如下图所⽰的查找关键字13的过程：（查找过程每次在左右⼦树中做出选择，减少⼀半的⼯作量）书中给出了查找过程的递归和⾮递归形式的伪代码：1 TREE_SEARCH(x,k)2 if x=NULL or k=key[x]3 then return x4 if(k<key[x])5 then return TREE_SEARCH(left[x],k)6 else7 then return TREE_SEARCH(right[x],k)1 ITERATIVE_TREE_SEARCH(x,k)2 while x!=NULL and k!=key[x]3 do if k<key[x]4 then x=left[x]5 else6 then x=right[x]7 return x（2）查找最⼤关键字和最⼩关键字 根据⼆叉查找树的特征，很容易查找出最⼤和最⼩关键字。
DP入门（2）——DAG上的动态规划
DP⼊门（2）——DAG上的动态规划有向⽆环图（DAG,Directed Acyclic Graph）上的动态规划是学习动态规划的基础。
很多问题都可以转化为DAG上的最长路、最短路或路径计数问题。
⼀、DAG模型【嵌套矩形问题】问题：有n个矩形，每个矩形可以⽤两个整数a、b描述，表⽰它的长和宽。
矩形X(a , b)可以嵌套在矩形Y(c , d)中当且仅当a<c,b<d,或者b<c,a<d(相当于把矩形X旋转90°)。
例如(1,5)可以嵌套在(6, 2)内，但不能嵌套在(3, 4)内。
你的任务是选出尽可能多的矩形排成⼀⾏，使得除了最后⼀个之外，每个矩形都可以嵌套在下⼀个矩形内。
如果有多解，矩形编号的字典序应尽量⼩。
分析：矩形之间的“可嵌套”关系是⼀个典型的⼆元关系（我的理解是两个矩形之间存在关系），⼆元关系可以⽤图来建模。
如果矩形X可以嵌套在矩形Y⾥，就从X到Y连⼀条有向边。
这个有向图必然是⽆环的，因为⼀个矩形⽆法直接或间接地嵌套在⾃⼰内部。
换句话说，它是⼀个DAG。
这样，所要求的便是DAG上的最长路径。
【硬币问题】问题：有n种硬币，⾯值分别为V1, V2, ..., V n，每种都有⽆限多。
给定⾮负整数S，可以选⽤多少个硬币，使得⾯值之和恰好为S？输出硬币数⽬的最⼩值和最⼤值。
1 <= n <= 100, 0 <= S <= 10000, 1 <= V i <= S。
分析：此问题尽管看上去和嵌套矩形问题很不⼀样，但本题的本质也是DAG上的路径问题。
将每种⾯值看作⼀个点，表⽰“还需要凑⾜的⾯值”，则初始状态为S，⽬标状态为0。
若当前在状态 i，每使⽤⼀个硬币 j，状态便转移到i - V j。
补充：这个模型和上⼀题类似，但也有⼀些明显地不同之处：上题并没有确定路径的起点和终点（可以把任意矩形放在第⼀个和最后⼀个），⽽本题的起点必须为S，终点必须为0。
动态规划及其应用(二)
前一颗珠子头标记为m，尾标记为r 后一颗珠子头标记为r，尾标记为n 聚合后的珠子头标记为m，尾标记为n
给定一个项链，求最大能释放多少能量 n <= 100 NOIP 2006 senior p1
能量项链
区间DP
先考虑链上的问题 区间[i,j]无论如何操作，最后聚合出的珠子的标记是固定的 枚举决策分界点k，区间[i,k]和区间[k+1,j]分别聚合成一颗 珠子后，两者再聚合 破环成链 等长复制一遍 DP一遍后取最值
除最后一位外，r的每一位严格小于它右边相邻的那一 位。
f[i][j]表示长度为i且最低位不超过j的数的个数 递推方程 f[i][j] = f[i][j-1] + f[i-1][j-1]
答案统计
Σ f[i][2^k - 1]，i∈[1, w/k ] （下取整） 枚举最高位x，Σ f[w/k][2^k – 1 - x]
条件 A：对于所有的i，g2������ > g2������ −1，且g2������ > g2������ +1； 条件 B：对于所有的i，g2������ < g2������ −1，且g2������ < g2������ +1。
请问，栋栋最多能将多少株花留在原地 1 <= n <= 100,000, 0 <= hi <= 1,000,000 NOIP 2013 senior day2 p2
游戏中，乌龟棋子自动获得起点格子的分数，并且在后续 的爬行中每到达一个格子，就得到该格子相应的分数。 求小明最多能得到多少分 N <= 350， M <= 120 NOIP2010 senior p2
运筹学第三版课后习题答案 (2)
运筹学第三版课后习题答案第一章：引论1.1 课后习题习题1a)运筹学是一门应用数学的学科，旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域，如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划，优化供应链管理，提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题，优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域，如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中，可以使用运筹学方法优化仓储和运输的布局，提高货物的运输效率。
在生产计划中，可以使用运筹学方法优化产品的生产数量和生产周期，降低生产成本。
在供应链管理中，可以使用运筹学方法优化订单配送和库存管理，提高供应链的效率。
在流程优化中，可以使用运筹学方法优化业务流程，提高整体效率。
习题2在物流管理中，可以使用运筹学方法优化车辆的调度和路线规划，以提高运输效率和降低成本。
在生产计划中，可以使用运筹学方法优化生产线的安排和产品的生产量，以降低生产成本和提高产能利用率。
在供应链管理中，可以使用运筹学方法优化供应链各个环节的协调和调度，以提高整体效率和减少库存成本。
在流程优化中，可以使用运筹学方法优化业务流程的排布和资源的分配，以提高流程效率和客户满意度。
第二章：线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法，用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为：max c^T*xs.t. Ax <= bx >= 0其中，c是目标函数的系数向量，x是决策变量向量，A是约束矩阵，b是约束向量。
习题2使用线性规划方法可以解决许多实际问题，如生产计划、供应链管理、资源分配等。
Pascal动态规划-复习2
● （5）第三次计算结点为B1，B2，B3，而决 策输出结点可能为C1，C2，C3。仿前计算可 得Bl，B2，B3的决策路径为如下情况。 ● Bl:B1C1费用 12+8=20， 路径:B1+C1+D1+E B2:B2C1费用 6+8=14， 路径:B2+C1+D1+E B3:B2C2费用 12+7=19，路径:B3+C2+D2+E ● 此时也无法定下第一，二，三阶段的城市哪 三个将在整体的最优决策路径上。 ● （6）第四次计算结点为A，决策输出结点可 能为B1，B2，B3。同理可得决策路径为 ● A：AB2，费用5+14=19，路径 A+B2+C1+D1+E。 ● 此时才正式确定每个子问题的结点中，哪一 个结点将在最优费用的路径上。19将是最短 路径的结果 ● 显然这种计算方法，符合最优原理。 ● 子问题的决策中，只对同一城市（结点）比 较优劣。而同一阶段的城市（结点）的优劣 要由下一个阶段去决定。
数塔
● 如下图所示的数塔，从顶部出发，在每一结点可以选择向左下走或是 向右下走，一直走到底层，要求找出一条路径，使路径上的数的和最 大。数塔层数用n表示，1<=n<=100。 ● 【分析】对于这一问题，很容易想到用枚举的方法（深度搜索法）去 解决，即列举出所有路径并记录每一条路径所经过的数字总和。然后 寻找最大的数字总和，这一想法很直观，很容易编程实现。 ● 但是当行数很大时，当三角形的行数等于100时，其枚举量之大是可 想而知的，用枚举法肯定超时，甚至根本不能得到计算结果，必须用 动态规划法来解。
动态规划适合解决什么样的问题
● 准确地说，动态规划不是万能的，它只适于解决一定条件的最优策略 问题。 ● (1)状态必须满足最优化原理； (2)状态必须满足无后效性 ● 1、动态规划的最优化原理是指无论过去的状态和决策如何，对前面 的决策所形成的当前状态而言，余下的诸决策必须构成最优策略。 ● 可以通俗地理解为子问题的局部最优将导致整个问题的全局最优在上 例最短路径问题中，A到E的最优路径上的任一点到终点E的路径也必 然是该点到终点E的一条最优路径，满足最优化原理。 ● 动态规划的无后效性原则指某阶段的状态一旦确定，则此后过程的演 变不再受此前各状态及决策的影响。也就是说，“未来与过去无关”， 当前的状态是此前历史的一个完整总结，此前的历史只能通过当前的 状态去影响过程未来的演变。具体地说，如果一个问题被划分各个阶 段之后，阶段 I 中的状态只能由阶段 I+1 中的状态通过状态转移方程 得来，与其他状态没有关系，特别是与未发生的状态没有关系，这就 是无后效性。
延安我把你追寻第二段的意思
延安我把你追寻第二段的意思如何理解延安我把你追寻第二段的意思第二段，第二段定义的是动态规划（Dynamic Programming），它是一种运用分析最优化方法来求解复杂问题的数学优化技术。
动态规划通常用于处理有关求最优路径、最大值等问题，它可以对一个复杂问题拆分成多个相互依赖的子问题，在求解子问题时，会把已求得的结果缓存，以便在需要时快速使用。
第二段追寻，：追寻是一种行为，指的是一种通过识别和跟踪目标来实现特定目标的动作。
它是一种通过在时间空间上连续间断及行踪追踪来获得对象信息的方法。
也就是用各种方式搜索目标，并尽可能把握、掌握有关目标的信息。
第二段追寻延安，延安，位于中国陕西省北部的一座城市，曾是革命老区，也是革命家们的摇篮。
延安还是中华人民共和国的诞生地之一。
1935年，中国共产党政权正式宣布在延安建立。
延安经过几十年的革命斗争，成为一座充满激情和希望的城市，发挥着重要的历史作用。
延安代表着英雄和勇敢，象征着中国革命传统，受到全国人民的尊重。
许多中国革命老一辈，如毛泽东、朱德、周恩来等，都在延安闪耀过，逐渐成为中国革命史上不可磨灭的印记。
因此，延安可以被定义为中国革命的来源和根据地，是中国革命的象征和回忆。
延安我把你追寻第二段的意思，是：我追寻你，穿过历史的沙漠，穿越延安，就如旋律中的音乐，唤起我心中的追忆。
为什么需要延安我把你追寻第二段的意思这段话的意义如下：1. 我继续追寻我心中的延安，希望能够回到这个充满热情的地方。
2. 延安变得更加开放、多元化，令经济发展蓬勃发展，使其成为了一座中国当之无愧的科技新城。
3. 令更多的人受益于延安这座“古老而新”的城市，让其领略延安的传统文化和更新的内涵。
怎么进一步推进完成延安我把你追寻第二段的意思1、提升对延安文化历史研究和国际交流的热情，尽快开展关于延安文化历史及相关内容的学术讨论活动；2、选择一些能够真正体现延安文化历史的重要地方作为观光景点，让游客可以接触到延安的文化历史；3、建立国家级的延安文化遗产保护中心，制定一整套的延安文化遗产保护的政策；4、加大对延安文化遗产的研究，并进行一些形式多样的文化传承；5、推广延安纪念文化，发扬延安精神，增强世界各国人民对延安文化的认知和理解。
采用二阶动态规划算法的火力分配
Ｆｉｅ ｗｅ ｌ ｔ ｅ ａ ｅ ｏ Ｒａ ｋ Ｄｙ ｍ ｉ ｏ ａ ｍ ｉ ｇ Ａｌ ｒｔ ｒ ｐｏ ｒＡｌｏ ｍ ｎｔＢ ｓ ｄ ｏｎＴｗ — ｎ ｎａ ｃＰｒ ｇｒ ｍ ｎ ｇｏ ｉｈｍ
ｐｒ ｏｂｌ ｍ ，ａｎ ｎｃ ｅａ ｅｃａ ｃ ａ ｉ ｐｅ ｅ ｄ ｉ ｒ ｓ ｌ ｕｌ ｔｏｐ ｗｅ ｌ ｔ ｎ ； ｒ ｅ ｌ ｓｅ ｉ ｉ ｉ ｇ Ｔｗｏ ｒ ｎ ｙ ａ ｉ ｌ ｎ； ｕ ｔ ｒｔ ｒ ｅ ； ｒ ｅ ｎ ｉ ｅ ｃ ｕ ｔ ｒ ｙ ｒ ｓ Ｆｉｅ ｏ ｒ ｌ ｍｅ ｔ Ｔａ ｇ ｔ ｕ ｔ ｒｄ ｖ ｄ ｎ ； ａ ｏ ｃ ａ ｋ ｄ ｎ ｍ ｃ ｐ ａ Ｃｌ ｓｅ ａ ｇ ｔ Ｔａ ｇ ｔｉ ｓｄ ｌ ｓ ｅ
动 态规 划对 群 目标 分配 火 力 ，第二 阶 动态规 划对 各群 内 目标 分 配 火 力， 最后 综合 各 群 的分 配 方案 ，得 出火 力分 配 问
题 的解 。其 仿真 证 明 ，该 方法可 解 决在 来 袭 目标较 多 时动 态规 划 求解 火 力分 配计 算量 太 大的 问题 ，提 高 了计 算速度 。
Ａｂ ｔａ ｔ ｈ ｉｅ ｏ ｒ ａｌ ｔ ｎ ｄ ｐ ｅ ｗｏ ｒ ｎ ｙ ａ ｃ ｐ ｏ ｒ ｍ ｍｉ ｇ ａ ｇ ｒｔ ｍ，ｄ ｖ ｄ ｄ ｃ ｕ ｔ ｒ ｔ ｒ ｕ ｈ ｔ ｒ ｅ ｓ ｒ ｃ ：Ｔ ｅ ｆｒ ｐ ｗｅ ｌ ｍｅ ｔ ａ ｏ ｔｄ ｔ － ａ ｋ ｄ ｎ ｍｉ ｒ ｇ ａ ｏ ｎ ｌ ｏ ｉｈ ｉ ｉ ｅ ｌ ｓｅ ｈ ｏ ｇ ａ ｇ ｔ
ｐ ｏ ｒ ｍｍ ｉ ｇ ｄ ｓｒｂ ｔ ｄ ｆｒ ｐ ｗｅ ｏ ｈ ｌ ｓ ｅ ａ ｇ ｔ ａ ｄ ｔ ｅ ｓ ｃ ｎ ａ ｋ ｄ ｎ ｍｉ ｒ ｇ ａ ｒｇａ ｎ ｉｔｉ ｕ ｅ ｉｅ ｏ ｒｆ ｒｔ ｅ ｃ ｕ ｔ ｒｔ ｒ ｅ ； ｎ ｈ ｅ ｏ ｄ ｒ ｎ ｙ ａ ｃ ｐ ｏ ｒ ｍｍ ｉ ｇ ｄ ｓ ｒｂ ｔ ｄ ｆｒ ｐ ｗｅ ｎ ｉ ｔｉ ｕ ｅ ｉｅ ｏ ｒ ∑ ｌ ｌ ｆ ｒｅ ｃ ａ ｇ ｔｉ ｓｄ ｌ ｓｅ ； ｔｌ ｓ ． ｈ ｌｏ ｍｅ ｔｓ ｈ ｍｅ ｏ ｖ ｒ ｌ ｓ ｅ ｓ ｉ ｔ ｇ ＝ ｔ ｄ ｔ ｃ ｉ ｖ Ｏ ｖ ｎ ｆｆｒ ｐ ｗｅ ｎ ０ ａ ｈ ｔ ｒ ｅ ｎ ｉ ｅ ｃ ｕ ｔ ｒ ａ ａ ｔ ｔ ｅ ａ ｌ ｔ ｎ ｃ ｅ ｆｅ ｅ ｙ ｃ ｕ ｔ ｒｗａ ｎ ｅ ｒ ｅ ｏ ａ ｈ ｅ ｅ Ｓ ｌ ｉ ｇ ｏ ｉｅ ｏ ｒ ａ ａ ｌ ｔ ｎ ｕ ｓｉ ｎ ． ｅ ｓ ｍｕ ａ ｉ ｎ ｓ ｏ ｄ ｔ ａ ｈ ｓ ｍｅ ｈ ｄ ｃ ｕ ｄ ｔ ｏ ｖ ｙ ａ ｃ ｐ ｗｅ ｌ ｔ ｎ ａ ｃ ｌ ｔｏ ｏ ｉ ｌ ｍｅ ｔｑ ｅ ｔｏ ｓ Ｔｈ ｉ ｌ ｔ ｈ ｗｅ ｈ ｔｔ ｉ ｔ ｏ ｏ ｌ ｏ ｓ ｌ ｅ ｄ ｎ ｍｉ ｏ ｒａ ｌ ｍｅ ｔｃ ｌ ｕ ａ ｉ ｎ ｔ ｏ ｂ ｇ ｏ ｏ ｏ ＝
生物信息学 第三章：序列比对原理
blastx Search protein database using a translated nucleotide query tblastn Search translated nucleotide database using a protein query
tblastx
Search translated nucleotide database using a translated nucleotide query
一、序列比对打分
序列分析的目的是揭示核苷酸或氨基酸序列编码的 高级结构或功能信息目的。
二、打分矩阵
稀疏矩阵、相似性打分矩阵
（一）DNA打分矩阵
即两个序列中相应的核苷酸相同，计1分；否则计0分。 如果考虑颠换和置换，可采用以下打分矩阵
（二） 氨基酸序列打分矩阵
1.PAM矩阵（Dayhoff突变数据矩阵）
（二）直系同源、旁系同源
直系同源基因（orthologous gene）是指在不同物种 中有相同功能的同源基因，它是在物种形成过程中 形成的。
旁系同源基因（paralogous gene）是指一个物种内 的同源基因。
直系同源基因和旁系同源基因统称为同源基因 （homolog）。
第二节 序列比对打分方法
ClustalX的比对步骤: 1.加载要比对的序列文件 序列格式可以支持NBRF/PIR、EMBL/Swiss-Ppot、 FASTA、GDE、Clustal、MSF、RSF等。
2.多序列比对
3.比对结果输出
（二）T-Coffee工具 （三）MultAlin工具 （四）MAFFT工具
比对结果
（二）高级BLAST工具 1、PSI-BLAST（position specific interated BLAST）
实验二最长公共子序列（动态规划算法）
实验二最长公共子序列（动态规划算法）班级：08计算机科学与技术（1）班学号：E08620113 姓名：戴斌江机器号：实验二最长公共子序列问题一、实验目的：1、理解动态规划算法的概念；2、掌握动态规划算法的基本要素；3、掌握设计动态规划算法的步骤；4、通过应用范例学习动态规划算法的设计技巧与策略；二、实验内容及要求：1、使用动态规划算法解决最长公共子序列问题：给定两个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}，找出X和Y的最长公共子序列。
2、通过上机实验进行算法实现。
3、保存和打印出程序的运行结果，并结合程序进行分析，上交实验报告。
三、实验原理：动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程（decision process)最优化的数学方法。
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。
1957年出版了他的名著Dynamic Programming，这是该领域的第一本著作。
算法总体思想：1)动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题,先求解子问题，然后从这些子问题的解得到原问题的解。
2)与分治法不同的是，适合于用动态规划法求解的问题，经分解得到的子问题往往不是独立的。
子问题中存在大量的公共子问题，在分治求解过程中被多次重复计算，保存计算结果，为后面的计算直接引用，减少重复计算次数这就是动态规划的基本思想。
3)用动态规划算法求解问题，可依据其递归式以自底向上的方式进行计算。
在计算过程中，保存已解决的子问题的答案。
每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量重复计算，最终得到多项式时间算法。
《生产与运作管理》课程笔记 (2)
《生产与运作管理》课程笔记第一章：绪论一、生产与运作管理的基本概念1. 定义：生产与运作管理（Production and Operations Management, POM）是指对企业生产与运作活动进行系统的规划、组织、指挥、协调和控制，以有效地利用资源，实现产品和服务的高效、低成本、高质量生产，满足市场需求，提升企业竞争力。
2. 目标：生产与运作管理的主要目标包括：- 提高生产效率：通过优化生产流程，减少浪费，提高产出。
- 降低成本：通过成本控制和成本优化，减少生产成本。
- 保证产品质量：通过质量管理和控制，确保产品符合标准。
- 满足市场需求：及时响应市场变化，满足客户需求。
- 提高企业适应性：使企业能够快速适应外部环境的变化。
- 提升员工满意度：通过合理的工作设计，提高员工的工作满意度和生产力。
3. 范围：生产与运作管理涵盖以下关键领域：- 产品设计和管理：确保产品设计符合生产能力和市场需求。
- 生产过程规划：设计高效的生产流程和操作方法。
- 设备和设施管理：选择、维护和升级生产设备和设施。
- 物料管理：采购、储存和分配原材料和组件。
- 供应链管理：协调供应链中的各个环节，确保物料及时供应。
- 质量管理：确保产品和服务达到既定的质量标准。
- 库存控制：管理原材料、在制品和成品的库存水平。
- 生产计划和控制：制定和执行生产计划，监控生产进度。
二、生产过程与生产系统1. 生产过程：生产过程是将输入（原材料、信息、能源等）转换为输出（产品或服务）的一系列相互关联的活动。
生产过程的特点包括：- 连续性：生产活动在一定时间内连续进行，没有中断。
- 复杂性：涉及多个环节、多种设备和人员。
- 动态性：随着市场需求、技术进步等因素的变化而调整。
- 可变性：生产过程可能受到多种因素的影响，如设备故障、人员变动等。
2. 生产系统：生产系统是由生产过程、生产设施、生产人员、生产信息等多个子系统组成的整体。
生产系统的功能包括：- 转换功能：将输入转换为输出，实现价值增值。
技术文档二次规划（QP）样条路径
技术⽂档⼆次规划（QP）样条路径
参考：
Apollo的Planning分为参考线平滑、决策、路径规划、速度规划等部分。
从整体上来说，规划模块的架构分为两个部分：⼀部分负责对数据的监听、获取和预处理；另⼀部分负责管理各个优化模块。
数据进⼊后，对其综合处理为规划模块的内部数据结构，由任务管理器调度合适的优化器进⾏各个优化任务。
综合优化的结果，经过最终的验证后，输出给控制模块。
在设计上，实现了策略的可插拔，使得各个优化器可以灵活配置不同策略，提升迭代效率。
EM-Planner是具体的规划实施类，它基于⾼精地图、导航路径及障碍物信息作出实际的驾驶决策，包括路径、速度等⽅⾯。
⾸先使⽤DP（动态规划）⽅法确定初始的路径和速度，再利⽤QP（⼆次规划）⽅法进⼀步优化路径和速度，以得到⼀条更平滑的轨迹，既满⾜舒适性，⼜⽅便车辆操纵。
基于样条的车辆轨迹优化⼆次规划，为了寻求更优质更平滑，体感更好的路径，需要使⽤⼆次规划的⽅法寻找。
需要的限制条件有：曲率和曲率连续性、贴近中⼼线、避免碰撞。
将路径划分为n段，每段路径⽤⼀个多项式来表⽰。
每个样条段 i 都有沿着参考线的累加距离。
每段的路径默认⽤5阶多项式表⽰：
优化问题：
初始点约束：
终点约束：
平滑节点约束：
点采样边界约束：
在路径上均匀的取样m个点，检查这些点上的障碍物边界。
将这些约束转换为QP约束不等式，使⽤不等式：。
动态规划第5讲 - 二维资源分配问题
8.5 动态规划：二维资源分配问题设有两种原料，数量各为a 和b 单位，需要分配用于生产n 种产品。
如果第一种原料以数量x i 为单位，第二种原料以数量y i 为单位，用于生产第i 种产品，其收入为问题描述试问：应如何分配这两种原料于n 种产品的生产使总收入最大?此问题可写成静态规划问题：动态规划建模——逆推法用动态规划方法来解，状态变量和决策变量要取二维,s2,k)：的。
设状态变量为(s1,ks1,k——分配用于生产第k种产品至第n种产品的第一种原料的单位数量。
s2,k——分配用于生产第k种产品至第n种产品的第二种原料的单位数量。
决策变量为x k——分配给第k种产品用的第一种原料的单位数量。
y k——分配给第k种产品用的第二种原料的单位数量。
式中和分别表示用来生产第k +1种产品至第n 种产品的第一种和第二种原料的单位数量。
状态转移方程：允许决策集合：动态规划建模——逆推法表示以第一种原料数量为s 1,k 单位，第二种原料数量为s 2,k 单位，分配用于生产第k 种产品至第n 种产品时所得到的最大收入。
逆推关系为最后求得即为所求问题的最大收入。
动态规划建模——逆推法1）。
引入拉格朗日乘数λ，将二维分配问题化为满足条件其中λ作为一个固定的参数。
求解算法：拉格朗日乘数法令于是问题变为满足求解算法：拉格朗日乘数法则可证明为原问题的最优解。
这是一个一维分配问题，可用对一维的方法去求解。
由于λ是参数，因此，最优解x i 是参数λ的函数，相应的y i 也是λ的函数，即为其解。
如果求解算法：拉格朗日乘数法如果将调整λ的值(利用插值法逐渐确定λ)，直到满足为止。
这样的降维方法在理论上有保证，在计算上是可行的，故对高维问题，可用上述拉格朗日乘数法的思想来降低维数。
求解算法：拉格朗日乘数法求解算法：逐次逼近法的形式反复进行，直到满足某种要求为止。
设为满足的一个可行解，固定x 在x (0)，先对y 求解，则二维分配问题变为一维问题：可用对一维的方法来求解。
两鼠穿墙的解题方法
两鼠穿墙的解题方法（原创版3篇）目录（篇1）1.引言：介绍“两鼠穿墙”问题2.问题分析：解释问题的关键所在3.解决方案：详述两种解题方法4.总结：对解题方法进行评价和展望正文（篇1）一、引言“两鼠穿墙”是一个有趣的智力题，描述的是两只老鼠从一个墙的一侧挖洞，同时从另一侧开始挖洞，它们在什么情况下能够相遇？这个问题看似简单，却涉及到一些深刻的数学和物理原理。
二、问题分析这个问题的关键在于理解空间和时间的关系。
两只老鼠在挖洞的过程中，它们的位置和速度都是关键因素。
如果两只老鼠挖洞的速度和方向不同，它们可能无法相遇。
另外，如果它们在挖洞的过程中，墙的厚度发生变化，也会影响它们相遇的时间和位置。
三、解决方案有两种基本的解题方法。
第一种方法是使用数学模型，通过建立老鼠的位置和速度的方程，求解它们相遇的时间和位置。
这种方法需要一定的数学知识，但是对于理解问题的本质非常有帮助。
第二种方法是使用物理学原理，考虑老鼠挖洞的过程中的力学效应，如重力、摩擦力等，通过物理模拟求解它们相遇的时间和位置。
这种方法更加直观，也更容易理解。
四、总结“两鼠穿墙”问题提供了一个理解空间和时间关系的有趣视角。
虽然问题看似简单，但是解决它需要深入理解数学和物理原理。
无论是使用数学模型，还是物理学原理，都能够帮助我们找到老鼠相遇的时间和位置。
目录（篇2）1.引言：介绍两鼠穿墙问题2.两鼠穿墙问题的解决方法3.方法一：直接计算4.方法二：动态规划5.方法三：数学方法6.结论：总结三种解决方法正文（篇2）在数学领域，有趣的问题层出不穷。
今天我们要探讨的是一个有趣的问题——两鼠穿墙问题。
这个问题描述如下：有两只老鼠从相距 100 米的 A、B 两点出发，它们同时开始挖洞，每天挖洞的距离之和为 2 米。
假设它们挖洞的过程中是相互独立的，也就是说，它们不会互相干扰。
那么请问，这两只老鼠需要多少天才能挖穿墙壁，相遇在对方的洞里？为了解决这个问题，我们可以尝试以下三种方法：方法一：直接计算。
经典的动态规划入门练习题
动态规划入门练习题1.石子合并在一个圆形操场的四周摆放着N堆石子(N<= 100),现要将石子有次序地合并成一堆.规定每次只能选取相邻的两堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分.编一程序,由文件读入堆栈数N及每堆栈的石子数(<=20).(1)选择一种合并石子的方案,使用权得做N－1次合并,得分的总和最小;(2)选择一种合并石子的方案,使用权得做N－1次合并,得分的总和最大;输入数据:第一行为石子堆数N;第二行为每堆的石子数,每两个数之间用一个空格分隔.输出数据:从第一至第N行为得分最小的合并方案.第N+1行是空行.从第N+2行到第2N+1行是得分最大合并方案.每种合并方案用N行表示,其中第i行(1<=i<=N)表示第i次合并前各堆的石子数(依顺时针次序输出,哪一堆先输出均可).要求将待合并的两堆石子数以相应的负数表示.输入输出范例:输入:44 5 9 4输出:－４５９－４－８－５９－１３－９２２４－５－９４４－１４－４－４－１８２２最小代价子母树设有一排数，共ｎ个，例如：22 14 7 13 26 15 11.任意2个相邻的数可以进行归并,归并的代价为该两个数的和,经过不断的归并,最后归为一堆,而全部归并代价的和称为总代价,给出一种归并算法,使总代价为最小.输入、输出数据格式与“石子合并”相同。
输入样例：412 5 16 4输出样例：－１２－５１６４１７－１６－４－１７－２０３７2.背包问题设有ｎ种物品，每种物品有一个重量及一个价值。
但每种物品的数量是无限的，同时有一个背包，最大载重量为ＸＫ，今从ｎ种物品中选取若干件（同一种物品可以多次选取），使其重量的和小于等于ＸＫ，而价值的和为最大。
输入数据：第一行两个数：物品总数Ｎ，背包载重量ＸＫ；两个数用空格分隔；第二行N个数,为Ｎ种物品重量；两个数用空格分隔；第三行N个数,为N种物品价值; 两个数用空格分隔；输出数据：第一行总价值；以下N行，每行两个数，分别为选取物品的编号及数量；输入样例：4 102 3 4 71 3 5 9输出样例：122 14 13.商店购物某商店中每种商品都有一个价格。
2023noip题目
2023NOIP考题解析题目一：数据结构与算法本题主要考察的是对数据结构和算法的理解与运用。
给定一组数字序列，请设计一个算法，找出该序列中第k小的数字。
输入输入包括两行。
第一行为一个整数n，表示数字序列的长度。
第二行为n个以空格分隔的整数，表示数字序列。
输出输出一个整数，表示数字序列中第k小的数字。
样例输入89 2 4 7 1 5 3 8样例输出3题解思路为了找出第k小的数字，我们可以使用堆排序的算法。
首先，将输入的数字序列构建成一个小顶堆。
然后，依次将堆顶元素取出，并将其与堆尾元素进行交换，再对堆进行调整，直到取出k个数字为止。
具体实现步骤如下：1.将输入序列构建成一个小顶堆。
可以使用数组或者二叉堆来实现堆结构。
2.依次取出堆顶元素，并将其与堆尾元素进行交换。
3.对堆进行调整，以满足堆的性质。
4.重复步骤2和3，直到取出k个数字为止。
5.返回堆尾元素，即为第k小的数字。
时间复杂度分析构建小顶堆的时间复杂度为O(nlogn)，其中n为数字序列的长度。
每次调整堆的时间复杂度为O(logn)。
因此，该算法的时间复杂度为O(n+klogn)。
题目二：动态规划本题主要考察的是动态规划的思想和应用。
给定一个包含n个正整数的序列，要求选取一个长度至少为2的子序列，使得该子序列中元素之和最大。
输入输入包括两行。
第一行为一个整数n，表示序列的长度。
第二行为n个以空格分隔的正整数，表示序列。
输出输出一个整数，表示选取的子序列中元素之和的最大值。
样例输入6-2 1 -3 4 -1 2 1 -5 4样例输出6题解思路该题可以使用动态规划的思想来解决。
定义一个数组dp，dp[i]表示以第i个元素结尾的子序列中元素之和的最大值。
则 dp[i] = max(dp[i-1]+nums[i], nums[i])。
具体实现步骤如下：1.初始化一个长度为n的数组dp，初始值均为0。
2.根据动态规划的递推公式，计算dp数组的每个元素的值。
(二) 动态规划算法
(二) 动态规划算法目录- 几个动态规划问题中的术语- 阶段- 状态- 无后效性- 决策- 多阶段决策问题- 策略- 状态转移方程- 最优化原理/最优子结构性质- 动态规划引出- 基本思想- 适用情况- 基本步骤- 书面版- 细讲- 个人理解- 备忘录算法- 程序设计- 思维过程- 一般的算法设计模式- 经典运用# 先来说几个动态规划问题中的术语：动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。
多阶段决策问题的图示## 阶段把所给求解问题的过程恰当地分成若干个相互联系的阶段，以便于求解，过程不同，阶段数就可能不同．描述阶段的变量称为阶段变量。
在多数情况下，阶段变量是离散的，用k表示。
此外，也有阶段变量是连续的情形。
如果过程可以在任何时刻作出决策，且在任意两个不同的时刻之间允许有无穷多个决策时，阶段变量就是连续的。
在前面的图中，第一个阶段就是点A，而第二个阶段就是点A 到点B，第三个阶段是点B到点C，而第四个阶段是点C到点D。
## 状态状态表示每个阶段开始面临的不以人的主观意志为转移的自然或客观条件，也叫不可控因素。
在上面的例子中，状态是某个阶段的开始位置，它不仅是该阶段一条道路的起点，也是前一阶段一条分支的终点。
前面的例子(图)中，第一个阶段有一个状态即A，而第二个阶段有两个状态B1和B2，第三个阶段是三个状态C1，C2和C3，而第四个阶段又是一个状态D。
过程的状态通常可以用一个或一组数来描述，称为状态变量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
树形DP与优化方法
聚会的快乐
你要组织一个由你公司的人参加的聚会。你希 望聚会非常愉快，尽可能多地找些有趣的热闹 。但是劝你不要同时邀请某个人和他的上司， 因为这可能带来争吵。给定N个人(姓名，他幽 默的系数，以及他上司的名字)，编程找到能 使幽默系数和最大的若干个人。
【输入】 第一行一个整数N(N<100)。接下来有N 行，每一行描述一个人的信息，信息之间用 空格隔开。姓名是长度不超过20的字符 串，幽默系数是在0到100之间的整数。 【输出】 所邀请的人最大的幽默系数和。
三色二叉树（tro）
见文本
树形动态规划(皇宫看守)
Hale Waihona Puke 太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。皇宫以午门 为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状；某些宫殿间可以互相望 见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守， 在不同的宫殿安排看守所需的费用不同。可是陆小凤手上的经费不足，无论 如何也没法在每个宫殿都安置留守侍卫。编程任务：帮助陆小凤布置侍卫， 在看守全部宫殿的前提下，使得花费的经费最少。 数据输入：输入数据由文件名为INPUT.TXT的文本文件提供。输入文件中数 据表示一棵树，描述如下： 第1行 n，表示树中结点的数目。 第2行至第n+1行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号i （0<i<=n），在该宫殿安置侍卫所需的经费k，该边的儿子数m，接下来m 个数，分别是这个节点的m个儿子的标号r1，r2，...，rm。 对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且 标号不重复。数据输出：输出到OUTPUT.TXT文件中。输出文件仅包含一个 数，为所求的最少的经费。
（二）若i不属于V，i一定要能被i的某个儿子j 标号，这时求所有Vj（j为i的儿子）。若所有的 j都是j被j的儿子标号时最“省”（即所有Vj= Vj2），那么实际上按这样的方案没有一个j∈V, 造成了i不能被标号。 这时只要找一个"牺牲"最小的i的儿子j，把 方案Vj2换成Vj1。这样就求出了"覆盖以节点i 为顶点且不包括节点i的最佳节点集Vi2"。
要求覆盖以节点i为顶点的树的最佳方案Vi， 显然只需考虑节点i属于或不属于集合V两种 情况，两者择优即可。即Vi=min{Vi1，Vi2} （1表示属于，2表示不属于）
(一）若i∈V，则对于i的任一儿子j，也只 有属于或不属于集合V两种情况： （1）若j∈V，则问题转化到求Vj1的 小一级规模问题，转化成功； (2) 若j不属于V，则要不求Vj2，要 不就是j不能被j的任意一个儿子标号，则 求所有Vk（k为j的儿子），Vi1求好了。
状态转移方程
通过上面的分析，我们很容易得到下面这组状态转移方程： F(i)=min{F(i,1),F(i,2)} F(i,1)=Weight(i)+∑min{F(j),∑min{F(k,1),F(k,2)}} F(i,2)=∑F(j)；若所有F(j)<F(j,1)，则换取代价最小的F(j,2) （以上j为i儿子，k为j儿子）
【样例】 party.in party.out 5 8 BART 1 HOMER HOMER 2 MONTGOMERY MONTGOMERY 1 NOBODY LISA 3 HOMER SMITHERS 4 MONTGOMERY
分析
首先，很显然公司的人员关系构成了一棵树。设f[a]为 a参加会议的情况下，以他为根的子树取得的最大幽默 值；g[a]为a不参加会议的情况下，以他为根的子树取 得的最大幽默值。那么，状态转移方程就是： f[a]=g[b1]+g[b2]+…+g[bk]+1 g[a]=max(f[b1], g[b1])+max(f[b2], g[b2])+…+max(f[bk], g[bk]) 其中b1, b2, …, bk为a的子结点。 最后的答案就是max(f[root], g[root])，root是树根。
边界条件 F(i)=F(i,1) F(i,1)=Weight(i) F(i,2)=+∞ （以上i为叶子节点）
输入数据示例
输出数据示例 25
问题分析
求给定的带权树的符合下面条件的子顶点集合V： 1． 若点i∈V，则所有与i相邻的点j可被标号。 2． 任意一个点j，若j不属于V，则j可被标号。 3． S=∑（Weight[i]，i∈V），并且S最小。
考虑到树本身的特性：除了根节点外，每一个节点 都仅与该节点的父节点与儿子节点有关系；大多数 情况下，每个节点的状况都是由它的儿子节点的状 况决定的。这与动态规划的无后效性要求相符，再 加上本题求的又是最优方案，这一切都与动态规划 算法不谋而合。