邓肯张模型FORTRAN子程序源代码
邓肯-张模型参数求取
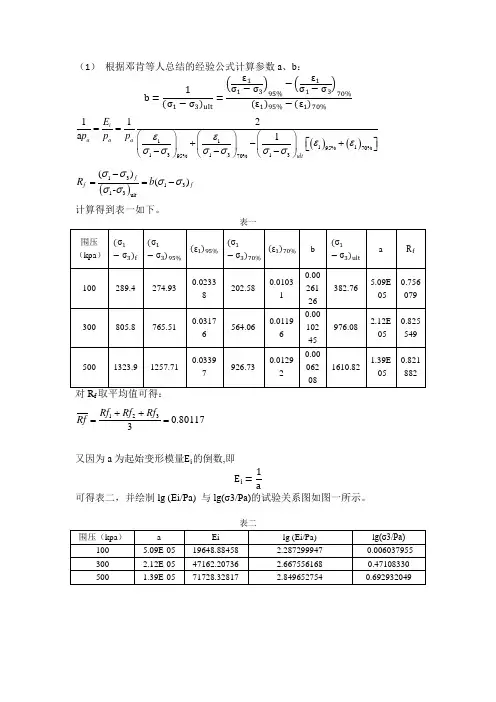
(1) 根据邓肯等人总结的经验公式计算参数a 、b :b =1(σ1−σ3)ult =(ε1σ1−σ3)95%−(ε1σ1−σ3)70%(ε1)95%−(ε1)70%()()111195%70%13131395%70%112a 1i a a a ultE p p p εεεεσσσσσσ==⎛⎫⎛⎫⎛⎫⎡⎤+-+ ⎪ ⎪ ⎪⎣⎦---⎝⎭⎝⎭⎝⎭()131313ult()()-ff fR b σσσσσσ-==-计算得到表一如下。
f 80117.03321=++=Rf Rf Rf Rf又因为a 为起始变形模量E i 的倒数,即E i =1a可得表二,并绘制lg (Ei/Pa) 与lg(σ3/Pa)的试验关系图如图一所示。
表二图一:承德中密砂lg (Ei/Pa) 与lg(σ3/Pa)的试验关系图对图一中的试验点进行拟合,得到lg (Ei/Pa) 与lg(σ3/Pa)的直线关系:y=0.8033x+2.2914.根据公式:E i=Kp a(σ3 p a )n可知K、n分别代表lg (Ei/Pa) 与lg(σ3/Pa)直线的截距和斜率,故可得K=2.2914;n=0.8033。
E-ν法在常规三轴试验中,轴向应变ε1与侧向应变—ε3之间也存在双曲线关系,经变换之后可得如下公式:−ε3ε1=f−Dε3由上式知—ε3/ε1与—ε3为直线关系,但实际上,二者并不是严格的直线关系,需先对试验结果进行取舍,然后选取某一区间进行拟合。
本文中选取试验曲线的后半部分进行拟合,得到不同围压下相应的拟合曲线,如下图所示。
图二:—ε3/ε1与—ε3关系曲线对应不同围压下的拟合曲线分别为:σ3=100kpa时,y=2.8211x+0.4719;σ3=300kpa时,y=2.8809x+0.4381;σ3=500kpa时,y=3.258x+0.4177.f和D分别为—ε3/ε1与—ε3直线的截距和斜率,结果如下表所示。
又因为νi=f=G -Flg (σ3/Pa )故可做νi—lg (σ3/Pa )关系曲线如下所示。
Fortran子程序.ppt

WRITE(*,*) I ENDIF ENDDO END
FUNCTION NUM(N, I)
SELECT CASE(I)
CASE(100)
第八章 子程序
语句函数 函数子程序 子例行程序 程序单元之间的数据传递 递归调用 数据共用存储单元与数据块子程序 内部子程序 模块
8.1 语句函数 语句函数——
PROGRAM EXAM1A X=1 FX=5*X**3-2*X**2+7*X+6
用一个语句定义的函数。WRITE(*,*) 'f(', X, ')=', FX
PARAMETER (N=20)
DIMENSION A(N)
INTEGER A
A(1)=17
!该语句及随后的三个语句生成数组A
DO I=2, 20
A(I)=MOD(19*A(I-1), 1024)
ENDDO
DO I=1, N-1 !二重循环完成对A的排序
DO J=I+1, N
CALL SWAP(A(I), A(J))
当未进行说明时,函数值的类型遵守I-N规则。 虚参的类型在函数体中说明,否则遵守I-N规则。
二、函数子程序的调用
P130 例8.4 用函数子程序的方法设计一个程序, 求50-100内的所有素数及其和。
分析:设计一个函数子程序 PRIME(N),函数 PRIME的值定义如下:
1 当n是素数时 prim e(n) 0 当n非素数时
注意:
函数用一条语句可以定义时,才用语句函数的 形式定义函数。
邓肯_张非线性模型研究及其在ANSYS中的实现

文章编号:1007 2284(2010)03 0076 04邓肯 张非线性模型研究及其在ANSYS 中的实现宿 辉1,2,党承华2,崔佳佳2(1.北京科技大学土木与环境学院,北京100083;2.河北工程大学水电学院,河北邯郸056021)摘 要:对工程领域使用广泛的邓肯 张非线性本构模型进行了研究,总结了国内外的研究现状及理论成果,针对其无法判定因结压力降低时的加载情况,提出了相应的变形模量的计算方法,同时考虑中主应力、土体抗拉强度的影响对模型进行了修正。
利用AP DL 编写程序实现了A N SYS 的材料本构模型的二次开发,运用重启动方法实现单元应力修正后数据重写入数据库,通过试验模拟对比分析验证了模型的适用性。
关键词:邓肯 张模型;抗拉强度;中主应力;应力分析 中图分类号:T U 470+.3 文献标识码:ADuncan Chang Nonlinear Elastic Model and Realization in ANSYSSU Hui 1,2,DANG Cheng hua 2,CUI Jia jia2(1.Schoo l of Civ il and Env iro nmen Engineering ,Beijing U niver sity o f Science and T echnolog y,Beijing 100083,China;2.Scho ol o f Water Resources and H ydropow er,Hebei U niv ersity of Engineering ,H andan 056021,H ebei Pro vince ,China)Abstract:Based on the pr esent research situation and theor etical r esults,research is do ne o n Duncan Chang no nlinear elastic mo del,w hich is applied w idely in engineer ing,.A cco rding t o the fact that Duncan Chang model can't judg e the lo ading situatio n w hile co n solidat ion pressure decr eases .T he model is mo dified cosidering the effect of int ermediate principal stress and tensile strength of so il.T he seco ndar y dev elo pment of mater ial co nstitut ive model in A N SYS is accomplished by utilizing the A PDL lang uag e.T hen t he r e start method is used to modify element str ess,the co rrected data is database rew ritten.A ser ies of compliance tests verify the accur a cy and applicability of the modified Duncan Chang nonlinear elastic mo del embedded AN SY S.Key words:Duncan Chang no nlinear elastic mo del;tensile str eng th;inter mediat e pr incipal stress;str ess analy sis 收稿日期:2009 05 18作者简介:宿 辉(1972 ),男,副教授,博士研究生,主要从事岩土工程及水工结构教学及研究工作。
第六讲 Fortran中的子程序

一、子例行程序的定义
子例行程序是以Subroutine 语句开头,并以End语句结束的一 个程序段,其定义的一般格式为:
Subroutine 子例行程序名(虚参表)
子例行程序体 end
2015/12/20 12
注意: (1)子例行程序的命名方法与变量相同。虚参由变量、数组 名(不能是数组元素,常数、表达式)充当,当有多个虚参 时,之间用“ ,” 分隔,没有虚参时子例行程序名后面的一对 括号可以省略; (2)子例行程序的设计方法与函数子程序相同,但不能有对 子例行程序名的赋值语句(因为其名字没有值)。
第六讲 Fortran中的子程序
实际中的程序由若干个程序单元组成,但是有且只有一个主 程序( Program main ),其它的都是子程序。子程序是构造 大型实用程序的有效工具,设计程序要善于利用子程序,因 此,本讲学习Fortran中的子程序:函数子程序和子例行程序。 此外,在Fortran中还有一种类似与函数子程序的语句函数。
2015/12/20 15
分析:牛顿迭代公式为:
program newton f(x)=7*x**4+6*x**3-5*x**2+4*x+3 f ( xn ) df(x)=28*x**3+18*x**2-10*x+4 xn 1 xn ' f ( xn ) read*,x0,e !x0=-1.0,e=0.0001 x1=x0 首先要给个迭代初值 x0 , x2=x1-f(x1)/df(x1) 代入公式的右边计算 x1 , do while(abs(x1-x2)>e) 再把 x1 代入计算出 x2 , … , x1=x2 x2=x1-f(x1)/df(x1) 当第n次和第(n+1)次计算 end do 结果差不多时(在规定的 print*,x1,f(x1) 精度内),则计算结果就 end
本构模型之邓肯张模型

G , F 为试验常数,其确定见图(c)。
将式(16)微分,得:
d v 1 D ) f D f 3 ( i 1 1 v t 2 2 d ( 1 D ) ( 1 D ) 1 1 1
(19)
将式(4)、式(8)、式(10)和式(18)代入式 (19),则得到任一应力(σ1,σ3)时的泊松比的 邓肯-张计算公式:
R f 值一般在0.75~1.0之间
R 1 f b ( ) ( )f 1 3 u l t 1 2
(8)
将式(8)、式(4)代入式(3)中,得
1 1 Et Rf Ei 1 1 E ( ) 1 3 f i
t
(4)
这表明代表的是在这个试验中的起始变形 模量(初始切线模量)的倒数。
在式(1)中,如果 1 ,则:
(1 3 )ult 1 b
(5) (6)
或者 :
1 b (1 3 )ult
由此可看出b代表的是双曲线的渐进线所对应的极 限偏差应力 (1 3)ult 的倒数。
在试验中 1 不可能无限大,求取 (1 3)ult ;对于有峰值 ) ( ) 3 ) ( 3 ) 点的情况,取 ( 1 3 f 1 3 1 f 1 u l t 峰,这样 ( 定义破坏比 R f 为: (1 3 ) f Rf (7) (1 3 )ult
本构模型之邓肯张模型
主要是根据试验成果拟合推导得出
邓肯-张双曲线模型
• 该模型是一种建立在增量广义虎克定律 基础上的非线性弹性模型,可经反映应 力~应变关系的非线性,模型参数只有 8个,且物理意义明确,易于掌握,并 可通过静三轴试验全部确定,便于在数 值计算中运用,因而,得到了广泛地应 用。
有限元编程算例(fortran)【范本模板】
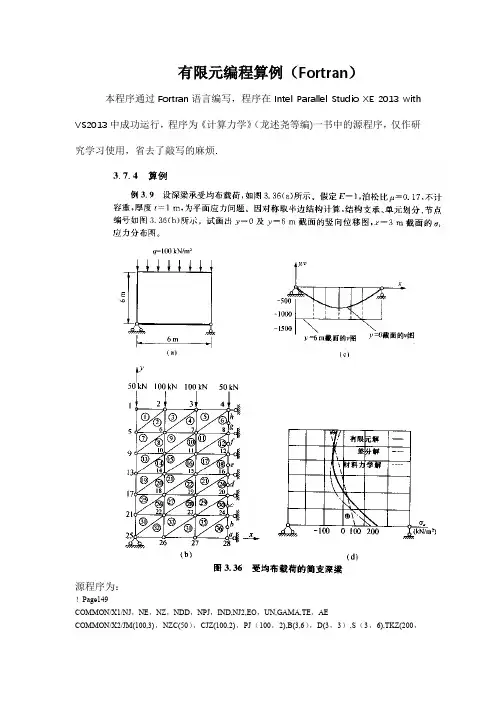
有限元编程算例(Fortran)本程序通过Fortran语言编写,程序在Intel Parallel Studio XE 2013 with VS2013中成功运行,程序为《计算力学》(龙述尧等编)一书中的源程序,仅作研究学习使用,省去了敲写的麻烦.源程序为:!Page149COMMON/X1/NJ,NE,NZ,NDD,NPJ,IND,NJ2,EO,UN,GAMA,TE,AECOMMON/X2/JM(100,3),NZC(50),CJZ(100,2),PJ(100,2),B(3,6),D(3,3),S(3,6),TKZ(200,20),EKE(6,6),P(200)OPEN(5,FILE=’DATAIN’)!OPEN(6,FILE=’DATAOUT’,STATUS=’NEW')CALL DATAIF(IND.EQ.0)GOTO 10EO=EO/(1.0—UN*UN)UN=UN/(1。
0—UN)10 CALL TOTSTICALL LOADCALL SUPPORCALL SOLVEQCALL STRESSPAUSE!STOPENDSUBROUTINE DATACOMMON/X1/NJ,NE,NZ,NDD,NPJ,IND,NJ2,EO,UN,GAMA,TE,AECOMMON/X2/JM(100,3),NZC(50),CJZ(100,2),PJ(100,2),B(3,6),D(3,3),S(3,6),TKZ(200,20),EKE(6,6),P(200)READ(5,*)NJ,NE,NZ,NDD,NPJ,INDNJ2=NJ*2NPJ1=NPJ+1READ(5,*)EO,UN,GAMA,TEREAD(5,*)((JM(I,J),J=1,3),I=1,NE)READ(5,*)((CJZ(I,J),J = 1,2),I=1,NJ)!Page150READ(5,*)(NZC(I),I=1,NZ)READ(5,*)((PJ(I,J),J=1,2),I=1,NPJ1)WRITE(6,10)(I,(CJZ(I,J),J=1,2),I=1,NJ)10 FORMA T(4X,2HNO,6X,1HX,6X,1HY/(I6,2X,F7。
ABAQUS二次开发Duncan-Chang模型在粗粒料三轴试验中的应用
3.粗粒料三轴实验
粗粒料通常是指块石、碎石(或砾卵石)、石屑、石粉等粗颗粒组成的无粘性
2
混合料,或是粘性土中含有大量粗颗粒的混合土。《土工试验规程》(SL237-
含量(%)
46.2
38.4 15.4
试样直径 101mm,高度 200mm,采用击实制样,控制干密度取 ρ = 1.9g / cm3 。
进行 3 组常规三轴试验,围压分别为 200kPa、500kPa、800kPa,采用固结排水
剪,剪切速率取 0.001mm/s,固结和剪切过程均按《土工试验方法标准》(GB/T
Duncan-Chang 模型是目前岩土工程方面运用十分广泛的岩土体本构模型, 其能够很好地反映土体非线性变形特征。其参数具有比较明确的物理意义,可教 容易由常规三轴试验得到。本文将用 2 次开发邓肯—张模型来模拟高围压三轴排 水实验。
2. Duncan-Chang 模型
1970 年Duncan、Chang提出了邓肯E-V双曲线非线性弹性模型,该模型属于 变弹性模型,其理论基础是基于广义虎克定律基础上的增量线弹性模型,这种模 型假定:土体变形虽然是弹性的,但是在微小变形时,变形可以看作是线性的, 并且服从增量线性的各向同性广义虎克定律。其基本假设依然保留了弹性理论中
的斜率或截距得到。在拟合过程中,得到的参数是综合 3 组试验数据的结果,所
4
以高围压 0.8MPa 下模拟的曲线大部分在试验曲线以下,而围压 0.2MPa、0.5MPa 的情况下模拟曲线大部分在试验曲线以上。如果试验的过程严格安照规范的规 定,操作过程在没有失误的情况下,排除了人为因素,一定能得到很好的模拟效 果。
fortran子程序【精选】
parameter (n1=3,n2=3,n3=3)
dimension a(n1,n2)
dimension b(n2,n3),c(n1,n3)
open(5,file='input.dat')
call getmat(a,n1,n2)
call getmat(b,n2,n3)
call matpro(a,n1,n2,b,n3,c)
20 continue end
real w(5,5) call readin(w)
输入矩阵 1,2,3,4,5 2,3,4,5,1
call opp(w,x1,x2) write(*,100) x1,x2 100 format(1x,'The two sum of',
3,4,5,1,2
$ ' oppusite angles elements:',
subroutine sub(ch) charact...er*(*) ch end
11
(4)如果实参是变量或数组元素,在调用子程序时, 对应的虚实参数实际上将共用同一存储单元。
program main
subroutine sub(x,a)
integer a,c(3)
integer x,a
data c/3*0/
4,5,1,2,3 5,1,2,3,4
$ /1x,'x1=',f8.2,' x2=',f8.2) end
9
主要区别:
1. 形式不一样(function、subroutine、call),无虚参 时括号使用不一样。
2. 子程序名的意义不一样。函数子程序名代表函数值, 通过其传递数据,需要类型说明;而子例行程序名仅 为了调用使用,通过虚实参传递数据。
ADINA软件中邓肯—张模型的二次开发与应用
ADINA软件中邓肯—张模型的二次开发与应用
陈志坚;江涛;陈松
【期刊名称】《水电能源科学》
【年(卷),期】2007(25)2
【摘要】根据AD INA提供的用户子程序,用FORTRAN编写了邓肯—张E-v本构模型,给出了模型开发的方法和步骤,并用常规三轴压缩试验对模型进行了检验。
检验结果表明,开发的模型正确合理、计算精度较理想,可应用于实际工程计算以解决复杂的非线性土工问题。
【总页数】3页(P65-67)
【关键词】ADINA;邓肯-张模型;二次开发
【作者】陈志坚;江涛;陈松
【作者单位】河海大学土木工程学院
【正文语种】中文
【中图分类】TU411;TP311.5
【相关文献】
1.邓肯-张E-B模型的ANSYS二次开发及应用 [J], 孙明权;陈姣姣;刘运红
2.Duncan-Chang E-υ模型在ADINA软件中的开发与应用 [J], 陈志波;朱俊高;陈浩锋
3.邓肯-张模型开发及其在面板坝计算中的应用 [J], 宋志宇;李斌;董莉莉;梁春雨
4.邓肯-张EB模型参数求解的二次优化法 [J], 陈立宏
5.一种改进邓肯张模型及其在土石坝数值模拟中的应用 [J], 邵东琛
因版权原因,仅展示原文概要,查看原文内容请购买。
应用MATLAB确定邓肯-张双曲线模型中的K,n参数
应用MATLAB确定邓肯-张双曲线模型中的K,n参数简介:接合承德中密砂常规三轴试验数据,介绍应用Matlab语言编写计算及绘图程序来处理试验数据的方法,可显著提高试验研究的数据处理效率和结果的可视化程度。
关键字:Matlab 三轴试验邓肯-张模型1 前言基于广义胡克定律的线弹性理论形式简单,参数少,物理意义明确,而且在工程界有广泛深厚的基础,得以应用于许多工程领域中。
早期土力学中的变形计算主要是基于线弹性理论的,只有在计算机得到迅速发展之后,非线性理论模型才得到较广泛的应用。
邓肯-张模型是建立在增量广义胡克定律基础之上的变模量的弹性模型,可以反映土变形的非线性,并在一定程度上反映土变形的弹塑性,很容易为工程界所接受,加之所用参数和材料参数不多,物理意义明确,只需用常规三轴压缩试验即可确定这些参数及材料常数适应的土类比较广,所以该模型为岩土工程界所熟知,并得到了广泛的应用,成为土的最为普及的本构模型之一。
本文主要是应用MATLAB编写计算及绘图程序来处理承德中密砂常规三轴试验数据。
2 基于MATLAB的计算过程实现现场的观测数据经过采集和整理后,按照一定的格式把数据存储在数据文件中,然后可以使用MATLAB丰富的数值运算功能可以非常容易地编制出数据处理程序,先用函数fope n()打开数据文件,fid=fopen(‘filename’,’r’)再用fscanf 函数依次从文件中读取格式化数据来完成对各变量地赋值,其使用语法为:matrix=fscanf(fid,format)。
本文由于数据不是太多,所以在计算过程中没有采取调用存储文件地形式。
直接在计算过程中输入试验数据计算。
2.1 数据的处理对第一组数据,通过编写Matlab语言,由轴向应变和应力差的试验数据可以作出~()和~双曲线关系图形,主要用到的MATLAB命令为:plot(x1,y1);axis([0 0.04 0 3]) ;hold on%(1)plot(x1, x1./y1);a=polyfit(x1, x1./y1,1);t1=0:0.001:0.07;plot(x1, x1./y1,'.',t1,a(1)*t1 +a(2))%(2)其中x1代表第一组轴向应变,x2代表第一组应力差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
邓肯张模型FORTRAN子程序源代码
SUBROUTINE UMA T(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
1 RPL,DDSDDT,DRPLDE,DRPLDT,STRAN,DSTRAN,
2 TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,MATERL,NDI,NSHR,NTENS,
3 NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,CELENT,
4 DFGRD0,DFGRD1,NOEL,NPT,KSLAY,KSPT,KSTEP,KINC)
C
INCLUDE 'ABA_PARAM.INC'
C
CHARACTER*80 MATERL
DIMENSION STRESS(NTENS),STATEV(NSTA TV),
1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
3 PROPS(NPROPS),COORDS(3),DROT(3,3),
4 DFGRD0(3,3),DFGRD1(3,3)
C
DIMENSION PS(3),DSTRESS(NTENS),TDSTRESS(NTENS),TSTRESS(NTENS) PARAMETER (ONE=1.0D0,TWO=2.0D0,THREE=3.0D0,SIX=6.0D0)
K=PROPS(1)
N=PROPS(2)
RF=PROPS(3)
C=PROPS(4)
FAI=PROPS(5)/180.0*3.1415926
G=PROPS(6)
D=PROPS(7)
F=PROPS(8)
KUR=PROPS(9)
PA=PROPS(10)
DFAI=PROPS(11)/180.0*3.1415926
S1S3O=STATEV(1)
S3O=STATEV(2)
SSS=STATEV(3)
CALL GETPS(STRESS,PS,NTENS)
FAI=FAI-DFAI*LOG10(S3O/PA)
CALL GETEMOD(PS,K,N,RF,C,FAI,ENU,PA,KUR,EMOD,S,S3O,G,D,F
1 ,SSS,S1S3O)
EBULK3=EMOD/(ONE-TWO*ENU)
EG2=EMOD/(ONE+ENU)
EG=EG2/TWO
EG3=THREE*EG
ELAM=(EBULK3-EG2)/THREE
CALL GETDDSDDE(DDSDDE,NTENS,NDI,ELAM,EG2,EG)
TDSTRESS=0.0
CALL GETSTRESS(DDSDDE,TDSTRESS,DSTRAN,NTENS)
DO 701 I1=1,NTENS
TSTRESS(I1)=STRESS(I1)+TDSTRESS(I1)*0.5
701 CONTINUE
CALL GETPS(TSTRESS,PS,NTENS)
CALL GETEMOD(PS,K,N,RF,C,FAI,ENU,PA,KUR,EMOD,S,S3O,G,D,F,
1 SSS,S1S3O)
EBULK3=EMOD/(ONE-TWO*ENU)
EG2=EMOD/(ONE+ENU)
EG=EG2/TWO
EG3=THREE*EG
ELAM=(EBULK3-EG2)/THREE
CALL GETDDSDDE(DDSDDE,NTENS,NDI,ELAM,EG2,EG)
DSTRESS=0.0
CALL GETSTRESS(DDSDDE,DSTRESS,DSTRAN,NTENS)
DO 702 I1=1,NTENS
STRESS(I1)=STRESS(I1)+DSTRESS(I1)
702 CONTINUE
CALL GETPS(STRESS,PS,NTENS)
CALL GETEMOD(PS,K,N,RF,C,FAI,ENU,PA,KUR,EMOD,S,S3O,G,D,F,
1 SSS,S1S3O)
EBULK3=EMOD/(ONE-TWO*ENU)
EG2=EMOD/(ONE+ENU)
EG=EG2/TWO
EG3=THREE*EG
ELAM=(EBULK3-EG2)/THREE
CALL GETDDSDDE(DDSDDE,NTENS,NDI,ELAM,EG2,EG)
IF(PS(3).GT.S3O)S3O=PS(3)
IF((PS(1)-PS(3)).GT.S1S3O)S1S3O=PS(1)-PS(3)
IF(S.GT.SSS)SSS=S
STA TEV(1)=S1S3O
STA TEV(2)=S3O
STA TEV(3)=SSS
END
SUBROUTINE GETPS(STRESS,PS,NTENS)
INCLUDE 'ABA_PARAM.INC'
DIMENSION PS(3),STRESS(NTENS)
CALL SPRINC(STRESS,PS,1,3,3)
DO 310 I=1,2
DO 320 J=I+1,3
IF(PS(I).GT.PS(J))THEN
PPS=PS(I)
PS(I)=PS(J)
PS(J)=PPS
END IF
320 CONTINUE
310 CONTINUE
DO 330 K1=1,3
PS(K1)=-PS(K1)
330 CONTINUE
RETURN
END
SUBROUTINE GETEMOD(PS,K,EN,RF,C,FAI,ENU,PA,KUR,EMOD,S,S3O
1 ,G,D,F,SSS,S1S3O)
INCLUDE 'ABA_PARAM.INC'
DIMENSION PS(3)
S=(1-SIN(FAI))*(PS(1)-PS(3))
IF(PS(3).LT.0) THEN
PSFEI=0.1
ELSE
PSFEI=PS(3)
END IF
S=S/(2*C*COS(FAI)+2*PSFEI*SIN(FAI))
IF(S.GE.0.99) THEN
S=0.99
END IF
AA=D*(PS(1)-PS(3))
AA=AA/(K*PA*((S3O/PA)**N))
AA=AA/(1-RF*S)
ENU=G-F*LOG10(S3O/PA)
ENU=ENU/(1-AA)/(1-AA)
IF(ENU.GT.0.49)ENU=0.49
EMOD=K*PA*((S3O/PA)**N)*((1-RF*S)**2)
IF(S.LT.SSS.AND.(PS(1)-PS(3)).LT.S1S3O)THEN
EMOD=KUR*PA*((S3O/PA)**N)
END IF
END
SUBROUTINE GETFEI(STRESS,SMISES,NTENS,NDI)
INCLUDE 'ABA_PARAM.INC'
DIMENSION STRESS(NTENS)
SMISES=STRESS(1)**2+STRESS(2)**2+STRESS(3)**2+
1STRESS(4)**2+STRESS(5)**2+STRESS(6)**2
SMISES=SQRT(SMISES)
RETURN
END
SUBROUTINE GETDDSDDE(DDSDDE,NTENS,NDI,ELAM,EG2,EG)
INCLUDE 'ABA_PARAM.INC'
DIMENSION DDSDDE(NTENS,NTENS)
DO 20 K1=1,NTENS
DO 10 K2=1,NTENS
DDSDDE(K2,K1)=0.0
10 CONTINUE
20 CONTINUE
DO 40 K1=1,NDI
DO 30 K2=1,NDI
DDSDDE(K2,K1)=ELAM
30 CONTINUE
DDSDDE(K1,K1)=EG2+ELAM
40 CONTINUE
DO 50 K1=NDI+1,NTENS
DDSDDE(K1,K1)=EG
50 CONTINUE
RETURN
END
SUBROUTINE GETSTRESS(DDSDDE,STRESS,DSTRAN,NTENS)
INCLUDE 'ABA_PARAM.INC'
DIMENSION DDSDDE(NTENS,NTENS),STRESS(NTENS),DSTRAN(NTENS) DO 70 K1=1,NTENS
DO 60 K2=1,NTENS
STRESS(K2)=STRESS(K2)+DDSDDE(K2,K1)*DSTRAN(K1)
60 CONTINUE
70 CONTINUE
RETURN
END。
