超静定结构力法
用力法求解超静定结构

用力法求解超静定结构概述超静定结构是指结构中的支座和约束条件多于结构自由度的情况。
用力法是一种经典的结构分析方法,常用于求解超静定结构。
本文将介绍用力法求解超静定结构的基本原理和步骤,并通过实例加以说明。
一、基本原理用力法的基本原理是根据平衡条件和变形约束,通过假设未知力的大小和方向,建立力的平衡方程和变形方程,解出未知力和结构的变形。
用力法适用于各种类型的结构,包括梁、柱、桁架等。
二、步骤用力法求解超静定结构的步骤如下:1. 选择合适的剖面根据结构的几何形状和约束条件,选择合适的剖面,将结构分割为若干个部分。
2. 假设未知力的方向和大小根据结构的特点和约束条件,假设未知力的方向和大小。
通常,未知力的方向可以根据结构的几何形状和外力的作用方向来确定,而未知力的大小则需要通过力的平衡方程来求解。
3. 建立力的平衡方程根据假设的未知力和结构的几何形状,建立力的平衡方程。
平衡方程包括力的平衡条件和力的矩平衡条件。
4. 建立变形方程根据结构的变形情况和约束条件,建立变形方程。
变形方程可以根据结构的刚度和约束条件来确定。
5. 解方程将力的平衡方程和变形方程联立,解方程组得到未知力和结构的变形。
6. 检验结果将求解得到的未知力和结构的变形代入原平衡方程和变形方程中,检验结果的准确性。
如果结果符合平衡和变形的要求,则求解成功;如果结果不符合要求,则需要重新假设未知力并重新求解。
三、实例分析为了更好地理解用力法求解超静定结构的步骤和原理,下面以一个简单的梁结构为例进行分析。
假设有一根悬臂梁,在梁的自重和外力作用下,需要求解支座反力和梁的变形。
1. 选择合适的剖面选择悬臂梁的剖面,将梁分割为两个部分:悬臂部分和支座部分。
2. 假设未知力的方向和大小假设支座反力的方向向上,大小为R。
3. 建立力的平衡方程根据力的平衡条件,可以得到悬臂部分的平衡方程:R - F = 0,其中F为梁的自重。
4. 建立变形方程根据梁的几何形状和约束条件,可以建立悬臂部分的变形方程,得到悬臂部分的弯矩和挠度。
材料力学-力法求解超静定结构

力法求解超静定结构时,可以根据计算结果优化结构设计,提高结构的强度和稳定性。
结论与总结
力法是求解超静定结构的有效方法,通过合理应用材料力学基础和力法的原理,我们能够准确求解反力分布并 分析结构的应力情况。
样例分析
结构:桥梁
使用力法求解桥梁上的悬臂梁,计算主梁的支座反 力和悬臂梁的应力分布。
结构:楼房
将力法应用于楼房结构,确定楼板的支座反力并分 析楼梯的受力情况。
实用提示和技巧
1 标定自由度
在应用力法时,正确标定结构的自由度是成功求解反力的重要步骤。
2 验证计算结果
对计算得到的反力进行验证,确保结果的准确性,避免错误的设计决策。
材料力学-力法求解超静 定结构
超静定结构的定义
超静定结构是指具有不止一个不可靠支持反力的结构。它们挑战了传统的结构分析方法,需要使用力法进行求 解。
材料力学基础
材料力学研究材料的受力和变形规律,包括弹性力学、塑性力学和损伤力学。 这些基础理论为力法求解超静定结构提供了必要的工具。
力法的原理
力法是一种基于平衡原理和支座反力法则的结构分析方法。它通过对超静定结构施加虚位移,建立受力平衡方 程,求解未知反力。
超静定结构应用力法求解的步骤
1
确定结构类型
了解结构是否为超静定结构,并确定不
计算反力
2
可靠支持反力的个数。
根据力法原理,建立并求解受力平衡方
程,计算未知反力。
3
验证平衡
通过检查受力平衡方程是否满足等式的
确定应力分布
4
要求,验证计算的反力是否正确。
பைடு நூலகம்
根据已知反力和结构的几何特性,计算 并绘制应力分布图。
超静定结构解法力法.pptx

P
EI
EI
l
P
解:
X1
l
X1=1
Pl
P
1 0
11 X1 1P 0 11 l 3 / 3EI
1P Pl 3 / 2EI
X1 3P / 2()
M M1 X1 M P
l
M1
Pl
MP
第8页/共21页
3 Pl M 2
力法基本思路小结
解除多余约束,转化为静定结构。多余约 束代以多余未知力——基本未知力。
分析基本结构在单位基本未知力和外界因 素作用下的位移,建立位移协调条件——力 法方程。
从力法方程解得基本未知力,由叠加原理 获得结构内力。超静定结构分析通过转化为 静定结构获得了解决。
第9页/共21页
将未知问题转化为 已知问题,通过消除已 知问题和原问题的差别, 使未知问题得以解决。 这是科学研究的 基本方法之一。
X1
X2
X3
X1
X2
X3
去掉一个链杆或切断 一个链杆相当于去掉 一个约束
X1 X2
X3
第12页/共21页
X2 X1
X3
X3
X2 X1
X3 X1
X1 X2 X3
X2
去掉一个固定端支 座或切断一根弯曲 杆相当于去掉三个 约束.
将刚结点变成铰结 点或将固定端支座 变成固定铰支座相 当于去掉一个约束.
几何可变体系不能 X3 作为基本体系
M
1 0
1 11 1P 0
11 X1 11
力法 方程
11 X1 1P 0
1 11 l 3 / 3EI
1P ql 4 / 8EI
X1 3ql / 8() M M1 X1 M P
力法求解超静定结构的步骤

力法求解超静定结构的步骤:
1、先判定其超静定次数,(含多余联系数),去掉原结构的所有多余联系,用相应的多余力代替,得一静定的基本结构(形式可能很多,尽量简单);
2、根据基本结构在原荷载及所有多余力共同作用下,在每一个去掉的多余联系处位移和原结构相应位置的已知位移相同,建立力法典型方程;
3、求方程所有系数和自由项,(静定结构的位移计算)积分法或图乘法,写出基本结构X i∑=在单位力及原荷载分别单独作用下的内力表达式或作出内力图;
4、解方程,求出所有多余力;
5、作最后内力图(静定结构的计算问题)梁、刚架:M N P 组合结构:
6、校核,两方面:平衡条件(截取结构中+ X i N i ∑=M P →Q→N 桁架:N +M i M=0 )∑Y=0 ∑ X=0 ∑刚结点、杆件或某一部分,应满足;变形协调条件(多余约束处位移是否与已知位移相等)
注:选取基本结构的原则:
(1)基本结构为静定结构;
(2)选取的基本结构应使力法方程中系数和自由项的计算尽可能方便,并尽量使较多的副系数和自由项为0
(3)较易绘M 图及MP 图。
第五章力法超静定结构概述(PDF)
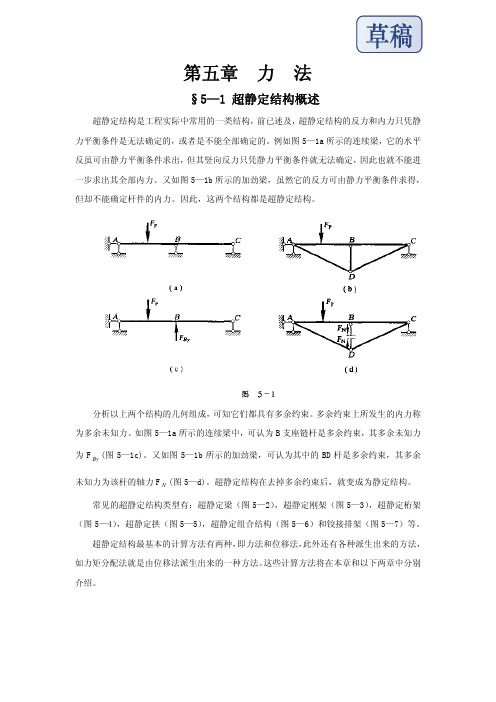
第五章 力 法§5—1 超静定结构概述超静定结构是工程实际中常用的一类结构,前已述及,超静定结构的反力和内力只凭静力平衡条件是无法确定的,或者是不能全部确定的。
例如图5—1a所示的连续梁,它的水平反虽可由静力平衡条件求出,但其竖向反力只凭静力平衡条件就无法确定,因此也就不能进一步求出其全部内力。
又如图5—1b所示的加劲梁,虽然它的反力可由静力平衡条件求得,但却不能确定杆件的内力。
因此,这两个结构都是超静定结构。
分析以上两个结构的几何组成,可知它们都具有多余约束。
多余约束上所发生的内力称为多余未知力。
如图5—1a所示的连续梁中,可认为B支座链杆是多余约束,其多余未知力(图5—1c)。
又如图5—1b所示的加劲梁,可认为其中的BD杆是多余约束,其多余为FBy未知力为该杆的轴力F(图5—d)。
超静定结构在去掉多余约束后,就变成为静定结构。
N常见的超静定结构类型有:超静定梁(图5—2),超静定刚架(图5—3),超静定桁架(图5—4),超静定拱(图5—5),超静定组合结构(图5—6)和铰接排架(图5—7)等。
超静定结构最基本的计算方法有两种,即力法和位移法,此外还有各种派生出来的方法,如力矩分配法就是由位移法派生出来的一种方法。
这些计算方法将在本章和以下两章中分别介绍。
§5—2 力法的基本概念在掌握静定结构内力和位移计算的基础上,下面来寻求分析超静定结构的方法。
先举一个简单的例子加以阐明。
设有图5—8a 所示一端固定另一端铰支的梁,它是具有一个多余约束的超静定结构。
如果以右支座链杆作为多余约束,则去掉该约束后,得到一个静定结构,该静定结构称为力法的基本结构。
在基本结构上,若以多余未知力代替所去约束的作用,并将原有荷载q 作用上去,则得到如图5—8b 所示的同时受荷载和多余未知力作用的体系。
该体系称为力法的基本体系。
在基本体系上的原有荷载是已知的,而多余力是未知的。
因此,只要能设法先求出多余未知力,则原结构的计算问题即可在静定的基本体系上来解决。
超静定结构内力计算.pptx

μ
MBC= 0.429×(-24) = -10.3kNm
传递弯矩:
c MCB= 0
c
MAB= 0.5×(-13.7) = -6.85kNm
最后杆端弯矩:
MCB= 0
MAB= MFAB+ MCAB = -66.85kNm
MBA= MFBA+ MμBA = 46.3kNm
MBC= MFBC+ MμBC = -46.3kNm
M
f AB
3 16
Pl
1 ql2 8
A
B
P A
3 Pl 16
B
M
f BA
3 16
Pl
1 ql2 8
A
B
M
f AB
1 8
ql 2
M
f BA
1 8
ql 2
第17页/共24页
1、计算各杆的固端 弯矩Mf
MfAB=0
M
f BA
1 8
ql 2=1/8×4×62=18
MfBC=-1/8PL=-1/8×30×6=-22.5 MfCB=1/8PL=1/8×30×6=22.5
所以,结点角位移的数目 等于该结构的刚结点数!
由于A、B、C为固定端支座,所以 其位移均已知为零,不需作为未知量; 而同一刚结点处各杆的杆端转角相等, 所以每个刚结点处只有一个独立的结 点转角未知量。故上图刚架只有一个 结点转角未知量。
第5页/共24页
2、独立结点线位移
在微弯状态下,假定受弯直杆两端之间距离在变形 前后保持不变,即杆长保持不变。
A
SAB = 3 i
B
A
SAB = i
θ =1
= B
A
B
当θ ≠ 1时: MAB = SAB θ
用力法解超静定结构

ቤተ መጻሕፍቲ ባይዱ
n1 X1 n2 X 2 nn X n np 0
(三)力法典型方程中系数和自由项的计算
1、主系数δii — 表示基本结构由于 Xi 1的单独作用,在Xi 的作用点并沿Xi的方向产生的位移; 图A
ii
M
2 i
dx
EI
2、副系数δij —iiijijip表的示作基MMM用EM本EEIiii2E点MMiIIMd结Ix并jjpd构dx沿dxx由Xi于的X方j 向 1产的生单的独位作移用;,图在B Xi
例2:试用力法计算图示超静定刚架,并绘内力图。
解: 1.选择基本体系
2.建立力法方程
d11X1+D1P=0
3.计算系数和自由项,绘 M1和MP图
11
1 EI
1 2
l
l
2 3
l
2
2l 3 3EI
1P
1 EI
1
2
l ql 2
2 3
l2
2 3
l
ql 2 8
l
2
17ql 4
24EI
4.计算X1 5.绘内力图
=1
结构称为力法基本结构
基本结构
力法基本方程 — 利用基本体系的变形状态与原结构
一致的条件所建立的确定多余未知
力的方程
BACK
11X1 1P 0
11
M1M1 dx 1 (1 l l 2 l) l3
EI
EI 2
3
3EI
1P
M1M p dx 1 (1 l 1 ql 2 3 l) ql 4
ql3
24EI l
1 ql2 8
3EI
5、绘内力图 M M1X1 M p V V1 X1 Vp
一次超静定结构的力法典型方程

一次超静定结构的力法典型方程在我们生活的这个世界里,结构物无处不在,房子、桥梁、甚至那看似简单的秋千,都跟结构有着千丝万缕的关系。
说到超静定结构,哎呀,这可是一个既神秘又让人抓狂的概念。
你可能会想,什么是超静定?是不是跟超人有关系?其实不是,超静定结构的意思就是,它的稳定性和受力情况并不是那么简单,通过一些力法的经典方程,我们能一探究竟。
想象一下,你的朋友跟你说他要建个大房子,你的第一反应肯定是:这得稳得住呀,风一吹可别塌了。
说到这里,超静定结构就显得尤为重要了。
好了,咱们来聊聊力法,听起来挺高大上的,但其实呢,就是用简单的力的平衡来搞定这些复杂的结构。
想象一下,你在玩积木,拼拼凑凑,突然发现有个地方歪了,这可怎么办?这时候,你得用一些巧妙的办法来调整。
力法的经典方程就像是你的调节工具,它帮助你找出哪些地方受力不均,哪里需要加固。
就像人喝酒,喝多了总得找个地方坐下,太累了可不行。
大家知道吗,超静定结构其实可以用几个基本的力法方程来描述。
我们得了解个基本的概念,结构的自由度。
自由度听起来高深,其实就是结构能在什么情况下发生变形。
就像一只小鸟,想飞就飞,想栖就栖,但超静定结构可没这么容易。
这里有个小诀窍,咱们常用的牛顿第二定律就可以派上用场,这可是万金油,万能的。
简单来说,就是力等于质量乘以加速度,哎,这可真是个简单粗暴的真理。
再说了,力法的方程其实就是在用一些简单的数学式子,来帮我们找出各个构件的受力情况。
你想啊,建筑结构就像一个大家庭,每个成员都有自己的责任和角色。
如果有人分担过多的压力,那家里可就不太平了。
想象一下,家里的洗衣机坏了,大家伙儿都在忙,结果呢,阳台的窗户也跟着受到了影响,哎,这可就麻烦了。
力法就是要确保每个成员都在适当的负荷下,不然可就得重新分配任务了。
你看,在这些方程中,有时候会出现一些神秘的符号,比如力的方向、大小,甚至是一些角度。
这就像打麻将,牌面上的每一张都要考虑清楚。
你不能只想着自己要胡,得看看别人怎么出牌。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、补充转化条件——力法的基本方程
MA
FAx
A
FAy
A
FP C
FP
B X1
B
FP
A
C
B
静定结构
A
B
C
X1
基本体系
基本结构
基本体系转化为原来超静定结构的条件是:基本体系沿
多余未知力X1方向的位移D1应与原结构位移ΔB相同,即
Δ1 = ΔB = 0 这个转化条件是一个变形条件或称位移条件,也就是
计算多余未知力时所需要的补充条件。
x2
x1 x2
x1
x3
x3
x3
x2
x1
(a)
(a1)
(a2)
(3 次)
x2 x2
或
x1
x3
(14 次)
或
(1 次)
(6 次)
(4 次)
§ 2 力法的基本概念
一、力法的基本思路:把超静定结构的计算问题转化为静
定结构的问题,即利用已熟悉的静定结构的计算方法达到计 算超静定结构的目的。
1、找出关键问题——力法的基本未知量
X2
n=6 超静定刚架
X1
X1
X5
X6
X3
三铰刚架
X1
X2
X3 X4
X6
X4 X6
X5
二悬臂折梁
X2 X3
X4
简支刚架
X6 X5
对同一超静定结构,可以采取不同的方式移去多余约束,而 得到不同的静定结构,但是多余约束的数目总是相同的,因 而所确定的结构超静定次数也是唯一的。
例
试确定图(a)、(b)所示结构的基 本未知量。
§1 超静定结构的组成和超静定次 数
• 超静定结构的组成
• 超静定次数
一、超静定结构
1、超静定结构的两大特征 从两个方面把它与静定结构作一个对比 :
(1)在几何组成方面:静定结构是没有多余约束的几何不变 体系,而超静定结构则是有多余约束的几何不变体系
(2)在静力分析方面:静定结构的支座反力和截面内力都 可以用静力平衡条件唯一地确定,而超静定结构的支座反 力和截面内力不能完全由静力平衡条件唯一地加以确定
二、超静定次数的确定
力法是以结构中的多余约束力为基本未知量的,一个 结构的基本未知量数目就等于结构的多余约束数目。 因此,力法计算首先要找出结构的多余约束。
超静定结构中的多余约束数目,称为超静定次数,用n 表示。
确定结构超静定次数最直接的方法是解除多余约束 法,即将原结构的多余约束移去,使其成为一个 (或几个)静定结构,则所解除的多余约束数目就 是原结构的超静定次数。
FP q
FP
FP
FP
FP
FP
FP
q
FP
①
X1 X1
X2 X2
③
②
④
X1
总起来说,约束有多余的,内力(或支座反力)是超
静定的,这就是超静定结构区别于静定结构的两大基
本特征。凡符合这两个特征的结构,就称为超静定结
构。
2பைடு நூலகம்超静定结构的两种约束
(1)必要约束:对维持体系的几何不变性不可缺少的约 束,称为必要约束。
MA A
FAx
FAy
FP B
C
X1
FP
A
C
B
静定结构
图中的超静定结构与静定结构相比较,其不同之处在于:在支
座B处多了一个多余未知力X1,这就造成了该结构的超静定性。 只要能设法求出这个X1,则剩下的问题就纯属静定问题了
2、寻求过渡途径——力法的基本体系
MA
FP
FP
A FAx
B
A
C
B
C
FAy
FP
X1
静定结构
A
B
A
B
C
X1
基本体系
基本结构
将图示结构的多余约束移去,而代之以多余未知力X1,并保留 原荷载所得到的结构,称为力法的基本体系。与之相应,把结 构的多余约束并连同荷载一起移去后所得到的结构,称为力法 的基本结构。
基本体系本身既是静定结构,又可用它代表原来的超静定结构。 因此,它是由静定结构过渡到超静定结构的有效途径。
解除超静定结构的多余约束,归纳起来有以下几种方式:
1)移去一根支杆或切断一根链杆, 相当于解除一个约束。
2)移去一个不动铰支座或切开一个 单铰,相当于解除两个约束。
X1
X2 X1
X1 X1
X1 X1 X2 X2
3)移去一个固定支座或切断一根梁 式杆,相当于解除三个约束。
4)将固定支座改为不动铰支座或 将梁式杆中某截面改为铰结,相当 于解除一个转动约束。
第二部分 超静定结构 第六章 力法
• §1 超静定结构的组成和超静定次数 • §2 力法的基本概念 • §3 超静定刚架和排架 • §4 超静定桁架和组合结构 • §5 对称结构的计算 • §6 两铰拱 • §7 无铰拱(自学) • §8支座移动和温度改变时的计算 • §9 超静定结构位移的计算 • §10超静定结构计算的校核
X3 X2
X1
X1
X1 X1 X3 X3
X2
X1
在解除多余约束判断结构的超静定次数时,应特别注意:既须 移去全部多余约束,又要保留每个必要约束,以保证结构成为 没有任何多余约束的几何不变体系,亦即成为静定结构。
(1)刚性联结的封闭框格,必须沿某一截面将其切断。 (2)去掉多余联系的方法有多种,但所得到的必须是几 何不变体系;几何可变、瞬变均不可以。
Δ1 = ΔB = 0 应用叠加原理把条件写成显含多余未知力Xi的展开形式。
Δ1=Δ1P+Δ11=0
Δ1为基本体系在荷载与未知力X1共 同作用下沿X1方向的总位移; Δ1P为基本结构在荷载单独作用下 沿X1方向的位移; Δ11为基本结构在未知力X1单独作 用下沿X1方向的位移。
(2)多余约束:对维持体系的几何不变性不是必需的约 束,称为多余约束。
多余约束中的约束力称为多余约束力,一般用Xi (i=1,2,…,n)表示。多余约束对结构的作用可以用相 应的多余约束力代替 。多余约束虽然不改变体系的几 何组成性质,但多余约束的存在,将影响结构的内力 与变形的大小及分布规律。
3、超静定结构的五种类型
X2
X2
X4
X4
X3
X1
X1
对于图示结构,水平支座链杆不可去掉,否则就将变成几何可
变体系;如果只去掉一根竖向支座链杆,则其中的闭合框格仍
然具有三个多余约束。还必须把该闭合框格再切开一个截面,
这时才成为静定结构。因此,原结构总共有四个多余约束,即
为四次超静定体系。
图示体系是六次超静定结构:
X1
X2 X4
1)超静定梁 3)超静定拱
2)超静定刚架 4)超静定桁架
5)超静定组合结构
4、分析超静定结构的两个基本方法
力法和位移法是分析超静定结构的两个基本方法。 力法是提出较早、发展最完备的计算方法,同时也是 更为基本的方法。
位移法的提出较力法稍晚些,是在20世纪初为了计算 复杂刚架而建立起来的。
在上述两种基本方法的基础上,还曾演变出多种渐近 法和近似法,主要用以克服当年因计算手段滞后给手 算工作带来的困难。属于位移法类型的渐近解法—— 力矩分配法和无剪力分配法;以及近似解法——分层 计算法和反弯点法,至今仍具有工程实用价值,
