结构力学 力法计算超静定结构
结构力学 力矩分配法计算超静定结构
力法和位移法是求解超静定结构的两种基本方法。两种方法的共同特点都是 要列方程和解联立方程，计算烦琐。而力矩分配法是建立在位移法基础上的一 种渐近解法，计算过程按照重复步骤进行，结果逐渐接近真实解答。它无须解 联立方程而直接计算出杆端弯矩，方法简便，适合手算。适用范围是连续梁和 无侧移刚架的内力计算。
情景二 用力矩分配法计算连续梁 学习能力目标
掌握力矩分配法计算连续梁并绘制弯矩图。
项目表述
运用力矩分配法计算多跨连续梁结构。
学习进程
情景二 用力矩分配法计算连续梁
项目实施
案例 3 – 17 图 3 – 62a 所示为两跨梁，试用力矩分配法求杆端弯矩，并作 M 图。
解答：（1）计算分配系数 同一结点各杆分配系数之和等于 1，把算好的μ 值填在表格 3 – 5中B结点处。 （2）计算固端弯矩（查表 3 – 4） （3）放松刚结点 B 进行力矩分配 （4）计算传递弯矩 （5）计算杆端弯矩 把同一杆端的固端弯矩、分配弯矩和传递弯矩相加（代数和），即得杆端弯
情景一 力矩分配法的基本原理和要素
知识链接
加于刚结点 1 的外力矩按分配系数分配给各杆的 1 端（近端），称 其 为分配弯矩。
3．传递系数 C 如图 3 – 60 所示，当外力矩 M 加于结点 1 时，该结点发生转角.1 ， 于是各杆近端和远端都将产生杆端弯矩，这些杆端弯矩值如下
情景一 力矩分配法的基本原理和要素
解答：① 求分配系数。 ② 锁住结点 B、C，求各杆的固端 M。 ③ 先放松结点 C，按单结点直接把M=150kN.m进行分配、传递，此时 C
暂时平衡，将结果填入表中。求出此时结点B的不平衡力矩。 ④ 再放松结点 B，将（ - MB ）进行分配、传递，此时 B 暂时平衡，而由
朱慈勉结构力学力法
6.46 EA
kN
(
)
2 5 m 1 15
2 5 m 1 15
C2E 4.A 23kNm
θD
6.46kN EA
1 m 1 1 m 1 35 35
例6-12 求图示组合结构C点的竖向位移ΔC和AD与BD杆间的相对转角
ΔθD。忽略受弯杆的轴向变形。 已知AD和BD杆：EA EI m2
2次超静定
9
选取基本结构为切断竖杆:
X 1h
t0
1 EA
1 kl
§6-7超静定结构的位移计算
F E N F N d A s k 0 F G Q F Q d A s M E M d I s F R c
1)载作用下的位移计算
F N F Nd P s EA
k 0F G Q F Qd P A s
M M P ds EI
求超静定结构因温度改变、支座移动产生的位移时， 若选原结构建立虚拟力状态，计算将会更简单。
EI, l,t0 ,Δt
①
M、Q、N
EMIht、ENAt0、G kQA
P=1
②
T 2 1 1 R *c W 21
c M * E M I h t d s N * E N A t0 d s Q * G kd Q
2次超静定
9
解：⑴ 确定超静定次数;
⑵ 用力法求解, 并作M图和FN图; ⑶ 选取基本结构为铰结体系求位移;
⑷ 求AD杆与BD间的相对转角:
⑸ 施加单位荷载并求各杆轴力:
D
FN1FN l EA
1 m 1
35m 25m 1 1 .8 9 k N 1 .3 4 k N 3 5
E A 1 5
1 m 1 35
b h
结构力学第六章 力法
四、n次超静定结构的力法典型方程
i1X1 i2 X 2 in X n iP 0(i 1、2、、n)
符号意义同前。 求解内力(作内力图)的公式：
M M1X1 M2X2 Mn Xn M P
FQ FQ1X1 FQ2 X2 FQn Xn FQP
FN FN1 X1 FN 2 X 2 FNn X n FNP 作内力图可以延用第三章的作法：由M→FQ→FN。
通常做法：拆除原结构的所有多余约束，代之 以多余力X，而得到静定结构。
规则： 1）去掉或切断一根链杆，相当于去掉一个约束； 2）去掉一个简单铰，相当于去掉两个约束； 3）去掉一个固定支座或切断一根梁式杆，相当于去 掉三个约束； 4）在梁式杆上加一个简单铰，相当于去掉一个约束。
10
例： a)
X1
X2
37
2、列 力法方程
1211XX11
12 X 2 22 X 2
1P 2P
0 0
（B 0） （C 0）
讨论方程和系数的物理意义。
q
A
D
Δ1P B
C
A
X1=1
δ11 δ21
D
B
C
A
δ12
X2=1 δ22
D
B C
38
位移方程(力法方程)
ΔφB=0 ——B左右截面相对转角等于零。 ΔφC=0 —— C左右截面相对转角等于零。
d)
原结构
X2
X1
X1
X2
n=2
13
e)
原结构
X1 X1 n=1
f)
原结构
n=3
X1
X3
X2
特别注意：不要把原结
构拆成几何可变体系。此
结构力学- 力法
0
X1 4X2
0
解方程得：
X1
1 15
ql 2
(
)
X2
1 60
ql2 (
)
3. 作内力图 1) 根据下式求各截面M值，然后画M图。
M M1X1 M2X2 MP
23
ql2 15
A
C
B
ql2 60
11ql 2 120
D M图
2) 根据M图求各杆剪力并画FQ图。
AB杆： MB 0
FQAB
26
2. 方程求解
q
B
C
ql 2 8
A
MP图
1P
1 E1I1
2 3
l
1 ql 2 8
1 2
ql3 ql3 24E1I1 24E2I2k
2P 0
X1=1 1 E1I1 l
1B
C
E2I2 l
A
M1图
B
E1I1 l C
E2I2 l
X2=1
A
M 2图
1
27
X1=1 1 E1I1 l
1B
C
E2I2 l
A
M1图
B
E1I1 l C
E2I2 l
X2=1
A
1 M2图
11
1 E1I1
1 2
1 l
2 3
1
1 E2 I 2
1 2
1
l
2 3
1
l l l E1I1 E2I2 l k 1 3E1I1 3E2I2 3 E1I1E2I2 3E2I 2 k
( E1I1 k) E2 I2
12
21
1 E2 I2
△iP—荷载产生的沿Xi方向的位移
浅析超静定结构计算中力法与位移法的异同
浅析超静定结构计算中力法与位移法的异同作者：赵浩楠来源：《科学与财富》2019年第17期摘要：力法和位移法是结构力学中计算超静定结构的两种基本方法，这两种计算方法既有相同之处，又有不同之处，本文从二者的基本原理、基本未知量、基本体系及典型方程等方面对比分析力法与位移法在结构计算中的异同。
关键词：超静定结构；力法；位移法；异同在实际工程计算中，大多数结构都是超静定的，结构力学计算通常包括两个部分：内力计算和位移计算，力法和位移法在结构力学中是计算超静定结构的两种基本方法，二者既有相同的地方也有许多不同之处。
相同之处在于二者的分析依据相同，并且最终目的都是为了求解出结构的内力和支座反力；不同之处主要是在于两者的基本原理、基本未知量、基本体系和典型方程不同。
1 力法与位移法对比分析之同1.1 分析依据超静定结构计算中，力法和位移法是常用的两种计算方法。
所谓的超静定结构即指具有多余约束的几何不变体系、基于静力平衡条件不能唯一确定内力和反力的结构。
力法和位移法不仅考虑静力平衡条件，还考虑了变形协调条件及物理条件，从而对超静定结构进行求解。
1.2 目的力法和位移法都是综合利用静力平衡条件、变形协调的几何条件、应力与应变间本构关系的物理条件，根据各自的简单基本结构和关于基本未知量的基本方程，先求解出基本未知量，再求出剩余未知量，最终求解出实际工程中常见的超静定结构各截面的内力和支座反力。
力法和位移法都是综合利用静力平衡条件、变形协调及物理关系三个方面的条件，使各自基本体系与原结构的受力、变形情况一致，从而应用基本体系建立相应的典型方程以达到分析原结构的目的。
2 力法与位移法对比分析之异2.1 基本原理结构在一定的荷载作用下，其内力与位移有一定的关系，简单来说，在分析超静定结构时，力法是先求出结构内力，然后计算其相应的位移；而位移法是先确定位移，再根据位移求出结构内力。
力法的基本原理是：通过撤除多余约束把多余未知力作为基本未知量，将分析超静定结构转化为分析相应的基本结构，然后根据多余约束处的变形协调条件（位移条件）建立力法基本方程，求出基本未知量后即可通过静力平衡条件求出结构的全部内力。
《结构力学习题集》(上)第四章超静定结构计算——力法
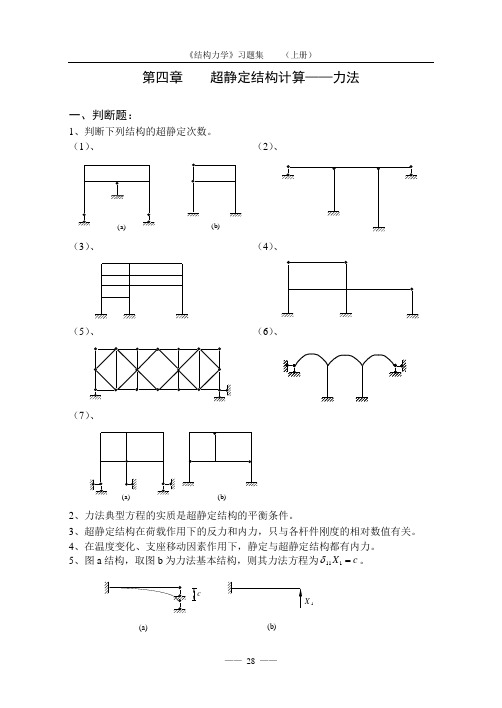
第四章 超静定结构计算——力法一、判断题：1、判断下列结构的超静定次数。
（1）、 （2）、(a )(b)（3）、 （4）、（5）、 （6）、（7）、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下，静定与超静定结构都有内力。
5、图a 结构，取图b 为力法基本结构，则其力法方程为δ111X c =。
(a)(b)X 16、图a 结构，取图b 为力法基本结构，h 为截面高度，α为线膨胀系数，典型方程中∆12122t a t t l h =--()/()。
t 21t l Ah(a)(b)X 17、图a 所示结构，取图b 为力法基本体系，其力法方程为。
(a)(b)1二、计算题：8、用力法作图示结构的M 图。
3mm9、用力法作图示排架的M 图。
已知 A = 0.2m 2，I = 0.05m 4，弹性模量为E 0。
qa a11、用力法计算并作图示结构的M 图。
ql /212、用力法计算并作图示结构的M 图。
q3 m4 m13、用力法计算图示结构并作出M 图。
E I 常数。
（采用右图基本结构。
）l 2/3l /3/3l/314、用力法计算图示结构并作M 图。
EI =常数。
3m 3m2m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l lql l17、用力法计算并作图示结构M 图。
E I =常数。
18、用力法计算图示结构并作弯矩图。
161kNmmmm19、已知EI = 常数，用力法计算并作图示对称结构的M 图。
ql lqa a21、用力法作图示结构的 M 图 。
EI = 常数。
2ql22、用力法作M 图。
各杆EI 相同，杆长均为 l 。
23、用力法计算图示结构并作M 图。
EI = 常数。
4m2kN24mmm24、用力法计算并作出图示结构的M 图。
E = 常数。
20kN3m 4m 3m26、用力法计算图示结构并作M 图。
力法的计算步骤和举例
q a2
a
3 4
a
19qa4 4 8Ε Ι
2F
1 1.5ΕΙ
1 2
q a2
a
1 2
a
q a4 6ΕΙ
4）解方程求多余未知力。
5 6
Χ1
1 3
Χ2
19 qa 48
0
12 1 3 Χ1 9 Χ2 6 qa 0
Χ1
7 16
qa
Χ2
3 32
qa
5）绘制内力图。利用叠加公式M M1X1 M2 X2 MF
Ι1 Ι2
Χ 2
ql2 8
0
4）解方程求多余未知
力。令
Ι 2 /Ι1 k
Χ1
ql2 4
k2 3k 4
Χ2
ql 4
k 3k
4
负号表示未知力
和
1
的实际方向与所设方向相
2
反。
5）绘制弯矩图。由叠加公式 M M1X1 M2X2 MF 计 算各控制截面上的弯矩值,用叠加法绘制最后弯矩图， 如图5.14（f）所示。
４.解力法方程求多余未知力。 ５.绘制原结构的内力图。
一、超静定梁和超静定刚架
1.超静定梁
【例5.1】 图5.13(a)所示为一两端固定的超静定梁,全 跨承受均布荷载q的作用,试用力法计算并绘制内力图。
【解】 1）选取基本结构。如图5.13(b)所示。
q
A
EI
B
l
X1
q
X2
X3
A
B
l
(a)原结构
(b)基本结构
【解】1）选取基本结构。如图 5.15（b）所示。 2）建立力法方程。C点的水 平和竖向位移为零
结构力学力法
怎么 求X1 呢？
力法
二、力法的基本方程
位移条件:基本结构转 化为原结构的条件是：基 本结构在原有荷载和多余
A 原结构
未知力共同作用下，在去
掉多余约束处的位移应与
原结构中相应的位移相等。
A
〓
FP
B
FBLeabharlann FPB即1 0
基本体系
当ΔB=Δ1=0
X1 =><>=> FB
F1
F1
X2
X 1 X2 X 1
二次超静定
F1
F1
二次超静定
X1 X2
力法
3） 切断一根梁式杆或去掉一个固定端支座，相当 于去掉三个约束。
F1
F1 X3 X2 X3
X1
X1
X2
三次超静定
F1
F1
三次超静定
X3
X1
X2
力法
4）将刚性连接改为单铰连接或把固定端支座改为铰 支座，相当于去掉一个约束。
F1
Δ1——基本结构在荷载与多余未知力X1共同作用下，B点沿 X1方向的总位移
力法
111 10 A
Δ11——基本结构在多余未知 力X1单独作用下，B点沿X1方向 的位移；
Δ1P——基本结构在荷载单独 作用下，B点沿X1方向的位移。
〓
FP
+
FP
B
FB
X1
Δ11 X1
Δ1P
力法
δ11 X1=1
↓
B
Δ1P
X10.94k5N X24.79k3N
(5) 求各杆的最后内力
各柱的弯矩图可按悬臂梁直接作出。
力法
结构力学计算超静定梁结构力学PPT学习教案
Δ1 =0
(a)
第6页/共61页
等式左端表示基本结构在作用点的竖向线位移(沿方向 等式左端表示基本结构在作用点的竖向线位移(沿方向的
位移)，等号右端表示原结构在B点的 竖向线 位移。 设、分 别表示基本结构在及荷载单独作用时 ，作用 点沿方 向的位
移，其符号都以沿假定的方向为正， 见图7-4(c)、(d)，根 据 叠加原理，变形协调条件式(a)可写为
图7-5
由于虚拟状态的 M 图与 M 1 图相同，故
11
M 1 M ds 1 (1 l l 2 l) l3
EI
EI 2
3
3EI
1P
M 1M P ds EI
1 [1 l (2 l Fl l Pl )]
EI 6 2
2 22
5Fl 3
48EI
(5) 解力法方程。
X1
q
C X1
"基本体系"
在力法中把原超静定结构称 (c) A
为原结构，去掉多余联系后
11
B
C
X1
的静定结构称为基本结构。
q
(d)
所去掉的多余联系，则以相 A
B
C
ip
应的多余未知力X1来代替。
图7-
第5页/共61页
4
这样，基本结构就同时承受着荷载和多余未知力X1的作用， 基本结构在原有荷载和多余未知力X1共同作用下的体系称为 力法的基本体系。现在分析一下如何计算X1 。对原结构讲它 代表B支座反力，是一个被动力，而对基本结构来讲它是一
链杆不是多余约束。
(a)
(b)
(c)
(d)
A
B
A
B X1
力法求解超静定结构的步骤
力法求解超静定结构的步骤在结构力学中，超静定结构是指不仅能同时满足静力学平衡条件，而且还有多余的约束力，因此外加一个作用力时其约束力不会被破坏。
力法求解超静定结构是求解这类结构体系的一种有效方法，下面是力法求解超静定结构的步骤。
步骤1：建立超静定结构的外部受力与内力等效关系超静定结构的约束力有多余的约束力，即力学平衡条件所无法求解的约束力。
因此，我们需要建立超静定结构的外部受力与内力等效关系，通过已知的受力条件推导约束力的作用，确定超静定结构的内力状态。
步骤2：建立超静定结构的位移方程或应力方程建立超静定结构的位移方程或应力方程，是力法求解超静定结构的关键步骤之一。
位移方程的建立可以基于杆件测量法或截面受力法，应力方程的建立可以基于材料本构关系和边界条件等。
步骤3：解超静定结构的位移方程或应力方程解超静定结构的位移方程或应力方程，可以采用数值解法和解析解法两种方法。
数值解法主要包括矩阵法、有限元法、边界元法等，解析解法则借助微积分和常微分方程等数学方法进行求解。
步骤4：计算超静定结构的内力与应变通过已解出的位移或应力，可以计算得到超静定结构的内力状态和应变分布。
同时，超静定结构的内力状态也可以用于检验该结构的可靠性以及对超静定结构进行所需的修理和维护。
步骤5：检验超静定结构的可靠性超静定结构的可靠性检验，是通过计算得到的内力状态来评估该结构是否满足设计和使用要求的一项重要工作。
该步骤可以基于强度理论、变形理论等方法，利用计算机强度分析软件来实现。
，力法求解超静定结构是求解这类结构体系的一种常用方法。
通过以上步骤的实施，我们可以获得超静定结构的内力状态，进而检验该结构的可靠性。
结构力学课件超静定结构概述
② 仅有未知力作用 —— Δ11 = ？
Δ11
X1
1
11 11 X1 l
11
M1M1 dx l 3
EI
3EI
M1 X1 1
q
q
＝ （3）X1 基本方程
+ 1P
Δ11
X1
1 11 1P 0
11 11 X1
物理意义 是什么？
11 X1 1P 0
X
1P
11
力法的基本方程 变形协调方程
2. 力法的基本原理 基本未知量 X1
作图示结构的弯矩图。（只考虑微小的弯曲变形，忽略轴向变形 和剪切变形）
q A
EI,l
Δ1＝0
q
B
X1＝？
q
1P
可求
+
Δ11 11 11 X1
X1
X1
11
可求
1
（1）基本概念
q A
EI,l
B
Δ1=0
原结构
q
X1 基本体系
基本结构
基本结构：去掉多余约束得到的几何不变体系。 基本体系：基本结构在荷载和未知多余力共同作用下的体系。
M M1 X1 MP
FQ , FN
q
＝
X1
q
+ 1P
Δ11
X1
叠加原理
M1 X1 MP M
ql2 2
+
ql 2
=8
l
M1 X1 1
MP
ql2 M
3ql
16
8
请自己完成 FQ , FN 图。
（4）力法计算步骤
（1）确定基本未知量，即多余未知力（X1）； （2）去掉多余约束，形成基本结构；
结构力学-第五章-力法4
§5-7 最后内力图的校核
例： 试校核图示刚架的弯矩图其是否有误。
M C B
2M /5 C 3M /5 M /5
A
l
B
M
1
3M /5
B X1 = 1
EI= 常数
A l/ 2
M
2M /5
A
M1 图
解:(1)平衡条件校核。 取刚结点C 为隔离体,满足平衡条件。 (2)校核位移条件。 检验C 结点两个端面间的相对转角位移 Δ C 是否为零, 任取一基本结构作图M 1 ，令 M 1 与M 相图乘得： 2m m 1 1 l 3m 2 1 ml ml 5 5 Δ C [ 1 l 1] [ ]0 EI 2 2 5 3 2 EI 10 10
小 结
小
结
力法是求解超静定结构最基本的方法。力法的基本原 理是将原超静定结构中的多余约束解除，代之以相应的未 知约束反力。原结构就变成了在荷载及多余未知力作用下 的静定结构。这个静定结构称为原结构的基本体系 , 多余 未知力称为原结构的基本未知数。根据基本体系中多余未 知力作用点的位移应与原结构一致的条件，即多余约束处 的位移谐调条件，建立位移协调方程。这就是力法典型方 程。方程中的基本未知数是体系的多余未知力。这种以未 知力为基本未知数的求解超静定结构的方法就称为力法。 由于基本体系满足位移谐调条件 , 因此基本体系的内力 与变形便与原超静定结构完全一致。利用位移约束条件解 出多余未知力是力法的关键 , 求出多余未知力后便将超静 定问题转化为静定问题了。以后的计算便与静定结构的求 解完全一样。
§5-7 最后内力图的校核
结论：亦满足给定位移条件，原弯矩图是正确的。
X1 = 1
C B
A
也可取图悬臂刚架作基本结构，计算B点水平位 移△xB 是否为零。
结构力学【王焕定】1.超静定结构-力法基本原理
11 X1 12 X 2 13 X 3 1 0 21 X1 22 X 2 23 X 3 2 31 X1 32 X 2 33 X 3 3 a
其中1 , 2 , 3 为由于支座移动所产生的位移, 即 i FRici
单位基本未知力引起的弯矩图和反力
1 ( Δbl )1Δ、bl Δ,2Δ、2Δ 3Δ等(于bl )多 少bl？, 3 0 δ
EI
力法典型方程为：
FP
基
本
体
11 X1 12 X 2 13 X 3 1P 0
系
21 X1 22 X 2 23 X 3 2P 0
31 X1 32 X 2 33 X 3 3P 0
单位和荷载弯矩图 Mi , MP 为：
FP
FPab l
由于
M
3
0,
FQ3 0
FN1 FN2 FNP 0
h2 2EI
hl 2EI
问题：如何建立如下基本结构的典型方程？
X3 X1 X2
基本体系2
X3 X1 X2
基本体系3
X3 X1 X2
i i
基本体系2
11 X1 12 X 2 13 X 3 1 b 21 X1 22 X 2 23 X 3 2 a 31 X1 32 X 2 33 X 3 3
所以
13 31 23 32 3P 0
又由于
33
M 32ds EI
FN23ds EA
M P图
k
FQ23ds GA
l EA
0
于是有
X3 0
两端固支梁在竖向荷载作用下没有水平反力
典型方程改写为
11 X1 21 X1
12 X 2 22 X 2
1P 2P
0 0
05-3结构力学 第五章 超静定结构的内力和位移计算(5.2节 位移法)ok
如： 1 2
3
1 2
1
3
这样即可使12、13杆 成为单跨超静定梁
2、附加链杆支座约束：为使杆件两端相对线位移被约束而在结点上附加的约 束阻止结点移动的装置。
如：1
3
用“
” 表示
2 1 3
结构变形时，显然13杆可沿水平方向移动， 同时刚结点1也可能发生转角，要使各杆独立成为 单跨超静定梁。 需在1结点上附加刚臂约束 同时还需加附加链杆支座以阻止13杆的水平线 位移。
r11Z 1+ r12Z 2+ · · · · + r1nZ n+R1P=0
位移法 – 刚度法
ri j=rj i
反力互等定理
位移法典型方程，简称为位移法方程 – 结构的刚度方程
主系数，rii>0 r12 ...... r1n Z1 R1P r11 r Z R r ...... r 2P 22 2n 2 21 ri j=rj i 反力互等定理 0 ...... ...... ...... ...... rn 2 ...... rnn Z n RnP rij=rji，Rip，>0，=0，<0 rn1
F M AB ql 2 / 12 F M BA ql 2 / 12
F A l/2 l/2 B
Fl/8 A
Fl/8
F M AB Fl / 8
B
F M BA Fl / 8
q
ql2/8 B A B
F M AB ql 2 / 8
A
F A l/2 l/2 B
3Fl/16 A B
EI=
Z1 Z2
EI=
结构力学力法
1）
iP, ij
2）由位移互等定理
ij ji ；
ij
位移的方向 对称方阵
产生位移的原因
3） ij 表示柔度，只与结构本身和基本未知力的选择有关，与外荷载无关；
4）柔度系数及其性质
. 1n 11 12 .......... .......... . 22 2n 21 .......... .......... .......... ...... .......... . n2 nn n1
1 p 11 0
1 p 11 X 1 0
力法基本未知量X1、基本体系、基本结构、基本方程。
7
q
q
EI
l
X1
ql 2 2
1P
（b）
11
（c） X 1 1
X1
11
（a）
1、力法基本未知量－X 1 2、力法基本体系－悬臂梁
3、力法基本方程－
11 X 1 1 p 0 11 11 X 1 11 X 1 1P 0
1P , 11
MP
l
X1 1
M1
4、系数与自由项
M 1M P ql4 1P dx EI 8 EI
5、解方程
M 1M 1 l3 11 dx EI 3 EI
l3 ql4 X1 0 3 EI 8 EI
8
X1
3 ql 8
3 X 1 ql 8
q
ql 2 2
X2 1
M 2 m
4、 解方程 18
3m
M P kN m
2.67 M X X 1 2.67 kN 1 1 X 2 1.11kN
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
子项目一 力法计算超静定结构
情景一 超静定结构的基本特征
学习能力目标
1. 能够解释力法的基本概念。 2. 能够确定超静定的次数，得到静定的基本结构。 3. 了解超静定结构的特点。
项目表述
试分析如图 3 – 1 所示超静定结构，确定它的超静定次数。
情景一 超静定结构的基本特征 学习进程
情景一 超静定结构的基本特征 知识链接
② 去掉一个固定铰支座（图 3 – 6a）或拆去一个单铰相当于去掉两个约束（图 3 – 6b），可用两个多余未知力代替。
情景一 超静定结构的基本特征 知识链接
③ 去掉一个固定支座（图 3 – 7b）或切断一刚性杆（图 3 – 7c），相当于去掉 三链接
③ 超静定结构的内力和各杆的刚度比有关，而静定结构则不然。在计算超静定 结构时，除了用静力平衡条件外，还要用到结构的变形条件建立补充方程。而 结构的变形条件与各杆的刚度有关，在各杆的刚度比值发生变化时，结构各部 分的变形也相应变化，从而影响各杆的内力重新分布。利用在超静定结构中， 刚度大的部分将产生较大的内力，刚度较小的部分内力也较小的特点，可以通 过改变杆件刚度的方法来达到调整内力数值的目的。 ④ 在局部荷载作用下，超静定结构与静定结构相比，具有内力分布范围大，内 力分布较均匀，峰值小，且变形小、刚度大的特点。如图 3 – 9a 所示是三跨连 续梁在荷载 F 作用下的弯矩图和变形曲线，由于梁的连续性，两边跨也产生内 力和变形，最大弯矩在跨中为 0.175Fl。图 3 – 9b 所示是多跨静定梁在荷载 F 作用下的弯矩图和变形曲线，由于铰的作用，两边跨不产生内力和变形，最大 弯矩在跨中为 0.25Fl，约为前者的 1.4 倍。
情景一 超静定结构的基本特征 知识链接
④ 将刚性连接改成单铰连接（图 3 – 8a）或将固定支座改为固定铰支座（图 3 – 8b），相当于去掉一个转动约束，用一个多余未知力代替。
情景一 超静定结构的基本特征
知识链接
3．超静定结构的特点 ① 在超静定结构中，除荷载作用外，支座移动、温度变化、材料收缩、构件的制 造误差等非荷载因素都会在结构中引起内力，而非荷载因素在静定结构中不会引 起内力。这是因为超静定结构中存在多余约束，当受到这些因素的影响而发生位 移时，将受到多余约束的制约，因而相应地产生内力。在工程中，连续梁可能由 于地基的不均匀沉降而产生有害的附加内力，可以设置温度缝、沉降缝等构造措 施减小内力对结构的不利影响。反之，在桥梁施工中可以通过改变支座高度来调 整其内力，从而达到合理分布。 ② 由于多余约束的存在，超静定结构比静定结构具有较强的防护能力。因为静定 结构的任一约束遭到破坏后，立即变成几何可变体系，完全丧失承载能力。而超 静定结构在多余约束遭到破坏后，仍为几何不变体系，能继续承受荷载。
情景一 超静定结构的基本特征
知识链接
再从几何构造看，图 3 – 2a 所示梁多余一个支座链杆，图 3 – 3a 中 所示桁架多余两根腹杆。因此两个结构都为超静定结构。
由此可见，超静定结构在静力方面的特征是单凭静力平衡条件不能确 定其全部反力和内力，而在几何构造上的特征是具有多余约束。常见的 超静定结构有超静定梁（图 3 – 4a）、超静定刚架（图 3 – 4b）、超静 定桁架（图 3 – 4c）、超静定拱（图 3 – 4d）及超静定组合结构（图3 – 4e）。
情景一 超静定结构的基本特征
知识链接
2．超静定次数的确定 超静定结构中多余约束的数目，称为超静定次数。确定超静定次数是力法计
算的首要工作。例如，图 3 – 2 所示结构有一个多余约束，超静定次数为 1 ； 图 3 – 3 所示结构有两个多余约束，超静定次数为 2。
超静定结构去掉多余结束的方式，归纳起来有如下几种： ① 去掉一个可动铰支座（图 3 – 2）或切断一根链杆（图 3 – 3 和图 3 – 5）相 当于去掉一个约束，用一个多余未知力代替。
超静定结构有多少个多余约束，相应地就有多少个多余未知力。超静定结构 在几何不变体系的前提下，去掉多余约束，用多余未知力来代替，使原结构变 为一个受已知外力和多余约束力共同作用下的静定结构，这个静定结构称为原 超静定结构的基本结构。原超静定结构称为原结构。我们若能求出 X1、X2 的 具体值，则基本结构中的其余未知量（如内力、位移）均随之可求出。可见， 多余未知力的确定是求解超静定结构的关键。因此，我们把多余未知力作为基 本未知量。
项目实施
去掉超静定结构的约束时，应注意： ① 去掉多余约束后基本结构必须是几何不变体系。即为了保证结构的几何不变 性，某些约束是绝对不能去掉的，如图 3 – 11a 所示连续梁支座 A 的水平链杆 是不能去掉的，否则基本结构就变成几何可变体系，如图 3 – 11b 所示。
情景一 超静定结构的基本特征 知识链接
情景一 超静定结构的基本特征
知识链接
1．力法求解超静定结构的概念 应用力法对超静定结构进行分析计算需拆除超静定结构的多余约束。如图 3
– 2a 中的链杆支座 B（或 A），以及图 3 – 3a 中的两根腹杆 1、2，同时用 X1 表示拆除链杆的未知反力；用 X1、X2 表示拆除的腹杆的未知内力，使其从结构 形式上成为静定结构，如图 3 – 2b 及图 3 – 3b 所示。
情景一 超静定结构的基本特征 知识链接
情景一 超静定结构的基本特征
项目实施
显然，对于同一个超静定结构，可以通过去掉不同的多余约束，得到不同的 基本结构形式。例如图 3 – 10a 所示的超静定结构，可以通过去掉不同的多余 约束，得到如图 3 – 10b、c 所示两个不同的基本结构。
情景一 超静定结构的基本特征
情景一 超静定结构的基本特征
知识链接
前面讨论和研究的都是静定结构的计算，本项目我们将研究超静定结构的内 力和位移的求解方法。从受力上看，如果未知的支座反力或各截面的内力不能 完全由静力平衡条件唯一地确定，就称为超静定结构。如图 3 – 2a 所示连续梁 和图 3 – 3a 所示的桁架就是超静定结构。