第二章第十一节变化率与导数、导数的计算
《2.11变化率与导数、导数的计算》 教案
教学过程一、课堂导入1.从近几年的高考试题来看,导数的几何意义是高考的热点.2.题型既有选择题、填空题,又有解答题,难度中档左右.3.命题切入点:在考查导数的概念及其运算的基础上,又注重考查与解析几何结合的相关知识.二、复习预习导数的概念、几何意义及其运算是运用导数解决问题以及导数在实际生活中的应用的基础,虽然相关知识点的考查为A,B级,但是在许多综合题目中都会涉及本节知识点,需要学生在运用本节知识点理解题意的基础上进一步的运用导数。
对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的作用,在实施化简时,要注意变换的等价性,避免不必要的失误.对于某些不满足求导法则条件的函数,可适当进行恒等变形,步步为营,使解决问题水到渠成.三、知识讲解考点1 导数的概念函数)(x f y =在0x x =处的导数一般地,函数)(x f y =在0x x =处的瞬时变化率是xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim 0000,称其为函数)(x f y =在0x x =处的导数,记作)(0x f '.考点2 导函数当x 变化时,)(x f '称为)(x f 的导函数,则xx f x x f y x f x ∆-∆+='='→∆)()(lim)(000特别提醒:注意)(x f '与)(0x f '的区别,)(x f '是一个函数,)(0x f '是常数,)(0x f '是函数)(x f '在点0x 处的函数值.考点3 导数的几何意义函数)(x f y =在0x x =处的导数的几何意义,就是曲线)(x f y =在点),(00y x P 处的切线的斜率,过点P 的切线方程为:))((000x x x f y y -'=-.特别提醒:求函数)(x f y =在点),(00y x P 处的切线方程与求函数)(x f y =过点),(00y x P 的切线方程意义不同,前者切线有且只有一条,且方程为))((000x x x f y y -'=-,后者可能不只一条.考点4 几种常见函数的导数考点5 导数运算法则(1))()(])()([x g x f x g x f '±'='±; (2))()()()(])()([x g x f x g x f x g x f '+'='; (3))()()()()(])()([2x g x g x f x g x f x g x f '-'=',)0)((≠x g考点6 复合函数的导数(理)设函数)(x ϕμ=在点x 处有导数)(x ϕμ'=',函数)(μf y =在点x 的对应点μ处有导数)(μf y '=', 则复合函数))((x f y ϕ=在点x 处也有导数,且x x y y μμ'⋅'='四、例题精析【例题1】【题干】求下列函数的导数(1)y=x+x5+sin xx2;(2)y=(x+1)(x+2)(x+3);(3)y=11-x+11+x;(4)y=cos 2xsin x+cos x.【解析】(1)∵y =x 12+x 5+sin x x 2=x 32-+x 3+sin xx 2,∴y ′=(x 32-)′+(x 3)′+(x -2sin x )′=-32x 52-+3x 2-2x -3sin x +x -2cos x .(2)y =(x 2+3x +2)(x +3)=x 3+6x 2+11x +6,∴y ′=3x 2+12x +11.(3)∵y =11-x +11+x =21-x ,∴y ′=⎝ ⎛⎭⎪⎫21-x ′=-2(1-x )′(1-x )2=2(1-x )2.(4)y =cos 2xsin x +cos x =cos x -sin x ,∴y ′=-sin x -cos x .【例题2】【题干】求下列复合函数的导数:(1)y=(1+sin x)2;(2)y=ln x2+1;(3)y=1(1-3x)4;(4)y=x1+x2.【解析】(1)y ′=2(1+sin x )·(1+sin x )′=2(1+sin x )·cos x .(2)y ′=(ln x 2+1)′ =1x 2+1·( x 2+1)′ =1x 2+1·12(x 2+1)12-·(x 2+1)′=xx 2+1.(3)设u =1-3x ,y =u -4.则y x ′=y u ′·u x ′=-4u -5·(-3)=12(1-3x )5. (4)y ′=(x 1+x 2)′=x ′·1+x 2+x () 1+x 2′=1+x 2+x 21+x 2=1+2x21+x 2 .【例题3】【题干】已知函数f (x )=2 x +1(x >-1),曲线y =f (x )在点P (x 0,f (x 0))处的切线l 分别交x 轴和y 轴于A ,B 两点,O 为坐标原点.(1)求x 0=1时,切线l 的方程;(2)若P 点为⎝ ⎛⎭⎪⎫-23,233,求△AOB 的面积.【解析】(1)f′(x)=1x+1,则f′(x0)=1x0+1,则曲线y=f(x)在点P(x0,f(x0))的切线方程为y-f(x0)=1x0+1(x-x0),即y=xx0+1+x0+2x0+1.所以当x0=1时,切线l的方程为x-2y+3=0.(2)当x=0时,y=x0+2x0+1;当y=0时,x=-x0-2.S△AOB=12⎪⎪⎪⎪⎪⎪x0+2x0+1·(x0+2)=(x0+2)22 x0+1,∴S△AOB =⎝⎛⎭⎪⎫-23+222 -23+1=839.【例题4】【题干】若函数f (x )=sin ⎝ ⎛⎭⎪⎫3x +π6+θ(0<θ<π),且f (x )+f ′(x )是奇函数,则θ=________.【答案】 π2【解析】∵f (x )=sin ⎝ ⎛⎭⎪⎫3x +π6+θ, ∴f ′(x )=3cos ⎝ ⎛⎭⎪⎫3x +π6+θ. 于是y =f ′(x )+f (x )=sin ⎝ ⎛⎭⎪⎫3x +π6+θ+3cos ⎝ ⎛⎭⎪⎫3x +π6+θ =2sin ⎝ ⎛⎭⎪⎫3x +π6+θ+π3=2sin ⎝ ⎛⎭⎪⎫3x +θ+π2 =2cos(3x +θ),由于y =f (x )+f ′(x )=2cos(3x +θ)是奇函数,∴θ=k π+π2(k ∈Z ).又0<θ<π,∴θ=π2.四、课堂运用【基础】1.(2013·永康模拟)函数y=f(x)的图象如图所示,则y=f′(x)的图象可能是()解析:选D据函数的图象易知,x<0时恒有f′(x)>0,当x>0时,恒有f′(x)<0.2.已知t为实数,f(x)=(x2-4)(x-t)且f′(-1)=0,则t等于() A.0 B.-1C.12D.2解析:选C f′(x)=3x2-2tx-4,f′(-1)=3+2t-4=0,t=1 2.3.(2013·大庆模拟)已知直线y=kx与曲线y=ln x有公共点,则k的最大值为()A.1 B.1 eC.2e D.2e解析:选B从函数图象知在直线y=kx与曲线y=ln x相切时,k取最大值.y′=(ln x)′=1x =k,x=1k(k≠0),切线方程为y-ln 1k =k⎝⎛⎭⎪⎫x-1k,又切线过原点(0,0),代入方程解得ln k=-1,k=1e.【巩固】4.已知f(x)=x2+2xf′(1),则f′(0)=________.解析:f′(x)=2x+2f′(1),∴f′(1)=2+2f′(1),即f′(1)=-2. ∴f′(x)=2x-4.∴f′(0)=-4.答案:-45.若曲线f(x)=ax5+ln x存在垂直于y轴的切线,则实数a的取值范围是________.解析:曲线f (x )=ax 5+ln x 存在垂直于y 轴的切线,即f ′(x )=0有正实数解.又∵f ′(x )=5ax 4+1x ,∴方程5ax 4+1x =0有正实数解.∴5ax 5=-1有正实数解.∴a <0.故实数a 的取值范围是(-∞,0).答案:(-∞,0)【拔高】6.求下列各函数的导数: (1)(x )′=12x 12-;(2)(a x )′=a 2ln x ;(3)(x cos x )′=cos x +x sin x ;(4)⎝ ⎛⎭⎪⎫x x +1′=1x +1,其中正确的有( )A .0个B .1个C .2个D .3个解析:选B根据函数的求导公式知只有(1)正确.7.函数y=x2(x>0)的图象在点(a k,a2k)处的切线与x轴的交点的横坐标为a k+1,其中k∈N*.若a1=16,则a1+a3+a5的值是________.解析:∵y ′=2x ,∴点(a k ,a 2k )处的切线方程为y -a 2k =2a k (x -a k ).又该切线与x 轴的交点为(a k +1,0),∴a k +1=12a k ,即数列{a k }是等比数列,首项a 1=16,其公比q =12.∴a 3=4,a 5=1.∴a 1+a 3+a 5=21.答案:218.如图,从点P1(0,0)作x轴的垂线交曲线y=e x于点Q1(0,1),曲线在Q1点处的切线与x轴交于点P2.再从P2作x 轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,Q1;P2,Q2;…;P n,Q n,记P k点的坐标为(x k,0)(k=1,2,…,n).(1)试求x k与x k-1的关系(k=2,…,n);(2)求|P1Q1|+|P2Q2|+|P3Q3|+…+|P n Q n|.解:(1)设点P k -1的坐标是(x k -1,0),∵y =e x ,∴y ′=e x ,∴Q k -1(x k -1,e x k -1),在点Q k -1(x k -1,e x k -1)处的切线方程是y -e x k -1=e x k -1(x -x k -1),令y =0,则x k =x k -1-1(k =2,…,n ).(2)∵x 1=0,x k -x k -1=-1,∴x k =-(k -1),∴|P k Q k |=e x k =e -(k -1),于是有|P 1Q 1|+|P 2Q 2|+|P 3Q 3|+…+|P n Q n |=1+e -1+e -2+…+e -(n -1)=1-e -n 1-e -1=e -e 1-ne -1,即|P 1Q 1|+|P 2Q 2|+|P 3Q 3|+…+|P n Q n |=e -e 1-ne -1.课程小结1.函数求导的原则对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误.2.曲线y=f(x)“在点P(x0,y0)处的切线”与“过点P(x0,y0)的切线”的区别与联系(1)曲线y=f(x)在点P(x0,y0)处的切线是指P为切点,切线斜率为k=f′(x0)的切线,是唯一的一条切线.(2)曲线y=f(x)过点P(x0,y0)的切线,是指切线经过P点.点P可以是切点,也可以不是切点,而且这样的直线可能有多条.。
高中数学全程复习方略 2

(6)(ax)′=_a_x_l_n_a_(a>0);
1
(7)(lnx)′=_x _;
1
(8)(logax)′=__x _l n_a _(a>0且a≠1).
【即时应用】
(1)y=x-5,则y′=______.
(2)y=4x,则y′=______.
(3)y=log3x,则y′=______.
(4)y= s i n ,则y′=______.
②方法一:
y′= (ex1)(ex1)(ex1)(ex1)
(ex1)2
=
ex(ex1)(ex1)ex (ex1)2
2ex (ex1)2.
方法二:∵y= exex1121ex21,
∴y′= 1 ( e,即x2y1′)=
2ex . (e x 1)2
【反思·感悟】准确熟练地掌握基本初等函数的导数和导数的运 算法则,根据所给函数解析式的特点,确定求导方法.
( D ) 1
【解题指南】利用导数的几何意义,(1)可以直接求出切线斜率;
(2)先求出切线方程,得到与y轴交点的纵坐标;(3)求切线与直
线y=0和y=x的交点,进一步求面积.
【规范解答】(1)选B.
y′= cosx (sinxcosx)sinx(cosxsinx)
(sinxcosx)2
=
(sinx
f(x)g(x)f(x)g(x)
(3)[ f x ]′=______[_g_(x_)_]2______(g(x)≠0).
g (x )
【即时应用】
(1)y=x3+sinx,则y′=_______.
(2)y=x4-x2-x+3,则y′=_______.
(3)y=(2x2+3)·(3x-2),则y′=_______. (4)f(x)= e x ,则f′(x)=_______.
变化率与导数、导数的计算

课堂互动讲练
【规律总结】 函数的导数与导 数值的区别与联系:导数是原来函数 的导函数,而导数值是导函数在某一 点的函数值,导数值是常数.
课堂互动讲练
考点二 导数的运算
1.运用可导函数求导法则和导 数公式,求函数y=f(x)在开区间(a, b)内的导数的基本步骤: (1)分析函数y=f(x)的结构和特 征; (2)选择恰当的求导法则和导数公 式求导; (3)整理得结果.
三基能力强力
4.(教材习题改编)已知f(x)=13 -8x+x2,且f′(x0)=2.则x0= ________.
5 2 答案: 2
三基能力强力
5.(2009年高考江苏卷改编)已知 点P在曲线C:y=x3-10x+3上,过 点P的切线垂直于直线x+2y+3=0, 则点P的坐标为________. 答案:(-2,15),(2,-9)
【思路点拨】 首先要判断已知 点是否在曲线上,再根据切线的斜率 即导数值列方程解决问题.
课堂互动讲练
【解】 (1)∵f(2)=23+2-16=-6, ∴点(2,-6)在曲线上. ∵f′(x)=(x3+x-16)′=3x2+1, ∴在点(2,-6)处的切线的斜率为 k=f′(2)=3×22+1=13. ∴切线的方程为y=13(x-2)+(-6). 即y=13x-32. 4分
课堂互动讲练
高考检阅
(本题满分 10 分)已知函数 f(x)= ax-6 的图象在点 M(-1,f(-1))处的切 2 x +b 线方程为 x+2y+5=0,求函数 f(x)的解 析式.
课堂互动讲练
解:由M(-1,f(-1))在x+2y+ 5=0上得 -1+2f(-1)+5=0,即f(-1)= -2. -a-6 也即 =-2.① 4分 1+b a(x2+b)-2x(ax-6) f′(x)= ,由 2 2 (x +b) 1 f′(-1)=- 得 2
变化率与导数导数的计算

变化率与导数导数的计算一、变化率与导数的关系在数学中,变化率是指一个量相对于另一个量的变化程度,常用来衡量两个变量之间的关系。
而导数则是描述函数在其中一点上的变化率的概念。
在一个数学函数中,比如说y=f(x),x和y分别代表自变量和因变量。
那么,当x发生微小变化Δx时,对应的y值也会发生一定的变化Δy。
这时,我们可以计算出y随着x的变化而变化的速率,也就是变化率。
变化率可以通过求平均变化率和瞬时变化率来进行计算。
平均变化率指的是通过两个点之间的变化率来计算,可以用Δy/Δx来表示。
而瞬时变化率则是在其中一点上的变化率,通过取Δx趋近于0时的极限来计算,也就是导数。
二、导数的定义与计算导数是用来衡量函数在其中一点上的变化率的数值,用dy/dx来表示。
导数的定义是:f'(x) = lim(Δx→0) (f(x+Δx) - f(x))/Δx导数表示函数f(x)在x点处的瞬时变化率。
导数可以用各种方法进行计算,其中最常用的方法包括求导法则和导数的性质。
1.求导法则(1)常数法则:如果c是一个常数,那么d(c)/dx = 0。
(2)幂法则:如果f(x) = x^n,那么d(f(x))/dx = nx^(n-1)。
(3)和差法则:如果f(x)=u(x) ± v(x),那么d(f(x))/dx =d(u(x))/dx ± d(v(x))/dx。
(4)乘法法则:如果f(x) = u(x)v(x),那么d(f(x))/dx =u(x)d(v(x))/dx + v(x)d(u(x))/dx。
(5)除法法则:如果f(x) = u(x)/v(x),那么d(f(x))/dx =(v(x)d(u(x))/dx - u(x)d(v(x))/dx)/v(x)^2(6)复合函数法则:如果f(x) = g(u(x)),那么d(f(x))/dx =g'(u(x))d(u(x))/dx。
2.导数的性质(1)导数的和差性:(f(x)±g(x))'=f'(x)±g'(x)。
高考数学复习课件变化率与导数导数的运算课件理北师大版
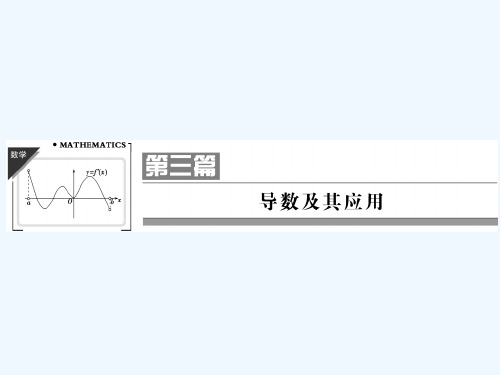
(3)gfxx′=
f′xgx-fxg′x [gx]2
(g(x)≠0).
6.复合函数的求导法则
复合函数y=f(φ(x))的导数和函数y=f(u),u=φ(x)的导数间的
关系为yx′=[f(φ(x))]′=f′(u)φ′(x).
一个区别 曲线 y=f(x)“在”点 P(x0,y0)处的切线与“过”点 P(x0,y0)的 切线的区别: 曲线 y=f(x)在点 P(x0,y0)处的切线是指 P 为切点,若切线斜率 存在时,切线斜率为 k=f′(x0),是唯一的一条切线;曲线 y= f(x)过点 P(x0,y0)的切线,是指切线经过 P 点,点 P 可以是切 点,也可以不是切点,而且这样的直线可能有多条.
值记为f′(x):f′(x)=
,则f′(x)是关于x
的函数,称f′(x)为f(x)的导函数,通常也简称为导数.
4.基本初等函数的导数公式 若f(x)=c,则f′(x)=0; 若f(x)=xα(α∈R),则f′(x)=αxα-1; 若f(x)=sin x,则f′(x)=cos x; 若f(x)=cos x,则f′(x)=-sin x; 若f(x)=ax(a>0,且a≠1),则f′(x)= axln a ;
设函数y=f(x),当自变量x从x0到x1时,函数值从f(x0)变到f(x1);
函数值y关于x的平均变化率为ΔΔyx=fxx11--xf0x0=fx0+ΔΔxx-fx0,
当x1趋于x0,即Δx趋于0时,如果平均变化率趋于一个固定的
值,则这个值为函数y=f(x)在x0点的导数,记为f′(x0)= x1l→imx0
[解答示范] (1)当a=-1时,f(x)=ln x+x+2x-1,
x∈(0,+∞).所以f′(x)=x2+xx2-2,x∈(0,+∞), (1分)
变化率与导数、导数的计算 (共31张PPT)

4. 若 f x cosx,则 f ' x sin x ;
6. 若 f x ex ,则 f ' x ex ;
1 7. 若 f x loga x, 则 f x ; x lna 1 ' 8. 若 f x ln x, 则 f x . x
3x2sin x-x3-1cos x y′ = sin2x
考点一
导数的运算 (基础送分型考点——自主练透)
[必备知识]
1.基本初等函数的导数公式 (xα)′=αxα-1,(sin x)′=cos x,(cos x)′=-sin x,(ax)′ 1 1 =a ln a,(e )′=e ,(logax)′= ,(ln x)′=x. xln a
'
(二)小题查验
判断正误
(1)sin
π π ′=cos 3 3
(× ) (× )
(√ )
1 1 (2)若(ln x)′=x,则x′=ln x
(3)(3x)′=3xln 3
基础盘查三
导数四则运算法则
(一)循纲忆知
能利用导数的四则运算法则求解导函数.
知识小结
1. 由常函数、幂函数及正、余弦函数经加、
f(x0 +Δx)- f(x0 ) k = f(x0 )= lim Δx→ 0 Δx
切线方程:
y - f(x 0 ) = f (x 0 )(x - x 0 )
作用:
确定x = x 0处切线的斜率,从而确 定切线的方程.
(二)小题查验
1.判断正误
(1)f′(x0)是函数y=f(x)在x=x0附近的平均变化率 ( × )
求下列函数的导数. (1)y=x2sin x; 1 (2)y=ln x+x; (3)y= cos x ; ex
课时变化率与导数导数的计算

第二章 函数、导数及其应用
2.导函数
当x变化时,f′(x)称为f(x)的导函数,则f′(x)= y′ =
fx+Δx-fx
liΔmx→0
Δx
.
【思考探究】 f′(x)与f′(x0)相同吗? 提示: f′(x)与f′(x0)不相同;f′(x)是一个函数,f′(x0)是常数,f′(x0)是 函数f′(x)在点x0处的函数值. 3.导数的几何意义
(2)Δy=x+4Δx2-x42=-4xΔ2xx2+x+ΔxΔ2x,
ΔΔyx=-4·x22xx++ΔΔxx2,
∴liΔmx→0 ΔΔyx=liΔmx→0 -4·x22xx++ΔΔxx2=-x83.
工具
第二章 函数、导数及其应用
求函数的导数要准确地把函数分割为基本初等函数的和、差、积、 商及其复合运算,再利用运算法则求导数.在求导过程中,要仔细分析 函数解析式的结构特征,紧扣法则,联系基本初等函数求导公式,对于 不具备求导法则结构形式的要适当变形.
3.函数y=xcos x-sin x的导数为( )
A.xsin x
B.-xsin x
C.xcos x
D.-xcos x
解析: y′=(xcos x)′-(sin x)′
=x′cos x+x(cos x)′-cos x
=cos x-xsin x-cos x=-xsin x.
答案: B
工具
第二章 函数、导数及其应用
.
工具
第二章 函数、导数及其应用
1.(2010·全国新课标卷)曲线y=x3-2x+1在点(1,0)处的切线方程为
()
A.y=x-1
B.y=-x+1
C.y=2x-2
D.y=-2x+2
解析: ∵点(1,0)在曲线y=x3-2x+1上,且y′=3x2-2,
高中数学变化率与导数 导数的计算讲义

3.1-3.2 变化率与导数 导数的计算一、导数的概念1、平均变化率:函数y =f(x)在x 0处的变化量△y =f(x 0+△x)-f(x 0)与自变量的变化量△x =(x 0+△x)-x 0的比:xy ∆∆=x x f x x f ∆-∆+)()(00。
2、函数在x =x 0处导数的定义: 一般地,设函数y =f(x)在x 0附近有定义,当自变量在x =x 0的附近改变量为△x 时,函数值的改变量为△y =f(x 0+△x)-f(x 0),如果△x 趋近于0时,平均变化率x y ∆∆=x x f x x f ∆-∆+)()(00趋近于一个常数m ,即0lim →∆x xy∆∆=lim →∆x xx f x x f ∆-∆+)()(00=m ,这个常数m 叫做函数f(x)在点x 0处的瞬时变化率。
函数..f(x)....在点..x .0.处的瞬时变化率又称为函数............y .=.f(x)....在.x .=.x .0.处的导数....。
记作: f ˊ(x 0)或y ˊ|0x x =,即: f ˊ(x 0) =lim →∆x xx f x x f ∆-∆+)()(00=0lim x x →∆1212)()(x x x f x f --(1)、函数y =f(x)在x 0处有导数(即导数存在),则说函数f(x)在x 0处可导。
(2)、函数y =f(x)在开区间(a ,b )内每一点x 都是可导的,则说函数f(x)在区间(a ,b )可导。
3、导函数的定义:xy∆∆表示函数的平均改变量,它是Δx 的函数,而f ˊ(x 0)表示一个确定的数值,即f ˊ(x 0)=xyx ∆∆→∆lim 0。
当x 在区间(a ,b )内变化时,f ˊ(x)便是x 的一个函数,我们称它为f(x)在(a ,b )的导函数(简称导数)。
y =f(x)导函数有时记作y ˊ,即f ˊ(x) =y ˊ=lim →∆x xx f x x f ∆-∆+)()(。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当t=1时,v=-6×1=-6.
返回
[冲关锦囊]
根据导数的定义,求函数y=f(x)在x=x0处导数的方法是 (1)求函数值的增量Δy=f(x0+Δx)-f(x0); (2)求平均变化率ΔΔxy=fx0+ΔΔxx-fx0;
(3)计算导数f′(x0)= lim x0
Δy Δx.
返回
[精析考题]
[例2] (2019·江西高考)若f(x)=x2-2x-4ln x,则f ′(x)>0
(1)曲线y=f(x)在点P(x0,y0)处的切线是指P为切点,切线 斜率为k=f′(x0)的切线,是唯一的一条切线.
(2)曲线y=f(x)过点P(x0,y0)的切线,是指切线经过P 点.点P可以是切点,也可以不是切点,而且这样的 直线可能有多条.
返回
返回
[精析考题] [例1] 用定义法求下列函数的导数. (1)y=x2; (2)y=x42.
1.函数求导的原则 对于函数求导,一般要遵循先化简,再求导的基本原则, 求导时,不但要重视求导法则的应用,而且要特别注意 求导法则对求导的制约作用,在实施化简时,首先必须 注意变换的等价性,避免不必要的运算失误.
返回
2.曲线y=f(x)“在点P(x0,y0)处的切线”与“过点P(x0,y0) 的切线”的区别与联系
2020 第二章第十一节变化率与导数、导数的计算
返回
返回
返回
返回
(2)几何意义:
函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y=f(x)上 点 (x0,f(x0处)) 的 切线的斜率.(瞬时速度就是位移函数
s(t)对时间t的导数)相应地,切线方程为 y-y0=f′(x0)(x-x0) .
返回
原函数 f(x)=logax f(x)=lnx
导函数 f′(x)= 1
xlna f′(x)= 1
x
返回
三、导数的运算法则 1.[f(x)±g(x)]′= f′(x)±g′(x) ; 2.[f(x)·g(x)]′= f′(x)g(x)+f(x)g′(x) ;
3.[gfxx]′=
f′xgx-fxg′x [gx]2
返回
解析:∵y′=2x,∴在点(ak,a2k)处的切线方程为 y-a2k=2ak(x-ak), 又该切线与x轴的交点为(ak+1,0), 所以ak+1=12ak,
返回
即数列{ak}是等比数列,首项a1=16,其公比q=12, ∴a3=4,a5=1, ∴a1+a3+a5=21.
答案: 21
返回
返回
2.函数f(x)的导函数
称函数f′(x)=
fx+Δx-fx为f(x)的导函数.
lim
Δx→0
Δx
返回
二、基本初等函数的导数公式
原函数 f(x)=c(c为常数) f(x)=xn(n∈Q*)
f(x)=sinx f(x)=cosx f(x)=ax
f(x)=ex
导函数 f′(x)= 0 f′(x)= nxn-1 f′(x)= cosx f′(x)= -sinx f′(x)= axlna f′(x)= ex
解:(1)∵s=8-3t2, ∴Δs=8-3(1+Δt)2-(8-3×12)=-6Δt-3(Δt)2, v =ΔΔst=-6-3Δt.
返回
(2)定义法:质点在t=1时的瞬时速度
v= lim x0
ΔΔst=
lim
x0
(-6-3Δt)=-6.
导数公式法:质点在t时刻的瞬时速度
v=s′(t)=(8-3t2)′=-6t.
返回
[自主解答] (1)因为ΔΔxy=fx+ΔΔxx-fx
=x+ΔΔxx2-x2
=x2+2x·ΔxΔ+x Δx2-x2=2x+Δx,
所以y′= lim x0
ΔΔy=
lim
x0
(2x+Δx)=2x.
返回
(2)Δy=x+4Δx2-x42=-4xΔ2xx2+x+ΔxΔx2 ,
ΔΔxy=-4·x22xx+ +ΔΔxx2,
A.1
B.2
C.e
D.1e
解析:由题意知y′=ex,故所求切线斜率k=ex|x=0=
e0=1
答案:A
返回
2.(教材习题改编)某汽车的路程函数是 s(t)=2t3-12gt2(g=10
m/s2),则当 t=2 s 时,汽车的加速度是
()
A.14 m/s2
B.4 m/s2
C.10 m/s2
D.-4 m/s2
∴ lim x0
ΔΔxy=
lim
x0
-4·x22xx+ +ΔΔxx2=-x83.
返回
[巧练模拟]——————(课堂突破保分题,分分必保!) 1.一质点运动的方程为s=8-3t2.
(1)求质点在[1,1+Δt]这段时间内的平均速度; (2)求质点在t=1时的瞬时速度(用定义及导数公式两 种方法).
返回
() 返回
4.(教材习题改编)已知函数f(x)=13-8x+ 2x2,且f′(x0) =4,则x0的值为________. 解析:∵f′(x)=-8+2 2x,∴-8+2 2x0=4. ∴x0=3 2. 答案:3 2
返回
5.函数y=x2(x>0)的图象在点(ak,a)处的切线与x轴 的交点的横坐标为ak+1,其中k∈N*.若a1=16,则 a1+a3+a5的值是________.
(g(x)≠0).
返回
[理]四、复合函数的导数 设u=v(x)在点x处可导,y=f(u)在点u处可导,
则复合函数f[v(x)]在点x处可导,且f′(x)= f′(u)·v′(x) ,即y′x= y′u·u′x .
返回
返回
1.(2011·江西高考)曲线y=ex在点A(0,1)处的切线斜率为( )
返回
解析:由v(t)=s′(t)=6t2-gt,a(t)=v′(t)=12t-g,得t=2 时,a(2)=v′(2)=12×2-10=14(m/s2). 答案: A
返回
3.函数y=xcos x-sin x的导数为
A.xsin x
B.-xsin x
C.xcos x
D.-xcos x
解析: y′=(xcos x)′-(sin x)′ =x′cos x+x(cos x)′-cos x =cos x-xsin x-cos x=-xsin x. 答案: B
的解集为
()
A.(0,+∞)
B.(-1,0)∪(2,+∞)
C.(2,+∞)
D.(-1,0)
返回
[自主解答] f′(x)=2x-2-4x=2x-2xx+1>0. ∵x>0,∴x>2.
[答案] C
返回
[巧练模拟]———————(课堂突破保分题,分分必保!)
