浸润线的计算方法
上游式尾矿堆积坝浸润线计算探讨
上游式尾矿堆积坝浸润线计算探讨一、前言根据《选矿厂尾矿设施设计规范》（ZBJ1-90)(下简称《尾矿规范》）规定,尾矿坝设计必须进行渗流计算。
渗流计算的目的是提供各种工况的浸润线、逸出渗透坡降和渗透流量，以供分析坝坡静力(动力)抗滑稳定性和渗透稳定性，确定排渗设施的结构断面。
对渗流计算的方法，《尾矿规范》提出:1、2级山谷型尾矿坝应按三维计算或由模拟试验确定；3级以下尾矿坝应按附录三进行；渗流计算中要考虑尾矿滩面放矿水流的影响。
首先应指出，尾矿堆积类型除上游式外还有中线法和下游式(包括一次筑坝法）,规范提出的浸润线计算方法仅针对上游式是因为上游式尾矿库占我国尾矿库总数的绝大多数，本应是规范的重点，同时中线式尾矿库因下游坝体是旋流分级的粗尾砂，颗粒较均匀，渗透系数大,坝基设置可靠的排渗层,浸润线基本上在排渗层内。
而下游式或一次筑坝的尾矿库,尾矿不堆坝，堆存尾矿的浸润线对基本坝体的安全已不重要。
其次，尾矿库的类型除山谷型外，还有傍山型和平地型，它们与山谷型的区别就是堆积坝体浸润线面的前沿宽度与下游逸出宽度基本一致，不存在山谷型尾矿库平面上渗流集中的三维问题。
《尾矿规范》通过化引滩长和化引库水位仅解决滩面放矿水流的问题。
既然着重提出山谷型尾矿库就必然有三维计算问题,关于三维计算是否必须进行,未要求论证。
第三，上游式尾矿库以中、低浓度放矿时,滩面（包括水下）尾矿沿程自然分级，按平均粒经大小，渐变形成尾中砂、尾细砂、尾粉砂、尾粉土、尾粉质粘土和尾粘土.因其物理力学指标有明显变化，可以进行概化分区。
上游式尾矿库尾矿排放按规定在堆积坝轴线长度上定间距轮流进行均匀放矿，实践早已证明,均匀是相对的,即使在放矿口间距范围相对于放矿口仍是集中放矿，矿浆进入滩面，迅速成为毫米级厚度薄层流体,由于放矿顺序、放矿时间、每次堆积高度、滩面水流的游弋，都有一定的随意性，尾矿各土层必然会普遍形成毫米级年轮状夹层和局部较厚层的粗、细透镜体。
水工专业浸润线计算的理论分析
水工专业浸润线计算的理论分析作者：姜连超来源：《今日湖北·下旬刊》2015年第04期摘要通过已知水库以及土石坝资料，根据坝内各部分渗流状况相同的特点，将坝体分为若干段，应用达西定理解决土坝渗流问题，用简易的Excel计算，得出该土石坝的浸润线方程。
本文为实践教学提供数据和理论支撑，保证了水工教学的实用性。
关键词达西定理浸润线实用性土石坝的渗流计算主要确定坝体的浸润线的位置，为坝体的稳定分析和布置观测设备提供依据；同时确定坝体与坝基的渗透流量，以估算水库的渗漏损失，而且还要确定坝体和坝基渗流区的渗透坡降，检查产生渗透变形的可能性，以便取适合的控制措施。
一、斜墙土石坝浸润线计算（一）已知材料水库水位（1）正常蓄水位 475.50m（2）设计洪水位（P=1%）480.00m（3）校核洪水位（P=0.1%）. 481.00m（4）汛期运行水位 472.00m（5）极限死水位 467.00m2、挡水坝下游水位（1）设计洪水位 458.70m（2）校核洪水位 460.30m（3）正常尾水位 452.00m（4）最高尾水位 450.00m上游坝坡坡率为：1：2.5下游坝坡坡率为：1：2.25（二）计算示意图（图1）（三）基本公式根据达西定理，假定任一铅直过水断面内各点渗透坡降均相等，可推出公式：式中S为浸润线的水平投影长度，m；H1为上游水深，m；为下游水深，m；H1为渗透系数，其中k1=0.3，k2=0.01；m1为大坝上游坡率，m1=2.5；m2为棱体排水内侧坡率，m2=1；h为溢出点高度，€%a为斜墙与坝底夹角，。
其中s=d-m1H1+e；e=（0.5～0.6）h；€%d=。
（四）浸润线计算使用CAD软件，根据已知条件绘制大坝剖面简图，式中，€%]值，€%a值，d值都由图上直接量出，单宽流量q值由Excel表格试算得出。
带入浸润线方程y2=h2-x中，得出浸润线方程，最终计算表格如表1：通过以上计算，即可求出该土石坝在正常水位，设计水位以及校核水位下的浸润线方程，从而进行接下来的渗流稳定分析。
在河水位骤降条件下某滑坡浸润线计算与稳定性研究
第４ ９卷 第 ３期 ２ ０ １ ３ 年 ３月
甘 肃 水 利 水 电 技 术
ＧＡ ＮＳ Ｕ ＷＡ Ｔ Ｅ Ｒ Ｒ Ｅ ｓ ＯＵ Ｒａ Ａ ＮＤ ＨＹＤ ＲＯＰ ＯＷＥ Ｒ Ｔ Ｅ ｃＨ ＮＯＬ ＯＧＹ
Ｖｏ １ ． ４ ９． Ｎｏ ． ３ Ｍａ ｒ ． ． ２ ０ １ ３
组 砂岩 中 ，富水 性受 构造 和地 貌等 因素 控制 。研 究 区地下 水赋 存 于极不 均匀 黏性 土夹 碎块 石 土 中。滑 坡 区地 下水 主要 接受 大气 降水 补 给 。河 流 为最低 侵 蚀 基 准面 ， 大气 降水 入渗第 四系地层 ， 经 渗 流后 主要 以泉 的形式 排 泄至河 流 。简分 析试 验得 出滑 坡堆 积 体 地 下水 和地表 河水 对混 凝土 无腐 蚀 。
性 的主要 因素 ， 揭 示了该 滑坡 的形成机制 。 提 出了在 河水位 变化条件 下该滑坡 地下水浸润线与滑坡稳定性计算模型 与计算方法 ， 得 出 了在 河水位骤 降条件 下该 滑坡 地下水浸润 线曲线 图， 计算 出了该 滑坡在 不 同工况下的稳定性 系数 及 剩余下滑力。河流水位升降影响坡体地下水浸润线 ， 改 变岩 土体非饱和 区， 影 响岩 土体软弱层抗 剪强度和滑坡稳
水 和基 岩裂 隙水 两类 。松 散岩 类孔 隙水 主要 赋存 于
第 四系粉质 黏 土夹碎 块石 土 中 。 孔 隙度 较大 ． 透水 性 较 好 。基岩 风化 裂 隙水 主要赋 存 于 白垩 系下 统苍 溪
内。 仪 陇一 巴 中一 平 昌莲 花状 构 造带 之 鼻状 背斜 南 东
翼 近核 部 。该滑 坡处 于 阶梯状 宽 台一 峡 谷低 山 区 ， 出 露 地层 主要 为第 四系残 坡积 土 （ Ｑ 柑 ） 和 白垩 系下 统
浸润线名词解释
浸润线名词解释
浸润线是渗透水流表面与土坝横断面的交线。
其以下土体处于饱和状态，颗粒重量为有效重量，同时受渗流水的渗透力作用，故坝体内浸润线位置的高低及形状对坝体的应力、土料的抗剪强度、坝坡稳定及土料的渗透稳定性影响较大。
其位置的确定是土坝渗流分析及稳定分析的重要内容，如何有效地降低浸润线的位置也是实际工程中的研究课题。
浸润线是水从土坝（或土堤）迎水面，经过坝体向下游渗透所形成的自由水面和坝体横剖面的相交线；土体中渗流水的自由表面的位置，在横断面上为一条曲线。
渗流在坝体内的自由面称为浸润面，坝体横剖面与浸润面的交线称为浸润线。
压渗流中重力水的自由表面线。
它属于平面问题。
土石坝浸润线计算
坝体渗流量 总渗流量
0 5 0.25 21 0 4.621595 37 8.4 2 2 4.621595 115.5399 115.5399
cm/s m cm/s m m m m m
X Y
-2.31 -1.63 0.394 3.775 10.82 14.59 22.03 30.82 40.96 52.46 0 2.5 5 7.5 10 12.5 15 17.5 20 22.5
K0： T： K： H1： H2： h0： L： △L1： m1： m2： h'0： qd： q：
地基渗透系数 透水地基厚度 坝体渗透系数 坝前水深 坝后水深
褥垫始点垂线上至浸润线高（考虑渗透地基） 褥垫始点至游水位与坝坡交点垂线的水平距离
[m1/(2m1+1)]*H1 上游坝坡比1∶m1 下游坝坡比1∶m2
注：坐标原点为褥垫起始点(坝内 )(x轴向上游为正，y轴向上为正) 坝前水位至坝底距离 坝后水位至坝底距离 h0＝q/(K+K0/0.44) 褥垫起始点：褥垫在坝内最靠近上游点 复核： x=0时，y=1.7144=h0 L‘=L+△L1= 45.4 m 等于当y=H1时对应的X值
m h‘0＝[(△L1+L)2+H12]0.5-(△L1+L) cm2/s qd＝K*h0'*100 cm2/s qj＝K0*T*100*(H1-H2)/(L+m1*H1+0.88*T)
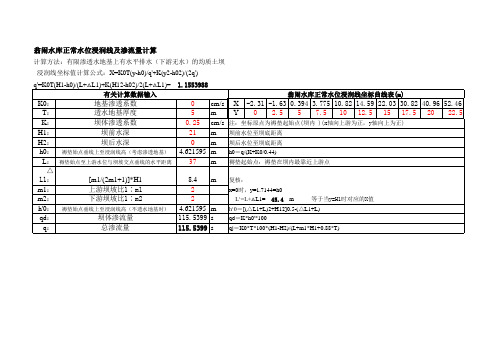
翁闹水库正常水位浸润线及渗流量计算
计算方法：有限渗透水地基上有水平排水（下游无水）的均质土坝 浸润线坐标值计算公式：X=K0T(y-h0)/q'+K(y2-h02)/(2q') q'=K0T(H1-h0)/(L+△L1)+K(H12-h02)/2(L+△L1)= 有关计算数据输入 1.1553988 翁闹水库正常水位浸润线坐标曲线表( 翁闹水库正常水位浸润线坐标曲线表(m)
渗流分析 浸润线
------------------------------------------------------------------- 计算项目: 渗流问题公式法 1-------------------------------------------------------------------[ 计算条件 ]土堤顶部宽度b = 4.000(m)土堤顶部高度h = 10.000(m)上游坡坡率1:m1 = 2.000下游坡坡率1:m2 = 2.000堤身渗透系数k = 0.240(m/d)上游水位h1 = 9.000(m)下游水位h2 = 0.000(m)心墙上游堤顶宽度 = 0.500(m)心墙顶部宽度 = 3.000(m)心墙底部宽度 = 7.000(m)心墙渗透系数 = 0.005(m/d)不透水地基[ 中间计算结果 ]L = 261.000(m)腖= 3.600(m)浸润线计算公式原点= 43.234(m)浸润线起点x坐标 = 18.000(m)浸润线终点x坐标 = 43.234(m)注：中间计算结果的含义参见规范E.2.1条。
[ 最终计算结果 ]下游出逸点高度h0 = 0.383(m)单位宽度渗流量q = 0.037(m3/d.m)浸润线计算结果:X(m) Y(m)心墙上游土堤段浸润线:18.456 8.93118.912 8.92319.368 8.91519.824 8.90720.280 8.899心墙下游土堤段浸润线:25.021 2.39328.664 2.14832.306 1.87035.949 1.54239.591 1.12443.234 0.383比降计算结果:下游出溢点A的比降: 0.447 下游坡脚B的比降: 0.500。
库水作用下浸润线的确定
公式的修正 (消除用一维代替二维引起的误差)
当水平距离大于一倍 下降高度时，坡角对 浸润线的影响很小 当水平距离大于一倍 下降高度时，一维公 式的计算结果大于有 限元的结果，并且两 者的曲线大致相互平 行。
30 浸润线高度(m) 25 20 15 10 5 0 0 25 50 75 100 125 150 175 200 225 250 275 计算公式 有限元(坡角为56.3°) 有限元(坡角为28.6°) 有限元(坡角为90°) 有限元(坡角为45°)
h x ,t
水平距离(m)
h0,t + ηV0 t (−0.1091λ4 + 0.7501λ3 − 1.9283λ2 + 2.2319λ ) = (λ ≥ 2) h0,t + ηV0 t
(0 ≤ λ < 2)
修正系数
9 . 2989 β η = 0 . 0066 β + 0 . 8218 ( β < 0 . 088 ) ( β ≥ 0 . 088 )
1 修正系数η 0.8 η= 0.0066β+ 0.8218 0.6 η= 9.2989β 0.4 0.2
β =
µv
k
0 0 1 2 3 4 5 6 7 下降速度指标β 8 9 10 11
7
试验验证
1.50 1.35 水头高度(m) 1.20 1.05 0.90 0.75 0.60 4 5 6 7 8 测压管编号 9 10 11 12 t=0min t=10min t=20min t=5min t=15min
8
试验验证
结论： 结论： 计算公式与试验值吻合，表明计算公式是正确的。 9
3、 程序编制及算例分析 、
堤防渗流计算(有详细的计算过程和程序)
q/k = (7.8^2-2.8^2)/(2×(65.943-5×2.8)) = 0.5102 m
q/k = 0.5011 = 0.5011 m
平均q/k = (0.5102+0.5011)/2 = 0.5057 m
平均渗流量qD = 0.5057×0.00001 = 5.06E-06 m3/s/m
透水地基底高程▽底 = 7 = 7 m 不透水地基顶高程
上游水位▽1 = 24.8 = 24.8 m
下游水位▽2 = 18 = 18 m
棱体顶高程 = 19 = 19 m 到下游堤脚
棱体临水坡坡率m3 = 2 = 2 / 1:m3
渗透系数k = 1.00E-05 = 1.00E-05 m/s
浸润线方程 y=SQRT(6.4516+1.4144x)
下游坝坡最大渗出坡降J = 1/3 = 0.333 / 1/m2
附录E.2.2 不透水堤基 均质土堤 下游设褥垫式排水
项目 计算式 数值 单位 备注
上游坡度m1 = 3 = 3 / 1:m1
下游坡度m2 = 5 = 5 / 1:m2
4.总渗流量 = 0.00000506+0.0000308 = 3.59E-05 m3/s/m
5.浸润线计算
h01 = 1 = 1 m
h02 = 10 = 10 m
步长 = 0.001 = 0.001 m
精度 = 0.001 = 0.001 m
试算得到h0 = 2.0361 = 1.894 m 程序计算
q/k = (7.8^2+1.398^2)/(2×51.943) = 0.604 m
浸润线计算-110
h0： 褥垫始点垂线上至浸润线高（考虑渗透地基） 1.714419 m L： 褥垫始点至上游水位与坝坡交点垂线的水平距离 52.9 m △L1： [m1/(2m1+1)]*H1 9.642857 m m1： m2： h'0： qd： q： 上游坝坡比1∶m1 下游坝坡比1∶m2
K0： T： K： H1： H2：
地基渗透系数 透水地基厚度 坝体渗透系数 坝前水深 坝后水深
0.00121 5 0.00164 22.5 0
c 15.35 22.18 30.49 39.98 50.67 62.54 m Y 0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 cm/s 注：坐标原点为褥垫起始点(坝内 )(x轴向上游为正，y轴向上为正) m 坝前水位至坝底距离 m
褥垫始点垂线上至浸润线高（不透水地基时）
3 2.8 3.924119 m
坝体渗流量 总渗流量
0.643556 cm2/s K*h0'*100 0.75263 cm2/s qd+K0*T*100*(H1-H2)/(L+m1*H1+0.88*T)
湖朗水库正常水位浸润线及渗流量计算
计算方法：有限渗透水地基上有水平排水（下游无水）的均质土坝 浸润线坐标值计算公式：X=K0T(y-h0)/q'+K(y2-h02)/(2q') q'=K0T(H1-h0)/(L+△L1)+K(H12-h02)/2(L+△L1)= 0.0086096 有关计算数据输入 湖朗水库正常水位浸润线坐标曲线表(m)
渗流计算内容
三、渗流计算内容（一）不透水地基均质坝渗流分析(1)下游有水而无排水或设贴坡排水情况(2)下游设有褥垫排水的情况或下游设有棱体排水且下游无水的情况(2)下游有堆石棱体排水且下游有水的情况（二）不透水地基心墙坝渗流分析计算时忽略上游坝壳段的水头损失，并将心墙简化为等厚的矩形断面，下游坝壳段与均质坝同样处理。
心墙简化为矩形，心墙段的单宽渗流量为：(1)假定下游坝壳逸出点位于下游水位与堆石内坡的交点A ，则坝壳内单宽流量表达式为：(2)由q= q1=q2，联立方程（1）和（2），可求出q 和h 。
下游坝壳的浸润线方程为：（三）有限深度透水地基土石坝渗流分析计算有限深透水地基上土石坝的渗流时，为简化计算，坝体内渗流仍可用上述不透水地基上土石坝的渗流计算方法确定渗流量及浸润线，坝基渗流则按有压渗流计算。
坝体渗流量与坝基渗流量之和即为总渗流量。
1、均质坝假设坝体的单宽流量为q1，坝基的渗透系数为kT ，透水地基深度为T ，单宽流量为q ′，上下游水头分别为H1和t 。
由达西定理可得地基内单宽流量q ′：将上式从上游面（x=0，y=H1）到下游面（x=L ，y=t ）积分得：)2/()(2211δh H k q c -=Lt h k q 2/222）（-=)2/(22q y h k x ）（-=LL可表示为L= L0+0.88T，式中0.88T为考虑进出口流线弯曲的影响的修正系数。
则通过坝体与坝基的总单宽流量为：2、心墙坝①地基上有混凝土防渗墙的心墙坝设心墙、砼防渗墙、下游坝壳、透水地基的渗透系数分别为kc、kD、k、kT 。
通过防渗心墙和地基砼防渗墙的渗流量为：(1)通过防渗心墙后的坝壳和地基防渗墙后的地基的渗流量为:(2)由q=q1=q2，联立求解式(1)和(2)即可得q和h 。
②地基上有截水槽的心墙坝，截水墙与心墙材料相同。
通过防渗心墙和地基截水墙的渗流量为：通过防渗心墙后的坝壳和地基截水墙后的地基的渗流量与地基中有混凝土防渗墙的心墙坝相同。
心墙坝浸润线简化计算方法
心墙坝浸润线简化计算方法作者：肖钧升沈振中于洋来源：《南水北调与水利科技》2016年第01期摘要：通过理论分析和数值计算，在考虑坝体与防渗墙的相对渗透系数关系的基础上，提出了估算心墙坝坝体浸润线的一种简化计算方法，给出了浸润线位置的拟合公式。
以白鸭山水库大坝为例，将该简化方法与有限元法的计算结果进行对比，表明该简化方法合理、可行。
这一简化计算方法可大大减少中小型水库大坝在进行除险加固方案比选时的计算工作量。
关键词：土石坝；渗流特性；除险加固；相对渗透系数；心墙坝；坝体浸润线中图分类号：TV223 文献标志码：A 文章编号：16721683（2016）01011405Simplified method for core dam saturation line calculationXIAO Junsheng1，2，SHEN Zhenzhong1，2，YU Yang2（1.State Key Laboratory of HydrologyWater Resources and Hydraulic Engineering，Hohai University，Nanjing 210098，China；2.The College of Water Conservancy and Hydropower，Hohai University，Nanjing 210098，China）Abstract：The saturation line position is one of the main bases for flow characteristics evaluation of earth rock dams，which must be calculated before the comparing and selecting the appropriate antiseepage reinforcement program of dangerous earthrock dam.Considering the relationship between the relative permeability coefficient of the dam and the cutoff wall，a simplified calculation method was proposed to estimate the saturation line of the core dam by theoretical analysis and numerical calculation.A fitting formulation was developed to calculate the position of the saturation lines.The simplified calculation methods proved to be reasonable when comparing with the results of finite element methods based on the dam of Baiyashan Reservoir.The simplified calculation method can significantly reduce the computational workload when comparing and selecting the reinforcement program of small and mediumsized reservoir dams.Key words：earth rock dam；flow characteristics；danger control and reinforcement；relative permeability coefficient；core dam；dam saturation line目前中国已建成水库大坝9万余座，其中土石坝[1]约占93%。
渗流计算案例
渗流计算
一、计算情况选择
渗流计算应考虑下列水位组合情况：
（1）上游正常高水位与下游相应的最低水位。
（2）上游设计洪水位与下游相应的水位。
（3）上游水位为3
1坝高处。
二、渗流分析的方法
采用水力学法进行土石坝渗流计算，将坝内渗流分为若干段，应用达西定律和杜平假设，建立各段的运动方程式，然后根据水流的连续性求解渗透流速，渗透流量和浸润线等。
三、计算断面及公式
本设计仅对河槽处最大断面进行渗流计算。
计算公式采用表4-1-4中的不透水地基情况。
四、单宽流量计算
表4-2-7 单宽流量计算表
①正常蓄水位情况下，浸润线方程：x y 92.735.757-= x ∈（0，95，63） 列表(4-2-8)如下，绘于图4-2-3。
表4-2-8 正常蓄水位情况下浸润线表
图4-2-3正常蓄水位情况下渗流及稳定计算图
②设计水位情况情况，浸润线方程为52.6333.10+=x y x ∈（0，84，58） 列表(4-2-9)如下，绘于图4-2-4。
表4-2-9 设计洪水位情况浸润线表
图4-2-4设计洪水位情况下渗流及稳定计算图
③上游水位为1/3坝高处浸润线方程：x
115-
=x∈（0，142,97）
.
13
y81
.0
列表(4-2-10)，绘于图4-2-5。
1坝高处浸润线表
表4-2-10 上游水位为
3
图4-2-5上游水位为1/3坝高处情况下渗流及稳定计算图。
土石坝边坡稳定分析与计算方法
土石坝边坡稳定分析与计算方法1 稳定性理论分析土坝的稳定性破坏有滑动、液化及塑性流动三种状态。
〔1〕坝坡的滑动是由于坝体的边坡太陡，坝体填土的抗剪强度太小，致使坍滑面以外的土体滑动力矩超过抗滑力矩，因此发生坍滑或由于坝基土的抗剪强度缺乏，因此坝体坝基一同发生滑动。
〔2〕坝体的液化是发生在用细砂或均匀的不够严密的砂料作成的坝体中，或由这种砂料形成的坝基中。
液化的原因是由于饱和的松砂受振动或剪切而发生体积收缩，这时砂土孔隙中的水分不能立即排出，局部或全部有效应力即转变为孔隙压力，砂土的抗剪强度减少或变为零，砂粒业就随着水的流动向四周流散了。
〔3〕土坝的塑性流动是由于坝体或坝基内的剪应力超过了土料实际具有的抗剪强度，变形超过了弹性限值，不能承受荷重，使坝坡或者坝脚地基土被压出或隆起，因此使坝体的坝基发生裂缝、沉陷等情况。
软粘性土的坝或坝基，假设设计不良，就容易产生这种破坏。
进展坝坡稳定计算时，应该杜绝以上三种破坏稳定的现象，尤其前两种，必须加以计算以及研究。
2 PC1500程序编制根据及计算方法2.1 编制根据及使用情况综述PC1500程序在计算方法方面采用了瑞典条分法和考虑土条程度侧向力的简化毕肖甫法。
从对土料物理力学指标的不同选用又可分为总应力法，有效应力法和简化有效应力法。
程序规定，计算公式中无孔隙水压力为总应力法；计入孔隙水压力为有效应力法；令孔隙水压力一项为零而将孔隙水压力包含在土体重量的计算之中，称为简化有效力法[1]。
分别考虑了稳定渗流期，施工期，水位降落期三种情况。
程序按照“水工建筑物抗震设计标准〞，“碾压土石坝设计标准〞编制。
2.2 计算方法所谓网格法，要计算假设干滑弧深度，对每一滑弧度计算过程如下：以给定滑弧圆心为中心，以大步长向四周由49个点，逐一计算，找出平安系数最小的点，以该点为中心，以小步长向四周布49个点，计算后就找出相应该滑弧深度的最小平安系数。
混合法是先用网格法。
将大步长布下的49个点算完后，找出平安系数最小的点，转入优选法计算。
测压管法监测土坝浸润线.
职业教育水利水电建筑工程专业《水利工程管理技术》测压管法监测土坝浸润线《水利工程管理技术》项目组2015年4月测压管法监测土坝浸润线土坝建成蓄水后，由于水头的作用，坝体内必然产生渗流现象。
水在坝体内从上游渗向下游，形成一个逐渐降落的渗流水面，称为浸润面（属无压渗流）。
浸润面在土石坝横截面上只显示为一条曲线，通常称为浸润线。
土坝浸润面的高低和变化，与土坝的安全稳定有密切关系。
土坝设计中先需根据土石坝断面尺寸、上下游水位以及土料的物理力学指标，计算确定浸润线的位置，然后进行坝坡稳定分析计算。
由于设计采用各项指标与实际情况不可能完全符合设计要求等，因此，土坝设计运用时的浸润线位置往往与设计计算的位置有所不同。
如果实际形成的浸润线比设计计算的浸润线高，就降低了坝坡的稳定性，甚至可能造成滑坡失稳的事故。
为此，观测掌握坝体浸润线的位置和变化，以判断土石坝在运行期间的渗流是否正常和坝坡是否安全稳定，是监视土石坝安全运用的重要手段，一般大中型土坝水库都必须予以重视，认真进行。
为掌握土坝在运行期间的渗透情况，应在坝体埋设测压管，进行浸润线观测。
测压管法是在坝体选择有代表性的横断面，埋设适当数量的测压管，通过测量测压管中的水位来获得浸润线位置的一种方法。
一、测压管布置土坝浸润线观测的测点应根据水库的重要性和规模大小、土坝类型、断面型式、坝基地质情况以及防渗、排水结构等进行布置。
一般选择有代表性、能反映主要渗流情况以及预计有可能出现异常渗流的横断面，作为浸润线观测断面。
例如选择最大坝高、老河床、合龙段以及地质情况复杂的横断面。
在设计时进行浸润线计算的断面，最好也作为观测断面，以便与设计进行比较。
横断面间距一般为100～200m，如果坝体较长、断面情况大体相同，可以适当增大间距。
对于一般大型和重要的中型水库，浸润线观测断面不少于3个，一般中型水库应不少于2个。
每个横断面内测点的数量和位置，以能使观测成果如实地反映出断面内浸润线的几何形状及其变化，并能描绘出坝体各组成部位如防渗排水体、反滤层等处的渗流状况。
第九章 渗流
裘皮 幼公 式
h0
无压均匀流场
u v kJ ki
整个流场各点 流速相等
3、流量
Q v0 ki0
矩形河槽
Q bh0ki
1
q kh0i
2
二、地下水渐变流
1、断面流速分布？ 任一断面流速分布 为矩形；不同断 面平均流速不等
非均匀渗流场
2、渐变渗流的基本微分方程
h z z dz h dh hw hw H dH H dH ids dh dH dh 所以 J i ds ds
k 2 2 s h1 h2 2q
dh Q q ds k kh
h1 h2 q s k 2
k 2 2 q h1 h2 2s
2
2
逆坡略
第四节 集水廊道和井
一、集水廊道
井和集水廊道，是吸取地下水源的建筑物，应用 甚广。从这些建筑物中抽水，会使附近天然地下 水位降落，也起着排水的作用。
正坡为a型和b型， 平坡为b0型， 负坡为 b 型。
a型为壅水曲线，上游以N—N线为渐近线， 下游趋于水平线。b型为降水曲线，上游以 N—N线为渐近线，下游从理论上与槽底正 交，由下游具体边界条件确定。
b0和 b 型为降水曲线，上游趋于水平线， 下游从理论上与槽底正交，由下游具体边 界条件确定。
二、地下水的形态
汽态水：以蒸汽状态存在于土壤孔隙中的水 附着水：以极薄的分子层吸附在土颗粒周围 薄膜水：以厚度不超过分子作用半径的膜层包围着土颗粒 毛细水：保持在土壤毛细管中的水 重力水：重力作用下沿土壤孔隙运动的水，渗流研究的主 要对象。
三、渗透性质与岩土分类
理正岩土使用手册-渗流分析
选择渗流计算所采用的方法（有限元分析法与公式法）：
图2.2-2 计算项目选择
2.2.3 增加计算项目
点击【工程操作】菜单中的【增加项目】菜单或“增”按钮来新增一个计算项目。
I:/…/06渗流分析（一二三）.htm
2/10
2010-5-26
06渗流分析（一二三） 图2.2-3 增加计算项目界面
10/10
2010-5-26
06渗流分析（四）
第四章 有限元法编制原理
4.1 编制依据
⑴《渗流计算原理及应用》顾慰慈 编著 中国建材工业出版社 2000.08； ⑵《土工原理与计算》（第二版）河海大学 钱家欢 殷宗泽 主编 中国水电出版社 1996.05； ⑶《渗流数值计算与程序应用》毛昶熙 段祥宝 李祖贻 主编 河海大学出版社 1999.01； ⑷《有限单元法原理与应用》（第二版）朱伯芳 编著 中国水利水电出版社1998.10。
H1 —— 上游水位（m）； H2 —— 下游水位（m）； h0 —— 下游出逸点高度（m）； m1 —— 上游坡坡率； m2 —— 下游坡坡率；
b —— 土堤顶部宽度（m）； H —— 土堤高度（m）； L —— （m）； ΔL —— （m）； L1 —— （m）。
7/10
2010-5-26
06渗流分析（一二三）
3.3.3 图形查询辅助工具
1． 图 形 查 询 工 具 栏
图3.3-2 计算结果图形查询界面
2． 图 形 查 询 快 捷 菜 单 在图形结果查询窗口单击鼠标右键，弹出图形查询快捷菜单，可以方便地查看图形。
3． 【 图 形 查 询 】 菜 单
3.4 计算书的编辑修改
5.2 一般稳定渗流计算方法
贝忙水库浸润线方程计算表
正常蓄水位1741H1H2A0L单宽流量公式一F(A0)=q/k=(H1^2-(A0+8.20 1.7536.63F(A0)0.876024使用条件H2为0单宽流量公式二F(A0)=q/k=A0/2F(A0)0.875用两公式输入不同的A0试算当两公式算出来的F(A0)相同是的A0就是所要求的A0式中H1为水深H为坝高M1为上游坡比M2为下游坡比B为坝顶宽度D为水面到坝顶的距离A0浸润线溢出点距坝浸润线方程x=k/2q（H1^2-z^2)H11/F(A0)zHI1/F(A0)z x8.2 1.14285728.2 1.1428571438.208.2 1.1428577.28.808.2 1.142857 6.216.468.2 1.142857 5.222.978.2 1.142857 4.228.348.2 1.142857 3.232.578.2 1.142857 2.235.668.2 1.142857 1.7536.678.2 1.1428578.2 1.1428576.9618.79849.3992设计洪水位1741.13H1H2A0L单宽流量公式一F(A0)=q/k=(H1^2-(A0+8.330 1.8236.212F(A0)0.912356使用条件H2为0单宽流量公式二F(A0)=q/k=A0/2F(A0)0.91用两公式输入不同的A0试算当两公式算出来的F(A0)相同是的A0就是所要求的A0式中H1为水深H为坝高M1为上游坡比M2为下游坡比B为坝顶宽度D为水面到坝顶的距离A0浸润线溢出点距坝浸润线方程x=k/2q（H1^2-z^2)H11/F(A0)zHI1/F(A0)z x8.33 1.09890128.33 1.0989018.3308.33 1.0989017.338.608.33 1.098901 6.3316.118.33 1.098901 5.3322.528.33 1.098901 4.3327.828.33 1.098901 3.3332.038.33 1.098901 2.3335.148.33 1.098901 1.8236.318.33 1.0989018.33 1.09890169.3889校核洪水位1741.16H1H2A0L单宽流量公式一F(A0)=q/k=(H1^2-(A0+8.360 1.8436.104F(A0)0.921006使用条件H2为0单宽流量公式二F(A0)=q/k=A0/2F(A0)0.92用两公式输入不同的A0试算当两公式算出来的F(A0)相同是的A0就是所要求的A0式中H1为水深H为坝高M1为上游坡比M2为下游坡比B为坝顶宽度D为水面到坝顶的距离A0浸润线溢出点距坝浸润线方程x=k/2q（H1^2-z^2)H11/F(A0)zHI1/F(A0)z x8.36 1.08695728.36 1.0869578.3608.36 1.0869577.368.5434828.36 1.086957 6.3616.000018.36 1.086957 5.3622.369588.36 1.086957 4.3627.652198.36 1.086957 3.3631.847848.36 1.086957 2.3634.956548.36 1.086957 1.8436.143498.36 1.0869578.36 1.0869576.9621.448m1λh1a0sθ20.4285718.9 1.75533.1888227q1408.522891死水位1735H1H2A0L单宽流量公式一F(A0)=q/k=(H1^2-(A0+2.200.153.18F(A0)0.045412使用条件H2为0单宽流量公式二F(A0)=q/k=A0/2F(A0)0.05用两公式输入不同的A0试算当两公式算出来的F(A0)相同是的A0就是所要求的A0式中H1为水深H为坝高M1为上游坡比M2为下游坡比B为坝顶宽度D为水面到坝顶的距离A0浸润线溢出点距坝浸润线方程x=k/2q（H1^2-z^2)H11/F(A0)zHI1/F(A0)z x8.362022.220 2.202.220 1.2342.2200.2482.2200.148.32.220 4.36-141.6962.2203.36-64.4962.220 2.36-7.2962.220 1.8414.5442.2202.2206.96-43.6016m1λh1a0sθl L130.4285714298.2 1.7530.2616158q 4.30050.9500949.50094E-0714.7758636314.77586363M1H1D B M2F(A0)=q/k=(H1^2-(A0+H2)^2)/2L28.2 1.283LF(A0)=q/k=A0/236.63 3.514286 2.4 3.2822.95 5.685.914286距离A0浸润线溢出点距坝脚的高度（要是H2不为0那就是离下游水面的高度）H2为下游水深L为计算点至溢出点的水平8.13540.651818.518171808.18.200.008.207.208.807.208.96.2016.46 6.207.96.96 5.2022.97 5.20 6.91815.06 4.2028.34 4.20 5.93.2032.57 3.204.92.2035.66 2.203.9以上方程适用于土石坝 1.7536.67 1.75 2.98.973 1.92.33333320.76667 1.7551818.51817.131808.1M1H1D B M2F(A0)=q/k=(H1^2-(A0+H2)^2)/2L28.33 1.0783LF(A0)=q/k=A0/236.212 3.57 2.14 3.33222.74 5.4725.7128.55距离A0浸润线溢出点距坝脚的高度（要是H2不为0那就是离下游水面的高度）H2为下游水深L为计算点至溢出点的水平8.13540.651818.58.3308.3318177.338.607.331808.1 6.3316.11 6.338.9 5.3322.52 5.3310.4 4.3327.82 4.336.96 3.3332.03 3.331815.06 2.3335.14 2.331.8236.31 1.82以上方程适用于土石坝8.9732.33333320.76667M1H1D B M2F(A0)=q/k=(H1^2-(A0+H2)^2)/2L28.36 1.04831818.51817.181808.1LF(A0)=q/k=A0/236.104 3.582857 2.08 3.34422.68 5.4245.66285728.31429距离A0浸润线溢出点距坝脚的高度（要是H2不为0那就是离下游水面的高度）H2为下游水深L为计算点至溢出点的水平8.13540.651818.58.3608.3618177.368.547.361808.1 6.3616.00 6.368.9 5.3622.37 5.3610.4 4.3627.65 4.366.96 3.3631.85 3.361815.06 2.3634.96 2.361.8436.14 1.84以上方程适用于土石坝8.97302.33333320.76667l L1tg16k36.63 3.4411760.511E-13M1H1D B M2F(A0)=q/k=(H1^2-(A0+H2)^2)/2L2 2.28.2831818.51817.181808.1LF(A0)=q/k=A0/253.180.94285716.40.8827.917.2817.3428686.71429距离A0浸润线溢出点距坝脚的高度（要是H2不为0那就是离下游水面的高度）H2为下游水深L为计算点至溢出点的水平8.13540.651818.58.3608.3618177.368.547.361808.1 6.3616.00 6.368.9 5.3622.37 5.3610.4 4.3627.65 4.366.96 3.3631.85 3.361815.06 2.3634.96 2.361.8436.14 1.84以上方程适用于土石坝8.97302.33333320.76667tg16k0.28670.000001H A0H29.4 1.7508.75计算点至溢出点的水平距离H A0H29.4 1.8209.19.1计算点至溢出点的水平距离H A0H29.4 1.8409.29.2计算点至溢出点的水平距离H A0H29.40.100.50.5计算点至溢出点的水平距离。
土石坝浸润线计算
计算方法：有限渗透水地基上有水平排水（下游无水）的均质土坝
浸润线坐标值计算公式：X=K0T(y-h0)/q'+K(y2-h02)/(2q')
q'=K0T(H1-h0)/(L+△L1)+K(H12-h02)/2(L+△L1)=
有关计算数据输入
K0：
地基渗透系数
T：
透水地基厚度
21 m 坝前水位至坝底距离
0
m 坝后水位至坝底距离
4.621595 m h0＝q/(K+K0/0.44)
37 m 褥垫起始点：褥垫在坝内最靠近上游点
8.4 m 复核：
2
x=0时，y=1.7144=h0
2
L‘=L+△L1= 45.4 m
等于当y=H1时‘0＝[(△L1+L)2+H12]0.5-(△L1+L)
K：
坝体渗透系数
H1：
坝前水深
H2：
坝后水深
h0： 褥垫始点垂线上至浸润线高（考虑渗透地基）
L： 褥垫始点至上游水位与坝坡交点垂线的水平距离
△
L1：
[m1/(2m1+1)]*H1
m1：
上游坝坡比1∶m1
m2：
下游坝坡比1∶m2
h'0： 褥垫始点垂线上至浸润线高（不透水地基时）
qd：
坝体渗流量
q：
总渗流量
115.5399 scm2/ qd＝K*h0'*100
115.5399 s
qj＝K0*T*100*(H1-H2)/(L+m1*H1+0.88*T)
1.1553988
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
浸润线的计算
7.4.1 瑞典条分法
7.4.1.1基本假定与公式
条分法是将滑动土体竖直分成若干土条，把土条当成刚体，分别求作用于各土条上的力对圆心的滑动力矩和抗滑力矩，然后按下式求土坡的稳定安全系数F s。
其原理是条分法可认为整体圆弧法s n是
l(x,y)的函数，无法求理论解，是一个边值问题，应通过数值计算解决。
一个简化解决方法是将滑动土体分成条。
实际是一种离散化计算方法。
代替法：用浸润线一下，坡外水位以上所包围的同体积的水重对滑动圆心的力矩来代替渗流力对圆心
7.4.2.3 安全系数
7.4.2.4简化毕肖普法的特点
①假设条块间作用力只有法向力没有切向力；
②满足滑动土体整体力矩平衡条件；
③满足各条块力的多边形闭合条件，但不满足条块的力矩平衡条件；
④满足极限平衡条件；
⑤得到的安全系数比瑞典条分法略高一点。
7.4.3 普遍条分法
7.4.3.1条分法基本原理
条分法的基本思路就是将滑动土体沿竖向分成若干土条，视所有土条为刚体，对每个土条进行受力分析，分别求出作用在各土条上的滑动力（矩）和抗滑力（矩），然后得到土坡的稳定安全系数。
很显然，要求解土条的受力，是一个超静定的问题。
划分的土条数越多，则超静定次数越高。
要使问题以求解，常用的做法是对土条间的作用力进行一些可以接受的简化假定，以减少未知量个数或增加方程数。
目前的多种条分法，其差别就在于采用了不同的简化假定。
这些简化假定大体上分为三类：①不考虑土条间作用力或仅考虑其中的一个作用力，如瑞典条分法和简化毕肖普法；②假定土条间力的作用方向或规定Pi与hi的比值，折线滑动面方法则属于此类；③假定土条间的作用位位置，即规定hi的大小，如等于侧面高度的1/2或1/3，通用条分法就属于这一类。