华师大货币银行学微观金融运行货币时间价值与现金流贴
《货币银行学》第三章 利息和利率

利率期限结构理论
理论必须能够解释的三个经验事实: • 不同期限的债券,其利率随时间变化一起波动; • 短期利率低,收益率曲线更倾向于向上倾斜;
IS线和LM线的交点表示货币市场和产品时 常同时达到均衡的利率和产出组合,由此决定的 利率为均衡利率,对应的产出为均衡产出。
理论特点:
1、与前三种理论比较,考虑到收入的因素;
2、克服了古典学派利率决定理论只考虑商品市 场均衡的缺陷,又克服了凯恩斯学派利率理论只 考虑货币市场均衡的缺陷,同时还克服了可贷资 金利率理论在兼顾两个市场时忽视两个市场各自 均衡的缺陷,因而该模型被认为是解释名义利率 决定过程的最成功的理论。
四、可贷资金理论
同时考虑了凯恩斯的货币因素和古典学派 的实质因素。该理论认为,利率是由可贷资金的 供给和需求的均衡点所决定的。
可贷资金的供给主要有两个来源:一是当 前的储蓄;二是实际货币供给量的变动。
可贷资金的需求主要也有两个方面:一是 当前的投资需求;二是货币贮藏的需求。
用公式表示: DL =I+ΔMD SL =S+ΔMS 当可贷资金供求双方相互作用达到平衡时,
3、若某人每年存入1万元,年利率为1%,10年后此人存 款余额为多少?
4、某企业期望6年后折旧基金余额为100万元,该企业从 今年开始,按3%的利率计息,每年应提折旧基金为多 少?
5、某客户有合格票据200万元到商业银行贴现,还差60天 到期,若按月息3‰扣除贴现利息,银行实付贴现额为 多少?
第二节 利率的决定
三、利率的应用——货币的时间价值
资金的时间价值,是指同样数额的资金在不同的时 间点上具有不同价值。资金的时间价值一般都是按照复 利方式计算的。
货币时间价值有两种表现形式: 其相对数是指扣除风险报酬和通货膨胀贴水后的平 均资金利润率或平均报酬率; 其绝对数即时间价值额是资金在生产经营过程中带 来的真实增殖额,即一定数额的资金与利息率的乘积。
关于金融与金融学

关于金融与金融学一、金融的定义金融(finance)是一个经济学的概念和范畴。
现代经济生活中,人们每天都离不开金融并频繁地使用“金融”这个词。
但是,目前理论界对于金融的含义却存在较大的分歧,没有统一的定义。
简单地说,金融就是资金的融通,即是由资金融通的工具、机构、市场和制度构成的有机系统,是经济系统的重要组成部分。
根据金融系统中个体与整体的差异,可以把金融划分为微观金融和宏观金融两部分。
微观金融(micro—finance)是指金融市场主体(投资者、融资者;政府、机构和个人)个体的投融资行为及其金融资产的价格决定等微观层次的金融活动;宏观金融(macro—finance)则是指金融系统各构成部分作为整体的行为及其相互影响以及金融与经济的相互作用。
金融作为资金融通活动的一个系统,是以各个微观主体个体的投融资行为为基础,工具、机构、市场和制度等构成要素相互作用并与经济系统的其他子系统相互作用的一个有机系统。
二、金融学及其学科体系兹维·博迪和罗伯特·C.莫顿在他们合著的《金融学》一书中,定义“金融学是研究人们在不确定的环境中如何进行资源的时间配置的学科”。
它实际上是研究微观金融主体个体的金融决策行为及其运行规律的学科,因此也可称为“微观金融学”。
显然,这是与狭义的金融概念相对应的狭义的金融学概念,也是目前西方使用较多的金融学的既念。
但是,既然金融包括微观金融和宏观金融,金融学就不能仅研究微观金融运行而不研究宏观金融运行。
也就是说,金融学不能只研究金融主体个体的行为,而不研究金融系统整体的行为。
整体行为是个体行为的集合,但并不是简单的相加;而个体行为又是以整体行为为前提和基础的行为,两者紧密相关。
因此,广义的金融学就是研究资金融通活动,包括金融主体的个体行为和金融系统整体行为及其相互关系和运行规律的科学。
它是经济学的一个重要分支。
它既包括以微观金融主体行为及其运行规律为研究对象的微观金融学的内容,还包括以金融系统整体的运行规律及其各构成部分的相互关系为研究对象的宏观金融学的内容。
第03讲 货币的时间价值与利率

中央财经大学金融学院
(2009)
11
➢利息的实质
2. 现代经济学关于利息的基本观点
利息实质已经不再是现代经济学的研究重点, 目前的研究更加侧重于对利息补偿的构成以 及对利率影响因素的分析。
其基本观点就是将利息看作投资者让渡资本 使用权而索取的补偿或报酬,该补偿一般包 括两部分:放弃投资于无风险资产的机会成 本的补偿和对风险的补偿,即:
1.利率的计算:单利与复利(续)
连续复利及其公式
பைடு நூலகம்
Lim (1
r
n
)
er
n
n
这里n为计息次数,r为利率。
中央财经大学金融学院
(2009)
21
案例:单利的计算
A银行向B企业发放了一笔金额为100万、期限 为5年、年利率为10%的贷款,如果按照单利 计息的话,则到期后B企业应该向A银行偿还的 利息和本利和分别为50万元和150万元。其具 体计算公式分别为:
从非货币因素考察
✓ 重商主义时期,配第、洛克、孟德斯鸠等从货币 是财富的角度得出利息是由货币产生的。之后, 巴本(1690)提出利息是资本的租金,这与土地 的租金相似。诺斯、马西、休谟等发展了该理论, 认为借贷的不是货币而是资本,利息应该是资本 利润的一部分。
✓ 亚当·斯密综合了巴本等人的观点,在《国富论》 中从产业资本的角度,指出利息是产业利润的一 部分。在利息的性质上,他们都强调实物因素的 作用。
中央财经大学金融学院
(2009)
18
货币的时间价值与利息
➢信用与货币的时间价值 ➢利息的实质 ➢利息与收益的一般形态 ➢金融交易与货币的时间价值 ➢现金流贴现分析与投资决策
中央财经大学金融学院
货币银行学名词解释

货币银行学名词解释名词解释1、铸币:是指经国家证明,具有一定重量和成色,并铸成一定形状的金属铸块。
2、金本位制:是指以黄金作为本位货币的一种货币制度。
3、基准利率:在多种利率并存的利率体系中,通常有一个起决定作用的利率,这个利率被称为基准利率。
4、货币时间价值:是指当前所持有的一定量货币比未来获得的等量货币具有更高的价值。
5、逆向选择:是在交易之前发生的信息不对称问题,那些最可能造成不利结果即造成信贷风险的借款人,常常是那些寻找贷款最积极、最可能得到贷款的人。
6、道德风险:是在交易之后出现的信息不对称问题,指的是放贷者发放贷款后将面对借贷者从事那些从放款者观点来看并不期望进行的风险较大的活动。
7、交易成本:即从事金融交易所花费的时间和金钱。
8、信息成本:投资者搜寻有效的项目,对其投资效益进行评估,并且亲自监督实施与贷款人签订的合同所耗费的识别成本和监督与实施成本共同构成了信息成本。
9、担保:担保人所做出的在缔约一方不履行或违反合同条款时而代付一笔确定款项的承诺。
10、承诺:是银行与贷款客户达成的一种具有法律约束力的正式契约,银行将在正式的有效承诺期内,按照双方商定的金额、利率,随时准备应客户的需要提供信贷便利,同时,作为提供承诺的报酬,银行通常要向借款人收取一定的承诺佣金。
11、流动性风险:是指金融机构不能如期满足客户提款取现,或不能如期偿还流动负债而导致的风险。
12、信用风险:是指债务人一方不履行合约,不按期偿还本金和利息而造成的风险。
13、原始存款:是客户用现金、其他行的支票或者汇票等存入而形成的存款,可增加其准备金,是银行或投资的基础。
14、派生存款:是商业银行在原始存款的基础上发放贷款或者投资时所创造的存款。
15、消费物价指数(CPI):是根据家庭消费的具有代表性的商品和劳务的价格变动状况而编制的物价指数。
16、生产者价格指数(PPI):是根据企业所购买的商品的价格变化状况编制而成的指数。
货币银行学2-7
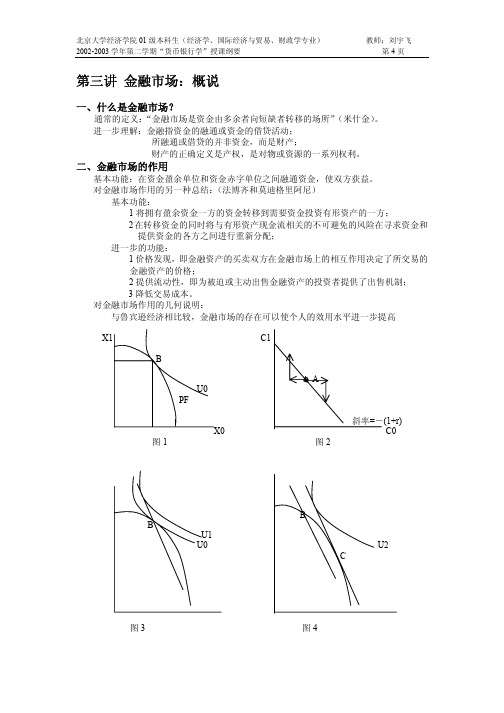
第三讲金融市场:概说一、什么是金融市场?通常的定义:“金融市场是资金由多余者向短缺者转移的场所”(米什金)。
进一步理解:金融指资金的融通或资金的借贷活动;所融通或借贷的并非资金,而是财产;财产的正确定义是产权,是对物或资源的一系列权利。
二、金融市场的作用基本功能:在资金盈余单位和资金赤字单位之间融通资金,使双方获益。
对金融市场作用的另一种总结:(法博齐和莫迪格里阿尼)基本功能:1将拥有盈余资金一方的资金转移到需要资金投资有形资产的一方;2在转移资金的同时将与有形资产现金流相关的不可避免的风险在寻求资金和提供资金的各方之间进行重新分配;进一步的功能:1价格发现,即金融资产的买卖双方在金融市场上的相互作用决定了所交易的金融资产的价格;2提供流动性,即为被迫或主动出售金融资产的投资者提供了出售机制;3降低交易成本。
对金融市场作用的几何说明:与鲁宾逊经济相比较,金融市场的存在可以使个人的效用水平进一步提高X1 C1BAU0PF斜率=-(1+r)X0 C0图1 图2BBU1U0 U2C图3 图4三、金融市场的结构1参与者:资金盈余单位/资金赤字单位/金融中介(存款机构+合约性机构+投资性机构)证券市场机构(投资银行/证券经纪商/证券自营商/证券交易所)[问题]:如何多角度辨析证券市场机构的“非金融中介”特点?2直接金融和间接金融:各自的利弊及相对重要性[问题]:你是否同意下面的说法:直接金融迅速发展,取代间接金融已成大势所趋?3金融工具(金融资产/金融产品):货币市场工具:短期国债(Treasury Bills);再购回协议(repos);可转让存单(negotiable bank certificates of deposit);商业票据;银行承兑票据(banker’sacceptance);联邦基金(federal funds)资本市场工具:股票(优先股和普通股);债券;抵押贷款(mortgages);消费者贷款和银行商业贷款(consumer and bank commercial loans);衍生工具:远期合约;期货合约;期权合约;互换合约4一级市场与二级市场:[问题]:企业通过一级市场已完成融资,二级市场何以重要?5第一市场和第二市场(交易所市场和场外市场[OTC])四、金融工具供求的基本原理需求方面:资产选择理论基本思路是:收益既定,追求低风险;风险既定,追求高收益。
2012 54《金融学》导言

3、从国际金融市场上来去匆匆的 hot 钱)以及沃伦· 巴菲特 的神话。 热钱对一国经济的冲击。 美元汇率的变化如何影响世界经济?
money(热
金融全球化的事实。全球范围内配置资源。
每个人都会恐惧和贪婪,我不过是“在别人恐惧的 时候贪婪,在别人贪婪的时候恐惧”罢了。
导 论 第一篇:导论篇 第一章 金融体系概述 第二章 货币和货币制度 第二篇:微观金融运行Ⅰ——投资与融资 第三章 第四章 第五章 货币的时间价值 金融资产 金融投资与融资
课时 2
4 4 6 4 6
2014-4-24
26
第三篇:微观金融运行Ⅱ-机构与市场 第六章 金融机构 4
第七章 金融市场 第四篇 宏观金融运行 第八章 货币需求 第九章 货币供给
1、从银行漂亮的办公大厦到引人入胜甚至眩目的股票债券市场、
期货市场、各种神秘的衍生证券交易。(银行凭什么?市场 有什么用?)
银行为何居于至关重要的地位? 银行到底是怎样运作的?为人们的资源配置提供怎样的服 务? 银行也会出现危机? 20世纪70年代美国的马丁·迈耶说: 从地平线上看到的第一座建筑物就是银行。
2014-4-24
货币供求及其均衡、通货膨胀与通货紧缩、货币政 18 策、金融危机、国际金融等
可概括为: 金融学就是研究金融系统运行规律(如何融通货币和货
币资金)的科学,包括金融主体的个体行为和金融系统 整体行为及其相互关系和运行规律的科学 。
Finance:
The study of how the financial system coordinates and channels the flow of funds from lenders to borrowers – and vice versa – and how new funds are created by financial intermediaries in the borrowing process.
金融方面的读书笔记
金融方面读书笔记【篇一: 金融读书笔记】最近读了戴国强主编《货币金融学》, 写了些读书笔记, 与您交流一下, 不足之处请批评指正。
邓小平指出: “金融很关键, 是现代经济关键。
金融搞好了, 一着棋活, 全盘皆活。
”这深刻地说明了金融在现代经济中特殊地位及举足轻重作用。
金融是指与货币资金金融通用相关一切活动, 它包含货币制度设计、信用管理、银行、证劵、保险等金融机构经营、金融市场运作、货币政策制订与落实、参与国际融资等。
在市场机制下, 大家经过货币资金融通与配置优化, 可提升其她社会资源配置效率, 从而更有效地促进商品生产和交换。
各国经济发展史都雄辩地证实, 一国金融活动有效程度会直接对该国经济发展产生深刻地乃至决定性影响。
一国要成为经济强国, 也必需拥有发达金融体系, 离开发达金融体系支撑, 是不可能成为真正经济强国。
能够说, 现代经济实质上是金融经济。
现代金融制度起源于威尼斯, 关键人员是罗马帝国及当初欧洲贵族理财代理人, 犹太人是这些人是关键组成部分。
当初欧洲货币是金属, 有金和银, 信用货币还没有出现。
现在来解释一下信用货币形式和实质。
信用货币最早形式是汇票和本票。
包含企业汇票、银行汇票, 企业本票, 银行本票。
因为中世纪欧洲金、银量长久不增加, 整个社会中缺乏货币供给, 商品经济十分落后。
含有大量金、银只能是部分贵族和皇族、教会高层。
部分善于理财人就代理这些贵族发高利贷。
利率高达20%--30%, 谁会去借这些高利贷呢, 当然商大家利润率必需大于利率才会去借债, 这就是从事东方贸易商人, 东方贸易利润率可高达300-500%。
目前, 中国经济已经进入一个非常关键发展时期。
跨入新世纪, 加入wto对中国经济发展, 尤其是对中国金融业地发展来说, 既提供了良好机遇, 又带来了严峻挑战。
经过多年努力, 中国金融业即使有了想当大规模, 不过, 同国际金融业地发展要求相比, 不管是在实务操作水平上, 还是在管理经验上, 我们都还有很大差距, 还有很多问题需要我们从理论和实践上加以处理。
重点推荐货币银行学教材参考书
1.货币银行学(MONEY AND BANKING)——现代经济学管理学教科书系列作者:易纲、吴有昌著易纲、海闻主编2.货币金融学(第七版)(经济科学译丛)[美]弗雷德里克·S·米什金 2006-12-313.《金融学》作者:(美)兹维·博迪罗泊特·C·莫顿4.金融学投资·机构·管理(美)斯坦利·G.伊肯思(Stanley G.Eakins)著曹廷贵译5.金融市场与机构(第5版高等院校双语教材)作者:(美)弗雷德里克·S·米什金//斯坦利·G·埃金斯|译者:贾玉革6.货币银行与经济(第6版)/当代经济学系列丛书/当代经济学教学参考书系作者:(美)托马斯·梅耶//詹姆斯·S.杜森贝里//罗伯特·Z.阿利伯|主编:陈昕|译者:林宝清//洪锡熙|校注:林宝清书籍内容简介1.货币银行学(MONEY AND BANKING)——现代经济学管理学教科书系列作者:易纲、吴有昌著易纲、海闻主编出版社:上海人民出版社ISBN: 7208032750出版时间: 1999-9第1版书籍介绍:本书试图将现代货币银行理论与中国的具体实践有机地融合起来,从而形成一个既反映现代货币银行理论的优秀成果,又具有中国特色的货币银行学体系。
针对国内同类教科书大多只编重制度性和操作性方面内容的特点,我们试图在理论性内容方面有所加强。
本书结合课程内容设计了28个专栏,这些专栏有助于增强学生对所学内容的感性认识,培养学生关注现实问题的兴趣。
由于篇幅所限,同时也考虑到绝大多数高校的经济类院系都开设了专门的国际金融课程。
本书是“现代经济学管理学教科书系列”之一。
该教科书系列的主编易纲先生在编著本书时,力求了联系世界经济和中国经济的实际,在充分体现理论深度的同时注重教材的实用性。
本书共分6篇;基本概念;金融机构与金融市场;货币供求及利率决定;货币与经济;金融与经济发展;货币政策。
《金融学》答案第四章 货币的时间价值与现金流贴现分析
CHAPTER 4THE TIME VALUE OF MONEY AND DISCOUNTED CASH FLOW ANALYSISObjectives∙To explain the concepts of compounding and discounting, future value and present value.∙To show how these concepts are applied to making financial decisions.Outline4.1Compounding4.2The Frequency of Compounding4.3Present Value and Discounting4.4Alternative Discounted Cash Flow Decision Rules4.5Multiple Cash Flows4.6Annuities4.7Perpetual Annuities4.8Loan Amortization4.9Exchange Rates and Time Value of Money4.10Inflation and Discounted Cash Flow Analysis4.11Taxes and Investment DecisionsSummary∙Compounding is the process of going from present value (PV) to future value (FV). The future value of $1 earning interest at rate i per period for n periods is (1+i)n.∙Discounting is finding the present value of some future amount. The present value of $1 discounted at rate i per period for n periods is 1/(1+i)n.∙One can make financial decisions by comparing the present values of streams of expected future cash flows resulting from alternative courses of action. The present value of cash inflows less the present value of cash outflows is called net present value (NPV). If a course of action has a positive NPV, it is worth undertaking.∙In any time value of money calculation, the cash flows and the interest rate must be denominated in the same currency.∙Never use a nominal interest rate when discounting real cash flows or a real interest rate when discounting nominal cash flows.How to Do TVM Calculations in MS ExcelAssume you have the following cash flows set up in a spreadsheet:A B1t CF20-1003150426053706NPV7IRRMove the cursor to cell B6 in the spreadsheet. Click the function wizard f x in the tool bar and when a menu appears, select financial and then NPV. Then follow the instructions for inputting the discount rate and cash flows. You can input the column of cash flows by selecting and moving it with your mouse. Ultimately cell B6should contain the following:=NPV(0.1,B3:B5)+B2The first variable in parenthesis is the discount rate. Make sure to input the discount rate as a decimal fraction (i.e., 10% is .1). Note that the NPV function in Excel treats the cash flows as occurring at the end of each period, and therefore the initial cash flow of 100 in cell B2 is added after the closing parenthesis. When you hit the ENTER key, the result should be $47.63.Now move the cursor to cell B7to compute IRR. This time select IRR from the list of financial functions appearing in the menu. Ultimately cell B7 should contain the following:=IRR(B2:B5)When you hit the ENTER key, the result should be 34%.Your spreadsheet should look like this when you have finished:A B1t CF20-1003150426053706NPV47.637IRR34%Solutions to Problems at End of Chapter1.If you invest $1000 today at an interest rate of 10% per year, how much will you have 20 years from now,assuming no withdrawals in the interim?2. a. If you invest $100 every year for the next 20 years, starting one year from today and you earninterest of 10% per year, how much will you have at the end of the 20 years?b.How much must you invest each year if you want to have $50,000 at the end of the 20 years?3.What is the present value of the following cash flows at an interest rate of 10% per year?a.$100 received five years from now.b.$100 received 60 years from now.c.$100 received each year beginning one year from now and ending 10 years from now.d.$100 received each year for 10 years beginning now.e.$100 each year beginning one year from now and continuing forever.e.PV = $100 = $1,000.104.You want to establish a “wasting” fund which will provide you with $1000 per year for four years, at which time the fund will be exhausted. How much must you put in the fund now if you can earn 10% interest per year?SOLUTION:5.You take a one-year installment loan of $1000 at an interest rate of 12% per year (1% per month) to be repaid in 12 equal monthly payments.a.What is the monthly payment?b.What is the total amount of interest paid over the 12-month term of the loan?SOLUTION:b. 12 x $88.85 - $1,000 = $66.206.You are taking out a $100,000 mortgage loan to be repaid over 25 years in 300 monthly payments.a.If the interest rate is 16% per year what is the amount of the monthly payment?b.If you can only afford to pay $1000 per month, how large a loan could you take?c.If you can afford to pay $1500 per month and need to borrow $100,000, how many months would it taketo pay off the mortgage?d.If you can pay $1500 per month, need to borrow $100,000, and want a 25 year mortgage, what is thehighest interest rate you can pay?SOLUTION:a.Note: Do not round off the interest rate when computing the monthly rate or you will not get the same answerreported here. Divide 16 by 12 and then press the i key.b.Note: You must input PMT and PV with opposite signs.c.Note: You must input PMT and PV with opposite signs.7.In 1626 Peter Minuit purchased Manhattan Island from the Native Americans for about $24 worth of trinkets. If the tribe had taken cash instead and invested it to earn 6% per year compounded annually, how much would the Indians have had in 1986, 360 years later?SOLUTION:8.You win a $1 million lottery which pays you $50,000 per year for 20 years, beginning one year from now. How much is your prize really worth assuming an interest rate of 8% per year?SOLUTION:9.Your great-aunt left you $20,000 when she died. You can invest the money to earn 12% per year. If you spend $3,540 per year out of this inheritance, how long will the money last?SOLUTION:10.You borrow $100,000 from a bank for 30 years at an APR of 10.5%. What is the monthly payment? If you must pay two points up front, meaning that you only get $98,000 from the bank, what is the true APR on the mortgage loan?SOLUTION:If you must pay 2 points up front, the bank is in effect lending you only $98,000. Keying in 98000 as PV and computing i, we get:11.Suppose that the mortgage loan described in question 10 is a one-year adjustable rate mortgage (ARM), which means that the 10.5% interest applies for only the first year. If the interest rate goes up to 12% in the second year of the loan, what will your new monthly payment be?SOLUTION:Step 2 is to compute the new monthly payment at an interest rate of 1% per month:12.You just received a gift of $500 from your grandmother and you are thinking about saving this money for graduation which is four years away. You have your choice between Bank A which is paying 7% for one-year deposits and Bank B which is paying 6% on one-year deposits. Each bank compounds interest annually. What is the future value of your savings one year from today if you save your money in Bank A? Bank B? Which is the better decision? What savings decision will most individuals make? What likely reaction will Bank B have? SOLUTION:$500 x (1.07) = $535Formula:$500 x (1.06) = $530a.You will decide to save your money in Bank A because you will have more money at the end of the year. Youmade an extra $5 because of your savings decision. That is an increase in value of 1%. Because interestcompounded only once per year and your money was left in the account for only one year, the increase in value is strictly due to the 1% difference in interest rates.b.Most individuals will make the same decision and eventually Bank B will have to raise its rates. However, it isalso possible that Bank A is paying a high rate just to attract depositors even though this rate is not profitable for the bank. Eventually Bank A will have to lower its rate to Bank B’s rate in order to make money.13.Sue Consultant has just been given a bonus of $2,500 by her employer. She is thinking about using the money to start saving for the future. She can invest to earn an annual rate of interest of 10%.a.According to the Rule of 72, approximately how long will it take for Sue to increase her wealth to $5,000?b.Exactly how long does it actually take?SOLUTION:a.According to the Rule of 72: n = 72/10 = 7.2 yearsIt will take approximately 7.2 years for Sue’s $2,500 to double to $5,000 at 10% interest.b.At 10% interestFormula:$2,500 x (1.10)n = $5,000Hence, (1.10)n = 2.0n log 1.10 = log 2.0n = .693147 = 7.27 Years.095310rry’s bank account has a “floating” interest rate on certain deposits. Every year the interest rate is adjusted. Larry deposited $20,000 three years ago, when interest rates were 7% (annual compounding). Last year the rate was only 6%, and this year the rate fell again to 5%. How much will be in his account at the end of this year?SOLUTION:$20,000 x 1.07 x 1.06 x 1.05 = $23,818.2015.You have your choice between investing in a bank savings account which pays 8% compounded annually (BankAnnual) and one which pays 7.5% compounded daily (BankDaily).a.Based on effective annual rates, which bank would you prefer?b.Suppose BankAnnual is only offering one-year Certificates of Deposit and if you withdraw your moneyearly you lose all interest. How would you evaluate this additional piece of information when making your decision?SOLUTION:a.Effective Annual Rate: BankAnnual = 8%.Effective Annual Rate BankDaily = [1 + .075]365 - 1 = .07788 = 7.788%365Based on effective annual rates, you would prefer BankAnnual (you will earn more money.)b.If BankAnnual’s 8% annual return is conditioned upon leaving the money in for one full year, I would need tobe sure that I did not need my money within the one year period. If I were unsure of when I might need the money, it might be safer to go for BankDaily. The option to withdraw my money whenever I might need it will cost me the potential difference in interest:FV (BankAnnual) = $1,000 x 1.08 = $1,080FV (BankDaily) = $1,000 x 1.07788 = $1,077.88Difference = $2.12.16.What are the effective annual rates of the following:a.12% APR compounded monthly?b.10% APR compounded annually?c.6% APR compounded daily?SOLUTION:Effective Annual Rate (EFF) = [1 + APR] m - 1ma.(1 + .12)12 - 1 = .1268 = 12.68%12b.(1 + .10)- 1 = .10 = 10%1c.(1 + .06)365 - 1 = .0618 = 6.18%36517.Harry promises that an investment in his firm will double in six years. Interest is assumed to be paid quarterly and reinvested. What effective annual yield does this represent?EAR=(1.029302)4-1=12.25%18.Suppose you know that you will need $2,500 two years from now in order to make a down payment on a car.a.BankOne is offering 4% interest (compounded annually) for two-year accounts, and BankTwo is offering4.5% (compounded annually) for two-year accounts. If you know you need $2,500 two years from today,how much will you need to invest in BankOne to reach your goal? Alternatively, how much will you need to invest in BankTwo? Which Bank account do you prefer?b.Now suppose you do not need the money for three years, how much will you need to deposit today inBankOne? BankTwo?SOLUTION:PV = $2,500= $2,311.39(1.04)2PV = $2,500= $2,289.32(1.045)2You would prefer BankTwo because you earn more; therefore, you can deposit fewer dollars today in order to reach your goal of $2,500 two years from today.b.PV = $2,500= $2,222.49(1.04)3PV = $2,500= $2,190.74(1.045)3Again, you would prefer BankTwo because you earn more; therefore, you can deposit fewer dollars today in order to reach your goal of $2,500 three years from today.19.Lucky Lynn has a choice between receiving $1,000 from her great-uncle one year from today or $900 from her great-aunt today. She believes she could invest the $900 at a one-year return of 12%.a.What is the future value of the gift from her great-uncle upon receipt? From her great-aunt?b.Which gift should she choose?c.How does your answer change if you believed she could invest the $900 from her great-aunt at only 10%?At what rate is she indifferent?SOLUTION:a. Future Value of gift from great-uncle is simply equal to what she will receive one year from today ($1000). Sheearns no interest as she doesn’t receive the money until next year.b. Future Value of gift from great-aunt: $900 x (1.12) = $1,008.c. She should choose the gift from her great-aunt because it has future value of $1008 one year from today. Thegift from her great-uncle has a future value of $1,000. This assumes that she will able to earn 12% interest on the $900 deposited at the bank today.d. If she could invest the money at only 10%, the future value of her investment from her great-aunt would only be$990: $900 x (1.10) = $990. Therefore she would choose the $1,000 one year from today. Lucky Lynn would be indifferent at an annual interest rate of 11.11%:$1000 = $900 or (1+i) = 1,000 = 1.1111(1+i)900i = .1111 = 11.11%20.As manager of short-term projects, you are trying to decide whether or not to invest in a short-term project that pays one cash flow of $1,000 one year from today. The total cost of the project is $950. Your alternative investment is to deposit the money in a one-year bank Certificate of Deposit which will pay 4% compounded annually.a.Assuming the cash flow of $1,000 is guaranteed (there is no risk you will not receive it) what would be alogical discount rate to use to determine the present value of the cash flows of the project?b.What is the present value of the project if you discount the cash flow at 4% per year? What is the netpresent value of that investment? Should you invest in the project?c.What would you do if the bank increases its quoted rate on one-year CDs to 5.5%?d.At what bank one-year CD rate would you be indifferent between the two investments?SOLUTION:a.Because alternative investments are earning 4%, a logical choice would be to discount the project’s cash flowsat 4%. This is because 4% can be considered as your opportunity cost for taking the project; hence, it is your cost of funds.b.Present Value of Project Cash Flows:PV = $1,000= $961.54(1.04)The net present value of the project = $961.54 - $950 (cost) = $11.54The net present value is positive so you should go ahead and invest in the project.c.If the bank increased its one-year CD rate to 5.5%, then the present value changes to:PV = $1,000= $947.87(1.055)Now the net present value is negative: $947.87 - $950 = - $2.13. Therefore you would not want to invest in the project.d.You would be indifferent between the two investments when the bank is paying the following one-year interestrate:$1,000 = $950 hence i = 5.26%(1+i)21.Calculate the net present value of the following cash flows: you invest $2,000 today and receive $200 one year from now, $800 two years from now, and $1,000 a year for 10 years starting four years from now. Assume that the interest rate is 8%.SOLUTION:Since there are a number of different cash flows, it is easiest to do this problem using cash flow keys on the calculator:22.Your cousin has asked for your advice on whether or not to buy a bond for $995 which will make one payment of $1,200 five years from today or invest in a local bank account.a.What is the internal rate of return on the bond’s cash flows? What additional information do you need tomake a choice?b.What advice would you give her if you learned the bank is paying 3.5% per year for five years(compounded annually?)c.How would your advice change if the bank were paying 5% annually for five years? If the price of thebond were $900 and the bank pays 5% annually?SOLUTION:a.$995 x (1+i)5 = $1,200.(1+i)5 = $1,200$995Take 5th root of both sides:(1+i) =1.0382i = .0382 = 3.82%In order to make a choice, you need to know what interest rate is being offered by the local bank.b.Upon learning that the bank is paying 3.5%, you would tell her to choose the bond because it is earning a higherrate of return of 3.82% .c.If the bank were paying 5% per year, you would tell her to deposit her money in the bank. She would earn ahigher rate of return.5.92% is higher than the rate the bank is paying (5%); hence, she should choose to buy the bond.23.You and your sister have just inherited $300 and a US savings bond from your great-grandfather who had left them in a safe deposit box. Because you are the oldest, you get to choose whether you want the cash or the bond. The bond has only four years left to maturity at which time it will pay the holder $500.a.If you took the $300 today and invested it at an interest rate 6% per year, how long (in years) would ittake for your $300 to grow to $500? (Hint: you want to solve for n or number of periods. Given these circumstances, which are you going to choose?b.Would your answer change if you could invest the $300 at 10% per year? At 15% per year? What otherDecision Rules could you use to analyze this decision?SOLUTION:a.$300 x (1.06)n = $500(1.06)n = 1.6667n log 1.06 = log 1.6667n = .510845 = 8.77 Years.0582689You would choose the bond because it will increase in value to $500 in 4 years. If you tookthe $300 today, it would take more than 8 years to grow to $500.b.You could also analyze this decision by computing the NPV of the bond investment at the different interest rates:In the calculations of the NPV, $300 can be considered your “cost” for acquiring the bond since you will give up $300 in cash by choosing the bond. Note that the first two interest rates give positive NPVs for the bond, i.e. you should go for the bond, while the last NPV is negative, hence choose the cash instead. These results confirm the previous method’s results.24.Suppose you have three personal loans outstanding to your friend Elizabeth. A payment of $1,000 is due today, a $500 payment is due one year from now and a $250 payment is due two years from now. You would like to consolidate the three loans into one, with 36 equal monthly payments, beginning one month from today. Assume the agreed interest rate is 8% (effective annual rate) per year.a.What is the annual percentage rate you will be paying?b.How large will the new monthly payment be?SOLUTION:a.To find the APR, you must first compute the monthly interest rate that corresponds to an effective annual rate of8% and then multiply it by 12:1.08 = (1+ i)12Take 12th root of both sides:1.006434 = 1+ ii = .006434 or .6434% per monthOr using the financial calculator:b.The method is to first compute the PV of the 3 loans and then compute a 36 month annuity payment with thesame PV. Most financial calculators have keys which allow you to enter several cash flows at once. This approach will give the user the PV of the 3 loans.Note: The APR used to discount the cash flows is the effective rate in this case, because this method is assuming annual compounding.25.As CEO of ToysRFun, you are offered the chance to participate, without initial charge, in a project that produces cash flows of $5,000 at the end of the first period, $4,000 at the end of the next period and a loss of $11,000 at the end of the third and final year.a.What is the net present value if the relevant discount rate (the company’s cost of capital) is 10%?b.Would you accept the offer?c.What is the internal rate of return? Can you explain why you would reject a project which has aninternal rate of return greater than its cost of capital?SOLUTION:At 10% discount rate:Net Present Value = - 0 + $5,000 + $4,000 - $11,000 = - 413.22(1.10)(1.10)2 (1.10)3c.This example is a project with cash flows that begin positive and then turn negative--it is like a loan. The 13.6% IRR is therefore like an interest rate on that loan. The opportunity to take a loan at 13.6% when the cost of capital is only 10% is not worthwhile.26.You must pay a creditor $6,000 one year from now, $5,000 two years from now, $4,000 three years from now, $2,000 four years from now, and a final $1,000 five years from now. You would like to restructure the loan into five equal annual payments due at the end of each year. If the agreed interest rate is 6% compounded annually, what is the payment?SOLUTION:Since there are a number of different cash flows, it is easiest to do the first step of this problem using cash flow keys on the calculator. To find the present value of the current loan payments:27.Find the future value of the following ordinary annuities (payments begin one year from today and all interest rates compound annually):a.$100 per year for 10 years at 9%.b.$500 per year for 8 years at 15%.c.$800 per year for 20 years at 7%.d.$1,000 per year for 5 years at 0%.e.Now find the present values of the annuities in a-d.f.What is the relationship between present values and future values?SOLUTION:Future Value of Annuity:e.f.The relationship between present value and future value is the following:FV = PV x (1+i)n28.Suppose you will need $50,000 ten years from now. You plan to make seven equal annual deposits beginning three years from today in an account that yields 11% compounded annually. How large should the annual deposit be?SOLUTION:You will be making 7 payments beginning 3 years from today. So, we need to find the value of an immediate annuity with 7 payments whose FV is $50,000:29.Suppose an investment offers $100 per year for five years at 5% beginning one year from today.a.What is the present value? How does the present value calculation change if one additional payment isadded today?b.What is the future value of this ordinary annuity? How does the future value change if one additionalpayment is added today?SOLUTION:$100 x [(1.05)5] - 1 = $552.56.05If you were to add one additional payment of $100 today, the future value would increase by:$100 x (1.05)5 = $127.63. Total future value = $552.56 + $127.63 = $680.19.Another way to do it would be to use the BGN mode for 5 payments of $100 at 5%, find the future value of that, and then add $100. The same $680.19 is obtained.30.You are buying a $20,000 car. The dealer offers you two alternatives: (1) pay the full $20,000 purchase price and finance it with a loan at 4.0% APR over 3 years or (2) receive $1,500 cash back and finance the rest at a bank rate of 9.5% APR. Both loans have monthly payments over three years. Which should you choose? SOLUTION:31.You are looking to buy a sports car costing $23,000. One dealer is offering a special reduced financing rate of 2.9% APR on new car purchases for three year loans, with monthly payments. A second dealer is offering a cash rebate. Any customer taking the cash rebate would of course be ineligible for the special loan rate and would have to borrow the balance of the purchase price from the local bank at the 9%annual rate. How large must the cash rebate be on this $23,000 car to entice a customer away from the dealer who is offering the special 2.9% financing?SOLUTION:of the 2.9% financing.32.Show proof that investing $475.48 today at 10% allows you to withdraw $150 at the end of each of the next 4 years and have nothing remaining.SOLUTION:You deposit $475.48 and earn 10% interest after one year. Then you withdraw $150. The table shows what happensAnother way to do it is simply to compute the PV of the $150 annual withdrawals at 10% : it turns out to be exactly $475.48, hence both amounts are equal.33.As a pension manager, you are considering investing in a preferred stock which pays $5,000,000 per year forever beginning one year from now. If your alternative investment choice is yielding 10% per year, what is the present value of this investment? What is the highest price you would be willing to pay for this investment? If you paid this price, what would be the dividend yield on this investment?SOLUTION:Present Value of Investment:PV = $5,000,000 = $50,000,000.10Highest price you would be willing to pay is $50,000,000.Dividend yield = $5,000,000 = 10%.$50,000,00034. A new lottery game offers a choice for the grand prize winner. You can receive either a lump sum of $1,000,000 immediately or a perpetuity of $100,000 per year forever, with the first payment today. (If you die, your estate will still continue to receive payments). If the relevant interest rate is 9.5% compounded annually, what is the difference in value between the two prizes?SOLUTION:The present value of the perpetuity assuming that payments begin at the end of the year is:$100,000/.095 = $1,052,631.58If the payments begin immediately, you need to add the first payment. $100,000 + 1,052,632 = $1,152,632.So the annuity has a PV which is greater than the lump sum by $152,632.35.Find the future value of a $1,000 lump sum investment under the following compounding assumptions:a.7% compounded annually for 10 yearsb.7% compounded semiannually for 10 yearsc.7% compounded monthly for 10 yearsd.7% compounded daily for 10 yearse.7% compounded continuously for 10 yearsa.$1,000 x (1.07)10 = $1,967.15b.$1,000 x (1.035)20 = $1,989.79c.$1,000 x (1.0058)120 = $2,009.66d.$1,000 x (1.0019178)3650 = $2,013.62e.$1,000 x e.07x10 = $2,013.7536.Sammy Jo charged $1,000 worth of merchandise one year ago on her MasterCard which has a stated interest rate of 18% APR compounded monthly. She made 12 regular monthly payments of $50, at the end of each month, and refrained from using the card for the past year. How much does she still owe? SOLUTION:Sammy Jo has taken a $1,000 loan at 1.5% per month and is paying it off in monthly installments of $50. We could work out the amortization schedule to find out how much she still owes after 12 payments, but a shortcut on the financial calculator is to solve for FV as follows:37.Suppose you are considering borrowing $120,000 to finance your dream house. The annual percentage rate is 9% and payments are made monthly,a.If the mortgage has a 30 year amortization schedule, what are the monthly payments?b.What effective annual rate would you be paying?c.How do your answers to parts a and b change if the loan amortizes over 15 years rather than 30?EFF = [1 + .09]1238.Suppose last year you took out the loan described in problem #37a. Now interest rates have declined to 8% per year. Assume there will be no refinancing fees.a.What is the remaining balance of your current mortgage after 12 payments?b.What would be your payment if you refinanced your mortgage at the lower rate for 29 years? SOLUTION:Exchange Rates and the Time Value of Money39.The exchange rate between the pound sterling and the dollar is currently $1.50 per pound, the dollar interest rate is 7% per year, and the pound interest rate is 9% per year. You have $100,000 in a one-year account that allows you to choose between either currency, and it pays the corresponding interest rate.a.If you expect the dollar/pound exchange rate to be $1.40 per pound a year from now and are indifferentto risk, which currency should you choose?b.What is the “break-even” value of the dollar/pound exchange rate one year from now?SOLUTION:a.You could invest $1 today in dollar-denominated bonds and have $1.07 one year from now. Or you couldconvert the dollar today into 2/3 (i.e., 1/1.5) of a pound and invest in pound-denominated bonds to have .726667(i.e., 2/3 x 1.09) pounds one year from now. At an exchange rate of $1.4 per pound, this would yield 0.726667(1.4) = $1.017 (this is lower than $1.07), so you would choose the dollar currency.b.For you to break-even the .726667 pounds would have to be worth $1.07 one year from now, so the break-evenexchange rate is $1.07/.726667 or $1.4725 per pound. So for exchange rates lower than $1.4725 per pound one year from now, the dollar currency will give a better return.。
金融学货币银行学各章节复习汇总
金融学复习汇总一、判断题1.俗话说的“不要把鸡蛋放在一个篮子里〞表达的金融学原理是分散化投资可以降低风险。
〔A〕2.对于一个经济系统而言,金融体系必须是一个能自我平衡的体系,否则将会引发金融危机、经济危机乃至政治危机。
〔A〕3.20世纪90年代以来,传统的银行业务正在遭受来自证券业、保险和基金组织的侵蚀,世界金融体系越来越显得多元化,银行作为各国金融体系的信贷中心、结算中心和现金出纳中心的地位已不复存在。
〔B〕4.钱、货币、通货、现金都是一回事,银行卡也是货币。
〔B〕5.所谓“流通中的货币〞就是现金,即发挥支付手段职能的货币和发挥流通手段职能的货币的总和。
〔B〕6.信用货币虽然本身没有价值,但由于其能够发挥货币的职能,所以构成社会财富的组成局部。
〔A〕7.电子货币作为一种信用货币,预示着无现金社会的开展趋势,即完全没有货币的社会。
〔B〕8.目前,世界各国普遍以金融资产平安性的强弱作为划分货币层次的主要依据。
〔B〕9.我国M1层次的货币口径是:M1=流通中现金+定期存款。
〔B〕10.在纸币本位制下,如果在同一市场上出现两种以上可流通纸币,会导致实际价值较低的货币排斥实际价值高的货币的“劣币驱逐良币〞现象。
〔B〕11.货币制度最根本的内容是确定货币名称和货币单位,货币名称和货币单位确定了,一国的货币制度也就确定了。
〔B〕12.金融市场被称为国民经济的“晴雨表〞,这实际上指的就是金融市场的调节功能。
〔B〕13.资本市场是指以期限在1年以内的金融工具为交易对象的短期金融市场。
〔B〕14.金融产品的收益性与流动性一般是反向变动,收益性越强,流动性越差。
〔B〕15.我们经常说高风险高收益,是说只要投资者承当高风险,就可以获得高收益。
〔B〕1.商业银行创造信用的能力不受任何条件的限制。
〔B〕2.商业银行与其他金融机构的根本区别在于商业银行是唯一吸收活期存款、开设支票存款账户的金融中介机构。
〔A〕3.分业经营限制了商业银行的业务经营活力,不利于提高资金的配置与使用效率。
