第二章控制系统的数学模型例题
合集下载
拉普拉斯变换 例题解析

2、
线性系统特性──满足齐次性、可加性
z 线性系统便于分析研究。 z 在实际工程问题中,应尽量将问题化到线性系统范围内研究。 z 非线性元部件微分方程的线性化。 例:某元件输入输出关系如下,导出在工作点 α 0 处的线性化增量方程
y(α ) = E 0 cosα
解:在 α = α 0 处线性化展开,只取线性项:
& m + f mω m = M m ┈牛 力矩方程: J m ⋅ ω
顿 变量关系: u a
i − Mm ωm E b −− −
消去中间变量有:
&m + ωm = kmua Tmω
⎧T = J m R [R ⋅ f m + C e C m ] ⎪ m ⎨ ⎪k m = C m [R ⋅ f m + C e C m ] ⎩
0 0 -st − st =⎡ ⎣e f ( t ) ⎤ ⎦ − ∫ f ( t )de 0 0 − st =⎡ ⎣0-f ( 0 ) ⎤ ⎦ + s ∫ f ( t )e dt ∞ ∞ ∞
∞
∞
= sF ( s ) − f ( 0 ) =右
0
(n) ( n-2 ) n-1 n-2 ⎤ n ′ 进一步:L ⎡ ( 0 ) − f ( n −1) ( 0 ) ⎣ f ( t ) ⎦ = s F ( s ) − s f ( 0 ) − s f ( 0 ) − L − sf
s + 0.4
( s + 0.4 )
2
+ 12
2
=
s + 0.4 s + 0.8s + 144.16
2
6).已知F(s) =
3s 2 + 2s + 8 求f ( ∞ ) = ? f(0) = ? f(∞) = 1, f(0) = 0 s ( s + 2 ) ( s 2 + 2s + 4 )
自动控制原理第二章 控制系统的数学模型4

x
G
y
x
G
y
上图中, 两者都具有关系: 上图中, 两者都具有关系 y(s) = G(s)x(s)。支路对节点x 来说 是输出支路,对输出节点y来说是输入支路 来说是输入支路。 是输出支路,对输出节点 来说是输入支路。
2
信号流图的术语
[几个术语]: 输入节点(源点 : 输入节点 源点):只有输出支路 源点 的节点。 的节点。如: R,N。 , 。 输出节点(阱点 : 输出节点 阱点):只有输入支路 阱点 的节点。 的节点。如: C
4
信号流图的等效变换
串联支路合并: 串联支路合并:
a
b
ab
x3
x1
x2
a
x1
x3
并联支路的合并: 并联支路的合并:
x1
b
x2
x1
a+b
x2
b a 1 m bc
回路的消除: 回路的消除:
a
b
±c
x1 x2
x3
x1
x2
x3
5
信号流图的等效变换
混合支路的清除: 混合支路的清除:
x4 ad b
c
x4
ad bd
18
梅逊公式||例5 梅逊公式 例
[例5]:使用 例 :使用Mason公式计算下述结构图的传递函数 公式计算下述结构图的传递函数
G4
C ( s) E ( s) , R( s) R( s)
R
-
E G 1
H1
+
G2
+ -
G3
C
H2
[解]:在结构图上标出节点,如上。然后画出信号流图,如下: 解 :在结构图上标出节点,如上。然后画出信号流图,如下:
第2章 自动控制系统的数学模型(2)

1/R2
I2(s)
Uc
I2
1/C2S
Uc(s)
双RC网络动态结构图
2.4.2. 动态结构图的等效与简化
1 串联连接的传递函数
X 2 (S ) G2 (S ) X 3 (S ) X1(S) X 3 (S ) G1 (S ) X 1 (S ) G(S) G1 (S)G 2 (S)
X3(S) X2(S) G2(S) G1(S)
输出信号的拉氏变换 C ( s) 传递函数 输入信号的拉氏变换零初始条件 R(s)
设线性定常系统由下述n阶线性常微分方程描 述:
dn d n 1 d a0 n c(t ) a1 n 1 c(t ) a n 1 c(t ) a n c(t ) dt dt dt dm d m1 d b0 m r (t ) b1 m1 r (t ) bm1 r (t ) bm r (t ) dt dt dt
例 试绘制如图所示无 1 源网络的结构图i i1
Ui
i i1 i2 ui i 1R1 u0 u0 iR2 1 i2dt R1i1 c 由(1)式有 I1(S)
i2
C
பைடு நூலகம்
R1
R2
U0
解:
I(S) I1 (S) I 2 (S) (1) U i (S) I1 (S)R1 U 0 (S) (2) U 0 (S) R 2 I(S) (3) R 1I1 (S) 1 I2(S ) CS (4)
C (s) b0 s m b1 s m1 bm1 s bm M (s) G( s ) n n 1 R(s) a0 s a1 s an1 s an N ( s)
自动控制原理-第二章-控制系统的数学模型—结构图-信号流图-传递函数

(1)单位脉冲 (2)单位阶跃 (3)单位斜坡 (4)单位加速度 (5)指数函数 (6)正弦函数 (7)余弦函数
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
第二章控制系统的数学模型例题全

L ddt
Ac ost
L
Asint
A 2 S2
2
另一种解法:
设xt Acost, xs A s
s2 2
x0 Acost A t0
Lddt xt sx(s) x0
Lddt Acost
s s2
s
2
A
A 2
S2 2
7已知f t cost- cos2t,求Fs。 8已知f t 2e-tsin2t,求Fs。 9已知f t te-2t ,求Fs。 10已知f t t n ,求Fs。
dt
2已知Fs
ss
4
2
, 求f
t
。
3已知Fs 1 ,求f 0、f 。
sa
3已知Fs 1 ,求f 0、f 。
sa
f 0
lims Fs s
lims s
s
1 a
1
f
lims s0
s
1 a
0
• Using the laplace transform methodes solve the differential equations
第二章控制系统的数学模型 例题
1已知f t d Acost,求Fs。
dt
2已知f t 3t 4e2t ,求Fs。
3已知f t e3tsin4t,求Fs。
t
4已知f t Acostdt,求Fs。
0
5已知f t sint ,求Fs。
6已知f t 8e-100t - 5e-200t ,求Fs。
G1
-1
- G2
N1
C
G2
C 1 G 2 G 3
N1 1 G 2 G1G 2G3
西工大、西交大自动控制原理 第二章 控制系统的数学模型_2

5 比较点的移动 比较点的前移:
Rs
Cs
Rs
Cs
Gs
Gs
Qs
1 Qs
Gs
若要将比较点由方框后移至方框的前面,为保持信号 的等效,要在移动后的信号线上加入一个比较点所越 过的方框的倒数。
5 比较点的移动 比较点的后移:
Rs
Cs Gs
Rs Gs
Cs
Qs
Qs
G(s)
若要将比较点由方框前移至方框的后面,为保持信号的 等效,要在移动后的信号线上加入一个比较点所越过的 方框。
2-3 控制系统的结构图与信号流图
控制系统的结构图概述
控制系统的结构图(block diagram)是描述系统各元部 件之间信号传递关系的数学图形,表示了系统中各变量 间的因果关系以及对各变量所进行的运算。通过对系统 结构图进行等效变换(equivalent transform)后,可 求出系统的传递函数。
G1(s)
-1 H(s)
R(s)=0
f
(s)
C(s) F(s)
G2 ( s) 1 G2 (s)H (s)(1)G1(s)
G2 ( s) 1 G2 (s)G1(s)H (s)
G2(s) G2(s) 1 G(s)H(s) 1 Gk (s)
单位反馈系统H(s)=1,有
f
(s)
C(s) F(s)
若令:G(s) G1(s)G2(s) 为前向通路传递函数,
则:
B(s)
Gk (s) (s) G(s)H(s)
可见:系统开环传递函数Gk(s)等于前向通路传递函 数G(s)=G1(s)G2(s)与反馈通道传递函数H(s)的乘积。
R(S) ε(s) G1(s)
F(s)
基本要求-控制系统数学模型

航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
线性连续系统微分方程的一般形式
d c (t ) d c (t ) dc (t ) an an 1 ... a1 a0 c ( t ) n n 1 dt dt dt d m r (t ) d m 1r (t ) dr (t ) bm bm 1 ... b1 b0 r (t ) m m 1 dt dt dt
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
• 3.表示形式 a.时域:微分﹑差分﹑状态方程 b.复域:传递函数﹑结构图 c.频域:频率特性
三种数学模型之间的关系 线性系统
拉氏 傅氏 传递函数 微分方程 频率特性 变换 变换
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
自动控制原理
第二章控制系统的数学模型
题目变种3,寻求新解法
1 R1 cs I ( s) U ( s) U r ( s) c 1 R1 cs
Uc( s ) I (s) R2
联立,可解得: 微分方程为:
U c ( s) R2 (1 R1Cs) U r (s) R1 R2 R1 R2 Cs
微分方程的标准形式: 1、与输入量有关的项写在方程的右端; 2、与输出量有关的项写在方程的左端; 3、方成两端变量的导数项均按降幂排列
mx(t ) fx(t ) kx(t ) F (t )
航空
第二章控制系统的数学模型
电气系统三元件(知识补充)
电阻
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
2.为什么要建立数学模型: 只是定性地了解系统的工作原理和大致的 运动过程是不够的,还要从理论上对系统 性能进行定量的分析和计算。 另一个原因:许多表面上看毫无共同之处 的控制系统,其运动规律具有相似性,可 以用相同形式的数学模型表示。
自动控制原理
第二章控制系统的数学模型
线性连续系统微分方程的一般形式
d c (t ) d c (t ) dc (t ) an an 1 ... a1 a0 c ( t ) n n 1 dt dt dt d m r (t ) d m 1r (t ) dr (t ) bm bm 1 ... b1 b0 r (t ) m m 1 dt dt dt
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
• 3.表示形式 a.时域:微分﹑差分﹑状态方程 b.复域:传递函数﹑结构图 c.频域:频率特性
三种数学模型之间的关系 线性系统
拉氏 傅氏 传递函数 微分方程 频率特性 变换 变换
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
自动控制原理
第二章控制系统的数学模型
题目变种3,寻求新解法
1 R1 cs I ( s) U ( s) U r ( s) c 1 R1 cs
Uc( s ) I (s) R2
联立,可解得: 微分方程为:
U c ( s) R2 (1 R1Cs) U r (s) R1 R2 R1 R2 Cs
微分方程的标准形式: 1、与输入量有关的项写在方程的右端; 2、与输出量有关的项写在方程的左端; 3、方成两端变量的导数项均按降幂排列
mx(t ) fx(t ) kx(t ) F (t )
航空
第二章控制系统的数学模型
电气系统三元件(知识补充)
电阻
航空工程学院航空工程实验中心
自动控制原理
第二章控制系统的数学模型
2.为什么要建立数学模型: 只是定性地了解系统的工作原理和大致的 运动过程是不够的,还要从理论上对系统 性能进行定量的分析和计算。 另一个原因:许多表面上看毫无共同之处 的控制系统,其运动规律具有相似性,可 以用相同形式的数学模型表示。
自控例题解析1
.
The cofactor of the determinant along path 1 is evaluated by removing the loops that touch path 1 from . Therefore we have
and .
Similarly,the cofactor for path 2 is
= (2.3)
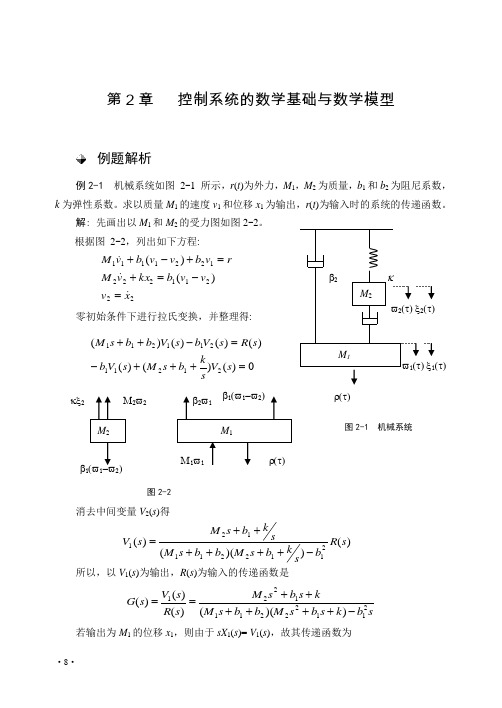
FIGURE2.1
Two-mass
Mechanical system.
electric circuit
analog C1=M1,
C2=M2,L=1/k,
R1=1/b1,
R2=1/b2.
(a)
v1R1v2
CurrentC1R1C2L
r(t)
(b)
Assuming the velocity ofM1is the output variable,we solve forV1(s) by matrix inversion or Cramer’s rule to obtain(2,3)
解:(1)在结构图上把需要引出的信号做出标记(如图2-52中的“O”所示),对应画出信号流图2-53所示。
(2)利用梅逊公式:当R1(s)单独作用时,系统有3条前向通道,3个回路,其中一组两两互不接触。
图2-52
图2-53 信号流图
故
R2(s)单独作用时对应有两条前向通路。
故
例2-18系统微分方程式如下:
The velocities, and ,of the mechanical system are directly analogous to the node voltages and of the electrical circuit. The simultaneous equations,assuming theinitial conditions are zero,
The cofactor of the determinant along path 1 is evaluated by removing the loops that touch path 1 from . Therefore we have
and .
Similarly,the cofactor for path 2 is
= (2.3)
FIGURE2.1
Two-mass
Mechanical system.
electric circuit
analog C1=M1,
C2=M2,L=1/k,
R1=1/b1,
R2=1/b2.
(a)
v1R1v2
CurrentC1R1C2L
r(t)
(b)
Assuming the velocity ofM1is the output variable,we solve forV1(s) by matrix inversion or Cramer’s rule to obtain(2,3)
解:(1)在结构图上把需要引出的信号做出标记(如图2-52中的“O”所示),对应画出信号流图2-53所示。
(2)利用梅逊公式:当R1(s)单独作用时,系统有3条前向通道,3个回路,其中一组两两互不接触。
图2-52
图2-53 信号流图
故
R2(s)单独作用时对应有两条前向通路。
故
例2-18系统微分方程式如下:
The velocities, and ,of the mechanical system are directly analogous to the node voltages and of the electrical circuit. The simultaneous equations,assuming theinitial conditions are zero,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章控制系统的数学模型 例题
d (1)已知f (t ) = (Acosωt ), 求F(s )。 dt − 2t (2)已知f (t ) = 3t + 4e , 求F(s )。
(3)已知f (t ) = e
t 0
3t
sin4t , 求F(s )。
(4)已知f (t ) = ∫ Acosωtdt, 求F(s )。 (5)已知f (t ) = sin (ωt + ϕ ), 求F(s )。 -100t - 200t (6)已知f (t ) = 8e - 5e , 求F(s )。
T T
Lb3D4037 求图示波形函数的拉氏变换。 求图示波形函数的拉氏变换。
f(t)
2 1 0 1 2 3 t
f ( t ) = 1( t − 1) +
1 1 t × 1(t − 1) − 2 × 1(t − 3) − t × 1(t − 3) 2 2 1 −s 1 −s 2 −3s 1 −3s F(s ) = e + 2 e − e _ 2 e s s 2s 2s e −s 1 e −3s 1 = 2 s + − 2 2s + 2 s 2 s
B(s) k2 = (s + 1 − j) = 4 − 3j A(s) s = −1+ j B(s) k3 = (s + 2) = -5 A (s) s = −2 B(s) k3 = (s + 4) = -3 A (s) s = −4 4 + 3j 4 - 3j 5 3 F(s) = + − − s +1+ j s +1− j s + 2 s + 4
− 2t
− 3e
− 4t
− 2t
− 3e
− 4t
− 3e
La3D5025 列写出如图 列写出如图D-12所示电路的微分方程, 所示电路的微分方程, 所示电路的微分方程 并写出传递函数。 并写出传递函数。
R1 C2
ui
i
C1
R2
u0
图D - 12
解:可列出系统的微分方程如下
1 d i( t ) = ( u i − u 0 ) + C1 ( u i − u 0 ) R1 dt u = iR + 1 idt 1 将微分方程作拉氏变换 0 C2 ∫
• Using the laplace transform methodes solve the differential equations
dx (t ) + x (t ) = 0, x (0 ) = 1 dt 解:sx (s ) − x (0 ) + x (s ) = 0 1 x (s )(s + 1) = 1,x (s ) = s +1 −t x (t ) = e
∴ f ( t ) = L [F(s)]
−1
= ( j) t
[4(e
− jt
(8cost + 6sint ) − 5e
+e
jt
) + 3j(e
+ (4 − 3j)e
− jt − 2t
− ( −1+ j) t jt
−e
)] − 5e
− 4t
− 5e
Lb3D5039求图示波形的拉氏变换 求图示波形的拉氏变换
f(t)
2a a 0 T 2T 3T t
a a f (t ) = a × 1(t ) + t × 1(t − T ) − t × 1(t − 2T ) − 2a × 1(t − 3T ) T T a a −Ts a − 2Ts 1 −Ts F(s ) = + 2 e − 2 e − 2a e s Ts s Ts
(
)
Lb3D2034求如图所示三角波的拉氏变换。 4 4 T 4 T 4 提示:f (t ) = 2 t − 2 t × 1 t − − 2 t × 1 t − + 2 × 1(t − T ) 2 T 2 T T T
f (t )
2 T
0
T 2
T
t
4 4 T 4 T 4 f (t ) = 2 t − 2 t × 1 t − − 2 t × 1 t − + 2 × 1(t − T ) 2 T 2 T T T 4 4 -2s 4 -2s 4 -Ts F(s ) = 2 2 − 2 2 e − 2 2 e + 2 2 e T s T s T s T s T - s 4 = 2 2 (1 - 2e 2 + e -Ts ) T s
Aω d L (Acosωt ) = L[− Aωsinωt ] = − 2 2 dt S +ω 另一种解法:
2
s 设x (t ) = Acosωt, x (s ) = A 2 2 s +ω x (0 ) = Acosωt t =0 = A d L x (t ) = sx (s) − x (0 ) dt d s Aω 2 L (Acosωt ) = s ⋅ 2 −A = − 2 2 dt s +ω S +ω2
La3D4023求函数 B(s) 20(s + 1)(s + 3) F(s) = = A(s) (s + 1 + j)(s + 1 + j)(s + 2)(s + 4)
的F(s )部分分式展开式和f (t )。
k3 k1 k2 k4 解:F(s) = + + + s +1+ j s +1− j s + 2 s + 4 B(s) k1 = (s + 1 + A(s) j) = 4 + 3j s = −1− j
2
(
)
3 A BS + C = + 2 S(S 2 + 2S + 5) S S + 2S + 5 3 3 S]S=0 = 5 S(S 2 + 2S + 5) 3 A BS + C 2 (S + 2S + 5) [ ]S= −1+ j2 = {[ + 2 (S 2 + 2S + 5)S=-1+ j2 ] } S S + 2S + 5 S(S 2 + 2S + 5) A =[ 3 [(-1 + j2) 2 + 2(-1 + j2) + 5] 3 [ ] = {5 + B(-1 + j2) + C} - 1 + j2 - 1 + j2 3 [(-3 - j4 − 2 + j4 + 5] 3 [ ]= 5 − B + j2B + C - 1 + j2 - 1 + j2 3 6 B = - ;C = − 5 5
Lb3D2033求如图D - 18所示方波的拉氏变换。
f(t)
1/T
T
t
提示:波形函数表达式为 1 1 f ( t ) = × 1(t ) − × 1(t - T ) T T
1 1 Q f ( t ) = × 1(t ) − × 1(t - T ) T T 1 1 -sT 1 − e = ∴ L(f ( t )] = 1 - e -sT Ts Ts Ts
(7 )已知f (t ) = cost - cos2t, 求F(s )。 -t (8)已知f (t ) = 2e sin2t, 求F(s )。 - 2t (9)已知f (t ) = te , 求F(s )。 n (10)已知f (t ) = t , 求F(s )。 − at (11)已知f (t ) = b(1 − e ), 求F(s )。
已知 s + 5s + 9s + 7 F(s ) = (s + 1)(s + 2)
3 2
求f (t )
s+3 G (s ) = s + 2 + (s + 1)(s + 2) d −t − 2t g(t ) = δ (t ) + 2δ (t ) + 2e − e dt
已知 2s + 12 F(s ) = 2 s + 2s + 5 求f (t )
已知 && + 2x + 5x = 3, x (0 ) = 0, x (0 ) = 0 & & x 求x (t )
3 s x (s ) + 2sx (s ) + 5x (s ) = s 3 x (s ) = 2 s s + 2s + 5 3 1 3 s+2 = ⋅ − ⋅ 2 5 s 5 s + 2s + 5 3 1 3 2 3 s +1 = ⋅ − ⋅ − ⋅ 2 2 5 s 10 (s + 1) + 2 5 (s + 1) 2 + 2 2 3 3 −t 3 −t x (t ) = − ⋅ e sin2t − ⋅ e cos2t 5 10 5
di (1)已知Ri(t) + L = u (t ) − e(t ), 求i(t )的拉氏式。 dt 4 (2)已知F(s ) = , 求f (t )。 s(s + 2 )
1 (3)已知F(s ) = , 求f (0)、f (∞ )。 s+a
1 (3)已知F(s ) = , 求f (0 )、f (∞ )。 s+a 1 f (0 ) = lim s ⋅ F(s ) = lim s ⋅ =1 s+a s →∞ s →∞ 1 f (∞ ) = lim s ⋅ =0 s+a s →0
d (1)已知f (t ) = (Acosωt ), 求F(s )。 dt − 2t (2)已知f (t ) = 3t + 4e , 求F(s )。
(3)已知f (t ) = e
t 0
3t
sin4t , 求F(s )。
(4)已知f (t ) = ∫ Acosωtdt, 求F(s )。 (5)已知f (t ) = sin (ωt + ϕ ), 求F(s )。 -100t - 200t (6)已知f (t ) = 8e - 5e , 求F(s )。
T T
Lb3D4037 求图示波形函数的拉氏变换。 求图示波形函数的拉氏变换。
f(t)
2 1 0 1 2 3 t
f ( t ) = 1( t − 1) +
1 1 t × 1(t − 1) − 2 × 1(t − 3) − t × 1(t − 3) 2 2 1 −s 1 −s 2 −3s 1 −3s F(s ) = e + 2 e − e _ 2 e s s 2s 2s e −s 1 e −3s 1 = 2 s + − 2 2s + 2 s 2 s
B(s) k2 = (s + 1 − j) = 4 − 3j A(s) s = −1+ j B(s) k3 = (s + 2) = -5 A (s) s = −2 B(s) k3 = (s + 4) = -3 A (s) s = −4 4 + 3j 4 - 3j 5 3 F(s) = + − − s +1+ j s +1− j s + 2 s + 4
− 2t
− 3e
− 4t
− 2t
− 3e
− 4t
− 3e
La3D5025 列写出如图 列写出如图D-12所示电路的微分方程, 所示电路的微分方程, 所示电路的微分方程 并写出传递函数。 并写出传递函数。
R1 C2
ui
i
C1
R2
u0
图D - 12
解:可列出系统的微分方程如下
1 d i( t ) = ( u i − u 0 ) + C1 ( u i − u 0 ) R1 dt u = iR + 1 idt 1 将微分方程作拉氏变换 0 C2 ∫
• Using the laplace transform methodes solve the differential equations
dx (t ) + x (t ) = 0, x (0 ) = 1 dt 解:sx (s ) − x (0 ) + x (s ) = 0 1 x (s )(s + 1) = 1,x (s ) = s +1 −t x (t ) = e
∴ f ( t ) = L [F(s)]
−1
= ( j) t
[4(e
− jt
(8cost + 6sint ) − 5e
+e
jt
) + 3j(e
+ (4 − 3j)e
− jt − 2t
− ( −1+ j) t jt
−e
)] − 5e
− 4t
− 5e
Lb3D5039求图示波形的拉氏变换 求图示波形的拉氏变换
f(t)
2a a 0 T 2T 3T t
a a f (t ) = a × 1(t ) + t × 1(t − T ) − t × 1(t − 2T ) − 2a × 1(t − 3T ) T T a a −Ts a − 2Ts 1 −Ts F(s ) = + 2 e − 2 e − 2a e s Ts s Ts
(
)
Lb3D2034求如图所示三角波的拉氏变换。 4 4 T 4 T 4 提示:f (t ) = 2 t − 2 t × 1 t − − 2 t × 1 t − + 2 × 1(t − T ) 2 T 2 T T T
f (t )
2 T
0
T 2
T
t
4 4 T 4 T 4 f (t ) = 2 t − 2 t × 1 t − − 2 t × 1 t − + 2 × 1(t − T ) 2 T 2 T T T 4 4 -2s 4 -2s 4 -Ts F(s ) = 2 2 − 2 2 e − 2 2 e + 2 2 e T s T s T s T s T - s 4 = 2 2 (1 - 2e 2 + e -Ts ) T s
Aω d L (Acosωt ) = L[− Aωsinωt ] = − 2 2 dt S +ω 另一种解法:
2
s 设x (t ) = Acosωt, x (s ) = A 2 2 s +ω x (0 ) = Acosωt t =0 = A d L x (t ) = sx (s) − x (0 ) dt d s Aω 2 L (Acosωt ) = s ⋅ 2 −A = − 2 2 dt s +ω S +ω2
La3D4023求函数 B(s) 20(s + 1)(s + 3) F(s) = = A(s) (s + 1 + j)(s + 1 + j)(s + 2)(s + 4)
的F(s )部分分式展开式和f (t )。
k3 k1 k2 k4 解:F(s) = + + + s +1+ j s +1− j s + 2 s + 4 B(s) k1 = (s + 1 + A(s) j) = 4 + 3j s = −1− j
2
(
)
3 A BS + C = + 2 S(S 2 + 2S + 5) S S + 2S + 5 3 3 S]S=0 = 5 S(S 2 + 2S + 5) 3 A BS + C 2 (S + 2S + 5) [ ]S= −1+ j2 = {[ + 2 (S 2 + 2S + 5)S=-1+ j2 ] } S S + 2S + 5 S(S 2 + 2S + 5) A =[ 3 [(-1 + j2) 2 + 2(-1 + j2) + 5] 3 [ ] = {5 + B(-1 + j2) + C} - 1 + j2 - 1 + j2 3 [(-3 - j4 − 2 + j4 + 5] 3 [ ]= 5 − B + j2B + C - 1 + j2 - 1 + j2 3 6 B = - ;C = − 5 5
Lb3D2033求如图D - 18所示方波的拉氏变换。
f(t)
1/T
T
t
提示:波形函数表达式为 1 1 f ( t ) = × 1(t ) − × 1(t - T ) T T
1 1 Q f ( t ) = × 1(t ) − × 1(t - T ) T T 1 1 -sT 1 − e = ∴ L(f ( t )] = 1 - e -sT Ts Ts Ts
(7 )已知f (t ) = cost - cos2t, 求F(s )。 -t (8)已知f (t ) = 2e sin2t, 求F(s )。 - 2t (9)已知f (t ) = te , 求F(s )。 n (10)已知f (t ) = t , 求F(s )。 − at (11)已知f (t ) = b(1 − e ), 求F(s )。
已知 s + 5s + 9s + 7 F(s ) = (s + 1)(s + 2)
3 2
求f (t )
s+3 G (s ) = s + 2 + (s + 1)(s + 2) d −t − 2t g(t ) = δ (t ) + 2δ (t ) + 2e − e dt
已知 2s + 12 F(s ) = 2 s + 2s + 5 求f (t )
已知 && + 2x + 5x = 3, x (0 ) = 0, x (0 ) = 0 & & x 求x (t )
3 s x (s ) + 2sx (s ) + 5x (s ) = s 3 x (s ) = 2 s s + 2s + 5 3 1 3 s+2 = ⋅ − ⋅ 2 5 s 5 s + 2s + 5 3 1 3 2 3 s +1 = ⋅ − ⋅ − ⋅ 2 2 5 s 10 (s + 1) + 2 5 (s + 1) 2 + 2 2 3 3 −t 3 −t x (t ) = − ⋅ e sin2t − ⋅ e cos2t 5 10 5
di (1)已知Ri(t) + L = u (t ) − e(t ), 求i(t )的拉氏式。 dt 4 (2)已知F(s ) = , 求f (t )。 s(s + 2 )
1 (3)已知F(s ) = , 求f (0)、f (∞ )。 s+a
1 (3)已知F(s ) = , 求f (0 )、f (∞ )。 s+a 1 f (0 ) = lim s ⋅ F(s ) = lim s ⋅ =1 s+a s →∞ s →∞ 1 f (∞ ) = lim s ⋅ =0 s+a s →0
