专题17 电场叠加(提高篇)(解析版)
高中物理电场叠加问题的几种解题技巧
2019第2期中（总第291期）例1：某绝缘球壳均匀带电+Q ，半径为R ，其球心处有一带电量为+q 的点电荷，其受力为零。
当于球壳上挖去一半径为r （r<<R ）的圆时，受力平衡被打破，试求此时点电荷的受力大小。
（静电力衡量为k ）解法1：该解法的思路我们称之为‘补偿法’，题干中说在球壳上挖掉一个圆孔，其作用相当于在圆孔处放置了一个带电量相当的负电荷，经过求解可以知道负电荷q ’的值为q ’=Q πr 2/4πR 2。
通过补偿法我们知道，挖去圆孔之前受力平衡，挖去之后所受力相当于在圆孔处放置等量异种电荷时点电荷所受的力，通过公式求解可得：F=KqQr 2/4R 2X1/R 2=KqQr 2/4R 4因为点电荷为正电荷，补偿小球带负电荷，所以力的方向是由圆心指向小孔。
解法2：另外的一种解法的思路是在球壳上挖去一个圆孔，其作用等效于在与小孔原点对称位置处放置一同性等量电荷，大小为：q ’=Q πr 2/4πR 2=Qr 2/4R 2，由此可求镜像电荷对点电荷的库仑力为F=KqQr 2/4R 4，方向由虚拟电荷指向点电荷，也就是由点电荷指向小圆孔。
例2：如下图所示：有一均匀带电圆环，带电量为+Q ，已知圆环半径为R ，现过圆形O 做圆环平面的垂线，于垂线上距原点O 长度为L 处取一点P ，试问P 点场强。
解法：该题可以使用微元法进行求解，微元法顾名思义，就是把整体拆分成微小的单元进行分析，使用微元法的前提是圆环形状规则，电荷分布均匀，这样假设圆环上的电荷密度为ρ，这样取圆环上一小段长度为Δ1，那么这个小段的带电量就是Δq=ρX Δl ，该小段近似看成一个点电荷，那么这段在P 处的场强E=k Δq/r 2,这个场强可以分为垂直圆环方向和平行圆环方向两个场强，圆环上的电荷对于P 点产生的场强在垂直方向互相抵消，水平方向叠加，所以这里只要求出水平方向的场强Ex 即可。
E x =Ecos θ=cos θk Δq/r 2。
【知识解析】电场叠加-完整版课件
解析：由点电荷的场强公式及电荷的对称分布，可推断出在正方体范 围内电场强度为零的点有体中心和各面中心。
再见
电场叠加
等量异种点电荷的电场
1.两点电荷连线上各点的场强方向从正电荷指 向负电荷，沿电场线方向场强先变小再变大。 2.两点电荷连线的中垂面(线)上，电场线的方 向均相同，即场强方向相同，且与中垂面(线) 垂直。 3.关于O点对称的两点A与A′、B与B′的场强等 大同向。
电场叠加
电荷量为＋q和－q的点电荷分别位于正方体的顶点，正方体范围内电场 强度为零的点有( ) D
电场叠加原理
电场叠加
多个点电荷在电场中某点的电场强度为 各个点电荷单独在该点产生的电场强度的 矢量和。
电场强度的叠加遵守平行四边形定则。
电场叠加
等量同种点电荷的电场
1.两点电荷连线中点O处的场强为零。 2.从两点电荷连线中点O沿中垂面(线)到无限远
，电场线先变密后变疏，即场强先变大后变 小。 3.两点电荷连线中垂线上各点的场强方向和该 直线平行。 4.关于O点对称的两点A与A′、B与B′的场强等大 反向。
电场的叠加解析电荷分布产生的电场的叠加效应
电场的叠加解析电荷分布产生的电场的叠加效应电场叠加是指当有多个电荷同时存在时，它们所产生的电场可以互相叠加的现象。
这种叠加效应可以通过分析电荷的分布和电场的特性来进行解析，从而计算出叠加电场的强度和方向。
本文将介绍电场叠加的基本原理和应用。
一、电场叠加原理电场的叠加原理是基于库仑定律和叠加原理的基础上得出的。
根据库仑定律，两个点电荷之间的电场强度与它们之间的距离和电荷量有关。
假设有n个电荷在同一空间中，那么每个电荷产生的电场都可以看作是其他（n-1）个电荷共同作用下的结果。
根据叠加原理，电场强度可以通过将每个电荷产生的电场矢量相加得到。
设第i个电荷qi位于坐标(xi, yi, zi)，观察点P位于坐标(x, y, z)，则第i个电荷对于观察点P产生的电场强度为：Ei = k * qi / r_i^2 * Ri，其中k为库仑常量，ri为观察点P到第i个电荷的距离，Ri为指向观察点P的单位矢量。
将每个电荷产生的电场矢量相加，最终得到观察点P处的总电场强度E：E = E1 + E2 + ... + En二、解析电荷分布产生的电场叠加效应对于复杂的电荷分布，可以利用叠加原理将其分解为若干个简单的电荷分布，然后对每个简单的电荷分布计算其产生的电场，最后再将它们进行叠加得到整个电荷分布产生的电场。
以均匀带电圆环为例，假设圆环半径为R，圆环电荷线密度为λ。
我们可以将圆环切割成无限多的小电荷dq，然后对每个小电荷dq计算其产生的电场，最后进行叠加。
根据对称性和积分计算的方法，可以得到圆环中心点P处的电场强度为：E = k * λ * z / (4π * ε * R^2 * (R^2 + z^2)^(3/2))其中，z为P点沿圆环轴线的垂直距离，ε为真空介质常数。
同样的方法可以应用于其他电荷分布，如均匀带电球体、直线电荷分布等。
三、电场叠加的应用电场叠加原理在电荷分析和电场计算中有着重要的应用。
通过合理地选择电荷分布的特性和叠加方法，可以解析出复杂场景中的电场分布。
电场的叠加Microsoft Word 文档
第1讲 电场的叠加一、基本方法----合成法【例1】．(单选)图中边长为a 的正三角形ABC 的三个顶点分别固定三个点电荷＋q 、＋q 、－q ，则该三角形中心O 点处的场强为( )．A.6kqa 2，方向由C 指向OB.6kqa 2，方向由O 指向C C.3kqa 2，方向由C 指向O D.3kqa 2，方向由O 指向C 答案 B 针对训练：1、如图所示，电量为＋q 和－q 的点电荷分别位于正方体的顶点，正方体范围内电场强度为零的点有( )．A ．体中心、各面中心和各边中点B ．体中心和各边中点C ．各面中心和各边中点D ．体中心和各面中心 答案 D二、巧解电场强度叠加的五种思维方法场强有三个公式：E ＝F q 、E ＝k Q r 2、E ＝Ud ，在一般情况下可由上述公式计算场强，但在求解带电圆环、带电平面等一些特殊带电体产生的场强时，上述公式无法直接应用。
这时，如果转换思维角度，灵活运用补偿法、微元法、对称法、等效法、极限思维法等巧妙方法，可以化难为易。
方法一、补偿法将有缺口的带电圆环补全为圆环，或将半球面补全为球面。
【例2】 均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场。
如图所示，在半球面AB 上均匀分布正电荷，总电荷量为q ，球面半径为R ，CD 为通过半球面顶点与球心O 的轴线，在轴线上有M 、N 两点，OM ＝ON ＝2R 。
已知M 点的场强大小为E ，则N 点的场强大小为( )A.kq2R 2－E B.kq 4R 2 C.kq4R 2－ED.kq2R2＋E 答案 A 针对训练：2、如图所示，半径为均匀带电圆形平板，单位面积带电量为，其轴线上任意一点（坐标为）的电场强度可以由库仑定律和电场强度的叠加原理求出：=2，方向沿轴。
现考虑单位面积带电量为的无限大均匀带电平板，从其中间挖去一半径为的圆板，如图2所示。
则圆孔轴线上任意一点（坐标为）的电场强度为 ( )A. 2B. 2C. 2D. 2 答案 A 方法二、微元法可将带电圆环、带电平面等分成许多微元电荷，每个微元电荷可看成点电荷，再利用公式和场强叠加原理求出合场强。
电场叠加 电场强度与电势差的关系含部分答案
一、应用等效和对称的思维方法求电场强度1．如图所示，带电量为+q 的点电荷与均匀带电薄板相距为2d ，点电荷到带电薄板的垂线通过板的几何中心。
若图中a 点处的电场强度为零，根据对称性，带电薄板在图中b 点处产生的电场强度大小为_______，方向________ 。
解析：因为Ea=0,故薄板与+q 产生的场强在该处大小相等、方向相反,即E 板=Eq=kq/d 2,同时可知,薄板也带正电,根据薄板形成电场的对称性,薄板在b 点的场强也为kq/d 2,方向水平向左.2．(2013·高考新课标全国卷Ⅰ，15题)如图，一半径为R 的圆盘上均匀分布着电荷量为Q 的电荷，在垂直于圆盘且过圆心c 的轴线上有a 、b 、d 三个点，a 和b 、b 和c 、c 和d 间的距离均为R ，在a 点处有一电荷量为q (q >0)的固定点电荷．已知b 点处的场强为零，则d 点处场强的大小为(k 为静电力常量)( )A ．k 3q R 2B ．k 10q 9R 2C ．k Q ＋q R 2D ．k 9Q ＋q 9R 2【解析】选B.本题应从点电荷产生的电场和电场的叠加角度解决问题．已知a 处点电荷和带电圆盘均在b 处产生电场，且b 处场强为零，所以带电圆盘在b 处产生的电场场强E 1与q 在b 处产生的电场场强E ab 等大反向，即E 1＝E ab ＝kqR2，带电圆盘在d 处产生的电场场强E 2＝E 1且方向与E 1相反，q 在d 处产生的电场场强E ad ＝kq(3R )2，则d 处场强E d ＝E 2＋E ad ＝kq R 2＋kq 9R 2＝k 10q9R2，选项B 正确．3、均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场．如图所示，在半球面AB 上均匀分布正电荷，总电荷量为q ，球面半径为R ，CD 为通过半球顶点与球心O 的轴线，在轴线上有M 、N 两点，OM=ON=2R ．已知M 点的场强大小为E ，则N 点的场强大小为（ ）A ．B ．C ．D ．4、N （N>1）个电荷量均为q(q>0)的小球，均匀分布在半径为R 的圆周上，示意如图，若移去位于圆周上P 点的一个小球，则圆心O 点处的电场强度大小为________,方向__________.(已知静电力常量为k)5．如图所示，用长为L 的金属丝弯成半径为r 的圆环，但在A 、B 之间留有宽度为d 的间隙，且d 《r 。
高考物理试题库 专题1.19 电场叠加(基础篇)(解析版)
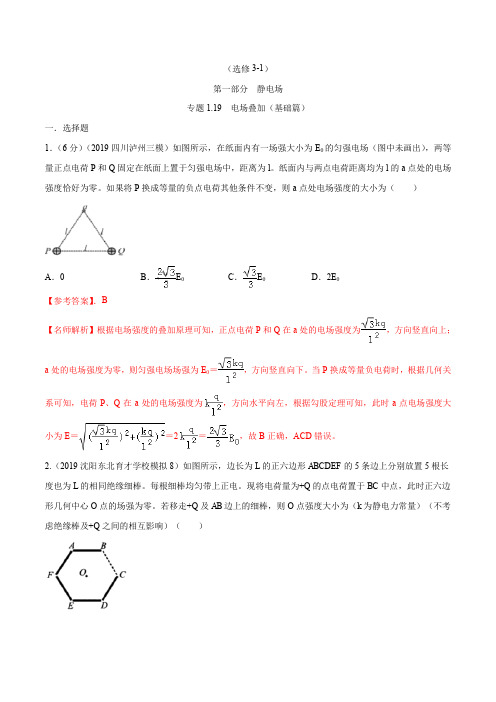
（选修3-1）第一部分静电场专题1.19 电场叠加（基础篇）一．选择题1．（6分）（2019四川泸州三模）如图所示，在纸面内有一场强大小为E0的匀强电场（图中未画出），两等量正点电荷P和Q固定在纸面上置于匀强电场中，距离为l。
纸面内与两点电荷距离均为l的a点处的电场强度恰好为零。
如果将P换成等量的负点电荷其他条件不变，则a点处电场强度的大小为（）A．0 B．E0C．E0D．2E0【参考答案】．B【名师解析】根据电场强度的叠加原理可知，正点电荷P和Q在a处的电场强度为，方向竖直向上；a处的电场强度为零，则匀强电场场强为E0＝，方向竖直向下。
当P换成等量负电荷时，根据几何关系可知，电荷P、Q在a处的电场强度为，方向水平向左，根据勾股定理可知，此时a点电场强度大小为E＝＝2＝，故B正确，ACD错误。
2.（2019沈阳东北育才学校模拟8）如图所示，边长为L的正六边形ABCDEF的5条边上分别放置5根长度也为L的相同绝缘细棒。
每根细棒均匀带上正电。
现将电荷量为+Q的点电荷置于BC中点，此时正六边形几何中心O点的场强为零。
若移走+Q及AB边上的细棒，则O点强度大小为（k为静电力常量）（不考虑绝缘棒及+Q之间的相互影响）（）A ．2kQ LB ．243kQ LCD 【参考答案】D【名师解析】每根细棒均匀带上正电，现将电荷量为+Q 的点电荷置于BC 中点，此时正六边形几何中心O 点的场强为零；根据点电荷电场强度公式可知，+Q 的点电荷在O 点的电场强度大小为E==；那么每根细棒在O 点的电场强度大小也为E=；因此+Q 及AB 边上的细棒在O 点的合电场强度大小E合=23L；其方向如下图所示：若移走+Q 及AB 边上的细棒，那么其余棒在O 点的电场强度大小为E′合；方向与图中方向相反，故ABC 错误，D 正确。
【关键点拨】根据点电荷电场强度公式E=k ，结合矢量的合成法则，及三角知识，即可求解。
考查点电荷的电场强度公式，掌握矢量的合成法则的内容，及三角知识的运用。
电场叠加原理
电场叠加原理
电场叠加原理是指在某个空间中，如果有多个电荷或电荷分布存在，那么在该空间中任一点的电场强度等于每个电荷或电荷分布所产生的电场强度的矢量和。
简言之，电场的叠加是线性的。
具体来说，如果在某一点P处有n个电荷qi（i=1,2,...,n），它们与该点的距离分别为ri，则该点处的电场强度可以表示为：
E=k*(q1/r1^2)*r1̂+k*(q2/r2^2)*r2̂+...+k*(qn/rn^2)*rn̂
其中，k为电场常数，r1̂、r2̂、...、rn̂分别为从电荷qi到点P的矢量方向，r1、r2、...、rn为它们的长度。
这一原理可以用于计算任意分布的电荷所产生的电场分布。
在实际应用中，我们可以将电荷分布离散化为若干小电荷，然后对每个小电荷的电场进行计算，并将结果进行叠加得到总电场分布。
需要注意的是，在考虑电场叠加时，应该同时考虑静电场和电磁场的叠加。
对于静电场，叠加原理适用于任意空间，而对于电磁场，则需要考虑相对论效应和场的传播特性等因素，可能会导致电磁场的非线性叠加。
总之，电场叠加原理是电学中的基本概念之一，它为我们计算和描述电场提供了重要的方法和工具。
在实际应用中，我们可以利用这一原理进行诸如电场分析、电场测量、电场模拟等方面的研究和设计。
高中物理：电场的叠加
高中物理：电场的叠加【知识点的认识】1．电场强度的三个公式及其叠加原理（1）三个公式的比较表达式比较E ＝E ＝k E ＝公式意义电场强度定义式真空中点电荷的电场强度决定式匀强电场中E 与U 关系式适用条件一切电场①真空②点电荷匀强电场比较决定因素由电场本身决定，与q 无关由场源电荷Q 和场源电荷到该点的距离r 共同决定由电场本身决定，d 是场中两点间沿场强方向的距离相同点矢量，单位：1N/C ＝1V/m（2）电场强度的叠加原理多个电荷在电场中某点的电场强度为各个点电荷单独在该点产生的电场强度的矢量和，这种关系叫电场强度的叠加．电场强度的叠加遵循平行四边形定则．在求解电场强度问题时，应分清所叙述的场强是合场强还是分场强，若求分场强，要注意选择适当的公式进行计算；若求合场强时，应先求出分场强，然后再根据平行四边形定则求解．【命题方向】题型一：电场强度的叠加问题例1：如图，一半径为R 的圆盘上均匀分布着电荷量为Q 的电荷，在垂直于圆盘且过圆心c 的轴线上有a 、b 、d 三个点，a 和b 、b 和c 、c 和d 间的距离均为R ，在a 点处有一电荷量为q （q ＞0）的固定点电荷．已知b 点处的场强为零，则d 点处场强的大小为（k 为静电力常量）（）A. B. C. D.分析；由题意可知，半径为R 均匀分布着电荷量为Q 的圆盘上电荷，与在a 点处有一电荷量为q（q＞0）的固定点电荷，在b点处的场强为零，说明各自电场强度大小相等，方向相反．那么在d点处场强的大小即为两者之和．因此根据点电荷的电场强度为即可求解．解：电荷量为q的点电荷在b处产生电场强度为，而半径为R均匀分布着电荷量为Q的圆盘上电荷，与在a点处有一电荷量为q（q＞0）的固定点电荷，在b点处的场强为零，则圆盘在此处产生电场强度也为．那么圆盘在此d产生电场强度则仍为．而电荷量为q的点电荷在d处产生电场强度为，由于都在d处产生电场强度方向相同，即为两者大小相加．所以两者这d处产生电场强度为，故B正确，ACD错误．故选：B．点评：考查点电荷与圆盘电荷在某处的电场强度叠加，紧扣电场强度的大小与方向关系，从而为解题奠定基础．。
电场强度叠加专题高三专题复习
电场强度叠加的基本方法命题研究：电场强度是描述电场力的性质的物理量，是电场中最基本、最重要的概念之一，高中阶段的学习对整个电场部分起了辅垫作用，而在高考中也是考试的热点。
求解电场强度的基本方法有：定义法E＝F/q，真空中点电荷场强公式法E＝KQ/r2，匀强电场公式法E＝U/d，矢量叠加法E＝E1+E2+E3……等。
但对于某些电场强度计算，必须采用特殊的思想方法。
现结合例题分析场强叠加的几种方法专项攻破：一．基本法遵循平行四边形定则（矢量合成）【典例1】图中a、b是两个点电荷，它们的电量分别为Q1、Q2，MN是ab连线的中垂线，P 是中垂线上，电荷连线上方的一点。
下列哪种情况能使P点场强方向指向MN的左侧？（）A.Q1、Q2都是正电荷，且Q1<Q2B.Q1是正电荷，Q2是负电荷，且Q1>|Q2|C.Q1是负电荷，Q2是正电荷，且|Q1|<Q2D.Q1、Q2都是负电荷，且|Q1|>|Q2|二．对称法对称法实际上就是根据某些物理现象、物理规律、物理过程或几何图形的对称性进行解题的一种方法，利用此法分析解决问题可以避免复杂的数学演算和推导，直接抓住问题的实质，有出奇制胜之效。
【典例2】如图所示，带电量为＋q的点电荷与均匀带电薄板相距为2d，点电荷到带电薄板的垂线通过板的几何中心。
若图中a点处的电场强度为零，根据对称性，带电薄板在图中b点处产生的电场强度大小为________，方向_________。
（静电力恒量为k）【典例3】ab是长为l的均匀带电细杆，P1、P2是位于ab所在直线上的两点，位置如图所示．ab上电荷产生的静电场在P1处的场强大小为E1，在P2处的场强大小为E2，则以下说法正确的是( )A．两处的电场方向相同，E1>E2B．两处的电场方向相反，E1>E2C．两处的电场方向相同，E1<E2D．两处的电场方向相反，E1<E2三、补偿法求解物理问题，要根据问题给出的条件建立起物理模型。
电场的叠加计算方法解析
电场的叠加计算方法解析电场在物理学中起着重要的作用。
了解电场的叠加计算方法对于理解和解决与电场相关的问题至关重要。
本文将解析电场的叠加计算方法，介绍其基本理论和应用。
1. 电场的定义和基本概念电场是由电荷所产生的力场，可以影响其周围空间中其他电荷的运动。
电场的强度用电场强度表示，定义为单位正电荷所受到的力大小。
电场强度的方向与力的方向一致。
电场强度可以用矢量表示。
2. 叠加原理电场满足叠加原理，即在同一位置的电场强度可以叠加。
这意味着，如果有多个电荷同时存在于某一点，那么在该点的总电场强度等于各个电荷在该点产生的电场强度的矢量和。
3. 点电荷的电场叠加计算方法点电荷的电场叠加计算方法是电场叠加计算的基本方法。
对于由多个点电荷组成的电场，可以通过以下步骤进行计算：(1) 分别计算每个点电荷在感兴趣位置上产生的电场强度矢量；(2) 将每个点电荷的电场强度矢量相加，得到总的电场强度矢量。
4. 导体的电场叠加计算方法对于导体上的电场叠加计算，需要考虑导体表面的电势分布。
导体内部的电势是均匀的，而导体表面上的电势是相等的。
因此，在计算导体上某一点的电场强度时，可以将导体上所有点电荷的电场强度矢量相加，并考虑导体自身的电势分布。
5. 连续分布电荷的电场叠加计算方法对于连续分布电荷的电场叠加计算，可以采用积分来表示电场强度的叠加。
首先，将电荷分布密度表示为一个函数，并将连续电荷分布区域分解为离散小元。
然后，对每个小元计算其在感兴趣位置上产生的电场强度矢量，并将所有小元的电场强度矢量积分求和，得到总的电场强度矢量。
6. 对称性在电场叠加计算中的应用在某些情况下，可以利用空间对称性或电荷分布的对称性来简化电场叠加计算。
例如，如果电荷分布具有球对称性，则可以利用球坐标系的对称性来简化电场叠加计算。
总结：本文对电场的叠加计算方法进行了解析，重点介绍了点电荷、导体和连续分布电荷的电场叠加计算方法。
通过了解叠加原理和利用对称性，可以更好地理解和应用电场叠加计算方法，解决与电场相关的问题。
专题17 电场叠加(提高篇)(解析版)
高考物理100考点最新模拟题千题精练（选修3-1）第一部分 静电场专题1.7. 电场叠加（提高篇）一．选择题1. （2020河北唐山一模）如图所示，正六边形的边长L ，六个顶点固定电量大小均为q 但是电性不同的正负点电荷，O 为六边形中心，abcd 分别为所在边的中点，取无限远处电势为零，下列说法正确的是A ．O 点场强大小为24kq LB ．O 点的电势为零C ．b 、c 两点电场强度相同D ．沿虚线由a 到d 电势一直降低【参考答案】：AB【命题意图】 本题以正六边形六个顶点点电荷产生的电场为情景，考查点电荷电场强度公式和场强叠加原理，电势叠加原理及其相关知识点，考查的核心素养是“运动和力”的观点、能量观点。
【解题思路】根据点电荷电场强度公式和场强叠加原理可得，O 点场强大小Eo=2k 2q L +2k 2q L cos60°+2k 2q L cos60°=4k 2q L，选项A 正确；取无穷远处电势为零，正六边形对角两个正负电荷在O 点产生电场的电势为零，根据电势叠加原理可知，正六边形六个顶点点电荷在六边形中心O 点产生电场的电势为零，选项B 正确；根据点电荷电场强度公式和场强叠加原理可知，b 点的电场强度方向向左，而c 点的电场强度方向沿边斜向左下，方向不同，b 、c 两点电场强度一定不相同，选项C 错误；在虚线ad 上，a 点电势最低，d 点电势最高，所以沿虚线由a 到d 电势一直升高，选项D 错误。
【关键点拨】电场强度是矢量，场强叠加按照矢量运算的平行四边形定则进行。
电势是标量，电势叠加按照代数法则进行。
2.（2019湖北鄂东南省级示范性高中教学联盟模拟）如图所示，真空有三个正点电荷q1、q2、q3，q1＝2q2＝2q3，它们固定在等边三角形的三个顶点A、B、C上，D、E、F分别为AB、AC、BC的中点，O为等边三角形中心，下列说法正确的是（）A．D、O两点场强大小相等B．一带负电的点电荷在E点的电势能小于该点电荷在F点的电势能C．若将q2、q3分别用﹣q2、﹣q3替换，O点场强大小变成之前的3倍D．若将q2、q3分别用﹣q2、﹣q3替换，O点的电势为0【参考答案】BCD【名师解析】由库仑定律及电场的叠加可判断A．D．O三点的场强大小及q2，q3电性变化前后O点场强的关系，根据电场力做功与电势能变化关系可知E，F两点的电势能大小关系，各点电荷在A，D，O三点产生的场强如图所示，由场强叠加原理知A，D，O三点场强不等故A错，将一负点电荷由E点沿直线移动到F点，电场力做负功，电势能增大故B正确，因为AO＝BO＝CO，所以q1在O点产生的场强为q2，q3两电荷在O点产生的场强的两倍，又因为q2，q3在o点的场强夹角为120°，故q2，q3在O点产生的合场强总是和q1在O点产生的场强共线，即先反向后同向，故改变电性后，O点的场强为原来的3倍，所以C对，电场中电场线总是由正电荷指向负电荷，且顺着电场线电势逐渐降低，正电荷周围电势为正，负电荷周围电势为负值，故O点电势为0，选项D正确。
高考专题---电场叠加问题-高考物理100考点最新模拟题---精校解析 Word版
100考点最新模拟题千题精练7- 2一．选择题1.（2017湖北天门等三市联考）如图所示，一边长为L 的立方体绝缘体上均匀分布着电荷量为Q 的电荷，在垂直于左右面且过立方体中心O 的轴线上有a 、b 、c 三个点，a 和b 、b 和O 、O 和c 间的距离均为L ，在a 点处固定有一电荷量为q (q <0)的点电荷．已知b 点处的场强为零，则c 点处场强的大小为(k 为静电力常量)A ．298L qk B ．2L Qk C ．2L qkD ．2910L qk【参考答案】D2.（2017北京昌平期末）关于电场强度，下列说法中正确的是 A ．由qFE =可知，电场中某点的场强大小E 与放置在该点的试探电荷所受电场力F 成正比，与电荷量q 成反比 B ．由2r QkE =可知，在以点电荷Q 为球心，以r 为半径的球面上各点处场强大小均相同C ．由dUE可知，匀强电场的场强大小E 等于电场中任意两点间的电势差U 与这两点间距离d 的比值 D ．电场中某点电场强度的方向与放置在该点的正电荷受到的电场力方向相同 【参考答案】BD3．(2016·南京模拟)均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场．如图所示，在半球面AB 上均匀分布的正电荷，总电荷量为q ，球面半径为R ，CD 为通过半球顶点与球心O 的轴线，在轴线上有M 、N 两点，OM ＝ON ＝2R.已知M 点的场强大小为E ，则N 点的场强大小为( )A .kq 2R 2－E B .kq 4R 2 C .kq 4R 2－E D .kq 4R2＋E 【参考答案】A【名师解析】把AB 右侧半球面补齐，即将电荷量分别为＋q 、－q 的两个半球面叠加在一起，AB 在N 点的场强相当于所带电荷量为2q 的完整的球壳在N 点的场强大小E 1减去多加的所带电荷量为－q 的半球面在N 点的场强大小E 2，E 2等于原电场在M 点的场强大小E ，则E N ＝E 1－E 2＝2qk (2R)2－E ，A 正确．4．(2016·江苏淮安高三期末)两个绝缘固定带等量正电的点电荷，其连线的垂直平分线上有A 、B 两对称点，如图所示。
2021届新高考物理第一轮复习课时强化训练：电场强度的叠加问题(解析版)
2021届新高考物理第一轮复习课时强化训练电场强度的叠加问题一、选择题1、MN 为足够大的不带电的金属板，在其右侧距离为d 的位置放一个电荷量为＋q 的点电荷O ，金属板右侧空间的电场分布如图甲所示，P 是金属板表面上与点电荷O 距离为r 的一点．几位同学想求出P 点的电场强度大小，但发现问题很难，经过研究，他们发现图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的．图乙中是两等量异号点电荷的电场线分布，其电荷量的大小均为q ，它们之间的距离为2d ，虚线是两点电荷连线的中垂线．由此他们分别对图甲P 点的电场强度方向和大小做出以下判断，其中正确的是( )A ．方向沿P 点和点电荷的连线向左，大小为2kqd r3B ．方向沿P 点和点电荷的连线向左，大小为2kq r 2－d 2r3C ．方向垂直于金属板向左，大小为2kqdr3D ．方向垂直于金属板向左，大小为2kq r 2－d 2r3解析：选C 据题意，从题图乙可以看出，P 点电场方向为水平向左；由题图乙可知，正、负电荷在P 点电场的叠加，其大小为E ＝2k qr2cosθ＝2k q r 2·d r ＝2k qdr3，故选项C 正确．2、均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场．如图所示，在半球面AB 上均匀分布着正电荷，总电荷量为q ，球面半径为R ，CD 为通过半球顶点与球心O 的轴线，在轴线上有M 、N 两点，OM ＝ON ＝2R .已知M 点的场强大小为E ，则N 点的场强大小为( )A.kq 2R 2－EB.kq 4R2 C.kq 4R 2－E D.kq 4R2＋E 解析：选A 若将带电荷量为2q 的完整球面的球心放在O 处，均匀带电的球面在球外空间产生的电场等效于电荷集中于球心处产生的电场，则在M 、N 点所产生的场强大小为E 1＝k ·2q 2R 2＝kq2R 2，由题意知左半球面在M 点产生的场强大小为E ，若只有右半球面，右半球面在N 点产生的场强大小也为E ，则N 点的场强大小为E 2＝kq2R2－E ，故选A.3、如图甲、乙所示，两个带电荷量均为q 的点电荷分别位于带电荷量线密度相同、半径相同的半圆环和34圆环的圆心，环的粗细可忽略不计．若图甲中环对圆心点电荷的库仑力大小为F ，则图乙中环对圆心点电荷的库仑力大小为( )A.32FB.12FC.22FD.32F 解析：选C 由题图甲中均匀带电半圆环对圆心点电荷的库仑力大小为F ，可以得出14圆环对圆心点电荷的库仑力大小为22F .将题图乙中的均匀带电34圆环分成三个14圆环，关于圆心对称的两个14圆环对圆心点电荷的库仑力的合力为零，因此题图乙中的34圆环对圆心点电荷的库仑力大小为22F，C正确．4、(多选)真空中有两点电荷q1、q2分别位于直角三角形的顶点C和顶点B上，D为斜边AB的中点，∠ABC＝30°，如图所示，已知A点电场强度的方向垂直AB向下，则下列说法正确的是( )A．q1带正电，q2带负电B．D点电势高于A点电势C．q1电荷量的绝对值等于q2电荷量的绝对值的二倍D．q1电荷量的绝对值等于q2电荷量的绝对值的一半解析：选AD A点电场强度的方向垂直AB向下，E A为A点的合场强，将E A分解到AC和AB方向如图所示，可知点电荷q1的电场强度方向由C指向A，则q1带正电，点电荷q2的电场强度方向由A指向B，则q2带负电，故A正确；由于A、D两点到q 1的距离是相等的，D 距离q 2更近，沿着电场线方向，电势逐渐降低，则D 点电势低于A 点电势，故B 错误；从图中可知设AB ＝2L ，则AC ＝AB sin 30°＝L ，从场强分解的图中可知E 2∶E 1＝sin 30°，即E 1＝2E 2，又E 1＝kq 1L 2，E 2＝kq 22L2，可得q 2＝2q 1，故C 错误，D 正确．5、(多选)如图所示，正六边形ABCDEF 的B 、D 两点各固定一个带正电、电荷量为 ＋q 的点电荷，F 点固定一个带负电、电荷量为－q 的点电荷，O 为正六边形的几何中心．则下列说法正确的是( )A ．O 点场强为0B ．C 点场强方向沿FC 方向 C ．电子在A 点电势能比在O 点小D ．OA 两点间电势差和OE 两点间电势差相等解析：选BD 根据点电荷的场强公式E ＝kqr2可知，三个点电荷在O 点产生的场强大小相等，合场强沿OF 方向，故A 错误；B 点和D 点两个正点电荷在C 点产生的合场强沿FC 方向，F 点的负点电荷在C 点产生的场强沿CF 方向，但距离较大，则C 点处合场强沿FC 方向，故B 正确；电子沿OA 运动时，OA 是BF 的中垂线，BF 两点放了等量异种电荷，所以这两个点电荷对电子作用力的合力方向垂直AO ，对电子不做功，D 处的电荷是正点电荷，对电子的作用力是引力，对电子做负功，所以三个电荷对电子做负功，则电子的电势能增大，电子在A 点电势能比在O 点大，故C 错误；根据对称性可知，电荷从O 点移到A 点、从O 点移到E ，电场力做功相同，所以OA 两点间电势差和OE 两点间电势差相等，故D 正确．6、(多选)已知均匀带电球体在其外部产生的电场与一个位于球心的、电荷量相等的点电荷产生的电场相同，而均匀带电球売在其内部任意一点形成的电场强度为零．如图所示，现有一半径为R 、电荷量为Q 的均匀带正电绝缘球体，M 、N 为一条直径上距圆心O 为12R 的两点，静电力常量为k ，则( )A ．M 、N 点的电场强度方向相同B ．M 、N 点的电场强度大小均为kQ2R2C ．M 、N 点的电场强度大小均为kQ8R2D ．M 、N 点的电势小于O 点的电势解析：选BD 根据均匀带电球壳在其内部任意一点形成的电场强度为零，知M 点的场强等于以O 圆心、半径为12R 的均匀球体在M 点产生的场强，这个球体之外的球壳在M 点产生的场强为零，这个球体所带电荷量为q ＝43πR 2343πR 3Q ＝Q 8，M 点的电场强度大小为E M ＝kqR 22＝kQ 2R 2，方向向左；根据对称性知N 点的电场强度大小也为kQ2R2，方向向右；O 点的场强为零，则MO 间场强方向向左，NO 间场强方向向右，所以M 、N 点的电势低于O 点的电势，故B 、D 正确，A 、C 错误． 7．(多选)如图所示，半径为R 的绝缘闭合球壳，O 为球壳的球心，球壳上均匀分布着正电荷，已知均匀带电的球壳在其内部激发的场强处处为零．现在球壳表面A 处取下一面积足够小、带电荷量为q 的曲面将其沿OA 连线延长线向上移动至B 点，且AB ＝R ，若球壳的其他部分的带电荷量与电荷分布保持不变，下列说法中正确的是( )A．把另一带正电的试探电荷从A点处移动到O点过程中系统电势能减少B．球壳剩余部分的电荷在球壳内部激发的电场的电场线由A点的对称点C点沿直线指向球壳内表面各点C．球壳内部电场的电场线由球壳各点沿曲线指向A点D．球心O点场强的大小为k 3q4R2解析：选CD 球壳表面A点处取一下面积足够小的带电荷量为q的曲面，相当于在球壳表面点A处放入等电荷密度、等面积的带负电荷的曲面，故球壳剩余部分的电荷在球壳内部激发的电场可以看作是两部分电荷电场的叠加，一部分是原球壳上均匀地分布的正电荷在内部激发的电场，处处为零；另一部分是球壳上位于A处的等量负点电荷激发的电场，故球壳剩余部分的电荷在球壳内部激发的电场就等同于只有一个负点电荷激发的电场，如图(a)所示，故B错误；同理，空间所有电荷在球壳内部激发的电场相当于两个等量异种电荷产生的电场，如图(b)所示，故A错误，C、D正确．8．如图所示，在点电荷－q 的电场中，放着一块带有一定电荷量、电荷均匀分布的绝缘矩形薄板，MN 为其对称轴，O 点为几何中心．点电荷－q 与a 、O 、b 之间的距离分别为d 、2d 、3d .已知图中a 点的电场强度为零，则带电薄板在图中b 点产生的电场强度的大小和方向分别为( )A.kq d 2，水平向右B.kqd 2，水平向左 C.kq d 2＋kq9d 2，水平向右 D.kq9d2，水平向右 解析：选A 薄板在a 点的场强与点电荷－q 在a 点的场强等大反向，故大小为E a ＝E 点＝kqd2，方向水平向左，由对称性可知，薄板在b 点的场强大小E b ＝E a ＝kq d2，方向水平向右，选项A 正确．9、如图所示，M 、N 为两个等量同种电荷，在其连线的中垂线上的P 点放一静止的点电荷q (负电荷)，不计重力，下列说法中正确的是( )A ．点电荷在从P 到O 的过程中，加速度越来越大，速度也越来越大B ．点电荷在从P 到O 的过程中，加速度越来越小，速度越来越大C ．点电荷运动在O 点时加速度为零，速度达最大值D ．点电荷越过O 点后，速度越来越小，加速度越来越大，直到粒子速度为零解析：选C 由等量同种电荷周围的电场线的分布可知，O 点场强为零，从O 点沿着中垂线向无穷远处延伸，场强先增大后减小，所以点电荷在从P 到O 的过程中，加速度可能先增大后减小，选项A 、B 错；但负电荷所受M 、N 点点电荷库仑力的合力方向竖直向下，到O 点一直加速，选项C 对；同理点电荷越过O 点后，速度越来越小，但加速度先增大后减小，选项D 错．10、已知均匀带电球体在球的外部产生的电场与一个位于球心的、电荷量相等的点电荷产生的电场相同．如图所示，半径为R 的球体上均匀分布着电荷量为Q 的电荷，在过球心O 的直线上有A 、B 两个点，O 和B 、B 和A 间的距离均为R .现以OB 为直径在球内挖一球形空腔，若静电力常量为k ，球的体积公式为V ＝43πr 3，则A 点处场强的大小为( )A.5kQ 36R 2B.7kQ 36R2 C .7kQ 32R 2 D .3kQ16R2 解析：选 B 把球形空腔补全，掌握均匀带电球体在A 处产生的电场强度为E 1＝k Q4R 2，把球形空腔看作均匀带电体，在A 处产生的电场强度为E 2＝k Q18R 2，根据叠加原理可知，图示的带电体在A 处产生的电场强度大小为E ＝E 1－E 2＝7kQ36R2，故B 选项正确．11、如图所示，有一带电荷量为＋q 的点电荷与均匀带电圆形薄板相距为2d ，此点电荷到带电薄板的垂线通过板的圆心．若图中a 点处的电场强度为零，则图中b 点处的电场强度大小是( )A ．k q 9d 2＋k q d 2B ．k q 9d 2－k q d2C ．0D ．k q d2解析：选A 点电荷在a 点产生的场强大小E ＝k qd2，方向向左，由题意，带电薄板在a 点产生的场强大小E ＝k q d2，方向向右．根据对称性，带电薄板在b 点产生的场强大小E ＝k qd 2，方向向左，点电荷在b 点产生的场强大小E ＝k q9d2，方向向左，根据场强的叠加原理，可知A 正确．二、非选择题12、如图所示，长l＝1m的轻质细绳上端固定，下端连接一个可视为质点的带电小球，小球静止在水平向右的匀强电场中，绳与竖直方向的夹角θ＝37°。
高中物理每日一点十题之电场强度 的叠加
高中物理每日一点十题之电场强度的叠加一知识点1.电场强度叠加原理在几个点电荷共同形成的电场中，电场中任意一点的总电场强度等于各个点电荷在该点各自产生的电场强度的矢量和.这就是场强叠加原理.2.注意(1)独立性——各个场源电荷产生的电场互不干扰.(2)叠加原理——只有同时作用在同一区域内的电场才可以进行叠加.电场强度叠加遵循平行四边形定则.3.一个半径为R的均匀带电球体(或球壳)在外部产生的电场，与一个位于球心的、电荷量相等的点电荷产生的电场相同.十道练习题（含答案）一、单选题（共10小题）1. 如图，xOy平面直角坐标系所在空间有沿x轴负方向的匀强电场(图中未画出)，电场强度大小为E.坐标系上的A、B、C三点构成边长为L的等边三角形．若将两电荷量相等的正点电荷分别固定在A、B两点时，C点处的电场强度恰好为零．则A处的点电荷在C点产生的电场强度大小为( )A. EB. EC. ED. E2. 如图，真空中a、b、c、d四点共线且等距．先在a点固定一点电荷＋Q，测得b点场强大小为E.若再将另一等量异种点电荷－Q放在d点，则( )A. b点场强大小为EB. c点场强大小为EC. b点场强方向向左D. c点场强方向向左3. 如图所示，M、N和P是以MN为直径的半圆弧上的三点，O点为半圆弧的圆心，∠MOP＝60°.电荷量相等、电性相反的两个点电荷分别置于M、N两点，这时O点电场强度的大小为E1；若将N 点处的点电荷移至P点，此时O点的场强大小为E2，则E1与E2之比为( )A. 1∶2B. 2∶1C. 2∶D. 4∶4. 如图所示，A、B、C三点的连线构成一个等腰直角三角形，∠A是直角．在B点放置一个电荷量为＋Q的点电荷，测得A点的电场强度大小为E.若保留B点的电荷，再在C点放置一个电荷量为－Q 的点电荷，则A点的电场强度大小等于( )A. 0B. EC. ED. 2E5. 如图所示，以O为圆心的圆周上有六个等分点a、b、c、d、e、f.等量正、负点电荷分别放置在a、d两处时，在圆心O处产生的电场强度大小为E.现改变a处点电荷的位置，关于O点的电场强度变化，下列叙述正确的是( )B. 移至b处，O处的电场强度大小减半，方向沿OdC. 移至e处，O处的电场强度大小减半，方向沿OcD. 移至f处，O处的电场强度大小不变，方向沿Oe6. 如图所示，a、b、c、d四个点在一条直线上，a和b、b和c、c和d间的距离均为R，在a点处固定一电荷量为Q的正点电荷，在d点处固定另一个电荷量未知的点电荷，除此之处无其他电荷，已知b点处的场强为零，则c点处场强的大小为(k为静止力常量)( )A. 0B. kC. kD. k7. 如图所示，A、B、C是直角三角形的三个顶点，∠A＝90°，∠B＝30°.在A、B两点分别放置两个点电荷q A、q B，测得C点的电场强度E c方向与AB平行．下列说法正确的是( )A. 点电荷q A、q B的电性可能都为正B. 点电荷q A、q B的电荷量大小之比是1∶2C. 点电荷q A、q B的电荷量大小之比是1∶4D. 点电荷q A、q B的电荷量大小之比是1∶88. 如图所示，直角三角形ABC的∠A＝37°，∠B＝90°，在A、B两点各放一个点电荷，则C点的电场强度大小为E，方向与AC垂直指向右下，sin 37°＝0.6，cos 37°＝0.8，则( )A. A、B两点处点电荷都带正电B. A点处点电荷带负电，B点处点电荷带正电C. A、B两点处点电荷的带电量之比为5∶3D. A、B两点处点电荷的带电量之比为4∶39. 如图所示，a、b、c、d分别是一个菱形(竖直放置)的四个顶点，∠abc＝120°，O点为菱形对角线的交点，现将三个电荷量均为＋Q的点电荷分别固定在a、b、c三个顶点上，下列说法正确的是( )A. d点电场强度的方向由O指向dB. O点电场强度的方向由d指向OC. d点的电场强度大于O点的电场强度D. d点的电场强度等于O点的电场强度10. 如图，真空中有三个电荷量相等的点电荷A、B、C，它们固定在等边三角形的三个顶点上，A、B 带正电，C带负电，三角形的中心O处的电场强度大小为E.当把点电荷C移至AB连线的中点D时，中心O处的电场强度大小为( )A. B. C. D.1. 【答案】B【解析】C点三个电场方向如图所示，根据题意可知E1cos 30°＋E2cos 30°＝E，又知道E1＝E2，故解得E2＝E，B正确．2. 【答案】B【解析】设ab＝bc＝cd＝L，＋Q在b点产生的场强大小为E，方向水平向右，由点电荷的场强公式得：E＝k，－Q在b点产生的场强大小为E1＝k＝E，方向水平向右，所以b点的场强大小为E b＝E＋E＝E，方向水平向右，故A、C错误；根据对称性可知，c点与b点的场强大小相等，为E，方向水平向右，故B正确，D错误．3. 【答案】B【解析】依题意，两点电荷在O点产生的场强大小均为，当N点处的点电荷移至P点时，O点场强如图所示，则合场强大小E2＝，故＝，选项B正确．4. 【答案】C【解析】正电荷Q在A点产生的电场强度为E，沿BA方向，负电荷Q在A点产生的电场强度也为E，方向沿AC方向，根据电场强度的叠加原理可知E合＝＝E，故C正确，A、B、D错误．5. 【答案】C【解析】由题意可得，正、负点电荷在O处产生的电场强度的大小都为，方向沿Od；当a处点电荷移至c处时，两点电荷在O处的电场强度方向的夹角为120°，合电场强度大小为，方向沿Oe，选项A错；同理，当a处点电荷移至b处时，O处的合电场强度大小为，方向沿Oe与Od的角平分线斜向上，选项B错；同理，当a处点电荷移至e处时，O处的合电场强度大小为，方向沿Oc，选项C对；同理，当a处点电荷移至f处时，O处的合场强大小为，方向沿Oc与Od的角平分线斜向下，选项D错．6. 【答案】B【解析】据题可知，点处的场强为零，说明点处和点处的两个点电荷在点处产生的场强大小相等、方向相反，则有：k＝k，得Q′＝4Q，电性与Q相同．则Q在c点处产生的场强大小E1＝k＝k，方向向右，Q′在c点处产生的场强大小E2＝k＝k，方向向左，故c点处场强的大小为E＝E2－E1＝k，B正确．7. 【答案】D【解析】放在A点和B点的点电荷在C处产生的电场强度方向分别在AC和BC的连线上，因C点电场强度方向与BA方向平行，放在A点的点电荷和放在B点的点电荷产生的电场强度方向只能如图所示，q A带负电，q B带正电，且E B＝2E A，即＝2，又由几何关系知：＝2，所以q A∶q B＝1∶8，故D正确，A、B、C错误．8. 【答案】C【解析】由于A点点电荷在C点产生的场强与AC平行，因此B点点电荷在C点的场强沿AC方向的分量与A点点电荷在C点的场强等大反向，因此场强E是B点点电荷在C点场强的分量，由此可以判断B点点电荷带负电，A点点电荷带正电，A、B项错误；设AC间的距离为r，则BC间的距离为0.6r，由k＝k sin 37°，解得q A∶q B＝5∶3，C项正确，D项错误．9. 【答案】A【解析】a、c两点的点电荷在d点叠加的电场强度的方向由O指向d，b点的点电荷在d点的电场强度的方向也由O指向d，所以d点电场强度的方向由O指向d，选项A正确；同理，O点电场强度的方向由O指向d，选项B错误；设菱形的边长为L，a点的点电荷在d点产生的电场场强在竖直方向的分量为E0y＝，由对称性及电场叠加原理知，d点的电场强度E d＝2×＋＝，同理得O 点的场强为E O＝＝，所以E d＜E O，选项C、D错误．10. 【答案】D【解析】设等边三角形的边长为L，由题意可知E＝2k＝2k＝，当把点电荷C移至AB连线的中点D时，中心O处的电场强度E′＝k－k＝－＝＝E，故选D.。
专题17 带电粒子(计重力)在电场中的运动(电磁学部分)(解析版)
专题17 带电粒子（计重力）在电场中的运动 压轴题一、单选题1．用长为1.4m 的轻质柔软绝缘细线，拴一质量为1.0×10－2kg 、电荷量为2.0×10-8C 的小球，细线的上端固定于O 点．现加一水平向右的匀强电场，平衡时细线与铅垂线成370，如图所示．现向左拉小球使细线水平且拉直，静止释放，则（sin370=0.6）（ ）A ．该匀强电场的场强为3.75×107N/CB ．平衡时细线的拉力为0.17NC ．经过0.5s ，小球的速度大小为6.25m/sD ．小球第一次通过O 点正下方时，速度大小为7m/s 【答案】C 【解析】AB ．小球在平衡位置时，由受力分析可知：qE=mgtan370，解得2681.010100.75/ 3.7510/2.010E N C N C --⨯⨯⨯==⨯⨯，细线的拉力：T=201.010100.125cos370.8mg T N N ⨯⨯===－，选项AB 错误； C ．小球向左被拉到细线水平且拉直的位置，释放后将沿着电场力和重力的合力方向做匀加速运动，其方向与竖直方向成370角，加速度大小为2220.125/12.5/1.010T a m s m s m ===⨯－，则经过0.5s ，小球的速度大小为v=at=6.25m/s ，选项C 正确；D ．小球从水平位置到最低点的过程中，若无能量损失，则由动能定理：212mgL qEL mv +=，带入数据解得v=7m/s ；因小球从水平位置先沿直线运动，然后当细绳被拉直后做圆周运动到达最低点，在绳子被拉直的瞬间有能量的损失，可知到达最低点时的速度小于7m/s ，选项D 错误．2．如图所示，一电荷量q =+3×10-5C 的小球，用绝缘细线悬挂于竖直放置足够大的平行金属板中的O 点，开关S 合上后，小球静止时细线与竖直方向的夹角θ=37°．已知两板间距d =0.1m ，电源电动势E =15V ，内阻r =0.5Ω，电阻R 1=3Ω，R 2=R 3=R 4=8Ω，．取g=10m/s 2，已知sin37°=0.6，cos37°=0.8．则以下说法正确的是( )A ．电源的输出功率为14WB ．两板间的电场强度的大小为140V/mC ．带电小球的质量5.6毫克D ．若增加R 1的大小，会有瞬时电流从右向左流过R 4 【答案】B 【解析】R 2=R 3=8Ω，并联后的电阻值为：R′＝12R 2=4Ω；由闭合电路的欧姆定律得：1152340.5E I A A R R r ==='++++；电源的输出功率P=EI-I 2r=15×2-22×0.5=28W ，故A 错误；两板间的电压为：U C =I （R 1+R 23）=2×（3+4）=14V ；两板间的电场强度为：14140/0.1C U E V m d ===，故B 正确；小球处于静止状态，所受电场力为F ，又F=qE ，由平衡条件得：水平方向 Tcosα-mg=0 ；竖直方向：Tsinα-qE=0； 得：m=37Eqgtan ︒=5.6×10-4kg ，故C 错误；若增加R 1的大小，电容两端电压增大，电容器充电，会有瞬时电流从左向右流过R 4，故D 错误．故选B ．3．如图所示，倾角为α的光滑斜面下端固定一绝缘轻弹簧，M 点固定有一个带电量为-q 的小球甲．整个装置处在场强大小为E 、方向沿斜面向下的匀强电场中．另一个带电量为+q 、质量为m 的小球乙，从N 点由静止释放后，沿着斜面向下运动．重力加速度为g ．则（ ）A ．小球乙返回时，有可能撞到小球甲B ．小球乙在N 点的加速度大小为sin qE mg mα+C ．小球乙刚接触弹簧时，速度最大D ．小球乙沿着斜面向下运动过程中，其电势能可能增加 【答案】D 【解析】A ．根据动能定理知，当小球乙返回到N 点，由于重力做功为零，匀强电场的电场力做功为零，电荷甲的电场对乙做功为零，则合力做功为零，则到达N 点的速度为零，所以小球乙不可能撞到小球甲，故A 错误；B ．设MN 两点之间的距离为0s ，根据牛顿第二定律得，小球在N 点的加速度220sin q qE mg k F s a m mα+-==合， 故B 错误；C ．当小球所受的合力为零时，速度最大，即22sin q qE mg k kx sα+=+，此时弹簧仍处于压缩状态，故C 错误；D ．小球乙沿着斜面向下运动过程中，匀强电场的电场力做正功，电荷甲产生的电场对乙做负功，两个电场力的合力不一定沿斜面向下，最终电场力可能做正功，也可能做负功，故电势能可能减少，也电势能可能增加，故D 正确．4．在光滑水平面上充满水平向右的匀强电场，被拉直的绝缘轻绳一端固定在O 点，另一端系着带正电的小球，轻绳与水平面平行，OB 与电场线平行．若小球从A 点由静止释放后，沿水平面摆动到B 点，不计空气阻力，则关于此过程，下列判断正确的是（ ）A ．小球的动能先变小后变大B ．小球的切向加速度一直变大C ．小球受到的拉力先变大后变小D ．小球受到的电场力做功的功率先增大后减小【答案】D 【解析】小球从A 点摆动到B 点的过程中，只有电场力做功且一直做正功，根据动能定理知小球的动能E k 一直增大，故A 错误；小球从A 点摆动到B 点的过程中轻绳与OB 的夹角设为θ，根据牛顿第二定律：sin qE ma θ=则小球的切向加速度为：1sin qE a mθ=，可知加速度随着θ的减小而减小，故B 错误；根据牛顿第二定律和向心力公式有：2v F qEcos m Lθ=－，可得小球受到的拉力大小为：2k F qEcos E L θ=+，cos θ、E k 均随着θ的减小而增大，可见F 一直增大，故C 错误；在A 点时小球的速率为零，电场力做功的瞬时功率为零，过B 点时小球的速度方向与电场力垂直，电场力做功的瞬时功率也为零，可见小球受到的电场力做功的功率先增大后减小，故D 正确．所以D 正确，ABC 错误．5．如图所示，绝缘轻弹簧的上端固定在天花板上的O 点，下端系一质量为m 、电荷量为q 的带正电小球,小球套在O 点正下方的水平光滑绝缘杆上,整个装置处于电场强度大小为E,方向沿杆向右的匀强电场中，现将小球以某个初速度从A 点运动到B 点，到B 点时与其在A 点时的弹簧弹カ大小相等，在小球从A 点运动到B 点的过程中，下列判断正确的是（ ）A ．小球在A 点时的速度大于在B 点时的速度 B ．小球的电势能一直减小,弹性势能先增大后减小C ．小球的加速度大小仅由电场力决定的位置有2个D ．弹簧弹力对小球做功的瞬时功率为零的位置有4个 【答案】C【解析】A. 小球从A 到B 的过程中，弹簧弹力做功为零，光滑杆无摩擦，杆处于水平位置中立不做功，故只有电场力做功；根据动能定理可得221122AB B A EqS mv mv =-，由于0AB EqS >，所以小球到达B 点时的速度大于A 点是的速度，故A 错误；B. 小球从A 到B 的过程中电场力一直做正功，所以小球的电势能一直减小，弹性势能先增大后减小再增大，故B 错误；C. 小球处于O 点正下方和小球受到的弹力为零的位置时，小球合力都是qE ，加速度都是qE/m ，所以小球的加速度大小为qE/m 的位置有2个，故C 正确；D.在O 点正下方弹力方向与速度方向垂直，弹力不做功，功率为零；在弹簧处于原长的位置弹力为零，则弹力的功率为零，所以弹簧测力计对小球做功的瞬间功率为零的位置有2个，故D 错误． 故选C.6．一个带正电荷量为q ，质量为m 的小球，从光滑绝缘的斜面轨道的A 点由静止下滑，小球恰能通过半径为R 的竖直圆形轨道的最高点B 而做圆周运动．现在竖直方向上的加如图所示的匀强电场，若仍从A 点由静止释放该小球，则（ ）A ．小球仍恰好能过B 点 B ．小球不能过B 点C ．小球通过B 点，且在B 点与轨道之间的压力不为0D ．以上说法都不对 【答案】A【解析】没有电场时，最高点速度设为v ，则2v mg m R=又根据机械能守恒定律2()122mg h R mv -=解得52h R =加上电场时，恰好过最高点需要的速度设为v′，则'2v mg qE m R+=解得'()mg qE Rv m+=而由动能定理得22212mg h R qE h R mv ---='（）（） 解得'()mg qE Rv m+=说明小球仍恰好能过B 点，球与轨道间无作用力。
高三高考一轮重点题型复习：带电粒子在叠加场中的运动问题
带电粒子在叠加场中的运动问题1．（2017全国Ⅰ，16）如图，空间某区域存在匀强电场和匀强磁场，电场方向竖直向上（与纸面平行），磁场方向垂直于纸面向里，三个带正电的微粒a ，b ，c 电荷量相等，质量分别为m a ，m b ，m c ，已知在该区域内，a 在纸面内做匀速圆周运动，b 在纸面内向右做匀速直线运动，c 在纸面内向左做匀速直线运动。
下列选项正确的是A ．a b c m m m >>B ． b a c m m m >>C ．c b am m m >> D ． a c b m m m >>【答案】B 2．（2019届河南省滑县高三第一学期第二次联考）如图所示,空间存在垂直纸面向里的匀强磁场,一带负电的物块在水平外力F 作用下沿粗糙水平面向右做匀加速直线运动,下列关于外力F 随时间变化的图象可能正确的是A ．B ．C ．D ．【答案】D 3．（2019届四川省成都市高中毕业班摸底测试）图示区域有方向竖直向下的匀强电场和水平向里的匀强磁场，一带正电的微粒以水平向右的初速度进入该区域时，恰能沿直线运动。
欲使微粒向下偏转，可采用的方法是A．仅减小入射速度B．仅减小微粒的质量C．仅增大微粒的电荷量D．仅增大磁场的磁感应强度【答案】A4．（2019届河南省中原名校高三第一次质量考评）如图所示，空间存在水平向左的匀强电场E和垂直纸面向外的匀强磁场B，在竖直平面内从a点沿ab、ac方向抛出两带电小球，不考虑两带电小球间的相互作用，两小球的电荷量始终不变，关于小球的运动，下列说法正确的是A．沿ab、ac方向抛出的小球都可能做直线运动B．若小球沿ac方向做直线运动，则小球带负电，可能做匀加速运动C．若小球沿ac方向做直线运动，则小球带正电，且一定是匀速运动D．两小球在运动过程中机械能均守恒【答案】AC5．（2019届安徽省合肥市高三上学期调研性检测）如图所示，空间某区域存在正交的匀强电场和匀强磁场，电场方向水平向左，磁场方向垂直纸面向里，在该区域内，一带电粒子在竖直面内可能沿竖直线AB或水平线CD运动。
高二物理提高：电势叠加
高二物理提高：电势叠加班级__________ 座号_____ 姓名__________ 分数__________一、知识清单1． 常见电场中的等势面等势面是平行线。
电场线平行的电场2． 同种、异种电荷等势面的区别不等量异种 不等量同种 Q a >Q bQ A <Q B大小及电势高低的关系是（A ．φa >φb ，E a ＝E b 2 C ．φa >φb ，E a ＝4E b 4． (2014·新课标全国Ⅰ·21)(多选)如图7所示，在正点电荷Q 的电场中有M 、N 、P 、F 四点，M、N 、P 为直角三角形的三个顶点，F 为MN 的中点，∠M ＝30°.M 、N 、P 、F 四点处的电势分别用φM 、φN 、φP 、φF 表示．已知φM ＝φN ，φP ＝φF ；点电荷Q 在M 、N 、P 三点所在平面内，则( ) A ．点电荷Q 一定在MP 的连线上 B ．连接PF 的线段一定在同一等势面上C ．将正试探电荷从P 点搬运到N 点，电场力做负功D ．φP 大于φM5． （2000春）如图所示，P 、Q 是两个电量相等的正的点电荷，它们连线的中点是O 、A 、B 的中垂线上的两点OA ＜OB ，用E A 、E B 、φA 、φB 分别表示A 、B 两点的场强和电势，则( ) A ．E A 一定大于E B ，φA 一定大于φB B ．E A 不一定大于E B ，φA 一定大于φB C ．E A 一定大于E B ，φA 不一定大于φB D ．E A 不一定大于E B ，φA 不一定大于φB6． (多选)一带负电粒子在电场中仅受电场力作用做匀速圆周运动，该电场可能是（ ）A ．匀强电场B ．正点电荷的电场C ．负点电荷的电场D ．等量同种正点电荷的电场7． （2012重庆卷）空中P 、Q 两点处各固定一个点电荷，其中P 点处为正点电荷，P 、Q 两点附近电场的等势面分布如图所示，a 、b 、c 、d 为电场中的四个点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021年高考物理100考点最新模拟题千题精练（选修3-1）第一部分 静电场专题1.7. 电场叠加（提高篇）一．选择题1. （2020河北唐山一模）如图所示，正六边形的边长L ，六个顶点固定电量大小均为q 但是电性不同的正负点电荷，O 为六边形中心，abcd 分别为所在边的中点，取无限远处电势为零，下列说法正确的是A ．O 点场强大小为24kq LB ．O 点的电势为零C ．b 、c 两点电场强度相同D ．沿虚线由a 到d 电势一直降低【参考答案】：AB【命题意图】 本题以正六边形六个顶点点电荷产生的电场为情景，考查点电荷电场强度公式和场强叠加原理，电势叠加原理及其相关知识点，考查的核心素养是“运动和力”的观点、能量观点。
【解题思路】根据点电荷电场强度公式和场强叠加原理可得，O 点场强大小Eo=2k 2q L +2k 2q L cos60°+2k 2q L cos60°=4k 2q L，选项A 正确；取无穷远处电势为零，正六边形对角两个正负电荷在O 点产生电场的电势为零，根据电势叠加原理可知，正六边形六个顶点点电荷在六边形中心O 点产生电场的电势为零，选项B 正确；根据点电荷电场强度公式和场强叠加原理可知，b 点的电场强度方向向左，而c 点的电场强度方向沿边斜向左下，方向不同，b 、c 两点电场强度一定不相同，选项C 错误；在虚线ad 上，a 点电势最低，d 点电势最高，所以沿虚线由a 到d 电势一直升高，选项D 错误。
【关键点拨】电场强度是矢量，场强叠加按照矢量运算的平行四边形定则进行。
电势是标量，电势叠加按照代数法则进行。
2.（2019湖北鄂东南省级示范性高中教学联盟模拟）如图所示，真空有三个正点电荷q1、q2、q3，q1＝2q2＝2q3，它们固定在等边三角形的三个顶点A、B、C上，D、E、F分别为AB、AC、BC的中点，O为等边三角形中心，下列说法正确的是（）A．D、O两点场强大小相等B．一带负电的点电荷在E点的电势能小于该点电荷在F点的电势能C．若将q2、q3分别用﹣q2、﹣q3替换，O点场强大小变成之前的3倍D．若将q2、q3分别用﹣q2、﹣q3替换，O点的电势为0【参考答案】BCD【名师解析】由库仑定律及电场的叠加可判断A．D．O三点的场强大小及q2，q3电性变化前后O点场强的关系，根据电场力做功与电势能变化关系可知E，F两点的电势能大小关系，各点电荷在A，D，O三点产生的场强如图所示，由场强叠加原理知A，D，O三点场强不等故A错，将一负点电荷由E点沿直线移动到F点，电场力做负功，电势能增大故B正确，因为AO＝BO＝CO，所以q1在O点产生的场强为q2，q3两电荷在O点产生的场强的两倍，又因为q2，q3在o点的场强夹角为120°，故q2，q3在O点产生的合场强总是和q1在O点产生的场强共线，即先反向后同向，故改变电性后，O 点的场强为原来的3倍，所以C对，电场中电场线总是由正电荷指向负电荷，且顺着电场线电势逐渐降低，正电荷周围电势为正，负电荷周围电势为负值，故O点电势为0，选项D正确。
故选：BCD。
3. (2018·山东省烟台市期末考试)如图所示，四个点电荷所带电荷量的绝对值均为Q，分别固定在正方形的四个顶点上，正方形边长为a，则正方形两条对角线交点处的电场强度()A ．大小为42kQ a 2，方向竖直向上 B ．大小为22kQ a 2，方向竖直向上 C ．大小为42kQ a 2，方向竖直向下 D ．大小为22kQ a 2，方向竖直向下 【参考答案】 C【名师解析】 一个点电荷在两条对角线交点O 产生的场强大小为E ＝kQ (22a )2＝2kQ a 2，对角线上的两异种点电荷在O 处的合场强为E 合＝2E ＝4kQ a 2，故两等大的场强互相垂直，合场强为E O ＝E 合2＋E 合2＝42kQ a 2，方向竖直向下，故选C.4．如图在半径为R 的圆周上均匀分布着六个不同的点电荷，则圆心O 处的场强大小和方向为A. ；由O 指向FB. ；由O 指向FC. ；由O 指向CD. ；由O 指向C【参考答案】B【名师解析】由点电荷的场强公式可知，在A、B、C、E、F五个位置的点电荷在O点产生的场强大小为，在D位移的点电荷在O产生的场强大小为，电场强度是矢量，求合场强应用平行四边形定则，作出电场强度的示意图，如图所示：最终O点的合场强为，方向由O指向F，故选B.5．均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场。
如图所示，在半球面AB上均匀分布正电荷，总电荷量为q，球面半径为R，CD为通过半球顶点与球心O的轴线，在轴线上有M、N两点，OM＝ON＝2R。
已知M点的场强大小为E，则N点的场强大小为()A.kq2R2－E B.kq4R2C.kq4R2－E D.kq4R2＋E 【参考答案】 A【名师解析】左半球面AB上的正电荷产生的电场等效为带正电荷为2q的整个球面的电场和带电荷－q的右半球面的电场的合电场，则E＝k·2q（2R）2－E′，E′为带电荷－q的右半球面在M点产生的场强大小。
带电荷－q的右半球面在M点的场强大小与带正电荷为q的左半球面AB在N点的场强大小相等，则E N＝E′＝k·2q（2R）2－E＝kq2R2－E，则选项A正确。
6.经过探究，某同学发现：点电荷和无限大的接地金属平板间的电场（如图甲所示）与等量异种点电荷之间的电场分布（如图乙所示）完全相同．图丙中点电荷q到MN的距离OA为L，AB是以电荷Q为圆心、L为半径的圆上的一条直径，则B点电场强度的大小是（）A. B. C. D.【参考答案】C7已知一个点电荷与足够大的金属板所形成的电场与等量异种点电荷连线的中垂线一侧的电场分布相同。
如图所示，在真空中的某竖直平面内固定一块足够大的接地金属板MN，在MN右侧与其相距2d处的P点放置一个所带电荷量为Q的正点电荷，从P点作平面的垂线，O点为垂足，A点为OP连线的中点，B 点为OP延长线上的一点，PB=d。
关于各点的电场强度，下列说法正确的是( )A. O点电场强度大小为kB. A点电场强度大小为kC. B点电场强度大小为kD. A、B两点电场强度大小相等，方向相反【参考答案】C【名师解析】金属板右侧的电场的电场线分布与等量异种电荷的电场线分布分别如图甲、乙所示：8.已知无限大的均匀带电面可产生垂直于该面的匀强电场（正的带电面场强方向背离该面、负的带电面场强方向指向该面），场强大小E=2πkσ，式中k为静电力常量，σ为电荷面密度（单位面积的带电量）。
现有如图所示的两个平行且可视为无限大的均匀带电面A和B，电荷的面密度分别为σ和-2σ（σ为正的常数），间距为d，空间中有C、D两点，CD连线垂直于带电面，C点到A面距离与D点到B面的距离均为，A 面接地。
关于C、D两点的场强大小和电势高低，下列说法中正确的是（）A. E C=E DB. E C>E DC. φ C=φDD. φ C>φD【参考答案】AD【名师解析】设A面产生电场的场强大小为E A=E0，由题意得B面产生电场的场强大小为E B=2E0，在C 点E C=E B-E A=E0，方向垂直指向A面。
同理在D点E D=E B-E A=E0，方向垂直指向B面，故A正确，B错误。
根据对称性，U CA=-U BD，又根据AB板间的场强方向指向B板，固有φA＞φB，因此φC＞φD，故C错误，D正确。
故选AD。
9.下列选项中的各绝缘直杆大小相同,所带电荷量已在图中标出,且电荷均匀分布,各直杆间彼此绝缘.坐标原点O处电场强度最大的是( )【参考答案】B【解析】设带电杆在O点产生的场强大小为E.所以坐标原点O处电场强度最大的是B. 所以B选项是正确的.10．如图所示，一带电荷量为+Q的均匀细棒，在过中点垂直于细样的直线上有a、b、d三点，a和b、b和c、c和d之间的距离均为L，在a处有一电荷量为-Q的固定点电荷。
已知d点处的电场强度为零，静电力常量为k，则b点处的电场强度大小为A. B. C. D.【参考答案】B【名师解析】电荷量为-Q的点电荷在d处产生电场强度为，方向向左在d点处的场强为零，根据电场的叠加原理可知细棍与-Q在d处产生电场强度大小相等，方向相反，11．一半径为R的半球面均匀带有正电荷Q,电荷Q在球心O处产生物的场强大小,方向如图所示.把半球面分为表面积相等的上、下两部分,如图甲所示,上、下两部分电荷在球心O处产生电场的场强大小分别为;把半球面分为表面积相等的左、右两部分,如图乙所示,左、右两部分电荷在球心O处产生电场的场强大小分别为.则( )A. B. C. D.【参考答案】A【名师解析】根据点电荷电场强度公式，且电荷只分布球的表面，对于图甲，虽表面积相同，但由于间距的不同，则上、下两部分电荷在球心O处产生电场的场强大小关系为，因电荷Q在球心O处产生物的场强大小，则，而，故A正确，B 错误；对图乙，半球面分为表面积相等的左、右两部分，是由于左右两个半个球壳在同一点产生的场强大小相等，则根据电场的叠加可知：左侧部分在O点产生的场强与右侧电荷在O点产生的场强大小相等，即．由于方向不共线，由合成法则可知，，故CD错误，故选A.12．如图所示，16个电荷量均为+q(q>0)的小球(可视为点电荷)，均匀分布在半径为R的圆周上若将圆周上P点的一个小球的电荷量换成-2q，则圆心0点处的电场强度为A. ，方向沿半径向左B. ，方向沿半径向右C. ，方向沿半径向左D. ，方向沿半径向右【参考答案】D【名师解析】圆心0点处的电场强度可以看成是P点-2q点电荷和与P对称的+q点电荷在O点电场强度的叠加。
根据点电荷电场强度公式和场强叠加原理，O点处的电场强度为E=kq/R2+ k·2q/R2=3 kq/R2，方向向右，选项D正确。
13．（湖北省襄阳市第五中学2016届高三5月高考模拟适应性考试（一）理科综合物理试题）已知静电场中某点的电势为标量：若取无穷远处电势为零，在一带电荷量为+q的点电荷的电场中，与点电荷相距r 处的电势为φ＝k q r ；如果某点处在多个点电荷所形成的电场中，则电势为每一个点电荷在该点所产生的电势的代数和。
如图所示，AB 是均匀带电的细棒，所带电荷量为＋Q 。
C 为AB 棒附近的一点，CB 垂直于AB 。
若取无穷远处电势为零，AB 棒上的电荷所形成的电场中，C 点的电势为φ0。
则AC 连线中点D 处的电势为A ．2φ0B ．2φ0C ．φ0D ．12φ0 【参考答案】A【名师解析】设φ0等效成AB 棒上的电荷集中于AB 中点P 处，图中E 是AP 的中点，由几何知识知：1 2ED PC =；带电量为+Q 的点电荷所形成的电场在C 点的电势为φ0，将AB 棒均分成两段，并看成两个点电荷，每个点电荷的电荷量为Q/2，由0Q k r ϕ=可知，每个电荷量为Q/2的点电荷在D 点产生电势为φ0，则两个点电荷在AC 连线中点D 处的电势为2φ0，故A 正确，BCD 错误；故选A.考点：电势的叠加【名师点睛】本题是信息题，要读懂题意，知道点电荷电势的公式0Q krϕ=，理解等效思维的运用是解题的关键，注意电势的代数和。