变压器的负载运行分析
变压器的空载运行及负载运行

N1I0 N1 I0 N1 I1L N2 I2
N1 I1L - N2 I2
其中I1L远远大于I0,大部分用来抵抗副边电流引起的磁通量变化。
当负载运行时可认为I1L=I1。
I1
I2 k
或 I1 I2
1 k
N2 N1
k为变压器变比
一、二次电流比近似与匝数成反 比。可见匝数不同,不仅能改变 电压,同时也能改变电流。
产业信息
中国变压器设备-尤其是特种变压器-已 走向世界成为“中国制造” 品牌
谢谢聆听
P0 = PFe + Pcu ≈ PFe
铁损耗分量
铁损耗分量:符号为I10P,供给铁磁材料 铁损(磁滞和涡流损耗),为有功分量
Part 2 空载运行分析
思考
如果误将变压器高低压侧接反,会发生什么异常现象?
变压器低压侧如果接到高压电源上,则铁心主磁 通Φm会增加,磁路饱和程度增加,因而励磁电流I0大 大增加,有可能烧毁线圈(励磁电流随磁路饱和程度 增加而急剧增大)
单相变压器空载运行示意图
Part 2 空载运行分析
空载电流的作用与组成
I10 I10Q I10P
励磁分量
励磁分量:符号为I10Q,用来建立主磁 通,相位与主磁通相同,为无功分量
变压器空载运行时,只从电源吸收少量有功功率P0, 用来供给铁心中铁损PFe和少量绕组铜损Pcu=R1I102 (可忽略不计)。容量越大,空载功率P0越小
Part 3 变压器的负载运行
变压器作用 通过对变压器负载运行的分析,可以清楚地看出变压器具有变电压、 变电流、变阻抗的作用。
• 变换电压 U1/U2≈E1/E2=k=N1/N2
• 变换电流 I1/I2≈N2/N1=1/k
变压器负载实验中的数据分析与评估

变压器负载实验中的数据分析与评估在变压器负载实验中,数据分析与评估是非常重要的环节。
通过对实验中所收集到的数据进行准确的分析和评估,可以评估变压器的性能和负载能力,从而为变压器在实际应用中的运行提供依据。
本文将对变压器负载实验中的数据分析与评估方法进行探讨。
一、数据采集与处理在进行变压器负载实验时,首先需要通过适当的仪器设备采集实验数据。
常用的数据采集设备包括电流表、电压表、功率表等。
这些设备可以实时测量变压器在负载运行过程中的电流、电压、功率等参数,并将数据记录下来。
在采集到数据后,需要进行适当的处理。
首先,对数据进行校验,确保数据的准确性和完整性。
其次,将采集到的数据按照时间顺序进行排序,以便后续的分析和评估。
最后,需要进行数据的清洗,去除异常值和噪声,确保数据的可靠性。
二、数据分析方法1. 负载特性分析负载特性分析是变压器负载实验中最常用的数据分析方法之一。
通过分析负载特性曲线,可以了解变压器在不同负载条件下的电流、电压、功率等参数的变化规律。
负载特性曲线通常以负载功率为横坐标,电流、电压等参数为纵坐标进行绘制。
负载特性分析可以揭示变压器的满载能力、超载能力以及负载平衡性等重要特性。
通过分析负载特性曲线,可以判断变压器是否能够满足实际应用中的负载要求,从而为变压器的选型和运行提供依据。
2. 效率分析效率是衡量变压器性能的重要指标之一,也是变压器负载实验中需要关注的内容之一。
通过分析变压器在不同负载条件下的效率曲线,可以了解变压器的能量转换效率。
效率曲线通常以负载功率为横坐标,效率为纵坐标进行绘制。
效率分析可以判断变压器在不同负载下的能量损耗情况,为变压器的运行和优化提供指导。
对于高效能的变压器,其效率曲线会相对平坦,能够在不同负载下保持较高的效率,从而减少能量损耗。
3. 温升分析在变压器负载实验中,温升是另一个需要进行分析的关键指标。
通过测量变压器在负载运行时的温度变化,可以了解变压器的散热能力和温升情况。
3.3单相变压器的负载运行
e1
N1
d
dt
e1
N1
d1
dt
e2
N2
d
dt
e2
N2
d2
dt
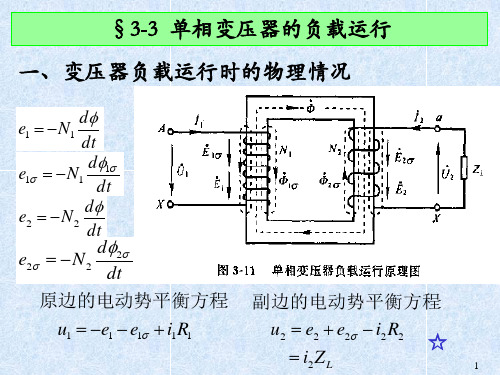
原边的电动势平衡方程: 副边的电动势平衡方程:
u1 e1 e1 i1R1
u2 e2 e2 i2R2 ☆
i2ZL
1
§3-3 单相变压器的负载运行
二、负载运行时的基本方程式
18
解 :(1)原、副边线电流: 变压器变比:
k U1N / 3 10000 25 U2N / 3 400
负载阻抗折算值:
ZL k 2ZL 252 (0.2 j0.07) 125 j43.75Ω
每相总阻抗:
Z zk ZL 1.546 j5.408125 j43.75Ω 126.546 j49.158 135.7621.23
X 2 k 2 X 2 3 0.055 0.165Ω
ZL k 2ZL 3 (4 j3) 12 j9Ω
14
根据题意,画出T形等值电路:
励磁阻抗:
Zm Rm jX m 30 j310 311.484.5
15
副边漏阻抗和负载阻抗和:
Z Z2 ZL 0.105 j0.165 12 j9 15.1837.1
『补例3-4』一台三相变压器,Y/y连接,SN=800kVA,U1N/U2N
=10000/400V;已知每相短路电阻rk=1.546,短路电抗xk=5.408
,该变压器原边接额定电压,副边接三相对称负载运行,每
相负载阻抗为:ZL=0.20+j0.07 。试用简化等值电路计算:
(1)变压器原、副边线电流; (2)副边线电压; (3)输入输出的有功功率及无功功率 (4)变压器效率
2-变压器负载运行
的大小
与空载运行时相比,负载时一次绕组的电流变化了,电源电压
不变,严格说来,负载时的
•
E
与空载时的不同。但在电力变压
1
器仍的然设还计是I中1N Z1I•0很U1小.仍,即存使在在U1额 E定1 由负载E1下 4运.44行fN1,I1Nm
比I0 大很多倍, 看出,空载、负
载与表运示空行。载,时其的主在磁数通值• m上的差数不值多差,仍别可很以小用,即同负一载个时符的号励I•磁0 N磁1或动势F• 0
因
,可认为 Zm
Z
' 2
Z
' L
无限Zm大而断开,于是等效电路变成了“一”型,
称为简化等效电路。如图:
单相变压器的负载运行
b.电压平衡方程式:
•
•
•
•
•
•
•
•
U1
I1
Z1
I 1 Z2'
U
' 2
I1
Z1
Z
' 2
U
' 2
I1 Zk
U
' 2
•
•
I1
I
' 2
•
•
U
' 2
Z
' L
单相变压器的负载运行
b.变压器接感性负载的相量图2-12a图:
单相变压器的负载运行
※相量图的绘制过程: 根据给定的条件不同,画法不同,但都是电压方程式 的相量图表示。
如给定U2, I2,cos2, k 及各参数,画图步骤为:
(((((((1234567)))))))根画在画画画E•1 据出出出出U•2'EU超•I2•'的•20' IE••前21相和E,•1,E量•910它/加I上Z•2的' m与,上,,主I其•I•1加画磁0R夹1上出通的,I角•2'U•相R•1再m为2' I量•,0加;和再上,2为加。它j上II••超11XjI•1;2前'得X2'到得•一m 出U•个1E•。2'铁耗;角;
变压器的负载运行解读

(3-39)
折算后,变压器负载运行时的基本方程式组可简化为如下的方程式组
U1 E1 I1z1 E1 I0zm U2 E2 I2 z2 U2 I2 zL E2 E1 I1 I2 I0
(3-40)
变压器的负载运行(续8)
2.等效电路
在将变压器副绕组的匝数折算为
与原绕组的匝数相等后,原、副绕组
负载增加时,I2 增加,副边磁动势N1 I2N2 增加,原
边电流的负载电流分量(-
N• I2
2
)也相应增加,
N
使 的其副产边生磁的动磁势动I2N势2 ,(以-维持NN12 I• 2励)磁1 Nl电得流以分抵量消增I0 加不了
变。可见,虽然变压器的原、副边没有直接的电
路联系,但负载电流的变化也会使原边电流相应
衡方程式。
变压器的负载运行(续2)
将磁动势平衡方程式表示成电流的形式,得
I
•
I
0
(
N
2
•
I2)
(3-26)
1
N
由上式看出,变压器负1 载运行时的原边电
流 I1 是大于变压器空载运行时的原边电流 I0 的, 它由反映主磁通 m 大小的励磁电流分量 I0 和反
映负载大小的负载电流分量(-
)组成。当 N • I2 2
s
s
s
图3.9 单相变压器负载运行 时的简化等效电路
变压器的负载运行(续9)
==308.00V例53/111,5已V其知,负一r1=载台0阻单.1抗相5为变,:压r2z器=L=的0.40数+2j43据为,。:x当S1N=外4.06k加.V2A7电,U压,1N /为xU22N 额定值时,用简化等效电路计算原、副边电流及副边电
工厂供配电知识点:变压器的负载运行

负载运行的物理状况 负载运行时的基本方程
一、负载运行的物理状况
一、负载运行的物理状况
当变压器二次绕组接上负载时,电动势E2将在二次绕组中产生电流I2 ,其方向与E2相同,随负载的变化而变化,I2流过二次绕组N2时建立磁动 势F2=I2N2。从电磁关系上来说, 变压器就从空载运行过渡到了负载运行 。F2也将在铁心内产生磁通,即此时铁心中的主磁通Φ不再单独由一次绕 组决定,而是由一次、二次绕组共同作用在同一磁路产生。磁动势F2的出 现使主磁通Φ趋于改变,随之电动势E1和E2也发生变化,从而打破了原来 空载运行时的平衡状态。在一定的电网电压 下,E1的改变会导致一次侧 绕组电流由空载时的I0改变为负载运行时的I1。但由于电源电压和频率不 变, 因而相应的主磁通也应保持不变。
二、变压器负载运行时的基本方程
(1)磁动势平衡方程式 变压器负载运行时,一次绕组磁动势F1和二次绕组磁
动势F2都作用在同一磁路上,如上图所示,于是根据磁路全电流 定律可得到变压器负载F运1 行F2时 F的0 磁动势方程式
这就是说,变压器负载运行时,作用在主磁路的两个 磁动势F1和F2构成了负载时的合成磁动势F0,从而由F0建立了铁 心内的主磁通。
三、变压器的空载电流和空载损耗
(2)电动势平衡方程式 由于实际上变压器的一、磁通在一、二次绕组中感应的电动势E1和E2外, 仅与一次绕组交链的一次漏磁通Φ1σ和与二次绕组交链的二次 漏磁通Φ2σ又在各自交链的绕组内产生漏感电动势E1σ和E2σ 。
课堂总结与练习
判断题: 1、负载运行时主磁通不再单独由一次绕组决定。 2、负载运行时二次绕组电流的变化不影响一次绕组电 流。 3、二次绕组输出功率变化的同时会引起一次绕组从电 网吸收功率的变化。
变压器的正常和异常运行分析
变压器的正常和异常运行分析变压器是电力系统中最常见的电气设备之一,它负责将高压电能传输到低压电网中。
正常运行的变压器具有高效、稳定和可靠的特点,但受到一些外部因素的影响时可能会出现异常情况。
本文将对变压器的正常和异常运行进行详细分析。
一、正常运行的变压器正常运行的变压器主要表现在以下几个方面:1.高效率:正常运行的变压器具有高效率的特点,其输入功率与输出功率之比接近于1,能够减少电能的损耗和浪费。
2.稳定的负载:变压器通常设计为满载运行时的最佳状态,负载范围内的运行能够保持其稳定性和正常工作。
3.温度稳定:变压器的运行温度通常受到限制,正常运行时变压器能够保持在正常工作温度范围内,不超过额定温度。
4.良好的绝缘性能:正常运行的变压器应具有良好的绝缘性能,能够阻止电流泄露和绝缘击穿。
5.正常的电流和电压:正常运行的变压器能够保持正常的电流和电压波形,不产生任何变形和失真。
6.低噪音和振动:正常运行的变压器应该具有低噪音和振动的特点,不会对周围环境和设备造成干扰。
二、异常运行的变压器异常运行的变压器可能会出现以下情况:1.过载:变压器工作在超过额定负载的情况下,会使变压器温升异常增加,导致绕组和绝缘材料受到损害。
2.短路:变压器的绕组出现短路时,会导致电流过大,可能引发火灾和爆炸等严重事故。
3.绝缘击穿:绝缘性能不良或外界形成高压波浪时,会导致绝缘击穿,引起变压器的短路和故障。
4.损耗增加:因为使用环境、冷却不良或过压等原因,变压器的损耗可能会增加,导致能量损耗增加和效率下降。
5.噪音和振动增加:异常运行的变压器会引起噪音和振动的增加,除了会影响周围环境外,还可能引发故障和损坏。
三、正常和异常运行的分析方法分析变压器的正常和异常运行,需要进行以下几个方面的工作:1.运行数据的监测和分析:对变压器的电流、电压和温度等运行数据进行监测和分析,可以及时发现可能存在的异常情况。
2.绝缘性能的测试和评估:定期测试变压器的绝缘性能,评估其绝缘系统的稳定性和可靠性,防止绝缘击穿和短路故障。
变压器的负载运行分析
变压器的负载运行分析引言变压器是电力系统中最为重要的设备之一,其主要作用是将一个电压值转换为另一个电压值,从而满足电力系统中不同电压等级之间的输电要求。
在电力系统中,变压器是高效能、大容量的电力设备。
在变压器的运行过程中,负载是影响其运行性能及寿命的重要因素之一。
因此,对变压器的负载运行进行分析及评估具有重要意义。
负载运行分析负载的分类在变压器的运行过程中,其负载可分为接触式负载和非接触式负载两种。
•接触式负载:指负责直接吸收有功负载的负载,如电阻炉、变频器等设备。
•非接触式负载:指变压器在运行过程中,所提供的磁场使得设备内的器件发生电磁感应而进行能量转换的负载,如电动机、照明设施等。
负载对变压器的影响在变压器运行过程中,负载对其性能有着较大的影响,对变压器的正常运行产生多种影响,如:•温升过高:当变压器的负载过大时,变压器的铁芯及线圈会产生大量的磁通量,导致变压器内部温度升高,如果超过了其所能承受的温度,就会对其安全运行造成威胁。
•电损失过多:变压器在运行过程中会出现电阻、铁损等不同种类的损失,这些损失会使得变压器的效率下降。
•电磁变化过大:当变压器负载过大,其放大比例也会变大,使得输出变化幅度增加,同时会使输出波形失真。
负载能力分析变压器能够承受的负载能力是衡量变压器运行稳定性及性能优异程度的重要标准。
通常是指容量,即变压器可以稳定输出的最大容量。
(与变压器的额定容量不同,因为额定容量为变压器的设计能力。
)因此,需要对变压器的负载能力进行分析和评价,以确定其稳定性及承载能力。
常用的评估方法是,通过实际检测,确定其能承载的最大负载,再结合变压器的设计特性,以此为依据来评估变压器的负载能力和稳定性。
负载评估方法对变压器的负载能力进行评估通常采用如下的方法:1.根据测量得出变压器的额定容量。
2.进行实际运行测试,通过测量变压器的温升和其他参数来确定变压器的实际负载。
3.采用已知的计算公式对实际负载进行计算和分析,以确定变压器的可承载能力。
变压器负载实验的结果分析与判断
变压器负载实验的结果分析与判断在电力系统中,变压器是起到调节电压的重要设备。
为了确保变压器的正常运行和性能稳定,我们需要进行负载实验来对其性能进行评估和判断。
本文将对变压器负载实验的结果进行分析和判断。
一、负载实验的目的负载实验的目的是通过加载一定负载,模拟实际运行条件下的工作情况,以评估变压器的电气性能和热特性。
通过实验得到的结果,可以用于判断变压器的运行状态、负载能力以及是否存在异常问题。
二、实验结果分析1. 输出电压和电流在负载实验中,我们需要测量输出电压和电流的数值。
通过对比实验结果和设计规格,可以判断变压器的电气性能是否正常。
如果输出电压和电流达到或接近设计要求,说明变压器的输出能力良好,符合预期。
2. 效率计算负载实验中,我们还可以计算变压器的效率。
变压器的效率可以通过输出功率与输入功率的比值计算而得。
效率越高,说明变压器的能量转换效率越好,损耗越小。
对比设计要求,可以判断变压器的能效性能。
3. 温度监测变压器在负载实验中应进行温度监测。
通过测量变压器的温度,可以判断变压器的热特性是否正常。
如果温度升高过快或超过设计要求,可能意味着变压器存在过载或冷却不良的问题,需要进一步分析和判断。
三、结果判断根据负载实验的结果分析,我们可以对变压器的运行情况进行判断和评估。
以下是几种常见情况的判断:1. 满足设计要求:如果变压器的输出电压和电流达到或接近设计要求,并且效率高,温度在合理范围内,那么可以判断变压器的性能正常,工作稳定。
2. 负载能力不足:如果在负载实验中,变压器出现输出电压和电流不达标,效率低下的情况,可能说明变压器的负载能力不足,需要进一步分析原因,如功率匹配不合适等。
3. 温度异常:如果变压器在负载实验中温度升高过快或超过设计要求,可能存在过载或冷却不良等问题,需要进行进一步检查和维修。
四、结果分析的意义通过对变压器负载实验结果的分析与判断,可以得出关于变压器性能和运行状态的结论。
变压器负载运行
' 2
E
' 2
&r I 1 1
& −E 1 &' −I 2 & I m
& I 1
& φ m
& & 90 0 的主磁通 φ (4)画出领先 E 1 m
& = −E & / Z 画出 I & , (5)根据 I m 1 m m
' I2 ' U2 ' ' I2 r2
副边绕组经折算 后,原来的基本 方程组成为:
& = −E & +I & ( R + jX ) U 1 1 1 1 1 &′ = E &′ − I & ′ ( R ′ + jX ′ ) U
2 2 2 2 2
已没有变比k !
& =I & +I &′ I 0 1 2 & =E &′ E 1 2 & = −I & ( R + jX ) E m m 1 0 &′ = I &′ Z ′ U
& I 1
r1
& I m
x1
&' x' −I 2 2
r2'
&' −U 2
& U 1
rm xm
' ZL
20
简化的等效电路
负载运行时, Im在I1N中所占的比例很小。在工程实际计算 中,忽略Im ,将激磁回路去掉, 得到更简单的阻抗串联电路
& I 1
r1
x1
&' x' −I 2 p; U 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图5.13 变压器的折算过程 考虑到图5.13a所示等值电路原、副方在电气上是相互独立的。为了简化计算,通 常将副方的绕组匝数由 N 2 提升至 N1 ,这样二次侧的各物理量均将发生相应的变化,这一 过程又称为折算。也就是说,将变压器的二次(或一次)绕组用另一个绕组来等
xm z m rm
2 2
(5-34) (5-35) (5-36)
变压器的变比为:
k
U1 U 20
B、短路试验
通过短路试验可以确定变压器的短路电阻 rk 和短路电抗 xk 。短路试验的试验接线如图 5.19a、b所示。
图5.19 变压器短路试验的接线图
根据额定电流时的试验数据,便可分别计算变压器的参数如下: 短路电阻为:
由于励磁阻抗很大,励磁电流很小,有时就将励磁支路舍掉,近似“Γ”型等效电路又可进 一步进行近似为简化等效电路,如图5.16所示。
图5.16 变压器的 简化等效电路
在变压器的简化等效电路中,令:
rk r1 r2 xk x1 x2 z k rk jxk
x 式中,rk 、 k 和 z k 分别称之为变压器的短路电阻、短路电抗和短路阻抗,即变压器 的副边短路时呈现的阻抗
(5-20)
漏电抗 x 2 或漏电感 L2 反映了副方漏磁路的情况。
C、变压器负载运行时的电磁关系
图5.12 变压器负载后的电磁过程
5.5 变压器的基本方程式、等值电路与 相量图
A、变压器的基本方程式
根据图5.11、图5.12以及正方向假定,利用基尔霍夫电压定律(KVL)便可获得原、副方 绕组电压平衡方程式的相量形式为:
变压器负载后,副方也存在漏磁通。同原方一样,副方漏磁路也可以用副方漏电抗来 描述,即: x2 L2 2fL2 。其中,副方漏电感为:
L2
N N 2 2 S 2 2 2 2 N 2 N 2 0 i2 N 2 i2 R 2 l 2
2 2
U 20 U 2 U 2N U 2 U 1N U 2 u 100% 100% 100% (5-47) U 2N U 2N U 1N
根据简化等效电路(图5.22a)和KVL得:
U1N U 2 I1 (rk jxK )
(5-48)
由此绘出相量图如图5.22所示。
(5-33)
考虑到 Z m z1 ,故有:
z0 z m
xm z m rm
2 2
(5-34) (5-35) (5-36)
变压器的变比为:
k
U1 U 20
B、短路试验
通过短路试验可以确定变压器的短路电阻 rk 和短路电抗 xk 。短路试验的试验接线如图 5.19a、b所示。
图5.19 变压器短路试验的接线图
(5-29)
经过折算后,变压器的基本方程式变为:
(5-30)
利用上式,并结合图5.13b便可获得变压器的T型等值电路如图5.14所示。
图5.14 变压器的T型等值电路
若忽略一次绕组漏阻抗压降的影响,T型等值电路可进一步简化为近似“Γ”型等效电 路,如图5.15所示。
图5.15 变压器的“Γ”型等效电路
rk 75 C
T0 75 rk T0
2
(5-43) (5-44)
z k 75 C r 2 k 75 C x k
定义: 阻抗电压或短路电压为 U kN z k 75 C I1N 。它有两种表示方法:
0
(1)短路电压百分比
z k 750 C I1N U kN uk 100% 100% U 1N U 1N
(5-23)
(5-24) (5-25) (5-26)
E2 kE2
电流:
U 2 kU 2
N I 1 I2 2 2 I2 N1 k
根据折算前后的磁势不变,得:
阻抗:
根据折算前后的有功功率和无功功率不变,得:
rI 2 2 k 2 r2 r2 2 I2
2
(5-27)
(5-42)
考虑到绕组电阻随环境温度的变化,按照技术标准,绕组的电阻值应折合到标准温 度 75 C ,而漏阻抗与温度无关。于是有:
rk 75 C
T0 75 rk T0
2
(5-43) (5-44)
z k 75 C r 2 k 75 C x k
定义: 阻抗电压或短路电压为 U kN z k 75 C I1N 。它有两种表示方法:
U 1 E1 (r1 jx1 ) I 1 E1 z1 I1 U 2 E2 r2 I 2 jx2 I 2 E 2 z 2 I 2
(5-21)
将式(5-9)、(5-13)、(5-18)和式(5-21)汇总得变压器负载后的基本方程式为:
x2 I 2 x2 k 2 x2 2 I2
同理,
2
(5-28)
z k 2 z2 2
U 1 E1 z1 I 1 U 2 E 2 z I 2 2 I1 I 2 I m E1 E 2 z m I m
0
(1)短路电压百分比
z k 750 C I1N U kN uk 100% 100% U 1N U 1N
(5-45)
(2)标幺值(Per Unit Value)
U kN z k 750 C I1N z k 750 C * u zk U 1N U 1N Z1N
* k
(5-46)
U 1 E1 z1 I 1 U 2 E 2 z 2 I 2 E1 z m I m N1 I1 N 2 I 2 N1 I m E1 N 1 k E2 N 2
(5-22)
B、变压器的等值电路
标幺值 = 实际值 / 基值 基值一般取额定值,标幺值就是实际值与基值的 比值。 使用标幺值得优点:
直观明了,直接反映变压器运行状态,例如 I * 1.5 说明过载了。 1 计算方便,便于性能比较。不论变压器大小、形状,其两个主要性能 指标的大小一般为 I0* 0.02 ~ 0.08 , Uk * 0.05 ~ 0.175 使用标幺值后,折算前后各量标幺值相同,无需折算,即: R2*=R2'*,I2*=I2'*,U2*=U2'*
上式与式(5-17)比较可得:
结论: 变压器负载后,一次侧电流有所增加。二次侧所需的负载 (电流)越大,一次侧供给的电流也就越大。 即变压器可以看作 为一种供需平衡关系。
式(5-17)写成相量形式为:
N1I1 N2 I 2 N1I0
(5-18)
B、变压器负载后副边漏磁路的电参数等效
N1i1 N 2i2 N1i0
(5-17)
上式可以理解为:随着负载电流的增加,一次侧必须增加相应的磁势(或电流),以抵 消二次侧磁势,才能维持空载时的磁通或磁势不变。于是有:
N1i1 N 2 i2 0
即:
N1 (i0 i1 ) N 2i2 N1i0
i1 i0 i1
其中,阻抗基值为 Z1N
U 1N I 1N
。
结论: 为减小二次侧电压随负载的变化,希望越小越好;但从减小 短路电流的角度看,希望越大越好。工程中应兼顾这两个因素。
5.6 变压器的等值电路参数的试验测定
变压器等值电路的参数可以通过空载和短路试验测得。
A、空载试验
通过空载试验可以确定变压器的变比 k 、激磁电阻 rm 和激磁电抗 xm 。空载试验的具体 接线如图5.18a、b所示。
C、变压器的相量图
根据变压器的基本方程式(5-30)绘出变压器带感性负载时运行时的相量图如图5.17所示。
图5.17 感性负载时变压器的相量图
结论: 变压器负载后其一次侧的功率因数角减小,功率因数得以提高。
5.6 变压器的等值电路参数的试验测定
变压器等值电路的参数可以通过空载和短路试验测得。
A、空载试验
效,同时,对该绕组的电磁量作相应的变换,以保持两侧的电磁关系不变。
折算的原则: 折算前后要保证电磁关系不变,即:(1)折算前后的磁势应 保持不变;(2)折算前后的电功率及损耗应保持不变。
根据上述原则,折算后的等值电路如图5.13b所示。 折算后副方各物理量分别按下式计算:
电压:
同理,
E2
N1 E2 kE2 E1 N2
rk pK IK
2
(5-38)
短路阻抗和短路电抗分别为:
Uk zk Ik
x k z k rk
2 2
(5-39)
(5-40)
对一、二次侧绕组的漏电抗值,可通过下式将漏阻抗近似分开:
x1
x 2
xk 2
(5-42)
考虑到绕组电阻随环境温度的变化,按照技术标准,绕组的电阻值应折合到标准温 度 75 C ,而漏阻抗与温度无关。于是有:
图5.22 变压器的简化等效电路及其相量图 借助于图5.22a,便可求出电压变化率为:
u (
I1N rk cos 2 I1N xk sin 2 ) 100% U1N
(5-49)
(rk * cos 2 xk * sin 2 ) 100%
5.4 变压器的负载运行分析
变压器负载后,二次侧的电流不再为零,从而导致铁心内部的电磁过程发生变化。
A、变压器负载运行时的磁势平衡方程式
图5.11 变压器的负载运行 考虑到负载运行时,一次侧绕组的电势平衡方程式为:
U1 E1 z1 I1
(5-16)
忽略漏阻抗压降的变化,则变压器负载前后的主磁通基本保持不变,因此,变压器负 载后的激磁磁势与空载时的激磁磁势基本相等。根据图5.11所示正方向,于是得变压器的 磁势平衡方程式为:
