七年级数学课时练答案下册
【★】人教版七年级下册数学课时练《5-3-2 命题、定理、证明》(含答案)
《5．3．2 命题、定理、证明》课时练一、选择题1．下列命题中，是假命题的为（）A．邻补角的平分线互相垂直B．平行于同一直线的两条直线互相平行C．如果一个角的两边分别平行于另一个角的两边，则这两个角一定相等D．平行线的一组内错角的平分线互相平行2．下列语句中，不是命题的是（）A．若两角之和为90°，则这两个角互补B．同角的余角相等C．作线段的垂直平分线D．相等的角是对顶角3．有下列命题：三角形的两边之和大于第三边；②相等的角是对顶角；③若a与b互为倒数，则ab=1；④绝对值等于本身的数是正数．其中真命题的个数是（）A．1 B．2 C．3 D．44．下列语句中，不属于命题的是（）A．若两角之和为90°，则这两个角互补B．同角的余角相等C．作线段的垂直平分线D．相等的角是对顶角5．下列语句中，不属于命题的个数是（）①延长线段AB；②自然数都是整数；③两个锐角的和一定是直角；④同角的余角相等．A．1B．2C．3D．46．下列命题中，是真命题的是（）A．在同一平面内，垂直于同一条直线的两条直线平行B．三角形的一个外角大于它的任何一个内角C．两条直线被第三条直线所截，同旁内角互补D．过一点有且只有一条直线与已知直线平行7．下列语句：①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③两条不相交的直线叫做平行线；④一个角的两边分别与另一个角的两边互相平行，则这两个角相等；⑤不在同一直线上的四个点最多可以画6条直线．其中错误的有（）A．2个B．3个C．4个 D．5个8．下列命题中是假命题的是（）A．同旁内角互补，两直线平行B．直线a⊥b，则a与b的夹角为直角C．如果两个角互补，那么这两个角一个是锐角，一个是钝角D．若a∥b，a⊥c，那么b⊥c二、填空题9．命题“两直线平行，同位角相等”的逆命题是命题．（填“真”或“假”）10．把命题“三角形的内角和等于180°”改写成“如果……那么……”的形式：如果，那么．11．如图，若∠1=∠2，则AB∥CD，这是命题（填“真”或“假”）．12．“如果ab=0，那么a=0”是命题．“如果a=0，那么ab=0” 是命题．13．命题“对顶角相等”的条件是．14．下列命题中：①若∣a∣=∣b∣，则a=b；②两直线平行，同位角相等；③对顶角相等；④内错角相等，两直线平行．是真命题的是．（填写所有真命题的序号）三、解答题15．试判断命题：“若一条直线上的两点到另一条直线的距离相等，则这两条直线平行”的真假，并说明理由．16．判断下列命题是真命题还是假命题，如果是假命题，请举出一个反例．（1）如果一个数是偶数，那么这个数是4的倍数．（2）两个负数的差一定是负数．17．用语言叙述这个命题：如图，直线AB，CD被EF所截，∠1＋∠2=180°，EM，FN分别平分∠BEF和∠CFE，则EM∥FN．18．对于同一平面内的三条直线a，b，c，给出下列论断：①a∥b；②b∥c；③a⊥b；④a∥c；⑤a⊥c．请以其中两个论断为条件，一个论断为结论，组成一个你认为正确的命题（至少写两个命题）．参考答案1．C．2．C．3．B．4．C．5．A．6．A7．B．8．C9．真．10．如果三个角是三角形的内角，那么它们的和等于180°．11．假．12．假；真；13．两个角是对顶角14．②③④15．解：假命题．图略，AB⊥BD于点B，CD⊥BD于点D，AB=CD，但AC与BD相交．16．解：（1）假命题．反例：6是偶数，但6不是4的倍数．（2）假命题．反例：（－5）－（－8）=＋3．17．解：如果两条直线平行，那么内错角的角平分线互相平行．18．解：答案不唯一，如：若a∥b，b∥c，则a∥c；若a∥b，a∥c则b∥c；若b∥c，a∥c，则a∥b；若a⊥b，a⊥c，则b∥c；若a⊥b，b∥c，则a⊥c；若b∥c，a⊥c，则a⊥b．。
2023-2024学年人教部编版初中七年级下册数学课时练《5.3.2 命题、定理、证明》(含答案)
第三课青春的证明 3.2青春有格一、单项选择题：1. 青春，我们敢想敢做，但青春并不意味着放纵，也要懂得选择。
下列有关“选择”的说法不正确的是( ) A. 只要自己愿意，就可作出各种选择 B. “羞恶之心”是我们明确行为选择的理由C. 我们要树立底线意识，违背道德或法律的行为坚决不做D. 要独立思考，明辨是非善恶，不盲目从众，作出正确的选择2. “世界那么大，我想去看看”，但世界又是纷繁复杂的，美丑、善恶交织在一起，这就要求我们“行己有耻”。
引导我们辨别是非、做出正确选择的主要因素是( )A. 恻隐之心B. 辞让之心C. 是非之心D. 羞恶之心3. 很多人觉得自己计划完不成，拖延，生活中养成种种恶习的根源在于自控力不强。
下列增强自控力的合理建议是( )①每天坚持做一些自己力所能及的事情①认真记录一些自己平时不关注的事情①尝试不做某些事情，纠正自己的行为①拒绝一切娱乐活动，专注提高学习成绩A. ①②③B. ①②④C. ①③④D. ②③④4. 后汉东莱太守杨震经过管辖地昌邑县时，县令王密送去十金，并说“暮夜无知者”。
杨震严词拒受，说：“天知，地知，你知，我知，何谓无知？”人们因此称他为“四知太守”。
杨震值得我们当代人学习的品质是( ) A. 自信，要相信自己的能力 B. 自爱，不做有损人格的事C. 自强，有不断进取的精神D. 自负，遇事有自己的主见5. “行己有耻”需要我们磨砺意志，拒绝不良诱惑，不断增强自控力。
我们要做到()①增强“我不要”的力量。
尝试不做某些事情，纠正自己的行为①增强“我想要”的力量。
每天坚持做一些自己未能做到的事情①加强自我监控。
认真记录一些自己平时不关注的事①面对挫折，半途而废A. ①①①B. ①①①C. ①①①D. ①①①6. “行己有耻”出自《论语·子路》。
春秋时期的孔子曾说：“行己有耻，使于四方，不辱君命，可谓士矣。
”下列行为中，没有做到“行己有耻”的是( )①拿别人的缺点、缺陷、姓名开玩笑②经常帮助同学，特别是身体残疾的同学③喜欢散播小道消息，专门讲同学的糗事④上课时给同学讲故事听，逗同学发笑A. ①①①B. ①①①C. ①①①D. ①①①7. 雨果说：“谁虚度了年华，青春就将褪色。
人教版七年级下册数学课时练《8.4 三元一次方程组的解法》试卷含答案
人教版七年级数学下册 第八章 二元一次方程组8.4 三元一次方程组的解法 课后练习一、选择题1．下列方程组是三元一次方程组的是（ ）A ．123x y y z z x +=⎧⎪+=⎨⎪-=⎩B ．02310x y z x yz y z ++=⎧⎪-=⎨⎪-=⎩C ．22154x y y z x z ⎧+=⎪+=⎨⎪-=⎩D ．563x y w z z x +=⎧⎪+=⎨⎪+=⎩2．三元一次方程5x y z ++=的正整数解有（ ）A ．2组B ．4组C ．6组D ．8组 3．已知代数式2ax bx c ++，当1x =-时，其值为4；当1x =时，其值为8；当x =2时，其值为25；则当3x =时，其值为（ ）．A ．4B ．8C ．62D ．524．若实数,,x y z 满足41233x y z x y z -+=⎧⎨-+=⎩，则6x y z ++=（ ） A ．3- B ．0 C ．3 D ．不能确定值 5．已知三个实数a 、b 、c 满足a+b+c ＝0，a ﹣b+c ＝0，则下列结论一定成立的是（ ） A ．a+b≥0 B ．a+c ＞0 C ．b+c≥0 D ．b 2﹣4ac≥06．如果方程组864x y y z z x +=⎧⎪+=⎨⎪+=⎩的解使代数式kx +2y ﹣3z 的值为8，则k ＝（ ）A ．13B ．﹣13C ．3D ．﹣37．为了奖励进步较大的学生，某班决定购买甲、乙、丙三种钢笔作为奖品，其单价分别为4元、5元、6元，购买这些钢笔需要花60元；经过协商，每种钢笔单价下降1元，结果只花了48元，那么甲种钢笔可能购买（ ）．A ．11支B ．9支C ．7支D ．5支 8．一对夫妇现在年龄的和是其子女年龄和的6倍，他们两年前年龄和是子女两年前年龄和的10倍，6年后，他们的年龄和是子女6年后年龄和的3倍，问这对夫妇共多少个子女？（ ）A ．1个B ．2个C ．3个D ．4个 9．小明妈妈到文具店购买三种学习用品，其单价分别为2元、4元、6元，购买这些学习用品需要56元，经过协商最后以每种单价均下调0.5元成交，结果只用了50元就买下了这些学习用品，则小明妈妈有几种不同的购买方法．（ ）A ．6B ．5C ．4D ．310．一个宾馆有二人间、三人间、四人间三种客房供游客租住，某旅行团25人准备同时租用这三种客房共9间，如果每个房间都住满，则租房方案共有（ ）A ．4种B ．3种C ．2种D ．1种二、填空题11．已知2234x y y z x z +++===-，则2x y z ++=________． 12．已知3203340x y z x y z -+=⎧⎨--=⎩，则::x y z =___________． 13．对于实数x ，y 定义新运算x y ax by cxy ⋅=++其中a ，b ，c 为常数，若123,234⋅=⋅=，且有一个非零常数d ，使得对于任意的x ，恒有x d x ⋅=，则d 的值是____．14．有一片牧场，草每天都在匀速地生长(即草每天增长的量相等)，如果放牧24头牛，则6天吃完牧草；如果放牧21头牛，则8天吃完牧草．设每头牛每天吃草的量是相等的，如果放牧16头牛，则__________天可以吃完牧草．15．重庆市举行了中学生足球联赛，共赛17轮（即每队均需比赛17场），记分办法是胜一场得3分，平一场得1分，负一场得0分．若文德中学足球队的积分为16分，且踢平场数是所负场数的整数倍，且胜、平、负的场数各不相同．则文德中学足球队共负____场．三、解答题16．解方程：（1）11425x y x y z x y z =+⎧⎪++=⎨⎪+-=⎩（2）3743225x y y z x z -=-⎧⎪+=⎨⎪-=-⎩ （3）1151x y z y z x z x y +-=⎧⎪+-=⎨⎪+-=⎩（4）::3:4:536x y z x y z =⎧⎨++=⎩ 17．已知方程组354x y a y z a z x a +=⎧⎪+=⎨⎪+=⎩①②③的解使得代数式23x y z -+的值等于-10，求a 的值．18．在等式2y ax bx c =++中，当1x =时，2y =-；当1x =-时，20y =；当32x =与13x =时，y 的值相等．求a ，b ，c 的值．19．在等式2y ax bx c =++中，当1x =-时，0y =；当5x =时，60y =；当x =0时，5y =-，求222a ab c ++的值．20．已知y ＝ax 2+bx +c ，当x ＝1时，y ＝8；当x ＝0时，y ＝2；当x ＝﹣2时，y ＝4． （1）求a ，b ，c 的值；（2）当x ＝﹣3时，求y 的值．21．阅读材料：我们把多元方程（组）的非负整数解叫做这个方程（组）的“好解”．例如：18x y =⎧⎨=⎩就是方程3x +y ＝11的一组“好解”；123x y z =⎧⎪=⎨⎪=⎩是方程组206x y z x y z -+=⎧⎨++=⎩的一组“好解”． (1)求方程x +2y ＝5的所有“好解”；(2)关于x ，y ，k 的方程组155327x y k x y k ++=⎧⎨++=⎩有“好解”吗？若有，请求出对应的“好解”；若没有，请说明理由．22．某工程由甲、乙两队合作需6天完成，厂家需付甲、乙两队共8700元，乙、丙两队合作需10天完成，厂家需支付乙、丙两队共8000元；甲、丙两队合作5天完成全部工程的23，此时厂家需付甲、丙两队共5500元．（1）求甲、乙、丙各队单独完成全部工程各需多少天？（2）若要不超过15天完成全部工程，问由哪队单独完成此项工程花钱最少？请说明理由．23．若一个四位正整数abcd 满足：a +d =b +c ，我们就称该数是“心想事成数”．比如：对于四位数5263，∵5+3=2+6，∵5263是“心想事成数”，对于四位数1276，∵1+6≠2+7，∵1276不是“心想事成数”．（1）直接写出最小的“心想事成数”和最大的“心想事成数”；（2）判断3625是否为“心想事成数”，并说明理由；（3）若一个“心想事成数”，满足个位上的数字是百位上的数字的两倍，且千位上的数字与十位上的数字之和能被8整除，请求出所有满足条件的“心想事成数”．参考答案1．A 2．C 3．D 4．A 5．D 6．A 7．D 8．C 9．D 10．B 11．-1012．9：5：313．414．1815．1或516．（1）653xyz=⎧⎪=⎨⎪=⎩；（2）2112xyz⎧⎪=-⎪=⎨⎪⎪=⎩；（3）683xyz=⎧⎪=⎨⎪=⎩；（4）91215xyz=⎧⎪=⎨⎪=⎩17．53a=-．18．6113abc=⎧⎪=-⎨⎪=⎩19．2220．（1）731132abc⎧=⎪⎪⎪=⎨⎪=⎪⎪⎩；（2）1221．(1)5xy=⎧⎨=⎩或31xy=⎧⎨=⎩或12xy=⎧⎨=⎩(2)有，96xyk=⎧⎪=⎨⎪=⎩或1014xyk=⎧⎪=⎨⎪=⎩或1122xyk=⎧⎪=⎨⎪=⎩或123xyz=⎧⎪=⎨⎪=⎩22．（1）甲、乙、丙各队单独完成全部工程分别需10天，15天，30天．；（2）由乙队单独完成此工程花钱最少．23．（1）最小的“心想事成数”为1010；最大的“心想事成数”为9999；（2）四位数3625是“心想事成数”，理由见解析；（3）所有满足条件的“心想事成数”有：3254，2468，7294，4040，8080。
2023-2024学年人教部编版初中七年级下册数学课时练《7.2.1 用坐标表示地理位置》(含答案)
人教版七年级下册数学《7．2．1用坐标表示地理位置》课时练学校：___________姓名：___________班级：___________一、选择题1．小明向同学介绍自己家的位置，下列表述最恰当的是（）A．在学校的东南方向B．在东南方向900米处C．距学校900米处D．在学校东南方向900米处2．象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“马”和“车”的点的坐标分别为(4，3)，(－2，1)，则表示棋子“炮”的点的坐标为( )A．(3，2) B．(1，3)C．(0，3) D．(－3，3)3．小张和小陈都在电影院看电影，小张的位置用(a，b)表示，小陈的位置用(x，y)表示，我们约定“排数在前，列数在后”，若小张恰在小陈的正前方，则( )A．a=x B．b=y C．a=y D．b=x4．如图是小李设计的49方格扫雷游戏，“★”代表地雷(图中显示的地雷在游戏中都是隐藏的)，点A可用(2，3)表示，如果小惠不想因点到地雷而结束游戏的话，下列选项中，她应该点()A．(7，2) B．(2，6) C．(7，6) D．(4，5)5．如图是某电视塔周围的建筑群平面示意图，这个电视塔的位置用A表示．某人由点B出发到电视塔，他的路径表示错误的是(注：街在前，巷在后)( )A．(2，2)→(2，5)→(5，6)B．(2，2)→(2，5)→(6，5)C．(2，2)→(6，2)→(6，5)D．(2，2)→(2，3)→(6，3)→(6，5)6．下列数据不能确定物体位置的是（）A．电影票5排8号B．东经118北纬40C．希望路25号D．北偏东307．海事救灾船前去救援某海域失火货轮，需要确定( )A．方位B．距离C．方位和距离D．失火轮船的国籍二、填空题8．某人从A点沿北偏东60︒的方向走了100米到达点B，再从点B沿南偏西10︒的方向走了100米到达点C，那么点C在点A的南偏东__度的方向上．9．课间操时，小华、小军、小刚的位置如图，小华对小刚说，如果我的位置用(－1，－2)表示，小军的位置用(1，－1)表示，那么你的位置可以表示成________．10．对于平面直角坐标系xOy中的点P（a，b），若点P的坐标为（a+kb，ka+b）（其中k为常数，且k ≠0），则称点P 为点P 的“k 属派生点”，例如：P （1，4）的“2属派生点”为P （1+2×4，2×1+4），即P ′（9，6）．若点P 在x 轴的正半轴上，点P 的“k 属派生点”为点P ′，且线段PP ′的长度为线段OP 长度的5倍，则k 的值为___．11．如图，一只甲虫在55⨯的方格（每小格边长为1）上沿着网格线运动．它从A 处出发去看望B ．C ．D 处的其它甲虫，规定：向上向右走为正，向下向左走为负、如果从A 到B 记为：(1,4)A B →++，从B 到A 记为：(1,4)B A →--，其中第一个数表示左右方向，第二个数表示上下方向．（1）图中A C →(______，______)，B C →(______，______)，C →______(1+，______)； （2）若图中另有两个格点M ．N ，且M A →(3,4)a b --，M N →(5,2)a b --，则N A →应记为______．12．如图，以灯塔A 为观测点，小岛B 在灯塔A 的北偏东45°方向上，距灯塔A 20 km 处． 若以小岛B 为观测点，则灯塔A 在小岛B 的 方向上，距小岛B km 处．三、解答题13．小兰和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图(如图)，可是她忘记了在图中标出原点和x 轴、y 轴，只知道游乐园的位置D 的坐标为(2，－2)，你能帮她求出其他各景点所在位置的坐标吗？14．图中标明了李明同学家附近的一些地方，已知李明同学家位于（-2，-1）．（1）建立平面直角坐标系，写出学校，邮局的坐标；（2）某星期日早晨，李明同学从家里出发，沿着（-1，-2）、（1，-2）、（2，-1）、（1，-1）、（1，3）、（-1，0）、（0，-1）的路线转了一下，写出他路上经过的地方；（3）连接他在（2）中经过的地点，你能得到什么图形？15．如图，对于平面直角坐标系中的任意两点A，B给出如下定义：过点A作直线m⊥x轴，过点B作直线n⊥y轴，直线m，n交于点C，我们把BC叫做A，B两点之间的水平宽，记作d1（A，B），即d1（A，B）＝|x A﹣x B|，把AC叫做A，B两点之间的铅垂高，记作d2（A，B），即d2（A，B）＝|y A﹣y B|．特别地，当AB⊥x轴时，规定A，B两点之间的水平宽为0，即d1（A，B）＝0，A，B两点之间的铅垂高为线段AB的长，即d2（A，B）＝|y A﹣y B|；当AB⊥y轴时，规定A，B两点之间的水平宽为线段AB的长，即d1（A，B）＝|x A﹣x B|，A，B两点之间的铅垂高为0，即d2（A，B）＝0；（1）已知O为坐标原点，点P（2，﹣1），则d1（O，P）＝，d2（O，P）＝．（2）已知点Q（3t，﹣2t+2）．①若点D（0，2），d1（Q，D）+d2（Q，D）＝5，求t的值；②若点D（﹣2t，3t），直接写出d1（Q，D）+d2（Q，D）的最小值．16如图，一只乌鸦从其巢(点O)飞出，飞向其巢东6km北10km的一点A，在该点它发现有一个稻草人，所以就转向，再向东8km北4km的地方B飞去．在那里它吃了一些谷物后立即返巢O，假设乌鸦总是沿直线飞行的，则乌鸦所飞的路径构成了一个三角形OAB（1）若点O的坐标为(0，0)，点A的坐标为(6，10)，写出点B的坐标．（2）试求三角形OAB的面积．17．如图，已知A、B两村庄的坐标分别为（2，2）、（7，4），一辆汽车在x轴上行驶，从原点O出发．（1）汽车行驶到什么位置时离A村最近？写出此点的坐标．（2）汽车行驶到什么位置时离B村最近？写出此点的坐标．（3）汽车行驶到什么位置时，距离两村的和最短？请在图中画出这个位置，并求出此时汽车到两村距离的和．参考答案1．D 2．B 3．B 4．D 5．A 6．B 7．B8．559．(3，1)10．±511．3+ 4+ 2+ 0 D 2- ()2,2--12．答案为：南偏西45°，20．13． 解：由题意可知，是以点F 为坐标原点(0，0)，射线FA 为y 轴的正半轴建立的平面直角坐标系，则音乐台的位置A(0，4)，湖心亭的位置B(－3，2)，望春亭的位置C(－2，－2)，牡丹园的位置E(3，3)14．（1）学校（1，3），邮局（0，-1）；（2）商店，公园，汽车站，水果店，学校，游乐场，邮局；（3）像一艘帆船15．（1）2，1；（2）①±1；②2．16．（1）(14,14)；（2）228km ．17．（1）汽车行驶到点（2，0）时离A 村最近，坐标是（2，0）；（2）汽车行驶到点（7，0）时离B 村最近，点的坐标是（7，0）；（3）汽车行驶到C （113，0）时，距离两村的和最短，。
人教版七年级下册数学课时练《7.1.1 有序数对》试卷含答案(1)
人教版七年级下册数学《7．1．1有序数对》课时练学校：___________姓名：___________班级：___________一、单选题1．如图所示，小亮从学校到家所走最短路线是( )A ．(2，2)→(2，1)→(2，0)→(0，0)B ．(2，2)→(2，1)→(1，1)→(0，1)C ．(2，2)→(2，3)→(0，3)→(0，1)D ．(2，2)→(2，0)→(0，0)→(0，1)2．以下有序数对书写正确的是（ ）．A ．()59、B ．5，6C ．(),x yD ．()a b3．共享单车提供了便捷、环保的出行方式．小白同学在北京植物园打开某共享单车APP ，如图，“”为小白同学的位置，“”为检索到的共享单车停放点．为了到达距离最近的共享单车停放点，下列四个区域中，小白同学应该前往的是（ ）A ．5DB ．5FC ．6FD ．7F4．如果一类有序数对(),x y 满足方程5y x =-，则下列数对不属于这类的是（ ）．A ．()3,2B ．()2,3C ．()6,1D ．()1,6-5．如图，小明从家到达学校要穿过一个居民小区，小区的道路均是正南或正东方向，则小明走下列线路不能到达学校的是( )A ．(0,4)→(0,0)→(4,0)B ．(0,4)→(4,4)→(4,0)C ．(0,4)→(3,4)→(4,2)→(4,0)D ．(0,4)→(1,4)→(1,1)→(4,1)→(4,0)6．在数轴上，用有序数对表示点的平移，若()2,1得到的数为1，()1,2-得到的数为3，则()3,5得到的数为（ ）．A ．8B ．2-C ．2D ．8-二、填空题7．如图，A 表示三经路与一纬路的十字路口，B 表示一经路与三纬路的十字路口，如果用(3，1)(3，2)(3，3)(2，3)(1，3)表示由A 到B 的一条路径，用同样的方式写出一条由A 到B 的路径：____________________．8．若某个电影院用()512，表示5排12号，则3排4号可以表示为____________． 9．如果有序数对(),a b 表示某栋楼房中a 层楼b 号房，那么有序数对()4,3和()3,4分别代表的是__________，______________．10．如图，李老师家在2街与2巷的十字路口附近，如果用(2，2)→(2，3)→(2，4)→(3，4)→(4，4)→(5，4)表示李老师从家到学校上班的一条路线．请你用同样的方式写出从家到学校的另外一种路线：____________________________________________________________．11．我们规定向东和向北方向为正，如向东走4米，再向北走6米，记作()4,6，则向西走5米，再向北走3米记作_________；数对()2,6--表示___________．12．教室5排2号可用有序数对(5,2)表示，则2排5号用数对可表示为__．三、解答题13．如图是某个小岛的简图，试用数的对表示出相关地点的位置．14．观察如图所示象棋棋盘，回答下列问题：（1）说出“将”与“帅”的位置；（2）说出“马3进4”（即第3列的“马”前进到第4列）后的位置．15．如图所示，点A表示3街与5大道的十字路口，点B表示5街与3大道的十字路口，如果用(3，5)→(4，5)→(5，5)→(5，4)→(5，3)表示由A到B的一条路径，那么你能用同样的方法写出由A到B的其他几条路径吗？请至少给出3种不同的路径．16．根据指令(s，A)(说明：s≥0，单位：厘米；0°≤A＜180°)，机器人在平面上能完成下列动作：先原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s，若机器人站在点M处，面对的方向如图所示．(1)给机器人下了一个指令(2，60°)，机器人移动到了B点，请你画出机器人从M点到B点的运动路径；(2)若机器人从M点运动到了C点，则给机器人下了一个什么指令？17．如图，在5×5的方格（每小格边长为1）内有4只甲虫A、B、C、D，它们爬行规律总是先左右，再上下．规定：向右与向上为正，向左与向下为负．从A到B的爬行路线记为：A→B（＋1，＋4），从B到A的爬行路线为：B→A（－1，－4），其中第一个数表示左右爬行信息，第二个数表示上下爬行信息，那么图中（1）A→C（，），B→D（，），C→ （＋1，）；（2）若甲虫A的爬行路线为A→B→C→D，请计算甲虫A爬行的路程；（3）若甲虫A的爬行路线依次为（＋2，＋2），（＋1，－1），（－2，＋3），（－1，－2），最终到达甲虫P处，请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置．18．郑州市区的许多街道习惯用“经几纬几”来表示．小颖所乘的汽车从“经七纬五”出发，经过“经六纬五”到达“经五纬一”．（1）在图上标出“经五纬一”的位置；（2）在图上标出小颖所乘汽车可能行驶的一条路线图．还有其他可能吗？（3）你能说出图中“华美达广场”的位置吗？参考答案1．B2．C3．C4．C5．C6．B7．(3，1)→(2，1)→(2，2)→(2，3)→(1，3)8．()34，9．4层楼3号房； 3层楼4号房10．答案不唯一：如(2，2)→(3，2)→(4，2)→(5，2)→(5，3)→(5，4)11．()5,3-； 向西走2米，再向南走6米12．()2,513．码头()4,3，营房()6,2，雷达()9,6，小广场()5,6，哨所1()5,9，哨所2()1,6【解析】根据题图可知，码头()4,3，营房()6,2，雷达()9,6，小广场()5,6，哨所1()5,9，哨所2()1,614．（1）“将”在第9行第5列，“帅”在第1行第5列；（2）第7行第4列【解析】（1）按照图中的表示数字，“将”在第9行第5列，“帅”在第1行第5列； （2）第7行第4列．15．答案见解析．【解析】答案不唯一，如：(1)(3，5)→(4，5)→(4，4)→(5，4)→(5，3)；(2)(3，5)→(4，5)→(4，4)→(4，3)→(5，3)；(3)(3，5)→(3，4)→(4，4)→(5，4)→(5，3)；(4)(3，5)→(3，4)→(4，4)→(4，3)→(5，3)；(5)(3，5)→(3，4)→(3，3)→(4，3)→(5，3)等．16．(1)画图略(2)指令(3，20°)【解析】（1）如图：（2）给机器人的指令是（3，20°）．17．（1）A→C（+3 ，+4 ），B→D（+3 ，-2 ），C→ D （＋1，-2 ）；（2）10；（3）见解析．【解析】解：（1）A→C（+3，+4）；B→D（+3，﹣2）；C→D（+1，﹣2）；（2）据已知条件可知：A→B表示为：（1，4），B→C记为（2，0）C→D记为（1，﹣2）；则该甲虫走过的路线长为1+4+2+0+1+2=10．答：甲虫A爬行的路程为10；（3）甲虫A爬行示意图与点P的位置如图所示：18．（1）“经五纬一”在广播大厦旁边的十字路口；（2）“经七纬五”“经六纬五”“经五纬五”“经五纬五”到达“经五纬一”；（3）“华美达广场”位于“经六路”与“纬三路”的十字路口附近【解析】解：（1）如图：“经五纬一”在广播大厦旁边的十字路口．（2）如图：从“经七纬五”到达“经五纬一”的路线不唯一．例如，“经七纬五”“经六纬五”“经五纬五”“经五纬五”到达“经五纬一”．（3）“华美达广场”位于“经六路”与“纬三路”的十字路口附近．。
人教版初一七年级下册数学课时练《5.3.2 命题、定理、证明》试题试卷 含答案
《5．3．2命题、定理、证明》课时练1．下列语句中，不是命题的是（）A．两点确定一条直线B．垂线段最短C．同位角相等D．作∠A的平分线2．下列语句中，是命题的是（）①若∠1＝60°，∠2＝60°，则∠1＝∠2；②同位角相等吗？③画线段AB＝CD；④一个数能被2整除，则它也能被4整除；⑤直角都相等．A．①④⑤B．①②④C．①②⑤D．②③④⑤3．命题“两直线平行，内错角相等”的题设是．4．把下列命题改写成“如果……那么……”的形式，并分别指出它们的题设和结论：（1）两点确定一条直线；（2）同角的补角相等；（3）两个锐角互余．5．下列命题中，是真命题的是（）A．若|x|＝2，则x＝2B．平行于同一条直线的两条直线平行C．一个锐角与一个钝角的和等于一个平角D．任何一个角都比它的补角小6．下列命题中，是假命题的是（）A．若|x|＝3，则x＝3B．垂线段最短C．同一平面内，两条直线的位置关系只有相交和平行两种D．两点确定一条直线7．判断命题“如果n＜1，那么n2－1＜0”是假命题，只需举出一个反例，反例中的n可以为（）A．－2 B．－12C．0 D.128．如图，BD平分∠ABC，若∠BCD＝70°，∠ABD＝55°.求证：CD∥AB.9．如图所示，如果∠1＝∠2，那么AB∥CD，这个命题是真命题吗？若不是，请你再添加一个条件，使该命题成为真命题，并说明理由．10．下列说法正确的是（）A．“作线段CD＝AB”是一个命题B．过一点作已知直线的平行线有且只有一条C．命题“若x＝1，则x2＝1”是真命题D．所含字母相同的项是同类项11．下列命题是假命题的是（）A．同角的余角相等B．内错角相等C．两点之间，线段最短D．同旁内角互补，两直线平行12．对于下列假命题，各举一个反例写在横线上．（1）“如果ac＝bc，那么a＝b”是一个假命题．反例：；（2）“如果a2＝b2，那么a＝b”是一个假命题．反例：．13．下列命题中，①若|a|＝b，则a＝b；②若直线l1∥l2，l1∥l3，则l2∥l3；③同角的补角相等；④同位角相等，是真命题的有（填序号）．14．把下列命题写成“如果……那么……”的形式，并判断其真假．（1）等角的补角相等；（2）不相等的角不是对顶角；（3）相等的角是内错角．15．如图直线EF分别与直线AB，CD交于点E，F.EM平分∠BEF，FN平分∠CFE，且EM ∥FN.求证：AB∥CD.16．如图，下列三个条件：①AB∥CD；②∠B＝∠C；③∠E＝∠F.从中任选两个作为条件，另一个作为结论组成一个真命题，并进行证明．17．（1）如图，DE∥BC，∠1＝∠3，CD⊥AB，求证：FG⊥AB；（2）若把（1）中的“DE∥BC”与结论“FG⊥AB”对调，所得的命题是否为真命题？试说明理由；（3）若把（1）中的“∠1＝∠3”与结论“FG⊥AB”对调呢？参考答案1．D2．A3．两条平行线被第三条直线所截，结论是内错角相等．4．（1）如果在平面上有两个点，那么过这两个点确定一条直线．题设：在平面上有两个点；结论：过这两个点确定一条直线．（2）如果两个角是同角的补角，那么它们相等．题设：两个角是同角的补角；结论：这两个角相等．（3）如果两个角是锐角，那么这两个角互余．题设：两个角是锐角；结论：这两个角互余．5．B6．A7．A8．证明：∵BD平分∠ABC，∠ABD＝55°，∴∠ABC＝2∠ABD＝110°.又∵∠BCD＝70°，∴∠ABC＋∠BCD＝180°.∴CD∥AB（同旁内角互补，两直线平行）．9．解：假命题，添加BE∥DF.∵BE∥DF，∴∠EBD＝∠FDN（两直线平行，同位角相等）．∵∠1＝∠2，∴∠EBD－∠1＝∠FDN－∠2.∴∠ABD＝∠CDN.∴AB∥CD（同位角相等，两直线平行）．10．C11．B12．（1）3×0＝（－2）×0；（2）32＝（－3）2．13．②③．14．解：（1）如果两个角是两个相等的角的补角，那么这两个角相等．是真命题．（2）如果两个角不相等，那么这两个角不是对顶角．是真命题．（3）如果两个角相等，那么这两个角是内错角．是假命题．15．证明：∵EM∥FN，∴∠FEM＝∠EFN.又∵EM平分∠BEF，FN平分∠CFE，∴∠BEF＝2∠FEM，∠EFC＝2∠EFN.∴∠FEB＝∠EFC.∴AB∥CD.16．解：答案不唯一，如：已知：AB∥CD，∠B＝∠C，求证：∠E＝∠F.证明：∵AB∥CD,∴∠B＝∠CDF.又∵∠B＝∠C，∴∠CDF＝∠C.∴EC∥BF.∴∠E＝∠F.17．解：（1）证明：∵DE∥BC，∴∠1＝∠2.又∵∠1＝∠3，∴∠2＝∠3.∴CD∥FG.∴∠BFG＝∠CDB.∵CD⊥AB，∴∠CDB＝90°.∴∠BFG＝90°.∴FG⊥AB.（2）真命题．理由如下：∵CD⊥AB，FG⊥AB，∴CD∥FG.∴∠2＝∠3.∵∠1＝∠3，∴∠1＝∠2.∴DE∥BC.（3）真命题．理由如下：同（2）可得∠2＝∠3.∵DE∥BC，∴∠1＝∠2.∴∠1＝∠3.。
【★】人教版七年级下册数学课时练《5-4 平移》(含答案)
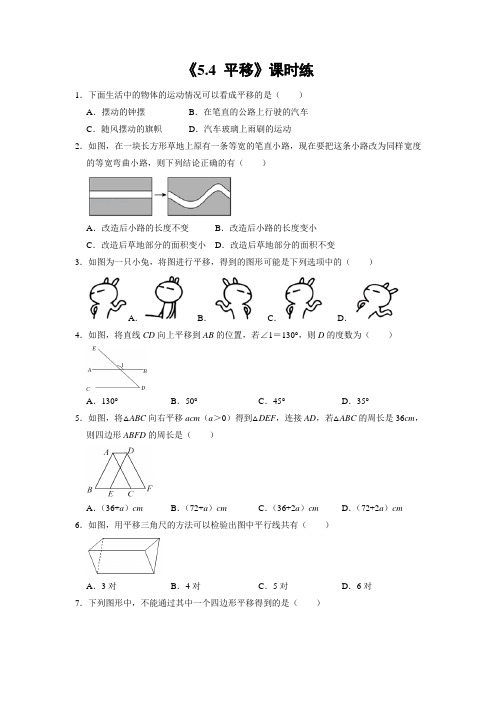
《5.4 平移》课时练1．下面生活中的物体的运动情况可以看成平移的是（）A．摆动的钟摆B．在笔直的公路上行驶的汽车C．随风摆动的旗帜D．汽车玻璃上雨刷的运动2．如图，在一块长方形草地上原有一条等宽的笔直小路，现在要把这条小路改为同样宽度的等宽弯曲小路，则下列结论正确的有（）A．改造后小路的长度不变B．改造后小路的长度变小C．改造后草地部分的面积变小D．改造后草地部分的面积不变3．如图为一只小兔，将图进行平移，得到的图形可能是下列选项中的（）A．B．C．D．4．如图，将直线CD向上平移到AB的位置，若∠1＝130°，则D的度数为（）A．130°B．50°C．45°D．35°5．如图，将△ABC向右平移acm（a＞0）得到△DEF，连接AD，若△ABC的周长是36cm，则四边形ABFD的周长是（）A．（36+a）cm B．（72+a）cm C．（36+2a）cm D．（72+2a）cm 6．如图，用平移三角尺的方法可以检验出图中平行线共有（）A．3对B．4对C．5对D．6对7．下列图形中，不能通过其中一个四边形平移得到的是（）A．B．C．D．8．将周长为8的△ABC沿BC方向右移2个单位长度得到△DEF，则四边形ABFD的周长为（）A．12 B．14 C．10 D．169．如图，一块形状为长方形ABCD的场地，长AB＝98米，宽AD＝46米，A、B两处入口E小路宽都为1米，两小路汇合处路口宽2米，其余部分种植草坪，那么草坪的面积为（）A．4320平方米B．4410平方米C．4416平方米D．4508平方米10．下面的每组图形中，左面的图形平移后可以得到右面图形的是（）A．B．C．D．11．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则平移的距离为（）A．3 B．4 C．5 D．612．如图，将△ABC沿BC方向平移得到△DEF，使点B的对应点E恰好落在边BC的中点上，点C的对应点F在BC的延长线上，连接AD．下列结论一定正确的是（）A．∠B＝∠F B．AC⊥DE C．BC＝DF D．AC平分DE 13．如图，将△ABE向右平移2cm得到△DCF．如果△ABE的周长是16cm，那么四边形ABFD 的周长是（）A．16 cm B．18 cm C．20 cm D．21 cm14．如图图形中，把△ABC平移后能得到△DEF的是（）A．B．C．D．15．如图是某公园里一处矩形风景欣赏区ABCD，长AB＝50米，宽BC＝25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为（）A．100米B．99米C．98米D．74米16．一个长方形花园，长为a，宽为b，中间有两条互相垂直的宽为c的路，则可种花的面积为．17．如图，将Rt△ABC沿BC方向平移得到Rt△DEF，如果AB＝12cm，BE＝5cm，DH＝4cm，则图中阴影部分面积为cm2．18．白云宾馆在装修时，准备在主楼梯上铺上红地毯．已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图所示，则购买这种地毯至少需要元．19．如图，一块长方形草地，长为20米，宽为10米，草地上有一条弯曲的小路（小路任何地方的宽度都是2米），请你写出小路部分所占的面积是米2．20．如图，边长为8cm的正方形ABCD先向上平移4cm，再向右平移2cm，得到正方形A′B′C′D′，此时阴影部分的面积为．21．如图，将三角形ABC水平向右平移得到三角形DEF，A，D两点的距离为1，CE＝2，∠A＝72°，则：（1）AC和DF的关系式为，．（2）∠1＝（度）；（3）BF＝．22．作图：△DEF是△ABC平移后的图形，F是C的对应点，画出△ABC．（保留画图痕迹）23．如图1，直线CB∥OA，∠A＝∠B＝120°，E，F在BC上，且满足∠FOC＝∠AOC，并且OE平分∠BOF．（1）求∠AOB及∠EOC的度数；（2）如图2，若平行移动AC，那么∠OCB：∠OFB的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值；参考答案1．B 2．D 3．C 4．B 5．C 6．D 7．D 8．A 9．A 10．D 11．A 12．D 13．C 14．A 15．C16．ab﹣ac﹣bc+c2．17．50．18．504．19．20．20．24cm2．21．AC＝DF，AC∥DF；108°；4．22．解：如图所示：△ABC即为所求．23．解：（1）∵CB∥OA∴∠BOA+∠B＝180°，∴∠BOA＝180°﹣120°＝60°，∵∠FOC＝∠AOC，OE平分∠BOF∴∠EOC＝∠EOF+∠FOC＝∠BOF+∠FOA＝（∠BOF+∠FOA）＝×60°＝30°；（2）不变．∵CB∥OA∴∠OCB＝∠COA，∠OFB＝∠FOA，∵∠FOC＝∠AOC∴∠COA＝∠FOA，即∠OCB：∠OFB＝1：2．。
数学课时练七年级下册答案人教版2020
数学课时练七年级下册答案人教版2020题型：选择题1.下列哪个小数是无限循环小数？A.0.12345B.0.131313…C.0.232323…D.0.1432182.若6m-2n=10，2m+n=11，则m的值为A. 3B. 1C. 2D. 43.在下列四个数中，与其它三个数的平均数不相等的是A. 20B. 18C. 15D. 124.一个长方形的长是3a,宽是4b，则它的周长为A. 5aB. 7aC. 12aD. 7b5.有两个数，它们的和是15，差是9，则这两个数分别为A.7和8B.6和3C.12和3D.9和6答案：1.B2.C3.C4.C5.D题型：填空题1.某班共50人，其中男生占(2/5)，则女生人数为\_\_\_\_\_\_人。
2.小明买了一部手机，原价是2000元，还打了8折，他需要支付的钱数是\_\_\_\_\_\_元。
3.一列火车长180米，以每秒72千米的速度通过隧道，需要通过多长的时间？4.一个4位数，各位数字之和为9，千位数减个位数等于3，则这个数是\_\_\_\_\_\_。
5.如图，矩形面积是20cm^2，则b=\_\_\_\_\_\_。
\begin{flushright}\includegraphics[scale=0.4]{geometry.png}\end{flushright}答案：1.302.16003.2.5秒4.10355.4题型：解答题1.解方程：(3/x)=(2/3)+(1/2x)2.画一张平行四边形ABCD，其中AB=10cm,BC=6cm，将其平移得到平面上的图形A'B'C'D'，其中AA'=5cm，A'B'与AB平行，B'C'与BC平行，求A'D'的长。
3.解如下一组不等式：\begin{cases}x+2y>6 \\y-2x<2\end{cases}4.求解下列方程：4(a-1)+5=17-3(a+4)5.如图，AB=AC，\angle A=90^\circ，AE是BC的中线，BD=8cm，求DE的长。
人教版数学七年级下册《5.4平移》课时练习（含答案）
（人教版）七年级下第五章 5.4 平移课时练（锦州中学）学校：姓名：班级：考号：评卷人得分一、选择题1. 将左图中的图案平移后,可以得到的图案是()A. B. C. D.2. 下列各网格中的图形是用其图形中的一部分平移得到的是()A. B. C. D.3. 如图,将周长为8的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD 的周长为()A. 6B. 8C. 10D. 124. 如图所示,△ABC平移到△DEF的位置,下列结论不成立的是( )A. AC=DFB. AD=BEC. AB=EFD. ∠C=∠F5. 两个三角形是通过平移得到的,下列说法错误的是( )A. 平移过程中,两三角形周长不变B. 平移过程中,两三角形面积不变C. 平移过程中,两三角形的对应线段一定相等D. 平移过程中,两三角形的对应边必平行1 / 86. 如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )A. 先把△ABC向左平移5个单位,再向下平移2个单位B. 先把△ABC向右平移5个单位,再向下平移2个单位C. 先把△ABC向左平移5个单位,再向上平移2个单位D. 先把△ABC向右平移5个单位,再向上平移2个单位7. 如图,将三角形ABC沿着XY方向平移一定的距离就得到三角形MNL,则下列结论:①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL,其中正确的有()A. 1个B. 2个C. 3个D. 4个8. 如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A'的坐标是()A. (6,1)B. (0,1)C. (0,-3)D. (6,-3)9. 某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )A. 甲种方案所用铁丝最长B. 乙种方案所用铁丝最长C. 丙种方案所用铁丝最长D. 三种方案所用铁丝一样长10. 如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.A. 5 050πB. 5 050π+101C. 5 055πD. 5 055π+101评卷人得分二、填空题,将点P(-1,4)向右平移2个单位长度后,再向下平移3个单位长度,得到点P1,则点P1的坐标为.12. 若线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,6),则点B(-5,-2)的对应点D 的坐标是.13. 已知△ABC的三个顶点坐标为A(4,5),B(-2,4),C(5,-7),将△ABC向左平移6个单位长度,则此时三个顶点的坐标分别为A,B,C.14. 如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是cm2.15.如图所示,大正方形ABCD内有一小正方形DEFG,对角线DF长为6 cm,已知小正方形DEFG3 / 8向东北方向平移3 cm就得到正方形D'E'BG',则大正方形ABCD的面积为.16. 1+1＝________.17. 如图,A,B的坐标为(2,0),(0,1).若将线段AB平移至A1B1,则a+b的值为.评卷人得分三、解答题,它们的总宽度是3米.总高度是2米,图中所成角度均为直角,现要在从A到B的台阶上铺上地毯,求地毯的总长度.19. (探究题)如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路,余下部分绿化,小路的宽为2 m,则绿化的面积为多少?20. 如图所示,已知在△ABC中,BC=4 cm,把△ABC沿BC方向平移2 cm得到△DEF.问:(1)图中与∠A相等的角有多少个?(2)图中的平行线共有多少对?请分别写出来.(3)BE∶BC∶BF的值是多少?21. (本小题满分8分)在平面上，七个边长均为1的等边三角形，分别用①至⑦表示(如图6).从④⑤⑥⑦组成的图形中，取出一个三角形，使剩下的图形经过一次平移，与①②③组成的图形拼成一个正六边形.(1)你取出的是哪个三角形？写出平移的方向和平移的距离；(2)将取出的三角形任意放置在拼成的正六边形所在平面上，问：正六边形没有被三角形盖住的面积能否等于5？请说明理由.222. 如图,在四边形ABCD中,AD∥BC,且AD<BC,△ABC平移到△DEF的位置.(1)指出平移的方向和平移的距离;(2)试说明AD+BC=BF.参考答案1. 【答案】A【解析】解答本题的关键是,根据平移不改变图形的形状和大小,且连接对应点的线段平行(或在同一条直线上)且相等来判断.2. 【答案】C【解析】由题意可知,只有C选项的图形是用其图形中的一部分平移得到的.5 / 83. 【答案】C【解析】根据题意,将周长为8的三角形ABC沿边BC向右平移1个单位得到三角形DEF,故AD=CF=1,AB+BC+AC=8,AC=DF,所以AB+BC+CF+DF+AD=8+1+1=10,即四边形ABFD的周长为10.4. 【答案】C【解析】根据平移的性质, 平移前后,两图形的大小不变、形状不变,因为△ABC 平移到△DEF的位置,得AC=DF,∠C=∠F,AB=DE.由AB=DE,得AB+BD=DE+BD,即AD=BE.所以选项A,B,D都成立,只有选项C不成立.5. 【答案】D【解析】在平移的过程中,两三角形的对应边必平行或在同一条直线上.6. 【答案】A【解析】三角形DEF在三角形ABC的左侧五个单位,下侧2个单位,故应该选A.7. 【答案】B【解析】由平移的性质可知①②正确,所以选B.8. 【答案】B【解析】因为A(3,-1),先向左平移3个单位,横坐标减3,再向上平移2个单位,纵坐标加2,故选B.9. 【答案】D【解析】由图形的平移可得出:甲所用铁丝的长度为:2a+2b,乙所用铁丝的长度为:2a+2b,丙所用铁丝的长度为:2a+2b,故三种方案所用铁丝一样长.10. 【答案】B【解析】动点M从O点出发到A点,在直线AB上运动了4个单位长度,在以O4为圆心的半圆运动了(π·1+π·2+π·3+π·4)个单位长度.∵100+1=4×25+1,点处运动的单位长度=4×25+(π·1+π·2+…+π·100)+1=101+5050π,∴动点M到达A101点处运动所需时间=(101+5050π)÷1=(101+5050π)秒.故选B.∴动点M到达A10111. 【答案】(1,1)【解析】根据点的坐标的平移规律,向右平移2个单位长度,即点的横坐标加2;向下平移3(1,1).个单位长度,即点的纵坐标减3,可得平移后点P的坐标为P112. 【答案】(0,1)【解析】点C(3,6),点A(-2,3),C的横坐标3=-2+5,C的纵坐标6=3+3,根据点的平移规律可知A点到C点,向右平移5个单位,向上平移了3个单位,按此平移由B点(-5,-2),可得D点坐标为(0,1).13. 【答案】(-2,5);(-8,4);(-1,-7)【解析】左右平移点的纵坐标保持不变,横坐标改变. △ABC向左平移6个单位长度,则三个顶点的纵坐标保持不变,横坐标分别减去6,得A (-2,5),B (-8,4),C (-1,-7).14. 【答案】168【解析】本题运用了转化思想,把不规则图形的面积转化为规则图形的面积.平移不改变图形的形状和大小,所以阴影部分的面积等于直角梯形ABCD的面积减去直角梯形EFMD的面积,也就是直角梯形DMGH的面积,所以阴影部分的面积为12×(24-6+24)×8=168(cm2).15. 【答案】812cm2【解析】如图所示.(1)根据平移的性质可知BF=3cm,所以正方形ABCD的对角线长为DF+FB=9cm,所以正方形ABCD的面积为12×9×9=812(cm2).16. 【答案】2【解析】1+1＝2.17. 【答案】2【解析】由B(0,1) 平移得B1(a,2)知将线段AB向上平移1个单位长度,由A(2,0)平移得A1(3,b)知将线段AB向右平移1个单位长度,则a=1, b=1.所以a+b=2.18.【答案】由平移的性质可知,把所有台阶的宽平移至BC上,发现总和恰好与BC相等,若把所有台阶的高平移到AC上,发现总和恰好与AC相等.所以地毯的总长度为3+2=5(米).19.【答案】如图所示,把两条小路平移到长方形地块ABCD的最上边和最左边,则余下部分EFCG是长方形.7 / 8∵CF =32-2=30(m),CG =20-2=18(m),∴长方形EFCG 的面积=30×18=540(m 2). 答:绿化的面积为540m 2.20.(1) 【答案】共有3个,分别是∠D ,∠EMC ,∠AMD.(2) 【答案】两对,AB ∥DE ,AC ∥DF.(3) 【答案】∵△ABC 沿BC 方向平移2 cm,∴BE =CF =2 cm . 又∵BC =4 cm, ∴BF =6 cm .∴BE ∶BC ∶BF =1∶2∶3.21.(1) 【答案】取出三角形⑦，由④⑤⑥组成的几何图形，向上平移的距离为1时，与①②③组成的图形拼成一个正六边形.(2) 【答案】记未被盖住的面积为S ，则S 能等于52.理由如下：正六边形的面积为S 正六角形＝6×√34＝3√32，正三角形的面积为S 正三角形＝√34，正三角形任意放置在正六边形所在平面，则S 最小＝S 正六边形－S 正三角形＝3√32－√34＝5√34， S 最大＝S 正六边形－0＝3√32＝6√34.因为√1004＝52，且6√34＝√1084＞√1004＞√754＝5√34.所以，S 能等于52.22.(1) 【答案】平移的方向是点A 到点D 的方向,平移的距离是线段AD 的长度;(2) 【答案】∵△ABC 平移到△DEF 的位置,∴CF=AD .∵CF+BC=BF ,∴AD+BC=BF .。
七年级下册数学课时训练答案人教版
七年级下册数学课时训练答案人教版1、设M=(x﹣3)(x﹣7)，N=(x﹣2)(x﹣8)，则M与N的关系为( ) [单选题] *A. M＜NB. M＞N(正确答案)C. M=ND. 不能确定2、在△ABC中,bcosA=acosB，则三角形为（）[单选题] *A、直角三角形B、直角三角形C、等腰三角形(正确答案)D、等边三角形3、37、已知A（3，﹣2），B（1，0），把线段AB平移至线段CD，其中点A、B分别对应点C、D，若C（5，x），D（y，0），则x+y的值是（）[单选题] *A．﹣1B．0C．1(正确答案)D．24、若(x+m)(x2-3x+n)展开式中不含x2和x项，则m，n的值分别为( ) [单选题] *A. m=3,n=1B. m=3,n=-9C. m=3,n=9(正确答案)D. m=-3,n=95、1、方程x2?-X=0 是（? ? ）? ? ? ? ? ? 。
[单选题] *A、一元一次方程B、一元二次方程(正确答案)C、二元一次方程D、二元二次方程6、46．若a+b＝7，ab＝10，则a2+b2的值为（）[单选题] *A．17B．29(正确答案)C．25D．497、21．在﹣5，﹣2，0，这四个数中最小的数是（）[单选题] *A．﹣5(正确答案)B．﹣2C．0D．8、2．线段是由线段平移得到的，点的对应点为，则点的对应点的坐标为（）[单选题] *A．(2,9)B(5,3)C(1,2)(正确答案)D(-9,-4)9、9．如图，下列说法正确的是（）[单选题] *A．直线AB与直线BC是同一条直线(正确答案)B．线段AB与线段BA是不同的两条线段C．射线AB与射线AC是两条不同的射线D．射线BC与射线BA是同一条射线10、7．已知点A(－2，y1)，B(3，y2)在一次函数y＝－x＋b的图象上，则( ) [单选题]* A．y1 > y2(正确答案)B．y1 < y2C．y1 ≤y2D．y1 ≥y211、如果四条不共点的直线两两相交，那么这四条直线（）[单选题] *A、必定在同一平面内B、必定在同一平面内C可能在同一平面内，也可能不在同一平面内(正确答案)D、无法判断12、下面哪个式子的计算结果是9﹣x2() [单选题] *A. (3﹣x)(3+x)(正确答案)B. (x﹣3)(x+3)C. (3﹣x)2D. (3+x)213、31、点A(-2,-3)关于y轴对称的点的坐标是（）[单选题] *(2,3)(-2,-3)(3,-2)(2,-3) (正确答案)14、11．小文买了一支温度计，回家后发现里面有一个小气泡（即不准确了），先拿它在冰箱里试一下，在标准温度是零下7℃时，显示为℃，在36℃的温水中，显示为32℃，那么用这个温度计量得的室外气温是23℃，则室外的实际气温应是（）[单选题] *A．27℃(正确答案)B．19℃C．23℃D．不能确定15、7. 3位同学准备去学校饭堂吃午饭，学校饭堂有2个，则不同的去法共有( )种．[单选题] *A. 2＋3=5种B.2×3=6种C.3×3=9种D.2×2×2=8种(正确答案)16、点A的坐标为（3，4），点B的坐标为（5，8），则它们的中点坐标是（D）[单选题] *A、（3，4）B、（3，5）C、（8，12）D、（4，6）(正确答案)17、420°用弧度制表示为（）[单选题] *7π/3(正确答案)-2π/3-π/32π/318、19．对于实数a、b、c,“a>b”是“ac2(c平方)>bc2(c平方) ; ”的（）[单选题] * A．充分不必要条件B．必要不充分条件(正确答案)C．充要条件D．既不充分也不必要条件19、5、若关于x的一元二次方程（a-1）x2+x+a2-1=0的一个根是0，则a的值是（）[单选题] *A、1B、-1(正确答案)C 、1或-1D、220、的单调递减区间为（）[单选题] *A、（-1,1）(正确答案)B、（-1,2）C、（-∞，-1）D、（-∞，+∞）21、若tan（π-α）>0且cosα>0，则角α的终边在（）[单选题] *A.第一象限B.第二象限C.第三象限D.第四象限(正确答案)22、300°用弧度制表示为（）[单选题] *5π/3(正确答案)π/62π/32π/523、掷三枚硬币可出现种不同的结果（）[单选题] *A、6B、7C、8(正确答案)D、2724、19．如图，共有线段（）[单选题] *A．3条B．4条C．5条D．6条(正确答案)25、6．下列各图中，数轴画法正确的是（）[单选题] *A．B．C．D．(正确答案)26、24.不等式x-3>5的解集为（）[单选题] *A. x > 1B. x > 2(正确答案)C. x > 3D. x > 427、22．如图棋盘上有黑、白两色棋子若干，找出所有使三颗颜色相同的棋在同一直线上的直线，满足这种条件的直线共有（）[单选题] *A．5条(正确答案)B．4条C．3条D．2条28、14、在等腰中，如果的长是的2倍，且三角形周长为40，那么的长是（）[单选题] * A．10B．16 (正确答案)C．10D．16或2029、40．若x+y＝2，xy＝﹣1，则（1﹣2x）（1﹣2y）的值是（）[单选题] *A．﹣7(正确答案)B．﹣3C．1D．930、已知直线l的方程为2x-y+7=0，（）是直线l上的点[单选题] *A、（2，3）B、（2，4）(正确答案)C、（2，-3）D、（-2，-3）。
人教版初一七年级下册数学课时练《5.2.1 平行线》试题试卷 含答案
《5．2．1平行线》课时练1．下列说法中，正确的是（）A．平面内，没有公共点的两条线段平行B．平面内，没有公共点的两条射线平行C．没有公共点的两条直线互相平行D．互相平行的两条直线没有公共点2．在同一平面内，两条直线的位置关系有（）A．两种：平行和相交B．两种：平行和垂直C．三种：平行、垂直和相交D．两种：相交和垂直3．在同一平面内，直线a与b满足下列条件，把它们的位置关系填在后面的横线上．（1）a与b没有公共点，则a与b ；（2）a与b有且只有一个公共点，则a与b ；（3）a与b有两个公共点，则a与b ．4．如图，完成下列各题：（1）用直尺在网格中完成：①画出直线AB的一条平行线；②经过C点画直线垂直于CD；（2）用符号表示上面①、②中的平行、垂直关系．5．若直线a∥b，b∥c，则a∥c的依据是（）A．平行公理B．等量代换C．等式的性质D．平行于同一条直线的两条直线平行6．点P，Q都是直线l外的点，下列说法正确的是（）A．连接PQ，则PQ一定与直线l垂直B．连接PQ，则PQ一定与直线l平行C．连接PQ，则PQ一定与直线l相交D．过点P只能画一条直线与直线l平行7．如图，在直线a的同侧有P，Q，R三点，若PQ∥a，QR∥a，则P，Q，R三点是（填“是”或“不是”）在同一条直线上，理由是．8．如图，P，Q分别是直线EF外两点．·QP·E F（1）过点P画直线AB∥EF，过点Q画直线CD∥EF；（2）AB与CD有怎样的位置关系？为什么？9．下列说法中，正确的有（）①过一点有无数条直线与已知直线平行；②经过直线外一点有且只有一条直线与已知直线平行；③如果两条线段不相交，那么它们就平行；④如果两条直线不相交，那么它们就平行．A．1个B．2个C．3个D．4个10．如图，在下面的方格纸中，找出互相平行的线段，并用符号表示出来：．11．如图所示，直线AB，CD是一条河的两岸，并且AB∥CD，点E为直线AB，CD外一点，现想过点E作河岸CD的平行线，只需过点E作的平行线即可，其理由是．12．在同一平面内，一条直线和两条平行线中的一条直线相交，那么这条直线与平行线中的另一条直线必．13．观察下图所示的长方体，回答下列问题．（1）用符号表示两棱的位置关系：A1B1AB，AA1AB，A1D1C1D1，AD BC；（2）AB与B1C1所在的直线不相交，它们平行线（填“是”或“不是”）．由此可知，在内，两条不相交的直线才是平行线．14．如图所示，在∠AOB内有一点P．（1）过点P画l1∥OA；（2）过点P画l2∥OB；（3）用量角器量一量l1与l2相交的角与∠O的大小有怎样的关系．15．如图，射线OA∥CD，射线OB∥CD，∠AOC＝13∠AOB，求∠AOC的度数．16．利用直尺画图：（1）利用图1中的网格，过P点画直线AB的平行线和垂线；（2）在图2的网格中画一个四边形，满足：①两组对边互相平行；②任意两个顶点都不在一条网格线上；③四个顶点都在格点上．参考答案1．D2．A3．（1）平行；（2）相交；（3）重合．4．解：（1）如图所示．（2）EF ∥AB ，MC ⊥CD ．5．D6．D7．是 经过直线外一点，有且只有一条直线与这条直线平行．8．解：（1）如图．（2）AB ∥CD ．理由：因为AB ∥EF ，CD ∥EF ，所以AB ∥CD （平行于同一条直线的两条直线平行）．9．A10．CD ∥MN ，GH ∥PN ．11．AB 平行于同一条直线的两条直线平行．12．相交．13．（1）A 1B 1∥AB ，AA 1⊥AB ，A 1D 1⊥C 1D 1，AD ∥BC ；（2）不是 同一平面14．解：（1）（2）如图所示．（3）l 1与l 2的夹角有两个：∠1，∠2．量得∠1＝∠O ，∠2＋∠O ＝180°，所以l 1与l 2的夹角与∠O 相等或互补．15．解：因为OA ∥CD ，OB ∥CD ，所以A ，O ，B 在同一条直线上． 所以∠AOB ＝180°．所以∠AOC ＝13∠AOB ＝13×180°＝60°． 16．解：（1）如图所示．CD ∥AB ，PQ ⊥AB ．（2）如图所示，答案不唯一．。
七年级数学下课时练习参考答案
七年级数学（下）课时练习参考答案8.1 角的表示一、选择题1．C 2．A 3．C二、填空题4．绕着它的端点从起始位置旋转到终止位置所成；始边；终边。
5．当角的终边与始边恰成一条直线是，所成的角；当射线旋转一周回到起始位置时，所成的角6．∠O，∠α，∠AOB；O；OA与OB 7．2三、解答题8．∠BAD；∠B；∠ACB；∠ACD; ∠D;∠CAD 9．(1)3 (2)6 (3)10 (4)288.2 角的比较一、选择题1．D 2．C 3．C二、填空题4．（1）∠AOC （2）∠AOD （3）∠BOC （4）∠BOD 5．90°6．70°三、解答题7．解：与题意可知∠AOB为平角即∠BOC+∠AOC=180°又∠BOC=2∠AOC，那么∠BOC=120°，又OD、OE三等分∠BOE那么∠BOC=3∠BOE，∠BOE=40°8．解：由题意知：∠AOB=∠AOC+∠BOC，又∠AOC=30°；∠BOC=50°那么∠AOB=80°，由题意知OD是∠AOB的平分线，那么∠BOD=12∠AOB=40°，又∠COD=∠BOC－∠BOD，所以∠COD=10°8.3 角的度量（1）一、选择题1．D 2．C 3．B 4．C二、填空题5．60；60 6．30°；6°7．37.5°8．25°19′三、解答题9．（1）32°15′36″ （2）35.43°10．(1)56°20′ (2)46°42′8.3 角的度量（2）一、选择题1．B 2．C 3．C 4．C二、填空题5．互余；互补6．14°7．90°8．50°三、解答题9．（1）32°（2）148°10．（1）∠AOB；∠COD（2）∠AOB=∠DOC因为同一个角的余角相等（3）有，∠BOE8.4 对顶角一、选择题1．B 2．B 3．D 4．C二、填空题5．∠AOD；∠3；∠COE 6．50°；130°7．135°；135°；45°；135°8．180°三、解答题9．∠BOC=105°10．∠AOM=40°8.5 垂直一、选择题1．C 2．D 3．D二、填空题4．（1）一；（2）垂线段5．∠1+∠2=90°6．（1）BE；CD （2）DC；BE三、解答题7．∠AOD=150°8．∠COE=27°第八章综合练习一、选择题1．B 2．B 3．B 4．B二、填空题5．（1）63°7′ （2）46°36′45″ 6．30°7．120°；30°8．180°三、解答题9．∠COE=145°10．∠EOG=59°9.1 同位角、内错角、同旁内角一、选择题1．B 2．D 3．A 4．B二、填空题5．AB；CE；BD；同位角；AB；AC；BC；同旁内角6．∠4，∠3，∠3 7．1；1；4 三、解答题8．∠1和∠E是同位角；∠2和∠3是内错角；∠3和∠E是同旁内角；第二步略。
人教版七年级下册数学课时练《7.1.2 平面直角坐标系》试卷含答案
人教版七年级下册数学《7．1．2 平面直角坐标系》课时练学校：___________姓名：___________班级：___________一、单选题1．在平面直角坐标系中，点 ()22,3P x +- 所在的象限是（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．点M （-3,4）离原点的距离是（ ）A ．3B ．4C ．5D ．73．已知点A （m+2，3m -6）在第一象限角平分线上，则m 的值为（ ）A ．2B ．-1C ．4D ．-24．如图，平面直角坐标系上有P 、Q 两点，其坐标分别为P （4，a ）、Q （b ，6）．根据图中P 、Q 两点的位置，判断点（﹣b ，a ﹣7）落在第（ ）象限．A ．一B ．二C ．三D ．四5．如果点P （m ，1-2m ）在第四象限，那么m 的取值范围是A ．0＜m ＜12B ．-12＜m ＜0 C ．m ＜0 D ．m ＞126．在平面直角坐标系中，对于坐标P （2，5），下列说法错误的是（ ）A ．P （2，5）表示这个点在平面内的位置B ．点P 的纵坐标是5C ．点P 到x 轴的距离是5D ．它与点（5，2）表示同一个坐标7．如图，下列各点在阴影区域内的是（ ）A ．（3，2）B ．（﹣3，2）C ．（3，﹣2）D ．（﹣3，﹣2）8．在平面直角坐标系中，点M(2，-3)在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限9．如图，若在象棋盘上建立平面直角坐标系，使“将”位于点（﹣1，﹣2），“炮”位于（﹣4，1），则“象”位于点（ ）A ．（1，2）B ．（﹣2，1）C ．（2，﹣2）D ．（1，﹣2）10．如图，在平面直角坐标系中，一动点从原点 O 出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点 ()10,1A ， ()21,1A ， ()31,0A ()42,0A ，……那么点 41n A + （ n 为自然数）的坐标为（ ）A ．()4,0nB ．()2,1nC ．()2,0nD ．()4,1n11．对点（x ，y ）的一次操作变换记为p 1（x ，y ），定义其变换法则如下：p 1（x ，y ）=（x+y ，x ﹣y ）；且规定P n （x ，y ）=P 1（P n ﹣1（x ，y ））（n 为大于1的整数）．例如：p 1（1，2）=（3，﹣1），p 2（1，2）=p 1（p 1（1，2））=p 1（3，﹣1）=（2，4），p 3（1，2）=p 1（p 2（1，2））=p 1（2，4）=（6，﹣2）．则p 2014（1，﹣1）=（ ） A ．（0，21006） B ．（21007，﹣21007） C ．（0，﹣21006）D ．（21006，﹣21006）12．如图，在平面直角坐标系 xOy 中，点 (1,0)P ．点 P 第1次向上跳动1个单位至点 1(1,1)P ，紧接着第2次向左跳动2个单位至点 2(1,1)P - ，第3次向上跳动1个单位至点 3P ，第4次向右跳动3个单位至点 4P ，第5次又向上跳动1个单位至点 5P ，第6次向左跳动4个单位至点6P ，……，照此规律，点 P 第2020次跳动至点 2020P 的坐标是（ ）A ．(506,1010)-B ．(505,1010)-C ．(506,1010)D ．(505,1010)二、填空题13．在平面直角坐标系中，点A （﹣3，6）到y 轴的距离为 ．14．在平面直角坐标系内，点P （m -3，m -5）在第四象限中，则m 的取值范围是 15．点 (1,2)P m m -- 在第四象限，则m 的取值范围是 ． 16．若点M （a+2，a -3）在y 轴上，则点M 的坐标为 ． 17．已知点P （3﹣m ，m ）在第二象限，则m 的取值范围是 ． 18．在平面直角坐标系中，点（﹣4，4）在第 象限．19．点E(a ，b)到x 轴的距离是4，到y 轴距离是3，且点E 在第四象限，则E 点坐标为 。
人教版七年级数学下册-《二元一次方程组》课时练习(有答案)
七年级数学8.1《二元一次方程组》课时练习一、选择题：1、在下列方程中：(1)8x －4y ＝5；(2)3x 2－2y ＝1；(3)2x＋3y ＝8；(4)2x ＋4y ＝3z ；(5)2xy ＋3x ＝0；(6)x 2＋y 3＝1.其中二元一次方程有( ) A ．1个 B ．2个 C ．3个 D ．4个2、某次知识竞赛共有20道题，规定：每答对一道题得+5分，每答错一道题得﹣2分，不答的题得0分，已知圆圆这次竞赛得了60分，设圆圆答对了x 道题，答错了y 道题，则（ ） A ．x ﹣y=20 B ．x +y=20 C ．5x ﹣2y=60 D ．5x +2y=603、由方程组⎩⎪⎨⎪⎧2x ＋m ＝1，y －3＝m 可得出x 与y 的关系是( ) A ．2x ＋y ＝4 B ．2x －y ＝4C ．2x ＋y ＝－4D ．2x －y ＝－44、下列方程组中，是二元一次方程组的是( )A.⎩⎪⎨⎪⎧2x ＋y ＝3，x －2y ＝5B.⎩⎪⎨⎪⎧12x －y 3＝1，xy ＝5C.⎩⎪⎨⎪⎧x －2y ＝1，x ＋3z ＝8D.⎩⎪⎨⎪⎧32x －23y ＝－1，x 3＋2y＝3 5、若方程x 2m －1＋5y 3n －2＝7是关于x ，y 的二元一次方程，则(m －n)2020＝( ) A. 0 B. 1 C. -1 D.无法确定6、已知⎩⎪⎨⎪⎧x ＝2，y ＝－3是关于x ，y 的二元一次方程ax －(2a －3)y ＝7的解，则a 的值为（ ） A. 2 B. 4 C.3 D.57、下列各组数是二元一次方程组⎩⎪⎨⎪⎧x ＋y ＝3，x －y ＝－1的解的是 ( ) A.⎩⎪⎨⎪⎧x ＝2，y ＝1 B.⎩⎪⎨⎪⎧x ＝1，y ＝2 C.⎩⎪⎨⎪⎧x ＝1，y ＝－2 D.⎩⎪⎨⎪⎧x ＝2，y ＝－1 8、学校八年级师生共466人准备参加社会实践活动．现已预备了49座和37座两种客车共10辆，刚好坐满．设49座客车x 辆，37座客车y 辆，根据题意可列出方程组（ ）A ．B ．C ．D ． 9、为奖励消防演练活动中表现优异的同学，某校决定用1200元购买篮球和排球，其中篮球每个120元，排球每个90元，在购买资金恰好用尽的情况下，购买方案有（ ） A ．4种 B ．3种 C ．2种 D ．1种10、已知⎩⎪⎨⎪⎧x ＝2，y ＝1是方程y ＝kx －3的一组解，则k ＝（ ） A. 2 B. -1 C.3 D.111、夏季来临，某超市试销A 、B 两种型号的风扇，两周内共销售30台，销售收入5300元，A 型风扇每台200元，B 型风扇每台150元，问A 、B 两种型号的风扇分别销售了多少台？若设A 型风扇销售了x 台，B 型风扇销售了y 台，则根据题意列出方程组为（ ） A ．B ．C ．D ．12、某单位购买甲、乙两种纯净水共用250元，其中甲种水每桶8元，乙种水每桶6元；乙种水的桶数是甲种水桶数的75%.设买甲种水x 桶，买乙种水y 桶，则所列方程组中正确的是( )A.⎩⎪⎨⎪⎧8x ＋6y ＝250，y ＝75%xB.⎩⎪⎨⎪⎧8x ＋6y ＝250，x ＝75%y C.⎩⎪⎨⎪⎧6x ＋8y ＝250，y ＝75%x D.⎩⎪⎨⎪⎧6x ＋8y ＝250，x ＝75%y 二、填空题：13、将一张面值100元的人民币，兑换成10元或20元的零钱，兑换方案有 种。
人教版七年级下册数学课时练《7.1.1 有序数对》(含答案)
答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。
２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。
相信你是最棒的！人教版七年级下册数学《7．1．1有序数对》课时练学校：___________姓名：___________班级：___________【笔记】1．有序数对:我们把有顺序的两个数a与b组成的数对，叫做，记作．2．理解有序数对注意:①不能随意交换两个数的．②有序数对的两个数是一个整体，中间用逗号隔开，外面有小括号．3．利用有序数对可以准确表示平面内的一个点．【训练】1．要确定珠穆朗玛峰的位置，需要知道珠穆朗玛峰的()A．高度B．经度C．纬度D．经度和纬度2．电影票上的“2排5号”如果用(2，5)表示，那么“5排2号”应该表示为() A．(2，5)B．(5，2)C．(-5，-2)D．(-2，-5)3．如图，小明从点O出发，先向西走40米，再向南走30米到达点M，如果点M的位置用(-40，-30)表示，那么(10，20)表示的位置是()A．点A B．点BC．点C D．点D4．下列说法中，能确定物体位置的是()A．天空中的一只小鸟B．电影院中18座C．东经120°，北纬30°D．北偏西35°方向5．如图是象棋棋盘的一部分，若帅的位置为(5，1)，相的位置为(7，1)，则炮的位置为()A．(1，1)B．(1，4)C．(2，4)D．(2，2)6．下列关于有序数对的说法正确的是()A．(3，4)与(4，3)表示的位置相同B．(a，b)与(b，a)表示的位置肯定不同C．(3，5)与(5，3)是表示不同位置的两个有序数对D．有序数对(2，2)与(2，2)表示两个不同的位置7．如图，雷达探测器测得六个目标A，B，C，D，E，F出现，按照规定的目标表示方法，目标C，F的位置分别表示为C(6，120°)，F(5，210°)，按照此方法在表示目标A，B，D，E的位置时，其中表示不正确的是()A．A(5，30°)B．B(2，90°)C．D(4，240°)D．E(3，60°)第7题图第8题图8．如图所示，一方队正沿箭头所指的方向前进，A的位置为三列四行，表示为(3，4);(1)B的位置是;(2)B左侧第二个人的位置是;(3)如果队伍向西前进，那么A北侧第二个人的位置是;(4)(4，3)表示的位置是．9．如图，①表示三经路与一纬路的十字路口，②表示一经路与三纬路的十字路口，如果用(3，1)→(3，2)→(3，3)→(2，3)→(1，3)表示由①到②的一条路径，用同样的方式写出另外一条由①到②的路径:(3，1)→→→→(1，3)．第9题图10．如图所示，A的位置为(2，6)，小明从A出发，经(2，5)→(3，5)→(4，5)→(4，4)→(5，4)→(6，4)，小刚也从A出发，经(3，6)→(4，6)→(4，7)→(5，7)→(6，7)，则此时两人相距几格?11．若定义:f(a，b)=(-a，b)，g(m，n)=(m，-n)，例如f(1，2)=(-1，2)，g(-4，-5)=(-4，5)，则g[f(2，-3)]可以表示为()A．(2，-3)B．(-2，3)C．(2，3)D．(-2，-3)12．如图所示，OP是一条射线，OA、OB、OC是三条线段．OA=a，OB=b，OC=c，∠BOP=30°，AO⊥BO，OC是∠AOB的角平分线．若B点可表示为(b，30°)，则A点和C点可分别表示为()A．(a，90°)，(c，90°)C．(a，120°)，(c，75°)D．(a，90°)，(c，75°)13．观察下列有序数对:(3，-1)，−5，7，−−9…，根据你发现的规律，第100个有序数对是．第14题图14．五子棋是一种两人对弈的棋类游戏，规则是:在正方形棋盘中，由黑方先行，白方后行，轮流弈子，首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者胜．如图，这一部分棋盘是两个五子棋爱好者的对弈图．若黑子A的位置记作(7，5)，则白子B的位置如何表示?黑方必须在哪个位置上落子，才不会让白方在短时间内获胜?15．如图，一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动．它从A处出发去看望B，C，D处的其他甲虫，规定:向上向右走为正，向下向左走为负．如果从A到B记为:A→B(+1，+4)，从B到A记为:B→A(-1，-4)，其中第一个数表示左右方向，第二个数表示上下方向．(1)图中B→C(，)，C→(+1，);(2)若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程;(3)若图中另有两个格点M，N，且M→A(3-a，b-4)，M→N(5-a，b-2)，则N→A应记作什么?16．我们知道，如果已知一点M相对于定点O的距离和方向，那么这个点就被唯一确定了．这就是说，我们可用角度和距离来确定平面上点的相对位置．第16题图在平面内取一个定点O，叫做极点，引一条射线OP，叫做极轴，再选定一个长度单位和角度的正方向(通常取逆时针方向)．对于平面内任一点M，用r表示线段OM的长度，θ表示从OP到OM的角度，r叫做点M的极径，θ叫做点M的极角，有序数对(r，θ)就叫做点M的极坐标，这样就在平面上建立了极坐标系．极坐标为(r，θ)的点M，可表示为M(r，θ)．建立极坐标系后，给定r和θ就可以在平面内唯一确定一点M．如图，如果点D的位置为(3，5)，点A的位置为(4，0)．(1)请表示点B与点C的位置;(2)若以(0，0)为极点O，OP为极轴，写出A点和B点的极坐标．参考答案【笔记】1．有序数对(a，b)2．位置【训练】1．D2．B3．B4．C5．C6．C7．D8．(1)(4，5)(2)(2，5)(3)(5，4)(4)C9．(2，1)(1，1)(1，2)(答案不唯一)10．此时两人相距3格11．B12．C13．(-201，1100)14．根据题意得白子B的坐标为(5，1);因为白方已把(4，6)，(5，5)，(6，4)三点凑成在一条直线，黑方只有在此三点两端任加一点即可保证不会让白方在短时间内获胜，即黑方必须在(3，7)或(7，3)上落子．15．(1)+20D-2(2)甲虫走过的路程为1+4+2+1+2=10．(3)∵M→A(3-a，b-4)，M→N(5-a，b-2)，∴3-a-(5-a)=-2，b-4-(b-2)=-2，∴点N向左走2个格点，向下走2个格点到点A，∴N→A应记为(-2，-2)．16．(1)B(0，3)，C(2，2)．(2)A(4，0°);B(3，90°)．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018-2019学年度初一年下学期期末质量检测数 学 试 题（满分：150分；考试时间：120分钟）一、选择题（每小题3分，共21分）．在答题卡上相应题目的答题区域内作答. 1．方程63-=x 的解是( )A ．2-=xB ．6-=xC ．2=xD ．12-=x 2．若a >b ，则下列结论正确的是（ ）.A.55-<-b aB. b a 33>C. b a +<+22D.33ba <3．下列图案既是中心对称图形，又是轴对称图形的是（ ）A ．B ．C ．D ．4．现有3cm 、4cm 、5cm 、7cm 长的四根木棒，任选其中三根组成一个三角形，那么可以组成三角形的个数是（ ） A ． 1 B ． 2 C ． 3 D ． 4 5．商店出售下列形状的地砖：①长方形；②正方形；③正五边形；④正六边形．若只选购 其中某一种地砖镶嵌地面，可供选择的地砖共有（ ） A ．1种 B ．2种 C ．3种 D ．4种6．一副三角板如图方式摆放，且∠1的度数比∠2的度数大50°，设1,2x y ︒︒∠=∠=，则可得方程组为（ ）50.180x y A x y =-⎧⎨+=⎩ 50.180x y B x y =+⎧⎨+=⎩ 50.90x y C x y =+⎧⎨+=⎩ 50.90x y D x y =-⎧⎨+=⎩7．已知，如图，△ABC 中，∠B =∠DAC ，则∠BAC 和∠ADC 的关系是（ ）A ．∠BAC ＜∠ADCB ．∠BAC =∠ADC C ． ∠BAC ＞∠ADCD ． 不能确定 二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答. 8．若25x y -+=，则________=y （用含x 的式子表示）． 9．一个n 边形的内角和是其外角和的2倍，则n ＝ ． 10．不等式93-x ＜0的最大整数．．．．解是 ． 第6题图 第7题图11．三元一次方程组⎪⎩⎪⎨⎧=+=+=+895x z z y y x 的解是 ．12．如图，已知△ABC ≌△ADE ，若AB =7，AC =3，则BE 的值为 ．13．如图，在△ABC 中，∠B =90°，AB =10．将△ABC 沿着BC 的方向平移至△DEF ，若平移的距离是3，则图中阴影部分的面积为 ．14．如图，CD 、CE 分别是△ABC 的高和角平分线，∠A ＝30°，∠B ＝60°，则∠DCE ＝______度．15．一次智力竞赛有20题选择题，每答对一道题得5分，答错一道题扣2分，不答题不给分也不扣，小亮答完全部测试题共得65分，那么他答错了 道题．16．如图，将长方形ABCD 绕点A 顺时针旋转到长方形AB ′C ′D ′的位置，旋转角为α (90<<αo )，若∠1=110°，则α=______°.17．如图所示，小明从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……，照这样下去，他第一次回到出发地A 点时，(1)左转了 次；（2）一共走了 米。
三、解答题（9小题，共89分）在答题卡上相应题目的答题区域内作答.18．（9分）解方程：62221+-=--y y y 19．（9分）解不等式3315+≤-x x ，并把解集在数轴上表示出来.20．（9分）解方程组：⎩⎨⎧=+=-16323y x y x21．（9分）解不等式组： 338213(1)8x x x-⎧+≥⎪⎨⎪--<-⎩（注：必须通过画数轴求解集）22．（9分）如图，在△ABC 中，点D 是BC 边上的一点，∠B =50°，∠BAD =30°，将△ABD沿AD 折叠得到△AED ，AE 与BC 交于点F . （1）填空：∠AFC = 度； （2）求∠EDF 的度数．23．（9分）如图所示的正方形网格中，每个小正方形的边长均为1个单位，△ABC 的三个顶点都在格点上． （1）在网格中画出△ABC 向下平移3个单位得到的△A 1B 1C 1； （2）在网格中画出△ABC 关于直线m 对称的△A 2B 2C 2； （3）在直线m 上画一点P ，使得||2PC PA -的值最大．第16题 ACDB E FDE AB CE DB C A第12题图 第13题图 第14题图第17题图24．（9分）为了美化环境，在一块正方形空地上分别种植四种不同的花草．现将这块空地按下列要求分成四块：⑴分割后的整个图形必须是轴对称图形；⑵四块图形形状相同；⑶四块图形面积相等．现已有两种不同的分法：⑴分别作两条对角线（如图中的图⑴）；⑵过一条边的四等分点作这边的垂线段（图⑵）（图⑵中两个图形的分割看作同一方法）．请你按照上述三个要求，分别在图⑶、图⑷两个正方形中画出另外两种不同的分割方法．．．．．．．．．．．．．（正确画图，不写画法）25．（13分）小明到某服装商场进行社会调查，了解到该商场为了激励营业员的工作积极性，实行“月总收入=基本工资+计件奖金”的方法，并获得如下信息：营业员A ：月销售件数200件，月总收入2400元； 营业员B ：月销售件数300件，月总收入2700元； 假设营业员的月基本工资为x 元，销售每件服装奖励y 元． （1）求x 、y 的值；（2）若某营业员的月总收入不低于3100元，那么他当月至少要卖服装多少件？ （3）商场为了多销售服装，对顾客推荐一种购买方式：如果购买甲3件，乙2件，丙1件共需350元；如果购买甲1件，乙2件，丙3件共需370元．某顾客想购买甲、乙、丙各一件共需多少元？26．（13分）在ABC ∆中，已知A α∠=.（1）如图1，ACB ABC ∠∠、的平分线相交于点D ．①当70α=时，BDC ∠度数= 度（直接写出结果）； ②BDC ∠的度数为 （用含α的代数式表示）；（2）如图2，若ABC ∠的平分线与ACE ∠角平分线交于点F ,求BFC ∠的度数（用含α的代数式表示）．（3）在（2）的条件下，将FBC ∆以直线BC 为对称轴翻折得到GBC ∆，GBC ∠的角平分线与GCB ∠的角平分线交于点M （如图3），求BMC ∠的度数（用含α的代数式表示）．AFAA2015-2016学年度初一年下学期期末质量检测数学试卷参考答案说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分.（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面得分数的二分之一；如属严重的概念性错误，就不给分. （三）以下解答各行右端所注分数表示正确做完涉及应得的累计分数. 一、选择题（每题3分，共21分）1.A2.B3.D4.C5.C6.C7.B 二、填空题（每题4分，共40分）8．52+x ；9．6；10．2； 11．⎪⎩⎪⎨⎧===632z y x ；12．4；13．30；14．15；15．5；16．20； 17．(1)11;(2)120.三、解答题：（89分） 18．（9分）解： 62221+-=--y y y )2(12)1(36+-=--y y y ………………3分 212336--=+-y y y ………………5分 321236--=+-y y y74=y …………………………8分 47=y …………………………9分 19．（9分）解不等式3315+≤-x x ，并把解集在数轴上表示出来. 解：1335+≤-x x ……………………2分 42≤x ………………………4分 2≤x ………………………6分它在数轴上的表示（略）（数轴正确1分，实心及方向2分）………………9分 20．（9分）解方程组：⎩⎨⎧⋯⋯=+⋯⋯⋯⋯=-）（）（2163213y x y x21．（9分）解：由（1）得13≥x ……………………3分 由（2）得2->x ……………………6分 方法一：用代入法解的得分步骤解：由（1）得 3+=y x （3）……3分 把（3）代入（2） 得1633(2=++y y ）解得2=y ………6分把2=y 代入（3） 得5=x ……8分方法二：用加减法解的得分步骤解：由（2）－（1）×2得 105=y …………………4分 2=y ……………6分 把2=y 代入（1）得5=x ……………………8分在数轴上表示两个解集（略）………7分所以原不等式组的解是：13≥x …………9分 22．（9分）解：（1）110； ………………………………………… 3分（2）解法一：∵∠B=50°，∠BAD=30°，∴∠ADB=180°-50°-30°=100°， ……… 5分 ∵△AED 是由△ABD 折叠得到，∴∠ADE=∠ADB=100°， …………………… 7分 ∴∠EDF=∠EDA+∠BDA-∠BDF=100°+100°-180°=20°. … 9分解法二： ∵∠B=50°，∠BAD=30°， ∴∠ADB=180°-50°-30°=100°， ……………………………………… 5分 ∵△AED 是由△ABD 折叠得到， ∴∠ADE=∠ADB=100°， …………………………………………………… 6分 ∵∠ADF 是△ABD 的外角， ∴∠ADF=∠BAD+∠B=50°+30°=80°，…………………………………… 7分 ∴∠EDF=∠ADE-∠ADF=100°-180°=20°. ……………………………… 9分（注：其它解法按步给分） 23．（9分）解：作图如下：24．（9分）答案不惟一．（注：画对一个得5分，两个得9分）25．（13分）解：（1）依题意得⎩⎨⎧=+=+27003002400200y x y x ………………………3分解得⎩⎨⎧==31800y x即x 的值为1800，y 的值为3．…………………………………………5分 （2）设他当月要卖服装m 件，由题意得：310031800≥+m ………………………………………………………8分 解得31433≥m ……………………………………………………………9分 ∵只能为正整数 ∴m 最小为434答：他当月至少要卖434件．………………………………………………10分 （3）设一件甲为a 元，一件乙为b 元，一件丙为c 元，则PACD BEF （1）正确画出△A 1B 1C 1． ………………3分 （2）正确画出△A 2B 2C 2． ………………6分 （3）正确画出点P ． ……………………9分⎩⎨⎧=++=++3703235023c b a c b a …………………………………………………………11分 将两等式相加得720444=++c b a 则180=++c b a答：购买一件甲、一件乙、一件丙共需180元．………………………………13分 26．（13分）解：（1）①125；②α2190+；………………………………4分 （2）∵BF 和CF 分别平分ABC ∠和ACE ∠ ∴ABC FBC ∠=∠21,ACE FCE ∠=∠21……………5分 ∴FBC FCE BFC ∠-∠=∠……………………………6分 )(21ABC ACE ∠-∠= A ∠=21……………………………………………7分 即α21=∠BFC ………………………………………………8分 （3）由轴对称性质知：α21=∠=∠BFC BGC ………………10分 由（1）②可得BGC BMC ∠+=∠2190………………12分 ∴α4190+=∠BMC ．……………………………………13分。