2011-2012第一学期八年级数学寒假作业4(等腰三角形)代丽

合集下载

《13.3.1等腰三角形》作业设计方案-初中数学人教版12八年级上册

《等腰三角形》作业设计方案（第一课时）一、作业目标本作业设计旨在通过《等腰三角形》的课程内容，使学生能够：1. 理解等腰三角形的定义及其性质。

2. 掌握等腰三角形的基本判定方法。

3. 能够运用等腰三角形的知识解决简单的实际问题。

二、作业内容本课作业内容主要围绕等腰三角形的概念和性质展开，具体包括：1. 基础概念：复习等腰三角形的定义，包括两条相等的边和两个相等的角。

2. 性质探索：探索等腰三角形的性质，如三线合一、基线定理等。

3. 题目练习：- 判断题：提供一系列关于等腰三角形定义的判断题，帮助学生巩固定义。

- 填空题：通过填空题形式，让学生理解和运用等腰三角形的性质。

- 应用题：设计实际问题，要求学生运用等腰三角形的知识进行解答。

三、作业要求为确保学生能够有效地完成本次作业，特提出以下要求：1. 认真阅读教材中关于等腰三角形的部分，并做好笔记。

2. 独立完成作业，不得抄袭他人答案。

3. 对于遇到的疑难问题，鼓励学生相互讨论或向老师请教。

4. 书写规范，答案清晰，逻辑性强。

5. 及时完成作业，不得拖延。

四、作业评价教师将对本次作业进行全面评价，包括：1. 准确性：评价学生对等腰三角形定义和性质的掌握程度。

2. 逻辑性：评价学生解题思路的清晰程度和逻辑性。

3. 创新性：鼓励学生尝试不同的解题方法，评价其创新性和实用性。

4. 规范性：评价学生的书写规范和答案的清晰度。

五、作业反馈为帮助学生更好地掌握《等腰三角形》的知识点，教师将根据学生的作业情况进行反馈：1. 对于普遍存在的问题，将在课堂上进行重点讲解。

2. 对于个别学生的问题，将进行个别辅导。

3. 鼓励学生在课堂上分享自己的解题方法和思路，促进同学之间的交流和学习。

4. 将优秀作业进行展示，供其他学生参考和学习。

六、附加建议为帮助学生更好地掌握等腰三角形知识，建议家长在家中辅助孩子进行以下活动：1. 与孩子一起探讨生活中的等腰三角形实例，加深对概念的理解。

2012年新人教版数学八年级(上)13.3.1 等腰三角形(1.等腰三角形的性质)

想一想:
刚才的证明除了能得到∠B＝∠C 你还能发现什么?
重合的线段 AB＝AC 重合的角
A
∠B ＝ ∠C.
∠BAD ＝ ∠CAD
∠ADB ＝∠ADC =90°
B D C
BD＝CD
AD＝AD
是真是假
猜想等腰三角形的底边上的高、底边上的中线、顶角的平分线互为重合.
A
1 2
（1）如图，AD⊥BC，AB＝AC. 求证：BD＝CD，∠1＝∠2. （2）如图，BD＝CD，AB＝AC. 求证：AD⊥BC，∠1＝∠2. （3）如图，∠1＝∠2，AB＝AC. B 求证：AD⊥BC，BD＝CD.
你的细心加你的耐心等于成功！
︸
C
H
B
3
2
D
∴△AEH≌△BEC(ASA) ∴AH=BC 即 AH=2BD
课后思考
如图，已知△ABC中，AB＝AC,F在AC上，在 BA的延长线上截取AE＝AF,求证：ED⊥BC
E
A
F
证明：∵AB＝AC，AE＝AF ∴∠B＝∠C，∠E＝∠AFE ∵∠E＋∠AFE＝∠BAC 又∵∠BAC＋∠B＋∠C＝180° ∴∠E＋∠AFE＋∠B＋∠C＝180° ∴∠E＋∠B＝1/2×180°＝90° ∴∠BDE＝90° ∴ED⊥BC
B
底边
C
等腰三角形中，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.
A C
A
图1
B
C
图2
B
已知：AB=AC
已知：CA=CB
说出每个三角形中的腰和底边；顶角和底角
小试牛刀
1、等腰三角形一腰为3cm,底为4cm, 则它的周长是

《17.1等腰三角形》作业设计方案-初中数学冀教版12八年级上册

《等腰三角形》作业设计方案（第一课时）一、作业目标本节课的作业设计旨在使学生：1. 理解等腰三角形的概念及性质。

2. 掌握等腰三角形中角与边的关系。

3. 学会利用等腰三角形的性质解决简单的几何问题。

二、作业内容等腰三角形作为初中数学的基础知识点，其实质在于其特殊性质。

因此，本课时的作业内容设计如下：1. 基础练习：要求学生根据等腰三角形的定义，判断给定的三角形是否为等腰三角形，并说明理由。

2. 角边关系探索：设计一系列问题，让学生通过计算和证明，掌握等腰三角形中两底角相等、底边上的中线、角平分线及垂直平分线的性质。

3. 应用题练习：通过实际情境或几何图形，设置几个关于等腰三角形的应用问题，如建筑物的支撑结构、道路标志的形状等，让学生运用所学知识解决问题。

4. 拓展提高：提供一些难度较高的题目，鼓励学生通过小组讨论或自主学习的方式探索答案，培养学生的探究能力和创新思维。

三、作业要求为确保学生有效完成作业，特提出以下要求：1. 认真审题：仔细阅读题目，明确题目要求。

2. 规范作答：书写要工整，步骤要完整，表述要准确。

3. 独立思考：在遇到问题时，首先尝试自己解决，不轻易放弃。

4. 合作交流：对于拓展题，可与同学交流想法和答案。

5. 及时订正：对于错题要及时订正，并总结解题方法。

四、作业评价对学生的作业进行评价时，应注重以下几个方面：1. 准确性：答案是否正确，是否符合题目要求。

2. 规范性：书写是否工整，步骤是否完整。

3. 创新性：在拓展题中是否展现出创新思维和独特见解。

4. 态度与努力：对待作业的态度是否认真，是否有努力解决问题的过程。

五、作业反馈作业反馈是提高教学效果的重要环节。

教师应对学生的作业进行批改，并做好以下反馈工作：1. 对错误进行及时纠正，并指导学生改正。

2. 对学生的优点和进步给予肯定和表扬。

3. 对共性问题进行课堂讲解，确保学生真正掌握知识点。

4. 收集学生的意见和建议，不断改进教学方法和作业设计。

八年级数学上册等腰三角形(习题及答案)(人教版)

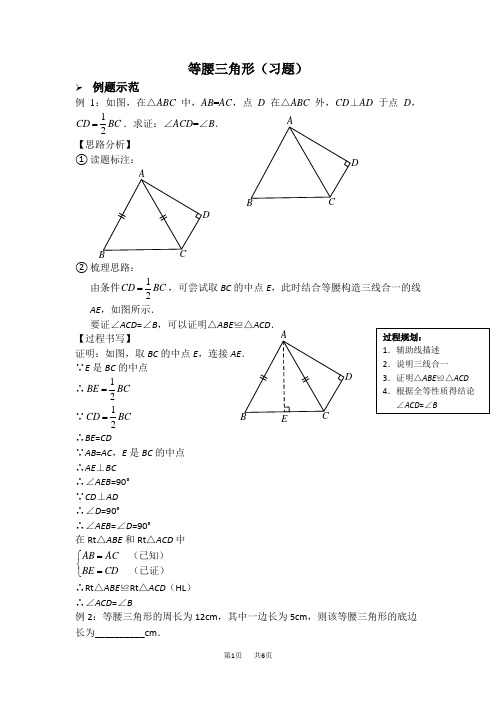
等腰三角形（习题）➢ 例题示范例1：如图，在△ABC 中，AB =AC ，点D 在△ABC 外，CD ⊥AD 于点D ，12CD BC =．求证：∠ACD =∠B ．【思路分析】 ① 读题标注： ABCD② 梳理思路：由条件12CD BC =，可尝试取BC 的中点E ，此时结合等腰构造三线合一的线AE ，如图所示．要证∠ACD =∠B ，可以证明△ABE ≌△ACD ．【过程书写】证明：如图，取BC 的中点E ，连接AE ．∵E 是BC 的中点∴12BE BC =∵12CD BC = ∴BE =CD∵AB =AC ，E 是BC 的中点 ∴AE ⊥BC ∴∠AEB =90° ∵CD ⊥AD ∴∠D =90°∴∠AEB =∠D =90°在Rt △ABE 和Rt △ACD 中 AB AC BE CD =⎧⎨=⎩（已知）（已证） ∴Rt △ABE ≌Rt △ACD （HL ） ∴∠ACD =∠B例2：等腰三角形的周长为12cm ，其中一边长为5cm ，则该等腰三角形的底边长为__________cm ．EA B C D A BCD【思路分析】等腰三角形一边长为5cm ，这一边可能是底，也可能是腰，故需分类讨论： ① 如果5cm 为底，则根据周长为12cm ，可知腰长为3.5cm ．此时两边之和大于第三边，这个三角形存在．② 如果5cm 为腰，则根据周长为12cm ，可知底边长为2cm ．此时两边之和大于第三边，这个三角形存在．综上，该等腰三角形的底边长为5cm 或2cm ． ➢ 巩固练习1. 已知：如图，在△ABC 中，AB =AC ，∠A =80°，求∠C 的度数．BA2. 如图，在△ABC 中，AB =AC ，BE ∥AC ，∠BDE =100°，∠BAD =70°，则∠E =______．ED CB ADC BA第2题图第3题图3. 已知：如图，在△ABC 中，AB =AC ，D 为AB 边上一点，若CD =AD =BC ，则∠A =_________．4. 如图，在△ABC 中，∠ABC 的平分线和∠ACB 的平分线相交于点E ，过点E作MN ∥BC ，交AB 于点M ，交AC 于点N ．若BM +CN =9，则线段MN 的长为（）N M ECBAA ．6B ．7C ．8D ．95. 已知：如图，在△ABC 中，AB =AC ，AD 是BC 边上的中线，点P 在AD 上．求证：PB=PC ．DCBAP6. 已知：如图，B ，D ，E ，C 在同一直线上，AB =AC ，AD =AE ．求证：BD =CE ．A B CDE7.已知等腰三角形的两边长分别为4和8，则该等腰三角形的周长为_________________．8.若等腰三角形的一个角比另一个角大30°，则该等腰三角形的顶角的度数为_____________．9.已知：如图，线段AB的端点A在直线l上，AB与l的夹角是30°，请在直线l上另找一点C，使△ABC是等腰三角形．这样的点能找几个？请找出所有符合条件的点．➢思考小结1.要证明边相等或角相等，可以考虑两种思路：①如果边或者角在两个三角形里面，则证明两个三角形__________；②如果边或角在一个三角形里面，证明三角形是_______三角形．2.将两个含30°角的三角板如图放置，则△ABD是_________三角形（“等腰”或“等边”），故AB_____BD，BC=____BD，所以BC=____AB，从而得到对于含有30°角的直角三角形，30°角所对的直角边是斜边的_______．ADCB【参考答案】➢巩固练习1.50°2.50°3.36°4. D5.证明略提示：利用等腰三角形三线合一的性质，得AD垂直平分BC，从而得到PB=PC 6.证明略提示：根据等边对等角可得∠B=∠C，∠ADE=∠AED，进而可得∠BAD=∠CAE，从而证明△ABD≌△ACE，根据全等三角形对应边相等，可得BD=CE7.208.80°或40°9.这样的点能找4个，作图略➢思考小结1.①全等②等腰2.等边，=，12，12，一半。

八年级数学上册第11章三角形等腰三角形课后作业 (新版)新人教版

等腰三角形1. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（）A. 6B. 7C. 8D. 92. 如图，在△ABC中，∠A=36°，AB=AC、BD平分∠ABC.若△ABD的周长比△BCD的周长多1厘米，则BD的长是（）A. 0.5厘米B. 1厘米C. 1.5厘米D. 2厘米3. 如图，在△ABC中，高AD和BE交于点H，且∠1=∠2=22.5°，下列结论：①∠1=∠3；②BD+DH=AB；③2AH=BH；④若DF⊥BE于点F，则AE-FH=DF.其中正确的结论是（）A. ①②③ B. ③④ C. ①②④ D. ①②③④4. 如图，在△ABC中，∠A=60°，∠ABC=50°，∠B、∠C的平分线相交于F，过点F作DE∥BC，交AB于D，交AC于E，那么下列结论正确的是（）①∠ACB=70°；②∠BFC=115°；③∠BDF=130°；④∠CFE=40°.A. ①②B. ③④C. ①③D. ①②③5. 如图，在△DAE中，∠DAE=40°，线段AE、AD的中垂线分别交直线DE于B和C两点，则∠BAC的大小是（）A. 100°B. 90°C. 80°D. 120°26. 如图，△ABC 中，D 是BC 的中点，DE ∥AB ，BF 平分∠ABC ，交DE 于点F ，若BC=6，则DF 的长是（）A. 2B. 3C. 25D. 47. 如图，在 Rt △ABC 中，∠B=90°.ED 是AC 的垂直平分线，交AC 于点D ，交BC 于点E ，已知∠BAE=30°，则∠C 的度数为.8. 如图所示，在△ABC 中，AB=AC ，∠A=36°，BC=2，BD 平分∠ABC ，DE ∥BC ，则AE=9. 如图，在△ABC 中，AD 平分∠BAC ，AD ⊥BD ，DE ∥AC 交AB 于E ，若AB=5，则DE 的长是.10. 如图，P 是等腰△ABC 的底边BC 上一点，过点P 作BC 的垂线，交AB 于点Q ，交CA的延长线于点R.判断△ARQ 是不是等腰三角形，并说明理由.11. 如图，△ABC中，BD、CE分别是AC、AB上的高，BD与CE交于点O.BE=CD（1）问△ABC为等腰三角形吗？为什么？（2）问点O在∠A的平分线上吗？为什么？12. 如图，在△ABC中，AD平分∠BAC.（1）若AC=BC，∠B：∠C=2：1，试写出图中的所有等腰三角形，并给予证明. （2）若AB+BD=AC，求∠B：∠C的比值.4等腰三角形课后作业参考答案1. 解析：由∠ABC 、∠ACB 的平分线相交于点E ，∠MBE=∠EBC ，∠ECN=∠ECB ，利用两直线平行，内错角相等，利用等量代换可∠MBE=∠MEB ，∠NEC=∠ECN ，然后即可求得结论.解：∵∠ABC 、∠ACB 的平分线相交于点E ，∴∠MBE=∠EBC ，∠ECN=∠ECB ，∵MN ∥BC ，∴∠EBC=∠MEB ，∠NEC=∠ECB ，∴∠MBE=∠MEB ，∠NEC=∠ECN ，∴BM=ME ，EN=CN ，∴MN=ME+EN ，即MN=BM+CN.∵BM+CN=9∴MN=9，故选D2. 解析：根据等腰三角形的判定定理，得△ABC 为等腰三角形，再根据三角形内角和定理和角平分线得∠BDC=72°，得出边之间的关系，从而求得BD 的长.解：由∠A=36°，AB=AC ，可得∠B=∠C=72°，∴∠ABD=∠CBD=36°，∠BDC=72°，∴AD=BD=BC ，由题意，（AB+AD+BD ）-（BD+BC+CD ）=1厘米，即 AC+2BD-2BD-CD=1厘米，即 AC-CD=AD=1厘米，即 BD=1厘米故选B.3. 解析：根据角平分线、高、等腰直角三角形的性质依次判断即可得出答案. 解：①∵∠1=∠2=22.5°，又∵AD 是高，∴∠2+∠C=∠3+∠C ，∴∠1=∠3，②∵∠1=∠2=22.5°，∴∠ABD=∠BAD ，∴AD=BD ，又∵∠2=∠3，∠ADB=∠ADC ，∴△BDH ≌△ADC ，∴DH=CD ，∵AB=BC ，∴BD+DH=AB ，③无法证明，④可以证明，故选C4. 解析：根据三角形内角和定理对①进行判断；根据角平分线的定义和三角形内角和定理可得到∠BFC=90°+21∠A=120°，则可对②进行判断；根据平行线的性质对③进行判断；先根据角平分线的性质得到∠BCF=21∠ACB=35°，然后根据平行线的性质对④进行判断.解：∵∠A=60°，∠ABC=50°，∴∠C=180°-∠A-∠ABC=70°，所以①正确；∵∠B 、∠C 的平分线相交于F ，∴∠BFC=90°+21∠A=120°，所以②错误； ∵DE ∥BC ， ∴∠BDF=180°-∠ABC=130°，所以③正确；∵CF 平分∠BCE ，∴∠BCF=21∠ACB=35°， ∵DE ∥BC ，∴∠CFE=∠BCF=35°，所以④正确.故选C5. 解析：由已知条件，利用了中垂线的性质得到线段相等及角相等，再结合三角形内角和定理求解.解：如图，∵BG 是AE 的中垂线，CF 是AD 的中垂线，∴AB=BE ，AC=CD∴∠AED=∠BAE=∠BAD+∠DAE ，∠CDA=∠CAD=∠DAE+∠CAE ，∵∠DAE+∠ADE+∠AED=180°∴∠BAD+∠DAE+∠DAE+∠CAE+∠DAE=3∠DAE+∠BAD+∠EAC=120°+∠BAD+∠EAC=180° ∴∠BAD+∠EAC=60°∴∠BAC=∠BAD+∠EAC+∠DAE=60°+40°=100°.故选A6. 解析：由中点的定义可以求出BD=21BC ，由角平分线的性质就可以得出∠ABF=∠CBF ，由平行线的性质就可以得出∠ABF=∠BFD.就有∠BFD=∠DBF ，得出DB=DF ，就可以得出结论.解：∵D 是BC 的中点，∴BD=21BC. ∵BC=6，∴BD=3.∵BF 平分∠ABC ，∴∠ABF=∠CBF.∵DE ∥AB ，∴∠ABF=∠BFD ，∴∠BFD=∠DBF ，∴BD=FD ，∴BF=3.6故选B.7. 解析：由已知条件，根据垂直平分线的性质，得到EA=EC ，进而得到∠EAD=∠ECD ，利用等腰三角形的性质和垂直平分线的性质解答解：∵ED 是AC 的垂直平分线，∴AE=CE ，∴∠EAC=∠C ，又∵∠B=90°，∠BAE=30°， ∴∠AEB=60°，又∵∠AEB=∠EAC+∠C=2∠C ，∴∠C=30°.故答案为308. 解析：由在△ABC 中，AB=AC ，∠A=36°，BC=2，BD 平分∠ABC ，DE ∥BC ，易求得△ADE ，△ABD 以及△BCD 是等腰三角形，则可得AE=AD=BD=BC.解：∵在△ABC 中，AB=AC ，∠A=36°，∴∠ABC=∠C=72°，∵BD 平分∠ABC ，∴∠ABD=∠DBC=36°，∴∠ABD=∠A ，∴BD=AD ，∵DE ∥BC ，∴∠AED=∠ADE=∠ABC=∠C=72°，∴AE=AD ，∴AE=BD ，∵∠BDC=180°-∠DBC-∠C=72°=∠C ，∴BD=BC=2，∴AE=2.故答案为：29. 解析：首先根据角平分线的性质与平行线的性质得出∠1=∠3，再利用等腰三角形的性质得出DE=21AB ，进而得出答案. 解：如图，∵AD 平分∠BAC ，∴∠1=∠2，∵DE ∥AC ，∴∠2=∠3，∴∠1=∠3，∴AE=ED ，又∵AD ⊥BD ，即∠3+∠4=90°，∴∠1+∠5=90°，∴∠4=∠5，∴BE=DE ，在Rt △ADB 中， DE=21AB=25故答案为：25 10. 解析：根据垂直求出∠C+∠R=90°，∠B+∠BQP=90°，再根据等边对等角求出∠B=∠C ，从而得到∠R=∠BQP ，再根据对顶角相等求出∠BQP=∠AQR ，然后求出∠R=∠AQR ，根据等角对等边可得AQ=AR ，从而判断出△ARQ 是等腰三角形.解：△ARQ 是等腰三角形.理由如下：∵RP ⊥BC ，∴∠C+∠R=90°，∠B+∠BQP=90°，∵AB=AC ，∴∠B=∠C ，∴∠R=∠BQP ，∵∠BQP=∠AQR ，∴∠R=∠AQR ，即△ARQ 是等腰三角形11. 解析：（1）先利用HL 证明Rt △BCD 与Rt △CBE 全等，然后根据全等三角形对应角相等可得∠ABC=∠ACB ，再根据等角对等边的性质可得AB=AC ，所以△ABC 是等腰三角形；（2）根据（1）中Rt △BCD ≌Rt △CBE ，然后利用全等三角形对应边相等可得BD=CE ，对应角相等可得∠BCE=∠CBD ，然后利用等角对等边可得BO=CO ，相减可得OD=OE ，再根据到角的两边距离相等的点在角的平分线上即可证明解：（1）△ABC 是等腰三角形.理由如下：∵BD 、CE 是△ABC 的高，∴△BCD 与△CBE 是直角三角形，在Rt △BCD 与Rt △CBE 中，BE=CD, BC=BC8∴Rt △BCD ≌Rt △CBE （HL ），∴∠ABC=∠ACB ，∴AB=AC ，即△ABC 是等腰三角形；（2）点O 在∠A 的平分线上.理由如下：∵Rt △BCD ≌Rt △CBE ，∴BD=CE ，∠BCE=∠CBD ，∴BO=CO ，∴BD-BO=CE-CO ，即OD=OE ，∵BD 、CE 是△ABC 的高，∴点O 在∠A 的平分线上（到角的两边距离相等的点在角的平分线上）12. 解析：（1）利用AC=BC 可直接得出△ABC 是等腰三角形，再利用三角形内角和定理求出∠B=∠ADB ，∠DAC=∠C ，即可得出△ABD 和△ADC 是等腰三角形.（2）此题有2种方法，方法1：在AC 上截取AE=AB ，连接DE ，求证△ABD ≌△ADE ，然后得到∠B=∠AED=∠EDC+∠C=2∠C 即可得出答案；方法2：延长AB 到E ，使AE=AC 连接DE ，利用“截长法”或“补短法”添加辅助线，将AC-AB 或AB+BD 转化成一条线段即可.解：（1）等腰三角形有3个：△ABC ，△ABD ，△ADC ，证明：∵AC=BC∴△ABC 是等腰三角形∴∠B=∠BAC∵∠B ：∠C=2：1∠B+∠BAC+∠C=180°∴∠B=∠BAC=72°，∠C=36°∵∠BAD=∠DAC=21∠BAC=36° ∴∠B=∠ADB=72°，∴△ABD 和△ADC 是等腰三角形（2）在AC 上截取AE=AB ，连接DE又∠BAD=∠DAE ，AD=AD∴△ABD ≌△ADE∴∠AED=∠B ，BD=DE∵AB+BD=AC∴BD=EC∴DE=EC∴∠EDC=∠C∴∠B=∠AED=∠EDC+∠C=2∠C 即∠B：∠C=2：1。

专题13.4等腰三角形【十大题型】-2024-2025学年八年级数学上册举一反三系[含答案]

试卷第 11 页，共 15 页
(1)求证： VBEC 是等腰三角形；
(2)用等式表示线段 AB、AC、BD 之间的数量关系，并证明．
②若 ÐCMD = 30° ， CD = 3 ，求 V BCM 的周长；
(2)若 BC = 8 ，且 V ABC 的面积为 40，求 VCDM 周长的最小值．
【题型 4 利用三线合一证明】
【例 4】
（23-24 八年级·辽宁锦州·期中）
13．如图，在 V ABC 中， AD 是 BC 边上的高线， CE 是中线，且 DG ^ CE 于 G ，
PA、PB、PC ，则图中有
个等腰三角形．
【变式 6-2】
（23-24 八年级·吉林白山·期中）
23．如图，在四边形 ABCD 中， AD ∥ BC ， AB = CD ， ÐBDC = ÐBCD ，点 E 是线段 BD
上一点，且 BE = AD ．
(1)求证： △ADB≌Байду номын сангаасEBC ；
(2)直接写出图中所有的等腰三角形．
专题 13.4 等腰三角形【十大题型】
【华东师大版】
【题型 1 利用等边对等角求解】
【题型 2 利用等边对等角进行证明】
【题型 3 利用三线合一求解】
【题型 4 利用三线合一证明】
【题型 5 格点中画等腰三角形】
【题型 6 找出图中的等腰三角形】
【题型 7 利用等角对等边证明等腰三角形】
【题型 8 利用等角对等边求边长或证明边相等】
（23-24 八年级·陕西西安·期末）
26．如图，在 V ABC 中， ÐACB = 90o ， CE 是斜边 AB 上的高，角平分线 BD 交 CE 于点
M ．求证： VCDM 是等腰三角形．

人教版八年级数学上等腰三角形性质教案导学案教学案教学设计课时作业试卷同步练习含答案解析

等腰三角形(1)【目标导航】1.掌握等腰三角形的概念、性质及其应用．2. 经历作（画）出等腰三角形的过程，•从轴对称的角度去体会等腰三角形的特点．3.通过学生的操作和思考，使学生掌握等腰三角形的相关概念，并在探究等腰三角形性质的过程中培养学生认真思考的习惯．【预习引领】1.2．等腰三角形是轴对称图形吗？请找出它的对称轴． 3．等腰三角形的两底角有什么关系？4．顶角的平分线所在的直线是等腰三角形的对称轴吗？5．底边上的中线所在的直线是等腰三角形的对称轴吗？•底边上的高所在的直线呢？【要点梳理】1．是等腰三角形． 2．等腰三角形的性质：性质1(等边对等角)；性质2互相重合．3．如图，在△ABC 中，AB =AC ，点D 在AC 上，且BD =BC =AD ．求：△ABC 各角的度数．【课堂操练】一、填空题1．在△ABC 中，AB =AC ．若∠A =50°，则∠B = °，∠C = °；若∠B =45°，则∠A = °，∠C = °；若∠C =60°，则∠A = °，∠B = °；若∠A =∠B ，则∠A = °，∠C = °． 2．（2011湖南邵阳）在△ABC 中，AB=AC ，∠B=50°，则∠A=_______．D C AB 253．等腰三角形的周长是24 cm ，一边长是6 cm ，则其他两边的长分别是． 4．在△ABC 中，AB =AC ，若AD 平分∠BAC ，则AD BC ， BD CD ． 5．（2011浙江省嘉兴）如图，在△ABC 中，AB =AC ，︒=∠40A ，则△ABC 的外角∠BCD ＝ °． 6．已知等腰三角形的腰长比底边多2cm ，并且它的周长为16cm ．这个等腰三角形的边长是．7．如图，在△ABC 中，AC =BC ，BD 是∠ABC 的平分线，且BD ＝DC ，则∠C 的度数为．（第7题）（第8题）8．如图，在△ABC 中，∠C =90°, AB 的垂直平分线交BC 于点D ，垂足为E ，∠CAD =2∠B ，则∠B = °9．如图所示，在△ABC 中，AD ⊥BC 于D ，请你添加一个条件，就可以确定△ABC 是等腰三角形，你添加是．（第9题）（第10题） 10．如图，在△ABC 中，AB =AC ，DE 是AB 的对称轴，△BCE 的周长为14，BC =6，则AB 的长为．二、解答题1．如图，△ABC 是等腰直角三角形（AB =AC ，∠BAC =90°），AD 是底边BC 上的高，标出∠B 、∠C 、∠BAD 、∠DAC 的度数，图中有哪些相等线段？2．如图，在△ABC 中，AB =AD =DC ，∠BAD = 26°，求∠B 和∠C 的度数．ED C B A D C B A D CAB DC A B NMCBAAE DCB DC B A ED C B A3．如图，在△ABC 中，AB =AC ，D 是BC 上一点，∠BAD =40°，E 是AC 上一点，AE =AD .求∠EDC 的度数．4．已知：如图，在△ABC 中，AB =AC ，AD 是外角∠CAE 的平分线．求证：AD ∥BC ．5．已知：如图，在△ABC 中，AB =AC ，点M 、N 在BC 上，且BM =CN ．求证：AM =AN ．E DCB A 26【课后操练】1．如图，D 、E 在BC 上，AD =BD ，AE =CE ，∠ADE =45°, ∠AED =110°，则∠B= °， ∠C= °．（第１题）（第２题） 2．如图，点D 在AC 上，AB =BD =DC ， ∠C=40°，则∠ABD ＝ °． 3．一等腰三角形的两边之比是1：2，周长是15 cm ，则它的底边长是 cm ，一腰长是 cm ． 4．已知一个等腰三角形两个内角的度数之比为1：4，则这个等腰三角形顶角的度数为．5．等腰三角形的一个外角是100°，它的顶角的度数是．6．已知：如图，在△ABC 中，AB =AC ，点D 、E 分别在AB 、AC 上，BE 、CD 相交于点O ，且BO =CO ．求证：BE =CD ．ED C B AD C B AOE D CBA7．如图，在△ABC 中，AB =AC ，BD =BC ， AD =DE =EB ．求∠A 的度数．8．已知：如图在△ABC 中，∠ACB ＝90°CD 是AB 边上的高，AE 分别交CB 、CD 于点E 、F ，且CE =CF ．求证：AE 平分∠BAC ．ED CB AF ED BA OF E D CB A279．已知：在△ABC 中，AB =AC ，AD ⊥BC 于点D ，E 是AD 延长线上一点，求证： BE =CE ．10．已知：如图， AD 是△ABC 的角平分线，点E 在AB 上，且AE ＝AC ，EF ∥BC 交AC 于点F ．求证：EC 平分∠DEF ． .【课外拓展】1．已知：在△ABC 中，AB =2AC ， AD 平分∠BAC , AD = BDEDC B A 28求证： CD ⊥AC ．2.（2011江苏扬州）已知：如图，锐角△ABC 的两条高BD 、CE 相交于点O ，且OB=OC ，（1）求证：△ABC 是等腰三角形；（2）判断点O 是否在∠B AC 的角平分线上，并说明理由。

八上等腰等边三角形(含答案)-

§14．3 等腰三角形1.等腰三角形知识要点1．有两条边相等的三角形是等腰三角形．相等的两条边叫做腰，另一条边叫做底边．两腰所夹的角叫做顶角，腰与底边的夹角叫做底角．2．三角形按边分类：三角形()⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形底边和腰不相等的等腰三角形等腰三角形等边三角形正三角形3．等腰三角形是轴对称图形，其性质是：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．4．等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．典型例题例：如图，五边形ABCDE 中AB=AE ，BC=DE ，∠ABC=∠AED ，点F 是CD 的中点．•求证：AF ⊥CD.分析：要证明AF ⊥CD ，而点F 是CD 的中点，联想到这是等腰三角形特有的性质，•于是连接AC 、AD ，证明AC=AD ，利用等腰三角形“三线合一”的性质得到结论．证明：连接AC 、AD 在△ABC 和△AED 中()()()AB AE ABC AED BC ED =⎧⎪∠=∠⎨⎪=⎩已知已知已知 ∴△ABC ≌△AED （SAD ） ∴AC=AD （全等三角形的对应边相等）又∵△ACD 中AF 是CD 边的中线（已知）∴AF ⊥CD （等腰三角形底边上的高和底边上的中线互相重合）EDC A B F练习题(第一课时)一、选择题1．等腰三角形的对称轴是（）A ．顶角的平分线B ．底边上的高C ．底边上的中线D ．底边上的高所在的直线2．等腰三角形有两条边长为4cm 和9cm ，则该三角形的周长是（） A ．17cm B ．22cm C ．17cm 或22cm D ．18cm3．等腰三角形的顶角是80°，则一腰上的高与底边的夹角是（） A ．40° B ．50° C ．60° D ．30° 4．等腰三角形的一个外角是80°，则其底角是（）A ．100°B ．100°或40°C ．40°D ．80°5．如图，C 、E 和B 、D 、F 分别在∠GAH 的两边上，且AB=BC=CD=DE=EF ，若∠A=18°，则∠GEF 的度数是（）A ．80°B ．90°C ．100°D ．108°ECAHFG二、填空题6．等腰△ABC 的底角是60°，则顶角是________度． 7．等腰三角形“三线合一”是指___________．8．等腰三角形的顶角是n °，则两个底角的角平分线所夹的钝角是_________． 9．如图，△ABC 中AB=AC ，EB=BD=DC=CF ，∠A=40°，则∠EDF•的度数是_____． 10．△ABC 中，AB=AC ．点D 在BC 边上（1）∵AD 平分∠BAC ，∴_______=________；________⊥_________；（2）∵AD 是中线，∴∠________=∠________；________⊥________；（3）∵AD ⊥BC ，∴∠________=∠_______；_______=_______．三、解答题11．已知△ABC 中AB=AC ，AD ⊥BC 于D ，若△ABC 、△ABD 的周长分别是20cm 和16cm ，•求AD 的长．12．如图，在四边形ABCD 中，AB=AD ，CB=CD ，求证：∠ABC=∠ADC.DCAB13．已知△ABC 中AB=AC ，点P 是底边的中点，PD ⊥AB ，PE ⊥AC ，垂足分别是D 、E ，• 求证：PD=PE.四、探究题14．如图，CD 是△ABC 的中线，且CD=12AB ，你知道∠ACB 的度数是多少吗？由此你能得到一个什么结论？请叙述出来与你的同伴交流．DCAB答案:1．D 2．B 3．A 4．C 5．B 6．607．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合 8．（90+12n ）° 9．70° 10．略 11．6cm 12．连接BD ，∵AB=AD ，∴∠ABD=∠ADB ．∵CB=CD ，∴∠CBD=∠CDB ．∴∠ABC=∠ADC 13．连接AP ，证明AP 平分∠BAC ．14．∠ACB=90°．结论：若一个三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形练习题(第二课时)一、选择题1．如图1，已知OC 平分∠AOB ，CD ∥OB ，若OD=3cm ，则CD 等于（）A ．3cmB ．4cmC ．1.5cmD ．2cmD C A BE D ABFEDCABH（1） (2) (3)2．△ABC 中AB=AC ，∠A=36°，BD 平分∠ABC 交AC 于D ，则图中的等腰三角形有（） A ．1个 B ．2个 C ．3个 D ．4个3．如图2，△ABC 中，∠ABC 与∠ACB 的平分线交于点F ，过点F 作DE ∥BC 交AB 于点D ，交AC 于点E ，那么下列结论：①△BDF 和△CEF 都是等腰三角形；②DE=BD+CE ；•③△ADE 的周长等于AB 与AC 的和；④BF=CF ．其中正确的有（） A ．①②③ B ．①②③④ C ．①② D ．①4．如图3，Rt △ABC 中，CD 是斜边AB 上的高，角平分线AE 交CD 于H ，EF ⊥AB 于F ，则下列结论中不正确的是（）A ．∠ACD=∠B B ．CH=CE=EFC ．CH=HD D ．AC=AF 二、填空题5．△ABC 中，∠A=65°，∠B=50°，则AB ：BC=_________．6．已知AD 是△ABC 的外角∠EAC 的平分线，要使AD•∥BC ，•则△ABC•的边一定满足________． 7．△ABC 中，∠C=∠B ，D 、E 分别是AB 、AC 上的点，•AE=•2cm ，•且DE•∥BC ，•则AD=________． 8．一灯塔P 在小岛A 的北偏西25°，从小岛A 沿正北方向前进30海里后到达小岛，•此时测得灯塔P 在北偏西50°方向，则P 与小岛B 相距________．三、解答题 9．如图，已知AB=AC ，E 、D 分别在AB 、AC 上，BD 与CE 交于点F ，•且∠ABD=•∠ACE ，求证：BF=CF ．E D CA BF10．如图，△ABC 中BA=BC ，点D 是AB 延长线上一点，DF ⊥AC 于F 交BC 于E ，• 求证：△DBE 是等腰三角形．ED CABF四、探究题11．如图，AF 是△ABC 的角平分线，BD ⊥AF 交AF 的延长线于D ，DE ∥AC•交AB 于E ，求证：AE=BE ．EDCABF答案:1．A 2．C 3．A 4．C 5．1 6．AB=AC 7．2cm 8．30海里9．连接BC ，∵AB=AC ，∴∠ABC=∠ACB ，又∵∠ABD=∠ACE ，∴∠FBC=∠FCB ，∴FB=FC 10．证明∠D=∠BED11．证明∠EAD=∠EDA ，∠EBD=∠EDB 分别得到AE=DE ，BE=DE2.等边三角形知识要点1．三条边都相等的三角形叫做等边三角形，也叫做正三角形．2．等边三角形的性质：•等边三角形的三个内角都相等，•并且每一个内角都等于60° 3．等边三角形的判定方法：（1）三条边都相等的三角形是等边三角形；（2）三个角都相等的三角形是等边三角形；（3）有一个角是60°的等腰三角形是等边三角形．4．在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．典型例题例：如图，△ABC是边长为1的等边三角形，BD=CD，∠BDC=120°，E、F分别在AB、AC上，且∠EDF=60°，求△AEF的周长．分析：由∠BDC=120°和∠EDF=60°得到∠BDE+∠CDF=60°，•从而想到把这两个角拼在一起构造全等三角形，即延长AC至点P，使CP=BE，证明△BDE≌CDP，然后证明△DEF≌△DPF，得到EF=PF，从而把△AEF的周长转化为用△ABC的边长表示．解：延长AC至点P，使CP=BE，连接PD．∵△ABC是等边三角形∴∠ABC=∠ACB=60°∵BD=CD，∠BDC=120°∴∠DBC=∠DCB=30°∴∠EBD=∠DCF=90°∴∠DCP=∠DBE=90°在△BDE和△CDP中BD CDDBE DCP BE CP=⎧⎪∠=∠⎨⎪=⎩∴△BDE≌△CDP（SAS）∴DE=DP，∠BDE=∠CDP∵∠BDC=120°，∠EDF=60°∴∠BDE+∠CDF=60°∴∠CDP+∠CDF=60°∴∠EDF=∠PDF=60°在△DEF≌△DPF中DE DPEDF PDF DF DF=⎧⎪∠=∠⎨⎪=⎩∴△DEF≌△DPF（SAS）∴EF=FP ∴EF=FC+BE ∴△AEF的周长=AE+EF+AF=AB+AC=2练习题一、选择题1．正△ABC的两条角平分线BD和CE交于点I，则∠BIC等于（）A．60° B．90° C．120° D．150°2．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；•③三个外角（每个顶点处各取一个外角）都相等的三角形；•④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A．①②③ B．①②④ C．①③ D．①②③④3．如图，D、E、F分别是等边△ABC各边上的点，且AD=BE=CF，则△DEF•的形状是（） A．等边三角形 B．腰和底边不相等的等腰三角形C．直角三角形 D．不等边三角形DA B F21EDCAB4．Rt△ABC中，CD是斜边AB上的高，∠B=30°，AD=2cm，则AB的长度是（）A．2cm B．4cm C．8cm D．16cm5．如图，E是等边△ABC中AC边上的点，∠1=∠2，BE=CD，则对△ADE的形状最准备的判断是（）A．等腰三角形 B．等边三角形 C．不等边三角形 D．不能确定形状二、填空题6．△ABC中，AB=AC，∠A=∠C，则∠B=_______．7．已知AD是等边△ABC的高，BE是AC边的中线，AD与BE交于点F，则∠AFE=______．8．等边三角形是轴对称图形，它有______条对称轴，分别是_____________．9．△ABC中，∠B=∠C=15°，AB=2cm，CD⊥AB交BA的延长线于点D，•则CD•的长度是_______．三、解答题10．已知D、E分别是等边△ABC中AB、AC上的点，且AE=BD，求BE与CD•的夹角是多少度？11．如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC•于点D ，•求证：•BC=3AD.D CAB12．如图，已知点B 、C 、D 在同一条直线上，△ABC 和△CDE•都是等边三角形．BE 交AC 于F ，AD 交CE 于H ，①求证：△BCE ≌△ACD ；②求证：CF=CH ；③判断△CFH•的形状并说明理由．EDABHF四、探究题13．如图，点E 是等边△ABC 内一点，且EA=EB ，△ABC 外一点D 满足BD=AC ，且BE 平分∠DBC ，求∠BDE 的度数．（提示：连接CE ）EDCA。

人教版八年级上册数学寒假作业：特殊三角形

特殊三角形复习一．填空题（每空2分，共20分） 1.等腰三角形的腰长是底边的43，底边等于12cm ，则三角形的周长为 cm 。

2.等腰三角形顶角为80°，则一腰上的高与底边所夹的角的度数为度。

3．如图在△ABC 中，点D,E 分别在AC,AB 上若AE=DE=DB=BC, 且∠ABC=100°,则∠A=_________。

4.已知三角形的三个角之比为1：2：3，则该三角形是____________。

5.在三角形中，如果两条直角边分别是3和4，那么斜边上的高线是____________。

6.一个三角形的三边的比为3：4：5，它的周长为36㎝，则它的面积为____________。

7.如图1，若∆ACD 的周长为7cm ，DE 为AB 边的垂直平分线，则AC+BC=_____ cm.8、如图2，在∆ABC 中，∠A=90︒，BD 是∠ABC 的平分线，DE 是BC 的垂直平分线，则∠C=_____． 9. 已知等腰三角形一边长为4cm ，另一边长为7cm ，此等腰三角形的周长为__________。

10. 等腰三角形的底角是____________。

(填“锐角、直角或钝角”) 二．选择题（共33分）1、如图3，已知在ABC ∆中，90ABC ∠=︒，30A ∠=︒，BD AC ⊥，DE BC ⊥，D 、E 为垂足，下列结论正确的是（）A 、AC=2AB B 、AC=8EC C 、CE=12BD D 、BC=2BD ．2. 如图4，已知∆ABC 是等边三角形，点O 是BC 上任意一点，OE 、OF 分别与两边垂直，等边三角形的高为1，则OE+OF 的值为（）．A ．12B ．1C ．2D ．不确定 3．三角形内到三角形各边的距离都相等的点必在三角形的（）A 中线上B 角平分线上C 高线上D 不能确定 4. 下列能断定△ABC 为等腰三角形的是（）A ．∠A=30º、∠B=60º B.∠A=50º、∠B=80º C ．AB=AC=2，BC=4 D.AB=3、BC=7，周长为13E DCBA(图1)(图2)ABCDE（图3）ABCOEF（图4）D C EA B第3题5. 若等腰三角形的底角比顶角大15︒，那么顶角为（）A ．45︒ B.40︒ C.55︒ D.50︒6．若等腰三角形的顶角为a ，则它一腰上的高与底边的夹角等于（）A.90°-aB.2a 90-︒ C. 2a 90-︒ D. 2a7．若三角形三边c b a ,,满足()()()0=---a c c b b a ，则该三角形是（）A ．等腰三角形 B.直角三角形 C.等边三角形 D.锐角三角形 8．用c b a ,,作三角形的三边，其中不能构成直角三角形的是（）A. 3,2,1===c b a B. 3,2,7===c b aC. 13,5,12===c b aD. 3,2,4===c b a9．若△ABC 三边长c b a ,,满足()05172=-+--+-+c b a b a ，则△ABC 是（）A ．等腰三角形 B. 等边三角形 C.直角三角形 D. 等腰直角三角形 10．下列条件中，不能判定两个直角三角形全等的是（）A ．两个锐角对应相等 B. 一条边和一个锐角对应相等 C.两条直角边对应相等 D. 一条直角边和一条斜边对应相等 11、如图5：ABC ∆中，D 点在BC 上,现有下列四个命题: ① 若AB=AC,则BC ∠=∠,②若AB=AC,12∠=∠，则,,AD BC BD DC ⊥= ③若,,AB AC BD CD ==则,12,AD BC ⊥∠=∠④若,,AB AC AD BC =⊥则,12,BD BC =∠=∠ 其中正确的有（）A 、1个B 、2个C 、3个D 、4个三．解答题（共34分）1.（6分）已知等腰三角形一腰上的中线将三角形的周长分成9cm 和15cm 两部分，求这个三角形的腰长和底边长。

等腰三角形八年级数学人教版(附答案)

等腰三角形中考频度：★★★★★ 难易程度：★★★☆☆1．等腰三角形的一个角是70°，它的底角的大小为 A ．70°B ．40°C ．70°或40°D ．70°或55°2．已知a 、b 、c 是ABC △的三条边，且满足22a bc b ac +=+，则ABC △是 A ．锐角三角形 B ．钝角三角形 C ．等腰三角形D ．等边三角形3．如图，在△ABC 中，AB =AC ，BD 是∠ABC 的平分线，DE ∥AB ，BE =5 cm ，CE =3 cm ，则△CDE 的周长是A ．15 cmB ．13 cmC ．11 cmD ．9 cm4．在下列给出的命题中，正确的命题有①等腰三角形的角平分线、中线和高重合；②等腰三角形两腰上的高相等；③等腰三角形最小边是底边；④一个等边三角形的高、中线、角平分线都分别相等；⑤等腰三角形都是锐角三角形． A ．1个 B ．2个 C ．3个D ．4个5．在△ABC 中，∠A =70°，∠B =55°，则△ABC 是 A ．钝角三角形 B ．等腰三角形 C ．等边三角形D ．等腰直角三角形6．等腰三角形一腰上的高与另一腰的夹角为20°，则这个等腰三角形的底角度数是 A ．70° B ．55° C ．35°D ．55°或35°△7．如图，正方形网格中，网格线的交点称为格点，已知A、B是两格点，如果C也是图中的格点，且使得ABC 为等腰三角形，则点C的个数有A．4个B．6个C．8个D．10个8．如图所示，△ABC为等边三角形，P为BC上一点，Q为AC上一点，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则对下面四个结论判断正确的是①点P在∠BAC的平分线上，②AS=AR，③QP∥AR，④△BRP≌△QSP．A．全部正确B．仅①和②正确C．仅②③正确D．仅①和③正确9．如图，△ABC中，∠ABC与∠ACB的平分线相交于点D，过点D作直线EF∥BC，交AB于点E，交AC 于点F．若BE=4，EF=7，则FC=__________．学+科网10．如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为__________．11．已知，a，b，c是△ABC的三边长，且满足|a–c|+|b–c|=0，则△ABC是__________三角形．12．如图，D是等边△ABC的AC边上的中点，点E在BC的延长线上，DE=DB，△ABC的周长是9，则∠E=__________°，CE=__________．13．如图，△ABC中AB=AC，EB=BD=DC=CF，∠A=40°，则∠EDF的度数是__________．14．等腰三角形的一腰的中线把三角形的周长分成16 cm和12 cm，则等腰三角形的底边长为__________．15．用一条长为20 cm的细铁丝能围成一边长为4 cm的等腰三角形吗？若能，请求出各边长；若不能，请说明理由．学科+网16．如图，四边形ABCD，AD BC∥，BAD∠的角平分线AE交CD于点F，交BC的延长线于点E，若点F 是CD的中点，求证：BF AF⊥．17．已知，如图所示，甲、乙、丙三个人做传球游戏，游戏规则如下：甲将球传给乙，乙将球立刻传给丙，然后丙又立刻将球传给甲．若甲站在∠AOB内的P点，乙站在OA上，丙站在OB上，并且甲、乙、丙三人的传球速度相同．问乙和丙必须站在何处，才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少？18．已知△ABC是等边三角形，点D是直线BC上一点，以AD为一边在AD的右侧作等边△ADE．（1）如图①，点D在线段BC上移动时，直接写出∠BAD和∠CAE的大小关系；（2）如图②，点D在线段BC的延长线上移动时，猜想∠DCE的大小是否发生变化．若不变请求出其大小；若变化，请说明理由．1．【答案】D【解析】若70°为顶角，则此等腰三角形的底角是（180°–70°）÷2=55°；若70°为底角，则此等腰三角形的底角为70°，综上，此等腰三角形的底角为70°或55°．故选D．2．【答案】C【解析】已知等式变形得：（a+b）（a-b）-c（a-b）=0，即（a-b）（a+b-c）=0，∵a+b-c≠0，∴a-b=0，即a=b，则△ABC为等腰三角形．故选C．5．【答案】B【解析】∵在△ABC中，∠A=70°，∠B=55°，∴∠C=180°–∠A–∠B=55°，∴∠B=∠C，∴△ABC是等腰三角形．故选B．6．【答案】D【解析】①如图①，∵AB=AC，∠ABD=20°，BD⊥AC，∴∠A=70°，∴∠ABC=∠C=（180°–70°）÷2=55°．②如图②，∵AB=AC，∠ABD=20°，BD⊥AC，∴∠BAC=20°+90°=110°，∴∠ABC=∠C=（180°–110°）÷2=35°．故选D．7．【答案】C【解析】如图，当△ABC为等腰三角形，则点C的个数有8个，故选C．8．【答案】A【解析】∵PR⊥AB于R，PS⊥AC于S．∴∠ARP=∠ASP=90°．∵PR=PS，AP=AP．∴Rt△ARP≌Rt△ASP．∴AR=AS，故②正确，∠BAP=∠CAP．∴点P在∠BAC的平分线上，故①正确．∴AP是BC边上的高和中线，即点P是BC的中点．依题可得∠PAQ=∠APQ=30°，∴∠PQS=∠PAQ+∠APQ=60°=∠BAC，∴PQ∥AB，故③正确．∵∠B=∠PQS=60°，∠BRP=∠QSP=90°，PR=PS，∴△BRP≌△QSP，故④正确．∴全部正确．故选A．9．【答案】3【解析】∵∠ABC，∠ACB的平分线相交于点D，∴∠ABD=∠DBC，∠ACD=∠DCB，∵EF∥BC，∴∠EDB=∠DBC，∠FDC=∠BCD，∴∠ABD=∠EDB，∠ACD=∠FDC，∴BE=DE，DF=CF，∴EF=DE+DF=BE+CF．∵BE=4，EF=7，∴CF=3．故答案为：3．12．【答案】30；3 2【解析】∵△ABC为等边三角形，D为AC边上的中点，∴BD为∠ABC的平分线，且∠ABC=60°，即∠DBE=30°，又DE=DB，∴∠E=∠DBE=30°．∵等边△ABC的周长为9，∴AC=3，且∠ACB=60°，∴∠CDE=∠ACB–∠E=30°，即∠CDE=∠E，∴CD=CE=12AC=32．故答案为：30；32．13．【答案】70°【解析】∵AB=AC，∠A=40°，∴∠B=∠C=70°，∵EB=BD=DC=CF，∴∠BDE=（180°-70°）÷2=55°，∠CDF=（180°-70°）÷2=55°，∴∠EDF=180°-55°-55°=70°．故答案为：70°．14．【答案】203cm或12 cm【解析】设等腰三角形的腰长是x，底边是y，根据题意得162122xxxy⎧+=⎪⎪⎨⎪+=⎪⎩或122162xxxy⎧+=⎪⎪⎨⎪+=⎪⎩，解得323203xy⎧=⎪⎪⎨⎪=⎪⎩或812xy=⎧⎨=⎩，经检验，均符合三角形的三边关系．因此三角形的底边是203或12．故答案为：203或12．16．【解析】∵AD∥BC，∴∠DAE=∠E，又∵∠DAE=∠BAE，∴∠E=∠BAE，∴BE=BA，在△DAF与△CEF中，∠DAE=∠E，∠DFA=∠CFE，DF=CF，∴△DAF≌△CEF，∴AF=EF，学-科网又∵BE=BA，∴BF⊥AF．17．【解析】如图所示，（1）分别作点P关于OA，OB的对称点P1，P2．（2）连接P1P2，与OA，OB分别相交于点M，N，因为乙站在OA上，丙站在OB上，所以乙必须站在OA上的M处，丙必须站在OB上的N处才能使传球所用时间最少．18．【解析】（1）∠BAD=∠CAE；理由：∵△ABC和△ADE是等边三角形，∴∠BAC=∠DAE=60°，∴∠BAD=∠CAE；（2）∠DCE=60°，不发生变化；理由如下：∵△ABC是等边三角形，△ADE是等边三角形，∴∠DAE=∠BAC=∠ABC=∠ACB=60°，AB=AC，AD=AE．∴∠ACD=120°，∠BAC+∠CAD=∠DAE+∠CAD，∴∠DAB=∠CAE．在△ABD和△ACE中，AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ACE（SAS），∴∠ACE=∠ABD=60°．∴∠DCE=180°–∠ACE–∠ACB=180°–60°–60°=60°．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2011-2012第一学期八年级数学寒假作业4(等腰三角形)
学号_____________ 姓名_________
一基础题
1，等腰三角形的一边长是6，另一边长是8，那么它的周长是（） A 、14 B 、22 C 、20 D 、20或22
2，已知等腰三角形的一个角等于42°，则它的底角为（）． A 、42 ° B 、69° C 、69°或84° D 、42°或69°
3，如图1，A B C △中，A B A C =，30A ∠= ，D E 垂直平分A C ，则BCD ∠的度数为（）Ａ．80 Ｂ．75 Ｃ．65 Ｄ．45 4，如图2，15A =
∠，AB BC CD DE EF ====，则D EF ∠等于（） A ．90
B ．75
C ．70
D ．60
图1 图2 图3 5，如图3，在Rt △ABC 中，∠C=90°，∠A=30°，AB ＋BC=12㎝，
则AB= ㎝
6，等腰三角形至少有a 条对称轴，至多有b 条对称轴，则b a -＝．二解答题
7，如图，在△ABC 中，DE 是AC 的垂直平分线，交BC 于D ，交AC 于E ， △ABD 的周长为15㎝，而AC ＝5㎝，求△ABC 的周长。

B
D
C E
A
第8
题图
B
C
B
A
8，一个等腰三角形的一个内角比另一个内角的2倍少30°，求这个三角形的三个内角的度数．
9，已知，在等腰三角形ABC ∆中，AB AC =，O 是底边BC 边上的中点， OD AB ⊥于D 点，OE AC ⊥于E 点，求证：A D A E =.
A
B
C
O
10, 如图：已知等边△ABC 中，D 是AC 的中点，E 是BC 延长线上的一点，且CE =CD ，DM ⊥BC ，垂足为M ，求证：M 是BE 的中点。

A
B
D
C
M E。