高中物理带电粒子在磁场中运动的多解问题 人教版
高中物理习题课带电粒子在磁场中运动的多解问题新人教版选修3

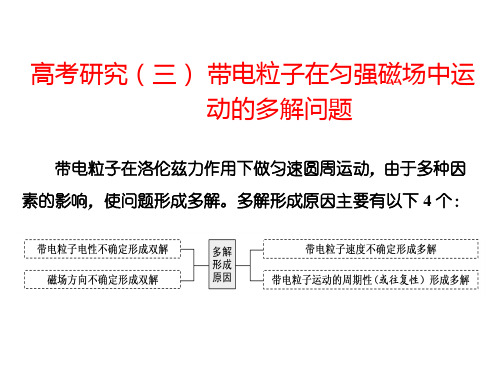
习题课三 带电粒子在磁场中运动的多解问题教学目标1.了解多解问题的常见成因,逐步熟悉处理多解问题的方法;2.强化“全圆”、“动圆”的概念,学会用好绘图工具快解问题。
教学过程:一.速度方向不变,大小改变【例题1】长为L ,间距也为L 的两平行金属板间有垂直向里的匀强磁场,如图所示,磁感应强度为B ,今有质量为m 、带电量为q 的正离子从平行板左端两班正中间以平行于金属板的方向射入磁场。
欲使离子不打在极板上,入射离子的速度大小应满足的条件是 ( )A.m qBL v 4<B.m qBL v 45>C.m qBL v >D.mqBL v m qBL 454<< 【解析】:由左手定则判得粒子在磁场中间向上偏,而作匀速圆周运动,很明显,圆周运动的半径大于某值r 1时粒子可以从极板右边穿出,而半径小于某值r 2时粒子可从极板的左边穿出,现在问题归结为求粒子能在右边穿出时r 的最小值r1以及粒子在左边穿出时r 的最大值r 2,由几何知识得:粒子擦着板从右边穿出时,圆心在O 点,有:r 12=L 2+(r 1-L /2)2得r 1=5L /4,又由于r 1=mv 1/Bq 得v 1=5BqL /4m ,∴v >5BqL /4m 时粒子能从右边穿出。
粒子擦着上板从左边穿出时,圆心在O '点,有r 2=L /4,又由r 2=mv 2/Bq =L /4得v 2=BqL /4m∴v 2<BqL /4m 时粒子能从左边穿出。
答案:AB【解后小结】本题只问带电粒子在洛伦兹力作用下飞出有界磁场时,由于粒子运动轨迹是圆弧状,因此,它可能穿过去了,也可能转过180o 从入射界面这边反向飞出,于是形成多解,在解题时一定要考虑周全。
【例题2】正离子从矩形磁场的D 点沿DA 方向、以各种不同的速率射入磁场,那么,这些正离子可能从矩形边界的什么位置射出?已知AD=a ,AB=1.5a 。
【解析】【解后小结】二.速度大小不变,方向改变【例题3】(05河北高考)如图,在一水平放置的平板MN 的上方有匀强磁场,磁感应强度的大小为B ,磁场方向垂直于纸面向里。
2018-2019学年高中一轮复习物理(人教版):第九单元 高考研究(三) 带电粒子在匀强磁场中运动的多解问题
返回
[例 2] [多选]如图所示, 一带负电的质点在
固定的正点电荷作用下绕该正电荷做匀速圆周 运动,周期为 T0,轨道平面位于纸面内,质点速 度方向如图中箭头所示。现加一垂直于轨道平面 的匀强磁场,已知轨道半径并不因此而改变,则( )
A.若磁场方向指向纸里,质点运动的周期将大于 T0 B.若磁场方向指向纸里,质点运动的周期将小于 T0 C.若磁场方向指向纸外,质点运动的周期将大于 T0 D.若磁场方向指向纸外,质点运动的周期将小于 T0
返回
[例 1]
如图所示,宽度为 d 的有界匀强磁场,
磁感应强度为 B, MM′和 NN′是它的两条边界。 现有质量为 m,电荷量为 q 的带电粒子,沿图示 方向垂直磁场射入。 要使粒子不能从边界 NN′射 出,则粒子入射速率 v 的最大值可能是多少。
返回
[解析] 若 q 为正电荷,轨迹是如图所示的上方与 NN′相切的 mv 1 圆弧,轨道半径:R= Bq 4 R 又 d=R- 2 Bqd 解得 v=(2+ 2) m 。
返回
[解析]
当磁场方向指向纸里时,质点所受的洛伦兹
力方向背离圆心,与库仑引力方向相反,则向心力减小, 由F
2π 2 R 向=m T
可知,当轨道半径 R 不变时,该质点运动
周期必增大;同理可得,当磁场方向指向纸外时,质点所 受的洛伦兹力指向圆心,则向心力增大,当 R 不变时,质 点运动周期减小。 [答案] AD
返回
[跟进训练] 2.[多选](2018· 商丘模拟)一质量为 m、电荷量为 q 的负电荷, 在磁感应强度为 B 的匀强磁场中,绕固定的正电荷沿固定 的光滑轨道做匀速圆周运动,若磁场方向垂直于它的运动 平面,且作用在负电荷的电场力恰好是磁场力的三倍,则 负电荷做圆周运动的角速度可能是 4qB A. m 3qB B. m 2qB C. m qB D. m ( )
带电粒子在磁场中运动之多解及周期运动问题

适用标准考点周期性与多解问题1.带电粒子电性不确立形成多解:受洛伦兹力作用的带电粒子,因为电性不一样,当速度同样时,正、负粒子在磁场中运动轨迹不一样,形成多解.如图 6 甲所示,带电粒子以速度v 垂直进入匀强磁场,如带正电,其轨迹为a,如带负电,其轨迹为 b .2.磁场方向不确立形成多解:有些题目只磁感觉强度的大小,而不知其方向,此时一定要考虑磁感觉强度方向不确立而形成的多解.如图乙所示,带正电粒子以速度 v 垂直进入匀强磁场,如 B 垂直纸面向里,其轨迹为 a,如 B 垂直纸面向外,其轨迹为 b .3.临界状态不独一形成多解:带电粒子在洛伦兹力作用下飞越有界磁场时,因为粒子运动轨迹是圆弧状,所以,它可能穿过去,也可能转过180 °从入射界面这边反向飞出,进而形成多解,如图丙所示.4.运动的周期性形成多解:带电粒子在局部是电场、局部是磁场的空间运动时,运动常常拥有来去性,进而形成多解,如图丁所示.一圆筒的横截面以下列图,其圆心为O.筒内有垂直于纸面向里的匀强磁场,磁感觉强度为B.圆筒下边有相距为 d 的平行金属板M 、N ,此中 M 板带正电荷, N 板带等量负电荷.质量为m、电荷量为q 的带正电粒子自M 板边沿的P 处由静止开释,经N 板的小孔S 以速度 v 沿半径 SO 方向射入磁场中.粒子与圆筒发生两次碰撞后仍从S 孔射出.设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的状况下,求:(1)M 、 N 间电场强度 E 的大小;(2)圆筒的半径 R.(3)保持M、N间电场强度 E 不变,仅将M 板向上平移,粒子仍从M 板边沿的P处由静止开释粒子自进入圆筒至从S 孔射出时期,与圆筒的碰撞次数n 。
1.以下列图,在纸面内有磁感觉强度大小均为B,方向相反的匀强磁场,虚线等边三角形ABC 为两磁场的理想界限。
三角形ABC 边长为 L,虚线三角形内为方向垂直纸面向外的匀强磁场,三角形外面的足够大空间为方向垂直纸面向里的匀强磁场。
带电粒子在磁场中运动的多解问题

带电粒子在磁场中运动的多解问题下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
本文下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Downloaded tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The documents can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!自古以来,人类对宇宙的探索从未停止。
2019届一轮复习人教版 带电粒子在磁场中运动的多解和临界问题 学案

知识回顾1.带电粒子在磁场中做圆周运动引起多解的原因(1)带电粒子的电性不确定形成多解,可能出现两个方向的运动轨迹.(2)磁场方向不确定形成多解,可能出现两个方向的运动轨迹.(3)临界状态不唯一形成多解,需要根据临界状态的不同分别求解.(4)圆周运动的周期性形成多解.2.带电粒子在磁场中运动临界问题的特点(1)带电粒子进入磁场时的速度方向不同,射出磁场的位置就会不同.(2)带电粒子在磁场中运动的速度大小不同,粒子的轨迹半径和运动时间就会不同.(3)粒子刚好穿出磁场边界的条件是带电粒子在磁场中的运动轨迹与边界相切.规律方法1.多解问题的解题方法和技巧(1)找出多解的原因.(2)画出粒子的可能轨迹,找出圆心半径的可能情况.(3)对于周期性形成的多解问题,注意n的可能限定范围.2.临界问题常用的结论(1)刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切.(2)当速度v一定时,弧长(或弦长)越长,圆心角越大,则带电粒子在有界磁场中运动的时间越长.(3)当速度v变化时,圆心角越大的,运动时间越长.3.处理带电粒子在有界磁场中运动的临界问题的技巧带电粒子进入有界磁场区域,其轨迹往往是一残缺圆,存在临界和极值问题,处理的方法是根据粒子的运动轨迹,运用动态思维,作出临界轨迹图,寻找几何关系,分析临界条件,然后应用数学知识和相应物理规律求解,分析临界问题时应注意:(1)从关键词、语句找突破口,审题时一定要抓住题干中“恰好”“最大”“至少”“不脱离”等词语,挖掘其隐藏的规律;(2)数学方法和物理方法的结合,如利用“矢量图”“边界条件”等求临界值.利用“三角函数、不等式的性质、二次方程的判别式”等求极值.例题分析【例1】 (2017年石家庄毕业检测)如图所示,宽度为d 的有界匀强磁场,磁感应强度为B ,MM ′和NN ′是它的两条边界.现有质量为m 、电荷量为q 的带电粒子沿图示方向垂直磁场射入.要使粒子不能从边界NN ′射出,求粒子入射速率v 的最大值可能是多少.【答案】v ′=-2Bqdm若q 为负电荷,轨迹是如图所示的下方与NN ′相切的34圆弧,则有:R ′=mv ′Bq,d =R ′+R ′cos45°,解得v ′=-2Bqdm .【例2】 如图所示,两垂直纸面向里的匀强磁场以MN 为边界,MN 边界上方磁场的磁感应强度大小B 1大于下方磁场的磁感应强度大小B 2(未知).有一长为l 的平直挡板与MN 重合,一比荷为c 的带正电粒子从挡板的中点O 处沿垂直挡板方向以速度v =cB 1lk (k 为偶数)进入上方磁场中,假设粒子与挡板发生碰撞并反弹过程没有能量损失,且粒子在下方磁场中运动时不会与挡板发生碰撞,粒子最终能回到出发点O ,不计粒子重力.若k =4,则粒子从挡板边缘进入下方磁场中.(1)试画出k =10时粒子的运动轨迹; (2)求两磁场的磁感应强度大小的比值B 1B 2.【答案】B 1B 2=k2+1【解析】 (1)粒子在上方磁场中运动时,有qvB 1=mv 2R 1得轨迹半径R 1=v cB 1=lk当k =10时,R 1=l10【例3】 如图所示,在xOy 平面内,有一个圆形区域,其直径AB 与x 轴重合,圆心O ′的坐标为(2a,0),其半径为a ,该区域内无磁场.在y 轴和直线x =3a 之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B .一质量为m 、电荷量为q 的带正电的粒子从y 轴上某点射入磁场.不计粒子重力.(1)若粒子的初速度方向与y 轴正向夹角为60°,且粒子不经过圆形区域就能到达B 点,求粒子的初速度大小v 1;(2)若粒子的初速度方向与y 轴正向夹角为60°,在磁场中运动的时间为Δt =πm3Bq ,且粒子也能到达B 点,求粒子的初速度大小v 2;(3)若粒子的初速度方向与y 轴垂直,且粒子从O ′点第一次经过x 轴,求粒子的最小初速度v min .【解析】 (1)因要求粒子不经过圆形区域就能到达B 点,故粒子到达B 点时速度方向竖直向下,则其轨迹的圆心必在x 轴正半轴上,如图 (1)所示.设粒子做圆周运动的半径为r 1,由几何关系得r 1sin30°=3a -r 1,又qv 1B =m v 21r 1,解得v 1=2qBa m(3)设粒子从C 点进入圆形区域,如图 (3)所示,O ′C 与O ′A 的夹角为θ,轨迹半径为r ,由几何关系得2a =r sin θ+a cos θ,故当θ=60°时,半径最小为r min =3a 又qv min B =mv 2minr min ,解得v min =3aBq m 。
人教版高中物理复习课件:带电粒子在磁场中运动的几个典型问题总结(共32张PPT)

圆形有界磁场
O
改变情景 深入挖掘
分组讨论:如果带电粒子的轨迹 半径等于圆形磁场半径,出射的 粒子有什么特点?
结论:任意方向射入 的粒子出射速度方向 均平行
圆形有界磁场
活学活用
如果带电粒子的轨迹半径等于圆 形磁场半径,平行射入的粒子会 有特点?
影响。下列图中阴影部分表示带电粒子可能经过的区域,
其中R=mv/qB,哪个图是正确的? ( )A
思考:从O点沿各方向射入的粒子 打到上边界上范围?(用R表示)
圆形有界磁场
O
v3
v2
v1
改变情景 深入思考
学生思考:指向圆心射入的粒子, 出射时速度方向有什么特点?
•深化提高
扩展圆——同向异速
Y
a
1.5a
X
当轨迹与某边界相切时,即为最终找出的临界情况,
在卷面上保留临界圆,由几何关系求解。
•深化提高
扩展圆——同向异速
Y
a
1.5a
X
当轨迹与某边界相切时,即为最终找出的临界情况,
在卷面上保留临界圆,由几何关系求解。
如图所示,M、N两板相距为d,板长为5d,两板不带电,板间有垂直纸面的匀强磁场,一
专题课:带电粒子在磁场中运动的 几个典型问题总结
产生条件 大小 方向
带电粒子在磁场中的运动(单边界、双边界、三角形、四边形、圆边界、临界问题、多解问题)(解析版)

带电粒子在磁场中的运动(单边界、双边界、三角形、四边形、圆边界、临界问题、多解问题)建议用时:60分钟带电粒子在磁场中的运动A.M带正电,N带负电B.M的速率小于N的速率A.1kBL,0°B3【答案】B【详解】若离子通过下部分磁场直接到达根据几何关系则有:R由:2v qvB mR=可得:qBLv kBLm==根据对称性可知出射速度与当离子在两个磁场均运动一次时,如图乙所示,因为两个磁场的磁感应强度大小均为根据洛伦兹力提供向心力,有:可得:122qBLv kBLm==此时出射方向与入射方向相同,即出射方向与入射方向的夹角为:通过以上分析可知当离子从下部分磁场射出时,需满足:此时出射方向与入射方向的夹角为:A.从ab边射出的粒子的运动时间均相同B.从bc边射出的粒子在磁场中的运动时间最长为C.粒子有可能从c点离开磁场D.若要使粒子离开长方形区域,速率至少为可见从ab射出的粒子做匀速圆周运动的半径不同,对应的圆心角不相同,所以时间也不同,故B.从bc边射出的粒子,其最大圆心角即与A .粒子的速度大小为2qBdmB .从O 点射出的粒子在磁场中的运动时间为C .从x 轴上射出磁场的粒子在磁场中运动的最长时间与最短时间之比为D .沿平行x 轴正方向射入的粒子离开磁场时的位置到得:R d=由洛仑兹力提供向心力可得:Bqv m=得:qBd v m=A 错误;A .如果0v v >,则粒子速度越大,在磁场中运动的时间越长B .如果0v v >,则粒子速度越大,在磁场中运动的时间越短C .如果0v v <,则粒子速度越大,在磁场中运动的时间越长D .如果0v v <,则粒子速度越大,在磁场中运动的时间越短【答案】B该轨迹恰好与y 轴相切,若上移,可知,对应轨迹圆心角可知,粒子在磁场中运动的时间越短,故CD .若0v v <,结合上述可知,飞出的速度方向与x 轴正方向夹角仍然等于A .粒子能通过cd 边的最短时间B .若粒子恰好从c 点射出磁场,粒子速度C .若粒子恰好从d 点射出磁场,粒子速度7.(2024·广西钦州·模拟预测)如图所示,有界匀强磁场的宽度为粒子以速度0v垂直边界射入磁场,离开磁场时的速度偏角为( )A.带电粒子在匀强磁场中做圆周运动的轨道半径为B.带电粒子在匀强磁场中做圆周运动的角速度为C.带电粒子在匀强磁场中运动的时间为D.匀强磁场的磁感应强度大小为【答案】B【详解】A.由几何关系可知,带电粒子在匀强磁场中做圆周运动的轨道半径为:A.该匀强磁场的磁感应强度B.带电粒子在磁场中运动的速率C.带电粒子在磁场中运动的轨道半径D.带电粒子在磁场中运动的时间C.根据几何关系可得:cos30aR = o所以:233R a =故C正确;AB.在磁场中由洛伦兹力提供向心力,即:A.从c点射出的粒子速度偏转角度最大C.粒子在磁场运动的最大位移为10.(2024·四川乐山·三模)如图所示,在一个半径为面向里的匀强磁场,O 为区域磁场圆心。
带电粒子在磁场中运动的多解问题

一质量为m,电量为q的负电荷在磁感应强度为B的匀强磁
场中绕固定的正电荷沿固定的光滑轨道做匀速圆周运动,若磁
场方向垂直于它的运动平面,且作用在负电荷的电场力恰好是
磁场力的3倍,则负电荷做圆周运动的角速度可能是( )
A. 4qB
m
B.
3qB m
C. 2qB
m
D. qB
m
解析:当负电荷所受的洛仑兹力与电场力方向相同时,
解: 由
qvB1
m
v2 R1
qvB2
m
v2 R2
得粒子在磁场B1、B2的轨道半径分别为
R1
1cm
d 4
R1
2cm
d 2
若粒子经过P点的轨迹如图6所示,则
T2
2R2
v0
t2
T2 2
联立解得粒子运动的时间
t2
2
106 s
若粒子经过P点的轨迹如图7所示,则
T1
2R1
v0
t1 T1
⑴ 明确多解原因。
⑵ 分别设每种多解原因成立,进行分析求解。
⑶ 求解过程同带电粒子在磁场中圆周运动的分析方法,即:
① 画出运动轨迹;确定圆心。
② 利用几何关系计算半径。 ③ 由 qvB m v2 和圆周运动等知识求解。 注意:粒子飞r 入、飞出对称边界时存在对称性。
11:10
圆心角 偏转角 圆心角 2弦切角
y
mv0 Bq
t1
1
360
T
④
vB B
1
若粒子带正电,运动时间
R
v0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
带电粒子在磁场中运动的多解问题
山东省郓城第一中学: 胡忠启 邮编:274700
带电粒子在洛仑兹力作用下做匀速圆周运动的问题一般有多解。
形成多解的原因有:
1. 带电粒子电性不确定
受洛仑兹力作用的带电粒子,可能带正电,也可能带负电。
当具有相同初速度时,正负粒子在磁场中的运动轨迹不同,导致形成双解。
例1. 如图1所示,第一象限范围内有垂直于xOy 平面的匀强磁场,磁感应强度为B 。
质量为m ,电量大小为q 的带电粒子在xOy 平面里经原点O 射入磁场中,初速度v 0与x 轴夹角θ=︒60,试分析计算:
(1)带电粒子从何处离开磁场?穿越磁场时运动方向发生的偏转角多大?
(2)带电粒子在磁场中运动时间多长?
分析:若带电粒子带负电,进入磁场后做匀速圆周运动,圆心为O 1,
粒子向x 轴偏转,并从A 点离开磁场。
若带电粒子带正电,进入磁场后做
匀速圆周运动,圆心为O 2,粒子向y 轴偏转,并从B 点离开磁场。
不论粒子带何种电荷,其运动轨道半径均为R mv Bq
=0。
如图2,有 带电粒子沿半径为R 的圆运动一周所用的时间为
(1)若粒子带负电,它将从x 轴上A 点离开磁场,运动方向发生
的偏转角θ1120=︒。
A 点与O 点相距:x R mv Bq ==330 若粒子带正电,它将从y 轴上B 点离开磁场,运动方向发生的偏转
角θ260=︒,B 点与O 点相距: y R mv Bq
==0 (2)若粒子带负电,它从O 到A 所用的时间为
若粒子带正电,它从O 到B 所用的时间为
2. 磁场方向不确定
磁感应强度是矢量。
如果题设只给出磁感应强度的大小,而未指出其方向,此时要考虑磁感应强度方向不确定而形成多解。
例2. 一质量为m ,电量为q 的负电荷在磁感应强度为B 的匀强磁场中绕固定的正电荷沿固定的光滑轨道做匀速圆周运动,若磁场方向垂直于它的运动平面,且作用在负电荷的电场力恰好是磁场力的三倍,则负电荷做圆周运动的角速度可能是( )
A. 4qB m
B. 3qB m
C. 2qB m
D. qB m
分析:依题中条件“磁场方向垂直于它的运动平面”,磁场方向有两种可能,且这两种可能方向相反。
在方向相反的两个匀强磁场中,由左手定则可知负电荷所受的洛仑兹力的方向也是相反的。
当负电荷所受的洛仑兹力与电场力方向相同时,根据牛顿第二定律可知
42
B q v m v R
=,得v BqR m =4
图 1 图2
此种情况下,负电荷运动的角速度为
当负电荷所受的洛仑兹力与电场力方向相反时,有
22
B q v m v R
=,得v BqR m =2 此种情况下,负电荷运动的角速度为
应选A 、C 。
3. 临界状态不惟一
带电粒子在洛仑兹力作用下飞越有界磁场时,由于粒子运动轨迹是圆弧状,因此穿越磁场的轨迹可能有多种情况。
例3. 如图3甲所示,A 、B 为一对平行板,板长为l ,两板距离为d ,板间区域内充满着匀强磁场,磁感应强度大小为B ,方向垂直纸面向里,一个质量为m ,带电量为+q 的带电粒子以初速v 0,从A 、B 两板的中间,沿垂直于磁感线的方向射入磁场。
求v 0在什么范围内,粒子能从磁场内射出? 分析:粒子射入磁场后受到洛仑兹力的作用,将做匀
速圆周运动,圆周运动的圆心在入射点的正上方。
要想使
粒子能射出磁场区,半径r 必须小于14
d (粒子将在磁场中转半个圆周后从左方射出)或大于某个数值(粒子将在磁场中运动一段圆弧后从右方射出)。
图3乙画出了两种
临界情况的轨迹示意图。
当粒子从左边射出时,若运动轨迹半径最大,则其圆心为图中O 1点,半径r d 14=。
因此粒子从左边射出必须满足r r ≤1。
由于r mv qB
=0 , 所以v rBq m 0= , 即v Bdq m 04≤ 当粒子从右边射出时,若运动轨迹半径最小,则其圆心为图中O 2点,半径为r 2。
由几何关系可得
因此粒子从右边射出必须满足的条件是
r r ≥2,即v d l qB dm
02244≥+() 所以当v Bdq m 04≤或v d l qB dm
02244≥+()时,粒子可以从磁场内射出。
4. 运动的重复性
带电粒子在部分是磁场,部分是电场的空间运动时,运动往往具有重复性,因而形成多解。
例4. 如图4所示,在x 轴上方有一匀强电场,场强为E ,方向竖直向下。
在x 轴下方有一匀强磁场,磁感应强度为B ,方向垂直纸面向里。
在x 轴上有一点P ,离原点的距离为a 。
现有一带电量+q 的粒子,质量为m ,从静止开始释放,要使粒子能经过P 点,其初始坐标应满足什么条件?(重力作用忽略不计)
图3
分析:要使粒子能经过P 点,其初始位置必须在匀强电场区域里。
由于没有明确粒子所在位置,讨论如下:
(1)若粒子从y 轴上由静止释放,在电场加速下进入磁场做半径为R 的匀速圆周运动。
由于粒子可能偏转一个、二个……半圆到达P 点,
故a nR n ==212(),… ①
设释放处距O 的距离为y 1,则有
q E y mv 1212= ② B q v m v R =2
③
由①、②、③式有
(2)若粒子在电场中的起点坐标为(x y ,2),依题意,有
当x a >,粒子不可能经过P 点;
当x a =,不论y 2取值如何,粒子均能经过P 点;
当x a <,则
a x nR n -==212(),…,
同理可得y B q a x n mE n 222
2812=-=()(),…。
图4。
