维纳滤波(最小均方滤波)
维纳滤波滤除同频的原理
维纳滤波滤除同频的原理1.引言1.1 概述维纳滤波是一种广泛应用于信号处理领域的滤波算法，其主要用途是去除同频干扰。
在实际应用中，我们经常会遇到不同信号混杂在一起的情况，即使这些信号具有相同的频率，但它们可能具有不同的相位和幅度。
这些干扰信号会对我们所关注的信号产生干扰，影响我们对信号的分析和处理。
维纳滤波通过对输入信号进行加权求和的方式，将干扰信号的影响最小化，使我们能够更准确地恢复出所关注的信号。
其基本原理是通过对干扰信号和所关注信号进行统计特性的估计，然后通过最小均方误差准则确定滤波器的加权系数，最终实现对干扰信号的抑制。
同频干扰是指具有相同频率的干扰信号对所关注的信号产生的干扰作用。
由于干扰信号与我们所关注的信号相同频率，传统的滤波器往往难以区分它们并准确滤除。
而维纳滤波通过对信号的统计特性进行建模，可以较好地区分干扰信号和所关注信号，并实现对同频干扰的有效抑制。
维纳滤波在通信领域、图像处理领域等都有广泛的应用。
在通信系统中，维纳滤波可以用于抑制同频干扰信号，提高系统的抗干扰性能，从而提高通信质量。
在图像处理领域，维纳滤波可以用于去除同频干扰造成的图像噪声，提高图像的清晰度和质量。
总之，维纳滤波是一种重要的信号处理技术，能够有效地滤除同频干扰。
通过对信号的统计特性进行建模和优化滤波器的参数，维纳滤波能够在干扰较严重的情况下提供较好的抑制效果。
在实际应用中，我们可以根据具体的信号特点和要求选择合适的维纳滤波算法，以达到更好的滤波效果。
1.2文章结构文章结构部分应描述整篇文章的组织结构和各个部分的内容。
在这篇文章中，可以按照以下方式来编写文章结构的内容：文章结构:本篇长文将按照以下结构组织内容:1. 引言1.1 概述1.2 文章结构: 本节将介绍文章的结构和各个部分的内容安排。
1.3 目的2. 正文2.1 维纳滤波的基本原理: 本节将介绍维纳滤波的基本原理，包括维纳滤波的数学模型和算法。
2.2 同频干扰的特点: 本节将探讨同频干扰的特点，包括其在信号处理中的影响和表现形式。
第2章 维纳滤波讲解
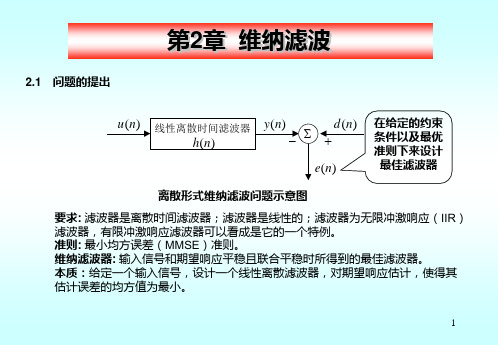
J min (w R 1p) T R ( w R 1p) J min (w w o ) T R (w w o )
（该式表明最佳权向量与最小均方误差的对应关系）
为使误差性能曲面的表达式简单化，定义权偏差向量为
T , w1 ,, w w w w o w0 M 1
结论：维纳滤波器所得最小均方误差等于期望响应的方差与滤波器输出方差的差值。
6
第2章 维纳滤波
2.4 横向滤波器的维纳解 2.4.1 横向滤波器的维纳-霍夫方程及其解
u (n)
u ( n 1)
z w0
1
z
1
u (n M 2)
z
1
u ( n M 1)
w1
wM 2
wM 1
u (n) ，当前输出 y (n) ，期望响应为 d (n) 滤波器的当前输入值： 重写维纳-霍夫方程
M 1 i 0
w
oi
r (i k ) p(k ) k 0,1,2,
定义横向滤波器的抽头输入 u(n), u(n 1),, u(n M 1) 的相关矩阵为Ｒ，则
p E[u(n)d (n)] [ p(0), p(1),, p(1 M )]T
则横向滤波器的维纳-霍夫方程式的矩阵表示形式为 Rwo p ，即维纳解为 w o R 1p 式中： w o [wo,0 , wo,1 ,, wo,M 1 ]T 是横向滤波器最优抽头权向量。
J J J J J , ,, 0 w w0 w1 wM 1
T
而 故可推出
J 2Rw(n) 2p
Rwo p ，与维纳-霍夫方程一致。
10
RLS、LMS及维纳滤波
图3.2 LMS算法下的误差信号以及滤波处理后的输出信号
图3.3维纳滤波的输入受干扰信号以及滤波输出信号
上图中红色是滤波后的输出信号，通过对比可以发现RLS算法下的输出信号比LMS算法下的输出信号要稳定的多。可以看到在RLS算法下的误差信号在迭代次数200次左右的时候变化较快较大，这是因为滤波器的阶数是200。可以看到在LMS算法下的输出信号在迭代次数200次以前是还没有达到收敛的，这是因为自适应滤波器的阶数是200阶，在200次之后，信号才是真正的滤波器的输出信号。由维纳滤波器的输出信号可以看到，在前200次，波形都是不稳定的，这是因为滤波器的阶数是200，在这之前还没有求得最佳的滤波器的系数，之后输出波形基本稳定，并且有效的抑制了噪声。但是基于维纳滤波器的求解过程中要求知道信号的统计特性，因此适用范围有限，并且计算自相关矩阵以及求其逆时需要占用极大的内存。
四
[1]张贤达．现代信号处理[M]．北京：清华大学出版社，2004．
[2]丁玉美．数字信号处理[M]．西安：西安电子科技大学出版社，2003．
[3]王正林，刘明．精通MATLAB 7[M]．北京：电子工业出版社，2006（7）．
五
课程设计
RLS、LMS及维纳滤波算法在噪声背景下的信号提取
院系：
专业：
学生姓名：
学号：
指导教授：
二○一三年十二月
一
噪声无处不在，在通信领域，噪声干扰是屡见不鲜的事情。前人做了很多从噪声中提取信号的相关工作。在本次实验中，主要是运用经典的最小均方误差方法，使用的是LMS准则，以及最小二乘方法，使用的是RLS准则，对这两种方法的降噪效果进行对比和分析。
3
最优估计之维纳滤波
设计目的：滤除按照统计方式干扰信号的噪声。
9
连续系统维纳滤波器的信息流程图 W ( s) Y(t)
＋ －
X(t)
＋ ＋
Z(t)
G(s)
e( t ) ˆ t X
V(t)
X(t) —— 有用随机信号； V(t) —— 随机干扰信号； G(s) —— 实际滤波器传递函数； W(s) —— 理想滤波器传递函数； ˆ t —— G(s) 的真实输出信号； X Y(t) —— W(s) 的理想输出信号。
ˆ t e(t ) Y (t ) X
W(s) = 1 ------ 滤波问题 s 预测问题 W ( s) e-----W(s) = s ------ 微分平滑问题
10
什么是维纳滤波
目的：设计传递函数G(s)，使e(t) 尽可能小。 ˆ t X (t ) X ˆ t 误差信号： e(t ) Y (t ) X
为求极值：
1 T 2 E e (t ) lim [ X ( t ) h ( ) z ( t ) d ] dt min 0 T 2T T 采用泛函变分方法。定 义泛函： 滤波器脉冲响应 h( ) 的函数， 2
定义在集合 h( ) 上的范函。
1 J [h( )] lim T 2T
S zx ( ) G ( j ) S zz ( )
G( j ) h(t )e jt dt
0
Rzx ( ) e j d Rzz ( ) e j d16
另一方面，可得：
ˆ X t h( ) Z (t )d
8
维纳滤波的特点
维纳滤波
维纳滤波7.2 维纳滤波从连续的(或离散的)输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波，而相应的装置称为滤波器。
根据滤波器的输出是否为输入的线性函数，可将它分为线性滤波器和非线性滤波器两种。
滤波器研究的一个基本课题就是:如何设计和制造最佳的或最优的滤波器。
所谓最佳滤波器是指能够根据某一最佳准则进行滤波的滤波器。
20世纪40年代，维纳奠定了关于最佳滤波器研究的基础。
即假定线性滤波器的输入为有用信号和噪声之和，两者均为广义平稳过程且知它们的二阶统计特性，维纳根据最小均方误差准则(滤波器的输出信号与需要信号之差的均方值最小)，求得了最佳线性滤波器的参数，这种滤波器被称为维纳滤波器。
在维纳研究的基础上，人们还根据最大输出信噪比准则、统计检测准则以及其他最佳准则求得的最佳线性滤波器。
实际上，在一定条件下，这些最佳滤波器与维纳滤波器是等价的。
因而，讨论线性滤波器时，一般均以维纳滤波器作为参考。
维纳滤波理论用于解决最小均方误差下的线性滤波问题。
设接收到(或观测到)的信号为随机信号(7-1)其中s(t)是未知的实随机信号，n(t)是噪声。
要设计的线性滤波器，其冲击响应为h(t, τ)，输入为x(t)，输出为，即(7-2)令为估计误差。
冲击响应h(t, τ)按最小均方误差准则确定，即h(t, τ)必须满足使(7-3)达到最小。
根据最小均方误差估计的正交条件，有以下关系成立(7-4)令(7-5)(7-6)则有(7-7)上述方程通常称为非平稳随机过程条件下的维纳-霍甫(Wiener-Kolmogorov)积分方程。
特别当x(t)，s(t)均为广义(或宽)平稳随机信号，而滤波器是线性时不变系统的情况下，x(t)与s(t)必为联合平稳，式(7-7)可写为(7-8)令，，则有(7-9)此处，“*”号表示卷积，对上式两边取Fourier变换，可得(7-10)(7-11)对于因果线性系统，有(7-12)采用完全相同的分析方法，推得因果平稳维纳-霍甫积分方程如下(7-13)(7-14)其中，表示的零、极点位于，表示的零、极点位于。
第八章 维纳滤波
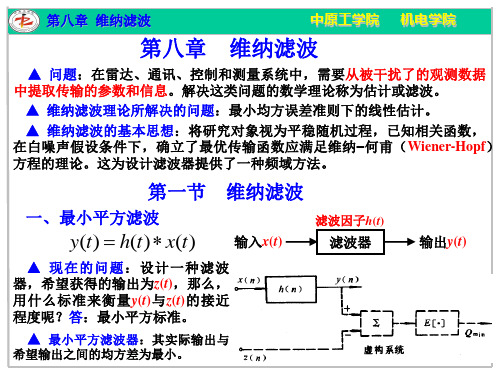
rxx(λ-k)
rzx(λ)
第八章 维纳滤波 维纳-何甫积分方 程式(离散形式)：
中原工学院
N xx
机电学院
h(k )r
k 0
N
( k ) rzx ( ) 或 h(k )rxx (k ) rzx ( )
k 0
自相关函数为偶函数
▲ 维纳滤波器 如果已知x(n)与所要求的输出信号z(n)，则当x(n)的自相关函 数和z(n)与x(n)的互相关函数为已知时，求解维纳-何甫方程，即可求得满足均 方误差最小的滤波因子h(n)。这就是按照最小平方准则设计的线性滤波系统， 它是一个最佳系统，通常称为维纳滤波器。 这是一个对 称 矩阵 。 卷积形式：
第八章 维纳滤波
中原工学院
机电学院
第二节
反滤波
一、回声鸣震现象及反滤波
问题的提出：在某些情况下（例如，在大礼堂内演讲，由于墙壁多次反射， 而造成回声交混，形成一片轰鸣声，使人们听不清讲话内容）所录取的信号， 可认为是原始信号经过几个物理系统（信号传输的路径或通道）作用的结果， 或者看成是源信号经过几个物理滤波器以串联形式滤波的结果。这时，采用 反滤波方法可以使真正源信号从干扰中恢复出来。
n n n n
期望输出s(n)与输入x(n)的互相关函数为
n n
rsx (k ) s(n k ) x(n) s(n k )[s(n) n(n)] rss (k )
如果以 Rss(ejω) 和 Rnn(ejω) 分别表示 rss(k) 和 rnn(k) 的频谱，即分别为 s(n) 和 n(n) 的功率谱，则在对维纳滤波的时间范围不加限制的情况下，由式H(ejω)=Rzs(ejω)/ Rxx(ejω)，可以得到维纳滤波器的频率响应应为：
IIR滤波FIR滤波及维纳滤波简介、程序及仿真结果
IIR 滤波器、FIR 滤波器与维纳滤波器所谓数字滤波器，是指输入、输出均为数字信号，通过一定运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分的器件。
数字滤波器从实现的网络结构或者从单位脉冲响应分类，可以分为无限脉冲响应（IIR ）滤波器和有限脉冲响应（FIR ）滤波器。
它们的系统函数分别为：1.1n N n z n h z H --=∑=10)()( 1.21.1中的H(z)成为N 阶IIR 滤波器，1.2中的H(z)称为(N-1)阶FIR 滤波器函数，这两种类型的设计方法有很大的区别。
IIR 数字滤波器的设计既可以从模拟滤波器的设计入手来进行，也可以直接利用指标参数，通过调用滤波器设计子程序或函数来进行。
可以利用脉冲响应不变法来设计IIR 数字低通滤波器，按照技术要求设计一个模拟低通滤波器，得到模拟低通滤波器的传输函数，再按一定的转换关系将传输函数转换成数字低通滤波器的系统函数H(z)。
设模拟滤波器的传输函数是s H a ()，相应的单位冲激响应是)(t h a ，对)(t h a 进行等间隔采样，采样间隔为T ，得到)(nT h a ，将h(n)= )(nT h a 作为数字滤波器的单位取样响应，那么数字滤波器的系统函数便是h(n)的z 变换，因此脉冲响应不变法是一种时域上的转换方法，它使h(n)在采样点上等于)(t h a∑=-=Ni iia s s A s H 1)( 1.3 ∑=--=Ni T s iz eA z H i 111)( 1.4 将s H a ()在s 平面上沿虚轴按照周期2pi/T 延括后，再按标准映射关系sT e z =，映射到z 平面上，就得到了H(z)。
脉冲响应不变法的优点是频率坐标变化时线性的，如果不考虑频率混叠现象，用这种方法设计的数字滤波器会很好的重现模拟滤波器的频率特性。
以下为用matlab 仿真的一个IIR 低通滤波器： % IIR Lowpass Use Butterworth % copyright by Etual clear;fs=20;fpass=4;fstop=5;∑∑=-=--=Nk kk Mk k k z a z b z H 101)(Ap=0.5;As=10;wp=2*pi*fpass/fs;ws=2*pi*fstop/fs;omegap=tan(wp/2);omegas=tan(ws/2);ep=sqrt(10^(Ap/10)-1);es=sqrt(10^(As/10)-1);N=ceil(log(es/ep)/log(omegas/omegap));omega0=omegap/ep^(1/N);K=floor(N/2);for i=1:Ktheta(i)=pi*(N-1+2*i)/(2*N);endfor i=1:KG(i)=omega0^2/(1-2*omega0*cos(theta(i))+omega0^2);endfor i=1:Ka1(i)=2*(omega0^2-1)/(1-2*omega0*cos(theta(i))+omega0^2);endfor i=1:Ka2(i)=(1+2*omega0*cos(theta(i))+omega0^2)/(1-2*omega0*cos(theta(i))+omeg a0^2);endif K<(N/2)G0=omega0/(omega0+1);a0=(omega0-1)/(omega0+1);endw=0:pi/300:pi;Hw2=1./(1+(tan(w/2)/omega0).^(2*N));plot(w/pi,Hw2);grid;图一IIR滤波器频谱图IIR数字滤波器能保留一些典型模拟滤波器优良的幅度特性，但设计中只考虑了幅度特性，没考虑相位特性，所设计的滤波器相位特性一般是非线性的。
维纳滤波器图像处理
维纳滤波器及其在图像处理中的应用摘要图像由于受到如模糊、失真、噪声等的影响，会造成图像质量的下降，形成退化的数字图像。
退化的数字图像会造成图像中的目标很难识别或者图像中的特征无法提取，必须对其进行恢复。
所谓图像复原就是指从所退化图像中复原出原始清晰图像的过程。
维纳波是一种常见的图像复原方法，该方法的思想是使复原的图像与原图像的均方误差最小原则恢复原图像。
本文进行了对退化图像进行图像复原的仿真实验，分别对加入了噪声的退化图像、运动模糊图像进行了维纳滤波复原，并给出了仿真实验效果以及结果分析。
实验表明退化图像在有噪声时必须考虑图像的信噪比进行图像恢复，才能取得较好的复原效果。
关键词：维纳滤波；图像复原；运动模糊；退化图像AbstractDue to factors such as blurring distorting and noising, image quality deteriorated and led to degenerated digital images which is getting harder to discern the target image or extract the image features. Wiener Filter is often used to recover the degraded image. The principle of the method expects to minimize the mean square error between the recovered image and original image. This paper carried out a restoration simulation experiments on degraded image,restoration of motion blurred images, and the result shows, SNR noise of the autocorrelation function for image restoration must be taken into consideration when restoring degraded images in a noise. Key words:Wiener Filter; motion blurred;degraded image;image restoration概述图像在形成、传输和记录的过程中都会受到诸多因素的影响,所获得的图像一般会有所下降，这种现象称为图像“退化”。
维纳维纳滤波实现模糊图像恢复知识讲解
维纳维纳滤波实现模糊图像恢复维纳滤波实现模糊图像恢复摘要维纳滤波器是最小均方差准则下的最佳线性滤波器，它在图像处理中有着重要的应用。
本文主要通过介绍维纳滤波的结构原理，以及应用此方法通过MATLAB函数来完成图像的复原。
关键词：维纳函数、图像复原一、引言在人们的日常生活中，常常会接触很多的图像画面，而在景物成像的过程中有可能出现模糊，失真，混入噪声等现象，最终导致图像的质量下降，我们现在把它还原成本来的面目，这就叫做图像还原。
引起图像的模糊的原因有很多，举例来说有运动引起的，高斯噪声引起的，斑点噪声引起的，椒盐噪声引起的等等，而图像的复原也有很多，常见的例如逆滤波复原法，维纳滤波复原法，约束最小二乘滤波复原法等等。
它们算法的基本原理是，在一定的准则下，采用数学最优化的方法从退化的图像去推测图像的估计问题。
因此在不同的准则下及不同的数学最优方法下便形成了各种各样的算法。
而我接下来要介绍的算法是一种很典型的算法，维纳滤波复原法。
它假定输入信号为有用信号与噪声信号的合成，并且它们都是广义平稳过程和它们的二阶统计特性都已知。
维纳根据最小均方准则，求得了最佳线性滤波器的的参数，这种滤波器被称为维纳滤波。
二、维纳滤波器的结构维纳滤波自身为一个FIR或IIR滤波器，对于一个线性系统，如果其冲击响应为()n h，则当输入某个随机信号)(nx时，Y(n)=∑-n )()(mnxmh式（1）这里的输入)()()(n v n s n x += 式（2）式中s(n)代表信号，v(n)代表噪声。
我们希望这种线性系统的输出是尽可能地逼近s(n)的某种估计，并用s^(n)表示，即)(ˆ)(y n sn = 式（3） 因而该系统实际上也就是s(n)的一种估计器。
这种估计器的主要功能是利用当前的观测值x(n)以及一系列过去的观测值x(n-1),x(n-2),……来完成对当前信号值的某种估计。
维纳滤波属于一种最佳线性滤波或线性最优估计，是一最小均方误差作为计算准则的一种滤波。
反卷积、低通滤波后的反卷积和维纳滤波python实现
反卷积、低通滤波后的反卷积和维纳滤波python实现反卷积（Deconvolution）是一种图像处理技术，用于恢复由于模糊或其他失真过程导致的图像质量下降。
低通滤波后的反卷积和维纳滤波是两种常用的去模糊方法。
下面分别介绍这三种方法的Python实现。
1. 反卷积反卷积的基本思想是将模糊图像与模糊核进行卷积运算，得到原始图像。
在Python中，可以使用OpenCV库中的deconvolve函数实现反卷积。
pythonimport cv2import numpy as np# 读取模糊图像和模糊核blurred_image = cv2.imread('blurred_image.jpg', cv2.IMREAD_GRAYSCALE)blur_kernel = np.array([[1, 4, 6, 4, 1], [4, 16, 24, 16, 4], [6, 24, 36, 24, 6], [4, 16, 24, 16, 4], [1, 4, 6, 4, 1]]) / 256 # 使用OpenCV的deconvolve函数进行反卷积deconv_image = cv2.deconvolve(blurred_image, blur_kernel)# 显示原始图像、模糊图像和反卷积后的图像cv2.imshow('Original Image', blurred_image)cv2.imshow('Blurred Image', deconv_image)cv2.waitKey(0)cv2.destroyAllWindows()2. 低通滤波后的反卷积低通滤波后的反卷积是在对模糊图像进行低通滤波后，再进行反卷积操作。
这里我们使用高斯滤波作为低通滤波器。
在Python中，可以使用OpenCV库中的GaussianBlur和deconvolve函数实现低通滤波后的反卷积。
维纳滤波与图像去噪
维纳滤波与图像去噪摘要首先选取对图像降噪比较有代表性的维纳滤波，在加有高斯噪声、椒盐噪声和乘性噪声的图像上进行处理，再将维纳滤波与中值滤波和均值滤波抑制噪声的效果进行比较，通过实验仿真及其处理效果，详细分析维纳滤波在图像去噪中的特点及各自作用的利弊。
关键词维纳滤波；中值滤波；均值滤波；图像去噪Wiener filtering and image denoisingLIMeng , ZHAOQi(Xi' an University of Posts and Telecommunications,School of communication and information engineering ，Xi ' an710000. Chin)Abstract: Select the first is a representative of wiener filtering for image noise reduction with gauss no ise and salt and pepper no ise and multiplicative no ise of image process ing, the n wie ner filtering and median filtering and mean filtering noise effect comparison, through the experimental simulation and the treatment effect, detailed analysis of wiener filtering in image denoising, the characteristics and the pros and cons of each role.Keywords: Wiener filtering,Median filtering,Mean filtering,Image denoising0引言图像在成像、传输、转换或存储的过程中会受到各种随机干扰信号即噪声的影响，从而会使画面变得粗糙、质量下降、特征淹没。
维纳滤波
表了一篇关于集合论的论文，将关系的理论 简化为类的理论的论文，在数理逻辑的发展 中占据一席之地。1919年维纳到麻省理工学 院数学系任教直至退休。1932年任正教授。
不満12岁中学毕业。 提出维纳滤波理论，开创了维纳信息论，创
立控制论。第二次世界大战期间，为了解决
第二章 维纳(Wiener)滤波
维纳生平
18岁获哈佛大学哲学博士学位。先后留学英 国剑桥大学和德国哥丁根大学，在罗索、哈 代、希尔伯特等著名数学家指导下研究逻辑 和数学。
罗索鼓励维纳选择把数学和物理、工程学结 合起来的研究方向。
1913年19岁维纳在＜剑桥哲学学会会刊＞发
N.维纳 （Norbert Wiener )
维纳滤波不能实时处理，其最大缺点是： 仅适用于一维平稳随机信号。这是由于 采用频域设计法所造成的。
因此，人们逐渐转向在时域内直接设计 最佳滤波器的方法。
11、维纳滤波器的应用
（1）通信的信道均衡器 （2）系统辨识 （3）最优线性预测
（1）通信的信道均衡器
在通信系统中，为了在接收器端补偿信 道传输引入的各种畸变，在对接收信号 进行检测之前，通过一个滤波器对信道 失真进行校正，这个滤波器称为信道均 衡器。
防空火力控制和雷达噪声滤波问题，1942年
建立维纳滤波理论。
本章内容
维纳滤波器的时域解 维纳滤波器的Z域解 维纳滤波器的预测器
第一节 引言
1、线性最佳滤波
滤波理论是估计理论的一个重要组成部分。 最佳线性估计理论：维纳滤波和卡尔曼滤波
理论，即：在线性滤波的前提下，以最小均 方误差为最佳准则。 采用最小均方误差准则的原因：其理论分析 比较简单，且可得到解析的结果。
5-1 维纳滤波与卡尔曼滤波---FIR滤波器
W ( z ) w(n) z n
n 0 p 1
ˆ (n) d (n) d
ˆ (n) w(k ) x(n k ) d
k 0 p 1
2．设观测信号x(n)为一高斯-马尔柯夫信号d(n)与其不 相关的白噪声v(n)的线性叠加。试设计二阶维纳一 步预测器。已知d(n)和v(n)的自相关函数分别为
rd (k ) (0.9)|k|
2
rv (k ) 0.64 (k )
作 业：
3. 设有噪声观测数据 x(n)=d(n)+v(n)，噪声v(n)是零均值 方差为1.05的白噪声，且信号和噪声不相关。信号 d(n)是AR(1)过程，由差分方程 d(n)=d(n-1)+w(n)产生 ，其中w(n)是零均值方差为0.182的白噪声。
最小正交性原理或投影原理1862fir维纳滤波器信号的线性最小均方估计称为wienerhopf方程1962fir维纳滤波器信号的线性最小均方估计2062fir维纳滤波器信号的线性最小均方估计由此设计的w将使均方误差达到最小均方误差dxdx2162fir维纳滤波器信号的线性最小均方估计若fir维纳滤波器写成非因果形式
预测: 取d(n)=x(n+D),且W(z)是因果的,则维纳滤 波器变成线性预测器，它由d(n)及其过去值来 预测估计x(n+D)。
na
n
n
nD
nb
n na
ˆ (n) x(n D) d x(k )w(n k ) w(k ) x(n k )
k na k 0
维纳滤波的python实现-概述说明以及解释
维纳滤波的python实现-概述说明以及解释1.引言1.1 概述概述部分的内容可以如下撰写：引言部分旨在介绍本文将要讨论的主题- 维纳滤波。
维纳滤波是一种常用的信号处理技术，广泛应用于各个领域，如图像处理、语音处理、雷达、通信等。
它是由卡尔·维纳于20世纪40年代提出的，被认为是非常优秀的信号处理方法之一。
维纳滤波的主要目的是通过消除或减弱信号中的噪声，以便更好地识别和分析感兴趣的信号成分。
噪声是信号处理中常见的问题之一，它在信号中引入了不必要的干扰和误差。
维纳滤波通过将输入信号与某种滤波器进行卷积运算，以抑制噪声并恢复信号的本来面貌。
在本文中，我们将通过使用Python语言来实现维纳滤波。
Python作为一种功能强大且易于使用的编程语言，被广泛应用于各个领域的科学计算和数据处理任务中。
通过Python，我们可以利用丰富的库和工具来实现维纳滤波算法，并进行各种实际应用的演示和验证。
本文的结构如下所示：首先我们将介绍维纳滤波的概念和原理，包括滤波器的设计思路和数学基础。
然后，我们将详细阐述如何使用Python 编程语言来实现维纳滤波算法，并给出相应的代码示例和详细的解释。
最后，我们将探讨维纳滤波的应用场景，介绍一些实际问题中使用维纳滤波的案例，并讨论可能的改进和扩展。
通过本文的阅读，读者将了解到维纳滤波的基本原理和使用方法，并有能力应用维纳滤波算法解决实际的信号处理问题。
同时，通过Python 的实现，读者还能够进一步探索和扩展维纳滤波算法，发现更多有趣的应用和研究方向。
希望本文能为读者提供一些关于维纳滤波和Python编程的启示，促进对信号处理领域的深入理解和探索。
1.2 文章结构本文主要介绍了维纳滤波算法在Python中的实现。
文章分为引言、正文和结论三个部分。
引言部分概述了本文的目的和意义，介绍了维纳滤波算法的概念，并概述了本文的结构。
正文部分分为两个小节。
首先，2.1节介绍了维纳滤波的概念，包括其基本原理和主要特点。
维纳滤波,最小二乘滤波,自适应滤波认知
主题：维纳滤波、最小二乘滤波、自适应滤波认知一、维纳滤波1. 维纳滤波是一种经典的线性滤波方法，它是以诺伯特·维纳（Norbert Wiener）命名的，主要用于信号和图像处理领域。
2. 维纳滤波是一种频域滤波方法，它利用信号和噪声的功率谱以及它们之间的相关性来进行滤波处理。
3. 维纳滤波通过最小化信号和噪声的均方误差来实现信号的恢复，能够有效地抑制噪声并增强信号的特征。
4. 维纳滤波的优点是对信噪比较低的图像有很好的处理效果，但缺点是对信噪比较高的图像处理效果较差。
二、最小二乘滤波1. 最小二乘滤波是一种基于统计原理的滤波方法，它通过对信号进行线性估计来实现滤波处理。
2. 最小二乘滤波与维纳滤波类似，都是以最小化均方误差为目标，但最小二乘滤波是基于时域的方法。
3. 最小二乘滤波将信号和噪声视为随机过程，利用信号和噪声的统计特性来进行滤波处理，能够提高信号的估计精度。
4. 最小二乘滤波的优点是对于信号和噪声的统计特性要求不高，处理效果比较稳定，但缺点是需要较强的计算能力和较大的样本量。
三、自适应滤波1. 自适应滤波是基于滑动窗口的滤波方法，它根据信号的局部特性动态调整滤波参数，适用于信号和噪声变化较大的场景。
2. 自适应滤波主要包括自适应均值滤波、自适应中值滤波、自适应加权滤波等不同类型，根据不同的信号特征选择相应的滤波方法。
3. 自适应滤波能够有效地抑制信号中的噪声和干扰，同时保留信号的边缘和细节特征，具有较好的空间适应性。
4. 自适应滤波的优点是能够根据信号的实际情况自动调整滤波参数，适用性广泛；但缺点是计算量大，实时性较差。
维纳滤波、最小二乘滤波和自适应滤波都是常用的信号和图像处理方法，它们各自具有特定的优点和适用场景。
在实际应用中，可以根据信号的特性和处理需求选择合适的滤波方法，以达到更好的处理效果。
对于不同的滤波方法，还可以结合其他技术手段进行改进和优化，以满足不同场景的需求。
维纳滤波（最小均方滤波）
维纳滤波（最⼩均⽅滤波）维纳滤波（最⼩均⽅滤波）避免逆滤波固有的弊端的另⼀种⽅法就是寻找图像的⼀种估值，使得和之间的均⽅误差最⼩。
均⽅误差最⼩准则是由维纳（Wiener）在1949年⾸先提出并⽤来对⼀维平稳时间序列进⾏估值。
因此这种⽅法被称为维纳滤波，也被称为最⼩均⽅误差滤波。
设、、分别为退化图像、原始图像和噪声，并设他们都是均匀随机的，且噪声的均值为零，并与图像不相关。
可以得到（3-6）式中，为维纳滤波器的点扩散函数。
按照均⽅误差最⼩准则，应该满⾜（3-7）为最⼩。
我们把称为已知时的线性最⼩均⽅估计。
将(2.2)带⼈(2.1)式，得到（3-8）可以证明当（3-9）时，式（3-7）取最⼩值。
经过证明可以得到维纳滤波的转移函数为（3-10）其中为噪声功率谱，为图像功率谱。
由式(2.5)可以看出，当没有噪声时，有，维纳滤波器就可以简化的看成是逆滤波器。
在有噪声的情况下，维纳滤波也⽤信噪功率⽐作为修正函数对逆滤波器进⾏了修正，但它在均⽅误差最⼩的意义上提供最佳恢复。
通常将噪声假设为⽩噪声，即噪声功率谱为常数，若在频谱空间上⾼频区下降⽐快得多，这种假设就近似正确。
于是可以认为常数（3-11）如果噪声时各态历经的，可以⽤⼀幅噪声图像进⾏计算从⽽求得，图像功率谱则可利⽤与原始图像统计性质相同的⼀类图像来确定。
如果不知道有关随机场的统计性质，也常⽤下式近似计算转移函数：（3-12）K是根据信噪⽐的某种先验知识来确定的常数。
下⾯是维纳滤波的复原效果：（a）原图（b）退化（c）复原图3-3 维纳滤波复原实验。
维纳滤波
维纳滤波维纳滤波又称为最小均方误差滤波，是由N.Wiener 在1942年提出的一种线性图像复原方法。
它的原理是对原始图像假设为f ，找出它的一个估计值，使得f 和估计图像之间的均方误差值最小，也就是实现了图像的去噪复原。
其误差度量的公式如式1.13所示(){}22e E f f =- （1.15） 我们假设噪声和图像没有任何关系，其中任意一个有零均值而且估计的灰度值是退化图像灰度级的线性函数。
那么在这样的情况下，式1.13中误差函数的最小值在频域中可以用下面的式子来表示：()()()()()()()22,1ˆ,,,,,/,f H u v F u v G u v H u v H u v S u v S u v η⎡⎤⎢⎥=⎢⎥+⎢⎥⎣⎦（1.16） 我们在针对运动中的模糊图像去噪复原过程中，维纳滤波对于反滤波法中H(u,v)零点的噪声放大问题完美的可以进行解决，但是也存在着一定的缺陷，例如无法消除图像模糊而导致信息不完整而造成的边缘误差。
维纳去卷积算法的设计在基本点上就决定了会存在着一定的局限性[16]：① 采用均方误差作为判断图像复原程度的标准，在数学计算上是较好的算法，但会导致我们所得的复原图像对于人类视觉上面的图像存在着一定的出入。
我们用标量的方式找到最好的滤波器。
人们希望能够找到滤除传统感染信号噪声的滤波器，这样维纳滤波器产生了。
② 对于退化函数具有空间可变、点扩散等性质的时候，经典的维纳滤波处理效果差强人意。
③ 对于非平稳的图像，如具有被边缘分开的平坦区域、噪声与图像局部灰度值相关等，维纳滤波无法较好的保证其滤波的效果。
假定线性滤波器的输入是有用信号和噪声的和，两者均为广义平稳过程且知它们的二阶统计特性，维纳方程是根据最小均方误差准则来求得最佳线性滤波器的参数，这种滤波器被称为维纳滤波器[5]。
实现维纳滤波的要求是：输入过程是广义平稳的；输入过程的统计特性是已知的。
维纳滤波器的优点是适合于更广泛的去噪滤波器，无论是在平稳随机过程或离散过程的都可应用。
matlab 维纳滤波代码
一、维纳滤波简介维纳滤波是一种经典的信号处理算法，主要用于图像去噪和恢复。
它基于最小均方误差准则，通过滤波器对输入信号进行处理，以减少噪声的影响并尽可能恢复原始信号的特征。
在 MATLAB 中，可以使用内置的函数或自行编写代码来实现维纳滤波。
二、维纳滤波的数学模型1. 维纳滤波的基本原理是利用频域上的滤波器对信号进行处理，其数学模型可以表示为：$$G(u,v) = H(u,v)F(u,v) + N(u,v)$$其中，$G(u,v)$ 是观测到的带噪声的图像的频谱，$H(u,v)$ 是系统的频率响应，$F(u,v)$ 是原始图像的频谱，$N(u,v)$ 是添加到图像中的噪声的频谱。
2. 根据维纳滤波的原理，可以通过以下公式计算维纳滤波器 $W(u,v)$： $$W(u,v) =\frac{1}{H(u,v)}\frac{|H(u,v)|^2}{|H(u,v)|^2+\frac{S_N(u,v)}{S_F(u,v )}}$$其中，$S_N(u,v)$ 是噪声功率谱，$S_F(u,v)$ 是原始图像功率谱。
三、MATLAB 中的维纳滤波函数MATLAB 提供了丰富的信号处理工具箱，其中包括了维纳滤波函数，可以方便地对图像进行去噪和恢复操作。
1. 在 MATLAB 中使用维纳滤波可以通过以下函数实现：```matlabJ = wiener2(I,[m n],noise_var);```其中，I 是输入图像，[m n] 是局部窗口的大小，noise_var 是噪声的方差。
2. 除了 wiener2 函数外，MATLAB 还提供了 imnoise 函数用于向图像中添加指定类型的噪声，可以配合维纳滤波进行实验和比较。
四、自行编写维纳滤波代码除了使用 MATLAB 提供的函数外，我们还可以根据维纳滤波的数学原理自行编写代码来实现算法。
1. 我们需要读取原始图像并将其转换为频域表示：```matlabI = imread('original.png');F = fft2(double(I));F = fftshift(F);```2. 计算噪声功率谱和原始图像功率谱：```matlabN = abs(fftshift(F_noise)).^2;S_f = abs(F).^2;```3. 接下来，根据维纳滤波的公式计算滤波器：```matlabWiener = (1./H).*(abs(H).^2./(abs(H).^2+(N./S_f)));```4. 将滤波器应用到输入图像的频谱上，并进行逆变换得到恢复图像： ```matlabF_restored = F .* Wiener;I_restored = ifft2(ifftshift(F_restored));```五、维纳滤波的应用场景维纳滤波在数字图像处理领域有着广泛的应用，尤其适用于受到高斯噪声影响的图像去噪和恢复。
914762-数字图像处理-第四章 图像复原-第4讲有约束复原-维纳滤波和约束最小平方滤波
M 1 N 1
(s) r 2 rTr
r2 (x, y)
x0 y0
在给定精度因子a的情况下，若调整s使得下式成立 ，
则认为恢复达到了要求
n 2 a≤ r 2 ≤ n 2 a
14
4.3 图像复原
噪声的特性：
若对噪声图像具有先验知识，则可求其均值和方差
1 M 1 N 1
mn
MN
x0
n(x, y)
y0
2 n
1 MN
M 1 N 1
[n(x,
x0 y0
y)
mn ]2
？ 实际上只要知道其均值和方差即可
n
2
MN (mn2
2 n
)
15
4.3 图像复原
约束最小平方滤波法恢复图像的 步骤：
(1) 根据先验知识，计算||n||2; 给s赋一初值；
(2)
R(u,v)
s | P(u, v) |2
G(u, v)
(7) 若 n 2 a ≤ r 2 ≤ n 2 a 成立，则停止迭代，并计算 Fˆ (u,v)
fˆ (x, y)
16
4.3 图像复原
例4.5采用约束最小平方滤波器法，对例4.4中相同的退化
图像进行恢复。
解答：模拟离焦模糊的高斯模板参数：方差为5 pixel，模
板是7x7 pixel的方模板。高斯噪声的均值为零，方差为 0.001。图 (a)为原始图像，图(b)是含噪声的离焦模糊图像。 根据公式计算，噪声的功率是409.6 . 图 (d)是用偏小的噪声功率值和的值(||n||2=205，σ =3)，图 (e) 是用偏大的噪声功率值和的值(||n||2=650，σ =7)分别恢复 的情况；s的初值取0.001，其迭代时的步长取0.01，精度因 子a=0.1||n||2。 图 (f)是采用真实的点扩散函数，和噪声功率(||n||2=409.6，σ =5) 时 迭 代 求 解 的 结 果 ， 精 度 因 子 a=0.1||n||2 ， s 的 初 值 取 0.001，其迭代时的步长取0.01，迭代终止时s= 0.1201。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（3-10）
其中������������������ (������, ������ )为噪声功率谱，������������������ (������, ������)为图像功率谱。由式(2.5)可以看出， 当没有噪声时，有P u, v = 1/H(u, v)，维纳滤波器就可以简化的看成是逆滤波 器。 在有噪声的情况下， 维纳滤波也用信噪功率比作为修正函数对逆滤波器进行 了修正，但它在均方误差最小的意义上提供最佳恢复。 通常将噪声假设为白噪声，即噪声功率谱������������������ (������, ������ )为常数，若������������������ (������, ������)在频 谱空间上高频区下降比������������������ (������, ������ )快得多，这种假设就近似正确。于是可以认为 ������������������ ������, ������ = ������������������ 0,0 = 常数（3-11） 如果噪声时各态历经的，可以用一幅噪声图像进行计算从而求得������������������ 0,0 ，
∞ ������(������ , ������ )������(������ −∞
− ������, ������ − ������ )������������������������（3-6）
式中，������(������, ������)为维纳滤波器的点扩散函数。按照均方误差最小准则，������ ^ x, y 应该满足 ������ 2 = ������ ������ ������, ������ − ������ ^ x, y
∞ ������(������ , ������)������(������ −∞ ∞ ������(������ , ������)������(������ −∞
− ������ , ������ − ������)������������������������
2
（3-8）
− ������ , ������ − ������)������������������������
ቤተ መጻሕፍቲ ባይዱ
（3-12） ������ ,������ |2 +������
K 是根据信噪比的某种先验知识来确定的常数。 下面是维纳滤波的复原效果：
（a）原图（b）退化
（c）复原 图 3-3 维纳滤波复原实验
维纳滤波（最小均方滤波）
避免逆滤波固有的弊端的另一种方法就是寻找图像f x, y 的一种估值 ������ ^ x, y ，使得f x, y 和������ ^ x, y 之间的均方误差最小。均方误差最小准则是由维纳 （Wiener）在 1949 年首先提出并用来对一维平稳时间序列进行估值。因此这种 方法被称为维纳滤波，也被称为最小均方误差滤波。 设g x, y 、f x, y 、n x, y 分别为退化图像、原始图像和噪声，并设他们都是 均匀随机的，且噪声的均值为零，并与图像不相关。可以得到 ������ ^ x, y =
2
= 0（3-9）
时，式（3-7）取最小值。 经过证明可以得到维纳滤波的转移函数为 P u, v = ������ (������ ,������) |������
1 |������ ������ ,������ |2 ������ ,������ |2 + ������������������ (������ ,������ )/������������������ (������ ,������ )
2
（3-7）
为最小。 我们把������ ^ x, y 称为已知g x, y 时f x, y 的线性最小均方估计。 将(2.2) 带人(2.1)式，得到 ������ 2 = ������ ������ ������, ������ − 可以证明当 ������ 2 = ������ ������ ������, ������ −
图像功率谱������������������ (������, ������ )则可利用与原始图像统计性质相同的一类图像来确定。如果 不知道有关随机场的统计性质，也常用下式近似计算转移函数： P u, v = ������ (������ ,������) |������
1 |������ ������ ,������ |2