一元二次方程方程专项训练 ---------动点问题
一元二次方程应用题动点问题
拓展与创新
例3如图，Rt△ABC中，∠B=90°，AC=10cm，BC=6cm，现有两个
动点P、Q分别从点A和点B同时出发，其中点P以2cm/s的速度，沿 AB向终点B移动；点Q以1cm/s的速度沿BC向终点C移动，其中一点 到终点，另一点也随之停止．连接PQ．设动点运动时间为x秒 （1）用含x的代数式表示BQ、PB的长度；
现在您正浏览在第12页，共14页。
课外延伸
4．有一边为5cm的正方形ABCD和等腰三角形PQR，PQ＝PR
＝5cm，QR＝8cm，点B、C、Q、R在同一直线l上，当C、Q
两点重合时，等腰三角形PQR以1cm/s的速度沿直线l按箭头方
向匀速运动，
（1）t秒后正方形ABCD与等腰三角形PQR重合部分的面积为5
新知探究
Rt△ABC中,AB=BC=12cm,动点P从A点出发,以2cm/s的速 度沿AB向B移动,通过点P作PR//BC,PQ//AC，求P出发几 秒时,四边形PQCR的面积等于20cm2?
∵0＜x＜6
2X
现在您正浏览在第5页，共14页。
2X
12-2X
例2 如图,在△ABC中∠B=90°,AB=6cm，
BC=3cm，点P以1的速度从点B开始沿
边BC向点C移动.如果点P、Q同时出发，几秒后
PQ之间的的距离等于 cm? 4 2
C
(2t)2(6t)2(42)2
↑ Q
t2 t2 5
A P→
现在您正浏览在第6页，共14页。
B t=2不符合题意，舍去
（2）当x为何值时，△PBQ为等腰三角形；
（3）是否存在x的值，使得四边形APQC的面积等于20cm2？若存在
，请求出此时x的值；若不存在，请说明理由．
一元二次方程与动点相结合的应用题
一元二次方程与动点相结合的应用题1. 一元二次方程的基础1.1 什么是它？首先，一元二次方程其实就是一个简单的数学公式，通常看起来像这样：( ax^2 + bx + c = 0 )。
听起来复杂，但别担心，简单几何图形就是它的代表，像一座优雅的抛物线。
你想象一下，抛物线就像你在公园滑滑梯，越滑越快，越滑越高，哈哈。
1.2 现实生活中的应用那么，这个方程有什么用呢？其实，它在我们的生活中无处不在。
比如说，建筑师在设计桥梁时，得考虑到材料的强度和形状，常常用到这种方程。
而且，当你打篮球时，投篮的轨迹也可以用它来描述。
是不是觉得这些数学知识跟你生活中的每一秒都有关系？2. 动点的神奇之旅2.1 动点是什么？接下来，让我们聊聊动点。
动点就像公园里那只自由自在的小鸟，随心所欲地在空中飞翔。
动点在数学中，通常指的是在某个规律下运动的点，位置会随着时间变化。
比如说，一个小球从高处掉下，位置就是不断变化的。
2.2 动点与一元二次方程的结合想象一下，小球从高处掉下，它的运动轨迹可以用一元二次方程来描述。
这个时候，你就能感受到数学的魅力了！当小球落地的瞬间，那一刹那就像是电影中的慢动作，让人无比期待。
你会发现，动点和一元二次方程就像是亲密无间的小伙伴，互相依赖，缺一不可。
3. 实际案例3.1 小朋友的投篮让我们来个实例。
想象一个小朋友正在公园里投篮，他抬起手，球在空中划出一个优美的弧线。
这个弧线的形状，正好可以用一元二次方程来描绘。
小朋友投篮时，势头和角度决定了球的飞行轨迹，而这一切都能用方程来算出来，真是太神奇了！3.2 从方程到答案假设小朋友投篮的方程是 ( y = x^2 + 4x )，这时候，我们可以通过解这个方程来知道，球在最高点时的高度有多高。
然后，利用这个高度，我们就可以知道这个小球是否能进篮筐。
就像在做一道美味的菜，得先调好配方，才能品尝到美味。
最后，结合一元二次方程与动点的故事，我们可以看到，数学不再是枯燥无味的，而是充满了生活的乐趣和探索的意义。
一元二次方程应用题动点问题2021完整版PPT
c（m1；）t秒后一正方样形AB时CD与间等腰三内角形，PQR假重合设部分的B面Q积=为x5，c求m时〔间t；x≠0〕，那么AP=2xcm，
3．如图，在矩形ABCD中，AB＝6米，BC＝8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从
CM=3xcm， 点C出发，沿CB向点B移动，设P、Q两点移动t秒（0<t<5）后，四边形ABQP的面积为S米2,（1）求面积S与时间t的关系式；
一样时间内，假设BQ=xcm〔x≠0〕，那么AP=2xcm，CM=3xcm，
解决有关“动点”的问题”方法
DN=x2cm． 一样时间内，假设BQ=xcm〔x≠0〕，那么AP=2xcm，CM=3xcm，
〔1〕用含x的代数式表示BQ、PB的长度；
〔2〕当x为何值时，△PBQ为等腰三角形；
〔3〕是否存在x的值，使得四边A形APQC的面积等于
20cm2？假设存在，请求出此时x的值；假设不存在
，请说明理由．
P
B
Q
C
自主完成
1.如图，△ABC中，∠C=90°，AC=8cm，BC=4cm，一动点P从C出发 沿着CB方向以1cm/S的速度运动，另一动点Q从A出发沿着AC方向 以2cm/S的速度运动，P，Q两点同时出发，运动时间为t〔s〕．
〔1〕当t为几秒时，△PCQ的面积是△ABC面积的四分之一？ 〔2〕△PCQ的面积能否为△ABC面积的一半？假设能，求出t的值
； 假设不能，说理由．
A
Q
C PB
自主完成
2、如图，在矩形ABCD中，BC=20cm，P，Q，M，N分别从A，
九年级中考《一元二次方程与实际问题》(面积问题 动点问题)经典题型专题提升练习
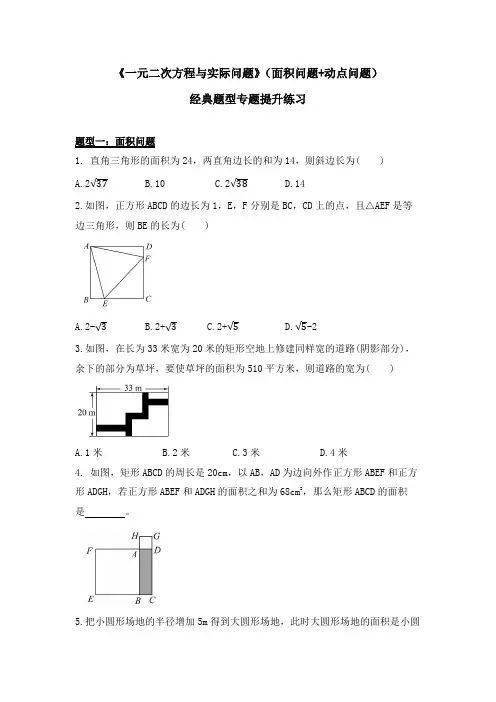
《一元二次方程与实际问题》（面积问题+动点问题）经典题型专题提升练习题型一：面积问题1. 直角三角形的面积为24，两直角边长的和为14，则斜边长为( )A.2√37B.10C.2√38D.142.如图，正方形ABCD的边长为1，E，F分别是BC，CD上的点，且△AEF是等边三角形，则BE的长为( )A.2-√3B.2+√3C.2+√5D.√5-23.如图，在长为33米宽为20米的矩形空地上修建同样宽的道路(阴影部分)，余下的部分为草坪，要使草坪的面积为510平方米，则道路的宽为( )A.1米B.2米C.3米D.4米4. 如图，矩形ABCD的周长是20cm，以AB，AD为边向外作正方形ABEF和正方形ADGH，若正方形ABEF和ADGH的面积之和为68cm2，那么矩形ABCD的面积是。
5.把小圆形场地的半径增加5m得到大圆形场地，此时大圆形场地的面积是小圆形场地的4倍，设小圆形场地的半径为xm，若要求出未知数x，则应列出方程________________.(列出方程，不要求解方程).6.如图所示，使用墙的一边(墙长7m)，再用13m的竹篱笆围三边，围成一个面积为20m2的矩形，设与墙相对的边长为xm，可得长、宽分别为。
7. 如图，已知点A是一次函数y=x-4的图象上的一动点，且矩形ABOC面积等于3，则点A的坐标为____________.8.如图,有一块矩形硬纸板,长30 cm,宽20 cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200 cm2?9. 在△ABC中，∠B=90°，AB=6cm，BC=3cm，点P从A点开始沿着AB边向点B 以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，如果P，Q分别从A，B同时出发：(1)经过多长时间，S△PQB =12S△ABC？(2)经过多长时间，P，Q间的距离等于4√2cm？题型二：动点问题1.如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD 方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为1cm2，则它移动的距离AA′等于( )A.0.5 cmB.1 cmC.1.5 cmD.2 cm2. 如图，过点A(2，4)分别作x轴，y轴的垂线，垂足分别是点M，N.若点P 从点O出发，沿OM做匀速运动，1min可到达M点.同时点Q从M点出发，沿MA 做匀速运动，1min可到达点A.若线段PQ的长度为2，则经过的时间为( )A.0minB.0.4minC.0.4min或0minD.以上都不对3. 如图，在△ABC中，∠ABC=90°，AB=8cm，BC=6cm.动点P，Q分别从点A，B 同时开始移动，点P的速度为1cm/s，点Q的速度为2cm/s，点Q移动到点C后停止，点P也随之停止运动.下列瞬时间中，能使△PBQ的面积为15cm2的是( )A.2 sB.3 sC.4 sD.5 s4. 如图，在Rt△ABC中，∠B=90°，AB=BC=12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC，则出发________s时，四边形DFCE的面积为20cm2.5. 如图，已知点A是一次函数y=x-4的图象上的一动点，且矩形ABOC面积等于3，则点A的坐标为____________.6. 如图，在矩形ABCD中，AB=4cm，BC=√2cm，点P从点A出发以1cm/s的速度移动到点B；点P出发秒后，点P，A的距离是点P，C距离的√3倍？7. 如图，某市区南北走向的北京路与东西走向的喀什路相交于点O处.甲沿着喀什路以4m/s的速度由西向东走，乙沿着北京路以3m/s的速度由南向北走.当乙走到O点以北50m处时，甲恰好到点O处.若两人继续向前行走，求两个人相距85m时各自的位置.8. 小岛A在码头B的正西方向，A，B相距40n mi l e.上午9点，一渔船和一游艇同时出发，渔船以20n mi l e/h的速度从B码头向正北出海作业，游艇以25n mi l e/h的速度从A岛返回B码头.一段时间后，渔船因故障停航在C处并发出信号.游艇在D处收到信号后直接向渔船驶去，上午11点到达C处.游艇在上午几点收到信号？9. 如图所示，A，B，C，D为矩形的四个顶点，AB=16cm，AD=6cm，动点P，Q 分别从点A，C同时出发，点P以3cm/s的速度向点B移动，一直到点B为止，点Q以2cm/s的速度向点D移动，一直到点D为止.(1)P，Q两点从出发开始，经过几秒时，四边形PBCQ的面积是33cm2？(2)P，Q两点从出发开始，经过几秒时，点P，点Q间的距离是10cm？10. 如图，在△ABC中，AB=6cm，BC=4cm，∠B=60°，动点P，Q分别从A，B 两点同时出发.分别沿AB，BC方向匀速移动；它们的速度分别为2cm/s和1cm/s.当点P到达点B时，P，Q两点停止运动.设点P的运动时间为t(s).求t 为多少时，△PBQ为直角三角形.。
一元二次方程——动点问题
Day5：一元二次方程之动点问题一元二次方程解决问题1．动点问题几何图形应用题，关键是将点的运动关系表示出来，找出未知量与已知量的内在联系，根据面积或体积公式列出方程.常见题型：选择题、解答题，求最值问题.易错点：找准动点的关系.中考回顾：常考，求最值或三角形为直角三角形等等.例1如图，点O 在线段AB 上，AO=1，OB=2，OC 为射线，且∠BOC=120°，动点P 以每秒2个单位长度的速度从点O 出发，沿射线OC 作匀速直线运动．设运动时间为t 秒，当△ABP 为直角三角形时，t 的值为（）A．t=1B．t=1或8﹣C．t=8D．t=1或8例2如图，已知△ABC中，∠B=90°，AB=5cm，BC=7cm，点P从点A开始沿AB边向点B以1cm/s 的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，当其中一点停止运动时，另一点也随之停止，其中P、Q不与A、B重合.（1）如果P、Q分别从A、B同时出发，那么几秒后，△PBQ的面积等于4cm2？（2）如果P、Q分别从A、B同时出发，那么几秒后，PQ的长度等于5cm？（3）在（1）中，△PBQ的面积能否等于7cm2？请说明理由.例3如图，在平面直角坐标系中，过原点O及点A（0,2）、C（6,0）作矩形OABC，∠AOC的平分线交AB于点D.点P从点O出发，以每秒2个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒，则当t为何值时，△PBQ为直角三角形？参考答案1.【答案】B【考点】本题考查了动点问题，结合三角形，注意画出图形，帮助理解．【解析】如图1，当∠PAB=90°时，∵∠BOC=120°，∴∠AOP=60°，∴∠APO=30°，∴OP=2OA=2，∵OP=2t，∴t=1；如图2，当∠APB=90°，过P 作PD⊥AB，∵∠OPD=120°﹣90°=30°，∴OD=12∴AD=AO﹣OD=1﹣t，在Rt△ABP 中，根据勾股定理得：AP 2+BP 2=AB 2，即（2+t）222+（1﹣t）2=32，解得：t=8﹣（负值舍去）；当∠ABP=90°时，此情况不存在；综上，当t=1或t=8﹣时，△ABP 是直角三角形．2.【答案】（1）1秒（2）2秒（3）不能【考点】一元二次方程在三角形中动点问题的应用.【解析】（1）设x 秒后，△PBQ 的面积等于4cm².此时，AP=x cm，PB=（5-x）cm，BQ=2x cm，由S △PBQ =4BQ PB 21=∙得()42-521=∙x x ，整理得0452=+-x x ，解得x 1=1，x 2=4.当x=4时，2x=8>7，不合要求.所以1秒后，△PBQ 的面积等于4cm².（2）设x 秒后，PQ 的长度等于5cm.由PB 2+BQ 2=5²得（5-x）²+（2x）²=5²整理得x²-2x=0，解得x 1=0（舍去），x 2=2.经检验，x=2符合要求，所以2秒后，PQ 的长度等于5cm.（3）不能.理由：设x 秒后，△PBQ 的面积等于7cm²，由题意得()72-521=∙x x ，整理得x²-5x+7=0，03-28-25<==∆，此方程无解，所以△PBQ 的面积不可能等于7cm².3.【答案】t=2或55+=t 或5-5=t 【考点】该题考查的是一元二次方程与直角坐标系结合的动点应用题型.【解析】过点P 作PG⊥OC，垂足为G.在Rt△POG 中，∵∠POG=45°，∴∠OPG=45°，∵OP=t 2，∴OG=PG=t，∴点P（t，t），又∵Q（2t，0），B（6,2），根据勾股定理可得PB²=（6-t）²+（2-t）²，QB²=（6-2t）²+2²，PQ²=（2t-t）²+t²=2t².在P、Q 移动过程中，PQ 始终与OD 垂直，容易得知∠BPQ 不可能等于90°.①若∠PQB=90°，则有PQ²+QB²=PB²，即2t²+[（6-2t）²+2²]=（6-t）²+（2-t）²，整理得4t²-8t=0，解得t 1=0（舍去），t 2=2，∴t=2.②若∠PBQ=90°，则有PB²+QB²=PQ²，∴[（6-t）²+（2-t）²]+[（6-2t）²+2²]=2t²，整理得t²-10t+20=0，解得t=5±5.∴当t=2或55+=t 或5-5=t 时，△PQB 为直角三角形.。
一元二次方程(动点问题)
7.动点问题例1：如图：在Rt △ACB 中，∠C=90°，点P 、Q 同时由A 、B 两点 出发分别沿AC 、BC 方向向 点C 匀速移动，它们的速度都是1m/s ，几秒后△PCQ 的面积为 Rt △ACB 面积的一 半？变式练习： 1、 如图：在△ABC 中，∠B=90°，点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动，点Q 从点B 开始，沿BC 边向点C 以2厘米/秒的速度移动，如果P 、Q 分别从A 、B 同时出发，几秒后△PBQ 的面积等于8平方厘米？AB C P Q 6cm 8cm2、如图，在△ABC 中，AB=6cm ，AC=12cm 动点D 从A 点出发到B 点为止，运动的速度为1cm/秒；同时动点E 从C 点出发到A 点为止，点E 运动的速度为2cm/秒那么当点A 、D 、E 为顶点的三角形与△ABC 相似时，运动的时间是（ ）3.如图，在矩形ABCD 中，AB=3，BC=4，点P 以每秒2个单位长度的速度从点C 出发，沿CA 向点A 运动；点Q 同时以每秒1个单位长度的速度从点A 出发，沿AB 向点B 运动,设P 、Q 两点移动t 秒（1）求△APQ 与△ABC 相似时t 的值（2）求四边形BCPQ 面积S 与时间t 的关系式（3）求△APQ 为等腰三角形时t 的值B CE D A例2：一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20 海里的圆形区10域(包括边界)都属台风区.当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里.若这艘轮船自A处按原速度继续航行，在途中会不会遇到台风?若会，试求轮船最初遇到台风的时间；若不会，请说明理由.变式练习：某军舰以20节的速度由西向东航行，一艘电子侦察船以30节的速度由南向北航行，它能侦察出周围50海里（包括50海里）范围内的目标。
(完整版)一元二次方程动点问题
一元二次方程动点问题息县五中敖勇1、在直角三角形ABC中,AB=BC=12cm，点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D作DE平行于BC,DF平行于AC,点E.F分别在AC,BC上,问：点D出发几秒后四边形DFCE的面积为20cm²？2、在△ABC中, AC=50cm, CB=40cm, ∠C=90°,点P从点A开始沿AC边向点C 以2cm/s 的速度移动, 同时另一点Q由C点以3cm/s的速度沿着CB边移动,几秒钟后, △PCQ的面积等于450cm²?3、在直角三角形ABC中，∠B=90°，AB=6厘米，BC=3厘米，点P从点A 开始沿AB边向点B以1cm/s的速度移动，点Q从B开始沿边BC向点C以2cm/s 的速度移动，若P、Q分别从A、B同时出发，几秒后PQ距离等于42厘米。
4、如图：在Rt△ACB中，∠C=90°，点P、Q同时由A、B两点出发分别沿AC、BC方向向点C匀速移动，它们的速度都是1m/s，几秒后△PCQ的面积为Rt △ACB面积的一半？变式训练1、在△ABC中，∠B=90°，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动。
若点P、Q分别从点A、B同时出发，经过多少时间，使△PBQ的面积等于8cm2？变式训练2.△ABC中，∠C=90°AB=10cm,AC=8cm,点P从点A开始出发，向点C 以2cm/s的速度移动，点Q从B点出发向点C以1cm/s的速度移动。
若P、Q分别同时从A、B出发，几秒后四边形APQB是△ABC面积的32。
5、已知：如图①，在Rt ACB△中，90C∠=o，4cmAC=，3cmBC=，点P由B 出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为(s)t（02t<<），解答下列问题：设AQP△的面积为y（2cm），求y与t之间的函数关系式；当t为何值时y是△ABC面积的53AC BPQ6c8c6、如图，在△ABC中，∠C＝90º，AC＝6cm，BC＝8cm，D、E分别是AC、AB 的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为1cm/s；同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t(0＜t＜4)s．解答下列问题：当点Q在B、E之间运动时，当t为何值时，PQ分四边形BCDE所成的两部分的面积之比为S△PQE∶S五边形PQBCD＝1∶29？7、等腰直角△ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与 AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm²?8、如图所示，已知在△ABC中，∠B=90°，AB=BC=5cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从B开始沿边BC向点C以2cm/s的速度移动，若一动点运动到终点，则另一个也随之停止。
一元二次方程中的动点问题
B 90 , AB 5 cm, BC 7 cm
点P从A点开始沿AB边向点B以1cm/s的速度移动， 点Q从点B开始沿BC边向点C以2cm/s的速度移 动. • （2）如果P,Q分别从A,B同时出发，那么几秒后， PQ的长度等于5cm？
• 1、已知：如图3-9-3所示，在△ABC中，
其它类型应用题：
5.在直角梯形ABCD中，AD∥BC，∠C=90°， BC=16，AD=21，DC=12，动点P从点D出发，沿 线段DA方向以每秒2个单位长度的速度运动， 动点Q从点C出发，沿线段CB 以每秒1个单位 长度的速度向点B运动. 点P、Q分别从点D、C 同时出发，当点P运动到点A时，点Q随之停止 运动，设运动时间为t秒. 问:当t为何值时，△BPQ是等腰三角形？ P D A 分类讨论思想
• 点P从A点开始沿AB边向点B以1cm/s的速度移动，
你还行吗
• 1、已知，如图所示，在三角形ABC中， B 90 , AB 5 cm, BC 7 cm • 点P从A点开始沿AB边向点B以每秒1cm的速度移动,点Q从点 B开始沿BC边向点C 以每秒2cm的速度移动。 • (3) 如果P、Q分别从A、B同时出发，那么几秒后，PQ的长 等于5cm.
Q C
B
2、如图，A、B、C、D为矩形的四个顶点， AB=16cn,AD=6cm，动点P、Q分别从点A、C 同时出发，点P以3cm/s的速度向点B移动，一 直到达B为止，点Q以2cm/s的速度向D移动。 （2）P、Q两点从出发开始到几秒时，点P和点Q 的距离是10cm？
A P D
Q
B
C
B 90 , AB 5 cm, BC 7 cm
点P从A点开始沿AB边向点B以1cm/s的速度移动， 点Q从点B开始沿BC边向点C以2cm/s的速度移 动. • 在（1）中，△PQB的面积能否等于7?说明理由
初中数学 一元二次方程的应用 动点问题
终点是 终点是
， 速度是 ， 速度是
。 。
， ，
3、P点从开始走过的路程是那一段？ Q点从开始走过的路程是那一段？ 4、 △ PCD的面积= ×
（哪条边？）
A
QC P
1、动点：P和Q
B
2、P的起点是 A 终点是 C ， 速度是 1cm/s Q的起点是 C 终点是 B ， 速度是 2cm/s 3、P点从开始走过的路程是那一段？ Q点从开始走过的路程是那一段？ 设 x s后 AP= X cm , CQ= 2X cm 4、 △PCQ的面积= CP=AC-AP =6-X AP CQ 。 。
B
Q
C
P
A
1、动点：P和Q 2、P的起点是 终点 是 ， 速度是 ， Q的起点是 终点 是 ， 速度是 ， 3、P点从开始走过的路程是那一 段？ 。 Q点从开始走过的路程是那一 段？ 。 4、 △ PCD的面积= × 。
C
Q
B
练习册 P32
P A度1m/s Q速度2m/s
， ，
½
CP × CQ （哪条边？） CQ=2X △ PCQ=9
A
QC P
• 解：设点P、Q出发x s后可使PCQ的面积为9 cm2 。依据题意得AP= x cm, PC=（6-x）cm, CQ=2X CM, 则由S △ PCQ= ½ ·PC · CQ可得 ½· （6-x）·2X=9 整理得 x2-6x+9=0 解得 x1=x2=3 答：、、、、、、、、、
一元二次方程的应用
动点问题
动点问题：
要从审题中明白以下关键点： 1、动点的起点， 从哪里出发？ 2、动点的终点，到哪里停止？ 3、动点在时间内 走过的路程是那一段，且路 程是多少？ （路程=速度×时间） 4、所构成的图形 面积怎么求？距离怎么求？ 5 、根据等量关系列出方程。
一元二次方程的应用(动点问题)
P53
练习 T2
牛刀小试 在矩形ABCD中,AB=6cm,BC=12cm,点P 从点A开始以1cm/s的速度沿AB边向点B移 动,点Q从点B开始以2cm/s的速度沿BC边 向点C移动,如果P、Q分别从A、B同时出发， 几秒后△ PQD的面积等于28cm2？
D C
Q
A P
B
牛刀小试
2、在直角三角形ABC 中,AB=BC=12cm，点D从点A开始以 2cm/s的速度沿AB边向点B移动,过 点D做DE平行于BC,DF平行于AC,点 E.F分别在AC,BC上,问：点D出发 几秒后四边形DFCE的面积为20cm2？
拓展提升：
P54 T7
（4）当x为何值时，四边形PQMN 为直角梯形？
有关“动点”的运动问题”
1)关键—— 以静代动把动的点进行转换, 变为线段的长度, 2)方法—— 时间变路程 求“动点的运动时间”可以转化为求“动点 的运动路程”，也是求线段的长度; 3）常找的数量关系——面积，勾股定理等； 由此,学会把动点的问题转化为静点的问题, 是解这类问题的关键.
习题速练：
动点问题
合作交流
例1 如图，在△ABC 中，∠C＝90°，AC＝6 cm，BC＝8 cm. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s的速度移动；同时点 Q沿 CB 边从点 C 向 终点 B 以 2 cm/s的速度移动，且当其中一点到达 终点时，另一点也随之停止移动. 问：(1)点 P，Q 出发几秒后， △PCQ 为等腰三角形？ （2）点P，Q出发几秒后， 可使△PCQ 的面积为9 cm2 ? △PCQ的面积能为10cm2? （3）当点P、Q出发几秒后， PQ的长度为 4 2 cm？
Ｅ Ａ
Ｄ
Ｃ F
一元二次方程-动点问题
二．经过多少时间后， S△PCQ的面积为 15cm2？
三．请用配方法说明，何 时△PCQ的面积最大， 最大面积是多少？
2．如图，用一块长为50cm、宽为30cm的长方形铁 片制作一个无盖的盒子，若在铁片的四个角截去四个 相同的小正方形，设小正方形的边长为xcm． （1）底面的长AB=_______cm，宽 BC=__________cm（用含x的代数式表示） （2）当做成盒子的底面积为300cm2时，求该盒子 的容积． （3）该盒子的侧面积S是否存在最大的情况？若存在， 求出x的值及最大值是多少？若不存在，说明理由．
想一想
(40 x 30)(600 10 x ) 10000. 1
答 : 每个台灯的定价应为50元或80元, 进 货 量 相 应 为5000个 或 200个.
某商场将进货价为30元的台灯以40元售出,平均每月 能售出600个.市场调研表明:当销售价为每上涨1元时, 其销售量就将减少10个.商场要想销售利润平均每月 达到10000元,每个台灯的定价应为多少元?这时应进 台灯多少个?
边形DFCE的面积为20cm2？
Ｃ
F
Ｅ
Ａ
Ｂ
Ｄ
3、如图,已知A、B、C、D为矩形的四个顶
点,AB=16㎝,AD=6㎝,动点P、Q分别从点A、C 同时出发,点P以3㎝/s的速度向点B移动,一直到
点B为止,点Q以2㎝/s的速度向点D移动.
（1）P、Q两点从出发开始几秒时, 四边形PBCQ的面积是33c㎡
D
P
（2）P、Q两点从出发开始到几秒时，
点P和点Q的距离是10cm？
的速度移动, 同时另一
点Q由C点以3cm/s的速
度沿着CB边移动,几秒钟
后, PCQ的面积等于
初中数学专题：利用一元二次方程解决几何中的三大动点问题
专题1.7 利用一元二次方程解决几何中的三大动点问题【苏科版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，可加强学生对利用一元二次方程解决几何中的三大动点问题的理解！【类型1 利用一元二次方程解决三角形中的动点问题】1．（2023春·广东江门·九年级校考期中）如图，在等腰中，，，动点P从点A出发沿向点B移动，作，，当的面积为面积的一半时，点P移动的路程为（）A．B．C．D．2．（2023春·浙江·九年级期末）如图，在等腰中，，动点P从点A出发沿折线向点终B以的速度运动，于点Q．设运动时间为，当s时，的面积为．3．（2023春•驻马店期末）如图，已知AG CF，AB⊥CF，垂足为B，AB=BC=3 ，点P是射线AG上的动点（点P不与点A重合），点Q是线段CB上的动点，点D是线段AB的中点，连接PD并延长交BF于点E，连接PQ，设AP=2t，CQ=t，当PQE是以PE为腰的等腰三角形时，t的值为．4．（2023春·广东江门·九年级校考期中）如图，是边长为6cm的等边三角形，动点，同时从，两点出发，分别沿，匀速移动，它们的速度都是2，当点到达点时，，两点都停止运动，设点的运动时间为，解答下列问题：(1)当为何值时，是以为直角的直角三角形？(2)是否存在，使四边形的面积是面积的若存在，求出的值；若不存在，请说明理由．5．（2023春·江苏宿迁·九年级统考期末）如图，在ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P 从点A出发沿边AB向点B以2cm/s的速度移动，同时动点Q从点B出发沿边BC向点C以4cm/s的速度移动，当P运动到B点时P、Q两点同时停止运动，设运动时间为ts．(1)BP＝cm；BQ＝cm；（用t的代数式表示）(2)D是AC的中点，连接PD、QD，t为何值时PDQ的面积为40cm26．（2023·浙江金华·九年级期中）如图，在中，厘米，厘米，于点D，动点P从点A出发以每秒1厘米的速度在线段上向终点D运动．设动点运动时间为t秒．（1）求的长；（2）当的面积为15平方厘米时，求t的值；（3）动点M从点C出发以每秒2厘米的速度在射线上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得？若存在，请求出t的值；若不存在，请说明理由．7．（2023春·九年级单元测试）如图，在Rt ABC中，∠BAC＝90°，AB＝AC＝16 cm，AD为BC边上的高，动点P从点A出发，沿A→D方向以cm/s的速度向点D运动，过P点作矩形PDFE(E点在AC上)，设ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t秒(0＜t＜8)．(1)经过几秒钟后，S1＝S2?(2)经过几秒钟后，S1＋S2最大？并求出这个最大值．8．（2023春·江苏淮安·九年级统考期中）Rt ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒（1）如图1，过点P作PD⊥AC，交AB于D，若PBC与P AD的面积和是ABC的面积的，求t的值；（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与ABC重叠部分的面积为8，求t的值．【类型2 利用一元二次方程解决四边形中的动点问题】1．（2023春·陕西渭南·九年级统考期末）如图，在矩形中，点是上的一个动点，把沿向矩形内部折叠，当点的对应点恰好落在的平分线上时，的长为．2．（2023春·河北邯郸·九年级统考期中）如图所示，A、B、C、D为矩形的四个顶点，，，动点P、Q分别从点A、C同时出发，点P以的速度向B移动，一直到达B为止；点Q以的速度向D移动．当P、Q两点从出发开始秒时，点P和点Q的距离是．（若一点到达终点，另一点也随之停止运动）3．（2023春·山东烟台·九年级统考期中）如图，在矩形中，，，动点P、Q分别以，的速度从点A，C同时出发，沿规定路线移动．(1)若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P，Q两点之间的距离是？(2)若点P沿着移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间的面积为？4．（2023春·浙江杭州·九年级期中）如图，点，分别在平行四边形的边，上，且，，，动点从点出发沿着线段向终点运动，同时点从点出发沿着折线段向终点运动，且它们同时到达终点，设点运动的路程为，的长度为，且（为常数，）．（1）求证：四边形是平行四边形．（2）求的长．（3）当时，①求的值；②连结，，当为直角三角形时，求所有满足条件的的值．5．（2023春·江西吉安·九年级校联考期中）如图，在ABD中，AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC（1）求证：四边形ABCD是菱形．（2）如果OA,OB(OA>OB)的长（单位：米）是一元二次方程的两根，求AB的长以及菱形ABCD的面积．（3）若动点M从A出发，沿AC以2m/s的速度匀速直线运动到点C,动点N从B 出发，沿BD以1m/s的速度匀速直线运动到点D，当M运动到C点时运动停止．若M、N同时出发，问出发几秒钟后，MON 的面积为？6．（2023春·浙江·九年级期中）如图，在四边形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动到C点返回，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t（秒）．（1）当t为何值时，四边形PQDC是平行四边形；（2）当t为何值时，以C，D，Q，P为顶点的四边形面积等于60cm2？（3）当0<t<10.5时，是否存在点P，使PQD是等腰三角形？若存在，请直接写出所有满足要求的t的值；若不存在，请说明理由．7．（2023春·浙江杭州·九年级校考期中）如图，平行四边形ABCD中，AB＝4cm，AD＝2cm，∠C＝30°．点P以2cm/s的速度从顶点A出发沿折线A﹣B﹣C向点C运动，同时点Q以1cm/s的速度从顶点A出发沿折线A﹣D﹣C向点C运动，当其中一个动点到达末端停止运动时，另一点也停止运动．设运动时间为ts．（1）求平行四边形ABCD的面积；（2）求当t＝0.5s时，APQ的面积；（3）当APQ的面积是平行四边形ABCD面积的时，求t的值．8．（2023春·广东惠州·九年级惠州一中校考开学考试）如图，AC是正方形ABCD的对角线，AD＝8，E是AC的中点，动点P从点A出发，沿AB方向以每秒1个单位的速度向终点B运动，同时动点Q从点B出发，以每秒2个单位的速度先沿BC方向运动到点C，再沿CD方向向终点D运动，以EP、EQ为邻边作平行四边形PEQF，设点P运动的时间为t秒（0＜t＜8）(1)当t＝1时，试求PE的长；(2)当点F恰好落在线段AB上时，求BF的长；(3)在整个运动过程中，当▱PEQF为菱形时，求t的值．9．（2023春·九年级单元测试）如图，正方形的边长为，动点从点出发，以的速度沿方向向点运动，动点从点出发，以的速度沿方向向点运动，若，两点同时出发，运动时间为．(1)连接，，，当为何值时，面积为(2)当点在上运动时，是否存在这样的的值，使得是以为腰的等腰三角形？若存在，请求出符合条件的的值；若不存在，请说明理由．10．（2023·江苏·九年级假期作业）如图，在矩形中，，，动点P、Q分别从点A、C同时出发，点P以的速度向点B移动，一直到点B为止，点Q以的速度向点D移动（点P停止移动时，点Q也停止移动）．设移动时间为t（s）．连接，．(1)用含t的式子表示线段的长：__________；__________．(2)当t为何值时，P、Q两点间的距离为？(3)当t为何值时，四边形的形状可能为矩形吗？若可能，求出t的值；若不可能，请说明理由．【类型3 利用一元二次方程解决坐标系中的动点问题】1．（2023春·陕西渭南·九年级统考期末）如图①，在矩形中，，对角线、相交于点，动点由点出发，沿运动，设点的运动路程为，的面积为，与的函数关系图像如图②所示，则边的长为（）A．3 B．4 C．5 D．62．（2023·河南驻马店·统考三模）如图，在平面直角坐标系中，矩形的边在y轴上，边在x轴上，点B的坐标是，D为边上一个动点，把沿折叠，若点A的对应点恰好落在矩形的对角线上，则点的坐标为（）A．B．C．D．3．（2023春·四川德阳·九年级统考期末）如图①，在中，于D，，，，点E 是上一动点（不与点A，D重合），在内作矩形，点F在上，点G、H在上，设，连接．(1)设矩形的面积为，的面积为，令，求y关于x的函数解析式；（要求写出自变量的取值范围）(2)如图②，点M是（1）中得到的函数图象上的任意一点，N的坐标为，，当为等腰三角形时，求点M的坐标．4．（2023春·广东佛山·九年级佛山市华英学校校考期中）如图，平面直角坐标系中，已知点，点，过点作轴的平行线，点是在直线上位于第一象限内的一个动点，连接，．(1)求出__________；(2)若平分，求点的坐标；(3)已知点是直线上一点，若是以为直角边的等腰直角三角形，求点的坐标.5．（2023春·广东江门·九年级江门市福泉奥林匹克学校校考期中）已知，如图：在直角坐标系中，正方形AOBC的边长为4，点D，E分别是线段AO，BO上的动点，D点由A点向O点运动，速度为每秒1个单位，E点由B点向O点运动，速度为每秒2个单位，当一个点停上运动时，另一个点也随之停止，设运动时间为t（秒）(1)如图1，当t为何值时，DOE的面积为6；(2)如图2，连接CD，与AE交于一点，当t为何值时，CD⊥AE；(3)如图3，过点D作DG OB，交BC于点G，连接EG，当D，E在运动过程中，使得点D，E，G三点构成等腰三角形，求出此时t的值6．（2023春·浙江·九年级期中）如图直角坐标系中直线与轴正半轴、轴正半轴交于，两点，已知，，，分别是线段，上的两个动点，从出发以每秒个单位长度的速度向终点运动，从出发以每秒个单位长度的速度向终点运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为（秒）．(1)求线段的长，及点的坐标；(2)为何值时，的面积为；(3)若为的中点，连接，，以，为邻边作平行四边形．是否存在时间，使轴恰好将平行四边形的面积分成两部分，若存在，求出的值．7．（2023春·浙江宁波·九年级校考期中）在平面直角坐标系中，A，B点的坐标分别为（0，4），（-4，0），点坐标为，点是射线BO上的动点，满足BE=1.5OP，以，为邻边作．（1）当m=2时，求出PE的长度；（2）当m﹥0时，是否存在m的值，使得的面积等于ABO面积的，若存在求出m的值，若不存在，请说明理由；（3）当点Q在第四象限时，点Q关于E点的对称点为Q′，点Q′刚好落在AB上时，求m的值（直接写出答案）．8．（2023春·浙江·九年级期中）如图1，在平面直角坐标系中，已知四边形的顶点，分别在轴和轴上．直线经过点，与轴交于点已知，，平分，交于点，动点从点出发沿着线段向终点运动，动点从点出发沿着线段向终点运动，，两动点同时出发，且速度相同，当点到达终点时点也停止运动，设．(1)求和的长；(2)如图，连接，，求证：四边形为平行四边形；(3)如图，连接，，当为直角三角形时，求所有满足条件的值．9．（2023春·浙江·九年级期中）如图1，已知，点O为坐标原点，点C在x轴的正半轴上．在中，边的角平分线交于点D．（1）求两点的坐标；（2）若点M是直线上的一个动点，点是坐标平面上的点，以点为顶点的四边形是菱形时，请直接写出点的坐标；（3）如图2，点P从点O出发，以每秒个单位长度的速度沿射线方向移动：同时点Q从点O出发，以每秒2个单位长度的速度沿射线方向移动，连结，设移动时间t秒．当t为何值时，是直角三角形．10．（2023春·重庆·九年级重庆市育才中学校联考期中）在平面直角坐标系中，直线l经过点和点．点C的横坐标为，点D为线段的中点．(1)求直线l的解析式．(2)如图1，若点P为线段上的一个动点，当的值最小时，求出点P坐标．(3)在（2）的条件下，点Q在线段上，若是等腰三角形，请直接写出满足条件的点Q的横坐标，并写出其中一个点Q的横坐标的求解过程．11．（2023春·河南南阳·九年级南阳市第三中学校考期末）如图，平行四边形位于直角坐标系中，为坐标原点，点，点交轴于点动点从点出发，沿方向以每秒1个单位长度的速度终点运动，同时动点从点出发，沿射线的方向以每秒2个单位长度的速度运动，当点运动到点时，点随之停止运动，运动时间为t（秒）．（1）用t的代数式表示：________，________（2）若以A，B，E，F为顶点的四边形是平行四边形时，求t的值．（3）当恰好是等腰三角形时，求t的值．12．（2023·辽宁沈阳·统考一模）已知：如图，在平面直角坐标系中，矩形AOBC的顶点C的坐标是（6，4），动点P从点A出发，以每秒1个单位的速度沿线段AC运动，同时动点Q从点B出发，以每秒2个单位的速度沿线段BO运动，当Q到达O点时，P，Q同时停止运动，运动时间是t秒（t＞0）．（1）如图1，当时间t＝秒时，四边形APQO是矩形；（2）如图2，在P，Q运动过程中，当PQ＝5时，时间t等于秒；（3）如图3，当P，Q运动到图中位置时，将矩形沿PQ折叠，点A，O的对应点分别是D，E，连接OP，OE，此时∠POE＝45°，连接PE，求直线OE的函数表达式．专题1.7 利用一元二次方程解决几何中的三大动点问题【苏科版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，可加强学生对利用一元二次方程解决几何中的三大动点问题的理解！【类型1 利用一元二次方程解决三角形中的动点问题】1．（2023春·广东江门·九年级校考期中）如图，在等腰中，，，动点P从点A出发沿向点B移动，作，，当的面积为面积的一半时，点P移动的路程为（）A．B．C．D．【答案】B【分析】设AP＝x cm，则PB＝（8−x）cm，求出∠A＝45°，∠APR＝90°，得到PR＝P A＝x cm，然后根据▱PQCR 的面积为ABC面积的一半列方程求解即可．【详解】解：设AP＝x cm，则PB＝（8−x）cm，∵∠B＝90°，AB＝BC＝8cm，∴∠A＝45°，∵PR BC，∴∠APR＝90°，∴PR＝P A＝x cm，∵▱PQCR的面积为ABC面积的一半，∴，解得：，∴点P移动的路程为4cm．故选：B．【点睛】本题主要考查了平行四边形的性质，一元二次方程的应用，根据几何图形的性质得出方程是解题的关键．2．（2023春·浙江·九年级期末）如图，在等腰中，，动点P从点A出发沿折线向点终B以的速度运动，于点Q．设运动时间为，当s时，的面积为．【答案】或【分析】利用等腰直角三角形的性质求出AB，设时间为秒，分和两种情况结合三角形面积分别计算．【详解】解：∵在等腰中，，，∴，，．∵于点．∴设当时间为秒时，的面积为．当时，，，，即，解得：或（舍去）．当时，，，，即，解得：或（舍去）．综上所述：当或秒时，的面积为．故答案为：或．【点睛】本题考查了等腰直角三角形的性质，勾股定理，三角形面积公式，解一元二次方程，解题的关键是理解点的运动情况，注意分类讨论．3．（2023春•驻马店期末）如图，已知AG CF，AB⊥CF，垂足为B，AB=BC=3 ，点P是射线AG上的动点（点P不与点A重合），点Q是线段CB上的动点，点D是线段AB的中点，连接PD并延长交BF于点E，连接PQ，设AP=2t，CQ=t，当PQE是以PE为腰的等腰三角形时，t的值为．【答案】或【分析】以B为原点、直线CF为x轴，直线AB为y轴，建立直角坐标系，先证明AP=BE，即可得E点坐标为(2t,0)，CQ=t，BQ=3-t，P点坐标为(-2t,3)，C点坐标为(-3,0)，A点坐标为(0,3)，Q点坐标为(t-2,0)，根据Q点在线段BC上，P点不与A点重合，可得0＜t＜3，进而有BE=2t，BQ=3-t，QE=BQ+EB=3+t，利用勾股定理有：，，，根据PQE是以PE为腰的等腰三角形，分类讨论：当PQ=PE时，当QE=PE时两种情况，即可求解．【详解】以B为原点、直线CF为x轴，直线AB为y轴，建立直角坐标系，如图，∵，AB⊥CF，∴AB⊥AG，∴∠GAB=∠ABF=90°，∵D点为AB中点，∴AD=BD，∴结合∠ADP=∠BDE可得APD≌△BED，∴AP=BE，∵AP=2t，∴BE=2t，∴E点坐标为(2t,0)，∵AB=BC=3，∴CQ=t，即BQ=3-t，P点坐标为(-2t,3)，C点坐标为(-3,0)，A点坐标为(0,3)，∴Q点坐标为(t-3,0)，∵Q点在线段BC上，P点不与A点重合，∴0＜t＜3，∵BE=2t，BQ=3-t，∴QE=BQ+EB=3+t，∴利用勾股定理有：，，，根据PQE是以为腰的等腰三角形，分类讨论：当PQ=PE时，有，整理：，解得（负值舍去），当QE=PE时，有，整理：，解得（0舍去），综上所述：t的值可以为，．故答案为：，．【点睛】本题考查了等腰三角形的性质、构建直角坐标系、勾股定理、全等三角形的判定与性质、一元二次方程的应用等知识，构建直角坐标系是快速解答此题的关键．解答时，需注意分类讨论的思想．4．（2023春·广东江门·九年级校考期中）如图，是边长为6cm的等边三角形，动点，同时从，两点出发，分别沿，匀速移动，它们的速度都是2，当点到达点时，，两点都停止运动，设点的运动时间为，解答下列问题：(1)当为何值时，是以为直角的直角三角形？(2)是否存在，使四边形的面积是面积的若存在，求出的值；若不存在，请说明理由．【答案】(1)1(2)不存在，理由见解析【分析】（1）当时，利用直角三角形的性质建立方程，解方程即可得；（2）假设存在某一时刻，使四边形的面积是面积的，从而可得，过点作于点，利用直角三角形的性质和勾股定理可得，再利用三角形的面积公式建立方程，然后利用一元二次方程根的判别式进行分析即可得出答案．【详解】（1）由题意得：，，为等边三角形，，当点到达点时，，则，∵，，，即，解得，符合题意；（2）不存在，使四边形的面积是面积的，理由如下：假设存在某一时刻，使四边形的面积是面积的，由（1）得：，，如图，过点作于点，，，，整理得：，此方程根的判别式为，方程无解，所以假设不成立，即不存在，使四边形的面积是面积的．【点睛】本题考查了等边三角形的性质、含角的直角三角形的性质、勾股定理、一元二次方程的应用等知识点，正确建立关于时间的方程是解题关键．5．（2023春·江苏宿迁·九年级统考期末）如图，在ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P 从点A出发沿边AB向点B以2cm/s的速度移动，同时动点Q从点B出发沿边BC向点C以4cm/s的速度移动，当P运动到B点时P、Q两点同时停止运动，设运动时间为ts．(1)BP＝cm；BQ＝cm；（用t的代数式表示）(2)D是AC的中点，连接PD、QD，t为何值时PDQ的面积为40cm2【答案】(1)（12﹣2t）；4t(2)t＝2或4【分析】（1）根据速度×时间=路程，列出代数式即可；（2）如图，过点D作DH⊥BC于H，利用三角形中位线定理求得DH的长度；然后根据题意和三角形的面积列出方程，求出方程的解即可．【详解】（1）根据题意得：AP＝2tcm，BQ＝4tcm，所以BP＝（12﹣2t）cm．故答案是：（12﹣2t）；4t．（2）如图，过点D作DH⊥BC于H，∵∠B＝90°，即AB⊥BC，∴AB∥DH，又∵D是AC的中点，∴BH=BC＝12cm，DH是ABC的中位线，∴DH AB＝6cm，根据题意，得-（12﹣2t）-（24﹣4t）×6-2t×12＝40，整理，得t2﹣6t+8＝0，解得：t1＝2，t2＝4，即当t＝2或4时，PBQ的面积是40cm2．【点睛】本题主要考查了一元二次方程的应用，解题的关键是读懂题意，找到关键描述语，列出等量关系．6．（2023·浙江金华·九年级期中）如图，在中，厘米，厘米，于点D，动点P从点A出发以每秒1厘米的速度在线段上向终点D运动．设动点运动时间为t秒．（1）求的长；（2）当的面积为15平方厘米时，求t的值；（3）动点M从点C出发以每秒2厘米的速度在射线上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得？若存在，请求出t的值；若不存在，请说明理由．【答案】（1）12厘米；（2）6秒；（3）存在t的值为2或或，使得S PMD=S ABC．【分析】①根据等腰三角形性质和勾股定理解答即可；②根据直角三角形面积求出PD×DC×=15即可求出t；③根据题意列出PD、MD的表达式解方程组，由于M在D点左右两侧情况不同，所以进行分段讨论即可，注意约束条件．【详解】解：（1）∵AB=AC=13，AD⊥BC，∴BD=CD=5cm，且∠ADB=90°，∴AD2=AC2-CD2∴AD=12cm．（2）AP=t，PD=12-t，又∵由PDM面积为PD×DC=15，解得PD=6，∴t=6．（3）假设存在t，使得S PMD=S ABC．①若点M在线段CD上，即0≤t≤时，PD=12-t，DM=5-2t，由S PMD=S ABC，即×(12−t)(5−2t)＝5，2t2-29t+50=0解得t1=12.5（舍去），t2=2．②若点M在射线DB上，即≤t≤12．由S PMD=S ABC得(12−t)(2t−5)＝5，2t2-29t+70=0解得t 1＝，t 2＝．综上，存在t的值为2或或，使得S PMD=S ABC．【点睛】此题关键为利用三角形性质勾股定理以及分段讨论，在解方程时，注意解是否符合约束条件．7．（2023春·九年级单元测试）如图，在Rt ABC中，∠BAC＝90°，AB＝AC＝16 cm，AD为BC边上的高，动点P从点A出发，沿A→D方向以cm/s的速度向点D运动，过P点作矩形PDFE(E点在AC 上)，设ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t秒(0＜t＜8)．(1)经过几秒钟后，S1＝S2?(2)经过几秒钟后，S1＋S2最大？并求出这个最大值．【答案】(1) t＝4 (2) t＝6【分析】分别根据运动方式列出面积S1,S2关于t的函数关系，第一问令面积相等，第二问配方求最值. 【详解】解：S1＝×8×t＝8t，S2＝t(8－t)＝－2t2＋16t，(1)由8t＝－2t2＋16t，解得t1＝4，t2＝0(舍去)，∴当t＝4秒时，S1＝S2(2)∵S1＋S2＝8t＋(－2t2＋16t)＝－2(t－6)2＋72，∴当t＝6时，S1＋S2最大，最大为72【点睛】关于x的两次三项式，可以配方化为只含一个变量的式子，再利用平方的非负性求最值,必要是需要引入二次函数的内容求最值.8．（2023春·江苏淮安·九年级统考期中）Rt ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒（1）如图1，过点P作PD⊥AC，交AB于D，若PBC与P AD的面积和是ABC的面积的，求t的值；（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与ABC重叠部分的面积为8，求t的值．【答案】（1）t1＝2，t2＝4；（2）t的值为或2时，重叠面积为8．【分析】（1）先求出ABC的面积，然后根据题意可得AP＝t，CP＝6﹣t，然后再PBC与P AD的面积和是ABC的面积的，列出方程、解方程即可解答；（2）根据不同时间段分三种情况进行解答即可.【详解】（1）∵Rt ABC中，∠ACB＝90°，AC＝BC＝6，∴S ABC＝×6×6＝18，∵AP＝t，CP＝6﹣t，∴△PBC与P AD的面积和＝t2+×6×（6﹣t），∵△PBC与P AD的面积和是ABC的面积的，∴t2+×6×（6﹣t）＝18×，解之，得t1＝2，t2＝4；（2）∵AP＝t，PQ＝2AP，∴PQ＝2t，①如图1，当0≤t≤2时，S＝（2t）2﹣t2＝t2＝8，解得：t1＝，t2＝﹣（不合题意，舍去），②如图2，当2≤t≤3时，S＝×6×6﹣t2﹣（6﹣2t）2＝12t﹣t2＝8，解得：t1＝4（不合题意，舍去），t2＝（不合题意，舍去），③如图3，当3≤t≤6时，S＝6×6﹣t2＝8，解得：t1＝2，t2＝﹣2（不合题意，舍去），综上，t的值为或2时，重叠面积为8．【点睛】本题考查了三角形和矩形上的动点问题，根据题意列出方程和分情况讨论是解答本题的关键.【类型2 利用一元二次方程解决四边形中的动点问题】1．（2023春·陕西渭南·九年级统考期末）如图，在矩形中，点是上的一个动点，把沿向矩形内部折叠，当点的对应点恰好落在的平分线上时，的长为．【答案】或【分析】过点A1作A1F⊥BC于F，根据等腰直角三角形的判定可得为等腰直角三角形，设CF==x，从而得出BF= 7－x，CA1=，然后根据折叠的性质可得AB==5，再利用勾股定理求出x，即可求出结论．【详解】解：过点A1作A1F⊥BC于F∵四边形ABCD为矩形，平分∴∴△为等腰直角三角形，设CF==x则BF=BC－CF=7－x，CA1==由折叠的性质可得AB==5在Rt中，即解得：x1=3，x2=4∴CA1=或故答案为：或．【点睛】此题考查的是矩形与折叠问题，掌握矩形的性质、折叠的性质、勾股定理、等腰直角三角形的判定及性质和解一元二次方程是解决此题的关键．2．（2023春·河北邯郸·九年级统考期中）如图所示，A、B、C、D为矩形的四个顶点，，，动点P、Q分别从点A、C同时出发，点P以的速度向B移动，一直到达B为止；点Q以的速度向D移动．当P、Q两点从出发开始秒时，点P和点Q的距离是．（若一点到达终点，另一点也随之停止运动）【答案】2或【分析】设当P、Q两点从出发开始x秒时，点P和点Q的距离是10cm，此时，，利用勾股定理即可得出关于x的一元二次方程，解之即可得出结论．【详解】解：设当P、Q两点从出发开始x秒时，点P和点Q的距离是，此时，，如图，过作于，∵四边形是矩形，∴四边形，是矩形，∴，，∴，则，根据题意得：，解得：，．答：当P、Q两点从出发开始到2秒或秒时，点P和点Q的距离是10cm．故答案为：2或．【点睛】本题考查了矩形的性质与判定，一元二次方程的应用以及勾股定理，利用勾股定理找出关于x的一元二次方程是解题的关键．3．（2023春·山东烟台·九年级统考期中）如图，在矩形中，，，动点P、Q分别以，的速度从点A，C同时出发，沿规定路线移动．(1)若点P从点A移动到点B停止，点Q随点P的停止而停止移动，问经过多长时间P，Q两点之间的距离是？(2)若点P沿着移动，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间的面积为？【答案】(1)或；(2)4秒或6秒．【分析】（1）过点P作于E，构造直角三角形，利用勾股定理即可求得；（2）根据点P的三个位置进行分类讨论，表示出的底和高，代入面积公式即可求得；【详解】（1）解：过点P作于E，设x秒后，点P和点Q的距离是．，∴，；∴经过或，P、Q两点之间的距离是；（2）解：连接．设经过后PBQ的面积为．①当时，，∴，即，解得；②当时，，，则，解得，（舍去）；③时，，则，解得（舍去）．综上所述，经过4秒或6秒，的面积为．【点睛】本题考查了动点问题，相关知识点有：勾股定理求长度，解一元二次方程等知识点，分类讨论是本题的解题关键．4．（2023春·浙江杭州·九年级期中）如图，点，分别在平行四边形的边，上，且，，，动点从点出发沿着线段向终点运动，同时点从点出发沿着折线段向终点运动，且它们同时到达终点，设点运动的路程为，的长度为，且（为常数，）．（1）求证：四边形是平行四边形．（2）求的长．（3）当时，①求的值；②连结，，当为直角三角形时，求所有满足条件的的值．【答案】（1）见解析；（2）8；（3）①2；②，，【分析】（1）根据已知证明即可得证；（2）根据题，当时，，令时，即可求得；（3）①当到达点时，点到达点，此时,则，令求得，可得，结合已知条件可得；②由①可得，是等边三角形，分情况讨论，当在上，时，根据含30度角的直角三角形的性质，可得；当时，过点分别作，垂足为,可得四边形是矩形，分别求得,根据勾股定理列出方程，解一元二次方程即可，当时，如图，过点作于点,同理通过勾股定理求得，当点在上时，观察图形可知不存在直角三角形．【详解】四边形是平行四边形；即四边形是平行四边形；（2）依题意，设点运动的路程为，的长度为，。
专题《一元二次方程中的动点问题专项训练(30道)》
专题一元二次方程中的动点问题专项训练（30道）【苏科版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，涵盖了一元二次方程中的动点问题所有类型！一．填空题（共7小题）1．（2022•峨边县模拟）在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒√2个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒，当t为时，△PQB为直角三角形．2．（2022春•衢江区校级期末）如图，B是AC上一点，且BC＝6cm，AB＝4cm，射线BD⊥AC，垂足为B，动点M从A出发以2cm/s的速度沿着AC向C运动，同时动点N从B出发以3cm/s的速度沿着射线BD向cm2，两动点运动了t（s），则t的值为．下运动，连接MN．当△BMN的面积为323．（2022•临清市一模）在Rt△ABC中，∠BAC＝90°，AB＝AC＝16cm，AD为BC边上的高，动点P从点A出发，沿A→D方向以√2cm/s的速度向点D运动．设△ABP的面积为S1，矩形PDFE的面积为S2，运动时间为t秒，则t＝秒时，S1＝2S2．4．（2022•于洪区校级模拟）如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝6cm，AB＝8cm，BC ＝14cm．动点P、Q都从点C同时出发，点P沿C→B方向做匀速运动，点Q沿C→D→A方向做匀速运动，当P、Q其中一点到达终点时，另一点也随之停止运动．若点P以1cm/s速度运动，点Q以2√2cm/s的速度运动，连接BQ、PQ．当时间t为秒时，△BQP的面积为24cm2．5．（2022秋•惠来县月考）如图，已知AB⊥BC，AB＝12cm，BC＝8cm．一动点N从C点出发沿CB方向以1cm/s的速度向B点运动，同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动，其中一点到达B点时另一点也随之停止，当△MNB的面积为24cm2时运动的时间t为秒．6．（2022秋•兰山区期末）如图，在Rt△ACB中，∠C＝90°，AC＝30cm，BC＝25cm，动点P从点C出发，沿CA方向运动，速度是2cm/s Q从点B出发，沿BC方向运动，速度是1cm/s，则经过s后，P，Q两点之间相距25cm．7．（2022秋•渭滨区期中）如图，A、B、C、D是矩形的四个顶点，AB＝16cm，BC＝6cm，动点P从点A出发，以3cm/s的速度向点B运动，直到点B为止；动点Q同时从点C出发，以2cm/s的速度向点D运动，当时间为时，点P和点Q之间的距离是10cm．二．解答题（共23小题）8．（2022秋•方城县期末）如图，已知等边三角形ABC的边长为6cm，点P从点A出发，沿A→C→B的方向以2cm/s的速度向终点B运动，同时点Q从点B出发，沿B→A的方向以1cm/s的速度向终点A运动．当点P运动到点B时，两点均停止运动．运动时间记为ts，请解决下列问题：（1）若点P在边AC上，当t为何值时，△APQ为直角三角形？（2）是否存在这样的t值，使△APQ的面积为2√3cm2？若存在，请求出t的值，若不存在，请说明理由．9．（2022秋•泗阳县期末）如图，在△ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P从点A出发沿边AB向点B以2cm/s的速度移动，同时动点Q从点B出发沿边BC向点C以4cm/s的速度移动，当P运动到B点时P、Q两点同时停止运动，设运动时间为ts．（1）BP＝cm；BQ＝cm；（用t的代数式表示）（2）D是AC的中点，连接PD、QD，t为何值时△PDQ的面积为40cm2？10．（2022春•淄川区期中）如图，在梯形ABCD中，AD∥BC，∠C＝∠D＝90°，BC＝16，CD＝12，AD ＝21．动点P从点D出发，沿线段DA的方向以每秒2个单位长度的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长度的速度向点B运动．点P，Q分别从点D，C同时出发，当点P运动到点A 时，点Q随之停止运动．设运动时间为t（s），当t为何值时，以B，P，Q三点为顶点的三角形为等腰三角形？11．（2022•红谷滩区校级模拟）如图所示，△ABC中，∠B＝90°，AB＝6cm，BC＝8cm．（1）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，如果P，Q分别从A，B同时出发，经过几秒，点P，Q之间的距离为√6cm？（2）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，如果P，Q分别从A，B同时出发，经过几秒，使△PBQ的面积等于8cm2？（3）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，几秒后，△PBQ的面积为1cm2？12．（2022秋•射阳县期末）如图，在矩形ABCD中，AB＝6cm，BC＝4cm，动点P从点A出发，以2cm/s的速度沿AB向点B移动，同时，点Q从点C出发，以1cm/s的速度沿CD向点D移动（点P到达点B停止时，点Q也随之停止运动），设点P运动时间为t秒．（1）试求当t为何值时四边形APQD为矩形；（2）P、Q两点出发多长时间，线段PQ的长度为5cm．13．（2022春•铜山区期末）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动．问：（1）几秒时△PBQ的面积等于8cm2；（2）几秒时△PDQ的面积等于28cm2；（3）几秒时PQ⊥DQ．14．（2022•宿迁三模）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点B出发沿线段BC、CD以2cm/s的速度向终点D运动；同时，点Q从点C出发沿线段CD、DA以1cm/s的速度向终点A运动（P、Q 两点中，只要有一点到达终点，则另一点运动立即停止）．（1）运动停止后，哪一点先到终点？另一点离终点还有多远？（2）在运动过程中，△APQ的面积能否等于22cm2？若能，需运动多长时间？若不能，请说明理由．15．（2022春•嘉兴期末）如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB＝6cm，AD＝2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/秒的速度向终点B移动，点Q以1厘米/秒的速度向D移动，当有一点到达终点时，另一点也停止运动．设运动的时间为t，问：（1）当t＝1秒时，四边形BCQP面积是多少？（2）当t为何值时，点P和点Q距离是3cm？（3）当t＝以点P、Q、D为顶点的三角形是等腰三角形．（直接写出答案）16．（2022秋•皇姑区校级月考）（1）求x2+6x+1的最小值；（2）求﹣2x2+6x+1的最大值；（3）如图，已知AB＝8，P上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，∠DAP＝60°，M，N分别是对角线AC，BE的中点，当点P在线段AB上移动时，设AP＝x，直接用含有x的代数式表示MN2，并直接写出MN2的最小值．17．（2022秋•宽城区校级月考）如图①，在矩形ABCD中，AB＝8，AD＝4．点P从点A出发，沿A→D→C→D运动，速度为每秒2个单位长度；点Q从点A出发向点B运动，速度为每秒1个单位长度．P、Q两点同时出发，点Q运动到点B时，两点同时停止运动，设点Q的运动时间为t（秒）．连接PQ、AC、CP、CQ．（1）点P到点C时，t＝；当点Q到终点时，PC的长度为；（2）用含t的代数式表示PD的长；（3）当三角形CPQ的面积为9时，求t的值．18．（2022春•大庆期中）如图，菱形ABCD中，AC，BD交于O，AC＝8cm，BD＝6cm，动点M从A出发沿AC方向以每秒2cm C，动点N从B出发沿BD方向以每秒1cm匀速直线运动到D，若M，N同时出发，问出发后几秒钟时，△MON的面积为菱形ABCD面积的11219．（2022秋•海州区校级月考）如图，在正方形ABCD中，AB＝5cm，动点P以√2cm/s的速度从点A出发，沿AC向点C移动，同时动点Q以1cm/s的速度从点C出发，沿CB向点B移动，设P、Q两点移动时间为ts（0＜t＜5）．在P、Q两点移动的过程中，PQ的长度能否等于√10cm？若能，求出此时t的值；若不能，请说明理由．20．（2022•曹县二模）如图，四边形ABCD中，AD∥BC，∠A＝90°，AD＝1cm，AB＝3cm，BC＝5cm，动点P从点B出发以1cm/s的速度沿BC的方向运动，动点Q从点C出发以2cm/s的速度沿CD方向运动，P、Q两点同时出发，当Q到达点D时停止运动，点P也随之停止，设运动的时间为ts（t＞0）（1）求线段CD的长；（2）t为何值时，线段PQ将四边形ABCD的面积分为1：2两部分？21．（2022秋•天宁区月考）如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．（1）求点Q的坐标；个平方单位？（2）当t为何值时，△APQ的面积为24522．（2022秋•镇江期中）在矩形ABCD中，AB＝12cm，BC＝6cm，点P从点A出发沿AB以2cm/s的速度向点B移动；同时，点Q从点B出发沿BC以1cm/s的速度向点C移动，点P运动到点B时，点Q也停止运动，几秒钟后△PQC的面积等于16cm2？23．（2022秋•丹阳市校级月考）如图，在△ABC中，∠B＝90°，AB＝BC＝10cm，点P从点A出发沿射线AB以1cm/s的速度做直线运动，点Q从点C出发沿射线BC以2cm/s的速度做直线运动．如果P，Q分别S△ABC？从A，B同时出发，经过几秒，S△PCQ=122524．（2022春•萧山区期中）如图，在Rt△ABC中，∠BCA＝90°，AC＝6cm，BC＝8cm．有一动点P从B 点出发，在射线BC方向移动，速度是2cm/s，在P点出发后2秒后另一个动点Q从A点出发，在射线AC 方向移动，速度是1cm/s．若设P出发后时间为t秒．（1）用含t的代数式分别表示线段AQ、PC的长度，并写出相应的t的取值范围．（2）连接AP、PQ，求使△APQ面积为3cm2时相应的t的值．（3）问是否存在这样的时间t，使AP平分∠BAC或者∠BAC的外角？如果存在，请求出t的值；如果不存在，请说明理由．25．（2022秋•营山县校级期中）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，问几秒钟时△PBQ的面积等于8cm226．（2022秋•淮安校级期中）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A沿边AB向点B 以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，问几秒后△PBQ的面积等于8cm2？27．（2022秋•武侯区期末）如图，AB＝200cm，O为AB的中点，OE⊥AB，P从A点以2cm/s的速度向B 运动，点Q从O点以3cm/s的速度运动向E运动，当P、Q两点运动多少时间时，△POQ的面积为1800cm2？28．（2022春•永嘉县期中）附加题（1）试用一元二次方程的求根公式，探索方程ax2+bx+c＝0（a≠0）的两根互为相反数的条件是．=．（2）已知x、y为实数，√3x−2+y2−4y+4=0，则xy（3）在直角梯形ABCD中，AD∥BC，∠C＝90度，BC＝16，AD＝21，DC＝12，动点P从点D出发，沿线段DA方向以每秒2个单位长度的速度运动，动点Q从点C出发，在线段CB以每秒1个单位长度的速度向点B运动．点P、Q分别从点D、C同时出发，当点P运动到点A时，点Q随之停止运动，设运动时间为t秒．①设△BPQ的面积为S，求S和t之间的函数关系式；②当t为何值时，以B、P、Q29．（2022秋•驻马店期末）如图，在矩形ABCD中，AB＝8cm，AD＝6cm，点F是CD延长线上一点，且DF＝2cm．点P、Q分别从A、C同时出发，以1cm/s的速度分别沿边AB、CB向终点B运动，当一点运动到终点B时，另一点也停止运动．FP、FQ分别交AD于E、M两点，连接PQ、AC，设运动时间为t（s）．（1）用含有t的代数式表示DM的长；（2）设△FCQ的面积为y（cm2），求y与t之间的函数关系式；（3）线段FQ能否经过线段AC的中点？若能，请求出此时t的值；若不能，请说明理由；（4）设△FPQ的面积为S（cm2），求S与t之间的函数关系式，并回答：在t的取值范围内，S是如何随t的变化而变化的？30．（2022春•文登区期中）如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝8cm，点P从A出发向C 以1cm/s的速度运动、点Q同时从C出发向B以1cm/s的速度运动，当一个点运动到终点时，该点停止运动，另一个点继续运动，当两个点都到达终点时也停止运动．？（1）几秒后，△CPQ的面积为Rt△ABC的面积的18（2）填空：①点经过秒，点P在线段AB的垂直平分线上．②点Q经过秒，点Q在∠BAC的平分线上．专题一元二次方程中的动点问题专项训练（30道）【苏科版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，涵盖了一元二次方程中的动点问题所有类型！一．填空题（共7小题）1．（2022•峨边县模拟）在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒√2个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒，当t为2或5+√5或5−√5时，△PQB为直角三角形．【分析】要使△PQB为直角三角形，显然只有∠PQB＝90°或∠PBQ＝90°，进而利用勾股定理分别分析得出PB2＝（6﹣t）2+（2﹣t）2，QB2＝（6﹣2t）2+22，PQ2＝（2t﹣t）2+t2＝2t2，再分别就∠PQB＝90°和∠PBQ＝90°讨论，求出符合题意的t值即可；【解答】解：作PG⊥OC于点G，在Rt△POG中，∵∠POQ＝45°，∴∠OPG＝45°，∵OP=√2t，∴OG＝PG＝t，∴点P（t，t），又∵Q（2t，0），B（6，2），根据勾股定理可得：PB2＝（6﹣t）2+（2﹣t）2，QB2＝（6﹣2t）2+22，PQ2＝（2t﹣t）2+t2＝2t2，①若∠PQB＝90°，则有PQ2+BQ2＝PB2，即：2t2+[（6﹣2t）2+22]＝（6﹣t）2+（2﹣t）2，整理得：4t2﹣8t＝0，解得：t1＝0（舍去），t2＝2，∴t＝2，②若∠PBQ＝90°，则有PB2+QB2＝PQ2，∴[（6﹣t）2+（2﹣t）2]+[（6﹣2t）2+22]＝2t2，整理得：t 2﹣10t +20＝0，解得：t ＝5±√5．∴当t ＝2或t ＝5+√5或t ＝5−√5时，△PQB 为直角三角形．故答案为：2或5+√5或5−√5．2．（2022春•衢江区校级期末）如图，B 是AC 上一点，且BC ＝6cm ，AB ＝4cm ，射线BD ⊥AC ，垂足为B ，动点M 从A 出发以2cm /s 的速度沿着AC 向C 运动，同时动点N 从B 出发以3cm /s 的速度沿着射线BD 向下运动，连接MN ．当△BMN 的面积为32cm 2，两动点运动了t （s ），则t 的值为 2−√22或2+√22或2+√62 ．【分析】分0＜t ＜2及2＜t ≤5两种情况考虑，当0＜t ＜2时，BM ＝（4﹣2t ）cm ，BN ＝3tcm ，根据△BMN 的面积为32cm 2，即可得出关于t 的一元二次方程，解之即可得出t 值；当2＜t ≤5时，BM ＝（2t ﹣4）cm ，BN ＝3tcm ，根据△BMN 的面积为3cm 2，即可得出关于t 的一元二次方程，解之取其符合题意的值即可得出结论．【解答】解：当0＜t ＜2时，BM ＝（4﹣2t ）cm ，BN ＝3tcm ，∴12（4﹣2t ）•3t =32，整理得：2t 2﹣4t +1＝0，解得：t 1=2−√22，t 2=2+√22；当2＜t ≤5时，BM ＝（2t ﹣4）cm ，BN ＝3tcm ，∴12（2t ﹣4）•3t =32，整理得：2t 2﹣4t ﹣1＝0，解得：t 3=2−√62（不合题意，舍去），t 4=2+√62． 综上所述，t 的值为2−√22或2+√22或2+√62． 故答案为：2−√22或2+√22或2+√62．3．（2022•临清市一模）在Rt △ABC 中，∠BAC ＝90°，AB ＝AC ＝16cm ，AD 为BC 边上的高，动点P 从点A 出发，沿A →D 方向以√2cm /s 的速度向点D 运动．设△ABP 的面积为S 1，矩形PDFE 的面积为S 2，运动时间为t 秒，则t ＝ 6 秒时，S 1＝2S 2．【分析】利用三角形的面积公式以及矩形的面积公式，表示出S 1和S 2，然后根据S 1＝2S 2，即可列方程求解．【解答】解：∵Rt △ABC 中，∠BAC ＝90°，AB ＝AC ＝16cm ，AD 为BC 边上的高，∴AD ＝BD ＝CD ＝8√2cm ，又∵AP =√2t ，则S 1=12AP •BD =12×8√2×√2t ＝8t ，PD ＝8√2−√2t ， ∵PE ∥BC ，∴∠AEP ＝∠C ＝45°，∠APE ＝∠ADC ＝90°，∴∠P AE ＝∠PEA ＝45°∴PE ＝AP =√2t ，∴S 2＝PD •PE ＝（8√2−√2t ）•√2t ，∵S 1＝2S 2，∴8t ＝2（8√2−√2t ）•√2t ，解得：t ＝6或0（舍弃）故答案是：6．4．（2022•于洪区校级模拟）如图，在直角梯形ABCD 中，AD ∥BC ，∠B ＝90°，AD ＝6cm ，AB ＝8cm ，BC ＝14cm ．动点P 、Q 都从点C 同时出发，点P 沿C →B 方向做匀速运动，点Q 沿C →D →A 方向做匀速运动，当P 、Q 其中一点到达终点时，另一点也随之停止运动．若点P 以1cm /s 速度运动，点Q 以2√2cm /s 的速度运动，连接BQ 、PQ ．当时间t 为 2 秒时，△BQP 的面积为24cm 2．【分析】由于点P 在线段CB 上运动，而点Q 沿C →D →A 方向做匀速运动，所以分两种情况讨论：①点Q 在CD 上；②点Q 在DA 上．针对每一种情况，都可以过Q 点作QG ⊥BC 于G ．由于点P 、Q 运动的时间为t （s ），可用含t 的代数式分别表示BP 、QG 的长度，然后根据三角形的面积公式列出S 与t 的函数关系式，并写出t 的取值范围，根据面积为24cm 2，列出方程，解方程并结合t 的范围取舍．【解答】解：如图1，过D 点作DH ⊥BC ，垂足为点H ，则有DH ＝AB ＝8cm ，BH ＝AD ＝6cm ．∴CH ＝BC ﹣BH ＝14﹣6＝8cm ．在Rt △DCH 中，∠DHC ＝90°，∴CD =√DH 2+CH 2=8√2cm ．当点P 、Q 运动的时间为t （s ），则PC ＝t ．①如图1，当点Q 在CD 上时，过Q 点作QG ⊥BC ，垂足为点G ，则QC ＝2√2t ．又∵DH ＝HC ，DH ⊥BC ，∴∠C ＝45°．∴在Rt △QCG 中，QG ＝QC •sin ∠C ＝2√2t ×sin45°＝2t ．又∵BP ＝BC ﹣PC ＝14﹣t ，∴S △BPQ =12BP ×QG =12（14﹣t ）×2t ＝14t ﹣t 2． 当Q 运动到D 点时所需要的时间t =2√2=√22√2=4．∴S ＝14t ﹣t 2（0＜t ≤4），当S ＝24时，14t ﹣t 2＝24，解得：t 1＝2，t 2＝12（舍）． ②如图2，当点Q 在DA 上时，过Q 点作QG ⊥BC ，垂足为点G ，则：QG ＝AB ＝8cm ，BP ＝BC ﹣PC ＝14﹣t ，∴S △BPQ =12BP ×QG =12（14﹣t ）×8＝56﹣4t ． 当Q 运动到A 点时所需要的时间t =2√2=√2+62√2=4+3√22． ∴S ＝56﹣4t （4＜t ≤4+3√22）， 当S ＝24时，56﹣4t ＝24，解得：t ＝8＞4+3√22，舍去， 综上，当t ＝2时，S ＝24，故答案为：2．5．（2022秋•惠来县月考）如图，已知AB ⊥BC ，AB ＝12cm ，BC ＝8cm ．一动点N 从C 点出发沿CB 方向以1cm /s 的速度向B 点运动，同时另一动点M 由点A 沿AB 方向以2cm /s 的速度也向B 点运动，其中一点到达B 点时另一点也随之停止，当△MNB 的面积为24cm 2时运动的时间t 为 2 秒．【分析】根据题意可知CN ＝tcm ，AM ＝2tcm ，进而可得出BN ＝（8﹣t ）cm ，BM ＝（12﹣2t ）cm ，根据△MNB 的面积为24cm 2，即可得出关于t 的一元二次方程，解之取其符合题意的值即可得出结论．【解答】解：根据题意可知CN ＝tcm ，AM ＝2tcm ，∴BN ＝（8﹣t ）cm ，BM ＝（12﹣2t ）cm ，∵△MNB 的面积为24cm 2，∴12×（12﹣2t ）×（8﹣t ）＝24， 整理得：t 2﹣14t +24＝0，解得：t 1＝2，t 2＝12（不合题意，舍去）．故答案为：2．6．（2022秋•兰山区期末）如图，在Rt △ACB 中，∠C ＝90°，AC ＝30cm ，BC ＝25cm ，动点P 从点C 出发，沿CA 方向运动，速度是2cm /s ；同时，动点Q 从点B 出发，沿BC 方向运动，速度是1cm /s ，则经过10 s 后，P ，Q 两点之间相距25cm ．【分析】设x 秒后P 、Q 两点相距25cm ，用x 表示出CP 、CQ ，根据勾股定理列出方程，解方程即可．【解答】解：设x 秒后P 、Q 两点相距25cm ，则CP ＝2xcm ，CQ ＝（25﹣x ）cm ，由题意得，（2x ）2+（25﹣x ）2＝252，解得，x 1＝10，x 2＝0（舍去），则10秒后P 、Q 两点相距25cm ．故答案是：10．7．（2022秋•渭滨区期中）如图，A 、B 、C 、D 是矩形的四个顶点，AB ＝16cm ，BC ＝6cm ，动点P 从点A 出发，以3cm /s 的速度向点B 运动，直到点B 为止；动点Q 同时从点C 出发，以2cm /s 的速度向点D 运动，当时间为 85s 或245s 时，点P 和点Q 之间的距离是10cm ．【分析】设当t 秒时PQ ＝10cm ，利用勾股定理得出即可．【解答】解：设当时间为t 时，点P 和点Q 之间的距离是10cm ，过点Q 作ON ⊥AB 于点N ，则QC ＝2tcm ，PN ＝（16﹣5t ）cm ，故62+（16﹣5t ）2＝100，解得：t 1=85，t 2=245， 即当时间为85s 或245s 时，点P 和点Q 之间的距离是10cm ，故答案为：85s 或245s ．二．解答题（共23小题）8．（2022秋•方城县期末）如图，已知等边三角形ABC 的边长为6cm ，点P 从点A 出发，沿A →C →B 的方向以2cm /s 的速度向终点B 运动，同时点Q 从点B 出发，沿B →A 的方向以1cm /s 的速度向终点A 运动．当点P 运动到点B 时，两点均停止运动．运动时间记为ts ，请解决下列问题：（1）若点P 在边AC 上，当t 为何值时，△APQ 为直角三角形？（2）是否存在这样的t 值，使△APQ 的面积为2√3cm 2？若存在，请求出t 的值，若不存在，请说明理由．【分析】（1）当点P 在边AC 上时，由题意知AP ＝2t ，AQ ＝6﹣t ，再分∠APQ ＝90°和∠AQP ＝90°两种情况分别求解即可；（2）分点P 在边AC 上和点P 在边AC 上两种情况，表示出S △APQ ，再根据△APQ 的面积为2√3cm 2列出关于t 的方程，解之即可．【解答】解：（1）∵△ABC 是等边三角形∴AB ＝BC ＝CA ＝6，∠A ＝∠B ＝∠C ＝60°，当点P 在边AC 上时，由题意知，AP ＝2t ，AQ ＝6﹣t ，当∠APQ ＝90°时，AP =12AQ ，即2t =12（6﹣t ），解得t ＝1.2，当∠AQP ＝90°时，AQ =12AP ，即6﹣t =12×2t ，解得t ＝3，所以，点P 在边AC 上，当t 为1.2s 或3s 时，△APQ 为直角三角形；（2）存在，①当点P 在边AC 上时，此时0≤t ≤3，过点P 作PD ⊥AB 于点D ，在Rt △APD 中，∠A ＝60°，AP ＝2t ，∴sin A =PD AP ，即sin60°=PD 2t =√32， ∴PD =√3t ，S △APQ =12AQ •PD =12（6﹣t ）•√3t ，由12（6﹣t ）•√3t =2√3得t 1=3+√5(不合题意，舍去)，t 2=3−√5； ②当点P 在边BC 上时，此时3≤t ≤6，如图，过点P 作PF ⊥AB 于点F ，在Rt △BPF 中，∠B ＝60°，BP ＝12﹣2t ，∴sin B =PF BP ，即sin60°=PF 12−2t =√32， ∴PF =√3(6−t)，S △APQ =12AQ •PF =12（6﹣t ）•√3(6−t)，由12（6﹣t ）•√3(6−t)=2√3得t 1＝4，t 2＝8（不合题意，舍去），因此，当t 的值是(3−√5)s 或4s 时，△APQ 的面积为2√3cm 2．9．（2022秋•泗阳县期末）如图，在△ABC 中，∠B ＝90°，AB ＝12cm ，BC ＝24cm ，动点P 从点A 出发沿边AB 向点B 以2cm /s 的速度移动，同时动点Q 从点B 出发沿边BC 向点C 以4cm /s 的速度移动，当P 运动到B 点时P 、Q 两点同时停止运动，设运动时间为ts ．（1）BP ＝ （12﹣2t ） cm ；BQ ＝ 4t cm ；（用t 的代数式表示）（2）D 是AC 的中点，连接PD 、QD ，t 为何值时△PDQ 的面积为40cm 2？【分析】（1）根据速度×时间＝路程列出代数式即可；（2）如图，过点D 作DH ⊥BC 于H ，利用三角形中位线定理求得DH 的长度；然后根据题意和三角形的面积列出方程，求出方程的解即可．【解答】解：（1）根据题意得：AP ＝2tcm ，BQ ＝4tcm ，所以BP ＝（12﹣2t ）cm ，故答案是：（12﹣2t ）；4t ；（2）如图，过点D 作DH ⊥BC 于H ，∵∠B ＝90°，即AB ⊥BC ．∴AB ∥DH ．又∵D 是AC 的中点，∴BH =12BC ＝12cm ，DH 是△ABC 的中位线． ∴DH =12AB ＝6cm ． 根据题意，得12×12×24−12×4t ×（12﹣2t ）−12×（24﹣4t ）×6−12×2t ×12＝40， 整理，得t 2﹣6t +8＝0．解得：t 1＝2，t 2＝4，即当t ＝2或4时，△PBQ 的面积是40cm 2．10．（2022春•淄川区期中）如图，在梯形ABCD 中，AD ∥BC ，∠C ＝∠D ＝90°，BC ＝16，CD ＝12，AD ＝21．动点P 从点D 出发，沿线段DA 的方向以每秒2个单位长度的速度运动，动点Q 从点C 出发，在线段CB 上以每秒1个单位长度的速度向点B 运动．点P ，Q 分别从点D ，C 同时出发，当点P 运动到点A 时，点Q 随之停止运动．设运动时间为t （s ），当t 为何值时，以B ，P ，Q 三点为顶点的三角形为等腰三角形？【分析】以B ，P ，Q 为顶点的三角形为等腰三角形有三种情况：当PB ＝PQ 时，当PQ ＝BQ 时，当BP ＝BQ 时，由等腰三角形的性质就可以得出结论．【解答】解：如图1，当PB ＝PQ 时，作PE ⊥BC 于E ，∴EQ =12BQ ， ∵CQ ＝t ，∴BQ ＝16﹣t ，∴EQ ＝8−12t ，∴EC ＝8−12t +t ＝8+12t ． ∴2t ＝8+12t ．解得：t =163．如图2，当PQ ＝BQ 时，作QE ⊥AD 于E ，∴∠PEQ ＝∠DEQ ＝90°，∵∠C＝∠D＝90°，∴∠C＝∠D＝∠DEQ＝90°，∴四边形DEQC是矩形，∴DE＝QC＝t，∴PE＝t，QE＝CD＝12．在Rt△PEQ中，由勾股定理，得PQ=√t2+144．16﹣t=√t2+144，解得：t=72；如图3，当BP＝BQ时，作PE⊥BC于E，∵CQ＝t，∴BP＝BQ＝BC﹣CQ＝16﹣t，∵PD＝2t，∴CE＝2t，∴BE＝16﹣2t，在Rt△BEP中，（16﹣2t）2+122＝（16﹣t）2，3t2﹣32t+144＝0，△＝（﹣32）2﹣4×3×144＝﹣704＜0，故方程无解．综上所述，t=163或72时，以B，P，Q三点为顶点的三角形为等腰三角形．11．（2022•红谷滩区校级模拟）如图所示，△ABC中，∠B＝90°，AB＝6cm，BC＝8cm．（1）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，如果P，Q分别从A，B同时出发，经过几秒，点P，Q之间的距离为√6cm？（2）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动，如果P，Q分别从A，B同时出发，经过几秒，使△PBQ的面积等于8cm2？（3）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，几秒后，△PBQ的面积为1cm2？【分析】（1）设经过x秒，点P，Q之间的距离为√6cm，根据勾股定理列式求解即可；（2）设经过y秒，使△PBQ的面积等于8cm2，由三角形的面积公式列式并求解即可；（3）分三种情况列方程求解即可：①点P在线段AB上，点Q在射线CB上；②点P在线段AB上，点Q 在射线CB上；点P在射线AB上，点Q在射线CB上．【解答】解：（1）设经过x秒，点P，Q之间的距离为√6cm，则AP＝x（cm），QB＝2x（cm），∵AB＝6cm，BC＝8cm∴PB＝（6﹣x）（cm），∵在△ABC中，∠B＝90°∴由勾股定理得：（6﹣x）2+（2x）2＝6化简得：5x2﹣12x+30＝0∵△＝（﹣12）2﹣4×5×30＝144﹣600＜0∴点P，Q之间的距离不可能为√6cm．（2）设经过x秒，使△PBQ的面积等于8cm2，由题意得：1（6﹣x）•2x＝82解得：x1＝2，x2＝4检验发现x1，x2均符合题意∴经过2秒或4秒，△PBQ的面积等于8cm2．（3）①点P在线段AB上，点Q在线段CB上设经过m秒，0＜m≤4，依题意有1（6﹣m）（8﹣2m）＝12∴m2﹣10m+23＝0解得；m1＝5+√2（舍），m2＝5−√2∴m＝5−√2符合题意；②点P在线段AB上，点Q在射线CB上设经过n秒，4＜n≤6，依题意有1（6﹣n）（2n﹣8）＝12∴n2﹣10n+25＝0解得n1＝n2＝5∴n＝5符合题意；③点P在射线AB上，点Q在射线CB上设经过k秒，k＞6，依题意有1（k﹣6）（2k﹣8）＝12解得k1＝5+√2，k2＝5−√2（舍）∴k＝5+√2符合题意；∴经过（5−√2）秒，5秒，（5+√2）秒后，△PBQ的面积为1cm2．12．（2022秋•射阳县期末）如图，在矩形ABCD中，AB＝6cm，BC＝4cm，动点P从点A出发，以2cm/s的速度沿AB向点B移动，同时，点Q从点C出发，以1cm/s的速度沿CD向点D移动（点P到达点B停止时，点Q也随之停止运动），设点P运动时间为t秒．（1）试求当t为何值时四边形APQD为矩形；（2）P、Q两点出发多长时间，线段PQ的长度为5cm．【分析】（1）根据矩形的对边相等得到AP＝PQ，由时间×速度＝路程求得线段AP、PQ的长度，然后等量关系AP＝PQ列出方程并解答；（2）过点P作PE⊥CD于点E，利用勾股定理列出关于t的方程，通过解方程求得答案．【解答】解：（1）∵四边形APQD为矩形，∴AP＝PQ，∴2t＝6﹣t，∴3t＝6，∴t＝2．（2）过点P作PE⊥CD于点E，∵∠A＝∠D＝∠DEP＝90°，∴四边形APED是矩形．∴AP＝DE＝2t，∴EQ＝CD﹣DE﹣CQ＝6﹣3t，在Rt△PQE中，PE2+EQ2＝PQ2，即（6﹣3t）2＝9，解得t1＝1，t2＝3，答：当出发1s或3s时，线段PQ的长度为5cm．13．（2022春•铜山区期末）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动．问：（1）几秒时△PBQ的面积等于8；（2）几秒时△PDQ的面积等于28cm2；（3）几秒时PQ⊥DQ．【分析】（1）表示出PB，QB的长，利用△PBQ的面积等于8cm2列式求值即可；（2）设出发秒x时△DPQ的面积等于28平方厘米，根据三角形的面积公式列出方程，再解方程即可；（3）如果PQ⊥DQ，则∠DQP为直角，得出△BPQ∽△CQD，即可得出BPCQ =BQCD，再设AP＝x，QB＝2x，得出6−x12−2x =2x6，求出x即可．【解答】解：（1）设x秒后△PBQ的面积等于8cm2．则AP＝x，QB＝2x．∴PB＝6﹣x．∴12×（6﹣x）2x＝8，解得x1＝2，x2＝4，答：2秒或4秒后△PBQ的面积等于8cm2；（2）设出发秒x时△DPQ的面积等于28cm2．∵S矩形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ＝S△DPQ∴12×6−12×12x−12×2x（6﹣x）−12×6×（12﹣2x）＝28，化简整理得x2﹣6x+8＝0，解得x1＝2，x2＝4，答：2秒或4秒后△PDQ的面积等于28cm2；（3）设x秒后PQ⊥DQ时，则∠DQP为直角，∴△BPQ∽△CQD，∴BPCQ =BQCD，设AP＝x，QB＝2x．∴6−x12−2x =2x6，∴2x2﹣15x+18＝0，解得：x=32或6，经检验x=32是原分式方程的根，x＝6不是原分式方程的根，当x＝6时，P点到达B点、Q点到达C点，此时PQ⊥DQ．答：32秒或6秒后PQ⊥DQ．14．（2022•宿迁三模）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点B出发沿线段BC、CD以2cm/s的速度向终点D运动；同时，点Q从点C出发沿线段CD、DA以1cm/s的速度向终点A运动（P、Q 两点中，只要有一点到达终点，则另一点运动立即停止）．（1）运动停止后，哪一点先到终点？另一点离终点还有多远？（2）在运动过程中，△APQ的面积能否等于22cm2？若能，需运动多长时间？若不能，请说明理由．【分析】（1）根据题意可以分别计算出两个点运动到终点的时间，从而可以解答本题；（2）先判断，然后计算出相应的时间即可解答本题．【解答】解：（1）点P 从开始到运动停止用的时间为：（12+6）÷2＝9s ，点Q 从开始到运动停止用的时间为：（6+12）÷1＝18s ，∵9＜18，只要有一点到达终点，则另一点运动立即停止，∴点P 先到终点，此时点Q 离终点的距离是：（6+12）﹣1×9＝9cm ，答：点P 先到终点，此时点Q 离终点的距离是9cm ；（2）在运动过程中，△APQ 的面积能等于22cm 2，当P 从点B 运动到点C 的过程中，设点P 运动时间为as ，∵△APQ 的面积能否等于22cm 2，∴12×6−2a×62−(12−2a)×a 2−(6−a)×122=22，解得，此方程无解；当点P 从C 到D 的过程中，设点P 运动的时间为（b +6）s ，∵△APQ 的面积能否等于22cm 2，∴12×6−(6+2b)×122−b(6−2b)2=22，解得，b 1＝1，b 2＝14（舍去），即需运动6+1＝7s ，△APQ 的面积能等于22cm 2．15．（2022春•嘉兴期末）如图，长方形ABCD （长方形的对边相等，每个角都是90°），AB ＝6cm ，AD ＝2cm ，动点P 、Q 分别从点A 、C 同时出发，点P 以2厘米/秒的速度向终点B 移动，点Q 以1厘米/秒的速度向D 移动，当有一点到达终点时，另一点也停止运动．设运动的时间为t ，问：（1）当t ＝1秒时，四边形BCQP 面积是多少？（2）当t 为何值时，点P 和点Q 距离是3cm ？（3）当t ＝ 3+√72，3−√72，65，−6+2√333． 以点P 、Q 、D 为顶点的三角形是等腰三角形．（直接写出答案）【分析】（1）如图1，当t＝1时，就可以得出CQ＝1cm，AP＝2cm，就有PB＝6﹣2＝4cm，由梯形的面积就可以得出四边形BCQP的面积；（2）如图1，作QE⊥AB于E，在Rt△PEQ中，由勾股定理建立方程求出其解即可，如图2，作PE⊥CD 于E，在Rt△PEQ中，由勾股定理建立方程求出其解即可；（3）分情况讨论，如图3，当PQ＝DQ时，如图4，当PD＝PQ时，如图5，当PD＝QD时，由等腰三角形的性质及勾股定理建立方程就可以得出结论．【解答】解：（1）如图1，∵四边形ABCD是矩形，∴AB＝CD＝6，AD＝BC＝2，∠A＝∠B＝∠C＝∠D＝90°．∵CQ＝1cm，AP＝2cm，∴AB＝6﹣2＝4cm．=5cm2．∴S=2(1+4)2答：四边形BCQP面积是5cm2；（2）如图1，作QE⊥AB于E，∴∠PEQ＝90°，∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴QE＝BC＝2cm，BE＝CQ＝t．∵AP＝2t，∴PE＝6﹣2t﹣t＝6﹣3t．在Rt△PQE中，由勾股定理，得（6﹣3t）2+4＝9，解得：t=6±√5．3如图2，作PE⊥CD于E，∴∠PEQ＝90°．∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴PE＝BC＝2cm，BP＝CE＝6﹣2t．∵CQ ＝t ，∴QE ＝t ﹣（6﹣2t ）＝3t ﹣6在Rt △PEQ 中，由勾股定理，得（3t ﹣6）2+4＝9，解得：t =6±√53． 综上所述：t =6−√53或6+√53；（3）如图3，当PQ ＝DQ 时，作QE ⊥AB 于E ，∴∠PEQ ＝90°，∵∠B ＝∠C ＝90°，∴四边形BCQE 是矩形，∴QE ＝BC ＝2cm ，BE ＝CQ ＝t ．∵AP ＝2t ，∴PE ＝6﹣2t ﹣t ＝6﹣3t ．DQ ＝6﹣t ．∵PQ ＝DQ ，∴PQ ＝6﹣t ．在Rt △PQE 中，由勾股定理，得（6﹣3t ）2+4＝（6﹣t ）2，解得：t =3±√72． 如图4，当PD ＝PQ 时，作PE ⊥DQ 于E ，∴DE ＝QE =12DQ ，∠PED ＝90°． ∵∠B ＝∠C ＝90°，∴四边形BCQE 是矩形，∴PE ＝BC ＝2cm ．∵DQ ＝6﹣t ，∴DE =6−t 2． ∴2t =6−t 2，解得：t =65；如图5，当PD ＝QD 时，∵AP ＝2t ，CQ ＝t ，∴DQ ＝6﹣t ，∴PD ＝6﹣t ．在Rt △APD 中，由勾股定理，得4+4t 2＝（6﹣t ）2，解得t 1=−6+2√333，t 2=−6−2√333（舍去）． 综上所述：t =3+√72，3−√72，65，−6+2√333． 故答案为：3+√72，3−√72，65，−6+2√333．16．（2022秋•皇姑区校级月考）（1）求x 2+6x +1的最小值；（2）求﹣2x 2+6x +1的最大值；（3）如图，已知AB ＝8，P 为线段AB 上的一个动点，分别以AP ，PB 为边在AB 的同侧作菱形APCD 和菱形PBFE ，点P ，C ，E 在一条直线上，∠DAP ＝60°，M ，N 分别是对角线AC ，BE 的中点，当点P 在线段AB 上移动时，设AP ＝x ，直接用含有x 的代数式表示MN 2，并直接写出MN 2的最小值．【分析】（1）将代数式配方，由于二次项系数大于0，代数式有最小值，根据配方式可得最小值；（2）将代数式配方，由于二次项系数小于0，代数式有最大值，根据配方式可得最大值；（3）连接PM 、PN ．首先证明∠MPN ＝90°，设P A ＝x ，则PB ＝8﹣x ，PM =12x ，PN =√3（4−12x ），构建二次函数，利用二次函数的性质即可解决问题．【解答】解：（1）x 2+6x +1＝（x +3）2﹣8，当x ＝﹣3时，x 2+6x +1有最小值，最小值是﹣8；（2）﹣2x 2+6x +1＝﹣2（x −32）2+112， 当x =32时，﹣2x 2+6x +1有最大值，最大值是112；（3）连接PM 、PN ．∵四边形APCD ，四边形PBFE 是菱形，∠DAP ＝60°，∴∠APC ＝120°，∠EPB ＝60°，∵M ，N 分别是对角线AC ，BE 的中点，∴∠CPM =12∠APC ＝60°，∠EPN =12∠EPB ＝30°， ∴∠MPN ＝60°+30°＝90°，设P A ＝x ，则PB ＝8﹣x ，PM =12x ，=√3（4−12x ），MN 2＝（12x ）2+[√3（4−12x ）]2＝x 2﹣12x +48＝（x ﹣6）2+12， ∴x ＝6时，MN 2有最小值，最小值为12，故答案为：12．17．（2022秋•宽城区校级月考）如图①，在矩形ABCD 中，AB ＝8，AD ＝4．点P 从点A 出发，沿A →D →C →D 运动，速度为每秒2个单位长度；点Q 从点A 出发向点B 运动，速度为每秒1个单位长度．P 、Q 两点同时出发，点Q 运动到点B 时，两点同时停止运动，设点Q 的运动时间为t （秒）．连接PQ 、AC 、CP 、CQ ．（1）点P 到点C 时，t ＝ 6 ；当点Q 到终点时，PC 的长度为 4 ；（2）用含t 的代数式表示PD 的长；（3）当三角形CPQ 的面积为9时，求t 的值．。
专题05动点问题与一元二次方程解析版
专题05 动点问题与一元二次方程1．如图，在△ABC 中，∠ABC ＝90°，AB ＝8cm ，BC ＝6cm ．动点P ，Q 分别从点A ，B 同时开始移动，点P 的速度为1cm /秒，点Q 的速度为2cm /秒，点Q 移动到点C 后停止，点P 也随之停止运动．下列时间瞬间中，能使△PBQ 的面积为15cm 2的是（ ）A ．2秒钟B ．3秒钟C ．4秒钟D ．5秒钟解：设动点P ，Q 运动t 秒后，能使△PBQ 的面积为15cm 2，则BP 为（8﹣t ）cm ，BQ 为2tcm ，由三角形的面积计算公式列方程得，12×（8﹣t ）×2t ＝15，解得t 1＝3，t 2＝5（当t ＝5时，BQ ＝10，不合题意，舍去）．∴动点P ，Q 运动3秒时，能使△PBQ 的面积为15cm 2．答案：B ．2．如图，Rt △ABC 中，∠B ＝90°，AC ＝10cm ，BC ＝8cm ，现有两个动点P 、Q 分别从点A 和点B 同时出发，其中点P 以1cm /s 的速度，沿AB 向终点B 移动；点Q 以2cm /s 的速度沿BC 向终点C 移动，其中一点到终点，另一点也随之停止．连接PQ ，若经x 秒后P ，Q 两点之间的距离为x 的值为 2或25 ．解：∵∠B ＝90°，AC ＝10cm ，BC ＝8cm ，∴AB ＝6cm ．∴BQ ＝2x ，PB ＝6﹣x ．∵P ，Q 两点之间的距离为∴BQ 2+PB 2＝PQ 2，∴（2x ）2+（6﹣x ）2＝（2，整理得，5x2﹣12x+4＝0，解得x1＝2，x2=2 5．答案：2或2 5．3．（易错题）一个正方体物体沿斜坡向下滑动，其截面如图所示．正方形DEFH的边长为2米，坡角∠A＝30°，∠B＝90°，BC＝6米．当正方形DEFH运动到什么位置，即当AE＝ 143 米时，有DC2＝AE2+BC2．解：如图，连接CD，设AE＝x米，∵坡角∠A＝30°，∠B＝90°，BC＝6米，∴AC＝12米，∴EC＝（12﹣x）米，∵正方形DEFH的边长为2米，即DE＝2米，∴DC2＝DE2+EC2＝4+（12﹣x）2，AE2+BC2＝x2+36，∵DC2＝AE2+BC2，∴4+（12﹣x）2＝x2+36，解得：x=143米．答案：14 3．4．如图，A、B、C、D为矩形的四个顶点，AB＝16cm，AD＝6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2cm/s的速度向D移动．（1）P、Q两点从出发开始到几秒时，四边形PBCQ的面积为33cm2；（2）P、Q两点从出发开始到几秒时，点P和点Q的距离是10cm．解：（1）设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2，则PB＝（16﹣3x）cm，QC＝2xcm，根据梯形的面积公式得12（16﹣3x+2x）×6＝33，解之得x＝5，（2）设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，作QE⊥AB，垂足为E，则QE＝AD＝6，PQ＝10，∵PA＝3t，CQ＝BE＝2t，∴PE＝AB﹣AP﹣BE＝|16﹣5t|，由勾股定理，得（16﹣5t）2+62＝102，解得t1＝4.8，t2＝1.6．答：（1）P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2；（2）从出发到1.6秒或4.8秒时，点P和点Q的距离是10cm．5．如图，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动．（1）如果P，Q同时出发，几秒钟后，可使PQ的长为（2）点P，Q在移动过程中，是否存在某一时刻，使得△PCQ的面积等于△ABC的面积的一半．若存在，求出运动的时间；若不存在，说明理由．解：（1）设x 秒钟后，可使PQ 的长为，由题意得：（6﹣x ）2+（2x ）2＝（2，解得：x ＝2或x =25，答：P 、Q 同时出发2或25秒钟后，可使PQ 的长为（2）不存在．理由：设y 秒时，△PCQ 的面积等于△ABC 的面积的一半，由题意得：12（6﹣y ）•2y =12×12×6×8，整理，得y 2﹣6y +12＝0，∵Δ＝36﹣4×12＜0，∴方程无解，即：不存在．6．如图，在直角坐标系xOy 中，四边形OACB 为矩形，C 点的坐标为（3，6），一个单位长度是1cm ，若点P 从O 点沿OA 向点A 以1cm /s 的速度运动，点Q 从点A 沿AC 以2cm /s 的速度运动，如果P ，Q 分别从O ，A 同时出发，问：（1）经过多长时间△PAQ 的面积为2cm 2？（2）△PAQ 的面积能否达到3cm 2？请说明理由；（3）经过多长时间，P 、Q ？解：（1）设经过xs，△PAQ的面积为2cm2，由题意得12（3﹣x）•2x＝2，解得x1＝1，x2＝2，所以经过1秒或2秒时，△PAQ的面积为2cm2；（2）设经过xs，△PAQ的面积为3cm2，由题意得12（3﹣x）•2x＝3，即x2﹣3x+3＝0，因为b2﹣4ac＝﹣3＜0，所以此方程没有实数根，所以△PAQ的面积不能达到3cm2；（3）设经过t秒，P、Q，根据题意得（2t）2+（3﹣t）2＝17，∴t1＝﹣0.8（不合题意舍去），t2＝2，答：经过2秒后，P、Q．7．（易错题）如图，长方形ABCD中（长方形的对边平行且相等，每个角都是90°），AB＝6cm，AD＝2cm，动点P，Q分别从点A，C同时出发，点P以2cm/s的速度向终点B移动，点Q以1cm/s的速度向点D移动，当有一点到达终点时，另一点也停止运动，设运动的时间为t（s），问：（1）当t＝1s时，四边形BCQP面积是多少？（2）当t为何值时，点P和点Q距离是3cm？（3）当t为何值时，以点P，Q，D为顶点的三角形是等腰三角形．解：（1）∵四边形ABCD是矩形，∴AB＝CD＝6cm，AD＝BC＝2cm，∠A＝∠B＝∠C＝∠D＝90°．∵CQ＝1cm，AP＝2cm，∴PB＝6﹣2＝4（cm）．∴S=(14)×22=5（cm2）．答：四边形BCQP面积是5cm2；（2）如图1，当t＜2时，作QE⊥AB于E，∴∠PEQ＝90°，∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴QE＝BC＝2cm，BE＝CQ＝t（cm）．∵AP＝2t（cm），∴PE＝6﹣2t﹣t＝（6﹣3t）cm．在Rt△PQE中，由勾股定理，得（6﹣3t）2+4＝9，解得：t∵t＜2，∴t=3．如图2，当t＞2时，作QE⊥CD于E，∴∠PEQ＝90°．∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴PE＝BC＝2cm，BP＝CE＝6﹣2t．∵CQ＝t，∴QE＝t﹣（6﹣2t）＝3t﹣6在Rt△PEQ中，由勾股定理，得（3t﹣6）2+4＝9，．解得：t=3∵t＞2，∴t=综上所述：t=（3）如图3，当PQ＝DQ时，作QE⊥AB于E，∴∠PEQ＝90°，∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴QE＝BC＝2cm，BE＝CQ＝t（cm）．∵AP＝2t，∴PE＝6﹣2t﹣t＝6﹣3t．DQ＝6﹣t．∵PQ＝DQ，∴PQ＝6﹣t．在Rt△PQE中，由勾股定理，得（6﹣3t）2+4＝（6﹣t）2，解得：t如图4，当PD＝PQ时，作PE⊥DQ于E，∴DE ＝QE =12DQ ，∠PED ＝90°．∵∠A ＝∠D ＝90°，∴四边形APED 是矩形，∴PE ＝AD ＝2cm ．DE ＝AP ＝2t ，∵DQ ＝6﹣t ，∴DE =6−t 2．∴2t =6−t 2，解得：t =65；如图5，当PD ＝QD 时，∵AP ＝2t ，CQ ＝t ，∴DQ ＝6﹣t ，∴PD ＝6﹣t ．在Rt △APD 中，由勾股定理，得4+4t 2＝（6﹣t ）2，解得t 1t 2．综上所述：t =或65或8．（易错题）如图所示，△ABC 中，∠B ＝90°，AB ＝6cm ，BC ＝8cm ．（1）点P 从点A 开始沿AB 边向B 以1cm /s 的速度移动，点Q 从B 点开始沿BC 边向点C 以2cm /s 的速度移动．如果P，Q分别从A，B同时出发，经过几秒，使△PBQ的面积等于8cm2？（2）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．（3）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，问几秒后，△PBQ的面积为1cm2？解：（1）设经过x秒，使△PBQ的面积等于8cm2，依题意有12（6﹣x）•2x＝8，解得x1＝2，x2＝4，经检验，x1，x2均符合题意．故经过2秒或4秒，△PBQ的面积等于8cm2；（2）设经过y秒，线段PQ能否将△ABC分成面积相等的两部分，依题意有△ABC的面积=12×6×8＝24，12（6﹣y）•2y＝12，y2﹣6y+12＝0，∵Δ＝b2﹣4ac＝36﹣4×12＝﹣12＜0，∴此方程无实数根，∴线段PQ不能将△ABC分成面积相等的两部分；（3）①点P在线段AB上，点Q在线段CB上（0＜m≤4），设经过m秒，依题意有12（6﹣m ）（8﹣2m ）＝1，m 2﹣10m +23＝0，解得m 1＝5m 2＝5经检验，m 1＝5+∴m ＝5②点P 在线段AB 上，点Q 在射线CB 上（4＜n ≤6），设经过n 秒，依题意有12（6﹣n ）（2n ﹣8）＝1，n 2﹣10n +25＝0，解得n 1＝n 2＝5，经检验，n ＝5符合题意．③点P 在射线AB 上，点Q 在射线CB 上（k ＞6），设经过k 秒，依题意有12（k ﹣6）（2k ﹣8）＝1，k 2﹣10k +23＝0，解得k 1＝5+k 2＝5经检验，k 1＝5∴k ＝5综上所述，经过（55秒，（5+PBQ 的面积为1cm 2．9．如图，已知矩形ABCD 的边长AB ＝3cm ，BC ＝6cm ．某一时刻，动点M 从A 点出发沿AB 方向以1cm /s 的速度向B 点匀速运动；同时，动点N 从D 点出发沿DA 方向以2cm /s 的速度向A 点匀速运动，问：（1）经过多少时间，△AMN 的面积等于矩形ABCD 面积的19？（2）是否存在时间t ，使△AMN 的面积达到3.5cm 2？若存在，求出时间t ；若不存在，说明理由．解：（1）设经过ts，△AMN的面积等于矩形ABCD面积的19，则DN＝2tcm，AM＝tcm，AN＝AD﹣DN＝（6﹣2t）cm，∴12AN•AM=19AD•AB，即12（6﹣2t）t=19×6×3，整理得：t2﹣3t+2＝0，即（t﹣1）（t﹣2）＝0，解得：t1＝1，t2＝2，则经过1s或2s，△AMN的面积等于矩形ABCD面积的1 9；（2）不存在，理由为：假设存在时间ts，使△AMN的面积达到3.5cm2，则12AN•AM＝3.5，整理得：2t2﹣6t+7＝0，∵Δ＝36﹣56＝﹣20＜0，∴方程没有实数根，则△AMN的面积不能达到3.5cm2．10．已知：如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．（1）如果P，Q分别从A，B同时出发，那么几秒后，△PBQ的面积等于6cm2？（2）如果P，Q分别从A，B同时出发，那么几秒后，PQ的长度等于5cm？（3）在（1）中，△PQB的面积能否等于8cm2？说明理由．解：（1）设经过x秒以后△PBQ面积为612×（5﹣x）×2x＝6整理得：x2﹣5x+6＝0解得：x＝2或x＝3答：2或3秒后△PBQ的面积等于6cm2（2）当PQ＝5时，在Rt△PBQ中，∵BP2+BQ2＝PQ2，∴（5﹣t）2+（2t）2＝52，5t2﹣10t＝0，t（5t﹣10）＝0，t1＝0（舍弃），t2＝2，∴当t＝2时，PQ的长度等于5cm．（3）设经过x秒以后△PBQ面积为8，1×（5﹣x）×2x＝82整理得：x2﹣5x+8＝0△＝25﹣32＝﹣7＜0∴△PQB的面积不能等于8cm2．11．（易错题）如图，在矩形ABCD中，BC＝20cm，P、Q、M、N分别从A、B、C、D出发沿AD，BC，CB，DA 方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．已知在相同时间内，若BQ＝xcm（x≠0），则AP＝2xcm，CM＝3xcm，DN＝x2cm．（1）当x为何值时，以PQ，MN为两边，以矩形的边（AD或BC）的一部分为第三边构成一个三角形；（2）当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形；（3）以P、Q、M、N为顶点的四边形能否为等腰梯形？如果能，求x的值；如果不能，请说明理由．解：（1）当点P与点N重合或点Q与点M重合时，以PQ，MN为两边，以矩形的边（AD或BC）的一部分为第三边可能构成一个三角形．①当点P与点N重合时，由x2+2x＝20，得x1=1，x2=1（舍去）．因为BQ+CM＝x+3x＝41）＜20，此时点Q与点M不重合．所以x1符合题意．②当点Q与点M重合时，由x+3x＝20，得x＝5．此时DN＝x2＝25＞20，不符合题意．故点Q与点M不能重合．所以所求x1．（2）由（1）知，点Q只能在点M的左侧，①当点P在点N的左侧时，由20﹣（x+3x）＝20﹣（2x+x2），解得x1＝0（舍去），x2＝2．当x＝2时四边形PQMN是平行四边形．②当点P在点N的右侧时，由20﹣（x+3x）＝（2x+x2）﹣20，解得x1＝﹣10（舍去），x2＝4．当x＝4时四边形NQMP是平行四边形．所以当x＝2或x＝4时，以P，Q，M，N为顶点的四边形是平行四边形．（3）过点Q，M分别作AD的垂线，垂足分别为点E，F．由于2x＞x，所以点E一定在点P的左侧．若以P，Q，M，N为顶点的四边形是等腰梯形，则点F一定在点N的右侧，且PE＝NF，即2x﹣x＝x2﹣3x．解得x1＝0（舍去），x2＝4．由于当x＝4时，以P，Q，M，N为顶点的四边形是平行四边形，所以以P，Q，M，N为顶点的四边形不能为等腰梯形．12．（易错题）如图，在边长为12cm的等边三角形ABC中，点P从点A开始沿AB边向点B以每秒钟1cm的速度移动，点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动．若P、Q分别从A、B同时出发，其中任意一点到达目的地后，两点同时停止运动，求：（1）经过6秒后，BP＝ 6 cm，BQ＝ 12 cm；（2）经过几秒后，△BPQ是直角三角形？（3）经过几秒△BPQ的面积等于2？解：（1）由题意，得AP＝6cm，BQ＝12cm．∵△ABC是等边三角形，∴AB＝BC＝12cm，∴BP＝12﹣6＝6cm．答案：6、12．（2）∵△ABC是等边三角形，∴AB＝BC＝12cm，∠A＝∠B＝∠C＝60°，当∠PQB＝90°时，∴∠BPQ＝30°，∴BP＝2BQ．∵BP＝12﹣x，BQ＝2x，∴12﹣x＝2×2x，∴x=12 5，当∠QPB＝90°时，∴∠PQB＝30°，∴BQ＝2PB，∴2x＝2（12﹣x），x＝6答6秒或125秒时，△BPQ是直角三角形；（3）作QD⊥AB于D，∴∠QDB＝90°，∴∠DQB＝30°，∴DB=12BQ＝x，在Rt△DBQ中，由勾股定理，得DQ=，=解得；x1＝10，x2＝2，∵x＝10时，2x＞12，故舍去∴x＝2．答：经过2秒△BPQ的面积等于2．13．（易错题）如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB＝6cm，AD＝2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/秒的速度向终点B移动，点Q以1厘米/秒的速度向D移动，当有一点到达终点时，另一点也停止运动．设运动的时间为t，问：（1）当t＝1秒时，四边形BCQP面积是多少？（2）当t为何值时，点P和点Q距离是3cm？（3）当t＝ ，，65，． 以点P、Q、D为顶点的三角形是等腰三角形．（直接写出答案）解：（1）如图1，∵四边形ABCD是矩形，∴AB＝CD＝6，AD＝BC＝2，∠A＝∠B＝∠C＝∠D＝90°．∵CQ＝1cm，AP＝2cm，∴AB＝6﹣2＝4cm．∴S=2(14)2=5cm2．答：四边形BCQP面积是5cm2；（2）如图1，作QE⊥AB于E，∴∠PEQ＝90°，∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴QE＝BC＝2cm，BE＝CQ＝t．∵AP＝2t，∴PE＝6﹣2t﹣t＝6﹣3t．在Rt△PQE中，由勾股定理，得（6﹣3t）2+4＝9，解得：t如图2，作PE⊥CD于E，∴∠PEQ＝90°．∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴PE＝BC＝2cm，BP＝CE＝6﹣2t．∵CQ＝t，∴QE＝t﹣（6﹣2t）＝3t﹣6在Rt△PEQ中，由勾股定理，得（3t﹣6）2+4＝9，解得：t综上所述：t=（3）如图3，当PQ＝DQ时，作QE⊥AB于E，∴∠PEQ＝90°，∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴QE＝BC＝2cm，BE＝CQ＝t．∵AP＝2t，∴PE＝6﹣2t﹣t＝6﹣3t．DQ＝6﹣t．∵PQ＝DQ，∴PQ＝6﹣t．在Rt△PQE中，由勾股定理，得（6﹣3t）2+4＝（6﹣t）2，解得：t如图4，当PD＝PQ时，作PE⊥DQ于E，∴DE＝QE=12DQ，∠PED＝90°．∵∠B＝∠C＝90°，∴四边形BCQE是矩形，∴PE＝BC＝2cm．∵DQ＝6﹣t，∴DE=6−t 2．∴2t=6−t 2，解得：t=6 5；如图5，当PD＝QD时，∵AP＝2t，CQ＝t，∴DQ＝6﹣t，∴PD＝6﹣t．在Rt△APD中，由勾股定理，得4+4t2＝（6﹣t）2，解得t1t2．综上所述：t=，6 5，，6 5，14．（易错题）等腰△ABC的直角边AB＝BC＝10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D．设P点运动时间为t，△PCQ的面积为S．（1）求出S关于t的函数关系式；（2）当点P运动几秒时，S△PCQ ＝S△ABC？（3）作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论．解：（1）当t＜10秒时，P在线段AB上，此时CQ＝t，PB＝10﹣t，∴S=12×t（10﹣t）=12（10t﹣t2），当t＞10秒时，P在线段AB得延长线上，此时CQ＝t，PB＝t﹣10，∴S=12×t（t﹣10）=12（t2﹣10t）．（2）∵S△ABC =12AB⋅BC=50，∴当t＜10秒时，S△PCQ =12(10t−t2)=50，整理得t2﹣10t+100＝0，此方程无解，当t＞10秒时，S△PCQ =12(t2−10t)=50，整理得t2﹣10t﹣100＝0，解得t＝5±，∴当点P运动5+S△PCQ ＝S△ABC．（3）当点P、Q运动时，线段DE的长度不会改变．证明：过Q作QM⊥AC，交直线AC于点M，易证△APE≌△QCM，∴AE＝PE＝CM＝QM，∴四边形PEQM是平行四边形，且DE是对角线EM的一半．又∵EM＝AC＝DE＝∴当点P、Q运动时，线段DE的长度不会改变．同理，当点P在点B右侧时，DE＝综上所述，当点P、Q运动时，线段DE的长度不会改变．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一元二次方程方程专项训练---------动点问题
D1．如图，等腰直角三角形ABC中，∠B＝90°，AB＝BC＝8cm，动点P从A出发沿AB向B移动，通过点P引PQ∥AC，PR∥BC，问当AP等于多少时，平行四边形PQCR的面积等于16cm2？设AP的长为xcm，列出关于x的方程．
D2．如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，若P点沿AB向B以lcm/s的速度移动，点Q从B沿BC向C以2cm/s的速度移动，问几秒后，△PBQ的面积为8cm2？
D3．如图，在矩形ABCD中，AB＝12cm，BC＝6cm，点P从A点出发沿AB以2cm/s的速度向点B移动，一直到达点B为止；同时，点Q从C点出发沿CD以1cm/s的速度向点D移动，当点P停止运动时，点Q也停止运动．（1）经过多长时间P、Q两点之间的距离是6cm？
（2）经过多长时间P、Q两点之间的距离是10cm？
D4．如图，△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从A沿AC边向C点以1cm/s的速度移动，在C点停止，点Q从C点开始沿CB边向点B以2cm/s的速度移动，在B点停止．
（1）如果点P，Q分别从A、C同时出发，经过几秒钟，使S△QPC＝8cm2？
（2）如果点P从点A先出发2s，点Q再从点C出发，经过几秒钟后S△QPC＝4cm2？
（3）如果点P、Q分别从A、C同时出发，经过几秒钟后PQ＝BQ？。