曲柄滑块机构的运动分析及应用精编WORD版
曲柄滑块机构及曲柄导杆机构的运动规律

曲柄滑块机构及曲柄导杆机构的运动规律
曲柄滑块机构和曲柄导杆机构都是常用的机构形式,在工业制造、机械设计等领域得到广泛应用。
它们的运动规律分别如下:
1. 曲柄滑块机构的运动规律
曲柄滑块机构由曲柄、连杆和滑块组成。
在机构运动过程中,曲柄转动,驱动连杆做直线往复运动,滑块则沿着滑道做往复运动。
曲柄滑块机构的运动规律可以简单描述为:曲柄绕定点转动时,连杆和滑块做往复直线运动。
具体来说,曲柄绕定点O转动一个角度θ,连杆就会做往复直线运动,滑块也沿着滑道做同样的往复运动。
2. 曲柄导杆机构的运动规律
曲柄导杆机构由曲柄、连杆和导杆组成。
在机构运动过程中,曲柄转动,驱动连杆做直线往复运动,导杆则做垂直于连杆方向的往复运动。
曲柄导杆机构的运动规律可以简单描述为:曲柄绕定点转动时,连杆做往复直线运动,导杆垂直于连杆方向做往复运动。
具体来说,曲柄绕定点O转动一个角度θ,连杆就会做往复直线运动,导杆则沿着垂直于连杆方向的轨迹做同样的往复运动。
总之,曲柄滑块机构和曲柄导杆机构都是常用的机构形式,它们的运动规律基于曲柄的旋转和连杆的直线往复运动,滑块或导杆则随之做相应的往复运动。
这些机构在工业制造、机械设计等领域有着广泛的应用。
曲柄滑块的原理及应用

曲柄滑块的原理及应用概述曲柄滑块是一种常见的机械传动装置,主要由曲柄、滑块和连杆组成。
利用曲柄旋转运动,通过连杆将旋转运动转化为直线运动,实现力的传递和工作机构的运动控制。
曲柄滑块具有结构简单、传动效率高等特点,广泛应用于各个领域。
原理曲柄滑块的原理基于连杆机构和曲柄的旋转运动转化为滑块的直线运动。
连杆将曲柄的旋转运动转化为滑块的往复直线运动,实现力的传递。
曲柄滑块的基本结构如下: - 曲柄:具有一端固定,并可以绕自身轴线旋转。
- 连杆:将曲柄的旋转运动转化为滑块的直线运动。
- 滑块:沿连杆的方向进行往复直线运动。
曲柄滑块的工作原理如下: 1. 曲柄通过旋转运动带动连杆运动。
2. 连杆将曲柄的旋转运动转化为滑块的直线运动。
3. 滑块完成往复直线运动,实现力的传递和工作机构的控制。
应用曲柄滑块由于其结构简单、传动效率高等特点,被广泛应用于各个领域,以下是曲柄滑块的几个常见应用示例:1. 内燃机曲柄滑块机构被广泛应用于内燃机的气缸机构中。
内燃机中的曲轴就是一个曲柄滑块机构,通过活塞的上下运动,将往复直线运动转化为曲轴的旋转运动,从而带动车辆驱动轮的转动。
2. 压力机曲柄滑块机构在压力机中也得到了广泛应用。
通过曲柄滑块机构转化运动,将旋转运动转化为直线压力运动,实现对工件的压制和成型。
3. 石油钻机在石油钻机中,曲柄滑块机构用于转动钻杆来实现钻孔。
曲柄滑块机构将旋转运动转化为往复线性运动,带动钻杆快速下压和快速抬起。
4. 壁画机器人曲柄滑块机构还被应用于壁画机器人。
通过控制曲柄滑块机构的运动,实现壁画机械臂的运动控制,完成复杂的绘制工作。
5. 自动包装机在自动包装机中,曲柄滑块机构常用于输送和抓取物品的功能。
通过控制曲柄滑块机构的运动,可以实现快速而准确的物品传递和抓取。
总结曲柄滑块是一种常见的机械传动装置,通过将曲柄的旋转运动转化为滑块的直线运动,实现力的传递和工作机构的控制。
曲柄滑块具有结构简单、传动效率高等优点,被广泛应用于内燃机、压力机、石油钻机、壁画机器人、自动包装机等领域。
曲柄滑块机构的设计3(3页)精编版
本篇再考察一道曲柄滑块机构的设计。
同样是给定行程速比系数来确定杆长。
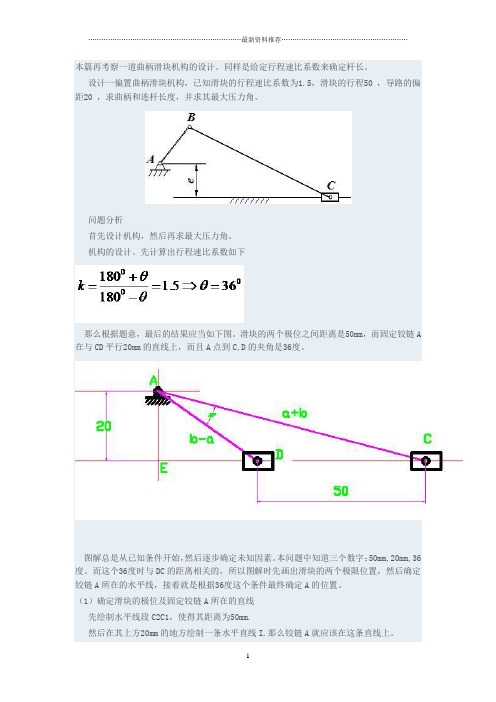
设计一偏置曲柄滑块机构,已知滑块的行程速比系数为1.5,滑块的行程50 ,导路的偏距20 ,求曲柄和连杆长度,并求其最大压力角。
问题分析首先设计机构,然后再求最大压力角。
机构的设计。
先计算出行程速比系数如下那么根据题意,最后的结果应当如下图。
滑块的两个极位之间距离是50mm,而固定铰链A 在与CD平行20mm的直线上,而且A点到C,D的夹角是36度。
图解总是从已知条件开始,然后逐步确定未知因素。
本问题中知道三个数字:50mm,20mm,36度。
而这个36度时与DC的距离相关的,所以图解时先画出滑块的两个极限位置,然后确定铰链A所在的水平线,接着就是根据36度这个条件最终确定A的位置。
(1)确定滑块的极位及固定铰链A所在的直线先绘制水平线段C2C1,使得其距离为50mm.然后在其上方20mm的地方绘制一条水平直线I.那么铰链A就应该在这条直线上。
(2)根据极位夹角确定铰链A所在的圆下面要根据极位夹角来确定A所在的曲线,这样,该曲线与上述曲线相交就可以唯一确定A点的位置。
A点到C1,C2形成的夹角是36度。
那么所有与C1,C2形成夹角为36度的点有什么特征呢?---圆周角具有这种特征。
从几何知道,在一个圆上面,对应于同一个圆弧的圆周角都相等。
基于这一点,过C2做直线垂直于C2C1,而作射线C1E与C2C1夹角为90-36=54度,二者交于点E,则C2EC1这个角度就是36度。
现在以C1E为直径做一个圆,则在该圆上任意取一点,该点与C2C1连线的夹角就都是36度,从而A点必然在该圆上面。
根据上述规则做出的上图发现,该圆与水平线I并不相交。
这意味着作图有问题。
实际上,刚才作的C1E在C2C1之下,所以导致不相交。
因此改变策略,在C2C1之上作C1E,使得它与C2C1的夹角为54度。
然后以C1E为直径作出一个圆。
该圆与直线I有两个交点:A1和A2。
曲柄滑块机构运动分析与力学计算

一、运动分析
S = Q sin R L ∴ ≈ Q cos ∴ = = ∴ = a
= L
R sin
+
L cos
−
R
cos ) + sin
α α
= ~
− →
L cos
cos
β β
)
R (1 −
α
= R sin =
L (1 −
β
= R L
β
= cos 1 − sin 1 2
λ
(1 − cos 2 α
cos
2 α 2 α )
)
(1 −
α α
λ
λ (1 −
cos
( 1 − cos dS = = dt
λ (1 −
= 2 α
)
dS d α + 1 2 ⋅
ω R sin
2
α
+
1 4
λ
⋅ 2
sin
2 α
σc =
g
设计时扭矩要照此要求
Q
转动副的摩擦 (轴颈摩擦)
力分析
r r r R21 = N 21 + F21
2 2 N 21 + F21 = N 21 1 + f 2
全反力 R21 =
N
Q
R21 − Q = 0 M d − R21 ⋅ ρ = 0
或
M d − F21 ⋅ r = 0
F21 ⋅ r f ρ= = R21 1+ f
→ R21 ⋅ ρ = F21 ⋅ r
Md
ω12
1
O N21
曲柄滑块原理的应用

曲柄滑块原理的应用简介曲柄滑块机构是一种常见的机械传动装置,利用曲柄的旋转运动和滑块的直线往复运动实现传递和转换动力。
它广泛应用于工程机械、汽车、机床等领域,具有结构简单、运动平稳等优点。
机械原理曲柄滑块机构由曲柄、滑块和链接杆组成。
曲柄是一个固定在旋转轴上的杆状零件,滑块则是直线往复运动的零件。
通过曲柄的旋转,使滑块沿着特定的轨迹运动,完成工作。
应用领域曲柄滑块机构在工程机械和汽车领域有着广泛的应用。
下面列举几个常见的应用案例:1.压力机:曲柄滑块机构被用于压力机中,通过滑块的往复运动,对工件进行加工、冲压、模具压制等工艺操作。
压力机的应用范围广泛,包括汽车制造、建筑、钢铁等行业。
2.发动机:汽车发动机中的活塞运动正是通过曲柄滑块机构实现的。
曲柄将发动机的旋转运动转换为活塞的直线往复运动,完成燃料的供给、爆发和排出的工作。
3.输送机:装载、输送和卸载物料是工业生产中常见的任务。
曲柄滑块机构可以用于实现输送机的往复运动,将物料或货物从一处运送到另一处。
4.工具机:曲柄滑块机构被广泛应用于工具机中,如剪床、冲床等。
通过滑块的往复运动,可以对工件进行切割、冲压、打孔等加工操作。
工作原理曲柄滑块机构的工作原理是利用曲柄的旋转运动来驱动滑块的直线往复运动。
下面是曲柄滑块机构的工作步骤:1.曲柄旋转:曲柄轴被连接到旋转动力源上(如电机),当电机启动后,曲柄开始旋转。
2.滑块运动:曲柄的旋转运动将通过曲柄销传递给滑块,使滑块沿着直线轨迹运动。
滑块的运动轨迹由曲柄的形状和滑块导向方式决定。
3.完成工作:滑块的直线往复运动可用于完成各种工作。
如在压力机中,滑块的下压能够对工件进行加工。
在发动机中,滑块的运动可以推动活塞进入燃烧室。
优点和局限性曲柄滑块机构作为一种常见的机械传动装置,具有以下优点:•结构简单:由于曲柄滑块机构由少量零件组成,因此结构简单,便于制造和维修。
•运动平稳:曲柄滑块机构的滑块运动往复平稳,具有较高的稳定性和可靠性。
曲柄滑块机构运动分析

曲柄滑块机构运动分析一、相关参数在图 1 所示的曲柄滑块机构中,已知各构件的尺寸分别为l 1100mm , l2300 mm,110rad / s,试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图 1 曲柄滑块机构二、数学模型的建立1、位置分析为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
将各矢量分别向X 轴和 Y 轴进行投影,得l1 cos 1l2 cos l1 sin 1l2 sin 2SC20(1)由式( 1)得2、速度分析将式( 1)对时间 t 求导,得速度关系l1 1 cos1l 22 cos20l1 1 sin1l 22 sin2v C(2)将( 2)式用矩阵形式来表示,如下所示l 2 sin 212l1 sin1l 2 cos 201l1 cos( 3).v C13、加速度分析将( 2)对时间 t 求导,得加速度关系三、计算程序1、主程序%1.输入已知数据clear;l1=0.1;l2=0.3;e=0;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%2.曲柄滑块机构运动计算forn1=1:721theta1(n1)=(n1-1)*hd;%调用函数 slider_crank 计算曲柄滑块机构位移、速度、加速度[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alpha1,l1,l2,e);endfigure(1);n1=0:720;subplot(2,3,1)plot(n1,theta2*du);title(' 连杆转角位移线图 ');xlabel('曲柄转角 \theta_1/\circ');ylabel('连杆角位移 /\circ');gridonsubplot(2,3,2)plot(n1,omega2);title(' 连杆角速度运动线图 ');xlabel('曲柄转角 \theta_1/\circ');ylabel('连杆角速度 /rad\cdots^{-1}');gridonsubplot(2,3,3)plot(n1,alpha2);title(' 连杆角加速度运动线图');xlabel('曲柄转角 \theta_1/\circ');ylabel('连杆角加速度 /rad\cdots^{-2}');gridonsubplot(2,3,4)plot(n1,s3);title(' 滑块位移线图 ');xlabel('曲柄转角 \theta_1/\circ');ylabel('滑块位移 /\m');gridonsubplot(2,3,5)plot(n1,v3);title(' 滑块速度运动线图 ');xlabel('曲柄转角 \theta_1/\circ');ylabel('滑块速度 /m\cdots^{-1}');gridonsubplot(2,3,6)plot(n1,a3);title(' 滑块加速度运动线图 ');xlabel('曲柄转角 \theta_1/\circ');ylabel('滑块加速度 /m\cdots^{-2}');gridon2、子程序function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);%计算连杆 2 的角位移和滑块 3 的线位移s3=l1*cos(theta1)+l2*cos(theta2);theta2=asin((e-l1*sin(theta1))/l2);%计算连杆 2 的角速度和滑块 3 的线速度A=[l2*sin(theta2),1;-l2*cos(theta2),0];B=[-l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);v3=omega(2);%计算连杆 2 的角加速度和滑块 3 的线加速度At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];alpha=A\(-At*omega+alpha1*B+omega1*Bt);alpha2=alpha(1);a3=alpha(2);四、程序运行结果及分析图 2 运动规律曲线图从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化范围大约在-20~20度之间,在 90°或 270°有极值,呈反正弦变化趋势;连杆的角速度变化范围大约在-3.3~3.3rad/s,在0°或 180°有极值,成反余弦变化趋势;连杆角加速度变化范围大约在 -35~35rad/s2,在 90°或270°有极值,呈正弦变化趋势。
曲柄滑块机构的结构
曲拐轴式曲柄滑块机构便于实现可调行程 且结构较简单,但由于曲柄悬伸,受力情
况较差,因此主要在中、小型机械压力机 上应用。
偏心齿轮工作时只传递扭矩,弯矩由芯轴承受,因此 偏心齿轮的受力比曲轴简单些,芯轴只承受弯矩,受
力情况也比曲轴好,且刚度较大。此外,偏心齿轮的
铸造比曲轴锻造容易解决,但总体结构相对复杂些。
为了保证滑块的运动精度,滑块的导向面应尽量长 ,因而滑块的高度要足够高,滑块高度与宽度的比 值,在闭式单点压力机上约为1.08~1.32 ,在开式压力机上则高达1.7左右。
滑块还应该越轻越好,质量轻的滑块上升时消耗的 能量小,可以减少滑块停止在上止点位置时的制动 力。
滑块还应有足够的强度,小型压力机的滑块常用HT200铸造。中 型压力机的滑块常用HT200或稀土球铁铸造,或用Q235钢板 焊接而成。
所以,偏心齿轮驱动的曲柄及滑块机构常用于大中型 压力机。
滑块与导轨结构
压力机上的滑块是一个箱形结构,它的上部与连杆连接,下面开有“ T”形槽或模柄孔,用以安装模具的上模。
滑块在曲柄连杆的驱动下,沿机身导轨上下往复运动,并直接承受上 模传来的工艺反力。
为了保证滑块底平面和工作台上平面的平行度,保 证滑块运动方向与工作台面的垂直度,滑块的导向 面必须与底平面垂直。(下平面的平面度,导向面的 平面度,下平面对导向面的垂直度,导向面对母线 的直线度)
综上所述,机身变形对冲压工艺的影响是至关重要的,必须给予重视 。不同刚度的压力机,在同样的工作负荷下,刚度小的变形大,刚度
大的变形小;而对同一台压力机,工作负荷越大,变形也越大。这是 在选择压力机时必须考虑的因素。
曲柄滑块机构的运动分析
S
R 1
cos
2
曲柄滑块机构运动分析与力学计算

sin( ) sin cos cos sin sin 1 2 sin 2 sin cos
(sin sin 2 )
2
M1
PAB R(sin
2
sin 2 )在下死点
0
PR(sin sin 2 )
2
M1(P, , R, L)
设计(公称压力)行程Sg ;设计(公称压力)角 g
Q
N
Q
Md
12
O
R21
1 2
N21
F21
以轴颈中心为圆心,为半径作的圆称为摩擦圆,
为摩擦圆半径。
三、实际机构扭矩计算
理想机构:不计弹性变形;不计配合间隙 不计摩擦;不计惯性力
sin (RA RB )
L
M
' 2
PAB
m2
m2 RA R sin( )
PAB 2
R0
PAB 2
R0
PAB R0
1 1 2 s in 2
2
s in 2 1 (1 c os 2 )
2
c os 1 1 2 (1 c os 2 )
4
S R(1 c os ) L 1 2 (1 c os 2 )
4
R (1 c os )
L R
1 4
(1 c os 2 )
R (1 c os )
PAB
P
sin(90 ) sin(90 )
PAB
P
coscos 源自由于在下死点附近,,很小M 2 PAB RA R0 R sin PAB P
当 0, 0
M 2 PRA R0 R sin
P R A
R0
RRA
L
RB
R L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲柄滑块机构的运动分析及应用精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(11071182)陈柯宇 (11071177)熊宇飞(11071174)张保开 (11071183)班级: 1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
是由曲柄(或曲轴、偏心轮)、连杆、滑块通过移动副和转动副组成的机构[4]。
曲柄滑块机构的特性及应用常用于将曲柄的回转运动变换为滑块的往复直线运动;或者将滑块的往复直线运动转换为曲柄的回转运动。
对曲柄滑块机构进行运动特性分析是当已知各构件尺寸参数、位置参数和原动件运动规律时,研究机构其余构件上各点的轨迹、位移、速度、加速度等,从而评价机构是否满足工作性能要求,机构是否发生运动干涉等。
曲柄滑块机构具有运动副为低副,各元件间为面接触,构成低副两元件的几何形状比较简单,加工方便,易于得到较高的制造精度等优点,因而在包括煤矿机械在内的各类机械中得到了广泛的应用,如自动送料机构、冲床、内燃机空气压缩机等 [5]。
对曲柄滑块机构选用不同构件为机架可演化成具有不同运动特性和不同用途的机构。
列如选取滑块为机架,则机构演化为移动导杆机构,下面以抽水机为例进行介绍。
抽水泵的Adams仿真图图中白色曲杆为原动件,红色直杆为从动件。
原动件位移曲线从动件位移曲线原动件速度曲线从动件速度曲线原动件加速度曲线从动件加速度曲线综上,曲柄滑块机构演化为移动导杆机构后可应用在手摇抽水机上改变力的方向和大小,从而使原动件与从动件的速度,加速度,位移截然不同,在大气压的作用下将水从井中抽出。
下图为曲柄滑块机构演化的偏心轮摇杆机构蓝色摇杆为研究对象摇杆质心的位移曲线摇杆质心的速度曲线摇杆质心的加速度曲线这套机构将输入运动偏心轮的圆周运动转化为输出运动摇杆的往复运动,可以作为汽车雨刷等需要摇杆做连续往复运动的机构曲柄滑块机构的分类根据结构特点,将其分成3大类:对心曲柄滑块、偏置曲柄滑块、偏心轮机构图2-1 对心曲柄滑块机构图2-2 偏置曲柄滑块机构图2-3 偏心轮机构偏心轮机构简介当曲柄长度很小时,通常把曲柄做成偏心轮,这样不仅增大了轴颈的尺寸,提高偏心轴的强度和刚度,而且当轴颈位于中部时,还可以安装整体式连杆,使得结构简化。
因此偏心轮广泛应用于传力较大的剪床、冲床、鄂式破碎机、内燃机等机械中[6]。
偏心轮机构可以实现复杂的非线性传动关系,且传动平稳,结构紧凑,动力平衡性好。
将偏心轮与连杆等机构组合应用,可实现单纯用连杆机构难以得到的复杂的运动特性。
是曲柄滑块机构是常用的机构型式。
生产实际中,如在滑块往复行程中具有匀速运动段,并有急回特性,则一般将有利于生产质量和生产率的提高。
冲压机的冲头(滑块),如能以匀速冲压工件成形、,则有益于冲压件加工质量的提高;牛头刨床的刨刀(滑块),如能以匀速刨削工件,则无疑会改善工件表面的加工质量,并提高刨刀的切削寿命(因切削刀均匀)。
但是,简单的对心曲柄滑块机构,当曲柄匀速回转时,其滑块是不具有急回特性和匀速运动段的;即便采用六杆以上的连杆机构,一般也只能实现近似的匀速运动。
现在采用偏心轮一曲柄滑块机构,则能以紧凑的机构型式实现上述运动特性[7]。
在海上能源综合开发平台上,采用这种偏心轮机构,通过滑块联动液压缸,用于将海风端水平轴旋转的机械能转化成活塞往复运动的机械能,进而转化成液压能。
图2-4 工作原理图曲柄滑块的动力学特性上图为曲柄滑块机构的受力分析示意图从曲柄r 传到连杆l 上的力p c 与滑块发出的压力p 之间,存在如下关系:p p c=ϕcos (3-1)曲柄颈A 处,沿半径方向的力p r 和p c的关系: p r =p c )cos(ϕθ+ (3-2)将上2式联立,可得到:p r=ϕϕθcos /)cos(+p (3-3) 曲柄颈沿r 方向承受与p r 力大小相等的压力。
曲柄颈沿圆周方向所受切线力p T 与半径r 的乘积,就是转矩T 。
T =p T*r (3-4) 根据上图可知:)sin(θϕ+=p p cT (3-5) 将(1)、(4)式代入(5)式,则r p T *cos /)sin(ϕϕθ+= (3-6)从上式求出P 。
r T p /1*)sin(/cos ϕθϕ+= (3-7)一般曲柄连杆机构l>4r ,所以,可将l 看成比r 大很多,即l>>r ,这时,ϕ角趋近于零。
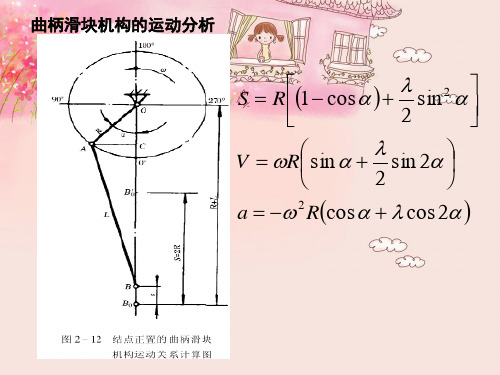
则上式可以写成:)sin /(θr T p = (3-8)按平面几何圆部分的勾股定理,可以导出r rs r s s r r /2/sin 222)(-=-=-θ ,将上式代入,则得: )1/2/(-=s r s T p [8] (3-9)曲柄滑块的运动学特性图3-2取A 点为坐标原点,x 轴水平向右。
在任意瞬时t ,机构的位置如图。
可以假设C 点的矢径为:=AC =AB +BC (3-10)C 点的坐标为其矢径在坐标轴上的投影:θθcos cos 3322r r x += (3-11)θθsin sin 3322r r y -= (3-12)根据图形可知:θθθλsin sin sin 22323*)/(==r r (3-13)所以: θλθθsin sin cos 22212123-=-= (3-14)式中,=λr r 32/是曲柄长与连杆长之比。
将上式代入x 的表达式中,并考虑到t ωθ=2,就得到了滑块的运动方程: t r r x t ωλωsin 1cos 22)(23-=+ (3-15)若将此式对时间求导数,其运算较繁琐。
在工程实际中,λ值通常不大(λ=1/4-1/6),故可在上式中将根式展开成λ2的幂级数并略去λ4起的各项而作近似计算:)(2cos t r ω=)]2(1[25.0cos 23t r ωλ--+ (3-16) )]2(25.0)([)25.01(cos cos 223t t x r r ωλωλ++-≈ (3-17)上式再对时间取导数,便可以得到速度和加速度的表达式:)]2(5.0)([sin sin 2t t x r ωλωωυ+-==• (3-18))]2()([cos cos 22t t a r ωλωυω+-==• (3-19)其中a x ,,υ都是t ωθ=2的周期函数[9]。
下面运用Adams 进行仿真模拟验证曲柄滑块的Adams 仿真模型滑块的位移曲线滑块的速度曲线滑块的加速度曲线经计算可知图像与表达式吻合。
在海上能源综合开发平台上,在已知海风端的输入轴颈,材质,转矩,通过上述原理设计出合理的曲柄滑块机构,得出驱动液压缸运动的滑块的位移,速度,加速度,压力,得到的结果便于液压缸的传动设计。
曲柄滑块机构运行中的振动与平衡在一切有质量、构件质心有加速度或构件有角加速度的机械中,都存在着惯性力。
例如:曲柄压力机在向下行程时,滑块出现“快落”,对传动系统产生撞击、振动,会降低传动零件的使用寿命。
机械在高速运转过程中,这种随机构运转而周期变化的强惯性作用将会在运动副中引起附加动压力。
这不仅将增加运动副中的摩擦力和构件的内应力,导致磨损加剧、效率降低,也影响构件的强度。
而且由于惯性力随机械的运转而作周期性变化,也会使机械及其基础产生强迫振动,从而导致机械工作质量和可靠性下降、零件材料内部疲劳损伤加剧,并由振动而产生噪声污染。
因此,研究机械高速运转中惯性力的变化规律,采用平衡设计和平衡试验的方法对惯性力加以平衡,以消除或减轻惯性力的不良影响,是减轻机械振动、改善机械工作性能、提高机械工作质量、延长机械使用寿命、减轻噪声污染的重要措施之一[10]。
曲柄滑块机构是最早获得广泛应用的连杆机构之一,在运转时各构件产生的惯性力会引起机座的强迫振动,加剧机器构件的磨损并产生噪声污染,降低机构的运动精度和平稳性。
因此,对这类机构平衡问题的研究很有必要。
从理论上讲,运用质量代换法可使这种机构的惯性力完全平衡。
但是这种平衡法会导致机械结构复杂化及其质量的增加,尤其是把配重安装在连杆上时,对机构更为不利。
因此,人们多采用惯性力部分平衡的方法来减小机构的振动[11]。
曲柄滑块机构中包含有作往复运动的滑块和作复合运动的连杆和作转动的曲柄,它们质心加速度以及角加速度的存在会导致周期性变化的振动力和振动力矩。
这种力和力矩将造成机械的强烈振动和噪声,加剧机件的磨损和疲劳失效,降低机构的运动精度和运动平稳性,限制了机械性能的提高。
