曲柄滑块机构运动分析1
曲柄滑块机构运动分析

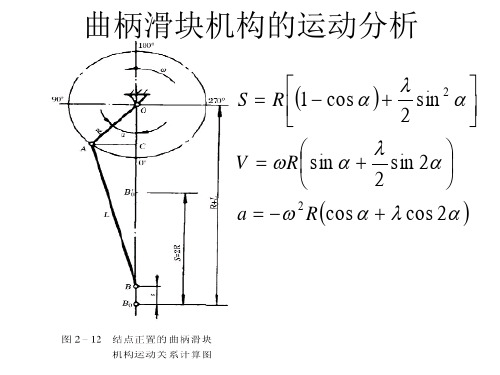
曲柄滑块机构运动分析一、相关参数在图1所示的曲柄滑块机构中,已知各构件的尺寸分别为mm l 1001=,mm l 3002=,s rad /101=ω,试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图1 曲柄滑块机构二、数学模型的建立1、位置分析为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
C S l l =+21将各矢量分别向X 轴和Y 轴进行投影,得sin sin cos cos 22112211=+=+θθθθl l S l l C(1)由式(1)得 ⎪⎪⎭⎫ ⎝⎛-=2112sin arcsin l l θθ 2211cos cos θθl l S C +=2、速度分析将式(1)对时间t 求导,得速度关系C v l l l l =--=+222111222111sin sin 0cos cos θωθωθωθω (2)将(2)式用矩阵形式来表示,如下所示 ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111122222cos sin . 0 cos 1 sin θθωωθθl l v l l C (3) 3、加速度分析将(2)对时间t 求导,得加速度关系⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111111222222222222sin cos 0 sin 0 cos 0 cos 1 sin θωθωωωθωθωαθθl l v l l a l l C C三、计算程序1、主程序%1.输入已知数据clear;l1=0.1;l2=0.3;e=0;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%2.曲柄滑块机构运动计算for n1=1:721theta1(n1)=(n1-1)*hd;%调用函数slider_crank计算曲柄滑块机构位移、速度、加速度[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alp ha1,l1,l2,e);endfigure(1);n1=0:720;subplot(2,3,1)plot(n1,theta2*du);title('连杆转角位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角位移/\circ');grid onsubplot(2,3,2)plot(n1,omega2);title('连杆角速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角速度/rad\cdots^{-1}');grid onsubplot(2,3,3)plot(n1,alpha2);title('连杆角加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角加速度/rad\cdots^{-2}');grid onsubplot(2,3,4)plot(n1,s3);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块位移/\m');grid onsubplot(2,3,5)plot(n1,v3);title('滑块速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块速度/m\cdots^{-1}');grid onsubplot(2,3,6)plot(n1,a3);title('滑块加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块加速度/m\cdots^{-2}');grid on2、子程序function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);%计算连杆2的角位移和滑块3的线位移s3=l1*cos(theta1)+l2*cos(theta2);theta2=asin((e-l1*sin(theta1))/l2);%计算连杆2的角速度和滑块3的线速度A=[l2*sin(theta2),1;-l2*cos(theta2),0];B=[-l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);v3=omega(2);%计算连杆2的角加速度和滑块3的线加速度At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];alpha=A\(-At*omega+alpha1*B+omega1*Bt);alpha2=alpha(1);a3=alpha(2);四、程序运行结果与分析图2 运动规律曲线图从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化X围大约在-20~20度之间,在90°或270°有极值,呈反正弦变化趋势;连杆的角速度变化X围大约在-3.3~3.3rad/s,在0°或180°有极值,成反余弦变化趋势;连杆角加速度变化X围大约在-35~35rad/s2,在90°或270°有极值,呈正弦变化趋势。
曲柄滑块机构的运动精度分析与计算

曲柄滑块机构的运动精度分析与计算宋亮;赵鹏兵【摘要】曲柄滑块机构是一种典型的四连杆机构,尽管设计时理论计算可以达到很高的精度,但是由于构件的制造误差及运动副的配合间隙等因素,会使机构在运动中产生输出误差,有时还会显著超出机构设计的允许误差.依据概率统计的相关理论进行机构设计,即考虑构件制造尺寸的随机误差,以保证机构运动的精度在允许的误差范围内.利用MATLAB进行仿真计算和实例研究,得出了理论设计和精度分析的计算结果.该方法准确、效率高、而且适合其它类型的机构设计,具有较大的工程实际应用价值.%Slider-crank mechanism is a typical four-bar linkage, in spite of the high precision when it' s calculated theoretically. The manufacturing error and kinematic pair clearance of the components will lead to the output error during the motion of the mechanism. Sometimes,it will significantly exceed the tolerance of the design. According to the probability and statistics theory, the mechanism is designed, that' s considering the random error of the component to make sure that the motion accuracy is in the allowed error range. Utilizing MATLAB to simulate and calculate based on case studies. and the theoretical design and accuracy analysis are obtained. This method is accurate and very efficiently, it also can be used in other kind of mechanism design, and it has much more practical value in engineering.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)010【总页数】5页(P2201-2205)【关键词】曲柄滑块机构;运动学;概率设计;等影响法;精度分析【作者】宋亮;赵鹏兵【作者单位】海军装备部,西安,710043;西北工业大学现代设计与集成制造技术教育部重点实验室,西安,710072【正文语种】中文【中图分类】TH112.1曲柄滑块机构是一种单移动副的四连杆机构,如图1和图2所示,分别为对心和偏心曲柄滑块机构。
曲柄(导杆)滑块机构设计分析正文.

目录1 引言1.1 选题的依据及意义·························································································(1)1.2 国内外研究概况及发展趋势··········································································(2)1.3 论文主要工作·······························································································(3)2 曲柄(导杆)滑块机构简介····································································(4)3 曲柄(导杆)滑块机构的运动学分析3.1 曲柄导杆滑块机构的运动分析······································································(5)3.1.1 机构装配的条件····················································································(6)3.1.2 建立数学模型·························································································(6)3.1.3 计算机辅助分析及其程序设计······························································(9)3. 2曲柄滑块机构的运动分析3.2.1 机构装配的条件·····················································································(25)3.2.2 建立数学模型·······················································································(25)3.2.3 计算机辅助分析及其程序设计·····························································(27)4 曲柄(导杆)滑块机构实验台装置设计4. 1 实验台结构·································································································(40)4.2 实验台硬件操作说明···················································································(41)4.3 用SolidWorks 2006实现实验台的立体图形················································(42)总结·········································································································(46)参考文献·········································································································(47)致谢·········································································································(48)1 引言1.1 选题的依据及意义1.曲柄(导杆)滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构的结构
• 闭式机身有整体式和组合式两种.闭式机身承 载能力大,刚度较好.所以,从小型精密压力机到 超大型压力机大都采用这种形式.
• 组合式〔见图b〕机身是用拉紧螺栓将上梁、 立柱和底座拉紧,紧固成为一体的,加工和运输 比较方便,大中型压力机应用较广.
• 整体式机身〔见图a〕,有时为了增强刚性也 有使用拉紧螺栓的.虽然整体式机身加工装配 工作量较小,但需要大型加工设备,运输也较困 难.因此,一般被限制在3000kN以下的压 力机上应用.
轴式的曲柄滑块机构在大型压力机上 的应用受到限制.
• 曲拐轴式曲柄滑块机构便 于实现可调行程且结构较 简单,但由于曲柄悬伸,受 力情况较差,因此主要在中、 小型机械压力机上应用.
• 偏心齿轮工作时只传递扭矩,弯矩 由芯轴承受,因此偏心齿轮的受力 比曲轴简单些,芯轴只承受弯矩,受 力情况也比曲轴好,且刚度较大.此 外,偏心齿轮的铸造比曲轴锻造容 易解决,但总体结构相对复杂些.所 以,偏心齿轮驱动的曲柄及滑块机 构常用于大中型压力机.
• 开式机身压力机的弹性变形、机身的角变 形使滑块下平面与垫板〔或工作台〕上平 面的平行度下降,引起模具的导柱导套和滑 块导轨过热,严重磨损,使加工出的零件精度 降低,尤其对压印加工或整形加工,这种不良 影响可以说是致命的缺陷,如后图a所示.
• 另外,角变形造成滑块的上下运动与工作 台〔或垫板〕上平面的垂直度的降低,将 使冲头和凹模倾斜一角度,促使模具间隙 不均匀,并产生水平方向的侧压力,不仅影 响冲压件的尺寸精度,而且还会加速模具 的磨损甚至使冲头折断,特别是对薄板冲 压加工工艺影响尤其严重,如后图b、c 所示.
• 压力机的工作台、垫板及滑块,在负荷状态下,如果 出现如下图所示那样的挠度,平面度就会被严重破 坏,尤其在双动或双点压力机中,这一点特别明显.
1.分析曲柄滑块机构机架长度及滑块偏置尺寸运动参数的影响。

1.分析曲柄滑块机构机架长度及滑块偏置尺寸运动参数的影响。
曲柄滑块机构是一种常见的转动运动转化为往复运动的机构。
机架长度和滑块偏置尺寸对该机构的运动参数有较大的影响。
首先,机架长度会影响机构的行程和速度。
机架长度越长,滑块往复运动的行程也就越大,同时速度也就越慢。
反之,机架长度越短,滑块往复运动的行程越小,速度也就越快。
因此,在实际设计中,应根据所需的行程和速度来选择合适的机架长度。
其次,滑块偏置尺寸会影响滑块的加速度和最大速度。
滑块偏置越大,滑块启动时的加速度就越大,最大速度也就越大。
但是,滑块偏置过大会导致机构的冲击振动较大,影响机构的稳定性和工作寿命。
因此,在实际设计中,应根据机构的要求选择合适的滑块偏置尺寸。
总的来说,机架长度和滑块偏置尺寸都是影响曲柄滑块机构运动参数的重要因素,在设计时需要综合考虑。
需要根据机构所要求的行程、速度、稳定性和工作寿命等方面的要求进行合理设计。
实验四 基于Simulink机构运动分析(1)
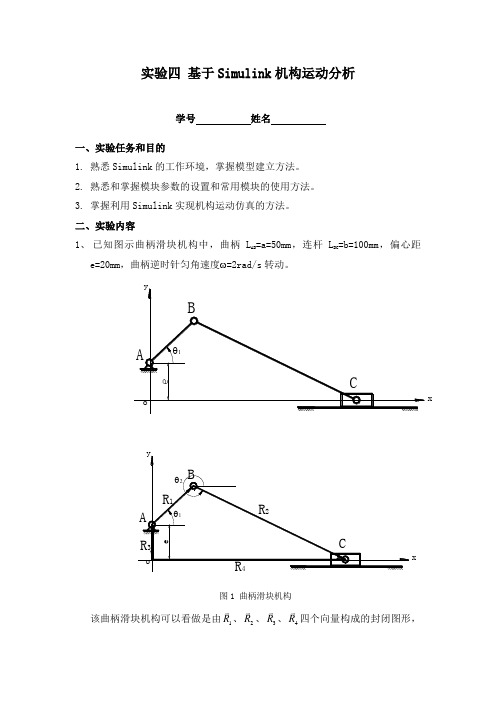
实验四 基于Simulink 机构运动分析学号 姓名一、实验任务和目的1. 熟悉Simulink 的工作环境,掌握模型建立方法。
2. 熟悉和掌握模块参数的设置和常用模块的使用方法。
3. 掌握利用Simulink 实现机构运动仿真的方法。
二、实验内容1、 已知图示曲柄滑块机构中,曲柄L AB =a=50mm ,连杆L BC =b=100mm ,偏心距e=20mm ,曲柄逆时针匀角速度ω=2rad/s 转动。
xx图1 曲柄滑块机构该曲柄滑块机构可以看做是由1R 、2R 、3R 、4R 四个向量构成的封闭图形,方向如图所示。
该机构的闭环位移矢量方程1234R R R R +=+上述矢量方程在x 和y 方向的投影方程1212cos cos (1)sin sin (2)c a b x a b eθθθθ+=⎧⎨+=-⎩ 对位移方程两边求一阶导数⎩⎨⎧=+=--)4(0cos cos )3(sin sin a 22112211θωθωθωθωb a v b C 上式可用于求解连杆角速度2ω和滑块速度C v⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--1111222cos sin 0cos 1sin θωθωωθθa a v b b C依此建立simulink 模型图2曲柄滑块机构Simulin 仿真模型其中(1) 计算连杆角速度和滑块速度的函数模块自定义函数模块vcslider.m源代码(2)计算连杆和滑块初始位置的函数模块自定义函数模块vcslider.m 源代码对上述曲柄滑块模型进行仿真。
2、 仿照上述曲柄滑块机构仿真方法,对图示曲柄摇杆机构进行建模仿真,要求用示波器显示CD 杆角位移4θ,角速度4ω和角加速度4α随曲柄转角(0~360°)变化曲线。
已知机构各构件尺寸100AB l mm =,200BC l mm =,200AD l mm =,150CD l mm =,原动件AB 以等角速度ω=10rad/s 逆时针方向转动,1θ初始位置为0。
曲柄滑块机构的运动精度分析与计算

⑥
2 1 SiT c. nn. 0 c. eh E gg 1
仪 表 技术
曲柄滑 块 机 构 的运 动 精 度 分析 与计 算
宋 亮 赵 鹏 兵。
( 海军装备部 , 西安 70 4 西北工业大学 现代设 计与集成 制造技术教育部重点实验室 , 10 3; 西安 70 7 ) 10 2
第1 1卷
第 1 0期
2 1 年 4月 01
科
学Байду номын сангаас
技
术
与
工
程
Vo.1 No 0 Ap . 011 1 1 .1 r2
17一 1 1 (0 1 1 —2 10 6 l 85 2 1 )02 0 —5
S inc ch oo y a d c e e Te n lg n Engn e i g ie rn
程 实 际应 用 价 值 。
关键词 曲柄滑块机 构
运 动学
概 率设计
等影响法
精度分析
中图法 分类号
T 1. H12 1;
文献标志码
A
曲柄 滑块 机构 是一 种单 移 动副 的 四连 杆 机 构 , 如 图 1和 图 2所示 , 分别 为对 心 和 偏 心 曲柄 滑 块 机
1 曲柄滑块机构的运动分析 ]
在 图 1和图 2所 示 的对心 曲柄滑 块机构 和偏 心
构 。它可 以用 来 实 现 转 动 和 移 动 之 间运 动 形 式 的 转换 和传 递 动 力 。 曲柄 滑 块 机 构 可 以测 量 的 长 度 是 曲柄 和连 杆 , 组成 移动 副 的滑 块 和导 路 两 个 构 件
图 2 偏 心 曲 柄滑 块 机 构
s= ± As , = / ± Av ,a -  ̄
曲柄滑块机构运动分析与力学计算

一、运动分析
S = Q sin R L ∴ ≈ Q cos ∴ = = ∴ = a
= L
R sin
+
L cos
−
R
cos ) + sin
α α
= ~
− →
L cos
cos
β β
)
R (1 −
α
= R sin =
L (1 −
β
= R L
β
= cos 1 − sin 1 2
λ
(1 − cos 2 α
cos
2 α 2 α )
)
(1 −
α α
λ
λ (1 −
cos
( 1 − cos dS = = dt
λ (1 −
= 2 α
)
dS d α + 1 2 ⋅
ω R sin
2
α
+
1 4
λ
⋅ 2
sin
2 α
σc =
g
设计时扭矩要照此要求
Q
转动副的摩擦 (轴颈摩擦)
力分析
r r r R21 = N 21 + F21
2 2 N 21 + F21 = N 21 1 + f 2
全反力 R21 =
N
Q
R21 − Q = 0 M d − R21 ⋅ ρ = 0
或
M d − F21 ⋅ r = 0
F21 ⋅ r f ρ= = R21 1+ f
→ R21 ⋅ ρ = F21 ⋅ r
Md
ω12
1
O N21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲柄滑块机构运动分析
一、相关参数
在图1所示的曲柄滑块机构中,已知各构件的尺寸分别为mm l 1001=,mm l 3002
=,s rad /101=ω,
试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图1 曲柄滑块机构
二、数学模型的建立
1、位置分析
为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
C S l l =+21
将各矢量分别向X 轴和Y 轴进行投影,得
0sin sin cos cos 22112211=+=+θθθθl l S l l C (1)
由式(1)得 ⎪⎪⎭
⎫ ⎝⎛-=2112sin arcsin l l θθ 2211cos cos θθl l S C +=
2、速度分析
将式(1)对时间t 求导,得速度关系
C v l l l l =--=+222111222111sin sin 0
cos cos θωθωθωθω (2)
将(2)式用矩阵形式来表示,如下所示
⎥⎦
⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111122222cos sin . 0 cos 1 sin θθωωθθl l v l l C (3) 3、加速度分析
将(2)对时间t 求导,得加速度关系
⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-11
11111222222222222sin cos 0 sin 0 cos 0 cos 1 sin θωθωωωθωθωαθθl l v l l a l l C C
三、计算程序
1、主程序
%1.输入已知数据
clear;
l1=0.1;
l2=0.3;
e=0;
hd=pi/180;
du=180/pi;
omega1=10;
alpha1=0;
%2.曲柄滑块机构力平衡计算
for n1=1:721
theta1(n1)=(n1-1)*hd;
%调用函数slider_crank计算曲柄滑块机构位移、速度、加速度
[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alpha1,l1,l2,e);
end
figure(1);
n1=0:720;
subplot(2,3,1)
plot(n1,theta2*du);
title('连杆转角位移线图');
xlabel('曲柄转角\theta_1/\circ');
ylabel('连杆角位移/\circ');
grid on
subplot(2,3,2)
plot(n1,omega2);
title('连杆角速度运动线图');
xlabel('曲柄转角\theta_1/\circ');
ylabel('连杆角速度/rad\cdots^{-1}');
grid on
subplot(2,3,3)
plot(n1,alpha2);
title('连杆角加速度运动线图');
xlabel('曲柄转角\theta_1/\circ');
ylabel('连杆角加速度/rad\cdots^{-2}');
grid on
subplot(2,3,4)
plot(n1,s3);
title('滑块位移线图');
xlabel('曲柄转角\theta_1/\circ');
ylabel('滑块位移/\m');
grid on
subplot(2,3,5)
plot(n1,v3);
title('滑块速度运动线图');
xlabel('曲柄转角\theta_1/\circ');
ylabel('滑块速度/m\cdots^{-1}');
grid on
subplot(2,3,6)
plot(n1,a3);
title('滑块加速度运动线图');
xlabel('曲柄转角\theta_1/\circ');
ylabel('滑块加速度/m\cdots^{-2}');
grid on
2、子程序
function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);
%计算连杆2的角位移和滑块3的线位移
theta2=asin((e-l1*sin(theta1))/l2);
s3=l1*cos(theta1)+l2*cos(theta2);
%计算连杆2的角速度和滑块3的线速度
A=[l2*sin(theta2),1;-l2*cos(theta2),0];
B=[-l1*sin(theta1);l1*cos(theta1)];
omega=A\(omega1*B);
omega2=omega(1);
v3=omega(2);
%计算连杆2的角加速度和滑块3的线加速度
At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];
Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];
alpha=A\(-At*omega+alpha1*B+omega1*Bt);
alpha2=alpha(1);
a3=alpha(2);
四、程序运行结果及分析
图2 运动规律曲线图
从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化范围大约在-20~20度之间,在90°或270°有极值,呈反正弦变化趋势;连杆的角速度变化范围大约在-3.3~3.3rad/s,在0°或180°有极值,成反余弦变化趋势;连杆角加速度变化范围大约在-35~35rad/s2,在90°或270°有极值,呈正弦变化趋势。
滑块位移变化范围大约在0.2~0.4m之间,在0°或180°有极值,呈反余弦变化趋势;滑块速度变化范围大约在-1~1m/s之间,大致上呈正弦变化趋势;滑块加速度变化范围大约在-13~6.9m/s2,在0°或180°有极值。
