曲柄滑块机构分析
曲柄滑块机构运动分析

曲柄滑块机构运动分析一、相关参数在图1所示的曲柄滑块机构中,已知各构件的尺寸分别为mm l 1001=,mm l 3002=,s rad /101=ω,试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图1 曲柄滑块机构二、数学模型的建立1、位置分析为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
C S l l =+21将各矢量分别向X 轴和Y 轴进行投影,得sin sin cos cos 22112211=+=+θθθθl l S l l C(1)由式(1)得 ⎪⎪⎭⎫ ⎝⎛-=2112sin arcsin l l θθ 2211cos cos θθl l S C +=2、速度分析将式(1)对时间t 求导,得速度关系C v l l l l =--=+222111222111sin sin 0cos cos θωθωθωθω (2)将(2)式用矩阵形式来表示,如下所示 ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111122222cos sin . 0 cos 1 sin θθωωθθl l v l l C (3) 3、加速度分析将(2)对时间t 求导,得加速度关系⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111111222222222222sin cos 0 sin 0 cos 0 cos 1 sin θωθωωωθωθωαθθl l v l l a l l C C三、计算程序1、主程序%1.输入已知数据clear;l1=0.1;l2=0.3;e=0;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%2.曲柄滑块机构运动计算for n1=1:721theta1(n1)=(n1-1)*hd;%调用函数slider_crank计算曲柄滑块机构位移、速度、加速度[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alp ha1,l1,l2,e);endfigure(1);n1=0:720;subplot(2,3,1)plot(n1,theta2*du);title('连杆转角位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角位移/\circ');grid onsubplot(2,3,2)plot(n1,omega2);title('连杆角速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角速度/rad\cdots^{-1}');grid onsubplot(2,3,3)plot(n1,alpha2);title('连杆角加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角加速度/rad\cdots^{-2}');grid onsubplot(2,3,4)plot(n1,s3);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块位移/\m');grid onsubplot(2,3,5)plot(n1,v3);title('滑块速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块速度/m\cdots^{-1}');grid onsubplot(2,3,6)plot(n1,a3);title('滑块加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块加速度/m\cdots^{-2}');grid on2、子程序function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);%计算连杆2的角位移和滑块3的线位移s3=l1*cos(theta1)+l2*cos(theta2);theta2=asin((e-l1*sin(theta1))/l2);%计算连杆2的角速度和滑块3的线速度A=[l2*sin(theta2),1;-l2*cos(theta2),0];B=[-l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);v3=omega(2);%计算连杆2的角加速度和滑块3的线加速度At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];alpha=A\(-At*omega+alpha1*B+omega1*Bt);alpha2=alpha(1);a3=alpha(2);四、程序运行结果与分析图2 运动规律曲线图从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化X围大约在-20~20度之间,在90°或270°有极值,呈反正弦变化趋势;连杆的角速度变化X围大约在-3.3~3.3rad/s,在0°或180°有极值,成反余弦变化趋势;连杆角加速度变化X围大约在-35~35rad/s2,在90°或270°有极值,呈正弦变化趋势。
曲柄(导杆)滑块机构设计分析正文.

目录1 引言1.1 选题的依据及意义·························································································(1)1.2 国内外研究概况及发展趋势··········································································(2)1.3 论文主要工作·······························································································(3)2 曲柄(导杆)滑块机构简介····································································(4)3 曲柄(导杆)滑块机构的运动学分析3.1 曲柄导杆滑块机构的运动分析······································································(5)3.1.1 机构装配的条件····················································································(6)3.1.2 建立数学模型·························································································(6)3.1.3 计算机辅助分析及其程序设计······························································(9)3. 2曲柄滑块机构的运动分析3.2.1 机构装配的条件·····················································································(25)3.2.2 建立数学模型·······················································································(25)3.2.3 计算机辅助分析及其程序设计·····························································(27)4 曲柄(导杆)滑块机构实验台装置设计4. 1 实验台结构·································································································(40)4.2 实验台硬件操作说明···················································································(41)4.3 用SolidWorks 2006实现实验台的立体图形················································(42)总结·········································································································(46)参考文献·········································································································(47)致谢·········································································································(48)1 引言1.1 选题的依据及意义1.曲柄(导杆)滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构的结构

工作原理
当曲柄绕固定轴转动 时,通过连杆带动滑 块做往复直线运动。
通过改变曲柄的转速 和转向,可以控制滑 块的往复运动速度和 方向。
曲柄的长度和安装位 置可以改变滑块的行 程长度和方向。
应用领域
内燃机
曲柄滑块机构广泛应用于内燃机的活塞运动,通过曲柄的转动使活塞 进行往复运动,实现内燃机的吸气、压缩、做功和排气过程。
可能是由于润滑不良、部件磨损或异物卡住引起 的。应检查润滑状况,清洁机构并更换磨损部件。
异响
可能是由于部件松动、润滑不良或部件损坏引起 的。应检查紧固件和润滑状况,必要时更换损坏 部件。
精度下降
可能是由于部件磨损、松动或导轨弯曲引起的。 应检查并调整部件的精度,必要时更换磨损部件 或修正导轨。
谢谢观看
热处理工艺
总结词
热处理工艺能够显著提高材料的机械性能,是曲柄滑块机构优化的重要环节。
详细描述
热处理工艺包括淬火、回火、表面淬火和化学热处理等。淬火可以提高材料的硬度和强度,回火则可以改善材料 的韧性和降低内应力。表面淬火可以强化材料表面的硬度,提高耐磨性。化学热处理可以改变材料表面的化学成 分,提高耐腐蚀性和疲劳强度。
曲柄滑块机构的结构
目录
• 曲柄滑块机构简介 • 曲柄滑块机构类型 • 曲柄滑块机构的设计 • 曲柄滑块机构的优化 • 曲柄滑块机构的维护与保养
01
曲柄滑块机构简介
定义与特点
定义
曲柄滑块机构是一种将曲柄的回 转运动转化为滑块的往复直线运 动的机构。
特点
结构简单,工作可靠,能实现精 确的直线运动,且运动范围较大 ,因此在各种机械装置中得到广 泛应用。
总结词
当曲柄绕机架转动时,导杆仅作直线往复运动的曲柄滑块机构。
1.分析曲柄滑块机构机架长度及滑块偏置尺寸运动参数的影响。

1.分析曲柄滑块机构机架长度及滑块偏置尺寸运动参数的影响。
曲柄滑块机构是一种常见的转动运动转化为往复运动的机构。
机架长度和滑块偏置尺寸对该机构的运动参数有较大的影响。
首先,机架长度会影响机构的行程和速度。
机架长度越长,滑块往复运动的行程也就越大,同时速度也就越慢。
反之,机架长度越短,滑块往复运动的行程越小,速度也就越快。
因此,在实际设计中,应根据所需的行程和速度来选择合适的机架长度。
其次,滑块偏置尺寸会影响滑块的加速度和最大速度。
滑块偏置越大,滑块启动时的加速度就越大,最大速度也就越大。
但是,滑块偏置过大会导致机构的冲击振动较大,影响机构的稳定性和工作寿命。
因此,在实际设计中,应根据机构的要求选择合适的滑块偏置尺寸。
总的来说,机架长度和滑块偏置尺寸都是影响曲柄滑块机构运动参数的重要因素,在设计时需要综合考虑。
需要根据机构所要求的行程、速度、稳定性和工作寿命等方面的要求进行合理设计。
曲柄滑块机构分析

Fx
A
60
B Fy
求解过程:
第一步:以曲柄1为研究对象进行受力分析,如图 所示:
X方向:F21*cos(60)+Fx+F=0 Y方向:Fy+F21*sin(60)=0 转矩平衡方程:F*OA-F21*OB*sin(60)=0 三个未知量,三个方程,则可求解得到F21,即 曲柄对连杆的作用力。
7
F4 F’x
D.其他情况
13
扩展1:曲柄滑块机构
M B
A C
D
14
扩展2:当杆长发生变化时,弹簧力会发生什 么变化?
D
F
D
F
200 100 B
A
C
500 100 B
A
C
D
F
200 100 B
A
C
15
课后作业2:教材P77,课后习题4
图2-128所示为曲柄导杆机构。已知曲柄长为 a=100mm,曲柄回转中心A与导杆摆动中心C的 距离为b=200mm。曲柄以ω=36(°)/s的角速 度匀速转动。 (1)试建立该曲柄导杆机构的虚拟样机模型。 (2)仿真机构的虚拟样机模型,并测量获取导杆 角度、角速度和角加速度的变化规律; (3)试根据仿真分析结果,计算求取机构的行程 速比系数
16
课后作业1:教材P77,课后习题5
在图2-129所示的对心曲柄滑块机构,已知曲柄为 100cmx10cmx5cm的钢质杆,连杆为200cmx10cmx5cm的用在曲柄上的 驱动力矩为M1=20N.m。 (1)试建立该曲柄滑块机构的虚拟样机模型; (2)请仿真机构的虚拟样机模型,并测量获取滑块3在0s-20s运 动时间内的位移、速度和加速度的变化规律。
曲柄滑块机构分析
曲柄滑块机构滑块速度计算

曲柄滑块机构滑块速度计算1. 曲柄滑块机构概述哎,大家好,今天咱们聊聊一个跟机械有关的玩意儿——曲柄滑块机构。
这听起来有点高大上,但其实它就像个机械界的小明星,常常在各种机器中大显身手。
简单来说,这个机构的主要功能就是把旋转的运动转化为直线的运动,听起来很简单吧?其实背后可是有一套复杂的运算呢!曲柄、滑块,各种零部件一起合作,像是在跳一支优雅的舞蹈,真是让人忍不住想拍手叫好。
1.1 机构的组成部分首先,我们得知道这个机构里都有什么。
最主要的有三个角色:曲柄、滑块和连杆。
曲柄就像是个大老板,负责旋转;滑块则是个勤勤恳恳的小员工,负责移动;而连杆嘛,就像是个好朋友,把它们俩紧紧联系在一起。
想象一下,如果没有连杆的帮助,曲柄和滑块就像两条平行线,永远无法相遇。
哎呀,这场舞蹈可就没法演下去了。
1.2 运动的过程好了,假设曲柄开始转动,滑块就会在导轨上来回移动。
这个过程中,滑块的速度可不是固定的哦,它会随着曲柄的转动而变化。
想象一下,滑块就像是乘坐过山车,随着曲柄的旋转,它的速度也是时快时慢,简直惊心动魄!所以,咱们得计算出滑块的速度,才能更好地控制整个机构的运行。
2. 滑块速度的计算说到计算,这可是个关键的环节。
咱们得用到一些公式,不用担心,这里没有高深的数学,咱们简单易懂地来。
首先,我们要知道曲柄的转动角度和半径。
假设曲柄的长度是R,转动角度是θ,那滑块的线速度V可以通过公式来计算。
用公式表示,就是 V = R * ω,其中ω是角速度,听起来复杂,其实就是曲柄转动的快慢。
2.1 角速度的理解说到角速度,其实就像是你骑自行车,越快转动脚踏板,车速自然就上来了。
对于我们的曲柄也是一样,转得快,滑块就移动得快。
再者,曲柄的旋转角度和滑块的移动距离也是有关系的,比如说转动一圈,滑块可能就往前走了一大段,这个就是“距离与角度”的关系,简单又形象。
2.2 速度变化的因素不过,滑块的速度可不是一成不变的哦!它会随着曲柄的转动位置而变化。
曲柄滑块机构运动分析与力学计算

一、运动分析
S = Q sin R L ∴ ≈ Q cos ∴ = = ∴ = a
= L
R sin
+
L cos
−
R
cos ) + sin
α α
= ~
− →
L cos
cos
β β
)
R (1 −
α
= R sin =
L (1 −
β
= R L
β
= cos 1 − sin 1 2
λ
(1 − cos 2 α
cos
2 α 2 α )
)
(1 −
α α
λ
λ (1 −
cos
( 1 − cos dS = = dt
λ (1 −
= 2 α
)
dS d α + 1 2 ⋅
ω R sin
2
α
+
1 4
λ
⋅ 2
sin
2 α
σc =
g
设计时扭矩要照此要求
Q
转动副的摩擦 (轴颈摩擦)
力分析
r r r R21 = N 21 + F21
2 2 N 21 + F21 = N 21 1 + f 2
全反力 R21 =
N
Q
R21 − Q = 0 M d − R21 ⋅ ρ = 0
或
M d − F21 ⋅ r = 0
F21 ⋅ r f ρ= = R21 1+ f
→ R21 ⋅ ρ = F21 ⋅ r
Md
ω12
1
O N21
曲柄滑块机构的结构
曲拐轴式曲柄滑块机构便于实现可调行程 且结构较简单,但由于曲柄悬伸,受力情
况较差,因此主要在中、小型机械压力机 上应用。
偏心齿轮工作时只传递扭矩,弯矩由芯轴承受,因此 偏心齿轮的受力比曲轴简单些,芯轴只承受弯矩,受
力情况也比曲轴好,且刚度较大。此外,偏心齿轮的
铸造比曲轴锻造容易解决,但总体结构相对复杂些。
为了保证滑块的运动精度,滑块的导向面应尽量长 ,因而滑块的高度要足够高,滑块高度与宽度的比 值,在闭式单点压力机上约为1.08~1.32 ,在开式压力机上则高达1.7左右。
滑块还应该越轻越好,质量轻的滑块上升时消耗的 能量小,可以减少滑块停止在上止点位置时的制动 力。
滑块还应有足够的强度,小型压力机的滑块常用HT200铸造。中 型压力机的滑块常用HT200或稀土球铁铸造,或用Q235钢板 焊接而成。
所以,偏心齿轮驱动的曲柄及滑块机构常用于大中型 压力机。
滑块与导轨结构
压力机上的滑块是一个箱形结构,它的上部与连杆连接,下面开有“ T”形槽或模柄孔,用以安装模具的上模。
滑块在曲柄连杆的驱动下,沿机身导轨上下往复运动,并直接承受上 模传来的工艺反力。
为了保证滑块底平面和工作台上平面的平行度,保 证滑块运动方向与工作台面的垂直度,滑块的导向 面必须与底平面垂直。(下平面的平面度,导向面的 平面度,下平面对导向面的垂直度,导向面对母线 的直线度)
综上所述,机身变形对冲压工艺的影响是至关重要的,必须给予重视 。不同刚度的压力机,在同样的工作负荷下,刚度小的变形大,刚度
大的变形小;而对同一台压力机,工作负荷越大,变形也越大。这是 在选择压力机时必须考虑的因素。
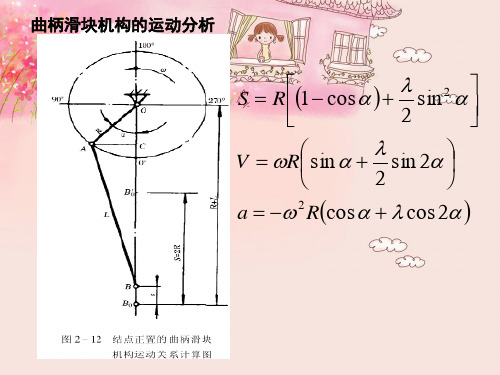
曲柄滑块机构的运动分析
S
R 1
cos
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械工程郑佳文学号:1508520102 任务:根据杆长判断机构类型,模拟仿真曲柄滑块机构运动,并绘制滑块速度及加速度图像。
源代码:
clear all
clc
l1=4,l2=10,e=0,w1=10;
if(e==0) & (l1>l2)
% load handel
% sound(y,Fs)
disp('当e=0时,l1需小于l2。
不满足杆长条件,请重新输入l1,l2,e的值')
elseif((e~=0)&(l1+e>l2))
% load handel
% sound(y,Fs)
disp('当e~=0时,l1+e需小于l2。
不满足杆长条件,请重新输入l1,l2,e的值') else
end
fai=linspace(0,2*pi);
for i=1:10:length(fai)
JGT2(fai(i),l1,l2,e,w1)
end
%%%%%%%%%%%计算滑块速度并绘制图像
figure (2)
fai=0:0.01:2*pi;
v=-l1.*sin(fai).*w1-(l2^2-(l1.*sin(fai)-e). ^2).^(-0.5)*(l1^2).*(l1.*sin(fai)-e).*sin(f ai).*cos(fai).*w1;
plot(fai,v,'-b')
title('滑块角度-速度图像')
xlabel('角度\phi/°')
ylabel('速度/m/s')
figure (3)
A=- l1.*cos(fai) -
(l1^2.*cos(fai).^2)./(l2^2 - (e -
l1.*sin(fai)).^2).^(1/2) - (l1.*sin(fai).*(e - l1.*sin(fai)))./(l2^2 - (e -
l1.*sin(fai)).^2).^(1/2) ...
- (l1^2.*cos(fai).^2.*(e -
l1.*sin(fai)).^2)./(l2^2 - (e -
l1.*sin(fai)).^2).^(3/2);
plot(fai,A,'-b')
title('滑块角度-加速度图像')
xlabel('角度\phi/°') ylabel('速度/m/s')
结果图:
-2
2
468
10
12
14
滑块位移图像
角度φ/°
滑块位移/
m
0123
4567
滑块角度-速度图像
角度φ/°
速度/m /s
0123
4567
-6
-5-4-3-2-1012
3滑块角度-加速度图像
角度 /°
速度/m /s。
