(完整版)第十三章(精编)轴对称知识点归纳并练习[]
新人教版八年级数学上册第十三章《轴对称》知识点归纳并练习

第十三章(精编)轴对称《轴对称、线段垂直平分线、、等腰三角形、等边三角形》轴对称图形如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,•这个图形就叫做轴对称图形,这条直线就是它的对称轴.有的轴对称图形的对称轴不止一条,如圆就有无数条对称轴.轴对称有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,•那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.图形轴对称的性质如果两个图形成轴对称,•那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.画一图形关于某条直线的轴对称图形的步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
轴对称与轴对称图形的区别轴对称是指两个图形之间的形状与位置关系,•成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.考点一、关于“轴对称图形”与“轴对称”的认识1.下列几何图形中,○1线段○2角○3直角三角形○4半圆,其中一定是轴对称图形的有【】A.1个B.2个C.3个D.4个2.图中,轴对称图形的个数是【】A.4个 B.3个 C.2个 D.1个3.正n 边形有___________条对称轴,圆有_____________条对称轴线段的垂直平分线 (1)经过线段的中点并且垂直于这条线段的直线,•叫做这条线段的垂直平分线(或线段的中垂线).(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,•与一条线段两个端点距离相等的点在这条线段的垂直平分线上.因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.考点二、线段垂直平分线的性质4.如图,△ABC 中,∠A =90°,BD 为∠ABC 平分线,DE ⊥BC ,E 是BC 的中点,求∠C 的度数。
第13章轴对称知识点
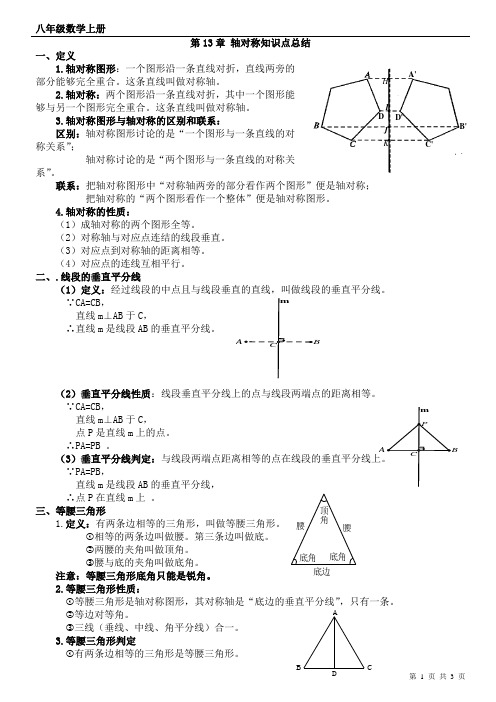
第13章 轴对称知识点总结一、定义1.轴对称图形:一个图形沿一条直线对折,直线两旁的部分能够完全重合。
这条直线叫做对称轴。
2.轴对称:两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。
这条直线叫做对称轴。
3.轴对称图形与轴对称的区别和联系:区别:轴对称图形讨论的是“一个图形与一条直线的对称关系”;轴对称讨论的是“两个图形与一条直线的对称关系”。
联系:把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称;把轴对称的“两个图形看作一个整体”便是轴对称图形。
4.轴对称的性质:(1)成轴对称的两个图形全等。
(2)对称轴与对应点连结的线段垂直。
(3)对应点到对称轴的距离相等。
(4)对应点的连线互相平行。
二、.线段的垂直平分线(1)定义:经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。
∵CA=CB ,直线m ⊥AB 于C ,∴直线m 是线段AB 的垂直平分线。
(2)垂直平分线性质:线段垂直平分线上的点与线段两端点的距离相等。
∵CA=CB ,直线m ⊥AB 于C ,点P 是直线m 上的点。
∴PA=PB 。
(3)垂直平分线判定:∵PA=PB ,直线m 是线段AB 的垂直平分线,∴点P 在直线m 上 。
三、等腰三角形1.定义:有两条边相等的三角形,叫做等腰三角形。
①相等的两条边叫做腰。
第三条边叫做底。
②两腰的夹角叫做顶角。
③腰与底的夹角叫做底角。
注意:等腰三角形底角只能是锐角。
2.等腰三角形性质:①等腰三角形是轴对称图形,其对称轴是“底边的垂直平分线”,只有一条。
②等边对等角。
③三线(垂线、中线、角平分线)合一。
3.等腰三角形判定①有两条边相等的三角形是等腰三角形。
m CA B D'D C'B'A'K J I H 底边底角底角顶角腰腰CBA②有两个角相等的三角形是等腰三角形。
四、等边三角形1.等边三角形定义:三条边都相等的三角形,叫做等边三角形。
说明:等边三角形就是腰和底相等的等腰三角形,因此,等边三角形是特殊的等腰三角形。
八年级第十三章《轴对称》知识点及典型例题

第十三章《轴对称》一、知识点归纳(一)轴对称和轴对称图形1、有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.2、轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
(对称轴必须是直线)3、对称点:折叠后重合的点是对应点,叫做对称点。
4、轴对称图形的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
类似的,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
连接任意一对对应点的线段被对称轴垂直平分.轴对称图形上对应线段相等、对应角相等。
5.画一图形关于某条直线的轴对称图形步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
(二)、轴对称与轴对称图形的区别和联系区别:轴对称是指两个图形之间的形状与位置关系,成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.联系:1:都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形,反之亦然。
(三)线段的垂直平分线(1)经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线)(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点在这条线段的垂直平分线上.(证明是必须有两个点)因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.(四)用坐标表示轴对称1、点(x,y)关于x轴对称的点的坐标为(-x,y);2、点(x,y)关于y轴对称的点的坐标为(x,-y);(五)关于坐标轴夹角平分线对称点P(x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是(y,x)点P(x,y)关于第二、四象限坐标轴夹角平分线y=-x对称的点的坐标是(-y,-x)(六)关于平行于坐标轴的直线对称点P(x,y)关于直线x=m对称的点的坐标是(2m-x,y);点P(x,y)关于直线y=n对称的点的坐标是(x,2n-y);(七)等腰三角形1、等腰三角形性质:性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。
轴对称知识点及习题

第十三章轴对称轴对称知识要点1.轴对称图形与轴对称轴对称图形:如果一个平面图形沿一条直线折叠;直线两旁的部分能够互相重合;这个图形就叫做轴对称图形.这条直线是它的对称轴.轴对称:把一个平面图形沿着某一条直线折叠;如果它能够与另一个图形重合;那么就说这两个图形关于这条直线成轴对称;这条直线叫做对称轴.2.轴对称的性质如果两个图形关于某条直线对称;那么对称轴是任何一对对应点所连线段的垂直平分线.3.线段的垂直平分线的性质和判定性质:线段垂直平分线上的点与这条线段两个端点的距离相等.判定:与一条线段两个端点距离相等的点;在这条线段的垂直平分线上.4.关于x轴、y轴对称的点的坐标的特点点x;y关于x轴对称的点的坐标为x;-y;点x;y关于y轴对称的点的坐标为-x;y;温馨提示1.轴对称图形是针对一个图形而言;是指一个具有对称的性质的图形;轴对称是针对两个图形而言;它描述的是两个图形的一种位置关系.2.在平面直角坐标系中;关于x轴对称的两个图形的对应点的横坐标相同;纵坐标互为相反数;关于y轴对称的两个图形的对应点的横坐标互为相反数;纵坐标相同.等腰三角形知识要点1.等腰三角形的性质性质1:等腰三角形的两个底角相等简写成“等边对等角”;性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合简写成“三线合一”.2.等腰三角形的判定方法如果一个三角形有两个角相等;那么这两个角所对的边也相等简写成“等角对等边”.3.等边三角形的性质和判定方法性质:等边三角形的三个内角都相等;并且每一个角都等于60°.判定方法1:三个角都相等的三角形是等边三角形.判定方法2:有一个角是60°的等腰三角形是等边三角形.4.直角三角形的性质在直角三角形中;如果一个锐角等于30°;那么它所对的直角边等于斜边的一半.温馨提示1.“等边对等角”和“等角对等边”只限于在同一个三角形中;在两个三角形中时;上述结论不一定成立.2.在应用直角三角形的性质时应注意以下两点:1必须是在直角三角形中;2必须有一个锐角等于30°.方法技巧1.等腰三角形的性质是证明两个角相等的重要方法;当要证明同一个三角形的两个内角相等时;可尝试用“等边对等角”.2.等腰三角形的判定是证明线段相等的一个重要方法;当要证明位于同一个三角形的两条线段相等时;可尝试用“等角对等边”.3.利用轴对称可以解决几何中的最值问题;本方法的实质是依据轴对称的性质以及两点之间线段最短和三角形两边之和大于第三边.13.1轴对称13.2画轴对称图形专题一轴对称图形1.2012·连云港下列图案是轴对称图形的是2.众所周知;几何图形中有许多轴对称图形;写出一个你最喜欢的轴对称图形是:______________________.答案不唯一3.如图;阴影部分是由5个小正方形组成的一个直角图形;请用两种方法分别在下图方格内涂黑两个小正方形;使它们成为轴对称图形.专题二轴对称的性质4.如图;△ABC和△ADE关于直线l对称;下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有A.0个 B.1个 C.2个 D.3个5.如图;∠A=90°;E为BC上一点;A点和E点关于BD对称;B点、C点关于DE对称;求∠ABC 和∠C的度数.6.如图;△ABC和△A′B′C′关于直线m对称.1结合图形指出对称点.2连接A、A′;直线m与线段AA′有什么关系3延长线段AC与A′C′;它们的交点与直线m有怎样的关系其他对应线段或其延长线的交点呢你发现了什么规律;请叙述出来与同伴交流.专题三灵活运用线段垂直平分线的性质和判定解决问题7.如图;在Rt△ABC中;∠ACB=90°;AB的垂直平分线DE交于BC的延长线于F;若∠F=30°;DE=1;则EF的长是A.3 B.2 C D.18.如图;在△ABC中;BC=8;AB的垂直平分线交BC于D;AC的垂直平分线交BC与E;则△ADE的周长等于________.9.如图;AD⊥BC;BD=DC;点C在AE的垂直平分线上;那么线段AB、BD、DE之间有什么数量关系并加以证明.专题四利用关于坐标轴对称点的坐标的特点求字母的取值范围10.已知点P-2;3关于y轴的对称点为Qa;b;则a+b的值是A.1 B.-1 C.5 D.-511.已知P1点关于x轴的对称点P23-2a;2a-5是第三象限内的整点横、纵坐标都为整数的点;称为整点;则P1点的坐标是__________.13.3等腰三角形13.4课题学习最短路径问题专题一等腰三角形的性质和判定的综合应用1.如图在△ABC中;BF、CF是角平分线;DE∥BC;分别交AB、AC于点D、E;DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长=AB+AC;④BF=CF.其中正确的是___________.填序号3.如图;已知△ABC是等腰直角三角形;∠BAC=90°;BE是∠ABC的平分线;DE⊥BC;垂足为D.1请你写出图中所有的等腰三角形;2请你判断AD与BE垂直吗并说明理由.3如果BC=10;求AB+AE的长.专题二等边三角形的性质和判定4.如图;在等边△ABC中;AC=9;点O在AC上;且AO=3;点P是AB上一动点;连接OP;以O为圆心;OP长为半径画弧交BC于点D;连接PD;如果PO=PD;那么AP的长是__________.5.如图.在等边△ABC中;∠ABC与∠ACB的平分线相交于点O;且OD∥AB;OE∥AC.1试判定△ODE的形状;并说明你的理由;2线段BD、DE、EC三者有什么关系写出你的判断过程.6.如图;△ABC中;AB=BC=AC=12 cm;现有两点M、N分别从点A、点B同时出发;沿三角形的边运动;已知点M的速度为1 cm/s;点N的速度为2 cm/s.当点N第一次到达B点时;M、N同时停止运动.1点M、N运动几秒后;M、N两点重合2点M、N运动几秒后;可得到等边三角形△AMN3当点M、N在BC边上运动时;能否得到以MN为底边的等腰三角形AMN 如存在;请求出此时M、N运动的时间.专题三最短路径问题7.如图;A、B两点分别表示两幢大楼所在的位置;直线a表示输水总管道;直线b表示输煤气总管道.现要在这两根总管道上分别设一个连接点;安装分管道将水和煤气输送到A、B两幢大楼;要求使铺设至两幢大楼的输水分管道和输煤气分管道的用料最短.图中;点A′是点A关于直线b的对称点;A′B分别交b、a于点C、D;点B′是点B关于直线a的对称点;B′A 分别交b、a于点E、F.则符合要求的输水和输煤气分管道的连接点依次是A.F和C B.F和E C.D和C D.D和E8.如图;现准备在一条公路旁修建一个仓储基地;分别给A、B两个超市配货;那么这个基地建在什么位置;能使它到两个超市的距离之和最小保留作图痕迹及简要说明。
初二数学上册(人教版)第十三章轴对称13.3知识点总结含同步练习及答案

描述:初二数学上册(人教版)知识点总结含同步练习题及答案第十三章 轴对称 13.3 等腰三角形一、学习任务1. 了解等腰三角形和等边三角形的概念.2. 掌握等腰三角形和等边三角形的性质定理和判定定理,掌握 角的直角三角形的性质.二、知识清单等腰三角形 等边三角形三、知识讲解1.等腰三角形等腰三角形有两条边相等的三角形叫做等腰三角形(isosceles triangle ).等腰三角形的性质① 等腰三角形的两个底角相等;② 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).三角形的边角对应关系在同一个三角形内,大边对大角,大角对大边.构造等腰三角形的方法30∘都填上)∠ADE=∠AED=2∠BAD34DE△BDE接 ,试判断 的形状,并说明理由.∠DBC描述:例题:2.等边三角形等边三角形三边都相等的三角形叫做等边三角形(equilateral triangle ),也属于等腰三角形.等边三角形的性质三个内角都相等,并且每一个角都等于 .等边三角形性质的推论在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半.等边三角形的判定① 三个角都相等的三角形是等边三角形;② 有一个角是 的等腰三角形是等边三角形.构造等边三角形的方法,.即 是等腰三角形.2∴∠DBC =∠E ∴BD =DE △BDE 60∘30∘60∘如图所示,在等边三角形 中, 和 的平分线相交于点 ,, 的垂直平分线分别交 于点 ,,求证: 是等边三角形.分析:根据垂直平分线的性质可知,,,由于 , 是角平分线,所以 ,再由于外角和定理,,所以 是等边三角形.证明: , 分别是 , 垂直平分线上的点,ABC ∠ABC ∠ACB O BO OC BC E F △OEF OE =BE OF =F C OB OC ∠OBC =∠OCB =30∘∠OEF =∠OF E =60∘△OEF ∵EF BO OC值为( )32A△ABC。
最新新编八年级数学上册第十三章轴对称知识点总结新版新人教

第十三章轴对称一、知识框架:二、知识清单:1.轴对称:⑴轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.这条直线称为它的对称轴.⑵两个图形成轴对称:把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.这条直线称为这两个图形的对称轴.⑶线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.2.轴对称的性质:对称的性质:①两个图形关于某一条直线对称,对称轴是任何一对对应点所连线段的垂直平分线.轴对称图形的对称轴是任何一对对应点连线段的垂直平分线.②关于某直线对称的两个图形是全等形.3.线段垂直平分线性质①线段垂直平分线上的点与这条线段两个端点的距离相等.②与一条线段两个端点距离相等的点在这条线段的垂直平分线上.③线段垂直平分线的作图a 分别以线段的两个端点为圆心,大于1/2线段的适当长度为半径画弧,两弧交于两个点;b 过两个交点作直线,则直线即为已知线段的垂直平分线.4.画已知图形的轴对称图形(步骤)a 过已知点A 作对称轴l 的垂线,垂足为O ,在垂线上截取OA',使OA'=OA ,则点A'是点A 的对称点;b 同理分别作出其它关键点的对称点;c 将所作的对称点依次相连,得到轴对称图形.5.关于坐标轴对称的点的坐标性质①关于x 轴对称的点横坐标不变,纵坐标互为相反数; 点P (,)x y 关于x 轴对称的点的坐标为'P (,)x y -.②关于y 轴对称的点纵坐标不变,横坐标互为相反数; 点P (,)x y 关于y 轴对称的点的坐标为"P (,)x y -.③关于原点对称的点横纵坐标分别互为相反数;点P (,)x y 关于原点对称的点的坐标为P 1()y ,x --.6.等腰三角形(1)等腰三角形:有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.(2)等腰三角形的性质(定理):①等腰三角形的两个底角相等(简写成“等边对等角”).②等腰三角形的顶角角平分线、底边上的中线,底边上的高相互重合.(简写成“三线合一”)(3)等腰三角形的判定(定理)如果一个三角形有两个角相等,那么这两个角所对的边也相等。
最新八年级数学第13章轴对称知识点
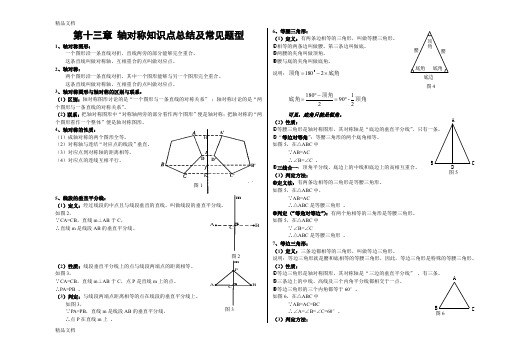
第十三章 轴对称知识点总结及常见题型1、轴对称图形:一个图形沿一条直线对折,直线两旁的部分能够完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
2、轴对称:两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
3、轴对称图形与轴对称的区别与联系:(1)区别:轴对称图形讨论的是“一个图形与一条直线的对称关系” ;轴对称讨论的是“两个图形与一条直线的对称关系”。
(2)联系:把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称;把轴对称的“两个图形看作一个整体”便是轴对称图形。
4、轴对称的性质:(1)成轴对称的两个图形全等。
(2)对称轴与连结“对应点的线段”垂直。
(3)对应点到对称轴的距离相等。
(4)对应点的连线互相平行。
5、线段的垂直平分线:(1)定义:经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。
如图2,∵CA=CB ,直线m ⊥AB 于C ,∴直线m 是线段AB 的垂直平分线。
(2)性质:线段垂直平分线上的点与线段两端点的距离相等。
如图3,∵CA=CB ,直线m ⊥AB 于C ,点P 是直线m 上的点。
∴PA=PB 。
(3)判定:与线段两端点距离相等的点在线段的垂直平分线上。
如图3,∵PA=PB ,直线m 是线段AB 的垂直平分线,∴点P 在直线m 上 。
6、等腰三角形:(1)定义:有两条边相等的三角形,叫做等腰三角形。
①相等的两条边叫做腰。
第三条边叫做底。
②两腰的夹角叫做顶角。
③腰与底的夹角叫做底角。
说明:底角顶角⨯-=2180顶角顶角底角21-902180︒=-︒=可见,底角只能是锐角。
(2)性质:①等腰三角形是轴对称图形,其对称轴是“底边的垂直平分线”,只有一条。
②“等边对等角”:等腰三角形的两个底角相等。
如图5,在△ABC 中 ∵AB=AC∴∠B=∠C 。
③三线合一:顶角平分线、底边上的中线和底边上的高相互重合。
人教版八年级数学上册第十三章-轴对称知识点总结及练习(无答案)

轴对称知识点总结及练习1、轴对称图形:一个图形沿一条直线对折,直线两旁的部分能够 ;这条直线叫做 。
互相重合的点叫 。
2、成轴对称:两个图形沿一条直线对折,其中一个图形能够与 完全重合;这条直线叫做对称轴。
3、轴对称图形与轴对称的区别与联系:(1)区别:轴对称图形讨论的是“一个图形与一条直线的对称关系” ;轴对称讨论的是“两个图形与一条直线的对称关系”。
(2)联系:把轴对称图形中“对称轴两旁的部分看作两个图形”便是两图成轴对称;把成轴对称的“两个图形看作一个整体”便是轴对称图形。
4、轴对称的性质:如图(1)成轴对称的两个图形 。
(2)连结“对应点的线段” 被对称轴 。
(3)对应点到对称轴的距离 。
(4)(4)对应点的连线互相 或在同一直线。
5、线段的垂直平分线:(1)定义:经过线段的中点且 的直线,叫做线段的垂直平分线。
符号语言:如图 ∵CA=CB ,直线m ⊥AB 于C , ∴直线m 是线段AB 的垂直平分线。
(2)性质: 。
∵直线m 垂直平分AB ,点P 是直线m 上的点。
符号语言:如图 ∴PA=PB 。
(3)判定:与线段两端点距离相等的点在线段的 上。
如图,∵PA=PB ,∴点P 在 上 。
6、等腰三角形: (1)定义:有两边 的三角形,叫做等腰三角形。
①相等的两条边叫做 。
第三条边叫做 。
②两腰的夹角叫做 。
③腰与底的夹角叫做 。
说明:底角顶角⨯-=2180 顶角顶角底角21-902180︒=-︒= (2)性质:①等腰三角形是轴对称图形,其对称轴是 ,一般有 条。
②等腰三角形的两个底角 ;简称 。
符号语言:如图,在△ABC 中 ∵AB=AC∴∠B=∠C (等边对等角)。
③三线合一:顶角平分线、 和 相互重合。
符号语言:如图,在△ABC 中 ∵AB=AC AD ⊥BC ∴(3)判定方法:①定义法:有两条边相等的三角形是等腰三角形。
如图5,在△ABC 中,∵AB=AC ∴△ABC 是等腰三角形 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十三章(精编)轴对称《轴对称、线段垂直平分线、、等腰三角形、等边三角形》轴对称图形如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,•这个图形就叫做轴对称图形,这条直线就是它的对称轴.有的轴对称图形的对称轴不止一条,如圆就有无数条对称轴.轴对称有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,•那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.图形轴对称的性质如果两个图形成轴对称,•那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.画一图形关于某条直线的轴对称图形的步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
轴对称与轴对称图形的区别轴对称是指两个图形之间的形状与位置关系,•成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.考点一、关于“轴对称图形”与“轴对称”的认识1.下列几何图形中,○1线段○2角○3直角三角形○4半圆,其中一定是轴对称图形的有【】A.1个B.2个C.3个D.4个2.图中,轴对称图形的个数是【】A.4个 B.3个 C.2个 D.1个3.正n 边形有___________条对称轴,圆有_____________条对称轴线段的垂直平分线 (1)经过线段的中点并且垂直于这条线段的直线,•叫做这条线段的垂直平分线(或线段的中垂线).(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,•与一条线段两个端点距离相等的点在这条线段的垂直平分线上.因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.考点二、线段垂直平分线的性质4.如图,△ABC 中,∠A =90°,BD 为∠ABC 平分线,DE ⊥BC ,E 是BC 的中点,求∠C 的度数。
ED BA5.如图,△ABC 中,AB =AC ,PB =PC ,连AP 并延长交BC 于D ,求证:AD 垂直平分BCAP6.如图,DE 是∆ABC 中AC 边的垂直平分线,若BC =8厘米,AB =10厘米,则∆EBC 的周长为【 】A.16厘米B.18厘米C.26厘米D.28厘米CEB DA7.如图,∠BAC =30°,P 是∠BAC 平分线上一点,PM ∥AC ,PD ⊥AC ,PD =30 , 则AM =MD P BCA轴对称变换由一个平面图形得到它的轴对称图形叫做轴对称变换.•成轴对称的两个图形中的任何一个可以看着由另一个图形经过轴对称变换后得到. 轴对称变换的性质(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样(2)经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点.(3)连接任意一对对应点的线段被对称轴垂直平分.作一个图形关于某条直线的轴对称图形(1)作出一些关键点或特殊点的对称点.(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形. 关于坐标轴对称点P (x ,y )关于x 轴对称的点的坐标是(x ,-y )点P (x ,y )关于y 轴对称的点的坐标是(-x ,y )关于原点对称点P (x ,y )关于原点对称的点的坐标是(-x ,-y )关于坐标轴夹角平分线对称点P(x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是(y,x)点P(x,y)关于第二、四象限坐标轴夹角平分线y=-x对称的点的坐标是(-y,-x)关于平行于坐标轴的直线对称点P(x,y)关于直线x=m对称的点的坐标是(2m-x,y);点P(x,y)关于直线y=n对称的点的坐标是(x,2n-y);考点三、轴对称变换及用坐标表示轴对称8.点 A(-3 ,2)关于 y 轴对称点的坐标是( )A (-3 ,-2)B (3 ,2)C (-3 ,2)D (2 ,-3)9.点P(a,b)关于 x 轴的对称点为P'(1,-6),则A、B的值分别为( )A 1 ,6B -1 ,-6C -1 ,6D 1 ,-610.点P关于x 轴对称点P'的坐标为(4,-5),那么点P关于y轴对称点P"的坐标为:A (-4,5)B (4,-5)C (-4,-5)D (-5,-4)11.平面内点A(-1,2)和点B(-1,6)的对称轴是( )A.x轴B.y轴C.直线y=4D.直线x=-112.下列关于直线 x=1 对称的点是( )A 点(0 ,-3)与点(-2 ,-3)B 点(2 ,3)与点(-2 ,3)C 点(2 ,3)与点(0 ,3)D 点(2 ,3)与点(2 ,-3 )13.已知A(-1,-2)和B(1,3),将点A向______平移_______个单位长度后得到的点与点B 关于y轴对称.14.如下图:若正方形 ABCD 关于 x 轴与 y 轴均成轴对称图形,点A的坐标为(2,1),标出点 B 、C 、D 的坐标分别为:B( , ),C( , ),D( , )。
15. 若A(m-1,2n+3)与B(n-1,2m+1)关于y轴对称,则m= ,n=16.已知a<0,那么点P(-a²-2,2-a)关于x轴对称的对应点P'在第象限三、解答题17.已知点M(1-a,2a+2),若点M关于x轴的对称点在第三象限,求a的取值范围?18.已知点A的坐标为(2x+y-3,x-2y)。
它关于x轴对称的点A'的坐标为(x+3,y-4),求点A关于y轴对称的点的坐标。
19.如图,从△ABC到△A′B′C′是进行的平移变换还是轴对称变换,如果是轴对称变换,找出对称轴,如果是平移变换,是怎样平移的?20.如图,△ABC,求顶点A、B、C关于y轴对称点的坐标并在坐标系中画出△ABC关于x轴对称的△EDF。
21.已知两点A(–1,2) B(3,1)(1)P点在X轴上移动。
求PA+PB的最小值。
(2)Q点在Y轴上移动。
求QA+QB的最小值。
(3)并求出P.Q的坐标。
考点四、作一个图形关于某条直线的轴对称图形(1)作出一些关键点或特殊点的对称点.(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形22.如图,Rt△ABC,∠C=90°,∠B=30°,BC=8,D为AB中点,P为BC上一动点,连接AP、DP,则AP+DP的最小值是23.已知等边△ABC,E在BC的延长线上,CF平分∠DCE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.若AP=PQ,求证∠APQ是多少度作点Q关于BE的对称点R,交BE于点H,从而可得ΔQCH≌ΔRCH,∠QCH=∠RCH=60度。
A ,C,R在同一直线上。
易证ΔPCQ≌ΔPCR,从而∠QPH=∠RPH,PR=PQ, ∠PQC=∠PRC.又由于AP=PQ,从而AP=PR,得到∠PRA=∠PAR∴∠BAP+∠PAC=∠PQC+∠QPC∴∠BAP=∠QPC即有:∠BAP+∠B=∠QPC+∠APQ即∠APQ=60º等腰三角形有两条边相等的三角形是等腰三角形.相等的两条边叫做腰,另一条边叫做底边.两腰所夹的角叫做顶角,腰与底边的夹角叫做底角.等腰三角形的性质性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.特别的:(1)等腰三角形是轴对称图形.(2)等腰三角形两腰上的中线、角平分线、高线对应相等.等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”). 特别的:(1)有一边上的角平分线、中线、高线互相重合的三角形是等腰三角形.(2)有两边上的角平分线对应相等的三角形是等腰三角形.(3)有两边上的中线对应相等的三角形是等腰三角形.(4)有两边上的高线对应相等的三角形是等腰三角形.考点五、等腰三角形的特征和识别24.如图,△ABC 中,AB =AC =8,D 在BC 上,过D 作DE ∥AB 交AC 于E ,DF∥AC 交AB 于F ,则四边形AFDE 的周长为______ 。
FE D AB C25.如图,△ABC 中,BD 、CD 分别平分∠ABC 与∠ACB ,EF 过D 且EF ∥BC ,若AB = 7,BC = 8,AC = 6,则△AEF 周长为【 】A. 15 B . 14 C. 13 D. 1826.如图,点B 、D 、F 在AN 上,C 、E 在AM 上,且AB =BC =CD =ED =EF,∠A=20o,则∠FEB=________度.27.已知等腰三角形一腰上的高与另一腰的夹角为40°,则它的一个底角的度数是_______ 28.如图:在△ABC中,AB=AC,AD⊥BC, DE⊥AB于点E, DF⊥AC于点F。
试说明DE=DF。
FCDBEA29.如图,E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD =CE.求证:△ABC是等腰三角形.30.已知:如图,△ABC中,∠ACB的平分线交AB于E,EF∥BC交AC于点F,交∠ACB的外角平分线于点G.试判断△EFC的形状,并说明你的理由.AB C DGFE等边三角形三条边都相等的三角形叫做等边三角形,也叫做正三角形.等边三角形的性质等边三角形的三个内角都相等,•并且每一个内角都等于60°等边三角形的判定方法(1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形.考点六、等边三角形的特征和识别31.下列推理中,错误的是【】A.∵∠A=∠B=∠C,∴△ABC是等边三角形B.∵AB=AC,且∠B=∠C,∴△ABC是等边三角形C.∵∠A=60°,∠B=60°,∴△ABC是等边三角形D.∵AB=AC,∠B=60°,∴△ABC是等边三角形32.如图,等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC,垂足为M。
求证:M是BE的中点。
33.已知△ABC是等边三角形,分别在AC、BC上取点E、F,且AE=CF,BE、AF交于点D,则∠BDF= _________度34.如图,D 、E 、F 分别是等边△ABC 各边上的点,且AD =BE =CF ,则△DEF•的形状是【 】A .等边三角形B .腰和底边不相等的等腰三角形C .直角三角形D .不等边三角形DAF角平分线的性质:在角平分线上的点到角的两边的距离相等.AB CP M N O角平分线的判定:到角的两边距离相等的点在角的平分线上.AB CP M N O三角形的角平分线的性质:三角形三个内角的平分线交于一点,并且这一点到三边的距离相等.考点七、30°所对的直角边是斜边的一半35.如图,是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC 、DE 垂直于横梁AC ,AB =8m ,∠A =30°,则DE 等于【 】A .1mB .2mC .3mD .4mEDCBA36.一张折叠型方桌如图甲,其主视图如图乙,已知AO =BO =40cm ,C0=D0=30 cm ,现将桌子放平,两条桌腿叉开的角度∠AOB 刚好为120°,求桌面到地面的距离是多少?乙ODCBA37.如图,AB =AC ,DE⊥AB 于E ,DF⊥AC 于F ,∠BAC=120o,BC =6,则DE +DF =38.在ABC △中,120AB AC A =∠=︒,,AB 的垂直平分线交BC 于点F ,交AB 于点E .如果1EF =,求BC 的长FEA39.已知:在△ABC 中,AB =AC ,∠BAC =120°,AB 的垂直平分线交AB 于E ,交BC 于F. 求证:CF =2BF.甲作图题专练1.如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.2.已知:A、B两点在直线l的同侧,试分别画出符合条件的点M.(1)如图,在l上求作一点M,使得|AM-BM|最小;作法:(2)如图,在l上求作一点M,使得|AM-BM|最大作法:(3)如图,在l上求作一点M,使得AM+BM最小.AC··DO B(4)如果两点位于直线异侧,请你去解决上述问题变式练习1、如图,已知直线MN与MN同侧两点A、B求作:点P,使点P在MN上,且∠APM=∠BPN2.如图点A、B、C在直线l的同侧,在直线l上,求作一点P,使得四边形APBC的周长最小;3.如图已知线段a,点A、B在直线l的同侧,在直线l上,求作两点P、Q(点P在点Q 的左侧)且PQ=a,四边形APQB的周长最小.4、已知:如图点M在锐角∠AOB的内部,在OA边上求作一点P,在OB边上求作一点Q,使得ΔPMQ的周长最小;5、已知:如图3-14,点M在锐角∠AOB的内部,在OB边上求作一点P,使得点P到点M的距离与点P到OA边的距离之和最小.6、一条河两岸有A、B两地,要设计一条道路,并在河上垂直于河岸架一座桥,用来连接A、B两地,问路线怎样走,桥应架在什么地方,才能使从A到B所走的路线最短?轴对称专题训练一、选择题(每题3分,共24分)1、下列图案中,不是轴对称图形的是()A B C D2、(易错易混点)下列长度的三线段,能组成等腰三角形的是 ( ) A . 1 1 2 B. 2 2 5 C. 3 3 5 D. 3 4 5 3.如图,已知AC ∥BD ,OA =OC ,则下列结论不一定成立的是 ( ) A . ∠B=∠D B. ∠A=∠B C. AD=BC D. OA=OB 4.(易错易混点)下列说法正确的是( ) A .等腰三角形的高、中线、角平分线互相重合 B .顶角相等的两个等腰三角形全等 C .等腰三角形一边不可以是另一边的二倍 D .等腰三角形的两个底角相等5、如图,ABC △与A B C '''△关于直线l 对称,且7848A C '∠=∠=°,°,则∠B 的度数为() A .48°B .54°C .74°D .78°6、如图所示,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D ′,C ′的位置.若∠EFB =65°,则∠AED ′等于A. 70°B. 65°C. 50°D. 25°7、已知M (a ,3)和N (4,b )关于y 轴对称,则2012()a b +的值为( ) A.1 B 、-1 C.20097D.20097-8、如图,∠BAC =110°若MP 和NQ 分别垂直平分AB 和AC ,则∠P AQ 的度数是( )A.20°B. 40°C. 50°D. 60° 二、填空题(每题3分,共24分)9.轴对称是指____个图形的位置关系;轴对称图形是指____个具有特殊形状的图形. 10、有一条对称轴的三角形是_______三角形,有三条对称轴的三角形是______三角形. 11. 如图,在∆ABC 中,090=∠A ,BD 是∠ABC 的平分线,DE 是BC 的垂直平分线,则∠C =____.12、(易错易混点)在△ABC 中,AB =AC ,AB 的垂直平分线与AC 所在的直线相交所得到锐角为50°,则∠B 等于_____________度.13、如图,在∆ABC 中,AB =AC ,050=∠A ,P 是∆ABC 内一点,且∠PBC = ∠PCA ,则∠BPC =_____.14、如图,△ABC 中,∠A =36°,AB =AC ,BD 平分∠ABC ,DE ∥BC ,则图中等腰三角形有_____________个.15、如图,△ABC 中,DE 是AC 的垂直平分线,AE =3cm ,△ABD 的周长为13cm ,则△ABC 的周长为____________.16.如图,点P 在∠AOB 的内部,点M 、N 分别是点P 关于直线OA 、OB •的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是20cm,则线段MN的长是___________.三、解答题(17-20题每题10分,21题12分)17、右图(实线部分)补成以虚线L为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案(不用写作法、保留作图痕迹).请用一句话说明你的画图思路18、如图,写出△ABC的各顶点坐标,并画出△ABC关于Y轴对称的△A1B1C1,写出△ABC关于X轴对称的△A2B2C2的各点坐标。
