非稳态法测材料导热性能的实验
非稳态导热例题

“非稳态导热”例题例题1:一温度为20℃的圆钢,长度为0.3m ,直径为60mm ,在一温度为1250℃的加热炉内被加热。
已知圆钢的导热系数为35 W/(m ∙K),密度为7800kg/m 3,比热容为0.460J/(kg ∙K),加热炉长为6m ,圆钢在其中匀速通过,其表面和炉内烟气间的表面传热系数为100 W/(m 2∙K)。
现欲将该圆钢加热到850℃,试求该圆钢在加热炉内的通过速度。
解 特征尺寸A V /为m 0136.0)1060(14.3413.0)1060(14.33.0)1060(14.3414124133322=⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯=⨯+=---d dL L d A V πππ 则毕渥数v Bi 为05.0211.01.0039.0350136.0100)/(v =⨯=<=⨯==M A V h Bi λ 因此可以采用集总参数法求解。
θθρτ0ln hA cV= 即s548.14 1250850125020ln 100)10460.0(78003=--⨯⨯=τ则该圆钢在加热炉内的通过速度为m /s 0109.014.5486===τL v例题2:两块厚度均为30mm 的无限大平板,初始温度为20℃,分别用铜和钢制成。
平板两侧表面的温度突然上升至60℃,计算使两板中心温度均达到56℃时两板所需时间之比。
已知铜和钢的热扩散率分别为610103-⨯m 2/s 和6109.12-⨯m 2/s 。
(125.0==铜钢钢铜a a ττ)例题3:无内热源、常物性的二维导热物体在某一瞬时的温度分布为x y t cos 22=。
试说明该导热物体在x =0,y =1处的温度是随时间增加而逐渐升高,还是逐渐降低?例题4:一初始温度为20℃的钢板,厚度为10cm ,密度为为7800kg/m 3,比热容为460.5 J/(kg ∙K),导热系数为53.5W/(m ∙K),放置到温度为1200℃的加热炉中加热,钢板与烟气间的表面传热系数为407 W/(m 2∙K)。
用闪光法测定不良导体的热导率

用以及使用注意事项后方可进行实验内容(2)。 (2) 调节光学系统:实验室已组装好光路的光学系统。 (a) 调节氙灯的三维微调架上有刻线,以便较快调节光学元件的共轴,使氙灯的电极中
∞
∑ V = 1 + 2 (−1)n ⋅ exp(−n2ω ). n=1
(5)
将(5)式作图表示,见图 2。
令V=1/2,求得ω=1.38。将对应的时间记为t1/2,可得扩散率 a=1.38L2/π2t1/2,
进而有热导率
(6)
λ=1.38ρL2/π2t1/2。
(7)
上述处理过程要满足的条件是:试样面积〉〉厚度,则侧面散热可忽略,可视为一维热
温度检测元件 试样
t1/2 ω=π2αtL2
图1
图2
方程(2)的解
∑ T (x, t)
=
Q ρcL
⎡ ⎢1 + ⎣
∞
2 cos
n=1
nπx L
⋅
sin(nπl / L) (nπl / L)
exp⎜⎜⎝⎛ −
n 2π L2
2
at ⎟⎟⎠⎞⎥⎦⎤ .
在试样背面 x= L 处温升可表示为
∑ T (L, t)
量为 Q 的脉冲在 t=0 时刻照射在试样表面(试样为薄片状,脉冲光沿垂直于圆面的轴线方向
辐照),且被试样均匀吸收,可以认为在距表面的微小距离 l 内样品温升为
T( x,0)=Q/ρcl (0<x<l),
T( x,0)=0
( l<x<L),
(1)
其中 Q 为单位面积吸收的能量,L 为样品厚度(L<< l)。当试样周围热损很小以至可以忽略
非稳态准稳态法测材料的导热性能实验

非稳态(准稳态)法测材料的导热性能实验非稳态(准稳态)法是一种测量材料导热性能的实验方法,它通过在材料的一侧施加热量,测量另一侧的热流量来计算材料的导热系数。
这种方法相对于稳态法,具有设备简单、操作方便、测量速度快等优点。
下面是关于非稳态(准稳态)法测材料的导热性能实验的详细描述。
一、实验目的本实验的目的是通过非稳态(准稳态)法测量材料的导热性能,包括导热系数、热扩散系数和比热容等参数。
这些参数对于材料的热设计、能源利用和工程应用具有重要意义。
二、实验原理非稳态(准稳态)法基于热传导的傅里叶定律,其基本公式为:q=-k AΔT/L,其中q为热流量,k为导热系数,A为传热面积,ΔT为两侧温度差,L为材料的厚度。
在实验中,通过测量材料的传热面积和两侧温度差,可以计算出材料的导热系数。
三、实验步骤1.准备材料:选择待测材料,并准备相应的支架、加热器和温度传感器等设备。
2.安装样品:将待测材料放置在支架上,将加热器和温度传感器分别与材料的两侧接触,并固定好。
3.开始测量:打开加热器,使加热器输出的热量均匀地施加到材料的左侧,同时使用温度传感器测量材料的右侧温度。
记录下加热时间和温度变化。
4.数据处理:根据测量的数据,绘制温度随时间变化的曲线。
通过曲线可以计算出材料的导热系数、热扩散系数和比热容等参数。
四、实验结果与分析通过实验测量和数据处理,我们可以得到待测材料的导热系数、热扩散系数和比热容等参数。
这些参数可以用来评估材料的导热性能和热特性。
例如,导热系数高的材料可以更好地传递热量,适用于需要高效散热的场合;比热容大的材料可以吸收更多的热量,适用于需要储存和释放热量的场合。
在分析实验结果时,需要注意以下几点:1.实验结果的准确性受到多种因素的影响,如测量设备的精度、环境温度和湿度等。
因此,需要对实验结果进行误差分析,以确定其可信度。
2.对于不同种类的材料,其导热性能和热特性可能存在差异。
因此,需要对不同种类的材料进行分别测量和分析。
非稳态平面热源法同时测量材料的导热系数和热扩散率

收 稿 日期 :060 - 2 0 -1 5 0
基金项 目: 国防科技重点实验室资助项 目( 目编号 :0 5S 16 .4 . a 2 5 。 项 2 0 J54 9 001Q V . ) 作者简介 : 于帆( 94一) 男, 16 , 教授 , 主要从事热物性测量和传热学技术的 正 06
1 引 言
导热系数 ( 或热导率 ) 直接表 征物质的导热能
a dT cnl e i , e i 00 3 n eh o g B rn B in 10 8 ; o y g jg
2 A rsaeR sac s tt o tr sadPoes gT cnlg ,e ig 20— 3—1 ,10 7 ) . eopc eerhI tue f e a n rcsi eh o y B rn 0 7 n i Ma i l n o 9 5 0 0 6
b a u n h e e au e r s o s n t e s e i n wi e s r p a e itn e f m h e t y me s r g t e tmp r t r e p n e i p cme t a s n o lc d a d sa c r i h h o t e h a
M e s r me to e ma n u tvt n a u e n fTh r lCo d ci iy a d The ma 船 i y f r r lDi t o
M a e il n Tr n in o . a e M eho t ra so a se tH tPl n t d
Ab t a t T e me s r me t r c p eo e t n i n t l emeh d, eh a o d c in mo e sr c h a u e n i i l f h a se t p n t r Ho — a t o t e t n u t d l pn h c o a d t e tmp r t r e p n e e u t n r n r d c d h e e p r na p a au a e n e t b i e n e e au e r s o s q ai sa e i t u e .T x e me tla p r t sh sb e s l h d h o o i a s a d p a t a a u e n s h v e n ma e w t o tr s h e r s l h w t a h e ma o — n r ci lme s r me t a e b e d i s me mae a .T e u t s o t e t r l n c h i l s h t h c
非稳态(准稳态)法测材料导热性能实验

非稳态(准稳态)法测材料的导热性能实验一、实验目的一、本实验属于创新型实验,要求学生自己选择不同原料、依照不同配比进行加工出新型实验材料,并对该材料的热物性(密度、导热系数、比热容、导温系数)进行实验测量。
2.快速测量绝热材料(不良导体)的导热系数和比热,把握其测试原理和方式。
3、把握利用热电偶测量温差的方式。
二、实验测试原理本实验是依照第二类边界条件,无穷大平板的导热问题来设计的。
设平板厚度为2δ,初始温度为t 0,平板两面受恒定的热流密度q c 均匀加热(如以下图所示)。
依照导热微分方程式、初始条件和第二类边界条件,关于任一刹时沿平板厚度方向的温度散布t(x ,τ)可由下面方程组解得;方程组的解为:式中:τ——时刻;λ——平板的导热系数;α——平板的导温系数;t 0——初始温度; —傅立叶准那么;δβμn n = ,n=1,2,3…;q c ——沿X 方向从端面向平板加热的恒定热流密度。
0),0(0),()0,(),(),(022=∂∂=+∂∂=∂∂=∂∂xt q x t t x t x x t a x t cτλτδτττ)1()]exp()cos(2)1(63[),(2211220o n n n n n c F x x q t x t μδμμδδδδατλτ--+--=-+∞=∑2δατ=F随着时刻τ的延长,F 0数变大,式(1)中级数和项愈小。
当F 0>时,级数和项变得很小,能够忽略,式(1)变成(2)由此可见,当F 0>后,平板遍地温度和时刻成线性关系,温度随时刻转变的速度是常数,而且处处相同。
这种状态即为准稳态。
在准稳态时,平板中心面X=0处的温度为:平板加热面X=δ处为:此两面的温差为: (3) 已知q c 和δ,再测出△t ,就能够够由式(3)求出导热系数:(4)事实上,无穷大平板是无法实现的,实验老是用有限尺寸的试件,一样能够为,试件的横向尺寸为厚度的6倍以上时,双侧散热对试件中心的温度阻碍能够忽略不计。
实验《导热系数测定》

实验二材料导热系数的测定一、实验目的1、巩固和深化不稳定导热过程的基本理论,学习用常功率平面热源法测定材料导热系数和导温系数的实验方法和技能。
2、测定试材的导热系数λ和导温系数α。
二、实验原理:稳态导热问题,即忽略温度随时间的变化,只考虑温度的空间分布。
即θ(x,y,z)而非稳态导热问题温度不仅在空间上有分布,而且随时间变化。
即θ(x,y,z,τ)根据不稳定导热过程的基本理论,初始温度均匀并为t0的半无限大均质物体,当表面边界被常功率热流q w加热时,同样引进过余温度θ=t-t0 ,温度场由以下导热微分方程求解:经过求解和变换,得出如下的关系式:(1)函数B(y)值()B y =(2)导温系数根据B(y)值查表得y 2值,则224d a y τ=' (m 2/h )d :薄试件的厚度 m (3)导热系数λ=(w/mk )上述各式中:(,)x θτ'' 经过时间τ'薄试件上表面过余温度; 1(0,)θτ 经过时间1τ薄试件下表面(热源面)过余温度;3(0,)θτ 经过时间3τ降温过程中下表面(热源面)过余温度; 2τ 关闭热源的时间;Q 加热器的功率 W/m 2Q=(V 标/10)2*A=I 2*A A=R/S式中: V 标 –与加热器串连的0.01Ω标准电阻两端的电压降 mv R 、S 分别为加热器的电阻及面积。
三、实验装置DRM-1型导热系数测定仪 适用于测定均质板状、粉末状材料的导热系数、导温系数和比热。
测试范围:3.5×10-2~1.7 W/mk ;电热烘干箱;秒表两只;干燥器;天平;卡尺(精度为0.02毫米)。
DRM-1型导热系数测定仪分三部分:1、试件部分:包括试件,试件台及夹具。
2、加热系统:包括晶体管稳压电源、加热器、0.01Ω标准电阻、电位差计和检流计。
3、温度测量系统:温度测量用铜-康铜热电偶,电偶产生的电信号用电位差计测出,通过查表得出温度值。
电芯导热系数测试标准

电芯导热系数测试标准
一、测试设备
电芯导热系数测试设备应符合相关标准和规定,具备温度控制、数据采集和数据处理等功能。
测试设备的精度、稳定性、可靠性和安全性应符合相关要求,确保测试结果的准确性和可靠性。
二、样品准备
1. 样品尺寸:电芯导热系数测试的样品尺寸应符合相关标准和规定,一般要求为长方形或圆形,长度、宽度和高度应符合测试设备的要求。
2. 样品质量:样品的质量应符合相关标准和规定,保证样品的代表性。
在测试前应对样品进行质量检测,确保其符合要求。
3. 样品处理:样品在测试前应进行预处理,包括清洁、干燥等,保证其表面质量和导热性能。
同时,应避免在测试过程中出现变形、开裂等现象。
三、测试方法
1. 稳态法:稳态法是一种常用的电芯导热系数测试方法,通过控制样品在不同温度下的热量平衡,测量样品在不同温度下的热流密度,从而计算出样品的导热系数。
稳态法具有较高的精度和可靠性,但测试时间长,需要样品的质量较大。
2. 非稳态法:非稳态法是一种较新的电芯导热系数测试方法,通过测量样品在不同时间点的温度变化,结合热扩散系数和比热容等参数,计算出样品的导热系数。
非稳态法具有测试时间短、样品质量小的优点,但精度和可靠性相对较低。
四、参数设置
1. 温度范围:在测试过程中,应根据样品的特性和测试要求设置合理的温度范围。
温度范围的设置应考虑样品的热膨胀系数、比热容等因素,避免出现热
冲击和过热等现象。
2. 压力范围:在测试过程中,应根据样品的特性和测试要求设置合理的压力范围。
压力范围的设置应考虑样品的机械性能和稳定性等因素,避免出现变形和破裂等现象。
传热学实验指导书---实验一(本部)
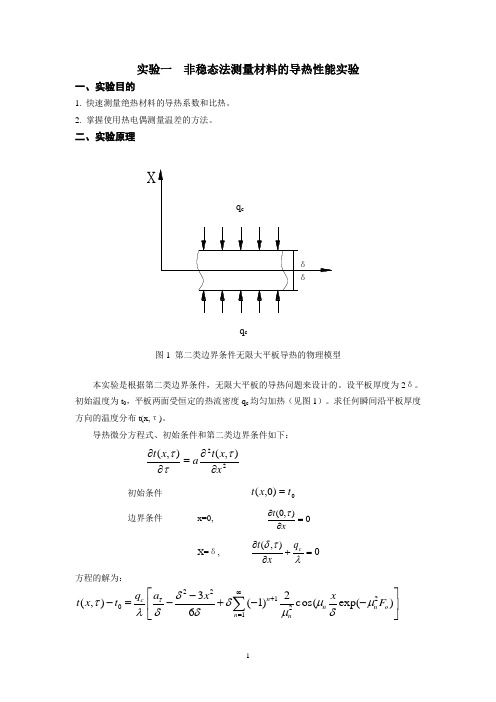
实验一 非稳态法测量材料的导热性能实验一、实验目的1. 快速测量绝热材料的导热系数和比热。
2. 掌握使用热电偶测量温差的方法。
二、实验原理X图1 第二类边界条件无限大平板导热的物理模型本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度为2δ。
初始温度为t 0,平板两面受恒定的热流密度q c 均匀加热(见图1)。
求任何瞬间沿平板厚度方向的温度分布t(x,τ)。
导热微分方程式、初始条件和第二类边界条件如下:22),(),(x x t a x t ∂∂=∂∂τττ初始条件 0)0,(t x t =边界条件x=0,0),0(=∂∂xt τX=δ,0),(=+∂∂λτδcq x t 方程的解为:⎥⎦⎤⎢⎣⎡--+--=-∑∞=+1221220)exp(cos(2)1(63),(n o n n n n c F x x a q t x t μδμμδδδδλττq c式中: t —温度; τ—时间; t 0 — 初始温度;ɑ — 平板的导温系数; μn — n π n=1,2,3,……2δτa Fo =— 傅立叶准则; q c— 沿方向从端面向平板加热的恒热流密度;随着时间t 的延长,Fo 数变大,上式中级数和项愈小。
当Fo>0.5时,级数和项变得很小,可以忽略,上式变成:)612(),(220-+-=-δτδτλδτa a q t x t c 由此可见,当Fo>0.5后,平板各处温度和时间成线性关系,温度随时间变化的速率是常数,并且到处相同。
这种状态称为准稳态。
在准稳态时,平板中心面x=0处的温度为:)61(),0(20-=-δτλδτa q t t c 平板加热面X=δ处为:)31(),(20+-=-δτλδτδa q t t c 此两面的温差为:λδττδcq t t t 21),0(),(=-=∆如已知q c 和δ,再测出t ∆,就可以由上式求出导热系数:tq c∆=2δλ式中,λ—平板的导热系数,oW /(m C)⋅ cq —沿x 方向给平板加热的恒定热流密度,2W /mδ—平板的厚度,mt ∆—平板中心面x=0处和平板加热面x=δ处两面的温差,o C又,根据热平衡原理,在准稳态有下列关系:式中,F —平板的横截面积ρ—试件材料的密度C —试件材料的比热—准稳态时的温升速率由上式可求得比热为:实验时, 以试件中心处为准。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 非稳态(准稳态)法测材料的导热性能实验
一﹑实验目的
1、测量绝热材料的导热系数和比热,掌握其测试原理和方法;
2、掌握使用热电偶测量温差的方法。
二﹑实验装置
实验装置见下图
三﹑实验原理
本实验是根据第二类边界条件, 无限大平板的导热问题来设计的设平板厚度为δ, 初始温度0t , 平板两面受恒定的热流密度c q 均匀加热求任何瞬间沿平板厚度方向的温度分布(,)
t x
τ导热微分方程式﹑初始条件和第二类边界条件如下:
2
2)
,(),(x
x t a x t ∂∂=∂∂τττ 0=τ时, 0t t = 0x =处, 0=∂∂x
t
δ±=x 处, c
q x
t =∂∂-λ
方程的解为:
22
03(,)[6c q a x t x t τδτλδδ--=-
12021
2(1)cos()exp()]n n n n x
F δμμμδ∞
+=+--∑ (1)
式中: τ—时间(s );
λ—平板的导热系数(0W m C ⋅); a —对流换热系数(2m ); n μ—πn (n=1,2,3,.....);
0F —2δ
τ
a (傅立叶准则);
0t —初始温度();
c q —沿x 方向从端面向平板加热的恒定热流密度(2W m )。
随着时间τ的延长, 0F 数变大,式(1)中级数和项愈小 当0F >0.5时, 级数和项变得很小, 可以忽略, 式(1)变成:
)6
1
2(),(220-+=-δδλδx at q t t x t c (2)
由此可见, 当0F >0.5后, 平板各处温度和时间成线性关系, 温度随时间变化的速率是
常数, 并且到处相同
这种状态称为准稳态。
在准稳态时, 平板中心面0x =处的温度为:)6
1
(),0(0-=
-δτλδτa q t t c 平板加热面x δ=处为:
)3
1
(),(20+=
-δτλδτδa q t t c (3) 此两面的温差为:
1(,)(0,)2c q t t t δ
δττλ
∆=-=⋅
如已知c q 和δ, 再测出t ∆, 就可以由式(3)求出导热系数:
t
q c ∆=
2δ
λ (4) 实际上,无限大平板是无法实现的,实验总是用有限尺寸的试件。
一般可认为,试件的横向尺寸为厚度的6倍以上时,两侧散热试件中心的温度影响可以忽略不计。
试件两端面中心处的温度差就等于无限大平板两端面的温度差。
根据势平衡原理,在准稳态时,有下列关系:
τ
ρδ
d dt CF F q c = 式中:F —试件的横截面(2
m );
C —为试件的比热(o J kg C ⋅); ρ—试件的密度(3kg m ); τ
d dt —准稳态时的温升速率(o
C ); 由上式可得比热: c
q C dt d ρδτ
= (τd dt 以试件中心处为准)
四﹑实验步骤
1﹑检查仪器并接通电源;
2、按下[功能/确认]键后,显示屏会出现(选择菜单),按[加/选择]键,选择项目后按[功能/确认]键确认;
3、待试件温度稳定后(约10分钟),每分钟记录一组数据;
4、第一次实验结束, 断开电源, 取下试件, 用电扇将加热器吹凉, 待其和室温平衡后才能继续做下一次实验试件不能连续做实验, 必须使其冷却至与室温平衡后, 才能再做下一次实验;
5、实验全部结束后, 必须切断电源, 一切恢复原状 五﹑数据处理
记录下列数据并将其它实验数据填入表1中
试件截面尺寸F : 0.00126 (2
m ) 试件厚度δ: 0.009 (m ) 试件材料密度ρ:1200 (3kg m )
加热温度
测试温度
准稳态时的温差t ∆()(平均值)
准稳态时的温升速率
τ
d dt
(o C ) 然后,计算出试件的导热系数λ(W m k ⋅)和比热C (o J kg C ⋅)。
