电路分析基础 上海交通大学出版社 习题答案第二章汇总
电路分析基础(英文版)课后答案第二章
2Some Circuit Simpli¯cationTechniquesDrill ExercisesDE2.116k64=12:8−;12:8+7:2=20−;20k30=12−[a]v=5(12)=60V[b]p5A(del)=(5)(60)=300W[c]i A=60=30=2A i C=3(64)=(80)=2:4Ai B=5¡2=3A p10−=(2:4)210=57:6WDE2.2[a]v o(no load)=200(75)=100=150V[b]75k150=50k−,therefore v o=200(50)=75=133:3V[c]i=200=25;000=8mA,p25k=(8£10¡3)2(25;000)=1:6W[d]Maximum dissipation at no load since v o is maximump=v2o75;000=0:3W2728CHAPTER2.Some Circuit Simpli¯cation TechniquesDE2.3v30=6+4(0:825)=9:3V;i30=v3030=0:31Ai6=i30+0:825=1:135A;i10=0:825+0:31=1:135A¡v30¡6i b+v20¡10i10=0¢::v20=9:3+16(1:135)=27:46Vi20=27:4620=1:373A;i5=i6+i20=2:508Ai30=0:31A;i6=1:135A;i10=1:135A;i20=1:373A;and i5=2:508ADE2.4Problems29i =7212=6A [a]v =7212(8)=48V ;i 120V =120¡57:620=3:12A [b]v a =6(9:6)=57:6V ;p 120V (del)=120i a =374:40WDE 2.5[a]110V source actingalone:R e =10(14)24=356−i 0=1105+35=6=13213Av 0o=µ356¶µ13213¶=77013V 4A source actingalone:5−k 10−=50=15=10=3−10=3+2=16=3−30CHAPTER2.Some Circuit Simpli¯cation Techniques 16=3k12=48=13−Hence our circuit reduces to:It follows thatv00a=4(48=13)=(192=13)Vandv00o=¡v00a(16=3)(10=3)=¡58v00a=¡(120=13)V¢::v o=v0o+v00o=77013¡12013=50V[b]p=v2o10=250WDE2.670-V source acting alone:v0=70¡4i0bi0s=v0b2+v010=i0a+i0b70=20i0a+v0bi0a=70¡v0b 20Problems31¢::i 0b=v 0b 2+v 010¡70¡v 0b 20=1120v 0b +v 010¡3:5v 0=v 0b+2i 0b ¢::v 0b =v 0¡2i 0b¢::i 0b =1120(v 0¡2i 0b )+v 010¡3:5or i 0b =1342v 0¡7042¢::v 0=70¡4µ1342v 0¡7042¶orv 0=322094=161047V 50-V source actingalone:v 00=¡4i 00bv 00=v 00b +2i 00bv 00=¡50+10i 00d ¢::i 00d=v 00+5010i 00s =v 00b 2+v 00+5010i 00b=v 00b 20+i 00s =v 00b 20+v 00b 2+v 00+5010=1120v 00b +v 00+5010v 00b =v 00¡2i 00b¢::i 00b =1120(v 00¡2i 00b )+v 00+5010or i 00b =1342v 00+10042Thus,v 00=¡4µ1342v 00+10042¶orv 00=¡20047V Hence,v =v 0+v 00=161047¡20047=141047=30V32CHAPTER2.Some Circuit Simpli¯cation Techniques ProblemsP2.1[a]p4−=i2s4=(12)24=576W p18−=(4)218=288W p3−=(8)23=192W p6−=(8)26=384W[b]p120V(delivered)=120i s=120(12)=1440W[c]p diss=576+288+192+384=1440WP2.2[a]From Ex.3-1:i1=4A,i2=8A,i s=12Aat node x:¡12+4+8=0,at node y:12¡4¡8=0[b]v1=4i s=48V v3=3i2=24Vv2=18i1=72V v4=6i2=48Vloop abda:¡120+48+72=0;loop bcdb:¡72+24+48=0;loop abcda:¡120+48+24+48=0P2.31R eq=16+110+115=1030=13;R eq=3−v(2+8+5)−=(20)(3)=60V;i(2+8+5)−=60=15=4A P5−=(4)2(5)=80WP2.4[a]R eq=2+2+(1=4+1=5+1=20)¡1=6−i g=120=6=20Av4−=120¡(2+2)20=40Vi o=40=4=10AProblems33 i(15+5)−=40=(15+5)=2Av o=(5)(2)=10V[b]i15−=2A;P15−=(2)2(15)=60W[c]P120V=(120)(20)=2:4kWP2.5[a]R eq=R k R=R22R=R2[b]R eq=R k R k R k¢¢¢k R(n R's)=R kR n¡1=R2=(n¡1)R+R=(n¡1)=R2nR=Rn[c]One solution:700−=200−+500−=1000=5+1000=2=1k−k1k−k1k−k1k−k1k−+1k−k1k−[d]One solution:5:5k−=5k−+0:5k−=2k−+2k−+1k−+0:5k−=2k−+2k−+2k−2+2k−4=2k−+2k−+2k−k2k−+2k−k2k−k2k−k2k−34CHAPTER2.Some Circuit Simpli¯cation TechniquesP2.6[a]12−k24−=8−Therefore,R ab=8+2+6=16−[b]1R eq=124k−+130k−+120k−=15120k−=18k−R eq=8k−;R eq+7=15k−1R ab=115k−+130k−+115k−=530k−=16k−R ab=6k−P2.7[a]For circuit(a)R ab=15k(18+48k16)=10−For circuit(b)1 R e =120+115+120+14+112=3060=12R e=2−R e+16=18−18k18=9−R ab=10+8+9=27−For circuit(c)48k16=12−12+8=20−20k30=12−12+18=30−30k15=10−10+10+20=40−R ab=40k60=24−[b]P a=20210=40WP b=144227=768WP c=62(24)=864WProblems35P2.8[a]5k20=100=25=4−5k20+9k18+10=20−9k18=162=27=6−20k30=600=50=12−R ab=5+12+3=20−[b]5+15=20−30k20=600=50=12−20k60=1200=80=15−3k6=18=9=2−15+10=25−3k6+30k20=2+12=14−25k75=1875=100=18:75−26k14=364=40=9:1−18:75+11:25=30−R ab=2:5+9:1+3:4=15−[c]3+5=8−60k40=2400=100=24−8k12=96=20=4:8−24+6=30−4:8+5:2=10−30k10=300=40=7:5−45+15=60−R ab=1:5+7:5+1:0=10−P2.9[a]R cond=845(0:0397)=33:5465−R total=2(1=2)R cond=33:5465−P loss=(2000)2(33:5465)=134:186MWP calif=800(2)¡134:186=1465:814MWE±ciency=(1465:814=1600)£100=91:61%[b]P calif=2000¡134:86=1865:814MWE±ciency=93:29%[c]P loss=(3000)2¢2¢(1=3)¢845¢(0:0397)=201:279MWP oregon=3000MW;P calif=3000¡201:279=2798:7MWE±ciency=(2798:70=3000)£100=93:29%P2.10i10k=(18)(15)40=6:75mAv15k=¡(6:75)(15)=¡101:25V i3k=18¡6:75=11:25mAv12k=¡(12)(11:25)=¡135Vv o=¡101:25¡(¡135)=33:75V36CHAPTER 2.Some Circuit Simpli¯cation TechniquesP 2.11[a]v 1k =11+5(30)=5V v 15k =1515+60(30)=6Vv x =v 15k ¡v 1k =6¡5=1V [b]v 1k =v s6(1)=v s =6v 15k=v s75(15)=v s =5v x =(v s =5)¡(v s =6)=v s =30P 2.1260k 30=20−i 30−=(25)(75)125=15A v o =(15)(20)=300V v o +30i 30=750V v g ¡12(25)=750v g =1050VP 2.135−k 20−=4−;4−+6−=10−;10k 40=8−;Therefore,i g =1258+2=12:5A i 6−=(40)(12:5)50=10A;i o =(5)(10)25=2A P 2.14[a]40k 10=8−i 75V =7510=7:5A 8+7=15−i 4+3−=7:5µ3045¶=5A15k 30=10−i o =¡5µ1050¶=¡1A[b]i 10−=i 4+3−+i o =5¡1=4AP 10−=(4)2(10)=160WP2.15[a]v9−=(1)(9)=9Vi2−=9=(2+1)=3Ai4−=1+3=4A;v25−=(4)(4)+9=25Vi25−=25=25=1A;i3−=i25−+i9−+i2−=1+1+3=5A;v40−=v25−¡v3−=25¡(¡5)(3)=40Vi40−=40=40=1Ai5k20−=i40−+i25−+i4−=1+1+4=6Av5k20−=(4)(6)=24Vv32−=v40−+v5k20−=40+24=64Vi32−=64=32=2A;i10−=i32−+i5k20−=2+6=8Av g=10(8)+v32−=80+64=144V:[b]P20−=(v5k20−)220=24220=28:8WP2.16[a]Let i s be the current oriented down through the resistors.Then,i s=V sR1+R2+¢¢¢+R k+¢¢¢+R nandv k=R k i s=R kR1+R2+¢¢¢+R k+¢¢¢+R nV s[b]i s=2005+15+30+10+40=2Av1=2(5)=10V v2=2(15)=30V v3=2(30)=60V v4=2(10)=20V v5=2(40)=80VP2.17[a]v o=2525(20)=20V[b]v o=255+R eR eR e=(20)(12)32=7:5k−v o=2512:5(7:5)=15V[c]v o25=2025=0:80[d]v o25=1525=0:60P2.18[a]No load:v o=R2R1+R2V s=¾V s¢::¾=R2R1+R2 Load:v o=R eR1+R eV s=¯V s¢::¯=R eR e+R1R e=R2R LR2+R L¢::¯=R2R LR1R2+R L(R1+R2)But R1+R2=R2¾¢::R1=R2¾¡R2¢::¯=R2R LR2³R2¾¡R2´+R L R2¾¯=R LR 2³1¾¡1´+R L ¾or ¯R 2µ1¾¡1¶+¯R L ¾=R L ¯R 2µ1¾¡1¶=R L Ã1¡¯¾!¢::R 2=(¾¡¯)¯(1¡¾)R LR 1=(1¡¾)¾R 2=þ¡¯¾¯!R L[b]R 1=(0:9¡0:7)0:63(126)k −=40k −R 2=(0:9¡0:7)(0:7)(0:1)(126)k −=360k −P 2.19[a]Let v o be the voltage across the parallel branches,positive at the upperterminal,theni g =v o G 1+v o G 2+¢¢¢+v o G N =v o (G 1+G 2+¢¢¢+G N )It follows thatv o =i g(G 1+G 2+¢¢¢+G N )The current in the k th branch is i k =v o G k ;Thus,i k =i g G k[G 1+G 2+¢+G N ][b]i 6:25=1142(0:16)[4+0:4+1+0:16+0:1+0:05]=32mAP 2.20R e =48£103=500−¢::XG =1500=2mS i 1=2i 2=2(10i 3)=20i 4i 2=10i 3=10i 4i 3=i 48=20i4+10i4+i4+i4=32i4¢::i4=832=0:25mAR4=v gi4=40:25£10¡3=16k−i3=i4=0:25mA ¢::R3=16k−i2=10i4=2:5mAR2=v gi2=42:5£10¡3=1:6k−i1=20i4=5mAR1=v gi1=45£10¡3=800−P2.21[a]i o=120=40k−=3mA[b]v a=(3)(20)=60Vi a=v a100=0:6mAi b=4¡3:6=0:4mAv b=60¡(0:4)(15)=54Vi g=0:4¡54=30=¡1:4mAp75V(developed)=(75)(1:4)=105mWCheck:p4mA(developed)=(60)(4)=240mWX P dev=105+240=345mWX P dis=(¡1:4)2(15)+(1:8)2(30)+(0:4)2(15)+(0:6)2(100)+(3)2(20)=345mWP2.22Apply source transformations to both current sources to geti o=¡66=¡1mAP2.23[a]¢::v o=1(240)=120V;i o=120=24=5A2[b]p300V=¡12:5(300)=¡3750WTherefore,the300V source is developing3.75kW.[c]¡10+i6−+7:5¡12:5=0;¢::i6−=15Av10A+4(10)+6(15)=0;¢::v10A=¡130Vp10A=10v10A=¡1300WTherefore the10A source is developing1300W.[d]X p dev=3750+1300=5050Wp4−=100(4)=400Wp40−=(7:5)2(40)=2250Wp6−=(15)2(6)=1350Wp42−=(5)2(42)=1050WX p diss=400+1350+2250+1050=5050W(CHECKS)P2.24Applying a source transformation to each current source yieldsNow combine the20V and10V sources into a single voltage source and the5−,4−and1−resistors into a single resistor to getNow use a source transformation on each voltage source,thuswhich can be reduced to¢::i o=(1:25)(8)=1A10P2.25First,¯nd the Th¶e venin equivalent with respect to R o.P2.26100−k25−=20−¢::i=400=5A60+20v0o=20i=100V100−k60−=37:5−i=50025+37:5=8Av00o=37:5i=300Vv o=v0o+v00o=100+300=400V P2.27i0o=10025=4A15−k30−=10−i00o=¡5025=¡2A¢::i o=i0o+i00o=4¡2=2A P2.2815=2i0¢+50i1+3i0¢Problems4715=2i 0¢+12i 02i 0¢=i 01+i 02;i 01=27=26A;i 0¢=51=26A¢::i 02=1213A;v 0o=9613V ¡2i 00¢=5i 001+3i 00¢¢::i 00¢=¡i 001i 002=i 00¢¡i 001=2i 00¢4i 002+(8+i 002)8=¡2i 00¢¢::i 002=¡6413A;i 001=3213A;i 00¢=¡3213A ¢::8+i 002=4013A ¢::v 00o=8µ4013¶=32013V ¢::v o =v 0o +v 00o =9613+32013=32V48CHAPTER2.Some Circuit Simpli¯cation TechniquesP2.29[a]The evolution of the circuit shown in Fig.P2.29is illustrated in the following steps:[b]Starting at the left end of the circuit and working toward the right end,aseries of source transformations yields:Problems49V R=4 4R (2R)=V R8P2.30[a]The evolution of the circuit in Fig.P2.30can be shown in two steps,thus:[b]Moving from left to right,a series of source transformations yields:50CHAPTER2.Some Circuit Simpli¯cation Techniquesv o=V R=84R(2R)=V R16Problems51 P2.31Eq.(2.34)v o=12V R(Switch1)Eq.(2.35)v o=14V R(Switch2)Eq.(2.36)v o=18V R(Switch3)Eq.(2.37)v o=116V R(Switch4)Given V R=16V:Switch Position v o12340000v o=0V000V R v o=116V R=1V00V R0v o=18V R=2V00V R V R v o=116V R+18V R=3V0V R00v o=14V R=4V0V R0V R v o=14V R+116V R=5V0V R V R0v o=14V R+18V R=6V0V R V R V R v o=14V R+18V R+116V R=7VV R000v o=12V R=8VV R00V R v o=12V R+116V R=9VV R0V R0v o=12V R+18V R=10VV R0V R V R v o=12V R+18V R+116V R=11VV R V R00v o=12V R+14V R=12VV R V R0V R v o=12V R+14V R+116V R=13VV R V R V R0v o=12V R+14V R+18V R=14VV R V R V R V R v o=12V R+14V R+18V R+116V R=15V52CHAPTER2.Some Circuit Simpli¯cation TechniquesThis page intentionally left blank。
《电路分析基础》习题参考答案
《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出，P2=6W吸收，P3=16W吸收，P4=-lOW发出，PS=-7W发出，PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开：UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合：12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
上海交通大学本科学位课程 电路基础 电路第2章_6
电路基础上海交通大学本科学位课程第二章 电路分析的基本方法“二端口”的串联口电流不因连接而破坏下a b a ba b1122,i i i i ==⇒=I I “二端口”A 和B 进行串联串联“二端口”的R 矩阵为各分“二端口”R 矩阵之和2u 2i 1i 1u a 2uABb 2ua 1ub 1ub 2ia 2ib 1ia 1ia a a a a a a 111121a a a a 221222b b b b b b b111121b b b b 221222u r r i u r r i u r r i u r r i ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦U R I U R I a b a b 11111a b a b 22222a a b b a b []u u u u u u u u u u ⎡⎤⎡⎤⎡⎤+⎡⎤===+⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦⎣⎦=+=+=U R I R I R R I RIa b∴=+R R R对较复杂“二端口”进行分析时，可将之分解成简单二端口的串联，使分析简化4113k ⎡⎤⎢⎥+⎣⎦302k ⎡⎤⎢⎥⎣⎦1111⎡⎤⎢⎥⎣⎦当口电流因连接受破坏时，前面的约束不成立3113⎡⎤⎢⎥⎣⎦2112⎡⎤⎢⎥⎣⎦4334⎡⎤⎢⎥⎣⎦1i k 31i 1211i k 31i 2111111111i 1i 12i 12i两个“二端口”间的串联连接是否有效，可通过有效性试验来判定。
当上两图中的电压表的读数都为零时，便可断定把A ，B 串联起来后不会破坏两端口电流的约束条件。
iAB1V iAB2V“二端口”电路含独立电源时的方程“二端口电路”含独立电源时的方程可以分两步考虑其中u 1oc 和u 2oc 都是在两端口开路时，由二端口中的独立源在两端口上产生的开路电压。
含独立源的二端口电路2u 1i 1u 2i 不含独立源二端口电路2'u 1i 1'u 2i 含独立源的二端口电路2ocu 1ocu 1oc 1111212oc 221222u u r r i u u r r i ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦求所示二端口电路的 r 参数方程。
C·A上传 【电路分析】第二章答案
。
***** 直流电路分析程序 ( DCAP 2.11 ) 成电 七系--胡翔骏 ***** 习题2-3
计算表明：电阻 R=4Ω时，电压u=6V，吸收功率 p=3W 。
2－4 电路如题图2－4所示。当开关S断开或闭合时，求电位器 滑动端移动时，a点电位的变化范围。
xt2-4A Circuit Data 元件 支路 开始 终止 控制 元 件 元 件 类型 编号 结点 结点 支路 数 值 数 值 V 1 1 0 15.000 R 2 1 2 1000.0 R 3 2 3 1000.0 R 4 3 0 1000.0 OC 5 2 0 独立结点数 = 3 支路数 = 5 结 点 电 压 V 1= 15.00 输出电压在5~10V之间变化 。 V 2= 10.00 V 3= 5.000 编号 类型 数值 支路电压 支路电流 支路吸收功率 1 V 15.00 U 1= 15.00 I 1= -5.0000E-03 P 1= -7.5000E-02 2 R 1000. U 2= 5.000 I 2= 5.0000E-03 P 2= 2.5000E-02 3 R 1000. U 3= 5.000 I 3= 5.0000E-03 P 3= 2.5000E-02 4 R 1000. U 4= 5.000 I 4= 5.0000E-03 P 4= 2.5000E-02 5 OC .0000 U 5= 10.00 I 5= .0000 P 5= .0000 各支路吸收功率之和 P = .0000
习题2-1c
u1 8V
u2 10V
2－2电路如题图2－2所示。已知电流i=2A，求电阻之值以及 5Ω电阻吸收的功率。
xt2-2 Circuit Data 元件 支路 开始 终止 控制 元 件 元 件 类型 编号 结点 结点 支路 数 值 数 值 R 1 1 0 5.0000 R 2 1 2 7.0000 R 3 2 0 36.000 R 4 2 3 6.0000 I 5 0 3 8.0000 独立结点数 = 3 支路数 = 5 ----- 给 输 出 变 量 值 , 求 元 件 数 值 ----你 选 择 的 输 出 变 量 值 I 3= 2.00 求 出 的 元 件 数 值 如 下 : 编号 类型 数值 1 数值 2 I 3 3 R 36.0002 1.99999 ***** 直流电路分析程序 ( DCAP 2.11 ) 成电 七系--胡翔骏 *****
电路分析基础,上海交大出版社,主编李秀平,主审胡耀华--答案(第1,2章)
《电路分析基础》课后习题答案第1章1-1 （a ）发出54W 功率；（b ）吸收50W 功率；（c ）发出220W 功率1-2 （a ）V U 9A -=; （b ）A I 2B -=; （c ）A I 6C =1-3 元件A 吸收54W 功率；元件B 发出24W 功率1-4 元件B 发出30W 功率；元件C 吸收15W 功率1-5 （2）元件1和2是电源，元件3,4,5是负载；（3）元件1发出140W 功率，元件2发出135W 功率，元件3吸收150W 功率，元件4 吸收80W 功率，元件5吸收45W 功率； 功率平衡1-6 A I 51=，A I 3=，电压源发出30W 功率，2Ω电阻吸收50W 功率，5Ω电阻吸收20W 功率，电流源发出40W 功率；电路功率平衡。
1-7 （a ）电压源吸收20W 功率，电流源发出20W 功率；（b ）电流源总是发出功率，20W;电阻总是吸收功率；R>0.8Ω时，电压源吸收功率；R=0.8Ω时，电压源既不吸收也不发出功率；R<0.8Ω时，电压源发出功率。
1-8（a ）电压源吸收45W 功率，电流源发出45W 功率；（b ）电压源总是发出功率; 电阻总是吸收功率；R>5Ω时，电流源发出功率；R=5Ω时，电流源既不吸收也不发出功率；R<5Ω时，电流源吸收功率。
1-9 A I A I A I A I 4;18;9;94321=-===1-10 A I 5.0=；Ω=34R ；V U S 34=1-11 （a ）Ω=2500R ；（b ）Ω=800R1-12 Ω=4R1-13 （a ）A I 2=；（b ）V U 4-=1-14 A I 4=1-15 Ω=6R1-16 mA I 51=；V U 15=1-17 （a ）V U 98=；A I 920=（b ）V U 13-= 1-18 V U 201=；V U 200=1-19 S 打开，V U A 6≈；S 闭合，V U A 2≈ 1-20 V U B 7200-= 第2章2-1 （a ）Ω=2ab R ；（b ）Ω=3ab R ；（c ）Ω=2ab R 2-2 Ω=7ab R2-3 V U 2=；V U 20ab =2-4 Ω=5R2-5 （a ）A I 1-=；（b ）V U 10=；（c ）A I 3= 2-6 Ω=4R2-7 mA I 2=2-8 V U 20=2-9 V U 6=2-10 A I 5.0-=2-11 当Ω=1R 时，A I 1=；当Ω=2R ，A I 6.0= 2-12 W P 4=2-13 V u oc 5.1=2-14 V u oc 6=2-15 （a ）Ω++=)5.0(2121ab R R R R R ；（b ）Ω=7ab R 2-16 （a ）Ω=1ab R ；（b ）Ω=5.2ab R2-17 （a ）Ω=5.0in R ；（b ）Ω=2ab R。
电路分析基础试题参考答案—II.doc
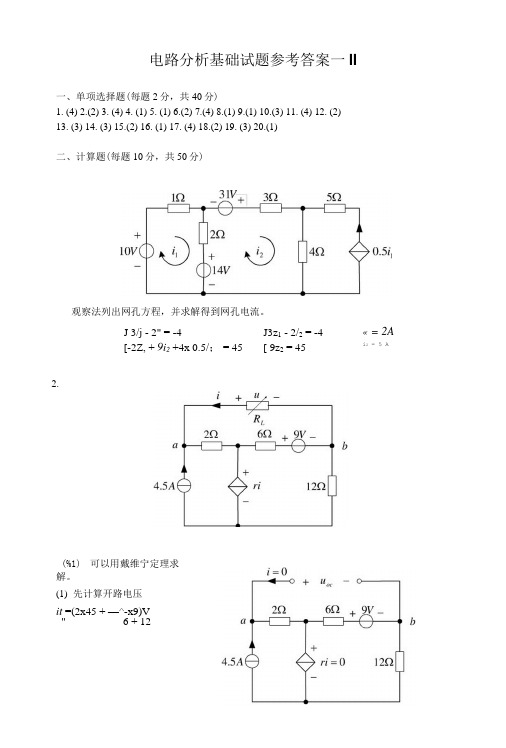
« = 2A i 2 = 5 A(%1) 可以用戴维宁定理求解。
(1) 先计算开路电压it =(2x45 + —^-x9)V " 6 + 12=9V + 6V = 15V电路分析基础试题参考答案一II一、单项选择题(每题2分，共40分)1. (4)2.(2)3. (4)4. (1)5. (1)6.(2)7.(4)8.(1)9.(1) 10.(3) 11. (4) 12. (2)13. (3) 14. (3) 15.(2) 16. (1) 17. (4) 18.(2) 19. (3) 20.(1)二、计算题(每题10分，共50分)观察法列出网孔方程，并求解得到网孔电流。
J 3/j - 2" = -4J3z 1 - 2/2 = -4 [-2Z, + 9i 2 +4x 0.5/； = 45[ 9z 2 = 452.(2)用外加电流源计算端口电压电流关系的方法计算输出电阻u s = 2i s +x 12i s = 10i sRo 隽= 10Q(3)用戴维宁等效电路代替单口网络，计算负载电阻电压u =—鱼—X15V10。
+ 凡当此=5。
时，u=5V。
当R=20Q 时，u =10V o(%1)也可以用网孔分析法求解。
J(2 + 6+R/)i-6« +2x4.5 = -9I —6i + (6+12)L =9 —12i(8 + R/)i-6i] =-18' 6i + 18L=9-1510+/?,LD・15R L u = -Rj i =10。
+幻R[ = 5Q u = 5 VR f = 20Q u = 10V(%1)也可以用结点分析法求解。
(0.5 + G/ )绮—0.5〃-)— G[ u3 = 4.5u2 = \2i< 1 1 1~G L U\_7W2+(7+TT+G L)W3 =T・5 o o 1Zi = G L(U3-U})r>0(0.5 + G/ )z, — 0.5w 7 ~G — 4.5v — 12G/] — 2"-)+ (3 + 12G L )I ，3 = — 18-12G z Wj —u 0 +12G j Wj = 0—180G, +13.5 -180G, -9 22.5 15/?, u = — “a = ----------- : -------------------- : ---- = -------------- = -------- :— V 3 15G/ +1.5 15G/ +1.5 15G/ +1.5 10 +/?z% =5Q/(0J = /(0J = 8A•/ \ 6 — 4 + 8 z(oo) = --------- A = 5A 21 八uT =—S = 0.55 2 z(r) = (5 + 3e -2z )A r>0w(r) = 2V-lQx ； = -(3 + 3。
电路分析基础课后习题答案(1-4章)-周围主编
9V
鹿胎膏的价格 /
9
第一章 基础知识 员工自评范文 /
1-42 ：如图所示电路，求：
（1）图(a)中电流
I
。
2
（2）图(b)中受控源提供的功率。
解：
I1 + I2
9 = 6 × (I1 + I2 ) + 3× I1 ⎩9 = 6 × (I1 + I2 ) + (−6I1)
−
5
2
功率及其正、负号的意义 员工自评范文 /
u 、i 关联参考方向 ⇒ p = ui ⎪⎫ ⎬
u 、i 非关联参考方向 ⇒ p =－ui
⇒
⎧⎪ ⎨
p
>
0
吸收（消耗）功率
⎪⎩ p < 0 产生（供出）功率
鹿胎膏的价格 /
3
第一章 基础知识 员工自评范文 /
⎭⎪
−
⇒ ⎧⎪⎨U1 =
2 3
V
⎪⎩R = 3 Ω
鹿胎膏的价格 /
13
第二章 等效变换分析法 员工自评范文 /
2-1 ：写出如图所示各电路的等效电阻R ab的表达式。 解：
R ab1 = ∞
R ab2 = 0 Ω
鹿胎膏的价格 /
US = Uab + Ubc + Ucd = 18× 3 +15×1− (−14) × R = 90 V
⇒ R = 1.5 Ω
鹿胎膏的价格 /
d −14 A
3A c b
6
第一章 基础知识 员工自评范文 /
1-26：在开关K断开和闭合两种情况下试求A点的电位。
4Ω I
1.5A 4Ω
29
第二章 等效变换分析法 1.5A 员工自评范文 /
习题参考答案-09487电路分析基础(第2版)
习题参考答案第1章习题1.1 t =7.5×105s1.2Q=6C1.3 I ab=30mA，I ba= -30 mA1.4U ab= -12V，U ba= 12V1.5 V O= -5V，V A=16V，V B=10V；U AB=6V，U BO=15V1.6 W=720kWh1.7 （1）I=6.818A；（2）W=1.125kWh；（3）0.776元1.8 （1）A汽车电池没电；（2）W=6kWh1.9 t =2500小时1.10（1）I=4A；（2）6666.7天1.11 I min=3.463A，I max=3.828A1.12 I=0.532mA1.14 （1）W=10.4kWh；（2）P=433.3W1.15 W=2333.3kWh1.16 （a）I=0.5A，P=1W；（b）I=2A，P=4W；（c）I= -1A，P= -2W；（d）I=1A，P=2W。
1.17 （1）I a= -1A；（2）U b= -10V；（3）I c= -1A；（4）P= -4mW。
1.18 （a）P=10 mW，吸收；（b）P=5sin2ωt W，吸收；（c）P= -10mW，产生；（d）P= -12W，产生。
第2章习题2.1 （a）20//20//20//20=5Ω；（b）300+1.8+（20//20）=311.8Ω（c）24k//24k+56k//56k=40k；（d）20+300+24k+（56k//56k）=52.32k2.2 R ab=10Ω2.3 S打开及闭合R ab=45Ω2.4 R0=11.25Ω2.5 （1）u2=400V；（2）u2=363.6V2.6 U0=8V，I0=0.2A2.7 （1）I1=0.136A，R1=806.67Ω；I2=0.364A，R2=302.5Ω（2）灯泡1超额定电压，灯泡2不能正常发光。
（U1=160V，U2=60V）2.8 P1=72 kW，P2=18kW2.9 U0/U S= -α/4；α=402.10 I1=3.2A，I2=4.8A，I3=2.4A，I4=9.6A2.11 I =0.1A ，U =2kV ，P =0.2kW 2.12 P =30W2.13 R 1=375Ω，R 2=257.1Ω 2.14 I =0.2A 2.15 U =1.333V 2.16 R =3Ω 2.17 P = -4W 2.18 P =9W （吸收） 2.19 I =5.77A 2.20 U =80V 2.21 U =14V 2.22 I S =9A ，I 0= -3A2.23 （a ）U =7V ，I =3A ；（b ）U =8V ，I =1A 2.24 AI 1191-=，AI 1112-=，AI 1183-=2.25 P S1= -112W （产生功率），P S2= -35.33W （产生功率） 2.26 I 1=2.5A ，I 2=0，I 1= -2.5A ， 2.27 VU322=2.28 U 0/U S = -8 2.29 U 0= -0.187V第3章 习题3.1 U 0=0.4995V3.2 （a ）0.5V ，0.5A ；（b ）5V ， 5A ；（c ）5V ，0.5A 3.3 I =1A 3.4 U =4V3.5 I = -1.32A ，P =17.43W 3.6 U ab =6V 3.7 U x = -0.1176V 3.8 I =1.5625mA3.9 （a ）R =50Ω，U OC =-20V ；（b ）R =15Ω，U OC =42V 3.10 I =1A 3.11 U ab =15V3.12 （a ）R =76.66Ω，U OC =8.446V ；（b ）R =72.97Ω，U OC =0.81V（c ）R =35.89k Ω，U OC =1.795V ；（d ）R =1.3k Ω，U OC =89.63V3.13 （a ）R ab =3.857Ω，U ab =4V ；（b ）R bc =3.214Ω，U bc =15V 3.14 U =7.2V 3.15 I =3A3.16 R AB =15.95Ω，U AB = -1.545V 3.17 U =12.3V 3.18 I =0.1mA 3.19 I =0.5A3.20 （a ）R =8Ω，I SC =2A ；（b ）R =20Ω，I SC =2.5A 3.21 （1）R =10Ω，U OC =0；（2）R =10Ω，I SC =0；（3）I x =0 3.22 R =3.33Ω，I SC = -0.4A ，I =2.4A3.23 （a ）R ab =2Ω，I ab =7A ；（b ）R cd =1.5Ω，I cd =12.67A 3.24 （1）R =22.5Ω，U OC =40；（2）R =22.5Ω，I SC =1.78A 3.25 （1）R =3.33Ω，U OC =10；（2）R =3.33Ω，I SC =3A ； 3.26 R =2k Ω，U OC = -80V 3.27 R =3Ω，U OC = 3V 3.28 R =-12.5k Ω，I SC = -20mA3.29 （1）R L =5.366Ω，P max =20.7mW ；（2）R L =727Ω，P max =3.975mW 3.30 R =1.6Ω，P max =0.625W 3.31 R =7.2Ω，P max =1.25W 3.32 R =20Ω，P max =0.1W 3.33 R =8k Ω，P max =1.152W3.34 （1）R =12Ω，U OC =40V ；（2）I =2A ；（3）R L =12Ω；（4）P max =33.33W 3.35 R =1k Ω 3.36 P =42.6W 3.37 R =8Ω，U OC =12V3.38 （1）I =1.286A ；（2）P max =8.1W3.39 （1）平衡；（2）R =5.62k Ω，P max =18.92mW 3.40 （1）R =20Ω；（2）R =37.14Ω，I max =69.2mA 3.41 I =-1A 3.42 I =16.67mA3.43 R x =1Ω；（4）P max =2.25W第4章 习题4.1 （1）3100C C d u u d t-+=；（2）i (0+)=10mA ；（3）i =10e -1000t （mA ）；（4）i |t=1.5ms =2.23mA ；W=5×10-5J 4.2 u C (0+)=50V ， i (0+)=12.5mA 4.3 u 1(0+)=-20V ，i (0+)=-2A4.5 0)0(05.0)0(==++C L u A i ，；sA ti L/1000d d 0-=+，sA tu C/105d d 40⨯=+4.6 （1）i 0（0+）=2A ，i 2（∞）=4A ；（2）i 0（t ）=（4 -2e -1000t ）A ；（3）t =2.3ms4.7 （1）i 1（0-）=0.2mA ，i 2（0-）=0.2mA ； （2）i 1（0+）=0.2mA ，i 2（0+）= -0.2mA ；（3）mAet i t61012.0)(-=；（4）mAet i t61022.0)(--=4.8 u c （0+）=20V ， i 1（0+）=5 mA ， i c （0+）=5mA 4.9 u c （0+）=24V ，i L （0+）=2A ，u （0+）=-8V 4.10 C =1μF4.11 τ充=R 2C ，τ放=（R 1+R 2）C4.12 i L =e -10t （A ），i 10Ω= i 20Ω=0.5e -10t （A ） 4.13 i L =1.6（1-e -10t ）（A ），u L =3.2e -10t ）（V ）i 2.5Ω=（1.6-1.28e -10t ）（A ），i 10Ω=0.32e -10t ）（A ） 4.14 )(3)(91000V et u t-=，mAe t i t9100032)(-=4.15 i =0.5e -5t （A ），u = -2.5e -5t （V ）4.16 （1）R =20k Ω，（2）C=0.05μF ，（3）τ=1ms ，（4）W =2.5×10-4J ，（5）t =0.112ms 4.17 u c （0+）=0，u R （0+）=20V ，i （0+）=2.857mA ，t =3.29ms 4.18 Aeet i tt)(133)(10005001---=4.19 i =8（1-e -2t ）（mA ），u C =40e -2t （V ），u R =40（1-e -2t ）（V ），i （τ）=5.06mA 4.20 ))(5.67120()(41000V et u tab -+=（ 0≤t ＜100ms ）))(857.12150()()(5.1710001V et u t t ab ---= （t 1=100ms ，t ＞100ms ）4.21 i =5-10e -1.69t （A ） 4.22 U = -0.368 4.23 i =15-10e -500t （A ） 4.24 u L =15e -7.5t （V ）4.25 u C =-10+20e -0.2t （V ）；t 0=3.46s4.26 u C =1+e -t （V ）（ 0≤t ＜1s ）；u C =0.5+0.868e -2（t-1）（V ）（t ≥1s ）；4.27 u = -12-54e -25t （V ） 4.28 i =0.6+0.332e -2t （A ） 4.29 u C =4+0.8e -t （V ）4.30 i L =0.833+4.167e -2t （A ） 4.32 8次，R=560kΩ第5章 习题5.1 （1）u ac =200sin ωt ，u bc =150sin （ωt+30o ），u dc =150sin （ωt+135o ），u ad =200sinωt -150sin （ωt+135o ） （2）ψu -ψi = -135o ，（3）ψu -ψi =45o5.2 （1） 7.13+j3.4 ； (2)6.9－j9.69 ； (3) －11+j19.1 ； (4) －69.28－j40 5.3 （1）10.63∠41.2°； (2) 150.95∠－144.57°； (3) 52∠-52°；(4) 3.22∠97.3° 5.4 （1）13.08∠126.6°； (2) 58.56∠－78.68° 5.5 （1）（a ）5∠53.13°， (b) 6∠105° ；（2）（a ）10sin （ωt -53.13o ），（b ）10sin （ωt +143.13o ）；（c ）-10cos （ωt ） 5.6 u 14=107.79V ；U 14=91V 5.7 mAt t i R )601000sin(23)(︒+=；At t i L )301000sin(26.0)(︒-=；mAt t i C )1501000sin(212)(︒+=5.8 （1）U m =170V ；（2）f =60Hz ；（3）ω=120πrad/s ；（4）-5π/6；（5）-150º；（6）16.67ms ；（7）t =9.03ms ；（8）u =170sin （120πt+60º）V ；（9）t =6.94ms ；（10）t =9.03ms 5.9 R =1Ω，u =14.1sin （314t+30º）V5.10 I =4.67A ，Q=1027.6Var ，i =6.6sin （314t-90º）A ；I =2.34A ，Q=513.8Var ，i =3.3sin （628t-90º）A 5.11 I =0.55A ，Q=121.6V ar ，i =0.78sin （314t+90º）A ；I =1.1A ，Q=243.1V ar ，i =1.56sin （628t+90º）A 5.12 U L =69.82V5.13 A I ︒∠=11.23707.0 ；i =sin （8000t+23.11º）A ； 5.14 V t u S )7.51000sin(205.10︒+= 5.15 （1）At i )87.36314sin(222︒+=，容性；（2）A t i)87.361256sin(222︒-=，感性5.16 At i)87.661000sin(210︒+=5.17 （1）AI m︒∠=4510 ，VU m ︒∠=45100ab ，VU m︒∠=135200bc ，VU m︒-∠=45100cd（3）i =10sin （20t +45o ）A ， u ab =100sin （20t +45o ）V ，u bc =200sin （20t +135o ）V ， u cd =100sin （20t -45o ）V5.18 AI ︒-∠=57.7132.61，AI ︒∠=0102，AI ︒∠=90103，AI ︒∠=43.1877.1005.19 （1）（a ）U =67.1V ；（b ）U =30V ；（c ）U =25V（2）（a ）U 1=12V ，U 2=0；（b ）U 1=12V ，U 2=0；（c ）U 1=0，U 2=0，U 3=12V 5.20 R =2.76k Ω 5.21 U 2=24V5.22 I =17.32A ，R =6Ω，X 2=2.89Ω，X C =11.55Ω 5.24 R =40Ω，L =15H5.25 I =5A ，Z =33.33-25j （Ω） 5.26 19.6819.7I A =∠-︒ ，198.433.43U V =∠︒ ，2196.856.59U V =∠︒ 5.27 U =113.2V ，I =0.377A第6章 习题6.1 （1）P =3400W ，Q =0；（2）P =155.29W ，Q =579.56Var ；（3）P = -2137.63W ，Q = -5873.1V ar 6.2 P us =7.5W ，P 4Ω=7.5W ，P 2Ω=2.5W 6.3 P =126.19W ，Q =180.2Var ，S =220V A 6.4 459.0cos 1=ϕ（超前）6.5 （1）P =60W ，Q = -80Var ，6.0cos =ϕ（超前）6.6 （1）Z 1=192∠53.13o Ω，Z 2=57.6∠-53.13o Ω，Z 3=320Ω（2）Z =51.83∠-30.26o Ω，864.0cos =ϕ（超前）6.7 P =573.19W 6.8 533.0cos =ϕ6.9 P =7.33kW ，Q = 1.197kVar ，987.0cos =ϕ6.10 Z =2.867∠38.74o Ω ，S =15.38kV A 6.11 818.0cos =ϕ，C =124.86μF6.12 （1）Q =32.91kVar ，S =86.51KV A ；（2）9248.0cos =ϕ；（3）I = 157.3A6.13 899.0cos =ϕ，C =574μF6.14 C =19.52μF 6.15 I = 16.1A ，982.0cos =ϕ，C =43.4μF6.16 9967.0cos =ϕ，P =1886.75kW6.17 64.0cos =ϕ，P =295.1W ，C =130.4μF6.18 （1）C =2.734mF ；（2）C =6.3mF 6.19 Z =75-j103.55（Ω）6.20 （1）Z =40-j8（Ω）；（2）P =66.61W 6.21 341.56元6.22 f =2.813kHz ，P =0.432W 6.23 I = 17.19A ，P =1559.77W第7章 习题7.1 （a ）a 、d 同名端，或b 、c 同名端；（b ）a 、c 、e 同名端，或b 、d 、f 同名端 7.2 2、3端连接，1、4端接220V 电源 7.3 （1）M=4mH ；（2）k=0.75；（3）M=8mH 7.4 开关闭合电压表正偏，开关打开电压表反偏 7.5 u 34 =31.4sin （314t -120º）V7.6 （a ）u 1 =cos t V ，u 2 = -0.25cos t V ；（b ）u 1 =2sin t V ，u 2 =2sin t V 7.7 M=52.87mH 7.8 （a ）221L M L L -=；（b ）221L M L L-=7.9545a bU V =︒ ，Z ab =j1000Ω，45ab I m A =-︒7.10 U ab =15V 7.11 At i )1510sin(231︒-=，i 2=07.12 n =32 7.13 N 2=100 7.14 P =315W7.15 n =2，I 1=41.67A ，I 2=83.33A 7.16 n =110，I 1=7.567mA7.17 R =10Ω，C =0.159nF ，L =0.159mH ，Q =100 7.18 I 2=12A7.19 （1）R =10Ω，C =3.19nF ，L =0.8mH ；（2）Q =50 7.20 L =160mH ， Q =4007.21 （1）R =4Ω，C =0.25μF ，L =40mH ，Q =100 ；（2）C （132.63μF ～331.57μF ） 7.22 （1） f （0.541MHz ～1.624MHz ）；（2）Q （68～204.1） 7.23 I 1=22.738nA ，I 2=2.145n A 7.24 f 0=899.53kHz ，f 0=937.83kHz第8章 习题8.1 （1）12730BU V=∠-︒ ，127150CU V=∠-︒ ；（2）22060ACUU V -=∠︒ ；（3）12790BCU U V +=∠-︒8.2 （1）V U V U V U CB A ︒∠=︒-∠=︒∠=1202201202200220 ，，（2），，，A I A I A I CB A ︒∠=︒∠=︒-∠=57.5686.1957.17686.1943.6386.19 8.3 （1）略；（2）I l =6.818A ，I N =0；（3）U 1=95.3V ，U 2=285V 8.4 I l =1.174A ，U l =376.49V 8.5 I l =30.1A ，I p =17.37A 8.6 △ I l =66A ，Y I l =22A ， 8.7 △连接，I l =65.82A ，I p =38A 8.8 I N =16.1A ，中线不能去掉。
电路分析基础2答案
一、选择题（本大题共 10 小题，每小题 3 分，共 30 分）
1. D 2. C 3. B 4. C 5. D 6. A 7. B 8. C 9. A 10. B
二、填空题（本大题共 10 小题，每小题 3 分，共 30 分）
1. 2H
2. 7V
3.幅值、角频率、初相位
4. 3A
5. 5V
3Ω
6Ω
I’
5A
2Ω
1Ω
(a)
I
'
1
6
// 6
3 //
3
2
2
5
4
A
（2）15V 电压源单独作用时，得图(b)电路
（2 分）
《电路分析基础》第 2 页 共 6 页
参考答案
+ 15V-
3Ω
6Ω
I”
2Ω
1Ω
(b)
I
"
3
15 (2
1)
//
6
6
6 2
1
2A
I I 'I" 4 2 2A
4. 解：（1）求 uoc，从 a、b 断开 RL，如图(a)所示
iL 2H
6Ω
3Ω
3A
(b)
uL ()
6
3
3
3
1
A
iL
(t
)
iL
()
[iL
(0
)
iL
()]e
t
iLf (t) 1 e4.5t A ，t≥0
（3）全响应，将零输入响应和全响应相加即为全响应。
i(t) iLx (t) iLf (t) 1 A
6．解：（1）
电路分析基础 习题答案
电路分析基础习题答案电路分析基础习题答案在学习电路分析的过程中，习题是非常重要的一部分。
通过解答习题，我们可以巩固所学的知识，加深对电路分析原理的理解。
下面我将为大家提供一些电路分析基础习题的答案，希望对大家的学习有所帮助。
习题一：请计算以下电路中电阻R1、R2、R3所受到的电压和电流。
习题一解答：根据欧姆定律，电压（V）等于电流（I）乘以电阻（R）。
所以我们可以用以下公式来计算电压和电流：V1 = I1 * R1V2 = I2 * R2V3 = I3 * R3假设电流I1 = 5A，电流I2 = 3A，电流I3 = 2A，电阻R1 = 10Ω，电阻R2 = 20Ω，电阻R3 = 30Ω。
那么我们可以得到以下结果：V1 = 5A * 10Ω = 50VV2 = 3A * 20Ω = 60VV3 = 2A * 30Ω = 60V所以电阻R1所受到的电压为50V，电阻R2所受到的电压为60V，电阻R3所受到的电压为60V。
习题二：请计算以下电路中电阻R1、R2、R3所受到的总电压和总电流。
习题二解答：根据基尔霍夫定律，电路中的总电压等于电压源的电压之和，总电流等于电路中的电流之和。
所以我们可以用以下公式来计算总电压和总电流：Vtotal = V1 + V2 + V3Itotal = I1 + I2 + I3假设电压源的电压为V = 100V，电流I1 = 5A，电流I2 = 3A，电流I3 = 2A。
那么我们可以得到以下结果：Vtotal = V1 + V2 + V3 = 50V + 60V + 60V = 170VItotal = I1 + I2 + I3 = 5A + 3A + 2A = 10A所以电阻R1、R2、R3所受到的总电压为170V，总电流为10A。
习题三：请计算以下电路中电阻R1、R2、R3所受到的功率。
习题三解答：根据功率公式，功率（P）等于电压（V）乘以电流（I）。
所以我们可以用以下公式来计算功率：P1 = V1 * I1P2 = V2 * I2P3 = V3 * I3假设电压V1 = 50V，电压V2 = 60V，电压V3 = 60V，电流I1 = 5A，电流I2 = 3A，电流I3 = 2A。
《电路分析基础》第2版-习题参考答案
《电路分析基础》各章习题参考答案《电路分析基础》各章习题参考答案第 1 章 习题参考答案习题参考答案1- 1 (1) 50W ; (2) 300 V 、25V, 200V 、75 V ; (3)2=12.5 QR a =100 Q, R 4=37.5 Q 1- 2 V A =8.5V =8.5V，， V m =6.5V =6.5V，， V B =0.5V =0.5V，， V C =- 12V ， V D =-19V =-19V，， V p =-21.5V =-21.5V，， U A B AB =8V =8V，， U B C BC =12.5=12.5，，U DA =-27.5V1-3 电源电源((产生功率产生功率))： A 、 B 元件；负载元件；负载元件；负载((吸收功率吸收功率))： C 、 D 元件；电路满足功率平衡元件；电路满足功率平衡元件；电路满足功率平衡 条件。
1-4 (1) V A =1 00V , V B =99V, V C =97V, V D =7V, V E =5V, V F =1V, U A F AF =99V, U C E CE =92V,U BE =94V, U BF =98V, U CA =- 3 V ； (2) V C =90V, V B =92V , V A =93V, V E =-2V, V F =-6V, V G =- 7V, U AF =99V, U CE =92V, U B E BE =94V, U B F BF =98V, U C A CA =- 3 V1-5 I 〜0.18A ,6 度，度，2.7 2.7 元 1- 6 I=4A ， I 1=11A =11A，，I 2=19A 1-7 (a) U=6V , , (b) U=24 V , (c) R=5Q , Q, (d) I=23.5A 1- 8 (1) i 6=-1A ； (2) u 4=10V, u 6=3 V ； (3) P 1=-2W 发出发出, P , P 2 2 =6W 吸收吸收, P , P 3 3 =16W 吸收吸收, ,P 4 =-10W 发出发出, P , P 5 5 =-7W 发出发出, P , P 6 6 =-3W 发出发出1- 9 I=1A, , U s =134V , R ~ 7.8Q 1- 10 S断开：断开：断开：U U AB =- 4.8V , U AO =- 12V , U BO =-7.2V ;S 闭合：闭合：闭合：U U AB = -12V, U A O AO = - 12V , U BO =0V 1- 11支路支路 3 3，节点，节点，节点 2 2，网孔，网孔，网孔 2 2 ，回路，回路，回路 3 3 1- 12节点电流方程：节点电流方程： (A) I (A) I 1 +I 3- I 6=0=0，，(B)I 6- I 5- I 7=0=0，，(C)I 5 +I 4-I 3=0 回路电压方程：① I6 R 6+ U S 5 S5 +I 5 R 5- U S 3 +1 3 3 R 3=0 ,②-15 R 5- U S 5+ I 7R 7- U S 4 =0 ,③-丨3 R 3+ U S3 + U S 4 S4 + I 1 1 R 2+ I 1 1 R 1=01- 13 UA B AB =11V , I 2=0.5A , l 3=4.5A , R 3~ 2.4 Q 1-14 VA =60V V C =140V V D =90V U A C AC =- 80V U AD =- 30V U CD =50V 1- 15 I 1=- 2A I 2=3A I 3=- 5A I 4=7A I 5=2A第 2 章 习题参考答案习题参考答案2- 1 1 2.42.4 Q 5 A 2- 2 (1) 4 V 2 V 1 V; (2) 40 mA 20 mA 10 mA 2-3 1.5 Q 2 A 1/3 A 2-4 6 Q 36 Q 2-5 2 2 A 1 A A 1 A 2-6 1 1 A A2-7 2 2 A A 2- 8 1 1 A A2- 9 I1 1 = -1.4 A I2 = 1.6 A I3 = 0.2 A 2- 10 I1 1 = 0 A I2 = -3 A P 1 = 0 W P 2 = -18 W 2-11 I i = -1 mA , I 2 = - 2 mA , E 3 = 10 V 2- 12 I 1 = 6 A , I 2 = -3 A ,I 3 = 3 A 2- 13 I1 1 =2 A , , I 2 = 1A , , I3 = 1 A , I4 =2 A , , I5 = 1 A 2-14 2-14 V V a = 12 V , I 1 = - 1 A ,I 2 = 2 A 2-15 2-15 V V a = 6 V , I 1= 1.5 A , I 2 = - 1 A ,I 3= 0.5 A 2-16 2-16 V V a = 15 V , , I 1 = - 1 A , , I 2 =2 A , , I 3= 3 A 2-17 2-17 I I 1 = -1 A ,, I 2 = 2 A 2-18 2-18 I I 1 =1.5 A , , I 2 = - 1 A , , I 3= 0.5 A 2-19 2-19 I I 1 =0.8 A , , I 2 = - 0.75 A , , I 3 = 2 A , I 4 = - 2.75 A , I 5 = 1.55 A 2-20 2-20 I I 3= 0.5 A 2-21 U o o = 2 V , R o = 4 Q ,Q, I 00 = 0.1 A 2-22 I 55 = -1 A 2-23 2-23 (1) I (1) I5 5 = 0 A , U ab = 0 V ; (2) I 5 5 = 1 A , U ab = 11 V 2-24 I L = 2 A2-25 I s s =11 A , , R 0 = 2 QQ 2-26 2-26 18 18 Q, - 2 Q ,Q, 12 Q 2-27 U == 5 V 2-28 I =1 A2-29 U == 5 V 2-30 I =1 A2-31 2-31 10 V 10 V ,, 180 Q 2-32 U 0 = 9 V , R 0 = 6 Q ,Q, U=15 V 第3章习题参考答案章习题参考答案3- 1 50Hz, 314rad/s, 0.02s, 141V, 100V, 120° 3-2 200V, 141.4V 3-3 u=14.1si n (314t-60 °V3- 4 (1) ®u1-贏2= 120° (2) ®1 = -90-90° °%= - 210°210°, , %1-屁=120=120° (不变° (不变) 3-5 (1) U^50 .^_90V , U 2 =50 .2.2 - 0 V ; ; (2) U 3=100 2 sin (3t+ 45 °)V , U, U 4=100 ■■ 2 sin ( ®t + 135 °)V 3- 6 (1) i 1=14.1 sin ( 72 °)A ;; (2) U 2=300 sin ( 3—60 °)V3- 7错误：(1),1),⑶，⑶，⑶，(4), (5) (4), (5) 3-8 (1) R ； (2) L ； (3) C; (4) R 3-9 i=2.82 sin (10t-30 °)A , Q~ 40 var , Q~ 40 var 3-10 u =44.9sin (3141-135 °V, Q=3.18 var 3- 11 (1) I=20A ; (2) P=4.4kW3- 12 (1)I ~ 1.4A , I 1.4 - 30 A； (3)Q~ 308 var, P=0W ; (4) i~ 0.98 sin (628t-30 °)A 3- 13 (1)I=9.67A , I =9.67450 A ,i=13.7 sin (314t+150 °) A ; (3)Q=2127.4 var, P=0W; (4) I C =0A3- 14 (1)C=20.3 尸;(2) I L = 0.25A ,l c = 16A第4章习题参考答案章习题参考答案4-1 (a) Z =5. 36.87 J, Y =0.2 / 36.87 S ; (b) ; (b) ZZ =2.5 - 2/ 45 门,Y =0.2.2/45 S 4- 2 Y=(0.06-j0.08) S , , R ~ 16.67 Q, X L =12.5 Q, L ~0.04 H 4-3 U R =6 0^0 V U L =8080//90 V , , U S =100100^^53.13 V 4-4 卩=2 0 £ 3 6.874-5 Z =100 =100 22^45 ；：；： ■,卩=1^0 A , , U R =100100^^0 V , U L =125125//90 V , , U C =2525/ /90 V 4-6 Y =0.25 2^45 S , U =4 “2/0 V ,卩R = .2. 0 A , , I L =0.^ 2 / 90 A , , I C =1.21.2..2/90 A4-7 ll =1 0.=1 0.「2 4 5，A U S =100 乙 90 V 4-8 (a) 30 V ; (b) 2.24 A 4-9 (a) 10 V ; (b) 10 A (b) 10 A 4-10 10 (a) (a) 10 V ; (b) 10 V (b) 10 V 4- 11 U=14.1 V4- 12 UL 1 =15 V , U C 2 =8 V , U S =15.65 V 4-13 4-13 U U X 1 =100 V , U 2 =600 V , , X 1=10Q, X 2=20 Q, X 3=30 Q 4-14 Z =20 .2 45 门，l =2. -45 A , h , h = 2 0 = 2 0 A , .2/-90 A , U ab ab==0V 4- 15 (1)1 =£2 2 A A , Z RC =5、2「，「， Z =5 10 门；门；(2) R (2) R =10 门，门，X X ^1010'J 'J4-16 P = 774.4 W , Q = 580.8 var, S = 968 V A- 4-17 l 1 = 5 A , l 2 = 4 A 4-18 4-18 I I 1 = 1 A , I 2 =2 A , l =.5. 26.565 A , S =44.72. -26.565 V V V A A 4-19 Z=10", I =190A I=190A ,U R2 =5 2 135 V , P =10 W 64-20 a =5X10 rad/s , p = 1000 = 1000 Q ,Q, Q = 100 , l = 2 mA , U R =20 mV , U L = U C = 2 V 4-21 30 =104 rad/s , p = 100 = 100 Q ,Q, Q = 100 , U = 10 V , I R = 1 mA , I L = I C = 100 mA 4-22 L 1 1 = 1 H , L 2 ~ 0.33 H 第5章习题参考答案章习题参考答案5- 3 M = 35.5 mH5- 4 301 =1000 rad/s ,3,302=2236 rad/s5-5 Z 1 = j31.4 Q , Q , Z 2 = j6.28 Q Q 5-6 Z r = 3+7.5 Q Q 5-7 M = 130 mH 5- 8 “2 二-2/45 A5- 9 U1 = 44.8 V 5- 10 M12 12 = 20 mH , 11 = 4 A 5- 11 U 2 = 220 V , I 1 = 4 A5- 12 n = 1.95- 13 N2 = 254 匝，匝，匝，N N3 = 72 匝 5- 14 n = 10 , P 2 = 31.25 mW章习题参考答案章习题参考答案(1) A 相灯泡电压为零，相灯泡电压为零，B B 、C 相各位为220V I L = I p = 4.4 A ，U p = 220 V ，U L = 380 V ，P = 2.3 kW (2) I p = 7.62 A ，I L = 13.2 A A 、C 相各为2.2A 2.2A，，B 相为3.8A U L = 404 VU A N =202202/ -/ -47 47 Vcos $ = 0.961 , Q = 5.75 kvar Z =334 28.4 门(1) I p p = 11.26 A , Z = 19.53 / 42.3 °Q; (2) I p p = I l l = 11.26 A , P = 5.5 kW U l = 391 Vi A =22 2sin(・t —53.13 ) Ai B =22 .2sin(・t —173.13 ) Ai C =22 2 sin(，t 66.87 ) AU V = 160 V(1) 负载以三角形方式接入三相电源负载以三角形方式接入三相电源(2) I — =3.8 T 2 -15 A , 1仁 =3.3.^-2/ ^-2/ 135 A , , 仁 =3.8、「2也105 AI A =3.8、. 6/「45 A , I B =3.8I Q 165 A , , I c =3.8.6. 75 AL = 110 mH , C = 91.9 mF 章习题参考答案章习题参考答案P = 240 W, Q = 360 var P = 10.84 W(1) i(t) 4.7sin( t 100 ) - 3sin3 t A(2) I ~ 3.94 A , U ~ 58.84 V , P ~ 93.02 W 0MU m n o L 1 r~2 ------------- 2u 2(t) msin(，t —-arctan 1)V , R 2 (丄J 2z 2 R '直流电源中有交流，交流电源中无直流直流电源中有交流，交流电源中无直流U 1=54.3 V , , R = 1 Q, L = 11.4 mH ;约为约为 8% 8% , , ( L'= 12.33 mH ) 使总阻抗或总导纳为实数使总阻抗或总导纳为实数((虚部为虚部为 0)0)的条件为的条件为的条件为 尺二尺二& = & = R x = Rx = ■ L/C ■ L/C G =9.39 折,C 2 =75.13 M F L 1 = 1 H , L 2 = 66.7 mHC 1 = 10 M F, C 2 2 = 1.25 M F章习题参考答案章习题参考答案第6 6-1 6-3 6-4 6-5 6-6 6-7 6-8 6-9 6-10 6-11 6-12 6-13 6-14 6- 15 第7 7- 1 7-2 7-3 7-4 7-5 7-6 7-7 7-87-9 7- 10 第88- 6 8-78-8i L (0+) = 1.5mA , U L (0+) = - 15V- 15V h (0+) = 4A , i 2(0+) = 1A , U L (0+) = 2V 2V ,i 1(s )= 3A , i 2(^)= 0, U L ()= 0 i 1 1 (0+) = 75mA , i 2(0+) = 75mA , i 3(0+) = 0, U L 1 (0+) = = 0, U L 2(0+) = 2.25V 2.25V6i c (t)二 2訂 A 4t U L (t) =6e _V u C (t) =10(1 _eg )V , i C (t) =56说*人 500t 貝 u C (t) =115e~ sin(866 亠60 ) V10t 10t 山⑴=12e - V , L(t) =2(1 —e — )A 1 1 t t U R (t) =~U s e 下2C V , U R (3 J - -U S e-V (1) T = 0.1s, (2) u c (t) =10e -V , (3) t = 0.1s u C (t) =10 _9e 」° V 10t _ i L (t) =5e 一 A (a)f(t) =1(t —t 。
电路分析基础习题上海交通大学出版社+部分习题答案
习 题如图所示的对称三相电路中，U 1=380V ，Z 1=80Ω，Z 2△=30+j40Ω，端线阻抗为零，求端线中的电流。
图解：在由负载Z 2所组成的三角形联结电路中，令00380∠=ABU & A Z U I AB 0002536.753500380-∠≈∠∠==&&相 因为负载三角形联结，所以相I I 32=，并且线电流比相电流滞后300028316.13)3053(36.7-∠=--∠⨯=I & 在由负载Z 1所组成的星形联结电路中，由00380∠=AB U &，得030220-∠=AU &，端线电流等于相线电流A Z U I 00113075.28030220-∠=-∠==相&& 所以A 相端线电流02195.73158316.133075.2-∠≈-∠+-∠=+=I I I A &&&如图所示电路，电源线电压U 1=380V 。
（1）如果图中各相负载的阻抗模都等于10Ω，是否可以说负载是对称的？（2）试求各相电流，并用电压与电流的向量图计算中性线电流。
（3）试求三相平均功率P 。
图解（1）不是对称三相电路。
对称三相电路是指三相负载阻抗相等的电路。
（2）令00220∠=AU &，则00120220,120220∠=-∠=C B U U && ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∠=∠∠==-∠=-∠-∠==∠=∠∠==A R U I A R U I A R U I C C C B BB A AA 00000000030229010120220302290101202200220100220&&&&&& A I I I I CB A N 0000001.600)13(2230223022022∠≈∠+=∠+-∠+∠=++=&&&& 030BI &CI &AI &030（3）三相平均功率WI U I U I U P P P P C C C B B B A A A C B A 484000122220cos cos cos =++⨯⨯=++=++=ϕϕϕ已知对称三相电路的星形负载阻抗Z =（165+j84）Ω，端线阻抗Z L =（2+j1）Ω，线电压U 1=380V 。
电路分析答案 第二章
R2
∞
R1 us
R1
uo R2 us
∞
R3
uo
题图 2.32 解 u+ = u− = u S 由分压公式
题图 2.33
u− =
R2 uo R1 + R2
uo R = 1+ 1 uS R2
2.33 求图示电路的输入电压与输出电压的关系。 解：因为 Rin = ∞ ，所以
2.7 求题图 2.7 电路的等效电阻 Rx 。
R
Rx
R
Rx
10Ω
10Ω
∞
r
r
Rx
7.5Ω
7.5Ω
(a) 图题 2.7 解：(a) Rx = R + r // Rx 得到一个一元二次方程，求解后即有（仅取正根）
(b)
Rx = ( R + R 2 + 4 Rr ) / 2
(b)利用上面的公式，求得
Rx = 15Ω
t = 1s 时， i (1) = i (0) + t = 2 s 时， i (2) = i (1) + t = 3s 时， i (3) = i (2) + t = 4 s 时， i (4) = i (3) +
1 3 1 3 u (t )dt = 5 + ∫ 0dt = 5 A ∫ L 2 4 2
1 4 1 4 u (t )dt = 5 + ∫ (10dt − 40)dt = 3.75 A ∫ L 3 4 3 2.25 题图 2.25 为三端网络， 端子用 a , d , e 标记， 已知 R = 1Ω ，C = 0.1 F，L = 0.5 H，u ab = sin(10t ) V，
电路分析基础(周围主编)第二章答案
2-2(1)．求图示电路在开关K 断开和闭合两种状态下的等效电阻ab R 。
解：先求开关K 断开后的等效电阻：()()Ω=++=9612//126ab R再求开关K 闭合后的等效电阻：()()Ω=+=86//1212//6ab R2-2(2)．求图示电路在开关K 断开和闭合两种状态下的等效电阻ab R 。
解：先求开关K 断开后的等效电阻：()Ω=+=384//4ab R再求开关K 闭合后的等效电阻：Ω==24//4ab R2-3．试求题图2－3所示电路的等效电阻ab R 。
（a ）解：题图2-3（a ）aΩ400ΩaΩΩa题图2-2（1）题图2-2（2）abΩ4Ω8240//360144ab R =ΩΩ=Ω（b ）解：40ab R =Ω题图2-3（b ）abab20Ω60Ωab40Ωab 20Ω60Ωab20ΩΩabΩΩabaabΩ2-25（1）. 求图示电路a 、b 两点间的等效电阻ab R 。
解：在图中画一条垂线，使左右两边对称，参见图中虚线所示。
显然虚线为等位线，没有电流流过，故图中电阻0R 可去掉，其等效电阻为：()()[]Ω=++=48//88//88ab R2-25（2）. 求图示电路a 、b 两点间的等效电阻ab R 。
解：此题与上题相同，只是其中电阻的阻值不同，但仍保持其对称性。
采用同样的方法处理，有：()()[]Ω=++=7124//22//66abR2-25（3）. 求图示电路a 、b 两点间的等效电阻ab R 。
解：在图中画一条垂线，使左右两边对称，参见图中虚线所示。
显然虚线为等位线，没有电流流过，故可将图中c 点分开，参见其等效图（题图2-25（3-1））所示，其等效电阻为：()[]R R R R R R R ab 9102//2//2//2=+=2-8．求图示电路的等效电压源模型。
（1）解：等效电压源模型如题图2-8（1-1）所示。
题图2-25（1）题图2-25（2）题图2-8（1） abV10题图2-8（1-1）题图2-25（3）题图2-25（3-1） R（2）解：等效电压源模型如题图2-8（2-1）和2-8（2-2）所示。
电路分析基础第二章答案
2-2(1)．求图示电路在开关K 断开和闭合两种状态下的等效电阻ab R 。
解：先求开关K 断开后的等效电阻：()()Ω=++=9612//126ab R再求开关K 闭合后的等效电阻：()()Ω=+=86//1212//6ab R2-2(2)．求图示电路在开关K 断开和闭合两种状态下的等效电阻ab R 。
解：先求开关K 断开后的等效电阻：()Ω=+=384//4ab R再求开关K 闭合后的等效电阻：Ω==24//4ab R2-3．试求题图2－3所示电路的等效电阻ab R 。
（a ）解：题图2-3（a ）aΩ400ΩaΩΩa题图2-2（1）题图2-2（2）abΩ4Ω8240//360144ab R =ΩΩ=Ω（b ）解：40ab R =Ω题图2-3（b ）abab20Ω60Ωab40Ωab 20Ω60Ωab20ΩΩabΩΩabaabΩ2-25（1）. 求图示电路a 、b 两点间的等效电阻ab R 。
解：在图中画一条垂线，使左右两边对称，参见图中虚线所示。
显然虚线为等位线，没有电流流过，故图中电阻0R 可去掉，其等效电阻为：()()[]Ω=++=48//88//88ab R2-25（2）. 求图示电路a 、b 两点间的等效电阻ab R 。
解：此题与上题相同，只是其中电阻的阻值不同，但仍保持其对称性。
采用同样的方法处理，有：()()[]Ω=++=7124//22//66abR2-25（3）. 求图示电路a 、b 两点间的等效电阻ab R 。
解：在图中画一条垂线，使左右两边对称，参见图中虚线所示。
显然虚线为等位线，没有电流流过，故可将图中c 点分开，参见其等效图（题图2-25（3-1））所示，其等效电阻为：()[]R R R R R R R ab 9102//2//2//2=+=2-8．求图示电路的等效电压源模型。
（1）解：等效电压源模型如题图2-8（1-1）所示。
题图2-25（1）题图2-25（2）题图2-8（1） abV10题图2-8（1-1）题图2-25（3）题图2-25（3-1） R（2）解：等效电压源模型如题图2-8（2-1）和2-8（2-2）所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.1 解：对节点列KCL 方程，得① 01=i② 032=+i i③ 0643=++i i i④ 6521i i i i =++⑤ 054=+i i对封闭面列KCL 方程，得②③④节点构成的闭合面：0541=++i i i③④⑤节点构成的闭合面：0321=++i i i②③④⑤节点构成的闭合面：01=i2.2 解：00543164218975645632432631521=+++=+-+=-+-=-+-=-++-=++-=++=++u u u u u u u u u u u u u u u u u u u u u u u u u u u2.3 解：对a 节点列KCL 方程，得A I I I I 123221441=-=-=+=对回路1列KVL 方程，得AI I I I I 45018212125062121255154==+++=+++ 对b 、c 、d 、节点列KCL 方程，得AI I I I I I A I I I I I I AI I I I I I 2)3(1143341623263512125546654=---=-==+-=-=-==+-=-=-=+=对回路2列KVL 方程，可求得UV U I I I U 242611236)3(4123646463=⨯-⨯++-⨯=++=+2.4 解：KCL ：00521654431=-+-=++-=+-I I I I I I I I IKVL ：23143205652643541=-+=++=--I I I I I I I I I2.5 解：利用支路电流法，对电路列出KCL 、KVL 方程，有 KCL ：5644326210i i i i i i i i i =++==++KVL ：333554411333222244666i R u i R i R i R u i R i R i R i R u i R s s s +=+=+++=+代入已知条件，解得：A i 956.05-=2.6 解：利用支路电流法，对电路列出KCL 、KVL 方程，有KCL ： c b e I I I +=KVL ：c c e e c ee b be b b b I R U I R U I R I R I R U ++=++=其中 b c I I β=代入已知条件，解方程得：AI A I AI e c b 3351016.11013.11027.2---⨯=⨯=⨯=2.7 解：假设网孔电流的参考方向如下图所示。
观察电路图，列出网孔方程如下所示822282640248321321321=++--=++=-+m m m m m m m m m I I I I I I I I I求解方程得到三个网孔电流AI A I AI m m m 4106321=-==根据KCL 即可求得各支路电流A I I I AI I I AI I AI I I AI I AI I m m m m m m m m m 6442106325214333162211=--==--===-=+-=-====2.8 解：假设网孔电流的参考方向，如图所示。
观察电路图，列出网孔方程没4313212105455113232121-=+-=-+-=-m m m m m m m I I I I I I I求解网孔方程得到三个网孔电流为A I A I AI m m m 325321-===从而，各支路电流为AI I I AI I I A I I AI I AI I m m m m m m m 5)3(2325325325214332211=--=-==-=-=-======2.9 解：假设网孔电流的参考方向如图所示。
观察电路图，列出网孔方程如下所示12224122441023812220321321321=+---=-+-=--m m m m m m m m m I I I I I I I I I求解网孔方程得到三个网孔电流为AI A I AI m m m 213321=-==再利用KCL 求得各支路电流AI I I AI I I AI I I AI I AI I AI I m m m m m m m m m 3214)1(3123213326215314332211-=--=-==--=-==-=-===-====2.10 解：假设网孔电流的参考方向如图所示，观察电路图，列出网孔方程，如下所示20204820424104081020321321321=+---=-+--=--m m m m m m m m m i i i i i i i i i求解网孔方程得到三个网孔电流为Ai i i Ai Ai A i m m m m m 6.19.05.264.3323321-=-=-=-=-=2.11 解：假设回路电流的参考方向如图所示，观察电路图，列出回路方程如下所示8)835(4886)863(1648326)642(2331221=-++=--+++-=-++i i i i i i i解方程得 A i i 4.23==2.12 解：假设回路电流的参考方向如图所示，观察电流图，列出回路方程如下所示Ii Ui i i i i i i i i 1.0510)105(42054)541(0104)10420(3213312321-==--+-=--++=--++解方程得 V U 5.276=2.13 解：标出节点电压参考方向，观察电路图，列出节点方程1021)6121132110421)2151(1221=-+++-=-+u u u u 2.14 解：标出节点电压参考方向，观察电路图，列出节点方程221)10121(11021)215111(1221=-+=-++u u u u 解方程得V u Vu 909.1009.921==故A u i A u i A u u i A u i 0909.110818.15909.02909.0110241321211====-=-==-=2.15 解：标出节点电压参考方向，观察电路图，列出节点方程201510141)41101(04151)2014151(5021233121u I I u u u u u u u ==--+=--++= 求方程得 V u U 322==2.16 解：当电压源作用时，对应的分电路如下图所示对回路1列KVL 方程，得A i i i 212663'''=+=+对假想回路2列KVL 方程，得（1Ω电阻上此刻无电流流过）V u Vu i 6123'''==+当电流源作用时，对应的分电路如下图所示A i 13633''=+⨯= 由KCL ，可知 A i 5231=+=对图示回路列KVL 方程，得V i i u 115661''''=+=+=根据叠加定理A i i i Vu u u 31217116''''''=+=+==+=+=2.17 解：当电流源单独作用时，分电路如下图所示V U 5)215453(6'=⨯+⨯⨯=当电压源单独作用时，分电路如下图所示V U 3)21369(6''=⨯+⨯=根据叠加定理 V U U U 8'''=+=2.18 解：根据齐性定理，电路中激励源同时增大2倍，电路中的响应也响应增大2倍，故V U 1628=⨯=2.19 解：当电压源单独作用时，分电路如下图所示对图示回路列KVL 方程，得''1'1'2)31(6I U U I =++=故 A I 1'= V U 313'-=⨯-=当电流源单独作用时，分电路如下图所示由KCL ，可知''''1''''144II I I -=+=对图示回路列KVL 方程，得''1''1''32I U I =+代入''''14I I -=，得''''1''3122I U I -=+且式中 ''''1I U = 故 A I 2''=此时 V I I U 6)4(33''''1''=-⨯== 根据叠加定理VU U U A I I I 363321''''''=+-=+==+=+=2.20 解：当电压源单独作用时，分电路如下图所示由电路可知 3''1U I =根据KCL ，可得3'''1''2U I I I I -=-=而 1226126'''2'+-=+=U I I U故 42''+=I U 当电流源单独作用时，分电路如下图所示由电路可知36''''1''''2U I U I ==根据KCL 可得623''''''2''1''+=+=+I U I I I根据叠加定理10210)(26242'''''''''+=++=+++=+=I I I I I U U U2.21 解：当电压源单独作用时，分电路如下图所示tV t U ab sin )215.2sin 5(1'=⨯⨯= 当电流源单独作用时，分电路如下图所示V e e U t t ab--=+⋅⨯=2.0)34343(1''根据叠加定理V e t U U U t ab ab ab )2.0(sin '''-+=+=2.22 解：（a ）该电路课通过电源等效变换，作如下化简（b ）2.23 解：与40Ω电阻相连的是如下图所示一端口电路利用电源等效变换，以上一端口电路可等效为戴维南等效电路，如图所示此戴维南等效电路与40Ω电阻相连，电阻上的电压U 为：V U 840604020-=+⨯-= 2.24 解：N 单口网络可等效为戴维南等效电路，（a ）（b ）电路可变换成下图所示电路（a ）图中 mA K UI 5.251=Ω=对（a ）图中回路1列KVL 方程，得mAI U I 320105.2223==+⨯根据KCL 可得mA I I I 5.05.23123=-=-= 对（a ）图中回路2列KVL 方程，得U RI u s =+3即 5.12105.03=⨯+-R u s （1） 对（b ）图中回路1列KVL 方程，得mAI I 820105.2443==⨯对（b ）图中回路2列KVL 方程，得5RI u s =而根据KCL 可知mA I I I 281045=-=-=故 R u s 3102-⨯= （2） 综合(1)(2)两式，可求得Ω==K R V u s 5102.25 解：AI rI 82411==且 A I 46242== 由KCL ，可得AI I I I 5121=+=+2.26 解：由KCL ，可得II I I I I I 232121+=+=+对图示回路列KVL ，得I I I I I I I I I 321121818121261812618222221-=-=++=+=而 I I I U 812)321(12122-=-== 此单口网络的戴维南等效电路如下图所示2.27 解：根据电源等效变换，将戴维南等效电路变换为诺顿等效电路。