计算方法第一章误差
1.《计算方法》-误差

《计算方法》教案(第一章误差)选用教材:普通高等教育“十一五”国家级规划教材《计算方法引论》(第三版)徐箤薇孙绳武编著主讲老师:刘鸣放2010年3月于河南大学一.基本内容提要1. 误差的来源2. 浮点数、误差、误差限和有效数字3. 相对误差和相对误差限4. 误差的传播5. 在近似计算中需要注意的一些问题二.教学目的和要求1. 熟练掌握绝对误差、绝对误差限、相对误差、相对误差限和有效数字的概念及其相互关系;2. 了解误差的来源以及误差传播的情况,掌握在基本算术运算中误差传播后对运算结果误差限的计算方法和函数求值中的误差估计;3. 理解并掌握几种减少误差避免错误结果应采取的措施,了解选用数值稳定的算法的重要性。
三.教学重点1.绝对误差、绝对误差限、相对误差、相对误差限和有效数字的概念及其相互关系,误差传播,减少误差避免错误结果应采取的措施。
四.教学难点1.误差传播;2. 数值稳定算法的选用。
五.课程类型新知识理论课;六.教学方法结合课堂提问,以讲授为主。
七.教学过程如下:Introduction1.《计算方法》课程介绍计算方法是用数值的方法研究研究科学与工程中的计算问题;它的内容主要包括:近似值的计算和误差估计两个方面;主要工具:计算机;地位:这门课已成为工科各专业,特别是计算机科学与技术、土木工程、机械、数学等专业的必修基础课。
2.发展状况几十年来,计算方法效率的提高是与计算机速度的提高几乎同步地、同比例地前进的。
这里简述一下国家重点基础研究计划项目(简称973项目)“大规模科学计算研究”(1999-2004)的主要内容,可以帮助同学们了解我国科学计算界所关心的问题。
此项目由石钟慈院士等人为首组织,集中了我国计算数学、计算物理、计算力学、计算机、以及材料、环境能源等领域60多名专家,跨学科,跨部门通力合作研究以下几个方面的主要内容:(1)复杂流体的高精度计算,含天气预报数值模拟研究;(2)新材料的物理性质机理多尺度计算研究,含超导、超硬度合金等问题的计算研究;(3)地质油藏模拟与波动问题及其反问题计算研究;(4)基础计算方法的理论创新与发展;(5)大规模计算软件系统的基础理论和实施。
计算方法 第1章 预备知识与误差分析

1. 误差的来源及误差类型 一般使用计算机解决实际问题须经过如下几个过程: 实际问题 数学模型 数值算法 程序设计 计算结果
根据实际问题建立数学模型的过程中通常会忽略某些次要因素而对问题进行简化, 由此 产生的误差称为模型误差; 很多数学模型都含有若干个参数, 而有些参数往往又是观测得到 的近似值, 如此取得的近似参数与真实参数值之间的误差称为参数误差或观测误差。 例如自 由落体运动规律的公式
nn
(1.2)
其矩阵形式可以表示为 Ax b, A R
, x, b R n ,由线性代数知识我们知道,当其系数
授课对象:北京工业大学计算机学院本科生
杨中华
2
编者:杨中华
计算方法讲稿
第一章 预备知识与误差分析
矩阵对应的行列式不等于零时,即 D 法则,有:
A 0 ,该线性方程组有唯一一组解,根据克莱姆
这个耗时数还不包括求解过程中的加减运算以及更耗时的读写内存数据操作所需要的时间。 但是如果用 Gauss 消去法求解此规模的线性方程组,其乘除法次数约仅为:
n3 n n 2 3060 3 3
(1.4)
从(1.3)与(1.4)式的巨大差距可以看出求解线性方程组用 Gauss 消去法非常有效, 因此对于稍 微大一点规模的线性方程组没有任何理由选择克莱姆法则解决此类问题。 对程序员的忠告:千万不要以为计算机的速度不是问题,选择数学方法不当可能让你 永远等不到最后的计算结果! 我们再看一个实例, 从中可以发现, 有时直接使用高等数学中给出的很简单明了的数学 表达式进行计算并不一定能够得到我们预期的结果。 例1.2 考虑导数的近似计算问题,根据导数的定义
计算方法讲稿
第一章 预备知识与误差分析
数值计算chapter1误差

显然,从相对误差看,近似值
x1
比
x
2
的精确程度要好得多.
例4 设 x 2.18是由准确值 x 经过四舍五入得到的近似值,
则 x的绝对误差限为 0.005 ,
相对误差限为
r
0.005 2.18
0.23%
注 凡是由准确值 x 经过四舍五入得到的近似值,其绝对误
差限取近似值末位数位的半个单位。
e S
2
D1
e D1
2
D2
e D2
10 0.05 5 0.1 0.5 1.5708 cm2
2
2
12
相对误差满足
er S
e S
S
1.5708 0.027 2.7% 58.905
即若取 S 58.905cm2作为圆环面积的近似值,则其绝对误差
不超过1.5708cm2 , 相对误差小于 2.7% .
注: ⑶ 相对误差和相对误差限都是无量纲数,常用百分数表示.
⑷
r
常用以下公式求:
r
x
.
5
例3 x1 100 2 的近似值 x1 100的相对误差限为
e1 x
e x1
x1
2 2% 100
x2 10 1 的近似值 x2 10 的相对误差限为
e2 x
ex2
x2
1 10% 10
再用舍入功能为八位的计算器计算,得结果为:
y 3.3921911108
19
由此,当相邻两数相减时,可考虑改变一下算法, 如
当
x1与
x 2 相近时,
ln
x1
ln
x2
ln
x1 x2
当 很小时, sinx sin x 2cos x sin
计算方法(1)-数值计算中的误差

* r
(
x)
1)乘方运算结果的相对误差增大为原值 x的p倍,降低精度.
2)开方运算结果的相对误差缩小为原值
x的1/q倍,精度得到提高.
三.算例的误差分析
x
3
2 2
1 1
24
§6 算法的数值稳定性
一.算法稳定性的概念
凡一种算法的计算结果受舍入误差的影 响小者称它为数值稳定的算法.
例4 解方程 x2 (109 1)x 109 0
方程精确解: x1 10 9 , x2 1
利用求根公式
x1,2
b
b2 4ac 2a
x1 10 9 , x2 0
25
当多个数在计算机中相加时,最好从
绝对值最小的数到绝对值最大的数依次相
加,可使和的误差减小.
二.算法的改进
2 2
1 1
3
计算结 果
2 7/5
2 17 /12
1 ( 2 1)6
2 6
0.0040960
5
6
0.00523278
5
12
2 99 70 2
1
1 0.16666667
6
3
6
1
5
6
0.00523278
12 6
计算方法
1
第一章 数值计算中的误差
§1 引言 §2 误差的种类及其来源 §3 绝对误差和相对误差 §4 有效数字及其与误差的关系 §5 误差的传播与估计 §6 算法的数值稳定性
第一章数值计算方法与误差分析

工具求出数学问题的数值解,并对算 法的收敛性、稳定性和误差进行分析 计算的全过程。
构建一个完整的数值算法,包含着以下环节: 1. 提出数值问题(即对对象建立数学模型) 2 .构思处理数值问题的基本思想(即提出理论) 3 .列出计算公式 4 .设计程序框图
5 .编制源程序并调试
I0=
∫01
ex-1dx=
ex-1|
1 0
=
1-e-1
≈0.6321
In= 1– nIn-1 (n=1, 2, … , 9)
用四位小数计算依次得到:
0.6321, 0.3679, 0.2642, 0.2074, 0.1704
0.1480, 0.1120, 0.2160, -0.7280, 7.5520
• 定义3 若近似值x*的绝对误差限是 某一位上的半个单位,该位到x*的第一 位非零数字一共有n位,则称近似值x*有 n位有效数字,或说x*精确到该位。
• 准确数本身有无穷多位有效数字, 即从第一位非零数字以后的所有数字都 是有效数字。
有效数字举例
• 如例1中的x*1,x*2 ,x*3,分别有1,3,5位有效数字。 • 实际上,用四舍五入法取准确值x 的前n位(不
• 为了既能表示近似数的大小,又能 表示近似数的精确程度,我们下面介绍 有效数字的概念(注意:有效数字既能 表示近似数的大小,又能表示近似数的 精确程度)。
半个单位的概念
•
我们知道,当x有很多位数字时,常常按照
“四舍五入”原则取前几位数字作为x的近似值x*。
• 例1 设 x = π = 3.1415926 …
一元二次方程 X2+2pX +q=0的求解方法
根据根与系数的关系可知
计算方法引论课后答案

计算方法引论课后答案第一章误差1.什么是模型误差,什么是方法误差?例如,将地球近似看为一个标准球体,利用公式 $A=4\pi r$ 计算其表面积,这个近似看为球体的过程产生的误差即为模型误差。
在计算过程中,要用到 $\pi$,我们利用无穷乘积公式计算 $\pi$ 的值:pi=2\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot\f rac{4}{5}\cdot\frac{6}{5}\cdot\frac{6}{7}\cdot\frac{8}{7}\cdot\ frac{8}{9}\cdot\cdots我们取前9项的乘积作为 $\pi$ 的近似值,得$\pi\approx3.xxxxxxxx5$。
这个去掉 $\pi$ 的无穷乘积公式中第9项后的部分产生的误差就是方法误差,也称为截断误差。
2.按照四舍五入的原则,将下列各数舍成五位有效数字:816.956,76.000,.322,501.235,.182,130.015,236.23.解:816.96,76.000,.501.24,.130.02,236.23.3.下列各数是按照四舍五入原则得到的近似数,它们各有几位有效数字?81.897,0.008,136.320,050.180.解:五位,三位,六位,四位。
4.若 $1/4$ 用 0.25 表示,问有多少位有效数字?解:两位。
5.若 $a=1.1062$,$b=0.947$,是经过舍入后得到的近似值,问:$a+b$,$a\times b$ 各有几位有效数字?已知 $da<\frac{1}{2}\cdot10^{-4}$,$db<\frac{1}{2}\cdot10^{-3}$,又 $a+b=0.\times10$。
begin{aligned}d(a+b)&=da+db\leq da+db=\frac{1}{2}\cdot10^{-4}+\frac{1}{2}\cdot10^{-3}=0.55\times10^{-3}<\frac{1}{2}\cdot10^{-2}end{aligned}所以 $a+b$ 有三位有效数字;因为 $a\timesb=0.xxxxxxxx\times10$。
数值计算方法1_误差

0 绪论
评分标准 考试
60%
作业 出勤
30%
10%
1.1 误差 – 来源
误差来源
原始误差-模型误差(忽略次要因素,如空气阻力)物理模型 ,数学模型 观测误差-获取模型参数的观测或实验过程中带来的误差 方法误差-截断误差(算法本身引起) 计算误差-舍入误差(计算机表示数据引起)
1.1 误差 – 来源
模型 长乘以宽
求面积
测量
尺子
近似 表达
虚线
取值
四舍五入
1.2 误差 – 分类
绝对误差
* 设 x* 为精确值, x 为近似值,e x x 为误差或绝对误差
例如:f ( x ) ln(x 1) 作Taylor展开,
(1)i 1 i (1) n x n 1 , 0 1 x n1 i (n 1)(1x) i1
方法二:
取前5项,截断误差已经小于10-5 。
1.5 误差 – 避免两个相近的数相减
方法一:
方法二:
1.6 误差 – 避免除数绝对值远小于被除数绝对值
除数减小,绝对误差增大
1.7 误差 – 防止大数吃小数 求根
1.7 误差 – 防止大数吃小数
如果用8位数计算机:
正确结果: 错误结果:
1.8 误差 – 尽量采用数值稳定性好的方法
方法一:迭代 正向计算
方法二:取中数 反向计算
1.8 误差 – 尽量采用数值稳定性好的方法
为 什 么 ?
Hale Waihona Puke 1.8 误差 – 尽量采用数值稳定性好的方法
方法一:迭代
方法二:取中数 反向计算
反向计算误差传播降低,方法一可否反向计算?
计算方法-误差
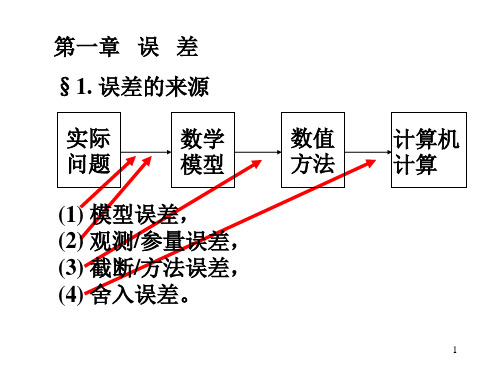
举例4:计算 tg(1.57079),tg(1.57078)
x 1.57079 , x* 1.57078
(x*) | x x* | 0.00001
r (x*) | (x x*) / x* | 6.410-6
| f ' (x*) | 1 3.8 109
c os2 ( x*)
15
( y*) | f ' (x*) | (x*) 3.8 104
| x * f ' (x*) / f (x*) |
1
9.6 104
s in( x*) c os (x*)
r ( y*) 0.6
y = tan(x) 1.580579134162482e+ 005
y* = tan(x*) 6.124900853150305e+ 004
( y*) =| y-y* | 9.680890488474515e+ 004
1 22
x2 2!
1 x2 3 x3 35 x4
22 2! 23 3! 24
4!
6.172839438271605e-16
3 23
x3 3!
35 24
x4 4!
6.1728394382716030948026634659e-16 3
• 举例3-1:计算机的精度限制(舍入误差)
-- 在matlab中运行计算:
f ( x1, x2 ) f ( x1*, x2 ) f ( x1*, x2 ) f ( x1*, x2*)
f
(1, x2 )
x1
( x1
x1*)
f
( x1*,2 )
x2
( x2
x2*)
f
( x1*, x2*) x1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:重力加速度常数g。g 9.80米 秒2 , g 980厘米 秒2
两者均有三位有效数字
g 9.80 0.5 102 米 秒2
g 980 0.5厘米 秒2
后者的绝对误差大,而相对误差分别为
0.5 102 0.5 和 9.80 980
两者相等,与量纲的选取无关
有效数字
取 r 5% 。
定理 2 若近似数 x 0.x1 x2
xn 10m ,的相对误差限
r
则它至少具有 n 位有效数字。 证 x 0.x1 x2 则 xx
1 10 ( n 1) 2( x1 1)
xn 10m 有 x ( x1 1) 10m 1
1. 2.
3.
4.
数值分析需要考虑哪些问题
1. 计算速度 例如:求解一个20阶线性方程组,20个未知量, 用加减消原法需3000次乘法运算,用行列式求 解需进行9.7*1020次运算,如果用每秒1亿次乘 法运算的计算机要30万年。 说明了算法方法的重要性 2. 存储量。大型问题有必要考虑 例如算法所需要保留的中间结果比较少,则可 以省下为保留中间结果所需要的额外的存储空 间。
0.3529 10 , 0.352900 10
2
2
当 x 0.a1a2
al
an 10m , ai为数字01 , , 2, , 9,a1 0.
其中,有效数字的个数是l,即 a1, , al是有效的。
则 e x x * 0.510
ml
有效数字:由绝对误差决定
此定理说明,相对误差限是由有效数字决定。
例:用 3.14 作为 的近似值,求其相 对误差。 解:四舍五入的近似值各位都是有效 数字,即 n=3,由定理 1 (31) r 10 0.17% 23 x 有两位有效数字,求其相对误差限。 解
2
误差的来源和基本概念
• 1. 误差的来源 模型误差:在建立数学模型过程中,不可能将所有因素 都考虑,必然要进行必要的简化,带来了与实际问题的 误差。不是数值方法考虑的问题 测量误差:测量已知参数时,数据带来的误差。也不是 数值方法考虑的问题 截断误差:在设计算法时,必然要近似处理,寻求简化。 这是计算数学考虑问题 舍入误差:计算机的字长是有限的,每一步运算均需四 舍五入,由此产生的误差称舍入误差。 数值分析主要讨论截断误差。测量误差看成初始的 舍入误差,数值分析也要从整体上讨论舍入误差的影响
1 因 n=2, r 10 ( n 1) 第 1 位 x1 未给出, 2 x1 1 1 10 ( n 1) 10 ( n 1) 5% 2 x1 2 1
x1 1 r x1 9
1 1 ( n 1) r 10 10 ( n 1) 0.56% , 2 x1 29
k 1
( xk )
数值计算中误差的传播
3. 四则运算中误差的传播:
( x1 x2 ) ( x1 ) ( x2 ); ( x1 x2 ) x1 ( x2 ) x2 ( x1 )
x1 x1 ( x2 ) x2 ( x1 ) 2 x2 x2
定 义 设 x * 的 近 似 值 x 0.x1 x2
xn 10m ,
1 x1 0 ,若 x 的绝对误差 x - x * 10 m n 2 则称近似值 x 为 x * 的有 n 位有效数字的近似值。 其中
x1 , x2 , , xn 是 x 的有效数字。近似值 x 具有 n 位有
现代复杂工程技术问题的解决步 骤
工程问题 数学模型 设计算法
问题解答
结果分析
上机计算
数值分析涉及的主要内容
• 计算机只能进行加减乘除四则运算和一些简单 的函数计算(即使函数也是通过数值分析方法 处理,转化为四则运算而形成的小型软件包) 数值代数:求解线性方程组和非线性方程组的 解法,分直接方法和间接方法 插值和数值逼近。离散的点上的函数值,想办 法得到点之间的值 数值微分和数值积分。很多函数无法求出积分, 利用数值方法求解 常微分方程和偏微分方程的数值解法
• 若近似值x的绝对误差限是某一位数的半个 单位,则说 x 精确到该位,若从该位到 x 的左面第一位非零数字一共有n位,则称近 似值x有n位有效数字。
例: 3.1415926535
3.14有三位有效数字 误差限 0.005 ;3.1416有五位有效数字, 误差限为0.00005
,
又例:0.003529是四位有效数字,0.00352900 6 是六位有效数字。前者的误差限为 0.5 10 , 8 后者为 0.5 10 ,写成标准的浮点数为:
1 0.25% 10 ( n 1) 2( x1 1)
x1 的取值范围是 1 到 9,由于 x1 未给出,取 x1=1,n= 3 x1=9,n=2 按最不利情况,x 至少有 2 位有效数字。
数值计算中误差的传播
1. 对函数的计算:
设x是x *的近似值。e( f ( x)) f ( x) f ( x*), 如果f ( x)可微,由泰勒公式得: 1 e( f ( x)) f '( x)( x x*) f ''( )( x x*) 2 2 1 故: e( f ( x)) f '( x) e( x) f ''( ) e 2 ( x) 2 忽略高项阶后可以得: e( f ( x)) f '( x) e( x)
效数字,它准确到第 n 位。
例:求 3.142 和 3.141 作为圆周率 的近似值有几位有效数字。 解: 3.142 0.000407
m n 3, n 4 。有 4 位有效数字。
1 0.0005 103 , m 1 , 2 1 10 2 , m 1 , 2
2. 3.
4.
误差的基本概念
• 绝对误差和绝对误差限 X*是精确值,x是它的一个近似值,称 e=x-x*是近似值x的绝对误差,简称误 差。绝对误差可正可负,是有量纲的。 误差是无法计算的,但可以估计出它 的一个上界。即 : x x * , 称 是近似值x的误差限
即x x* x
例如: 有毫米刻度的尺子, 读出的近似值的 误差,不会超过毫米的一半(半个毫米) 。 读出 35 毫米代表 34.5 到 35.5 之间。误差 是半个毫米,误差限是末位的半个单位。
相对误差和相对误差限
• 相对误差和相对误差限
e x x* 记作 称 为近似值x的相对误差, x* x*
er
相对误差是个相对数,是无量纲的,也可正 可负。相对误差的估计 er r
xn 10m 具有 n 位有效数字,
r
1 10 ( n 1) 2 x1
xn 10m ,有 x x1 10m 1 ,
又, x 有 n 位有效数字,即 x x *
1 10m n ,因此 2
1 mn 10 x x* 2 1 1 ( n 1) ( n 1) ,即 10 er 10 r x* x1 10 m 1 2 x1 2 x1
称 r为相对误差限 ,即:
x*
x x* x*
2
x*
r
实际计算中,x*未知,用x代替,两者的差为:
x
x* x
x* x
x*x x*
2
x r2 x*
例:用 3.14 作为 的近似值,求其相 对误差。 解:四舍五入的近似值 3.14 的绝对误 1 2 差 限 10 , 相 对 误 差 2 1 2 10 r 2 0.159% 3.14 x
2 18 9 18
b 4ac 10 4 10 10 10
9
又 109 1 109 ; 则
9 9 (109 ) 109 ( 10 ) 10 x1 109 , x2 0 2 2
数值分析需要考虑哪些问题
x2的值与精确解有天壤之别。若
b b 4ac 2c x2 2a b b 2 4ac 2 109 1与精确解相等 9 9 (10 ) 10
数值分析需要考虑哪些问题
3. 数值稳定性 在大量计算中,舍入误差是积累还是能控制, 这与算法有关。 例:一元二次方程 9 2 9 9 其精确解为 x 10 , x2 1 x (10 1) x 10 0 1
b b2 4ac 如用求根公式:x1,2 2a 和字长为8位的计算器求解,有
数值计算中误差的传播
2. 对多元函数的计算:
对多元函数f ( x1 , x2 , 是x , x ,
* 1 * 2 * n n
, xn ), 若x1 , x2 , f ( x1 , x2 , xk
, xn分别
, x 的近似值,则 , xn )
( f ( x1 , x2 , , xn ))
x x x
x
1 1 即 10 ( n 1) ( x1 1)10 m 1 10 m n , 2( x1 1) 2
它至少具有 n 位有效数字。
例 解
已知近似数 x 的相对误差限为 0.25%, 问 x 至少有几位有效数字? 由 r 0.25% ,根据定理,有
3.141 0.00059
0.005
m n 2, n 3 。有 3 位有效数字。
22 的近似值有几位有 例: 以 作为圆周率 7
效数字。
22 解: =3.142857……, π =3.141592……。 7
22 1 2 0.00126 10 。因为 m=1, 7 2
m-n=-2 ,所以 n=3,有 3 位有效数字。
