离散数学之命题符号化共35页文档
离散数学命题符号

离散数学命题符号一、离散数学命题符号的定义在离散数学中,命题是一个陈述句,可以判断为真或为假。
为了准确地表示命题,在离散数学中引入了命题符号。
命题符号主要用于表示命题的逻辑关系,以及对命题的运算。
1. 命题变量和命题符号离散数学中,命题变量被表示为字母,常用的命题变量包括p、q、r等。
命题符号则用来表示对命题变量的操作和运算关系。
常用的命题符号包括逻辑与(∧)、逻辑或(∨)、非(¬)等。
2. 逻辑连接词离散数学中,逻辑连接词用于将多个命题连接起来,形成复合命题。
常见的逻辑连接词有:- 逻辑与(∧):表示两个命题都为真时,复合命题为真;否则为假。
- 逻辑或(∨):表示两个命题至少一个为真时,复合命题为真;否则为假。
- 非(¬):表示对命题的否定。
3. 命题符号的优先级为了保证命题的运算顺序和结果的准确性,在离散数学中,命题符号有一定的优先级。
常见的命题符号优先级从高到低依次为:- ¬(非)- ∧(逻辑与)- ∨(逻辑或)二、离散数学命题符号的应用1. 命题的合取和析取在离散数学中,逻辑与(∧)和逻辑或(∨)的运算被广泛应用于命题的合取和析取。
- 合取:当多个命题同时为真时,可以使用合取运算符(∧)将这些命题合并成为一个复合命题。
例如,当p表示“今天下雨”、q表示“今天天气阴沉”时,合取命题p∧q表示“今天同时下雨并且天气阴沉”。
- 析取:当多个命题至少一个为真时,可以使用析取运算符(∨)将这些命题合并成为一个复合命题。
例如,当p表示“今天下雨”、q表示“今天天气阴沉”时,析取命题p∨q表示“今天下雨或者天气阴沉”。
2. 命题的否定在离散数学中,非(¬)运算符常用于对命题的否定。
如果p为真,则¬p为假;如果p为假,则¬p为真。
例如,若p表示“今天下雨”,则¬p表示“今天不下雨”。
3. 命题的复合运算通过组合使用逻辑连接词和命题符号,可以对多个命题进行复合运算。
离散数学符号表

《离散数学》符号表∀ 全称量词(任意量词)∃ 存在量词├ 断定符(公式在L 中可证)╞ 满足符(公式在E 上有效,公式在E 上可满足) ┐ 命题的“非”运算∧ 命题的“合取”(“与”)运算∨ 命题的“析取”(“或”,“可兼或”)运算 → 命题的“条件”运算↔ 命题的“双条件”运算的B A ⇔ 命题A 与B 等价关系B A ⇒ 命题A 与B 的蕴涵关系*A 公式A 的对偶公式wff 合式公式iff 当且仅当V 命题的“不可兼或”运算( “异或门” ) ↑ 命题的“与非” 运算( “与非门” ) ↓ 命题的“或非”运算( “或非门” ) □ 模态词“必然”◇ 模态词“可能”φ 空集∈ 属于(∉不属于)A μ(·) 集合A 的特征函数P (A ) 集合A 的幂集A 集合A 的点数n A A A ⨯⨯⨯ (nA ) 集合A 的笛卡儿积R R R =2 )(1R R R n n -= 关系R 的“复合”0ℵ 阿列夫零ℵ 阿列夫⊇ 包含⊃ 真包含∪ 集合的并运算∩集合的交运算 - (~)集合的差运算 ⊕集合的对称差运算 m + m同余加 m ⨯ m同余乘 〡限制 R x ][集合关于关系R 的等价类 A /R集合A 上关于R 的商集 )(A R π集合A 关于关系R 的划分 )(A R π集合A 关于划分π的关系 ][a元素a 产生的循环群 R a ][元素a 形成的R 等价类 r C由相容关系r 产生的最大相容类 I环,理想 )/(n Z模n 的同余类集合 )(mod k b a ≡a 与b 模k 相等 )(R r关系R 的自反闭包 )(R s关系R 的对称闭包 +R ,)(R t关系R 的传递闭包 *R ,)(R rt关系R 的自反、传递闭包.i H 矩阵H 的第i 个行向量j H . 矩阵H 的第j 个列向量CP 命题演绎的定理(CP 规则)EG 存在推广规则(存在量词引入规则)ES 存在量词特指规则(存在量词消去规则) UG 全称推广规则(全称量词引入规则) US 全称特指规则(全称量词消去规则) A I ,0R 恒等关系A 集合A 的补集X X 所有X 到自身的映射X Y 所有从集合X 到集合Y 的函数)(][A A K 集合A 的势(基数)R 关系r 相容关系 R 否关系R 补关系1-R (c R ) 逆关系S R 关系R 与关系S 的复合n nR R R R ,关系R 的n 次幂 r r B B B 222,⨯⨯ 布尔代数2B 的r 次幂r B 2 含有r 2个元素的布尔代数domf 函数f 的定义域(前域)ranf 函数f 的值域Y X f →: (Y X f −→−) f 是X 到Y 的函数),(y x GCD y x ,最大公约数),(y x LCM y x ,的最小公倍数 e 幺元θ 零元1-a 元素a 的逆元)(Ha aH H 关于a 的左(右)陪集 )(f Ker 同态映射f 的核(或称f 的同态核) A ,B ,C 合式公式⎪⎪⎭⎫ ⎝⎛k n 二项式系数⎪⎪⎭⎫ ⎝⎛p n n n n ,,,21 多项式系数[1,n] 1到n 的整数集合)1()1(][+--=k x x x x k)1()1(][-++=k x x x x kk n C 组合数),(v u d 点u 与点v 间的距离 )(v d 点v 的度数)(v d + 点v 的出度)(v d - 点v 的入度),(E V G = 点集为V ,边集为E 的图 G 图G 的补图G G '≅ 图G 与图G '同构*G 平面图G 的对偶图 W(G) 图G 的连通分支数 )(G κ 图G 的点连通度)(G λ 图G 的边连通度)(G δ 图G 的最小点度)(G ∆ 图G 的最大点度 A(G) 图G 的邻接矩阵 P(G) 图G 的可达矩阵 M(G) 图G 的关联矩阵 n K n 阶完全图m n K , 完全二分图C 复数集N 自然数集(包含0在内) +N 正自然数集P 素数集Q 有理数集+Q 正有理数集-Q 负有理数集R 实数集Z 整数集m Z ]}[,,]2[,]1{[m Set 集范畴Top 拓扑空间范畴Ab 交换群范畴Grp 群范畴Mon 单元半群范畴Ring 有单位元的(结合)环范畴 Rng 环范畴CRng 交换环范畴R-mod 环R 的左模范畴 mod-R 环R 的右模范畴 Field 域范畴Poset 偏序集范畴。
离散数学课件 4.1一阶逻辑命题符号化

第 10 页
四、符号化
例2 在一阶逻辑中将下面命题符号化。
(1)人都爱美。
(2)有人用左手写字。
个体域分别为:
(a) D为人类集合 (b) D为全总个体域
解: (a)设F(x):x爱美,G(x):x用左手写字,则
(1) xF(x) (2) xG(x)
, L(x,y): x与y跑得同样快。 (5) ﹁ x y(F(x) G(y) H(x, y)) (6) ﹁ x y(F(x) F(y) L(x, y))
第 16 页
总结和作业
➢ 小结 ◆ 理解个体词、谓词、量词的含义 ◆ 掌握一阶逻辑命题的符号化
➢ 作业(做书上)
课本63-64页 4(1) (3), 5(1) (3),6 (1) (3) (5)
第1 页
第四章 一阶逻辑基本概念
➢ 命题逻辑的局限性
在命题逻辑中,研究的基本单位是简单命题,对简单 命题不再进行分解,并且不考虑命题之间的内在联系和数 量关系。
➢ 一阶逻辑所研究的内容
为了克服命题逻辑的局限性,将简单命题再细分,分 析出个体词、谓词和量词,以期达到表达出个体与总体的 内在联系和数量关系。 ◆ §4.1一阶逻辑命题符号化 ◆ §4.2一阶逻辑公式及解释 ◆ §5.1一阶逻辑等值式与置换规则 ◆ §5.2一阶逻辑前束范式
第四章 一阶逻辑基本概念
➢ 苏格拉底三段论
◆ 所有的人都是要死的。 ◆ 苏格拉底是人。 ◆ 所以,苏格拉底是要死的。 试证明此推理。 解:令p:所有的人都是要死的,q:苏格拉底是人,r:苏格拉底 是要死的,则 前提:p,q 结论:r 推理的形式结构: p Ù q ® r
离散数学6.命题公式及符号化

若写成(PQ) (P R)时,当P为F,Q为F时,即天没下雨而我没 上街,此时我说的是假话,但是表达式 (PQ) (P R) 的真值却是
“T” ,因为此时(P R)的真值是“T”.
4
二、复合命题的符号化(翻译) 有了命题演算的合式公式的概念,我们可以把自然语言
中的有些语句(复合命题),翻译成数理逻辑中的符号形式. 基本步骤如下:
1)首先要明确给定命题的含义. 2)对于复合命题,找联结词,用联结词断句,分解出各
个原子命题. 3)设原子命题符号,并用逻辑联结词联结原子命题符号,
构成给定命题的符号表达式.
5
例2 说离散数学无用且枯燥无味是不对的. P:离散数学是有用的. Q:离散数学是枯燥无味的. 该命题可写成: (P∧Q). 例3 如果小张与小王都不去,则小李去. P:小张去. Q:小王去. R:小李去. 该命题可写成: (P∧Q)R. 如果小张与小王不都去,则小李去. 该命题可写成: (P∧Q)R, 也可以写成: (P∨QP∧Q, PR, P∨Q∧R,PQ ∨S , (P W) Q); 下面的式子才是合式公式:
(P∧Q),(PR),((P∨Q)∧R). 按照合式公式定义最外层括号必须写. 约定:为方便,最外层括号可以不写,上面的合式
公式可以写成: P∧Q,PR,(P∨Q)∧R.
命题公式及符号化
一、 命题公式
1.定义1-3.1 命题演算的合式公式
合式公式是由命题变元、命题常量、联结词和圆括号按 一定的逻辑关系联结起来的符号串.我们以如下递归的形 式来定义合式公式:
(1)单个命题变元是一个合式公式. (2)若A是合式公式,则┐A也是合式公式. (3)若A,B是合式公式,则(A∧B),(A∨B),(AB),
离散数学符号大全

离散数学符号大全├断定符(公式在L中可证)╞满足符(公式在E上有效,公式在E上可满足)┐命题的“非”运算∧命题的“合取”(“与”)运算∨命题的“析取”(“或”,“可兼或”)运算→ 命题的“条件”运算A<=>B 命题A 与B 等价关系A=>B 命题A与B的蕴涵关系A* 公式A 的对偶公式wff 合式公式iff 当且仅当↑ 命题的“与非” 运算(“与非门” )↓ 命题的“或非”运算(“或非门” )□模态词“必然”◇模态词“可能”φ 空集∈属于(??不属于)P(A)集合A的幂集|A| 集合A的点数R^2=R○R [R^n=R^(n-1)○R] 关系R的“复合”∪集合的并运算∩集合的交运算- (~)集合的差运算〡限制[X](右下角R) 集合关于关系R的等价类A/ R 集合A上关于R的商集[a] 元素a 产生的循环群I (i大写) 环,理想Z/(n) 模n的同余类集合r(R) 关系R的自反闭包s(R) 关系的对称闭包CP 命题演绎的定理(CP 规则)EG 存在推广规则(存在量词引入规则)ES 存在量词特指规则(存在量词消去规则)UG 全称推广规则(全称量词引入规则)US 全称特指规则(全称量词消去规则)R 关系r 相容关系R○S 关系与关系的复合domf 函数的定义域(前域)ranf 函数的值域f:X→Y f是X到Y的函数GCD(x,y) x,y最大公约数LCM(x,y) x,y最小公倍数aH(Ha) H 关于a的左(右)陪集Ker(f) 同态映射f的核(或称f同态核)[1,n] 1到n的整数集合d(u,v) 点u与点v间的距离d(v) 点v的度数G=(V,E) 点集为V,边集为E的图W(G) 图G的连通分支数k(G) 图G的点连通度△(G) 图G的最大点度A(G) 图G的邻接矩阵P(G) 图G的可达矩阵M(G) 图G的关联矩阵C 复数集N 自然数集(包含0在内)N* 正自然数集P 素数集Q 有理数集R 实数集Z 整数集Set 集范畴Top 拓扑空间范畴Ab 交换群范畴Grp 群范畴Mon 单元半群范畴Ring 有单位元的(结合)环范畴Rng 环范畴CRng 交换环范畴R-mod 环R的左模范畴mod-R 环R的右模范畴Field 域范畴Poset 偏序集范畴。
离散数学命题符号化课件
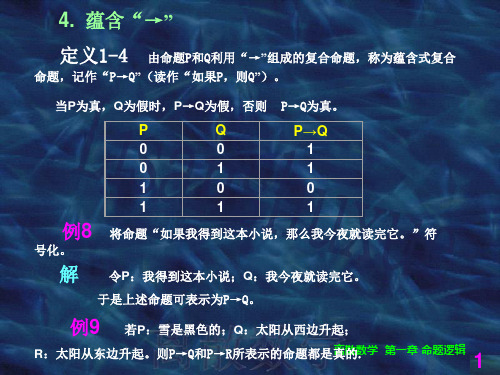
当P和Q的真值相同时,P↔Q取真,否则取假。
例10
P
Q
P Q
0
0
1
0
1
0
1
0
0
1
1
1
非本仓库工作人员,一律不得入内。
解
令P:某人是仓库工作人员;
Q:某人可以进入仓库。
则上述命题可表示为P↔Q。
离散数学 第一章 命题逻辑
8
例11 黄山比喜马拉雅山高,当且仅当3是素数
令P:黄山比喜马拉雅山高;Q:3是素数 本例可符号化为PQ
离散数学 第一章 命题逻辑
6
例. P: 月亮下山 Q: 3+3=6
则P→Q: 若月亮下山,则3+3=6 (并没有实质蕴含关系,仍承认)
Q→P: 叫做P→Q的逆命题 ┐P→┐Q : 叫做P→Q的反命题 ┐Q→┐P: 叫做P→Q的逆反命题
离散数学 第一章 命题逻辑
7
5.等值“↔”
定义1-5 由命题P和Q,利用“↔”组成的复合命题,称为等值式 复合命题,记作“P↔Q” (读作“P当且仅当Q”)。
21
2
條件否定¬(P→Q)的真值表:
P
Q
0
0
0
1
1
0
1
1
于是得到:¬(P→Q) 与 P∧¬Q 等价。
P∧¬Q 0 0 1 0
換個角度來看,既然下雨地就會溼;那麼如果地是乾的,就一定是沒有下雨。 下面的真偽值表可以反應這個關係:
P
Q
¬Q → ¬P
0
0
1
0
1
1
1
0
0
1
1
1
「非 Q則非P」為「若 P 則 Q」之逆否命題(contrapositive),和「若 P 則 Q 」 為等價之命題。我們稱 Q 為 P之必要條件。
命题符号化【范本模板】

命题符号化(1)杭州不是中国的首都。
(2) 张三虽然学习努力但成绩并不优秀。
解(1) 令P:杭州是中国的首都.则命题“杭州不是中国的首都"符号化为:┐P(2)令P:张三学习努力。
Q:张三成绩优秀。
则命题“张三虽然学习努力但成绩并不优秀。
”符号化为:P∧┐Q.合取运算特点:只有参与运算的二命题全为真时,运算结果才为真,否则为假。
自然语言中的表示“并且”意思的联结词,如“既…又…”、“不但…而且…"、“虽然…但是…”、“一面…一面…”等都可以符号化为∧。
注意:不要见到“与”或“和”就使用联结词∧ !下列命题符号化(1)北京不仅是中国的首都而且是一个故都p:北京是中国的首都. q:北京是一个故都。
p∧q:北京是中国的首都并且是一个故都.(2)牛启飞和林妹妹是好朋友P:牛启飞和林妹妹是好朋友(3) 王晓既用功又聪明。
(4) 王晓不仅聪明,而且用功。
(5) 王晓虽然聪明,但不用功。
(6)张辉与王丽都是三好生。
(7)张辉与王丽是同学。
解令 p:王晓用功,q:王晓聪明,则(3) p∧q(4) p∧q(5) p∧q.令 r :张辉是三好学生,s :王丽是三好学生(6) r∧s.(7)令 t : 张辉与王丽是同学,t 是简单命题 .设p,q为二命题,复合命题“p或q”称为p与q的析取式,记作p ∨q,符号∨称为析取联结词。
将下列命题符号化(1) 2或4是素数.(2) 2或3是素数.(3) 4或6是素数。
(4)小元元只能拿一个苹果或一个梨。
(5)王晓红生于1975年或1976年。
解令 p: 2是素数, q: 3是素数, r: 4是素数, s: 6是素数则(1),(2), (3) 均为相容或。
分别符号化为: p∨r ,p∨q,r∨s,它们的真值分别为 1, 1, 0. 而 (4),(5)为排斥或。
令 t :小元元拿一个苹果,u:小元元拿一个梨,则 (4)符号化为 (t∧u) ∨(t∧u)。
令v :王晓红生于1975年,w:王晓红生于1976年,则 (5) 符号化为 (v∧w)∨(v∧w)。
离散数学一阶逻辑命题符号化

§4.2一阶逻辑公式及解释
14/26
非逻辑符号: 个体词常项符号, 函数符号和谓词符号 逻辑符号: 个体词变项符号, 量词符号, 联结词符号和括号与逗号 定义 设L是一个非逻辑符号, 由L生成的一阶语言L的字母表 包括下述符号如下:
非逻辑符号 (1) L中的个体常项符号: a, b, c, …; ai , bi , ci ,… , i≥1 (2) L中的函词符号: f, g, h, …; fi , gi , hi ,… , i≥1 (3) L中的谓词符号: F,G, H,…; Fi ,Gi , Hi ,…, i≥1 逻辑符号 (4) 个体变项符号: x, y, z, …; xi , yi , zi ,…, i≥1 (5) 量词符号: , . (6) 联结词符号: ┐,∧,∨, →, ↔. (7) 逗号与括号: , , ( ) .
练习 函数f(x)在x=a处极限为b 任给小正数ε, 则存在正数 δ, 使得 当0<|x-a|<δ时, |f(x)-b|<ε成立 任意ε>0, 存在δ>0, 使得 当0<|x-a|<δ时, |f(x)-b|<ε成立 ∀ε(ε>0→ ∃δ(δ>0∧ ∀x(|x-a|<δ→|f(x)-b|<ε)))
定义 在公式 xA 和 xA中, 称 x 为指导变元, A为相
应量词的辖域. 在x 和 x 的辖域中, x的所有出现都 称为约束出现, A中不是约束出现的其它变项都称为 自由出现.
谓词续
6/26
④不含个体变项的谓词称为0元谓词. 例如 F(a), G(a,b), P(a1,a2,…,an)等. 当F, G, P等为谓词常项时, 0元谓词即为命题. 因此, 命题可看作特殊的谓词. 例 用0元谓词将下列命题符号化, 并讨论它们的真值. (1) 只有当2是素数时, 4才是素数; (2) 如果5大于4, 则4大于6.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、Байду номын сангаас力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
