高速精密角接触球轴承最小预紧载荷计算

合集下载

角接触球轴承计算预紧量

角接触球轴承计算预紧量角接触球轴承是一种常用的轴承类型，在机械设备中起到支撑和传递载荷的作用。

为了确保轴承的正常运行和寿命的延长，正确的预紧量是非常重要的。

本文将介绍角接触球轴承的预紧量计算方法，帮助读者了解如何在实际应用中正确设置预紧量。

一、角接触球轴承的结构和工作原理角接触球轴承由内外圈、滚动体（球）和保持架组成。

内外圈之间的接触角度通常为15°或25°，这决定了轴承的承载能力和刚度。

在工作时，滚动体在内外圈之间滚动，承受来自轴向和径向方向的载荷。

预紧量的设置可以调节轴承的刚度和摩擦，进而影响轴承的运行性能。

二、预紧量的定义和作用预紧量是指在安装轴承时，通过调整轴承内圈和外圈之间的间隙，使其产生一定的压力，从而保证轴承在工作时不会出现过大的游隙或过紧的情况。

适当的预紧量可以提高轴承的刚度和传递载荷的能力，减少滚动体的滑动和滚动接触应力，从而延长轴承的使用寿命。

三、计算预紧量的方法计算预紧量的方法有多种，下面分别介绍两种常用的方法。

1. 涉及轴向力和径向力的预紧量计算方法当轴承同时承受轴向力和径向力时，可以根据以下公式计算预紧量：Ax = kx * FxAr = kr * Fr其中，Ax和Ar分别为轴向力和径向力的预紧量，kx和kr为轴向力和径向力的预紧系数，Fx和Fr为轴向力和径向力。

2. 涉及转矩的预紧量计算方法当轴承承受转矩时，可以根据以下公式计算预紧量：M = kM * F其中，M为转矩，kM为转矩的预紧系数，F为轴向力。

在实际应用中，根据具体情况选择合适的计算方法，并根据设计要求和轴承的额定参数确定预紧系数的取值。

需要注意的是，预紧量的设置应该考虑到轴承的使用条件、工作环境和预期寿命等因素，综合考虑才能得出合理的预紧量数值。

四、预紧量的调整和检验在安装角接触球轴承时，预紧量的调整是非常重要的。

一般情况下，首先根据设计要求计算出初步的预紧量数值，然后在安装过程中逐步调整，直到达到合适的预紧量。

过盈配合量和预紧力对高速角接触球轴承刚度的影响

趋近量．
图１钢球与内、外圈接触刚度
Ｃｏｎｔａｃｔｒｉｇｉｄｉｔｉｅｓｂｅｔｗｅｅｎｂａｌｌｓａｎｄｒａｃｅｗａｙｓ
与内、外圈的接触刚度的轴向分量㈣，，ａ。分别为第Ｊ个钢球处于旋转状态时与内圈、外圈之间的动态
万方数据
第１２期
过盈配合量和预紧力对高速角接触球轴承刚度的影响
１３１７
不可能给出解析解，只能用数值解法．本文给出如流程图４所示的数值解法，图中轴承位移值的修正和球心坐标值的修正均采用牛顿一拉费逊方法．
Ｋｅｙｗｏｒｄｓ：ｉｎｔｅｒｆｅｒｅｎｃｅｆｉｔ；ａｘｉａｌｐｒｅｌｏａｄ；ｃｏｎｔａｃｔｒｉｇｉｄｉｔｙ；ｂｅａｒｉｎｇｒｉｇｉｄｉｔｙ
愁ｊ辫舢蠢誊誊ｉ渗≤｜ｊｊ｝ｊ÷漤添寨豢瀵黉攀
在机械运转中，为了使套圈严格定位，高速滚动球轴承与轴以及轴承座孔需要采用过盈配合，使配合面不产生间隙，由此产生了设计手册中的过盈配合量数据和一些近似公式．文献／－１～３］为了进一步
艿一Ｆ［鑫卜邝，㈤
力学分析提供了基础．
其中，Ｒ。为轴向预紧力，Ｇ一＾＋＾一１，ｚ为钢
球数．１．２赫兹接触刚度及轴承刚度参数
誓ｌ基鑫毽娩｜ｊ｜｜『；｜；Ｉ｛ｊｉ｝『｜誊ｉｌ｜ｉ
变化
ｌｌ毫｜毒；？ｉ誊ｉ毒誊誊
１．１滚动轴承过盈配合安装后的位移及接触角的
由赫兹接触理论，两接触物体的接触载荷和弹
性趋近量之间的关系为Ｂ７，１８］：
（图３）．在图３中，固定外圈沟曲率中心为坐标原点，根据变形几何关系，确定第Ｊ个钢球中心位置的变化有以下关系式［１
８Ｉ：
／—］
ｚ毛＋《一［（＾一０．５）Ｄｂ＋如］２＝０，
（Ａｑ—ｚ。，）２＋（Ａｑ—ｚｑ）２一
（１７）

角接触向心轴承轴向载荷的计算11

轴承1
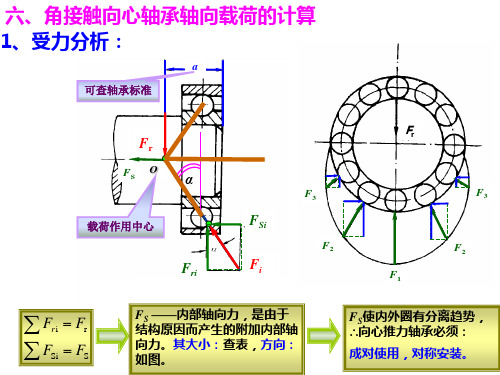
Fa1 3470.6 0.8677 0.35 Fr1 4000
由表查得X=0.40, 已知Y=1.7,中等冲击载荷，查表取fp＝1.6
则 P f p ( XFr1 YFa1 ) 1.6(0.4 1.7 3470.6) N 12000N 1 轴承2
Fa 2 1470.6 0.294 0.35 Fr 2 5000
C0 S0
X0
静径向载荷系数静轴向载荷系数
Y0
S0
静强度安全系数
例1、已知：FS1=1175 N，FS2=3290 N，FA=1020 N求： Fa1、 Fa2。解：
FrⅠ
FS2+FA = 3290+1020= 4310 ＞FS1， FS2
FrⅡ
FS1
→轴承Ⅰ被“压紧”
FA
，轴承Ⅱ被“放松”
正、反安装的简化画法
1 2
1
2
反装正装
六、滚动轴承的静强度计算目的：防止在载荷作用下产生过大的塑性变形。基本额定静载荷C0 ：滚动轴承受载后，在承载区内受力最大的滚动体与滚道接触处的接触应力达到一定值时的静载荷。当轴承同时承受径向力和轴向力时，需折算成当量静载荷P0，应满足
P0 X 0 Fr Y0 Fa
P f p ( XFr 2 YFa 2 ) 1.6(1 5000 0 1470.6) N 8000N 2
3、验算基本额定动载荷C 查表，取ft＝1.00 滚子轴承 10 / 3
12000 10 60 1500 5000 3 C' N 75014 145000 N 1.0 106
2
1
FS2 Fr2
FA

高速精密角接触球轴承刚度计算

3
+
0. 596
8
Rx Ry
F = 1. 527 7 + 0. 602 31n
Ry Rx
对 (1) 式求导数 , 可以得到赫兹接触刚度 K
为
K = 1. 5F - 1
9 2εR
12 πk E′
- 1/ 3
Q1/ 3
(2)
2 轴承刚度计算
已知轴承外加载荷 , 用牛顿 - 拉费逊法分别计算每个球的力平衡方程和位置相容方程组成非
叙词 :电磁轴承数字控制数字信号处理器 (DSP)
杜迎辉 ,邱明 , 蒋兴奇等. 高速精密角接触球轴承刚度计算. 轴承 ,2001 (11) :5～8
在分析轴承受力和变形的基础上 , 根据主轴轴承内部球与沟道接触载荷和接触角 , 提出了一种新的计算轴承径向、轴向和角刚度的方法 , 并分析计算了轴承旋转速度、预紧载荷和内外圈沟道曲率系数对轴承刚度的影响。附图 14 幅 ,表 1 个 ,参考文献 2 篇。
图 7 轴向刚度随预紧载荷的变化
图 4 旋转速度与轴向刚度的关系
轴承径向刚度、轴向刚度和角刚度随之增加。这是由于预载荷增加 , 不仅提高了球与内外圈沟道的接触角 ,而且提高了球与内外圈沟道的接触载荷 ,从而提高主轴轴承的径向刚度、轴向刚度和角刚度。
图 8 预紧载荷对角刚度的影响
滚动轴承中接触载荷和接触变形之间的关系是非线性的 ,因此 ,轴承刚度并非恒定。但过去许多人对刚度特性的计算过于简化[1] , 一般都是把轴承简化成等效弹簧 , 忽略了刚度随载荷的非线性变化、角刚度以及刚度随旋转速度变化等。即使考虑到上述因素 , 刚度计算误差也较大。本文在计算两种预紧方式即定位预紧和定压预紧、球与内外圈沟道接触载荷和接触角的基础上 , 计算了每个球与内外圈沟道接触点的接触刚度 , 根据轴承内部变形的几何关系 , 提出了一种新的轴承径向刚度、轴向刚度和角刚度的计算方法 ,并通过实例计算分析了轴承旋转速度、预紧载荷和内外圈沟道曲率系数对刚度的影响。所提出的机床主轴轴承刚度计算方法也适用于其他滚动轴承应用场合。

轴承预紧力对轴承性能及寿命的影响分析

轴承预紧力对轴承性能及寿命的影响分析作者：马更生丁开瑞张旭平来源：《山东工业技术》2016年第14期摘要：本文就转动机械中最常见的角接触轴承安装预紧力的作用、估算方法及对轴承性能的影响进行了深入阐述及探讨，对角接触轴承的安装起到了指导作用。

关键词：轴承；预紧力；估算；调整；性能；寿命DOI：10.16640/ki.37-1222/t.2016.14.1820 引言转动机械在现代工业中的应用非常广泛，作为转动机械的核心部件轴承的安装工艺直接关系到转动机械的安全运行。

本文就转动机械中最常见的角接触轴承安装预紧力的作用、估算方法及对轴承性能的影响进行了深入阐述及探讨，对角接触轴承的安装起到了指导作用。

1 概述滚动轴承根据不同的应用场合，装配时需要预留合适的工作游隙。

在大部分的情况下，工作游隙应为正值，但是如果需要提高轴系的旋转精度或刚性时，则经常采用负的工作游隙。

预紧就是在轴承装配时通过外部给予一定的预加负荷，消除轴承滚动体与内外环的间隙，使轴承出现弹性变形产生负的工作游隙。

预紧是减少轴因受力产生挠曲，促使轴承中的负荷分布更均匀，改善工作状态下受力状况的一种措施。

通过预紧还可对滚动体与内外环的磨损给予一定的补偿，降低设备在运行中产生的噪声，延长轴承的使用寿命。

2 需要进行预紧的场合一般来说，对于轴承定位精度要求高、旋转精度要求高、需要提高轴系刚性的高速精密运转的场合，以及高速轻载、温度变化较大、做往复运动的轴承配置或需要降噪减振的场合，均需要进行预紧，以便为轴承提供最小负荷。

例如精密机床的主轴轴承、减速机的轴承、汽车传动轴的小齿轮轴承、小型电机、低温设备、风机的轴承等，通常均需要在装配时进行预紧。

3 最小负荷的确定最小负荷的大小受到轴承的基本额定静负荷、最小轴向负荷系数Ka、转速n、轴承平均直径等的影响。

我们可以根据轴承手册提供的经验公式进行计算，例如单列角接触轴承的最小轴向负荷可通过公式进行计算。

如果轴承支撑的重量加外力达不到最小负荷，则必须通过调整轴承的预紧力施加额外的负荷。

主轴轴承预载荷的计算

根据轴向外载荷与预载荷的关系，合理选择并施加预载荷，就显得尤为重要。下文就轴承受力与变形关系进行分析，以指导合理加载预载荷，使轴承在空载和施加轴向外载荷情况下都能处于正常工作状态。
!" 刚性预载荷概述
图 # 所示的是 $ 套承载轴承和 # 套预载轴承刚性预
冷加工
! " " # 年第 $ % 期 # !" ! ! !" # $ % & ’ ! ( ) * + , -. / 0 1" 2 ( #
将表 ’ 中数据带入式（ ’ ），计算承载轴承和预载轴承变形量
"& *+"& ! !’) # $% &’ ( ’) * $ ( 3’* + " & ( 4+ ( " * ’ " & ( -./ * 0 " & # ,) ( 5
7"
8’ , &
7 -./
80 , &
计算时，设定 4 , 值， 4 9 是设计任务给的数据。分别计算出 !’ 和 !+ 值，两值之和即为承载轴承和预载轴承的总变形量，即存在如下关系 ! ! # !’ 4 !+ # !’) 4 !+) （0）
（’）式中! 3— — —串联轴承数量； — —轴向变形量（ 11）； !— 4 ,) — — —预载荷（ 2）； 5— — —球数； — —球径（ 11）； "— — —接触角（ 3 ）。 #— 串联轴承数量是指承载轴承数量或预载轴承数量。如图 ’ 中承载轴承数量为 + ，预载轴承数量为 ’ 。由于参与计算的轴承数量变化，由式（ ’ ）可知多个轴承串联的总变形要小于单个轴承的变形。计算时，根据轴承的组配，分别计算承载轴承组和预载轴承的变形量，总的变形量为承载轴承与预载轴承变形之和，即 ! ! # !’) 4 !+) 式中! !’) — — —预载荷状态下承载轴承变形量； — —预载荷状态下预载轴承变形量。 !+) — 例如：采用图 ’ 的组配，其中 + 套承载轴承是成对顺装轴承，一般可以从厂家直接购买，轴承型号相同，预载荷值用轴承间的隔圈高度差得到。轴承及按照工作需要选择的预载参数如表 ’ 所示，表中参数 4 ,) 是配制隔圈后预期得到的预载值。

角接触球轴承计算方法

角接触球轴承设计方法1 主题内容和适用范围本设计方法适用于外圈带琐口的特轻(1)、轻(2)窄、中(3)窄系列的36000、46000型及内、外圈均带琐口的轻(2)窄、中(3)窄系列的66000型角接触球轴承的产品设计。

轴承名称新代号旧代号分离型角接触球轴承 S71900S7000S720010069006loo6200角接触球轴承 71900c70007000AC7200C7200AC7200B73000C7300AC7300B103690036l0046100362004620066200363004630066300锁口在内圈上的角接触球轴承B7000CB7000ACB7200CB7200AC136100146100136200146200成对双联角接触球轴承71900C／DB71900C，DF71900C／DT7000C／DB7000C／DF(T)7000AC／DB(F，T)7200C／DB(F，T)7200AC／DB(F，n7200B／DB(F，T)7300C／DB(F，T)7300AC／DB(F，T)7300B／DB(F，T)1236900133690014369002361003(4)361002(3，4)461002(3，4)362002(3，4)462002(3，4)662002(3，4)363002(3，4)463002(3，4)663002 代号与含义KDW ：钢球直径系数F0 ：轴承径向额定静负荷系数 fc ：轴承径向额定动负荷系数 kd ．套圈挡边直径系数kt、δt ：装配锁口高度系数Kpi、kpe：内、外圈滚道直径系数εi、ε e：实体保持架内、外径引导间隙kc ：实体保持架内、外径系数3 设计要点整篇文章把dn≥0．6×10^6的称为高速，dn≥1．8×10^6的称为超高速。

结构形式优点缺点采用公司外圈单挡边、内圈双挡边．保持架外引导单挡边外圈有利于外圈沟道多余润滑剂流出，不仅减小润滑剂搅动摩擦．而且有利于降低接触SKF-7000FAG-B7000NSK-7000GMN-S6000外圈单挡边、内圈双挡边，保持架内引导与上面相比，由于采刚内圈烈挡边引导保持架，运动平稳。

角接触球轴承预紧与刚度

兰
＝三Ｚ
轴承
２０１５年６期
１—４
ＣＮ４１—１１４８／ＴＨＢｅａｉｎｒｇ２０１５，Ｎｏ．６
．．Ｉ产品设计与应用
角接触球轴承预紧与刚度
罗天宇，罗继伟
（１．河南科技大学机电工程学院，河南洛阳４７１００３；２．洛阳轴研科技股份有限公司，河南洛阳４７１０３９）
２．ＬｕｏｙａｎｇＢｅａｒｉｎｇＳｃｉｅｎｃｅ＆ＴｅｃｈｎｏｌｏｙｇＣｏ．，Ｌｔｄ．，Ｌｕｏｙａｎｇ４７１０３９，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：Ｔｈｅａｘｉａｌｉｇｒｉｄｉｔｙｃｌｃａｕｌａｔｉｏｎｏｆａｎｇｕｌａｒｃｏｎｔａｃｔｂａｌｌｂｅａｒｉｎｇｓｉｓｄｉｓｃｕｓｓｅｄ．Ｂａｓｅｄｏｎｐｒｅｌｏａｄａｎｄｉｇｒｉｄｉｔｙｏｆ
摘要：讨论了角接触球轴承轴向刚度的计算问题。在获得单列轴承预载荷与刚度基础上，利用轴承载荷、位移和刚度的相互关系确定了多联组配轴承的预载荷与刚度。分析了双联和多联组配轴承预载荷与刚度的相对
值，并与ＳＫＦ和ＮＳＫ公司进行了对比，结果表明，误差均在３％之内。关键词：角接触球轴承；多联组配；预载荷；刚度中图分类号：ＴＨ１３３．３３１；ＴＧ７６９文献标志码：Ａ文章编号：１０００— ３７６２（２０１５）０６— ０００１— ０４

角接触轴承当量动载荷计算

承尺寸、内部设计及作用于轴承上的力和力矩，而最大允许倾斜角应保证轴承内不会产生过
高的额外应力。
若内、外圈之间存在倾斜角将影响轴承寿命。同时，轴承运转精度下降，运转噪声增大。
径向当量动载荷
1）接触角为 15°的单列角接触球轴承单个轴承或串联配置（7000C、7000C/DT）
Pr=Fr
当 Fa/Fr≤e
单个轴承或串联配置（7000C、7000C/DT）
Por=0.5Fr+0.46Fa
Por= Fr
当 Por＜Fr 时
背对背、面对面配置（7000C/DB、7000 C/DF）
Por=Fr+0.92Fa
2) 接触角为 25°的单列角接触球轴承
单个轴承或串联配置（7000AC、7000AC/DT）
Por=0.5Fr+0.38Fa
Pr=0.44Fr+Yfa
当 Fa/Fr＞e
背对背、面对面配置（7000C/DB、7000 C/DF）
Pr=Fr+Y1Fa
当Fa/Fr≤e
Pr=0.72Fr+Y2Fa
当Fa/Fr＞e
计算系数e、Y、Y1、Y见附表 2. 2）接触角为 25°的单列角接触球轴承
单个轴承或串联配置（7000AC、7000AC/DT）
L10=(Cr/Pr)3 式中： L10
基本额定寿命
（106转）
Cr
径向基本额定动负荷
（N）
Pr
径向当量动负荷
（N）
安装尺寸
1. 轴和孔的最大单一圆角半径rasmax见附表 3
2. 挡肩高度最小值hmin见附表 3
3. 安装尺寸计算
轴或孔挡肩高度要比轴承倒角最大允许尺寸大，并与轴承端面平坦部分接触。轴

电机轴承预紧力计算公式

电机轴承预紧力计算公式在电机设计和制造过程中，轴承的预紧力是一个非常重要的参数。

预紧力的大小直接影响着轴承的使用寿命和性能。

因此，正确计算轴承的预紧力是非常重要的。

本文将介绍电机轴承预紧力的计算公式及其相关知识。

1. 轴承预紧力的作用。

轴承的预紧力是指在轴承安装时对轴承施加的一定压力，目的是消除轴承内部的游隙，保证轴承在工作时能够稳定地运转。

轴承的预紧力不仅可以提高轴承的刚度和精度，还可以减小轴承在工作时的振动和噪音，提高轴承的使用寿命。

2. 轴承预紧力的计算公式。

轴承的预紧力可以通过以下公式来计算：Fp = 0.3 × C × d。

其中，Fp表示轴承的预紧力，单位为N；C表示轴承的额定动载荷，单位为N；d表示轴承的直径，单位为mm。

3. 轴承额定动载荷的确定。

轴承的额定动载荷是指在标准试验条件下，轴承可以承受的极限载荷。

通常情况下，轴承制造商会在产品的技术参数中提供轴承的额定动载荷数值。

如果没有提供，也可以通过轴承的材料、尺寸和结构等参数来计算得出。

4. 轴承直径的确定。

轴承的直径是指轴承内圈或外圈的直径，通常情况下可以通过轴承的型号或者产品参数来确定。

在实际计算中，需要将轴承的直径转换为标准单位mm。

5. 轴承预紧力计算实例。

假设某电机轴承的额定动载荷为5000N，轴承直径为50mm，则可以通过上述公式计算得到轴承的预紧力为：Fp = 0.3 × 5000N × 50mm = 750N。

因此，该电机轴承的预紧力为750N。

6. 轴承预紧力的调整。

在实际使用中，轴承的预紧力需要根据具体情况进行调整。

通常情况下，可以通过调整轴承的安装方式、螺母的紧固力或者轴承座的设计来实现轴承预紧力的调整。

在调整过程中，需要注意不要使轴承的预紧力过大或者过小，以免影响轴承的使用寿命和性能。

7. 结语。

轴承的预紧力是影响轴承性能的重要参数，正确计算和调整轴承的预紧力对于提高电机的使用寿命和性能具有重要意义。

角接触球轴承的预紧技术

!产品设计与应用#角接触球轴承的预紧技术姜韶峰1,刘正士1,杨孟祥2(1.合肥工业大学,安徽　合肥　230009;2.洛阳轴承研究所,河南　洛阳　471039)摘要:介绍角接触球轴承预紧的类型及工作原理,给出了预紧选择原则和确定预紧力的计算方法。

对中低速组配轴承而言,其最小预紧力可根据轴承组配方式以及承受的额定外载荷确定。

关键词:角接触球轴承;主轴轴承;配置;预紧中图分类号:TH133.33 文献标识码:B 文章编号:1000-3762(2003)03-0001-04Preload Technique of Angular Contact B all BearingsJ I ANG Shao -feng 1,LI U Zheng -shi 1,Y ANG Meng -xiang 2(1.Hefei University of T echnology,Hefei 230009,China;2.Luoyang Bearing Research Institute ,Luoyang 471039,China )Abstract :The types and w orking principle of preload of the angular contact ball bearings are introduced ,the selection rules of the preload and calculation method of determining preload force are given.F or the medium and lower speed group match bearings ,the minimum preload force is determined by bearing group m ode and rating load.K ey w ords :angular contact ball bearing ;spindle bearing ;coupling ;preload 合适的预紧可以增加轴承的刚度、提高旋转精度、降低振动噪声、延长使用寿命。

角接触球轴承预紧具体措施

角接触球轴承预紧具体措施了解角接触球轴承预紧的具体方法。

下面分别给大家详细说明一下：角接触球轴承径向预紧：径向顶紧法多使用在承受径向负荷的圆锥孔轴承中，典型的例子是双列精密短圆柱滚子轴承利用螺母调整这种轴承相对于锥形轴颈的轴向位置，使内圈有合适的膨胀量而得到径向负游隙，这种方法多用于机床主轴和喷气式发动机中。

角接触球轴承轴向预紧：轴向预紧法大体上可分为定位预紧和定压预紧两种。

在定位预紧中，可通过调整衬套或垫片的尺寸，获得合适预紧量；也可通过测量或控制起动摩擦力矩来调得合适的预紧；还可直接使用预先调好预紧量的成对双联轴承来实现预紧的目的，此时一般不需用户再行调整，总之，凡是经过轴向预紧的轴承，使用时其相对位置肯定不会发生变化。

定压预紧是用螺旋弹簧、碟形弹簧等使轴承得到合适预紧的方法。

预紧弹簧的刚性—般要比轴承的刚性小得多，所以定压预紧的轴承相对位置在使用中会有变化，但预紧量却大致不变。

角接触球轴承定位预紧与定压预紧的比较在于预紧量相等时，定位预紧对轴承刚性增加的效果较大，而且定位预紧时刚性变化对轴承负荷的影响也小得多。

定位预紧在使用中，由于轴和轴承座的温度差引起的轴向长度差，内外圈的温度差引起的径向膨胀量以及由负荷引起的位移等的影响，会使预紧量发生变化；而定压预紧在使用中，预紧的变化可以不予考虑。

由于角接触球轴承和圆锥滚子轴承的径向游隙和轴向游隙之间有一定的关系，因此在涉及游隙的问题时，只需指定其中一个数值，在大部分的情况下是以轴向游隙为主要参数。

调整轴承的游隙或预紧时，可以在轴承达到零游隙后，通过拧松或锁紧轴上的螺母或轴承座中某些带螺纹的部件，如挡圈。

另一个方法是在内圈或外圈与挡肩之间的位置加上一些厚度经过计算的垫片或垫圈。

具体采用哪一种方法来进行游隙的测量或调整，通常是根据需要调整的数量而考虑和决定。

使用千分表是其中用来测量轴向游隙的方法，例如用于测量轮毂轴承的配置。

在测量或调整圆锥滚子轴承的游隙时，应先反复转动轴或轴承座数周，以确保滚子的大端面与内圈的挡边有良好的接触。

Koyo角接触轴承的预负荷计算

东莞安昂五金机电有限公司（安昂商城）
Koyo角接触轴承的预负荷计算
Koyo角接触轴承预负荷计算选择预负荷，最小预负荷的计算方法如下：
奥敏= 1.58R ± 0.5A（N）如作用于轴承径向负荷（N）对轴向负荷的轴承代理（N）通过通过球与直线之间的夹角中心平面（即公称接触角）直线滚珠和滚道接触点：
7000C A = 15 °7000AC A = 25 °7000B A = 40 °每个轴承的Koyo角接触轴承对这里计算。

其中“+”为工作轴向负荷，减少了原预定利润公司的价值符号，一个轴承；数字工作的轴向预负荷，使市民的原值增加盈余轴承。

两对Koyo角接触轴承预负荷量最小的奥敏两个轴承应取得两个最大选择值（装配经验的基础上，并普遍对预负荷50N）。

预负荷调整空运转试验。

角经大会检验合格后Koyo角接触轴承，应该为空运行速度测试，不小于2小时，温升不应超过15℃。

安昂传动传动世界。

轴承的预载荷计算

轴承的预载荷根据应用场合，有必要在轴承配置中加入正的或负的工作游隙。

在大多数应用场合，工作游隙应是正的，即在运行时，轴承应有剩余游隙，尽管很小，见“轴承的内部游隙”一节。

但是在很多情况下，例如机床主轴轴承、汽车车轴传动器上的小齿轮轴承、小型电动机轴承配置或作摇摆运动的轴承配置，需要负的工作游隙，即要加预载荷，来提高轴承配置的刚性或提高运行精度。

在空载或极轻负荷条件下与高速度运行的轴承，也建议应用预载荷，例如使用弹簧加压。

在这些情况下，预载荷起到为轴承提供最低负荷的作用，防止因滚动体打滑而造成轴承损坏，见“要求的最低负荷 ”。

轴承的预载荷--预载荷的种类根据轴承类型不同，预载荷可以是径向或轴向的。

例如，圆柱滚子轴承由于其设计特点只能承受径向预载荷，而推力球轴承与圆柱滚子推力轴承则只能承受轴向预载荷。

单列角接触球轴承与圆锥滚子轴承 (图35)一般要跟另一个同样类型的轴承一起背对背（a）或面对面（b）配置安装，这类轴承要加轴向预载荷。

深沟球轴承通常也要用轴向预载荷，要这样做，轴承的径向内部游隙应比正常值的要大（例如C3），这样，像角接触球轴承的情况一样，可以产生大于零的接触角。

对于圆锥滚子轴承与角接触球轴承来说，在轴承背对背布置时，其压力中心之间的距离L大于轴承中心之间的距离I（图36），在面对面布置时（图37），L小于I。

这就是说背对背布置的轴承即使轴承中心距离较短，也能够承受较大的倾覆力矩。

这类轴承中由力矩负荷产生的径向力以及所造成的轴承变形比面对面布置的轴承要小些。

如果在运行中轴的温升比轴承座高，根据安装过程中的环境温度而调整（设定）的预载荷将会增加，面对面布置的增加量大于背对背布置的增加量。

在两种情况下，径向热膨胀都起到减少游隙或增加预载荷的作用。

当轴承面对面布置时，径向热膨胀会增加这种趋势，而背对背布置时，则会减少这种趋势。

仅就背对背布置来说，轴承之间有一定距离，当轴承与相关部件的热膨胀系数相同时，径向与轴向热膨胀会相互抵消，因此预载荷不会改变。

双列角接触球轴承预紧力分析_蒋蔚

双列角接触球轴承预紧力分析洛阳轴承研究所(河南洛阳　471039)　蒋　蔚　孟庆伟　徐　浩【ABSTRACT 】In order to make fully ensure for utilizing perfor mance of double row angular contact ball bearings ,the pr eload must be applied on them .Because many host machines have the demands of high sensitivity and low friction moment for the kind of bearings ,the preload applied on it must be accu -rate .B y calculating and actual measuring ,these demands may be realized . 双列角接触球轴承可承受双向轴向载荷,具有较高的旋转精度和较大的刚性。

同时,由于其结构紧凑,安装简便,工艺性好而在航天、航空领域的某些特殊场合得到应用。

为使双列角接触球轴承的使用性能得到充分保证,对其施加一定的预紧力是必不可少的。

这与配对使用的角接触球轴承有类似之处,但由于双列角接触球轴承的内圈是双沟的,在设计和制造上有自己的独特性。

同时,主机对此类轴承多有高灵敏度和低摩擦力矩的要求,这就要求对其所施加的预紧力必须准确。

如果实际预紧力小于设计预紧力,则轴承的刚性不能满足要求;如果实际预紧力大于设计预紧力,则又破坏了轴承的高灵敏度性能,故此,对轴承施加的实际预紧力的准确性对于轴承的使用是至关重要的。

现以46 18CTN HVP5轴承(图1)为例进行分析。

图11　凸出量的测量与修研量的计算为使轴承达到一定的预紧力,首先需对轴承的凸出量进行测量。

成对使用的角接触球轴承对每套轴承仅测量一次凸出量,而双列角接触球轴承由于结构原因需进行两次凸出量测量。

角接触轴承的轴向载荷的计算

分目录
上一页
下一页
退出
滚动轴承的计算举例
2、求基本额定动载荷
C P
60 n 10 6
[Lh
]

3679
3
60 3000 10 6
4000
32974 N
3、选择轴承型号
由轴承手册，按内径d=40mm,选6308轴承Cr =40800N>C， C0=24000N,Fa/ C0=0.0375,仍满足
分目录
上一页
下一页
退出
2
Fd2
Fr
M
Fae
Fr2
派生轴向力Fd1和Fd2的大小可根据表13-7得。
1
Fd1 Fr1
分目录
上一页
下一页
退出
角接触轴承的轴向载荷计算
压紧、放松的确定
2
Fd2
Fr
1
M
Fae
Fd1
Fr2
Fr1
以轴和与其相配合的轴承内圈为分离体，如达到轴向平衡时，应
满足：Fae Fd 2 Fd1
退出
滚动轴承的静载荷计算
摆动、转速极低及短期受冲击的轴承会产生塑性变形。针对失效形式应进行静载荷计算。
基本额定静载荷：C0（Cor，Coa）使受载最大的滚动体与滚道接
触中心处引起的接触应力达到一定值（如向心球轴承为4200MPa）的载荷。
当量静载荷：P0
P0 X 0 Fr Y0 Fa
式中 X0、Y0分别为当量静载荷的径向、轴向载荷系数，其值可查轴承手册。
当 Fae Fd 2 Fd1 ，有两种情况：
当 Fae Fd 2 Fd1 时，则轴有向右窜动的趋势，相当于轴承 1

角接触球轴承-内部游隙-预载荷

角接触轴承-部游隙-预载荷单列角接触球轴承的部游隙只有在安装后才能获得，而且取决于相对另一个轴承的调节量。

该轴承在相反方向上提供轴向定位。

SKF任意配对轴承以三种不同游隙和预载荷等级生产。

带游隙的轴承组的等级为：–CA轴向游隙小于普通组；–CB普通级轴向游隙〔普通级〕；–CC轴向游隙大于普通组。

带CB游隙级的轴承为标准轴承，而一些较大的轴承带G级游隙。

其它可供选用的轴承游隙等级见方阵图1。

带游隙的SKF任意配对轴承可结合在包括任何数量轴承的轴承组中。

带预载荷的轴承组的等级为：–GA轻型预载荷〔标准〕；–GB中型预载荷；–GC重型预载荷。

带GA级预载荷的轴承为标准轴承〔方阵图1〕。

同带游隙的SKF任意配对轴承相比，带预载荷的轴承只能以两个轴承成组配对，否如此预载荷会增加。

游隙等级的数值见表1和表2。

预载荷游隙等级的数值见表3。

这些数值适用于背对背或面对面配对的未安装轴承组，涉与到游隙时，测量载荷为零配对轴承的额定转速，对于配对布置的轴承，产品表中提供的标准转速大约低于单列轴承的标准转速的20%。

配对轴承的载荷承受能力产品表中给出的轴承根本额定载荷和疲劳载荷极限值也适用于配对安装的轴承。

同单列轴承的关系如下〔配对布置的轴承直接靠在一起安装时有效〕：：所有轴承配置中的标准轴承和背对背或面对面配对的SKF Explorer轴承的根本额定动载荷C = 1,62 × C单列轴承串联配置的SKF Explorer轴承的根本额定动载荷C = 2 × C 单列轴承疲劳载荷极限P u = 2 × P u单列轴承轴向力确实定当施加径向载荷给单列角接触球轴承时，载荷从一条滚道传送到另一条时与轴承轴线构成一个角度，导致轴承产生部轴向力. 计算由两个单列轴承和/或串联布置的配对轴承组的当量载荷时，必须考虑到这一点。

各种轴承配置和载荷情况所需公式见表4。

只有在轴承之间的游隙调整到几乎等于零但也不加任何预负载的情况下，这些方程式才适用。

高速磨床主轴轴承预载荷的施加与测量计算

1 磨床主轴轴承装配形式及受力状况
磨床主轴轴承可以根据机床的不同和加工零件的不同而采取相适应的装配形式[1] 。常见的有如图 1
收稿日期 :2004 - 10 - 26 ;修回日期 :2004 - 12 - 06 基金项目 :浙江省教育厅基金资助项目 (20020189) 作者简介 :严峻 (1957 - ) ,男 ,浙江嘉兴人 , 副教授 , 理工学院副院长。研究方向为机械系统故障诊断与可靠性。
- 184.
(编辑 :朱学骏)
图 4 轴承 2 、3 的装配情况
这时内外圈隔垫厚度差为 ΔL =δ下2 +δ上3 (6) 轴承 4 、5 也是同向安装 , 可用轴承 1 、2 的方法计算 δ下4和测量 δ上5 , 内外圈隔垫厚度差为 ΔL =δ下4 - δ上5 。为准确起见 , 计算误差不得大
严峻 :高速磨床主轴轴承预载荷的施加与测量计算
轴承预紧方法是在组合的两轴承内外圈之间置以不同厚度的隔垫 , 借助内外隔垫的厚度差值得到不同的预载荷。因此 , 关键在于准确地确定内外圈隔垫的厚度差值 ΔL ,两差值又取决于两轴承内外圈的相对轴向位移量。下面以图 1 结构为例 ,介绍轴承预载荷的测量方法和工具。测前先把每个待测轴承做出标记 , 并精确地测量出每个轴承内外圈的宽度 H内、H外 , 做好记录。然后再按图 2 所示工具 , 分别测量出每个轴承内外圈端面的 δ差值。
所示的简支梁形式。前支承采用三联轴承作为固定支承 , 调整内
外隔垫的厚度可保证轴承的预载荷。后支承采用两套串联轴承作为浮动支承 , 后支承轴承的预载荷由弹簧确定。前轴承 1 、2 用来承受来自前端的轴向载荷 , 调整隔垫 15 、14 、13 、12 的厚度即可调整前轴承的预载荷。后轴承 4 、5 同向安装 , 外圈