如何理解电压增益相位频率特性曲线
频率特性
这些统称放大电路的频率响应。 这些统称放大电路的频率响应。 幅频特性偏离中频值的现象称为幅度频率失真; 相频特性偏离中频值的现象称为相位频率失真。 产生频率失真的原因是: 产生频率失真的原因是: 1.放大电路中存在电抗性元件 放大电路中存在电抗性元件, 1.放大电路中存在电抗性元件,例如 耦合电容、旁路电容、分布电容、 耦合电容、旁路电容、分布电容、变压 分布电感等; 器、分布电感等; 2.三极管的 是频率的函数。 2.三极管的β(ω)是频率的函数。 在研究频率特性时, 在研究频率特性时,三极管的低频小信号 模型不再适用,而要采用高频小信号模型。 模型不再适用,而要采用高频小信号模型。
1 1 式中 ω L = = 。 RC
RC 高通电路
τ
下限截止频率、 下限截止频率、模和相角分别为 f / fL 1 f0 = fL = Av = ϕ = 90o − arctg( f f ) 2πRC L 1 + ( f )2 fL
HPF
HPF
RC高通电路的频率响应 高通电路的频率响应
RC电路的电压增益: 电路的电压增益: 电路的电压增益 V ( s) R2 AVH ( s ) = o = Vi ( s ) R2 + 1 / sC 2
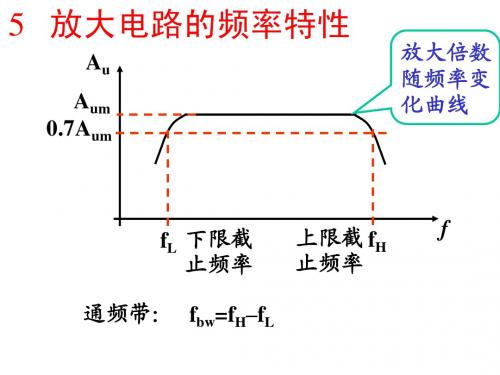
5 放大电路的频率特性
Au Aum 0.7Aum 放大倍数 随频率变 化曲线
fL 下限截 止频率 通频带: 通频带: fbw=fH–fL
上限截 fH 止频率
f
5.1 放大电路的频率特性概述
幅度频率特性
相位频率特性
幅频特性是描绘输入信号幅度 固定, 固定,输出信号的幅度随频率变化 而变化的规律。 而变化的规律。即 & &i &∣= ∣Vo /V∣= f (ω ) ∣A
电路基础原理三端口网络的特性与参数分析

电路基础原理三端口网络的特性与参数分析电路学是电子工程学科中的核心内容之一,而电路中的三端口网络则是电路学中的重要概念。
三端口网络是指具有三个输入或输出端口的电路,它在现实世界中有着广泛的应用。
本文将针对三端口网络的特性与参数进行分析,并探讨其在实际电路中的具体应用。
一、三端口网络的特性首先我们来了解三端口网络的基本特性。
三端口网络有三条输入输出路径,其中一条路径为输入,两条路径为输出。
三端口网络可以是简单的线性元件或复杂的小信号放大电路,它能够实现信号的传输和转换。
具体的特性表现为以下几个方面:1. 传输功能:三端口网络能够将输入信号进行传输和放大,保持其在输出路径上的一致性和稳定性。
传输功能是三端口网络最基本的特点之一。
2. 频率响应:三端口网络的频率响应是指其在不同频率下的传输效果。
不同频率下,三端口网络对信号的放大程度以及相位差会有所不同。
频率响应是评估三端口网络性能的重要指标之一。
3. 输入输出特性:三端口网络在输入和输出端口上具有一些特定的电压和电流特性。
输入输出特性可以描述三端口网络在不同工作状态下的响应情况,比如输入输出电阻、电压增益等。
二、三端口网络的参数分析三端口网络的参数分析是对其特性进行定量描述的过程。
通过对三端口网络进行参数分析,可以准确地了解其电气特性,并进行电路设计和优化。
常见的参数分析方法包括:1. 传输参数分析:传输参数是衡量三端口网络传输功能的重要指标。
传输参数包括乙、乙'参数,分别表示输出端口电流与输入端口电压之间的关系。
传输参数可以通过测量三端口网络的输入输出电压和电流,利用公式计算出来。
2. 常规参数分析:常规参数是对三端口网络输入输出特性的定量描述。
常规参数包括输入输出电阻、电压增益、相位差等指标。
这些参数可以通过实验测量或者电路仿真软件进行计算。
3. 频率响应分析:频率响应分析是对三端口网络在不同频率下的传输特性进行测量和分析。
通过将不同频率的信号输入三端口网络,测量输出信号的振幅和相位差,可以绘制出频率响应曲线。
电压放大倍数或电压增益

高 频 电 子 线 路
按带宽分:
1、窄频带放大器:
窄带放大器用LC谐振回路或集中选频滤波器做负 载,具有放大、选频的功能。其中心频率在(几百-
几百M)Hz范围内,频带宽度约(几~几十M)Hz。
2、宽带放大器: 用纯阻或变压器做负载,带宽较宽,越(几M~几 百M)Hz。
主讲 元辉
高 频 电 子 线 路
主讲 元辉
3.1.1
高 频 电 子 线 路
5.噪声系数
表征信号经放大后,信噪比变坏的程度。 噪声系数的定义是放大器的输入信噪比(输入端的信 号功率与噪声功率之比)与输出信噪比之比,即
psi pni NF pso pno
N F 通常是大于1的, N F 越接近于1,放大器的输出
噪声越小。 放大器中产生噪声的原因有放大器本身产生的噪声。 在多级级联的放大器中,前一、二级放大器的噪声对整 个放大器的噪声起决定作用。为了减少放大器的内部噪 声,在设计与制作时应当采用低噪声管,正确的选择工 作点电流,选用合适的电路等。
非谐振放大器:以传输线变压器作负载。
主讲 元辉
3.1
高 频 电 子 线 路
二、高频小信号放大器
按元器件分: 1、以分离元件为主的高频小信号调谐放大器(用 LC谐振回路作负载) 又可分为: 谐振放大器(频率可调,主要做高频放大级,接 收天线后第一级放大器)
中频(频带)放大器(频率固定的中放电路);
2、以集成电路为主的集中选频放大器(用集中选 择性滤波器做负载)。
高 频 电 子 线 路
第三章 高频小信号放大器
本章重点:高频小信号谐振放大器的 工作原理及性能指标计算。
难
点:谐振放大器的性能分析。
主讲 元辉
课件:第三章-1-频率特性基本概念及波特图

2. 一阶零点因子
Av2( j)
Av2 ( ) 20 lg 1 ( / z )2
2
(
)
arct
an
z
结的论贡:献| A是网v( j负络)的函| (d,数B)最的大每20为一lg 个-Av(一900) 度阶 2,极0lg在点1ω因=子 ω(zp负2处半为20轴-lg)415对度相,p位2
ω贡=献ω是p-就(2是0) d幅B0频/十 波a倍rc特频ta图n或的-z 转6da折rBc频/t倍an率频,p程在。ω>ωp 处对幅度的
(1 j )
Av (
j )
Av (0) (1
j
z
)
p
其中Av (0)
Avm
z p
(1 j )
Av (
j )
Av (0)
(1
j
z
)
表示成分贝形式:
p
其中Av (0)
Avm
z p
| Av ( j) | (dB) 20lg Av(0) 20lg
2
1
z
20lg
2
1
p
() 0 arctan arctan
零点:z1=0 z2=-σ2
极点:p1=-σ1
零极图为:
p2 ( n ) jn 1 2
p3 ( n ) jn 1 2
3.2.4 波特图绘制方法
波特图:用折线逼近幅度频率特性和相位频率特性, 频率轴采用对数刻度,幅值(以dB表示)和相位采用 线性刻度。
H( j) | H( j) | e j()
零点因子的波特图: H(1 j) j 1() 90 | H(1 j) | 或 | H(1 j) | 20lg(dB)
单级放大器及频率特性(2)

(Vo V1 )C gd1s gm1V1 Vo (Cs G) 0
由式(6.1)可得到:
V1
Vo
Cgd1s G Cs gm1 Cgd1s
把式(6.3)代入式(6.1),可得:
(6.2) (6.3)
Vi RS
Vo
[ RS1
(C gs1
Cgd1 )s][G gm1 C gd1s
图中Ci=Cgs1+Cgd1(1+gm1/G)
共源级的频率响应
根据KCL定理,对于上图所示的电路有:
Vo
( gm1 sC gd1 )V1 s(C Cgd1 ) G
V1
1/
1 / sCi sCi RS
Vi
由以上两式可以很简单地推导出其传输函数
为:
Av (s)
(sCi
(sC gd1 gm1 ) / RS
带宽估算(1)
为了求解其传输出函数,先忽略ro与Cdb(通过后 面的分析可以发现该假设是成立的)
将等效电路在下图中直线切开后求出右半图所示电 路的等效输入特性。
带宽估算(2)
密勒等效
假设Av(s)的零极点频率远高于要设计 的带宽,因此可以用直流值代替Av(s)
这就是所谓的“密勒等效” 在后续工作中需验证一下这个假设是否真正有效
求解方法
总述
对频率特性的研究一般是基于网络系统的传 输函数的零极点的研究。
由信号与系统的理论可知传输函数的零点决 定了系统的稳定程度,而传输函数的极点所 对应的就是系统的转折频率。
因此频率特性的研究主要是通过等效电路推 导出电路的传输函数,进而求出零、极点以 确定电路的频率特性。
以CS电路为例:电路及等效模型
总之,CL减小Vgs到Vo的增益,必然减小了Vi到Vo的增益。
电阻电路的频域分析方法

电阻电路的频域分析方法电阻电路是电路中最简单的一种元件组合形式,是电子电路中最基础、最重要的元件之一。
在电路分析中,我们常常需要对电阻电路进行频域分析,以研究电路在不同频率下的性能和响应。
本文将介绍电阻电路的频域分析方法,让我们一起来了解吧。
一、频域分析的基本概念频域分析是指将信号从时域转换到频域的过程,通过分析信号在不同频率下的幅度和相位差,来了解信号的频率特性和频率响应。
在电路分析中,频域分析可以帮助我们理解电路的滤波特性、频率响应以及稳态和暂态响应等。
二、电阻电路的频域分析方法电阻电路是由电阻元件构成的电路,其频域分析可以采用复数法或频域响应法。
1. 复数法复数法是一种基于复数理论的频域分析方法,它可以方便地描述电路中电流和电压的相位关系。
在复数法中,我们将电阻元件的电阻值表示为实数R,电压表示为复数V,电流表示为复数I。
复数法的基本原理是欧姆定律和基尔霍夫电压定律在复数域的推广,即U = IR。
通过复数法可以方便地计算电路中的电流、电压和功率等参数。
2. 频域响应法频域响应法是一种基于频率响应函数的分析方法,它通过计算电路在不同频率下的幅频特性和相频特性来描述电路的频率特性。
在频域响应法中,我们通常使用Bode图来表示电路的频率响应。
Bode图由振幅-频率特性曲线和相位-频率特性曲线组成,可以直观地显示电路在不同频率下的增益和相位信息。
通过分析Bode图,我们可以了解电路的截止频率、增益衰减、相位延迟等信息。
三、案例分析以一个简单的RC电路为例,我们来演示电阻电路的频域分析方法。
在一个串联的RC电路中,电路包含一个电阻R和一个电容C,输入信号为正弦信号Vin,我们的目标是分析输出信号Vout在不同频率下的响应。
首先使用复数法进行分析,设输入信号为Vin = A*sin(ωt),其中A为幅度,ω为角频率。
根据欧姆定律可得Vout = Vin * Z,其中Z为电路的阻抗,对于串联的RC电路,电路的阻抗为Z = R + 1/(jωC)。
手把手教你看懂波特图
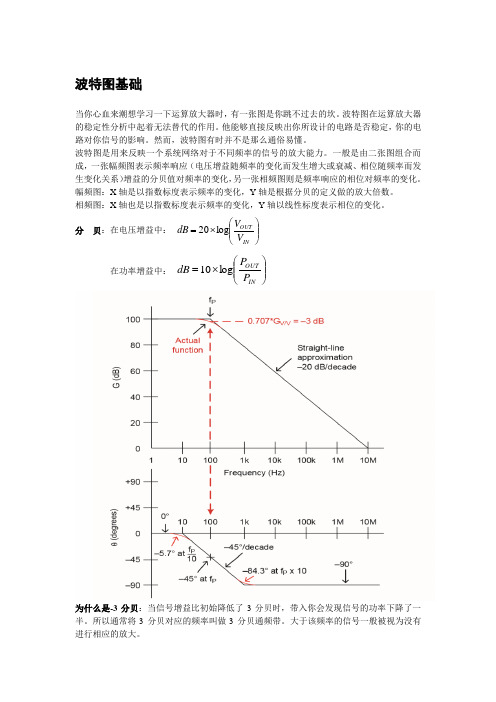
波特图基础当你心血来潮想学习一下运算放大器时,有一张图是你跳不过去的坎。
波特图在运算放大器的稳定性分析中起着无法替代的作用。
他能够直接反映出你所设计的电路是否稳定,你的电路对你信号的影响。
然而,波特图有时并不是那么通俗易懂。
波特图是用来反映一个系统网络对于不同频率的信号的放大能力。
一般是由二张图组合而成,一张幅频图表示频率响应(电压增益随频率的变化而发生增大或衰减、相位随频率而发生变化关系)增益的分贝值对频率的变化,另一张相频图则是频率响应的相位对频率的变化。
幅频图:X 轴是以指数标度表示频率的变化,Y 轴是根据分贝的定义做的放大倍数。
相频图:X 轴也是以指数标度表示频率的变化,Y 轴以线性标度表示相位的变化。
分 贝:在电压增益中: ⎪⎪⎭⎫ ⎝⎛⨯=IN OUT V V dB log 20 在功率增益中: ⎪⎪⎭⎫ ⎝⎛⨯=IN OUT P P dB log 10为什么是-3分贝:当信号增益比初始降低了3分贝时,带入你会发现信号的功率下降了一半。
所以通常将-3分贝对应的频率叫做-3分贝通频带。
大于该频率的信号一般被视为没有进行相应的放大。
下降速率:有十倍频程(decade )跟二倍频程(octave )两种基本单位,-20dB/decade 与-6dB/octave 是一样的,数学推导就不在这里叙述了。
零点与极点:单个极点响应在波特图上具有按 -20dB/decade 或-6db/octave 斜率下降的特点。
在极点位置,增益为直流增益减去3dB 。
在相位曲线上,极点在频率上具有-45°的相移。
相位在的两边以45°/decade 的斜率变化为0°和 -90°。
单极点可用简单RC 低通网络来表示。
单个零点响应在波特图上具有按+20dB/decade 或+6db/octave 斜率上升(对应于下降)的特点。
在零点位置,增益为直流增益加 3dB 。
在相位曲线上,零点在其频率上具有+45°的相移。
电路基础原理解惑电路的幅频特性和相频特性

电路基础原理解惑电路的幅频特性和相频特性电路的幅频特性和相频特性是电路工程中的重要概念,它们对描述电路的性能和行为起着关键作用。
在学习电路基础原理的过程中,理解并熟练运用幅频特性和相频特性是非常重要的。
本文将解析这两个概念的意义和具体应用。
幅频特性,又称为频率响应,描述的是电路在不同频率下对电压或电流的响应情况。
在交流电路中,信号的频率会对电路的行为产生影响。
幅频特性通常通过频率响应曲线来表达。
频率响应曲线可以显示电路在不同频率下的增益或损耗情况。
幅频特性可以帮助我们了解电路对不同频率信号的放大或衰减程度。
例如,放大器是一种常见的电路元件,它起到放大信号的作用。
通过分析放大器的幅频特性,我们可以了解到放大器在不同频率下的放大倍数,从而更好地设计和选择合适的放大器。
此外,幅频特性还可以帮助我们分析和解决电路中的各种问题。
例如,当我们遇到信号衰减或失真问题时,可以通过观察幅频特性来寻找问题所在。
若发现在问题频率附近出现衰减或失真,我们便可以针对性地进行电路修正或优化。
与幅频特性相对的是相频特性,又称为相位响应。
相频特性描述了电路对不同频率下信号的相位变化情况。
在交流电路中,信号的相位同样与频率有关。
相频特性通常通过相频响应曲线来表示。
相频特性可以帮助我们了解电路中信号的相位变化情况。
在某些应用中,信号的相位变化可能对系统的性能和稳定性产生重要影响。
比如,在音频信号处理中,我们希望保持信号的相位一致性,以避免声音的失真。
通过观察和分析相频特性,我们能够更好地了解电路对信号的相位变化情况,从而采取相应措施进行校正或补偿。
综上所述,电路的幅频特性和相频特性是电路工程中相当重要的概念。
通过研究幅频特性,我们能够更好地了解电路对不同频率信号的放大或衰减情况,从而为电路设计和选择提供依据。
而相频特性能够帮助我们分析信号的相位变化情况,从而优化电路设计,确保信号的准确传输。
在实际应用中,我们通常使用示波器、频谱仪等测试仪器来获取电路的幅频特性和相频特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何理解电压增益相位频率特性曲线
Q. "电压增益•相位-频率特性实例"曲线图中低频段的增益均为40dB,和电压增益Av值不符,这是什么原因?
A. 运算放大器的电压增益•相位vs频率特性曲线图一般反映闭环增益为40dB的非反相放大电路的特性。
开环增益的特性只反映在高频段。
为此,如Fig.1.的实线部分所示,低频段的电压增益均为40dB。
因为,这是一种便于操作的评估手段。
高频段特性与开环电路特性原理相同,因此一般根据Fig.1.,即可判断反馈环路的变化。
如另需低频段的开环电路特性曲线表,则可按照Fig.1.推算。
增益频率特性:
增益=将Av所对应的平行于频率数轴的直线AB与曲线图上原有的斜率为-20dB/dec的BC连接。
曲线ABC即为开环电路增益频率特性的推算值。
(频率数轴为对数,增益轴为直线,表示dB值)
相位频率特性曲线:
连接相位0°对应的直线DE和90°对应的直线GF。
当增益-频率特性曲线图上B点的频率为f1时,分别设置E,F两点,使F点的频率f2=10×f1,E点的频率为f3=f1/10,这时曲线DEFG 为开环电路的相位频率特性的近似值。
(频率数轴为对数,相位轴为直线)
Fig5_1.运算放大器低频段特性近似值计算方法。
