经典奥数专题:数与形(试题)数学六年级上册人教版
六年级数学上册《数与形》练习题及答案-人教版

六年级数学上册《数与形》练习题及答案-人教版一、发现规律,填补空白。
(共44分)1.把一个大正方形用“十”字形连续均分后剪开,所得的小正方形越来越多。
第15次均分剪开后所得的小正方形有多少个?(10分)1+3=4 1+3×2=7 1+3×3=10规律:解答:2.把一张纸连续对折,写出每次折成的一小块是整张纸的几分之几。
(8分)第1次 第2次 第3次)()( )()( )()( 如果像这样连续对折8次,折成的一小块是整张纸的)()(。
3.数一数,图中大小正方体的个数。
(单位:厘米)(10分)棱长:( ) ( ) 正方体个数:13+23=( ) 13+23+33=( )如果正方体的棱长为4,那么大小正方体的个数是( )个。
4.每个小正方形的顶点恰好在另一个正方形的中心,且边相互平行,求每个图形的周长。
(小正方形的边长为2厘米)(8分)( )厘米 ( )厘米 ( )厘米若有8个小正方形像上面这样叠放,所组成的图形的周长是( )厘米。
5.随着三角形个数的增加,涂色三角形的个数也在增加。
照这样接着画下去,第20个图形有( )个涂色的三角形。
(8分)1 3 6 10 二、想一想,选一选。
(共16分,每题8分。
)1.下图能够大概表示汽车由静止发动,加速到一定速度匀速行驶一段距离后减速上坡,再加速下坡,然后逐渐减速到匀速行驶的一个过程的是( )。
A.B. C. 2.汽车出发时,油箱内有30升油。
如果每小时耗油3升,则油箱内余油量(升)与行驶时间t (时)的关系图像,应是( )。
A. B. C.三、解决问题。
(共40分,每题10分。
)1.A 、B 、C 、D 、E 、F 六位同学见面,每两人之间都要握一次手。
到现在为止,A 握了5次,B 握了4次,最少的也握了2次。
这时6个人至少握了多少次?2.有一个正六边形点阵,如图,它的中心是一个点,算作第一层;第二层每边2个点,第三层每边3个点……这个六边形点阵第28层上面共有多少个点?第100层速度 时间 速度 时间 速度时间呢?3.一条马路长180米,小明和他的小狗分别以均匀的速度同时从马路的起点出发。
六年级数学(上)奥数思维拓展《数与形》测试题(含答案)

六年级数学(上)奥数思维拓展《数与形》测试题(含答案)一.选择题(共8小题)1.下面是用棋子摆成的“T”字形,第1个图中有5枚棋子,第2个图中有8枚棋子,第3个图中有11枚棋子,按此规律摆放,第()个图中有65枚棋子。
A.22B.13C.20D.212.下列图形都是由大小相同的黑点按一定规律组成的,第1个图中有1个黑点,第2个图中有5个黑点,第3个图中有9个黑点,第4个图中有13个黑点,按此规律排列,第16个图中有()个黑点。
A.51B.61C.55D.653.根据图形规律,第20个图案有()个基本图形。
A.20B.40C.41D.604.把长2cm,宽1cm的长方形一层、二层、三层…有规律地摆下去(如图),摆到第十层时,这个图形的面积是()cm2。
A.20B.110C.100D.905.如果1÷A=0.0606……,2÷A=0.1212……,3÷A=0.1818……。
那么7÷A=()A.0.2424……B.0.3636……C.0.4242……D.无法确定6.如图搭一个五边形需要5根小棒,每增加1个五边形多用4根小棒,像这样搭n个五边形需要()根小棒。
A.4n﹣1B.4n+1C.5n﹣1D.5n+17.我国明朝时期的《算法统宗》里讲述了一种“铺地锦”的乘法计算方法,例如计算62×37时,方法如下:上面右图是计算23×14的铺地锦方法,括号里应填的数是()A.10B.12C.0D.28.观察下列图形,则第n个图形中三角形的个数是()A.4n B.4n+4C.2n+2D.2n二.填空题(共8小题)9.如图规律排列第8幅点阵图中有个●,第n幅点阵图中有个●。
10.数学中规定:连接多边形任意两个不相邻顶点的线段叫做多边形的对角线。
正多边形……边数 456……一个顶点可画 对角线数量 123……对角线总数量259……聪聪是个喜欢思考的学生,他发现正多边形的对角线数量和正多边形的边数存在某种规律(如图),照这样的规律,正七边形共有 条对角线,正n 边形共有 条对角线。
人教版(六上)第八单元 数学广角——数与形 同步奥数(附答案)

第八单元 数学广角——数与形 同步奥数知识点:1.1+3+5+7+9+……+(2n-1)=n 22.2+4+6+8+10+……+2n=n ×(n+1)3.1+2+3+4+5+…(n-1)+n+(n-1)+…+5+4+3+2+1=n 24.平方差公式:a 2-b 2=(a+b)(a-b) 例题1.1=( )2 1+3=( )2 1+3+5=( )2(1)观察一下,上面的图形和对应的算式有什么关系?把算式补充完整。
(2)你能利用规律直接写一写吗?如果有困难,可以画图来帮助。
1+3+5+7=( )21+3+5+7+9+11+13=( )2=92练习1.先观察下面的图形和算式之间的关系,再填空。
OO O O OO O OO OO O O O O O O O O O O O O O O O O O O O (1) (2) (3) (4) 图(1):1=12 图(2):1+3=4=22 图(3):1+3+5=9=32图(4):1+3+5+7=( )=( )2 ……我会用:1+3+5+7+9+11+9+7+5+3+1=( )2+( )2=( ) 例题2.2=( )×( ) 2+4=( )×( ) ) (1)观察一下,上面的图形和对应的算式有什么关系?把算式补充完整。
(2)你能根据规律直接写一写吗?如果有困难,可以画图。
2+4+6+8=()×()2+4+6+8+10+12+14=()×()=10×11练习2.计算:2+4+6+8+10+……+98+100=()例题3.1+2+1=2 1+2+3+2+1=32 1+2+3+4+3+2+1=42 1+2+3+4+5+4+3+2+1=( )2练习3.计算:1+2+3+4+5+…+99+100+99+98+97+…+3+2+1=()例题4.下面每个图中最外圈各有多少个小正方形?22-02=() 42-22=() 62-42=() 82-62=()照这样接着画下去,第6个图形最外圈有()个小正方形;第n个图形最外圈有()个小正方形。
六年级上册人教版小学数学第八单元数学广角—数与形测试(包含答案解析)
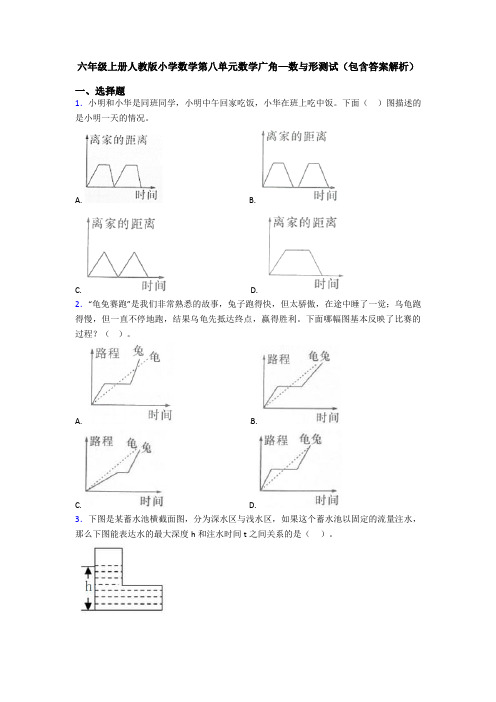
六年级上册人教版小学数学第八单元数学广角—数与形测试(包含答案解析)一、选择题1.小明和小华是同班同学,小明中午回家吃饭,小华在班上吃中饭。
下面()图描述的是小明一天的情况。
A. B.C. D.2.“龟免赛跑”是我们非常熟悉的故事,兔子跑得快,但太骄傲,在途中睡了一觉;乌龟跑得慢,但一直不停地跑,结果乌龟先抵达终点,赢得胜利。
下面哪幅图基本反映了比赛的过程?()。
A. B.C. D.3.下图是某蓄水池横截面图,分为深水区与浅水区,如果这个蓄水池以固定的流量注水,那么下图能表达水的最大深度h和注水时间t之间关系的是()。
A. B. C.D. 以上都不对4.根据图中的信息,第六个图案所对应的式子是( )A. 7+1B. 62+1C. 72+1D. 82+1 5.小明妈妈从家出发到超市,购物若干时间后再回到家。
下面比较准确地描述了这件事的图是(),A. B.C. D.6.下面每个图形都是由中的两个(可以相同)构成的。
观察各图形与它下面的数之间的关系.猜猜最右面图形下面的“?”表示( )。
A. 23B. 31C. 13D. 327.下图表示的是学校足球队乘车去体育馆训练,然后返回学校的过程,下面说法错误的是( )。
A. 体育馆距离学校5kmB. 去体育馆的车速是5千米/时C. 足球队在体育馆的时长是1.5时D. 返回学校用时0.5时8.按规律1,8,27,, 125,括号中的数应为()A. 30B. 64C. 80D. 1009.图是一辆面包车和一辆货车的运行情况,下列说法错误的是( )A. 出发时货车在面包车前50千米处B. 经过2小时货车追上面包车C. 货车平均速度为37.5千米/小时D. 面包车平均速度为12.5千米/小时10.甲与乙在一次赛跑中路程与时间的关系图如下,则正确的是()A. 甲比乙先出发B. 乙比甲跑的路程多C. 甲、乙两人的速度相同D. 甲先到达终点11.把正方形边长扩大到原来的2倍,所得到的图形周长是原图形周长的倍,面积是原图形的倍.()A. 2,4B. 2,1C. 2,2D. 4,4 12.某城市限定每户每月用水量不超过6吨时,每吨价格为2元;当用水量超过6吨时,超过部分每吨水价为3元,每户每月水费y(元)与用水量x(吨)的关系是图中的()A. B. C. D.二、填空题13.如图,在线段AB上,画1个点,可得3条线段;画2个不同点,可得6条线段;画3个不同点,可得10条线段;照此规律,画4个不同点,可得________条线段,画10个不同点,可得________条线段。
【奥数题】人教版小学数学六年级上册三角形中的计算奥数思维拓展(试题)含答案与解析
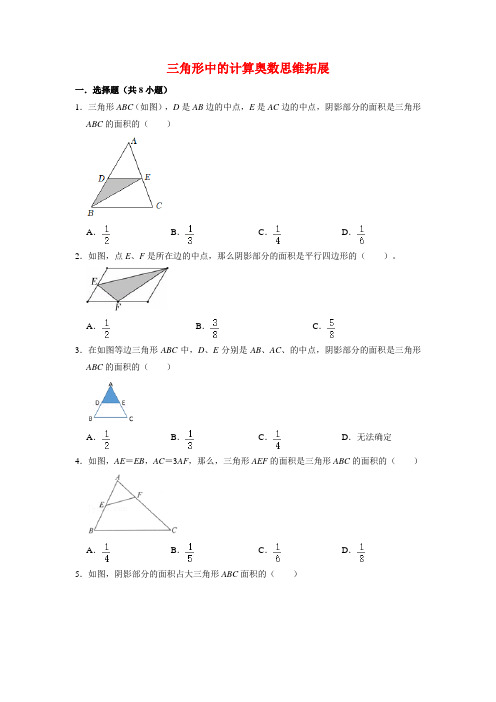
三角形中的计算奥数思维拓展一.选择题(共8小题)1.三角形ABC(如图),D是AB边的中点,E是AC边的中点,阴影部分的面积是三角形ABC的面积的()A.B.C.D.2.如图,点E、F是所在边的中点,那么阴影部分的面积是平行四边形的()。
A.B.C.3.在如图等边三角形ABC中,D、E分别是AB、AC、的中点,阴影部分的面积是三角形ABC的面积的()A.B.C.D.无法确定4.如图,AE=EB,AC=3AF,那么,三角形AEF的面积是三角形ABC的面积的()A.B.C.D.5.如图,阴影部分的面积占大三角形ABC面积的()A.B.C.D.无法确定6.如图,把三角形ABC的一条边延长一倍到D,把它的另一条边延长2倍到E,得到一个较大的三角形,那么,三角形ABC的面积是三角形ADE的面积的()A.B.C.D.7.如图中,DE=2BE,那么阴影部分面积是长方形面积的()A.B.C.8.如图,在三角形ABC中,E、D、G分别是AB、BC、AD的中点,图中与三角形ADE面积相等的三角形还有()A.0个B.1个C.2个D.3个二.填空题(共8小题)9.如图中阴影部分的面积是12平方厘米,BD:CD=4:5,三角形ADC的面积是平方厘米。
10.如图,三角形ABC的面积27cm2,,三角形AED的面积是cm2。
11.如图,AD=DB,AE=EF=FC。
已知阴影部分的面积是5平方厘米,三角形ABC的面积是平方厘米。
12.如图,直角梯形ABCD的上底是5厘米,下底是7厘米,高是4厘米,且三角形ADE、ABF和四边形AECF的面积相等,则三角形AEF的面积是.13.如图每个小长方形的长2厘米,宽1厘米,阴影部分面积占长方形面积的%.14.在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于平方厘米。
15.如图梯形中E是BC的中点,F是DC的中点,线段EF把梯形分成甲、乙两个部分,面积比是21:4,那么梯形的上底AB与下底CD的长度比是。
小学数学 人教版 6年级上册 《数与形》练习+详解

小学数学 人教版 6年级上册 《数与形》试题部分1. 如下图,用同样大小的黑色棋子按如图所示的方式摆图案,按照这样的规律摆下去,第20个图案需棋子______枚。
2. 看图数角。
11+2=______1+2+3=_______1+2+3+4=_______根据上面的规律,左图中一共有_____个角。
3. 下图是乐乐用火柴搭成的1条、2条、3条"金鱼"......则搭6条"金鱼"需要火柴_____根。
4.2=1×2;2+4=2×3;2+4+6=3×4;根据规律,下面式子( )=10×11.A. 2+4+6+8+10+12+14+16B. 2+4+6+8+10+12+14+16+18C. 2+4+6+8+10+12+14+16+18+20D. 2+4+6+8+10+12+14+16+18+20+225. 将长3cm ,宽1cm 的长方形如下图一层、两层、三层......地画下去,则第n 个图形的周长是_______cm 。
图形中有14个正方形,第四个图形中有30个正方形,第五个图形中有______个小正方形.7.观察下面已有的几个点阵图,按照规律,第10幅图有______个点。
8.如下图,第一个图形中有1个小正方形,第二个图形中有4个小正方形,第三个图形中有9个小正方形,第四个图形中有16个小正方形,第八个图形中有_____个小正方形.三个图形中有9个小正方形,第四个图形中有16个小正方形,第十个图形中有_______个小正方形.10.根据规律接着画:在第四幅图中有______个黑球,______个白球.11.下图都是由边长为1的小三角形组成的图形,按照规律摆下去,第四幅图有_______个小三角形.12.下面第三幅图中最外面一圈的正方形有______个。
13.摆一个正方形需要4根小棒,两个需要7根小棒,那么摆n个正方形需要()根小棒。
【奥数题】人教版小学数学六年级上册数与形奥数思维拓展(试题))含答案与解析
数与形奥数思维拓展(试题)一.选择题(共8小题)1.像如图这样继续画,第10组应该画()个。
A.81B.100C.1212.将正方形纸片按规律拼成如下的图案,第()个图案中恰好有45张纸片。
A.3B.5C.10D.113.把边长1cm的正方形按如图所示拼成各种图形。
当图形是4层时,它的周长是16cm。
如果图形有n层,它的周长是()cm。
A.4n B.5n C.6n4.如图,在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退。
开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能是下列数中的()A.5B.4C.3D.15.将黑色棋子按照一定规律排列成一系列如图所示的图案,第1个图中有8枚黑棋子,第2个图中有13枚黑棋子,第3个图中有18枚黑棋子,按照此规律,第9个图中有()枚黑棋子。
A.49B.48C.47D.466.把同样的小棒按下面的方式摆放,第9个图形需要()根小棒。
A.24B.27C.307.观察下面图形的规律,其中第1个图形由4个小正方形组成,第2个图形由7个小正方形组成,第3个图形由10个小正方形组成,…按此规律排列下去,则第n个图形由()个小正方形组成。
A.4n B.2n﹣1C.3n+1D.3n﹣18.如图所示,用白色小正方形和黑色长方形按照下面的摆法,组成不同的长方形。
当摆5个黑色长方形时,四周需要摆()个白色小正方形。
A.16B.20C.26D.36二.填空题(共8小题)9.如图,用小棒摆出若干个小正方形。
照这样的规律,摆n个小正方形需要根小棒;用100根小棒可以摆个这样的正方形。
10.观察如图规律,如果一幅图中涂色正方形是6个,那么空白正方形有个。
11.观察下面的图形并填空。
利用你发现的规律直接写出下面算式的结果:1992﹣1982=12.照此规律画下去,第n个图形共有个■,个□。
(常考题)人教版小学数学六年级上册第八单元数学广角—数与形测试题(答案解析)
(常考题)人教版小学数学六年级上册第八单元数学广角—数与形测试题(答案分析)一、选择题1.一只兔子和一条小狗从同一地址出发,同时开始向东运动,兔子的运动距离与时间关系如图中实线部分ABCD所示,小狗的运动距离与时间关系图象如图中虚线部分AD 所示。
则对于该图象以下说法正确的选项是()。
A. 小狗的速度一直比兔子快C. 图中 BC 段表示兔子在做匀速直线运动B整.个过程中小狗和兔子的均匀速度同样D. 在前 4 秒内,小狗比兔子跑得快2.以以下图a~d 是水滴进玻璃容器的表示图(滴水速度同样),以以下图中水的高度随滴水时间变化的状况(图中刻度、单位都同样),与表示图e~ h 表示的是容器c 容器相对应的统计图是()。
A. 图 e B图. f C图. g D图. h 3.礼拜天,林林从家出发到书店看了一会儿书,而后回到家里,下边第()幅图描绘的是林林的行为。
A. B. C.4.五年级一班同学礼拜一第一节课到二楼教室上数学课,第二节课到三楼语音室上英语课,第三节课到四楼美术室上美术课,第四节课到室外上体育课,下边第()幅图描绘了这一过程。
A.B.C.5.乐乐与同学们在老师的率领下到茶厂展开研学旅游活动.第一天她参加采茶叶体验活动.上午采茶叶 2 小时,吃过午餐后接着采茶叶 3 小时.下边能较正确地描绘这件事的是图()A. B.C. D.6.依据图中的信息,第六个图案所对应的式子是( )A. 7+ 1B. 62+ 1C. 72+1D. 82+ 1 7.察看数列的摆列规律,而后从四个选项中选出你以为最合理的一项,来填充空缺项:1 2 4 8 16()A. 32B. 24C. 64D. 20 8.下边各图是由棱长为 1 厘米的正方体拼成的,依据前三个图形表面积的摆列规律,第五个图形的表面积是()平方厘米。
A. 20B. 22C. 249.礼拜六小明和家人从家中出发,搭车0.5 小时后,到达离家10 千米远的植物园,旅游1 小时后,走出植物园,歇息 1 小时,而后搭车0.5 小时返回家中。
六年级数学上册 数学广角——数与形综合题 (试题) 人教版(含答案)
六年级同步经典题精练之数学广角——数与形综合题一.选择题(共8小题)1.找规律:,,,,,(),……括号里的数是。
A.B.C.2.先找出规律,再按规律选择答案。
85.47×1.3=111.11185.47×2.6=222.22285.47×3.9=333.33385.47×7.8=()A.444.444B.666.666C.888.888D.999.9993.小丁同学用三角形摆出了如图的图案,根据图形与数的规律接着摆下去,第(6)个图案中所用三角形总数为()个。
A.15B.21C..84.用火柴棒按如图的方式搭正方形,搭30个这样的正方形需要()根火柴棒。
A.120B.90C.915.周文用小棒以下面的方式摆六边形。
摆n个六边形要用小棒()根。
A.6n B.5n+1C.4n+36.根据史书的记载和考古材料发现:在算筹计数法中,以纵、横两种排列方式来表示单位数目。
其中横式表示数的方法如图所示。
那么,在算筹中用横式丧示“8”的图案是()A.B.C.D.7.按照下面3幅图的规律,如果每个圆的直径都是10厘米,那么第10个图形长()厘米。
A.50B.55C.95D.1008.四个同学观察上图后,分别说出了自己的发现。
()的想法正确。
A.只有丽丽B.只有丽丽和文文C.只有丽丽、平平、文文D.丽丽、平平、文文、欣欣二.填空题(共5小题)9.3÷16.5的商的小数部分第101位上的数字是。
10.观察规律,,,,,……这列数从左到右第100个数是。
11.根据111111÷37037=3,222222÷37037=6,333333÷37037=9,写出:444444÷37037=,555555÷37037=。
12.如图,用小棒摆图形,照这样摆下去,摆第7个图形需要根小棒,摆第n个图形需要根小棒。
13.瑞士中学教师巴尔末成功地从光谱数据、、、……中得到巴尔末公式,从而打开了光谱奥妙的大门。
第八单元 数学广角—数与形解决问题专项(题型专练)-六年级数学上册(答案解析)(人教版)
保密★启用前第八单元数学广角—数与形解决问题专项答案解析【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
发现及说明见详解【详解】①113 += 244②1117 ++= 2488③111115+++= 2481616…则:④111111 +++++= 2481664nn…发现:计算结果以最后一个分数的分母作分母,分子等于分母减1。
如图:依次选取余下的一半,就会出现这种情况:【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
3.(1)a+b;(a+b)2;(2)这四个图形的面积和是a2+b2+2ab;(3)我发现大正方形的面积等于这四个图形的面积之和,所以可以得出结论:(a+b)²=a²+b²+2ab。
【分析】(1)由图可知大正方形的边长为(a+b),根据正方形的面积公式S=a²,即可用字母表示出大正方形的面积;(2)根据长方形的面积公式S=a×b,正方形的面积公式S=a²,分别求出两个小长方形①和②的面积,两个小正方形③和④的面积,再将这四个图形的面积相加即可解答;(3)通过观察图形,可知大正方形的面积等于这四个图形的面积之和,用字母表示出来即可。
【详解】(1)大正方形的边长为(a+b);用字母表示大正方形的面积是:(a+b)²。
(2)①的面积a×b=ab②的面积a×b=ab③的面积a×a=a²④的面积b×b=b²ab+ab+a²+b²=a²+b²+2ab答:两个长方形①和②,两个小正方形③和④,这四个图形的面积和是a²+b²+2ab。
(3)答:我发现大正方形的面积等于这四个图形的面积之和,所以可以得出结论:(a+b)²=a²+b²+2ab。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典奥数专题:数与形(试题)数学六年级上册人教版一、选择题1.用小木棒按下图方式摆放图形,第⑧个图形需要()根小木棒。
A.33B.30C.36D.272.如下图,第5个图形是由()个小正方形拼成的。
A.16B.20C.25D.363.观察下面的点子图,如果按图中的规律画下去,第⑧个方框里应画()个点。
A.29B.31C.334.观察下图,请选择最适合的一个填入问号处,能使之呈现出一定的规律性的是()。
A.B.C.D.5.古希腊著名的毕达哥拉斯学派把1、3、6、10、15、21…这样的数称为“三角形数”,而把1、4、9、16、25、36…这样的数称为“正方形数”。
从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和。
下列等式中,不符合这一规律的是()。
A.25=9+16B.36=15+21C.49=21+28D.64=28+366.如下图所示,摆1个六边形要用6根小棒,摆2个六边形要用11根小棒,摆3个六边形要用16根小棒……,摆30个六边形要用()根小棒。
A.151B.179C.180二、填空题7.观察下图,这样的5张桌子连在一起可以坐( )人,按此规律连下去,坐96人需要( )张桌子。
8.请根据下图中的规律,按要求回答问题。
(1)第5个图形中白色三角形的个数有( )个。
(2)第10个图形中白色三角形的个数有( )个,黑色三角形的个数有( )个。
9.下面图形按一定规律排列,这样第⑥幅图中一共有( )个小正方形。
10.根据图中四幅图的规律,第5幅图中有( )个●,第n幅图中有( )个△。
……13.下面图形是由一些小正方形和实心圆按一定规律摆成的,第1个图中有4个实心圆,第2个图中有6个实心圆,第3个图中有8个实心圆……,按此规律,第7个图中有( )个实心圆。
14.用一根长48厘米的绳子在地上摆正方形。
当这根绳子摆出4个正方形时,正方形的总面积是( )平方厘米,当这根绳子摆出n个正方形时,正方形的边长是( )厘米。
三、解答题248163218.当当在计算“12+1×3×2+32、22+2×5×2+52、42+4×6×2+62 …”这样的算式时,她用“数形结合”的方法来探索:用算式中的数分别构造两个正方形和两个长方形。
她发现“这四个图形的面积相加正好是大正方形的面积”(如图所示)。
由此得出:图①:12+1×3×2+32=42图②:22+2×5×2+52=72图③:42+4×6×2+62=102(1)根据当当发现的规律填空:32+3×5×2+52=()。
162+16×19×2+192=()。
(2)你能根据当当发现的规律,把如图这个正方形分成四块,并用算式表示出来吗?()=9220.探索规律。
(1)观察上面的图,发现:图①空白部分小正方形的个数是22-12=2+1图②空白部分小正方形的个数是22=4+343图③空白部分小正方形的个数是52-42=()+()(2)像这样继续排列下去,你会发现一些有趣的规律,请你再写出一道算式:()。
(3)运用规律计算。
202-192+182-172+162-152+…+22-12。
参考答案:1.D【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)=6+3n-3×1=6+3n-3=3n+6-3=(3n+3)根当n=8时。
3n+3=3×8+3=24+3=27(根)所以,第⑧个图形需要27根小木棒。
故答案为:D【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
2.C【分析】观察图形,第1个图形是由1×1=1=12个小正方形拼成的,第2个图形是由2×2=4=22个小正方形拼成的,第3个图形是由3×3=9=32个小正方形拼成的,依次类推,可以看出第5个图形是由52个小正方形拼成的。
据此解答。
【详解】52=5×5=25(个)即第5个图形是由25个小正方形拼成的。
故答案为:C【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
3.A【分析】根据图示,第1个方框中的点为:1个;第2个方框中的点为:1+4=5(个);第3个方框中的点为:1+4+4=9(个);第4个方框中的点为:1+4+4+4=12(个);则第n个方框中的点为:1+4(n-1)=(4n-3)个。
据此解答。
【详解】第⑧个方框里应画的点数为:4n-3=4×8-3=32-3=29(个)则第⑧个方框里应画29个点。
故答案为:A【点睛】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
4.C【分析】观察可知,方框中的圆点数量如,中间4圆点可以呈现出一定的规律性,再根据圆点的呈现方式进行选择。
【详解】如图,具有一定的规律性。
故答案为:C【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.A【分析】根据“三角形数”的规律是:1,3,6,10,15,21,28,36,45…,而“正方形数”是两个相邻“三角形数”之和,据此逐项判断即可。
【详解】A.25=9+16;25=52,是正方形数,9和16不是三角形数,不符合规律,符合题意;B.36=15+21;36=62,是正方形数,15和21是相邻的三角形数,符合规律,不符合题意;C.49=21+28;49=72,是正方形数,21和28是相邻的三角形数,符合规律,不符合题意;D.64=28+36;64=82,是正方形数,28和36是相邻的三角形数,符合规律,不符合题意。
故答案为:A【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
6.A【分析】摆1个六边形需要156+=根小棒,摆2个六边形需要12511011+⨯=+=根小棒,摆3个六边形需要13511516+⨯=+=根小棒,,摆n 个六边形需要()15n +根小棒,据此解答即可。
【详解】摆30个六边形要用:1530+⨯1150=+151=(根)所以摆30个六边形要用151根小棒。
故答案为:A【点睛】本题考查数与形,解答本题的关键是找到题中的规律。
7. 24 23【分析】把左右两边的4人单独看,则一张桌子对应4个人,一张桌子坐4+1×4=8 (人) , 2张桌子坐4+2×4=12人,3张桌子坐4+3×4=16(人),则n 张桌子可以坐(4+4n )人,据此解答即可。
【详解】这样的5张桌子连在一起可以坐的人数为: 4+4n =4+4×5 =4+20 =24则这样的5张桌子连在一起可以坐24人; 4+4n =96解:4+4n -4=96-4 4n =92 4n÷4=92÷4 n =23则坐96人需要23张桌子。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
8.(1)10【点睛】掌握图形的变化规律是解题的关键。
13.16【分析】由图可知:第1个图中有4=2×(1+1)个实心圆,第2个图中有6=2×(2+1)个实心圆;第3个图中有8=2×(3+1)个实心圆……第n个图中有2×(n+1)个实心圆;将n=7代入计算即可。
11111=18(个)当n=10时,有10个绿色小正方形;蓝色小正方形有:2n+6=2×10+6=20+6=26(个)答:照这样接着画下去,第6个图形有6个绿色小正方形和18个蓝色小正方形。
第10个图形有10个绿色小正方形和26个蓝色小正方形。
道理:从图中发现规律:第n个图形有n个绿色小正方形,(2n+6)个蓝色小正方形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
18.(1)82,352(2)22+2×7×2+72图见详解【分析】根据题意,用算式中的数分别构造两个正方形和两个长方形。
这四个图形的面积相加正好是大正方形的面积,由此可知:图①:12+1×3×2+32=(1+3)2=42图②:22+2×5×2+52=(2+5)2=72图③:42+4×6×2+62=(4+6)2=102也就是说a2+2ab+b2=(a+b)2,据此规律解答即可。
【详解】(1)根据当当发现的规律填空:32+3×5×2+52=(3+5)2=82162+16×19×2+192=(16+19)2=352(2)你能根据当当发现的规律,把如图这个正方形分成四块,用算式表示出来如下:22+2×7×2+72=92;图如下:(2)白色三角形的个数:1+2+……+9=45(个)黑色三角形的个数:1+2+……+10=55(个)答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
20.(1)5;4(2)72-62=7+6(3)210【分析】观察算式规律可得:相邻两个数的平方差等于这两个数的和,由此按规律解答即可。
【详解】(1)52-42=5+4(2)72-62=7+6(答案不唯一)(3)202-192+182-172+162-152+…+22-12=20+19+18+17+…+3+2+1=(20+1)×20÷2=21×20÷2=420÷2=210【点睛】此题考查数与形结合的规律,进一步培养学生的观察能力和总结能力。
