六年级奥数专题:找规律
六年级找规律奥数题

六年级找规律奥数题
题目:找出下面每行、每列和每个九宫格中的数字,并将它们组成一个四位数。
一行:357,892
一列:461,983
一个九宫格:289,417,982,357
要求:每个数字必须被4个数字整除,且这些数字不能重复。
解法:
首先观察题目中的数字,可以发现每行、每列和每个九宫格中的数字都是唯一的。
其次,我们可以使用穷举法来寻找符合条件的数字。
从行入手,如果行中的第一个数字是357,则该数字不能被4个数字整除,因此无法继续向下寻找。
同理,从列入手,如果列中的第一个数字是892,则该数字不能被4个数字整除,因此无法继续向下寻找。
因此,我们可以将这个行、列和九宫格中所有数字都排除掉,然后再从下一个行、列和九宫格中开始寻找符合条件的数字。
最后,我们使用计算机程序来解决这个问题,可以大大加快搜索的速度。
具体地,我们可以使用一个数组来表示符合条件的数字,使用一个循环来搜索整个数组。
在搜索过程中,我们需要检查每个数字是否被4个数字整除,如果符合条件,则将其加入数组中。
时间复杂度:O(n^3)
拓展:
这个问题可以推广到更大的数字规模。
例如,如果有n行、m列和n个九宫格,我们需要找到符合条件的n位数。
我们可以使用类似的方法来解决,即使用一个数组来表示符合条件的数字,使用一个循环来搜索整个数组。
在搜索过程中,我们需要检查每个数字是否被4个数字整除,如果符合条件,则将其加入数组中。
如果数字的规模很大,那么搜索的时间复杂度将变得非常高。
因此,我们需要使用更高效的算法来解决这个问题。
小学奥数找规律知识点

小学奥数找规律知识点小学奥数是指小学生参加的数学奥赛比赛,题目难度较高,常常需要运用一些找规律的方法来解题。
在小学奥数中,找规律是一种重要的解题技巧,掌握了找规律的知识点,可以在解题时事半功倍。
本文将介绍小学奥数中常用的找规律的知识点。
一、数字序列的规律在小学奥数中,经常会给出一组数字的序列,要求找出其中的规律。
在解决这类问题时,我们可以首先观察数字序列的前几个数,看是否能够找到一些明显的规律。
比如,给定数字序列:2, 4, 6, 8, 10,我们可以发现每个数字都是前一个数字加2,因此规律是“加2”。
有时候数字序列的规律可能更加复杂,我们可以根据数字之间的差异来寻找规律。
例如,给定数字序列:1, 3, 6, 10,我们可以发现每个数字相对于前一个数字的差值递增,即1, 2, 3,因此规律是“差值递增”。
二、图形的规律小学奥数中常常会出现一些图形题目,要求找出图形之间的规律。
在解决这类问题时,我们可以先观察图形的形状、颜色、数量等特征,看是否能够找到一些规律。
例如,给定以下图形序列:△ △△ △△△ △△△△我们可以发现每一行图形的数量递增,因此规律是“数量递增”。
有时候图形的规律可能与位置有关,我们可以根据图形在位置上的变化来寻找规律。
比如,给定以下图形序列:□□ □□ □ □□ □ □ □我们可以发现每一行图形的位置与数量有关,因此规律是“位置与数量相关”。
三、数学运算的规律在小学奥数中,常常会出现一些涉及数学运算的题目,要求找出运算中的规律。
解决这类问题时,我们可以先观察数学运算的过程和结果,看是否能够找到一些规律。
例如,给定以下数学运算序列:2 +3 = 53 +4 = 74 +5 = 9我们可以发现每一组的结果都比前一组的结果大2,即组数与结果之间存在着一定的关系,因此规律是“结果与组数相关”。
有时候数学运算的规律可能与数的性质有关,我们可以根据数的性质来寻找规律。
比如,给定以下数学运算序列:6 × 1 = 66 × 2 = 126 × 3 = 18我们可以发现每一组的结果都是一个等差数列,因此规律是“结果是一个等差数列”。
(完整版)小学奥数找规律

小学奥数找规律一、知重点依照必定序次摆列起来的一列数,叫做数列。
如自然数列:1,2,3,4,⋯⋯双数列: 2,4, 6, 8,⋯⋯我研究数列,目的就是了数列中数摆列的律,并依照个律来填写空缺的数。
依照必定的序摆列的一列数,只需从的几个数中找到律,那么就能够知道其他全部的数。
找数列的摆列律,除了从相两数的和、差考,有要从、商考。
擅长数列的律是填数的关。
二、精精【例 1】在括号内填上适合的数。
(1)3,6,9,12,(),()(2)1,2,4,7,11,(),()(3)2,6,18,54,(),()1:在括号内填上适合的数。
(1)2,4,6,8,10,(),()(2)1,2,5,10,17,(),()(3)2,8,32,128,(),()(4)1,5,25,125,(),()(5)12,1,10,1,8,1,(),()【例 2】先找出律,再在括号里填上适合的数。
(1)15,2,12,2,9,2,(),()(2)21,4,18,5,15,6,(),()练习 2:按规律填数。
(1)2,1,4,1,6,1,( ),( )(2)3,2,9,2,27,2,( ),()(3)18,3,15,4,12,5,( ),( )(4)1,15,3,13,5,11,( ),()(5)1,2,5,14,(),()【例题 3】先找出规律,再在括号里填上适合的数。
(1)2,5,14,41,() (2)252,124,60,28,( )(3)1,2,5,13,34,( )(4)1,4,9,16,25,36,()练习 3:按规律填数。
(1)2,3,5,9,17,( ),()(2)2,4,10,28,82,( ),( )(3)94,46,22,10,( ),( )(4)2,3,7,18,47,(),()【例题 4】依据前方图形里的数的摆列规律,填入适合的数。
(1)10 7 12 9 145914111613(2)479 816 814 43249 3 27 (3)1243636 12练习 4:找出摆列规律,在空缺处填上适合的数。
六年级奥数——找规律
(3)1,8,27,(),125,()
(4)3,6,9,15,24,(),63,()
2、按照规律在括号里画出每组的第32个图形。
(1)◎□○◎□○◎□○……()
(2)○○○□○○○□○○○□……()
(3)△△△○○△△△○○……()
3、六(2)班同学在六一国际儿童节按下面的规律在教室里挂上气球。
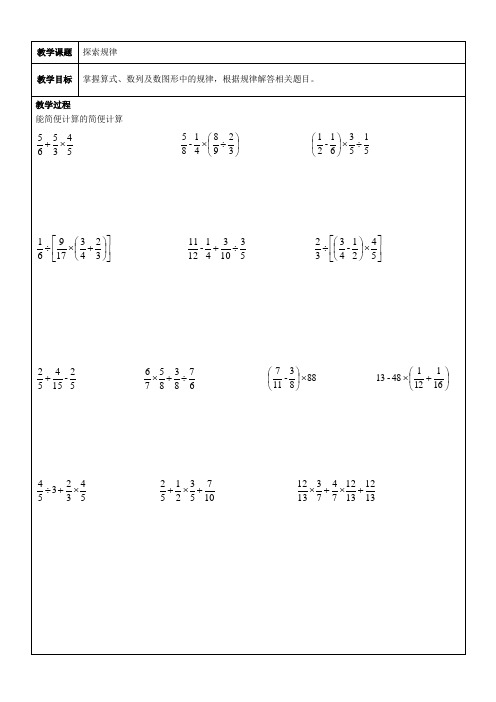
教学课题
探索规律
教学目标
掌握算式、数列及数图形中的规律,根据规律解答相关题目。
教学过程
能简便计算的简便计算
探索规律
一、算式中的规律
在数学算式中探索规律,应认真观察算式的特点,再观察结果的特点,从而根据规律完成这一类题。如:
二、数列中的规律
按一定次数排列的一列数叫做数列
1、规律蕴涵在相邻两数的差和倍数中。
六、搭配中的规律
搭配问题的解题思路类似于乘法原理,即做一件事情,完成它需要分成n个步骤,做第一步有 中不同的方法,,做第二步有 中不同的方法…,做第 步有 中不同的方法,那么完成这件事有
例1:先观察下列各式,找出规律再填空。
(1)12345679×9=111111111
(2)12345679×18=222222222
例4:小明在一个正方形的棋盘里摆棋子,他先把最外层摆满,用了40个棋子,最外层每边有多少棋子?如果他要把整个棋盘摆满,还需要多少棋子?
例5:由1,2,3,4,5五个数字组成的五位数共有120个,将它们从小到大排列起来,第95个数是()。
跟踪练习
1、你能发现下列各组数的规律吗?
(1)8,11,14,17,(),23,26
如:12,15,17,30,22,45,27,60,…第1,3,5,…项依次相差5,第2,4,6,…项依次相差15。
(完整版)六年级数学经典找规律专题

找规律专题一.解答题(共 30 小题)1.( 2015?深圳)在生活中,经常把一些同样大小的圆柱管如图捆扎起来,下面我们来探索捆扎时绳子的长度,图中,每个圆的直径都是 8 厘米,当圆柱管放置放式是 “单层平放 ”时,100 个时需要绳子厘米( π取 3)2.( 2015?龙泉驿区校级三模)摆一个六边形需要六根小棒,摆 2 个六边形需要 11根小棒, 3 个需要 16 根小棒 ⋯问:摆 10 个六边形需要 根小棒,摆 100 个六边形需要 根小棒,摆 n 个六边形需要 根小棒.3.( 2015 春?淮安校级期中)用计算器计算,再根据规律编写一道算式并直接写出得数. (24+25) ×5= ; (872+873 )×5= ; (2830+2831 )×5= ;( + ) × = .4.( 2015 春?射阳县校级期中)根据规律填数. 9×9+9=90 9876×9+6=888905.( 2015 春?成都校级期中)如图表示 “宝塔”,它们的层数不同,但都是由一样大的小三角 形摆成的.仔细观察后,请回答:(1)五层的 “宝塔”最下层包含多少个小三角形?六层呢?七层呢? n 层呢? (2)整个五层 “宝塔”一共包含多少个小三角形?六层呢?七层呢? n 层呢?共几个面在外面7.( 2015 春?盐城校级期中)用小棒如图的方式搭正方搭 1 个正方形要 4 根小棒,搭 2 个正方形要 7 根小棒. (1)搭 3 个正方形要 根小棒; (2)搭 8 个正方形要 根小棒; (3)搭 n 个正方形要根小棒.(4)现有 2014 根小棒,可以搭个正方形.98×9+8=890 987×9+7=889098765×9+5= 987654 ×9+4=形.捆扎后的横截面积如图所示:6.( 2015 春?西安校级期中)仔细观察,根据发现的规律把表格填完整.第几幅图1 2 3 5 n8.(2015春?团风县期中)一串珠子按照 3 颗黑珠,2颗白珠, 3 颗红珠,2颗蓝珠的顺序排列.(1)第14 颗珠子是珠子.(2)第998 颗珠子是颜色珠子.9.(2015 春?射阳县校级期中)想一想,填一填.用上面的图形在左边表里框出5个数,先算出这5 个数的和,再想想算出的和与中间一个数有什么关系?如果5个数的和为795,请在上面图形里写出这 5 个数.10.(2015 春?威宁县校级期中)表中一共有50个奇数,黑线框出的5 个数之和是115;仔细观察后回答问题.(1)你能发现每次框出的 5 个数的和与中间数有什么关系吗?(2)如果框出5 个数的和要是375,应该怎么框?(先在图中框一框,并在下面用文字说明)(3)能框出和是295的 5 个数吗?为什么?(4)一共可以框出多少个大小不同的和?11.(2015 春?株洲校级月考)不计算,运用规律在横线上填上合适的数.7×9=6377×9=693777×9=69937777×9=69993 777777777×9=1÷7=0.142857142857 ⋯2÷7=0.285714285714 ⋯3÷7=0.428571428571 ⋯4÷7=0.575÷7=0.76÷7=7÷7=12.(2014?涟水县模拟)观察与计算.计算: 1+2+3+ ⋯+99+100+99+98+ ⋯+3+2+1=14.(2014?宝安区校级模拟)观察下面 3 题的规律,然后算出( 1)( 2)两小题的结果. 1+2+1=2 ×2=41+2+3+2+1=3 ×3=91+2+3+4+3+2+1=161) 1+2+3+ ⋯+99+100+99+ ⋯+3+2+1=15.(2014?绍兴)有些题目可以通过观察找出规律,知道答案.按照下图算式的规律不变,如果商是 123456,括号中的 “减数 ”应该是 . (3﹣3)÷27=0 (33 ﹣ 6) ÷27=1 (333﹣9)÷27=12(3333﹣12)÷27÷=123.16.(2014?武平县)观察图形找规律:1)按照图形变化规律填表:正方形个 12345数直角三角 048形个数2)如果画 8 个正方形能得到个直角三角形,画 n 个正方形能得到个直角三角形.序号 ①②③④⑤数列 A 13 5 7 9数列 B 0149⑩81+⋯ + + +1+ + +⋯+ + + =13.(2014?金寨县校级模拟)找规律,填表. 2)+17.(2014?东莞)探寻规律.用这种瓷砖来铺设地面. 如果铺成一个 2×2 的正方形图案 (如图 ?),其中完整的圆共有 5 个, 如果铺成一个 3×3 的正方形图案 (如图 ?),其中完整的圆共有 13 个,如果铺成一个 4×4 的正方形图案(如图 ④ ),其中完整的圆共有 25 个.若这样铺成 一个 10×10 的正方形图案,则其中完整的圆共有个.你要研究的问题是:正方体个数与拼成的长方体表面积之间的关系.根据你的发现填空.当正方体个数为 10 时,所拼成的长方体表面积是平方厘米.当正方体个数为 a 时,所拼成的长方体表面积是 平方厘米. 当拼成的长方体表面积是 202 平方厘米时,正方体个数是 .20.(2014?成都)有甲、乙两个同样的杯子,甲杯装满水,乙杯是空的.第一次将甲杯里的杯中的 倒回甲杯, ⋯,这样反复倒 2015 次后,甲杯中的水是原来的几分之几?18.(2014?东台市)准备( (2)一个挨着一个排成一都是棱长为 1 厘米的正方体.19.(2014?长沙)在如图所示的数表中,第 100 行左边的第一个数是,第二次将乙杯中水的倒回甲杯,第三次将甲杯中的 倒回乙杯,第四次将乙1)每个21.(2014?陕西校级模拟)有一列数 2, 9, 8,2, 6, ⋯从第 3 个数起,每个数都是前面两 个数乘积的个位数字.例如第四个数就是第二、第三两数乘积 9×8=72 的个位数字 2.问这 一列数第 1997 个数是几?, , , ⋯则 是第 个分数.23.(2014?临夏县模拟)找规律填数. 1,4, 9, 16,, ,49, ,81.24.(2014?湖南模拟)分析推理找规律① 1+2+1=4② 1+2+3+2+1=9③ 1+2+3+4+3+2+1=16④ 1+2+ ⋯+49+50+49+ ⋯+2+1=⑤ 1+2+⋯+(n ﹣1)+n+(n ﹣1)+⋯+2+1=(n 为自然数)2 2 225.(2014?江油市校级模拟) 1+3=4=22,1+3+5=9=32,1+3+5+7=16=4 2,⋯1+3+5+⋯+(2n ﹣1) =20132,则 n=.26.(2014?宁远县校级模拟)如图,第 6 个图形一共由 个小三角形组成,第 n个图形,一共由 个小角形组27.( 2014?广州模拟) 为了美化城市, 某商场在门前的空地上用花盆按如图所示的方式搭正 方形.28.( 2014?台湾模拟) 如图所示,按一定规律用棉花棒摆放图案:第一组的图案用棉花棒 2 枝,第二组用棉花棒 7 枝,第三组用棉花棒 15 枝,如此类推,问第二十组的图案用棉花 棒多少枝﹖29.( 2014?成都校级模拟)下面的小点按如图所示的规律摆放:第 1 个图形有 6 个小点,第 2 个图形有 10 个小点,第 3 个图形有 16 个小点,第 4 个图形有 24 个点 ⋯,依次规律,第 10 个图形中点的个数是,, ,,22.(2014?江油市校级模拟)有一串数,成.1)填写下表 正方形的层数 该层所需花盆的个数1 2 3 4 5 4 122)按这种规律搭下去,搭第 n (n 为正整数)层正方形,需要 盆花.30.(2014?海安县模拟)用小棒按照如下的方式摆图形.摆 1 个八边形需要8 根小棒,摆 2 个八边形需要15 根小棒,⋯摆50 个八边形需要根小棒;如果摆这样的八边形用了771 根小棒,你知道摆了个八边形.。
六年级上奥数第一讲找规律

第一讲 找规律给出几个具体的、特殊的数、式或图形,要求找出其中的变化规律,从而猜想出一般性的结论.解题的思路是实施特殊向一般的简化;具体方法和步骤是(1)通过对几个特例的分析,寻找规律并且归纳;(2)猜想符合规律的一般性结论;(3)验证或证明结论是否正确,下面通过举例来说明这些问题. 开篇小练习:1、有一列数,观察规律,并填写后面的数,-5,-2,1,4,_______,________,________。
2、有一组数为:1111111,,,,,,234567---- …找规律得到第11个数是_________,第n 个数是__________3、小凡在计算时发现,11×11=121,111×111=12321,1111×1111=1234321,他从中发现了一个规律。
你能根据他所发现的规律很快地写出 111111111×111111111=______吗? 答案是___________________________。
4、四个同学研究一列数:1,-3,5,-7,9,-11,13,……照此规律,他们得出第n 个数分别如下,你认为正确的是 ( )A.2n -1B.1-2nC.(1)(21)nn -- D.1(1)(21)n n +--5、如图,是用积木摆放一组图案,观察图形并探索:第五个图案中共有 块积木,第n 个图形中共有 块积木.6、观察数列1,1,2,3,5,8,x ,21,y ,……,则2x-y=____________7、观察下列各式:1234567822,24,28,216,232,264,2128,2256,======== …,请你根据上述规律,猜想108的末位数字是_________.8、观察下列各式:3211=3323332333321231236123410+=++=+++=典型例题:一、数字排列规律题1、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __2、请填出下面横线上的数字。
找规律知识点六年级

找规律知识点六年级一、数列和规律数列是由一系列按照一定规律排列的数字组成的序列。
在六年级的数学学习中,其中一个重要的知识点就是寻找数列中的规律。
通过观察数列中的数字变化规律,我们可以预测数列的下一个数字,甚至推导出数列的通项公式。
例如,考虑以下数列:2, 4, 6, 8, ...我们可以发现,每个数字都比前一个数字大2。
因此,可以得出这个数列的通项公式为:a_n = 2n,其中a_n表示数列中的第n个数字。
二、常见的数列规律1. 等差数列:在等差数列中,每个数字与前一个数字之差都是一个常数,这个常数称为公差。
例如,考虑以下数列:3, 6, 9, 12, ...我们可以发现,每个数字都比前一个数字大3。
因此,这个数列的公差为3。
可以得出通项公式为:a_n = 3n。
2. 等比数列:在等比数列中,每个数字与前一个数字的比值都相等,这个比值称为公比。
例如,考虑以下数列:2, 4, 8, 16, ...我们可以发现,每个数字都是前一个数字乘以2。
因此,这个数列的公比为2。
可以得出通项公式为:a_n = 2^n。
3. 斐波那契数列:斐波那契数列中的每个数字都是前两个数字之和。
例如,考虑以下数列:1, 1, 2, 3, 5, 8, ...我们可以发现,每个数字都是前两个数字之和。
可以得出通项公式为:a_n = a_(n-1) + a_(n-2),其中a_1 = 1,a_2 = 1。
三、寻找数列规律的方法1. 观察数列中数字之间的增减关系。
可以通过计算相邻数字的差值或者比值,判断数列是否具有等差或等比的规律。
2. 观察数列中数字之间的差值或比值是否保持恒定。
如果是恒定的,那么可以得出数列的通项公式。
3. 尝试使用已知的数列类型来逼近要寻找规律的数列。
有时候,一个数列可以被近似表示为某种已知的数列类型。
4. 利用递推公式或递推关系式来求解数列的规律。
递推公式描述了数列中每个数字与前面数字之间的关系。
四、数列规律的应用1. 预测数列未知部分的数字。
六年级奥数专题:找规律

六年级奥数博题:找顺序之阳早格格创做共教们从三年级启初,便陆绝交战过许多“找顺序”的题目,比方创造图形、数字或者数表的变更顺序,创造数列的变更顺序,创造周期变更顺序等等.那一道的实质是通过创造某一问题的顺序,推导出该问题的估计公式.例1 供99边形的内角战.分解与解:三角形的内角战等于180°,但是99边形的内角战何如供呢?咱们把问题简化一下,先供四边形、五边形、六边形……的内角战,找一找其中的顺序.如上图所示,将四边形ABCD分成二个三角形,每个三角形的内角战等于180°,所以四边形的内角战等于180°×2= 360°;共理,将五边形ABCDE分成三个三角形,得到五边形的内角战等于180°×3=540°;将六边形ABCDEF分成四个三角形,得到六边形的内角战等于180°×4=720°.通过上头的图形及分解不妨创造,多边形被分成的三角形数,等于边数减2.由此得到多边形的内角战公式:n边形的内角战=180°×(n-2)(n≥3).有了那个公式,再供99边形的内角战便太简单了.99边形的内角战=180°×(99-2)=17460°.例2 四边形内有10个面,以四边形的4个顶面战那10个面为三角形的顶面,最多能剪出几个小三角形?分解与解:正在10个面中任与一面A,连结A与四边形的四个顶面,形成4个三角形.再正在剩下的9个面中任与一面B.如果B正在某个三角形中,那么连结B与B天方的三角形的三个顶面,此时三角形总数减少2个(睹左下图).如果B正在某二个三角形的大众边上,那么连结B与B天方边相对付的顶面,此时三角形总数也是减少2个(睹左下图).类似天,每减少一个面减少2个三角形.所以,共可剪出三角形 4+ 2× 9= 22(个).如果将例2的“10个面”改为n个面,其余条件没有变,那么由以上的分解可知,最多能剪出三角形4+2×(n-1)=2n+2=2×(n+1)(个).共教们皆了解圆柱体,如果将圆柱体的底里换成三角形,那么便得到了三棱柱(左下图);共理不妨得到四棱柱(下中图),五棱柱(左下图).如果底里是正三角形、正四边形、正五边形……那么相映的柱体便是正三棱柱、正四棱柱、正五棱柱……例3 n棱柱有几条棱?如果将没有相接的二条棱称为一对付,那么n棱柱公有几对付没有相接的棱?分解与解:n棱柱的底里战顶里皆是n边形,每个n边形有n个顶面,所以n棱柱公有2n个顶面.瞅察三棱柱、四棱柱、五棱柱的图形,不妨瞅出,每个顶面皆与三条棱贯串,而每条棱对接 2个顶面,所以n棱柱公有棱 2n×3÷2=3n (条).进一步瞅察不妨创造,n棱柱中每条棱皆与4条棱相接,与其余的3n-4-1 =(3n-5)条棱没有相接.公有3n条棱,所以没有相接的棱有 3n×(3n- 5)(条),果为没有相接的棱是成对付出现的,各估计一遍便沉复了一遍,所以没有相接的棱公有3n×(3n-5)÷2(对付).例4 用四条曲线最多能将一个圆分成几块?用100条曲线呢?分解与解:4条曲线时,咱们不妨试着绘,100条曲线便没有成能再绘了,所以必须觅找到顺序.如下图所示,一个圆是1块;1条曲线将圆分为2块,即减少了1块;2条曲线时,当2条曲线没有相接时,减少了1块,当2条曲线相接时,减少了2块.由此瞅出,要念分成的块尽管多,应当使后绘的曲线尽管与前里已绘的曲线相接.再绘第3条曲线时,应当与前里2条曲线皆相接,那样又减少了3块(睹左下图);绘第4条曲线时,应当与前里3条曲线皆相接,那样又减少了4块(睹左下图).所以4条曲线最多将一个圆分成1+1+2+3+4=11(块).由上头的分解不妨瞅出,绘第n条曲线时应当与前里已绘的(n—1)条曲线皆相接,此时将减少n块.果为一启初的圆算1块,所以n条曲线最多将圆分成1+(1+2+3+…+n)=1+n(n+1)÷2(块).当n=100时,可分成1+100×(100+1)÷2=5051(块).例5 用3个三角形最多不妨把仄里分成几部分?10个三角形呢?分解与解:仄里自己是1部分.一个三角形将仄里分成三角形内、中2部分,即减少了1部分.二个三角形没有相接时将仄里分成3部分,相接时,接面越多分成的部分越多(睹下图).由上图瞅出,新减少的部分数与减少的接面数相共.所以,再绘第3个三角形时,应使每条边的接面尽管多.对付于每个三角形,果为1条曲线最多与三角形的二条边相接,所以第3个三角形的每条边最多与前里2个三角形的各二条边相接,共可爆收3×(2×2)= 12(个)接面,即减少12部分.果此, 3个三角形最多不妨把仄里分成1+1+6+12= 20(部分).由上头的分解,当绘第n(n≥2)个三角形时,每条边最多与前里已绘的(n—1)个三角形的各二条边相接,共可爆收接面3×[(n—l)×2]=6(n—1)(个),能新减少6(n-1)部分.果为1个三角形时有2部分,所以n个三角形最多将仄里分成的部分数是2+6×[1+2+…+(n—1)]当n=10时,可分成2+3×10×(10—1)=272(部分).训练1.供12边形的内角战.2.五边形内有8个面.以五边形的5个顶面战那8个面为三角形的顶面,最多能剪出几个小三角形?3.已知n棱柱有14个顶面,那么,它有几条棱?4.n条曲线最多有几个接面?5.6条曲线与2个圆最多产死几个接面?6.二个四边形最多把仄里分成几部分?训练问案:1.1800°.2.19个.提示:与例2类似可得5+2×(8-1)=19(个).3.21条棱.提示:n棱柱有2n个顶面,3n条棱.4.n(n-1)÷2.解:1+2+3+…+(n-1)=n(n-1)÷2.5.41个.解:6条曲线有接面6×(6-1)÷2=15(个),每条曲线与二个圆各有2个接面,二个圆之间有2个接面,公有接面15+6×4+2=41(个).6.10部分.提示:睹左图.与例5类似,当绘第n(n≥2)个四边形时,每条边应与已绘的(n-1)个四边形的各2条边相接,共可爆收接面4×[(n-1)×2]=8(n-1)(个),新减少8(n-1)部分.果为1个四边形有2部分,所以n个四边形最多将仄里分成2+8×[1+2+…+(n-1)]=2+4n(n-1)(部分).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数专题:找规律
同学们从三年级开始,就陆续接触过许多“找规律”的题目,例如发现图形、数字或数表的变化规律,发现数列的变化规律,发现周期变化规律等等。
这一讲的内容是通过发现某一问题的规律,推导出该问题的计算公式。
例1 求99边形的内角和。
分析与解:三角形的内角和等于180°,可是99边形的内角和怎样求呢?我们把问题简化一下,先求四边形、五边形、六边形……的内角和,找一找其中的规律。
如上图所示,将四边形ABCD分成两个三角形,每个三角形的内角和等于180°,所以四边形的内角和等于180°×2= 360°;同理,将五边形ABCDE分成三个三角形,得到五边形的内角和等于180°×3=540°;将六边形ABCDEF分成四个三角形,得到六边形的内角和等于180°×4=720°。
通过上面的图形及分析可以发现,多边形被分成的三角形数,等于边数减2。
由此得到多边形的内角和公式:
n边形的内角和=180°×(n-2)(n≥3)。
有了这个公式,再求99边形的内角和就太容易了。
99边形的内角和=180°×(99-2)=17460°。
例2 四边形内有10个点,以四边形的4个顶点和这10个点为三角形的顶点,最多能剪出多少个小三角形?
分析与解:在10个点中任取一点A,连结A与四边形的四个顶点,构成4个三角形。
再在剩下的9个点中任取一点B。
如果B在某个三角形中,那么连结B与B所在的三角形的三个顶点,此时三角形总数增加2个(见左下图)。
如果B在某两个三角形的公共边上,那么连结B与B所在边相对的顶点,此时三角形总数也是增加2个(见右下图)。
类似地,每增加一个点增加2个三角形。
所以,共可剪出三角形 4+2× 9= 22(个)。
如果将例2的“10个点”改为n个点,其它条件不变,那么由以上的分析可知,最多能剪出三角形
4+2×(n-1)=2n+2=2×(n+1)(个)。
同学们都知道圆柱体,如果将圆柱体的底面换成三角形,那么便得到了三棱柱(左下图);同理可以得到四棱柱(下中图),五棱柱(右下图)。
如果底面是正三角形、正四边形、正五边形……那么相应的柱体就是正三棱柱、正四棱
柱、正五棱柱……
例3 n棱柱有多少条棱?如果将不相交的两条棱称为一对,那么n棱柱共有多少对不相交的棱?
分析与解:n棱柱的底面和顶面都是n边形,每个n边形有n个顶点,所以n棱柱共有2n个顶点。
观察三棱柱、四棱柱、五棱柱的图形,可以看出,每个顶点都与三条棱相连,而每条棱连接 2个顶点,所以n棱柱共有棱2n×3÷2=3n(条)。
进一步观察可以发现,n棱柱中每条棱都与4条棱相交,与其余的3n-4-1 =(3n-5)条棱不相交。
共有3n条棱,所以不相交的棱有3n×(3n- 5)(条),因为不相交的棱是成对出现的,各计算一遍就重复了一遍,所以不相交的棱共有
3n×(3n-5)÷2(对)。
例4 用四条直线最多能将一个圆分成几块?用100条直线呢?
分析与解:4条直线时,我们可以试着画,100条直线就不可能再画了,所以必须寻找到规律。
如下图所示,一个圆是1块;1条直线将圆分为2块,即增加了1块;2条直线时,当2条直线不相交时,增加了1块,当2条直线相交时,增加了2块。
由此看出,要想分成的块尽量多,应当使后画的直线尽量与前面已画的直线相交。
再画第3条直线时,应当与前面2条直线都相交,这样又增加了3块(见左下图);画第4条直线时,应当与前面3条直线都相交,这样又增加了4块(见右下图)。
所以4条直线最多将一个圆分成1+1+2+3+4=11(块)。
由上面的分析可以看出,画第n条直线时应当与前面已画的(n—1)条直线都相交,此时将增加n块。
因为一开始的圆算1块,所以n条直线最多将圆分成
1+(1+2+3+…+n)
=1+n(n+1)÷2(块)。
当n=100时,可分成
1+100×(100+1)÷2=5051(块)。
例5 用3个三角形最多可以把平面分成几部分?10个三角形呢?
分析与解:平面本身是1部分。
一个三角形将平面分成三角形内、外2部分,即增加了1部分。
两个三角形不相交时将平面分成3部分,相交时,交点越多分成的部分越多(见下图)。
由上图看出,新增加的部分数与增加的交点数相同。
所以,再画第3个三角形时,应使
每条边的交点尽量多。
对于每个三角形,因为1条直线最多与三角形的两条边相交,所以第3个三角形的每条边最多与前面2个三角形的各两条边相交,共可产生3×(2×2)= 12(个)交点,即增加12部分。
因此, 3个三角形最多可以把平面分成
1+1+6+12= 20(部分)。
由上面的分析,当画第n(n≥2)个三角形时,每条边最多与前面已画的(n—1)个三角形的各两条边相交,共可产生交点
3×[(n—l)×2]=6(n—1)(个),能新增加6(n-1)部分。
因为1个三角形时有2部分,所以n个三角形最多将平面分成的部分数是
2+6×[1+2+…+(n—1)]
当n=10时,可分成2+3×10×(10—1)=272(部分)。
练习
1.求12边形的内角和。
2.五边形内有8个点。
以五边形的5个顶点和这8个点为三角形的顶点,最多能剪出多少个小三角形?
3.已知n棱柱有14个顶点,那么,它有多少条棱?
4.n条直线最多有多少个交点?
5.6条直线与2个圆最多形成多少个交点?
6.两个四边形最多把平面分成几部分?
练习答案:
1.1800°。
2.19个。
提示:与例2类似可得5+2×(8-1)=19(个)。
3.21条棱。
提示:n棱柱有2n个顶点,3n条棱。
4.n(n-1)÷2。
解:1+2+3+…+(n-1)=n(n-1)÷2。
5.41个。
解:6条直线有交点6×(6-1)÷2=15(个),每条直线与两个圆各有2个交点,两个圆之间有2个交点,共有交点15+6×4+2=41(个)。
6.10部分。
提示:见右图。
与例5类似,当画第n(n≥2)个四边形时,每条边应与已画的(n-1)个四边形的各2条边相交,共可产生交点
4×[(n-1)×2]=8(n-1)(个),新增加8(n-1)部分。
因为1个四边形有2部分,所以n个四边形最多将平面分成2+8×[1+2+…+(n-1)]=2+4n(n-1)(部分)。
