数学物理方法快速学习资料及练习题
物理解题方法:数学物理法习题知识点及练习题及答案解析

物理解题方法:数学物理法习题知识点及练习题及答案解析一、高中物理解题方法:数学物理法1.一透明柱体的横截面如图所示,圆弧AED 的半径为R 、圆心为O ,BD ⊥AB ,半径OE ⊥AB 。
两细束平行的相同色光1、2与AB 面成θ=37°角分别从F 、O 点斜射向AB 面,光线1经AB 面折射的光线恰好通过E 点。
已知OF =34R ,OB =38R ,取sin 370.6︒=,cos 370.8︒=。
求:(1)透明柱体对该色光的折射率n ;(2)光线2从射入柱体到第一次射出柱体的过程中传播的路程x 。
【答案】(1)43;(2)54R 【解析】 【分析】 【详解】(1)光路图如图:根据折射定律sin(90)sin n θα︒-=根据几何关系3tan 4OF OE α== 解得37α︒=43n =(2)该色光在柱体中发生全反射时的临界角为C ,则13sin 4C n == 由于sin sin(90)sin530.8sin a C β︒︒=-==>光线2射到BD 面时发生全反射,根据几何关系3tan 82REH OE OH R R β=-=-=可见光线2射到BD 面时发生全反射后恰好从E 点射出柱体,有sin OBOGα= 根据对称性有2x OG =解得54x R =2.如图所示,质量为m=1kg 的物块与竖直墙面间动摩擦因数为=0.5,从t=0的时刻开始用恒力F 斜向上推物块,F 与墙面间夹角=37°,在t=0的时刻物块速度为0.(1)若F=12.5N ,墙面对物块的静摩擦力多大? (2)若F=30N ,物块沿墙面向上滑动的加速度多大?(3)若要物块保持静止,F 至少应为多大?(假设最大静摩擦力等于同样正压力时的滑动摩擦力,F 的计算结果保留两位有效数字)【答案】(1)0f =(2)25/a m s =(3)9.1F N = 【解析】试题分析:(1)设f 向上,37Fcos f mg ︒+=得0f =(2)根据牛顿第二定律可得cos37sin 37F F mg ma μ︒-︒-=,得25/a m s = (3)当物块即将下滑时,静摩擦最大且向上,cos37sin 37F F mg μ︒+︒=,得9.1F N =考点:考查了摩擦力,牛顿第二定律【名师点睛】在计算摩擦力时,首先需要弄清楚物体受到的是静摩擦力还是滑动摩擦力,如果是静摩擦力,其大小取决于与它反方向上的平衡力大小,与接触面间的正压力大小无关,如果是滑动摩擦力,则根据公式F N μ=去计算3.如图所示,一根一端封闭的玻璃管,内有一段长h =0.25m 的水银柱。
高考物理数学物理法解题技巧和训练方法及练习题

高考物理数学物理法解题技巧和训练方法及练习题一、数学物理法1.两块平行正对的水平金属板AB ,极板长0.2m L =,板间距离0.2m d =,在金属板右端竖直边界MN 的右侧有一区域足够大的匀强磁场,磁感应强度3510T B -=⨯,方向垂直纸面向里。
两极板间电势差U AB 随时间变化规律如右图所示。
现有带正电的粒子流以5010m/s v =的速度沿水平中线OO '连续射入电场中,粒子的比荷810C/kg qm=,重力忽略不计,在每个粒子通过电场的极短时间内,电场视为匀强电场(两板外无电场)。
求: (1)要使带电粒子射出水平金属板,两金属板间电势差U AB 取值范围;(2)若粒子在距O '点下方0.05m 处射入磁场,从MN 上某点射出磁场,此过程出射点与入射点间的距离y ∆;(3)所有粒子在磁场中运动的最长时间t 。
【答案】(1)100V 100V AB U -≤≤;(2)0.4m ;(3) 69.4210s -⨯ 【解析】 【分析】 【详解】(1)带电粒子刚好穿过对应偏转电压最大为m U ,此时粒子在电场中做类平抛运动,加速大小为a ,时间为t 1。
水平方向上01L v t =①竖直方向上21122d at =② 又由于mU qma d=③ 联立①②③得m 100V U =由题意可知,要使带电粒子射出水平金属板,两板间电势差100V 100V AB U -≤≤(2)如图所示从O '点下方0.05m 处射入磁场的粒子速度大小为v ,速度水平分量大小为0v ,竖直分量大小为y v ,速度偏向角为θ。
粒子在磁场中圆周运动的轨道半径为R ,则2mv qvB R=④ 0cos v v θ=⑤2cos y R θ∆=⑥联立④⑤⑥得20.4m mv y qB∆== (3)从极板下边界射入磁场的粒子在磁场中运动的时间最长。
如图所示粒子进入磁场速度大小为v 1,速度水平分量大小为01v ,竖直分量大小为v y 1,速度偏向角为α,则对粒子在电场中011L v t =⑦11022y v d t +=⑧ 联立⑦⑧得101y v v =101tan y v v α=得π4α=粒子在磁场中圆周运动的轨道半径为R ',则211mv qv B R ='⑨ 1mv R qB'=⑩ 带电粒子在磁场中圆周运动的周期为T12π2πR m T v qB'==⑪在磁场中运动时间2π(π2)2πt T α--=⑫联立⑪⑫得663π10s 9.4210s t --=⨯=⨯2.一透明柱体的横截面如图所示,圆弧AED 的半径为R 、圆心为O ,BD ⊥AB ,半径OE ⊥AB 。
数学物理方法快速学习资料与练习题

现代远程教育《数学物理方法》课程学习指导书作者:赵先林08年 2月课程学习方法指导为便于学员尽快进入本课程的学习,下面将简要介绍本课程的性质及基本要求,并给出学习方法指导。
一、课程的性质、目的和任务通过本课程的学习,使学生掌握复变函数、数学物理方程和特殊函数的基本理论、建模方法和计算方法,并能将数学结果联系物理实际,加深对物理理论的理解,为学习电动力学和量子力学等后继课程打下良好的基础。
二、课程教学的基本要求通过本课程的教学,学员应达到下列基本要求:1.掌握复变函数论的基本理论、微分和积分的方法、了解残数及其在积分中的应用2.掌握弦振动方程、热传导方程、电报方程的建模过程3.初步学会确定边界条件和初始条件4.熟练掌握分离变量法、达朗贝尔法、付里叶变换法和拉普拉斯变换法5.了解特殊函数的导出和意义三、学习方法建议学习本课程最基本的方法是课前预习,课后复习,多做习题。
针对课前预习时存在的问题,通过上课时认真的学习,并尝试运用上课时所学内容解决这些问题,或者通过课外指导书,仔细研究书中例题,在此过程中搞懂、会做课后习题,从而对课程内容有进一步认识。
此外,每章结束后,做好阶段性总结。
还要制定学习计划,善于自主学习。
学习中,既重视知识的记忆,也重视对知识的反思。
此外,为方便大家自主学习,现将教材及参考书罗列如下:(一)教材:《高等数学》(第四册).四川大学.高等教育出版社(二)参考书:1、《数学物理方法》,梁昆淼,高等教育出版社,第三版2、《数学物理方法教程》,刘志旺,高等教育出版社3、《数学物理方法学习指导》,姚端正,科学出版社希望各位学员善于这些教参书,能取得一个良好的成绩。
课程学习进度安排课程学习课时分配第一章复数和复变函数一、 章节学习目标1. 熟练掌握复数的运算。
2. 掌握复数的几种表示法及互换关系,能正确地求出复数的实部、虚部、模与辐角,了解共轭复数的性质。
3. 理解复数的几何意义。
4. 了解各种区域。
高中物理数学物理法的基本方法技巧及练习题及练习题
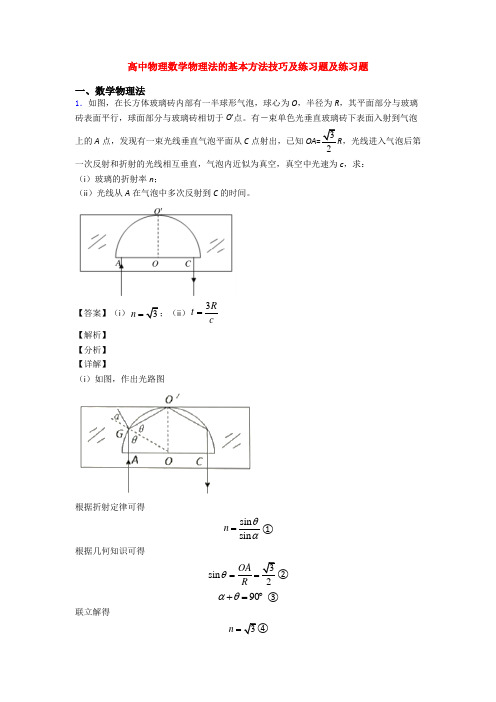
高中物理数学物理法的基本方法技巧及练习题及练习题一、数学物理法1.如图,在长方体玻璃砖内部有一半球形气泡,球心为O ,半径为R ,其平面部分与玻璃砖表面平行,球面部分与玻璃砖相切于O '点。
有-束单色光垂直玻璃砖下表面入射到气泡上的A 点,发现有一束光线垂直气泡平面从C 点射出,已知OA =32R ,光线进入气泡后第一次反射和折射的光线相互垂直,气泡内近似为真空,真空中光速为c ,求: (i )玻璃的折射率n ;(ii )光线从A 在气泡中多次反射到C 的时间。
【答案】(i )3n =;(ii )3t R c=【解析】 【分析】 【详解】(i )如图,作出光路图根据折射定律可得sin sin n θα=① 根据几何知识可得3sin 2OA R θ==② 90αθ+=︒ ③联立解得3n =玻璃的折射率为3。
(ii )光从A 经多次反射到C 点的路程322R Rs R R R =+++=⑤ 时间st c=⑥ 得3t R c=光线从A 在气泡中多次反射到C 的时间为3R c。
2.质量为M 的木楔倾角为θ,在水平面上保持静止,质量为m 的木块刚好可以在木楔上表面上匀速下滑.现在用与木楔上表面成α角的力F 拉着木块匀速上滑,如图所示,求:(1)当α=θ时,拉力F 有最小值,求此最小值; (2)拉力F 最小时,木楔对水平面的摩擦力. 【答案】(1)mg sin 2θ (2)12mg sin 4θ 【解析】 【分析】对物块进行受力分析,根据共点力平衡,利用正交分解,在沿斜面方向和垂直于斜面方向都平衡,进行求解采用整体法,对m 、M 构成的整体列平衡方程求解. 【详解】(1)木块刚好可以沿木楔上表面匀速下滑时,mg sin θ=μmg cos θ,则μ=tan θ,用力F 拉着木块匀速上滑,受力分析如图甲所示,则有:F cos α=mg sin θ+F f ,F N +F sin α=mg cos θ, F f =μF N联立以上各式解得:()sin 2cos mg F θθα=-.当α=θ时,F有最小值,F min=mg sin 2θ.(2)对木块和木楔整体受力分析如图乙所示,由平衡条件得,F f′=F cos(θ+α),当拉力F最小时,F f′=F min·cos 2θ=12mg sin 4θ.【点睛】木块放在斜面上时正好匀速下滑隐含摩擦系数的数值恰好等于斜面倾角的正切值,当有外力作用在物体上时,列平行于斜面方向的平衡方程,结合数学知识即可解题.3.如图所示,现有一质量为m、电荷量为e的电子从y轴上的()0,P a点以初速度v平行于x轴射出,为了使电子能够经书过x轴上的(),0Q b点,可在y轴右侧加一垂直于xOy 平面向里、宽度为L的匀强磁场,磁感应强度大小为B,该磁场左、右边界与y轴平行,上、下足够宽(图中未画出).已知002mv mveB eB<α<,L b<.求磁场的左边界距坐标原点的可能距离.(结果可用反三角函数表示)【答案】01(1cos)cotmvx b L aeBθθ⎡⎤=----⎢⎥⎣⎦(其中θ=arcsineBLmv)或222mv ax b aeB=--【解析】【分析】先根据洛伦兹力提供向心力求解出轨道半径表达式;当r>L时,画出运动轨迹,根据几何关系列式求解;当r≤L时,再次画出轨迹,并根据几何关系列式求解.【详解】设电子在磁场中做圆周运动的轨道半径为r,则2vmerBv=,解得0mvreB=(1)当r>L时,磁场区域及电子运动轨迹如图所示由几何关系有:0L eBL sin r mv θ== 则磁场左边界距坐标原点的距离为[]11x b L a r cos cot θθ=----() 解得:011mv x b L a cos cot eB θθ⎡⎤=----⎢⎥⎣⎦()(其中0eBL arcsin mv θ=) (2)当r≤L 时,磁场区域及电子运动轨迹如图所示由几何关系得磁场左边界距坐标原点的距离为222()x b r a r =--- 解得2022mv ax b a eB=-- 【点睛】本题关键分r >L 和r≤L 两种情况讨论,画出轨迹是关键,根据几何关系列方程求解是难点.4.一路灯距地面的高度为h ,身高为L 的人以速度v 匀速行走,如图所示: (1)试证明人的头顶的影子做匀速直线运动; (2)求人影的长度随时间的变化率。
(物理)高中必备物理数学物理法技巧全解及练习题

(物理)高中必备物理数学物理法技巧全解及练习题一、数学物理法1.如图所示,直角MNQ △为一个玻璃砖的横截面,其中90Q ︒∠=,30N ︒∠=,MQ 边的长度为a ,P 为MN 的中点。
一条光线从P 点射入玻璃砖,入射方向与NP 夹角为45°。
光线恰能从Q 点射出。
(1)求该玻璃的折射率;(2)若与NP 夹角90°的范围内均有上述同频率光线从P 点射入玻璃砖,分析计算光线不能从玻璃砖射出的范围。
【答案】(1)2;(2)312a - 【解析】 【详解】(1)如图甲,由几何关系知P 点的折射角为30°。
则有sin 452sin 30n == (2)如图乙,由折射规律结合几何关系知,各方向的入射光线进入P 点后的折射光线分布在CQB 范围内,设在D 点全反射,则DQ 范围无光线射出。
D 点有1sin n α=解得由几何关系知DQ EQ ED =-,12ED EP a ==,32EQ a = 解得31DQ a -=2.如图所示,空间有场强E =1.0×102V/m 竖直向下的电场,长L =0.8m 不可伸长的轻绳固定于O 点.另一端系一质量m =0.5kg 带电q =+5×10-2C 的小球.拉起小球至绳水平后在A 点无初速度释放,当小球运动至O 点的正下方B 点时绳恰好断裂,小球继续运动并垂直打在同一竖直平面且与水平面成θ=53°、无限大的挡板MN 上的C 点.试求:(1)小球运动到B 点时速度大小及绳子的最大张力; (2)小球运动到C 点时速度大小及A 、C 两点的电势差;(3)当小球运动至C 点时,突然施加一恒力F 作用在小球上,同时把挡板迅速水平向右移至某处,若小球仍能垂直打在档板上,所加恒力F 的最小值。
【答案】(1)30N ; (2)125V ; (3)0~127︒︒ 【解析】 【分析】 【详解】(1)小球到B 点时速度为v ,A 到B 由动能定理21()2mg qE L mv +=2()v F mg qE m L-+=解得42/v m s =F=30N(2)高AC 高度为h AC ,C 点速度为v 1152m/s sin v v θ==211()2AC mg qE h mv +=解得U =125V(3)加恒力后,小球做匀速直线运动或者匀加速直线运动,设F 与竖直方向夹角为α,当小球匀速直线运动时α=0,当小球匀加速直线运动时,F 的最小值为F 1,F 没有最大值1()sin 8N F mg qE θ=+=F 与竖直方向的最大夹角为180127αθ=︒-=︒ 0127α≤≤︒F ≥8N3.如图所示,在xoy 平面内y 轴右侧有一范围足够大的匀强磁场,磁感应强度大小为B ,磁场方向垂直纸面向外;分成I 和II 两个区域,I 区域的宽度为d ,右侧磁场II 区域还存在平行于xoy 平面的匀强电场,场强大小为E =22B qdm,电场方向沿y 轴正方向。
高中物理数学物理法技巧(很有用)及练习题

高中物理数学物理法技巧(很有用)及练习题一、数学物理法1.如图所示,在竖直边界1、2间倾斜固定一内径较小的光滑绝缘直管道,其长度为L ,上端离地面高L ,下端离地面高2L.边界1左侧有水平向右的匀强电场,场强大小为E 1(未知),边界2右侧有竖直向上的场强大小为E 2(未知)的匀强电场和垂直纸面向里的匀强磁场(图中未画出).现将质量为m 、电荷量为q 的小球从距离管上端口2L 处无初速释放,小球恰好无碰撞进入管内(即小球以平行于管道的方向进入管内),离开管道后在边界2右侧的运动轨迹为圆弧,重力加速度为g . (1)计算E 1与E 2的比值;(2)若小球第一次过边界2后,小球运动的圆弧轨迹恰好与地面相切,计算满足条件的磁感应强度B 0;(3)若小球第一次过边界2后不落到地面上(即B >B 0),计算小球在磁场中运动到最高点时,小球在磁场中的位移与小球在磁场中运动时间的比值.(若计算结果中有非特殊角的三角函数,可以直接用三角函数表示)【答案】(131;(23(23)m gL -;(3)36gL︒【解析】 【分析】根据题意,粒子先经过电场,做匀加速直线运动,在进入管中,出来以后做匀速圆周运动,画出物体的运动轨迹,再根据相关的公式和定理即可求解。
【详解】(1)设管道与水平面的夹角为α,由几何关系得:/21sin 2L L L α-== 解得:30︒=α由题意,小球在边界1受力分析如下图所示,有:1tan mg qE α=因小球进入边界2右侧区域后的轨迹为圆弧,则有:mg =qE 2解得比值:E 1 :E 2=3:1(2)设小球刚进入边界2时速度大小为v ,由动能定理有:2113sin302cos302mg L E q L mv ︒︒⋅+⋅=联立上式解得:3v gL =设小球进入E 2后,圆弧轨迹恰好与地面相切时的轨道半径为R ,如下图,由几何关系得:cos30+2L R R ︒= 代入数据解得:(23)R L =+洛伦兹力提供向心力,由牛顿第二定律得:20v qvB m R=代入数据解得:03(23)m gLB -=(3)如下图,设此时圆周运动的半径为r ,小球在磁场中运动到最高点时的位移为:2cos15S r ︒=⋅圆周运动周期为:2rT vπ=则小球运动时间为:712t T =解得比值:362cos15cos157712gL S r t Tπ︒==︒【点睛】考察粒子在复合场中的运动。
高中物理数学物理法技巧和方法完整版及练习题
高中物理数学物理法技巧和方法完整版及练习题一、数学物理法1.如图所示,在x ≤0的区域内存在方向竖直向上、电场强度大小为E 的匀强电场,在x >0的区域内存在方向垂直纸面向外的匀强磁场。
现一带正电的粒子从x 轴上坐标为(-2l ,0)的A 点以速度v 0沿x 轴正方向进入电场,从y 轴上坐标为(0,l )的B 点进入磁场,带电粒子在x >0的区域内运动一段圆弧后,从y 轴上的C 点(未画出)离开磁场。
已知磁场的磁感应强度大小为,不计带电粒子的重力。
求: (1)带电粒子的比荷; (2)C 点的坐标。
【答案】(1)202v qm lE=;(2)(0,-3t )【解析】 【详解】(1)带电粒子在电场中做类平抛运动,x 轴方向02l v t =y 轴方向212qE l t m=联立解得202v qm lE=(2)设带电粒子经过B 点时的速度方向与水平方向成θ角00tan 1yqE t v m v v θ===解得45θ=︒则带电粒子经过B 点时的速度02v v =由洛伦兹力提供向心力得2mv qvB r= 解得22mvr l qB== 带电粒子在磁场中的运动轨迹如图所示根据几何知识可知弦BC 的长度24L r l ==43l l l -=故C 点的坐标为(0,-3t )。
2.[选修模块3-5]如图所示,玻璃砖的折射率3n =,一细光束从玻璃砖左端以入射角i 射入,光线进入玻璃砖后在上表面恰好发生全反射.求光速在玻璃砖中传播的速度v 及入射角i .(已知光在真空中传播速度c =3.0×108 m/s ,计算结果可用三角函数表示).【答案】83310/2v m s =;3sin 3i =【解析】 【分析】 【详解】 根据c n v =,83310/v m s = 全反射条件1sin C n=,解得C=600,r =300, 根据sin sin i n r =,3sin i =3.质量为M 的木楔倾角为θ (θ < 45°),在水平面上保持静止,当将一质量为m 的木块放在木楔斜面上时,它正好匀速下滑.当用与木楔斜面成α角的力F 拉木块,木块匀速上升,如图所示(已知木楔在整个过程中始终静止).(1)当α=θ时,拉力F 有最小值,求此最小值; (2)求在(1)的情况下木楔对水平面的摩擦力是多少? 【答案】(1)min sin 2F mg θ= (2)1sin 42mg θ 【解析】 【分析】(1)对物块进行受力分析,根据共点力的平衡,利用正交分解,在沿斜面和垂直斜面两方向列方程,进行求解.(2)采用整体法,对整体受力分析,根据共点力的平衡,利用正交分解,分解为水平和竖直两方向列方程,进行求解. 【详解】木块在木楔斜面上匀速向下运动时,有mgsin mgcos θμθ=,即tan μθ= (1)木块在力F 的作用下沿斜面向上匀速运动,则:Fcos mgsin f αθ=+N Fsin F mgcos αθ+=N f F μ=联立解得:()2mgsin F cos θθα=-则当=αθ时,F 有最小值,2min F mgsin =θ(2)因为木块及木楔均处于平衡状态,整体受到地面的摩擦力等于F 的水平分力,即()f Fcos αθ='+当=αθ时,12242f mgsin cos mgsin θθθ='= 【点睛】木块放在斜面上时正好匀速下滑隐含动摩擦因数的值恰好等于斜面倾角的正切值,当有外力作用在物体上时,列平行于斜面方向的平衡方程,求出外力F 的表达式,讨论F 取最小值的条件.4.图示为一由直角三角形ABC 和矩形CDEA 组成的玻璃砖截面图。
高考物理数学物理法的基本方法技巧及练习题及练习题
高考物理数学物理法的基本方法技巧及练习题及练习题一、数学物理法1.如图所示,在竖直分界线MN 的左侧有垂直纸面的匀强磁场,竖直屏与MN 之间有方向向上的匀强电场。
在O 处有两个带正电的小球A 和B ,两小球间不发生电荷转移。
若在两小球间放置一个被压缩且锁定的小型弹簧(不计弹簧长度),解锁弹簧后,两小球均获得沿水平方向的速度。
已知小球B 的质量是小球A 的1n 倍,电荷量是小球A 的2n 倍。
若测得小球A 在磁场中运动的半径为r ,小球B 击中屏的位置的竖直偏转位移也等于r 。
两小球重力均不计。
(1)将两球位置互换,解锁弹簧后,小球B 在磁场中运动,求两球在磁场中运动半径之比、时间之比;(2)若A 小球向左运动求A 、B 两小球打在屏上的位置之间的距离。
【答案】(1)2n ,21n n ;(2)123rr n n -【解析】 【详解】(1)两小球静止反向弹开过程,系统动量守恒有A 1B mv n mv =①小球A 、B 在磁场中做圆周运动,分别有2A A A mv qv B r =,21B2B Bn mv n qv B r =②解①②式得A2Br n r = 磁场运动周期分别为A 2πmT qB=,1B 22πn m T n qB =解得运动时间之比为AA2BB122Tt nTt n==(2)如图所示,小球A经圆周运动后,在电场中做类平抛运动。
水平方向有A AL v t=③竖直方向有2A A A12y a t=④由牛顿第二定律得AqE ma=⑤解③④⑤式得2AA()2qE Lym v=⑥小球B在电场中做类平抛运动,同理有22B1B()2n qE Lyn m v=⑦由题意知By r=⑧应用几何关系得B A2y y r y∆=+-⑨解①⑥⑦⑧⑨式得123ry rn n∆=-2.如图,在长方体玻璃砖内部有一半球形气泡,球心为O,半径为R,其平面部分与玻璃砖表面平行,球面部分与玻璃砖相切于O'点。
高考物理数学物理法技巧和方法完整版及练习题
高考物理数学物理法技巧和方法完整版及练习题一、数学物理法1.如图所示,在竖直分界线MN 的左侧有垂直纸面的匀强磁场,竖直屏与MN 之间有方向向上的匀强电场。
在O 处有两个带正电的小球A 和B ,两小球间不发生电荷转移。
若在两小球间放置一个被压缩且锁定的小型弹簧(不计弹簧长度),解锁弹簧后,两小球均获得沿水平方向的速度。
已知小球B 的质量是小球A 的1n 倍,电荷量是小球A 的2n 倍。
若测得小球A 在磁场中运动的半径为r ,小球B 击中屏的位置的竖直偏转位移也等于r 。
两小球重力均不计。
(1)将两球位置互换,解锁弹簧后,小球B 在磁场中运动,求两球在磁场中运动半径之比、时间之比;(2)若A 小球向左运动求A 、B 两小球打在屏上的位置之间的距离。
【答案】(1)2n ,21n n ;(2)123rr n n -【解析】 【详解】(1)两小球静止反向弹开过程,系统动量守恒有A 1B mv n mv =①小球A 、B 在磁场中做圆周运动,分别有2A A A mv qv B r =,21B2B Bn mv n qv B r =②解①②式得A2Br n r = 磁场运动周期分别为A 2πmT qB=,1B 22πn m T n qB =解得运动时间之比为AA2BB122Tt nTt n==(2)如图所示,小球A经圆周运动后,在电场中做类平抛运动。
水平方向有A AL v t=③竖直方向有2A A A12y a t=④由牛顿第二定律得AqE ma=⑤解③④⑤式得2AA()2qE Lym v=⑥小球B在电场中做类平抛运动,同理有22B1B()2n qE Lyn m v=⑦由题意知By r=⑧应用几何关系得B A2y y r y∆=+-⑨解①⑥⑦⑧⑨式得123ry rn n∆=-2.如图所示,在xoy平面内y轴右侧有一范围足够大的匀强磁场,磁感应强度大小为B,磁场方向垂直纸面向外;分成I和II两个区域,I区域的宽度为d,右侧磁场II区域还存在平行于xoy平面的匀强电场,场强大小为E=22B qdm,电场方向沿y轴正方向。
数学物理方法复习资料及参考答案(二)
数学物理方法复习资料及参考答案(二)一、选择题:1. 函数()f x 以0z 为中心的Taylor 展开的系数公式为:( )A ξξξπd z f i k C c k ⎰-=)()(20 B !)(0)(k z f C k k =C ξξξπd z f i C c k k ⎰+-=10)()(21 D ξξξπd z f i k C c k k ⎰+-=10)()(2 2。
⎰=-l dz a z )(( ) (其中l 表示以为a 中心ρ为半径的周围)。
A i ⋅πB iC i ⋅-πD 0 3. 非齐次边界条件)(),(0t u t u l x x νμ====,转化为齐次边界条件的方法:( )A )()(tB x t A + B x t A )(C )(t BD x t B x t A )()(2+ 4。
)(t f 是定义在半无界区间),0(∞上的函数,⎩⎨⎧<<<=)(0)0()(t T T t ht f在边界条件0)0(='f 下,把)(t f 展为实数形式傅立叶积分:( ) Aw h 12π B w wT h cos 2π C w wT h sin 2π D wwTh cos 12-π 5. 齐次边界条件0,00====l x x xu u 的本征值和本征函数:( ) A ),3,2,1,0(cos )(,222 ===n l xn C x X l n nn n ππλB ),3,2,1(sin )(,222 ===n l xn C x X l n nn n ππλC ),3,2,1,0()21(cos )(,)21(222 =+=+=n l xn C x X ln n n n ππλD ),3,2,1,0()21(sin )(,)21(222 =+=+=n l xn C x X l n nn n ππλ6. 若集合是( ),则该集合是区域。
A 开集B 连通开集C 连通闭集D 连通集 7. 设a 是)(z f 的可去奇点,则有:( )Alim ()Z af Z →存在且有限 Blim ()Z af Z →不存在C )(z f 在a 点的主要部分只有有限项D )(z f 在a 点的主要部分有无限多项8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代远程教育《数学物理方法》课程学习指导书作者:先林08年2月课程学习方法指导为便于学员尽快进入本课程的学习,下面将简要介绍本课程的性质及基本要求,并给出学习方法指导。
一、课程的性质、目的和任务通过本课程的学习,使学生掌握复变函数、数学物理方程和特殊函数的基本理论、建模方法和计算方法,并能将数学结果联系物理实际,加深对物理理论的理解,为学习电动力学和量子力学等后继课程打下良好的基础。
二、课程教学的基本要求通过本课程的教学,学员应达到下列基本要求:1.掌握复变函数论的基本理论、微分和积分的方法、了解残数及其在积分中的应用2.掌握弦振动方程、热传导方程、电报方程的建模过程3. 初步学会确定边界条件和初始条件4.熟练掌握分离变量法、达朗贝尔法、付里叶变换法和拉普拉斯变换法5.了解特殊函数的导出和意义三、学习方法建议学习本课程最基本的方法是课前预习,课后复习,多做习题。
针对课前预习时存在的问题,通过上课时认真的学习,并尝试运用上课时所学容解决这些问题,或者通过课外指导书,仔细研究书中例题,在此过程中搞懂、会做课后习题,从而对课程容有进一步认识。
此外,每章结束后,做好阶段性总结。
还要制定学习计划,善于自主学习。
学习中,既重视知识的记忆,也重视对知识的反思。
此外,为方便大家自主学习,现将教材及参考书罗列如下:(一)教材:《高等数学》(第四册).大学.高等教育(二)参考书:1、《数学物理方法》,梁昆淼,高等教育,第三版2、《数学物理方法教程》,志旺,高等教育3、《数学物理方法学习指导》,端正,科学希望各位学员善于这些教参书,能取得一个良好的成绩。
课程学习进度安排课程学习课时分配第一章复数和复变函数一、 章节学习目标1. 熟练掌握复数的运算。
2.掌握复数的几种表示法及互换关系,能正确地求出复数的实部、虚部、模与辐角,了解共轭复数的性质。
3.理解复数的几何意义。
4. 了解各种区域。
5. 理解复函的极限与连续。
6. 知道复函极限存在与连续的充要条件。
二、 章节重点本部分学习的主要容包括复数、复变函数的基本概念、复球面与无穷远点三个部分。
掌握复数的几种表示方法。
分别为以下三种:1.复数的代数表示;2.复数的几何表示;3.复数的指数表示。
其中复数的几何表示与指数表示可以使有关复数的运算简化,从而达到能够正确解题的要求。
例如计算复数的乘幂及复数的方根时,运用复数的几何表示和指数表示就能快速计算出结果。
对复数的运算规则也需掌握,需明确实数中的运算规则在复数中同样是适用的。
本部分学习的主要容还包括复变函数的基本概念。
其中所涉及复变函数的极限与连续问题,是首先要了解的。
对于复函的极限定义与连续定义需要知道。
并且需要知道复变函数极限存在与连续的充要条件,即函数),(),()(y x iv y x u z f +=在点000iy x z +=连续的充分必要条件是二元实函数),(),,(y x v y x u 于),(00y x 连续。
这是本章的重中之重,一定要掌握它的定义、定理以及应用,对这一部分书本上的例题要会计算。
三、 章节考试大纲第一节 复数 复数域 复平面 复数的模与幅角 复数的乘幂与方根 第二节 区域与约当曲线 复变函数的概念 复变函数的极限与连续性 第三节 复球面 闭平面上的几个概念四、 章节练习题(一) 选择题1.z 为复数,则()。
A ln z 没有意义;B ln z 为周期函数;C Ln z 为周期函数;D ln()ln z z -=-。
2.由对数函数的定义有()。
A()1212Ln z z Lnz Lnz +=•B ()22Ln z Lnz = C1122z Ln Lnz Lnzz ⎛⎫=-⎪⎝⎭D 0Lnz Lnz -=(二)填空题1.复数1i +的幅角为,模为。
2.函数zw R =,将z 平面的图形;以原点为中心,R 为半径的圆,变为w 平面的图形为。
第二章解析函数一、章节学习目标1 理解复函的导数的概念、解析函数的概念。
2 掌握复变函数解析的充要条件,并能应用函数解析的充要条件判别函数的解析性和可导性。
3 了解解析函数与调和函数的关系;掌握从已知调和函数求出解析函数的方法。
4 了解指数函数、对数函数、三角函数、幂函数的定义和性质.二、章节重点、要点本部分学习的主要容包括解析函数的概念及哥西-黎曼条件、解析函数与调和函数的关系、初等解析函数三个部分。
知道解析函数的概念,并且要深入掌握哥西-黎曼条件,哥西-黎曼条件是本章容的重要部分。
哥西-黎曼条件为下列公式,.u v u vx y y x ∂∂∂∂==∂∂∂∂,记为C -R 条件。
知道C -R 条件后,对函数可微的充分必要条件能更进一步了解。
即函数),(),()(y x iv y x u z f +=在点000iy x z +=可微的充分必要条件是二元实函数),(),,(y x v y x u 于),(00y x 可微并满足C -R 条件。
这是本章的重点,要掌握它的定义、定理以及应用。
掌握解析函数和调和函数之间的关系。
知道任何一个在区域D 上解析的函数),(),()(y x iv y x u z f +=,其实部与虚部都是该区域上的调和函数。
即满足条件0022222222=∂∂+∂∂=∂∂+∂∂yvx v y u x u ,。
对已知实虚部,再求解函数的习题,或已知函数,虚部的题要掌握,要学会计算。
对于初等解析函数部分,一些基本的解析函数,如幂函数nz ,指数函数ze ,三角函数sin ,cos ,z z 双曲函数sinh ,cosh ,z z ,等等。
它们都可以看成是相应实变函数在复数域中的推广。
要掌握·如何将相应实变函数推广到复数域 ·这些函数的解析性·这些函数作为复变函数所特有的性质 并且掌握初等多值函数的计算。
三、章节考试大纲第一节 导数的定义 哥西-黎曼条件 解析函数的定义 第二节 共厄调和函数的求法 共厄调和函数的几何意义 第三节 初等单值函数 初等多值函数四、章节练习题(一)计算题1.已知1)(,332-=-=i f y y x u ,求解析函数iv u z f +=)(。
2.设ω=0arg(1)2z π≤-<,求(2),(),(0),()i i ωωωω-。
第三章哥西定理 哥西积分一、章节学习目标1.掌握复变函数积分的定义、基本性质及计算方法。
2.记住并能熟练地运用公式()2,10,1nli n dzn z a π=⎧=⎨≠-⎩⎰。
3.牢固地掌握哥西定理及其推广定理。
4.掌握哥西积分公式及其推广定理。
5.掌握解析函数的任意阶导数的存在性。
6.熟练地运用哥西积分公式和柯西导数公式计算复变函数的围道积分。
7.解析函数在平面场中的应用。
二、章节重点、要点本部分学习的主要容包括复变积分的概念及其简单性质、哥西积分及其推广、哥西积分公式及其推广、解析函数再平面场中的应用四个方面。
会计算一般的积分,并且要掌握哥西积分定理,知道哥西定理的使用条件和围。
若函数()f z 在单连通区域D 上解析,C 是D 的任意一条分段光滑的围线,则()0cf z dz =⎰。
在运用哥西定理解题的时候,要分清积分路径所包含的围,注意函数()f z 在区域D 是否解析。
只有当满足所有条件时,才能运用哥西定理。
对于哥西定理的推广这一部分的容是一样的运用原理。
此外,书本上例题5也是很重要的容,通过此例题的结论()2,10,1nli n dzn z a π=⎧=⎨≠-⎩⎰也可求积分的值,是很重要的结论。
因此需要将此结论深入理解并记住,并将书上例题掌握。
对于哥西积分公式⎰-=c d zf i z f ξξξπ)(21)(可以改写成()2()c f z dz if a z a π=-⎰这个公式表明,对于在某界闭域上解析的函数,它在区域一点的值可用它在边界上的值表示出来。
这是解析函数的一个基本性质。
借用此公式可以计算某些围线积分。
对解析函数在平面场中的应用部分需要掌握复位势的定义概念,并会计算例题。
三 、章节考试大纲第一节 哥西积分的定义及其计算方法 复变积分的简单性质第二节 哥西积分定理 不定积分 哥西积分定理推广到复围线的情形第三节 哥西积分公式 解析函数的无限次可微性 模的最大值原理 哥西不等式 维尔定理 摩勒纳定理第四节 什么叫平面场 复位势 举例四、章节练习题(一)选择题1.下列积分不为零的是()。
A 0.51z dz z π=+⎰; B 20.51z dz z π=-⎰;C10.5z dzz π=+⎰; D211z dz z π=-⎰。
(二) 填空题1.15z dzz ==+⎰。
(三)计算题1.计算积分⎰czdz Re ,其中积分路径如右图示,(1)C 为连结O 点到i +1点的直线段(2)C 为连结O 点到1点再到i +1点的折线2.计算cos .xx e dx x -∞-⎰3.计算积分⎰-=c z dzI 12, 此处C 是2=z 。
第四章解析函数的幂级数表示一、章节学习目标1.了解在复数围级数及级数的收敛、发散、绝对收敛、一致收敛及有关性质,会使用收敛判据。
2. 正确确定幂级数的收敛半径,并了解幂级数的性质。
3. 掌握泰勒级数与解析函数的关系及泰勒展开的方法。
4. 掌握罗朗级数与奇点存在的关系。
5. 罗朗级数展开的方法。
6. 理解其收敛半径与孤立奇点的关系。
7. 孤立奇点的类型。
8. 精确地判断孤立奇点的类型,掌握其特点。
二、章节重点、要点本部分学习的主要容包括函数项级数的基本性质、幂级数与解析函数、罗朗级数、单值函数的孤立奇点四个方面。
了解幂级数与解析函数的关系,知道解析函数可以表示成幂级数。
根据解析函数的解析围,有两种展开方法可将解析函数表示成幂级数。
(一) 泰勒定理设()f z 在区域D 解析, a D ∈,只要圆:K z a R -<含于D ,则()f z 在K能展成幂级数0()()nn n f z c z a ∞==-∑,其中系数()(),0,1,2,,!n n f a c n n ==并且展式是唯一的,此展式称为是()f z 在a 点的泰勒展式,这样确定的系数称为泰勒系数。
可通过上述定理将一个解析函数展开成幂级数。
泰勒展开总结:1、泰勒级数在解析圆域进行展开。
2、展开式是唯一的,可用各种方法展开。
3、展开式在其可展区域是收敛的。
(二)罗朗定理 在圆环:(0,)H r z a R r R <-<≥<∞的解析函数()f z 必可展成级数()()nn n f z c z a ∞=-∞=-∑其中11(),0,1,2,2()n n f c d n i a γζζπζ+==±±-⎰称为罗朗系数,右边的级数称为罗朗级数。
