信号与系统 冲激函数
阶跃函数和冲激函数

控制系统的性能优化
阶跃函数用于测试控制系统的 性能,通过观察系统对阶跃输 入的响应速度和超调量,可以
评估系统的性能。
冲激函数可用于分析系统的 频率响应,了解系统在不同 频率下的性能表现,为系统
性能优化提供依据。
通过调整控制系统的参数,结 合阶跃函数和冲激函数的特性, 可以优化控制系统的性能指标。
控制系统的故障诊断与修复
在图形上,冲激函数看起来像一个非 常窄的矩形脉冲。
应用场景
在信号处理中,冲激函数常被 用作单位冲激信号,用于表示 某一事件的发生或开始。
在物理学中,冲激函数可以用 于描述瞬间作用或力的作用, 例如碰撞或冲击。
在电路分析中,冲激函数可以 用于描述电路中的瞬态响应或 冲激响应。
03
阶跃函数与冲激函数的 比较
05
阶跃函数和冲激函数在 控制系统中的应用
控制系统的稳定性分析
01
阶跃函数用于分析控制系统的稳定性,通过观察系统
对阶跃输入的响应,可以判断系统是否稳定。
02
冲激函数可用于分析系统的零点和极点,进一步确定
系统的稳定性。
03
通过计算系统的传递函数,结合阶跃函数和冲激函数
的性质,可以判断系统在不同频率下的稳定性。
阶跃函数和冲激函数可用于检测控制系统的故障,通过观察系统对输入信号的响应变化,可以判断系 统是否存在故障。
阶跃函数和冲激函数还可以用于定位故障,通过分析系统在不同输入下的响应特性,可以确定故障发生 的位置。
在故障诊断的基础上,可以利用阶跃函数和冲激函数的特性,制定相应的修复措施,恢复控制系统的正 常运行。
04
阶跃函数和冲激函数在 信号处理中的应用
信号的分离与提取
信号与系统傅里叶变换对照表

信号与系统傅里叶变换对照表
傅里叶变换是信号与系统领域中非常重要的数学工具,它将一个时域信号转换为频域信号,可以帮助我们理解信号的频谱特性。
下面是一份傅里叶变换的对照表,列出了一些常见的信号和它们的傅里叶变换形式:
1. 单位冲激函数(单位脉冲):
时域表示,δ(t)。
频域表示,1。
2. 正弦函数:
时域表示,sin(2πft)。
频域表示,jπ[δ(f-f0) δ(f+f0)]
3. 余弦函数:
时域表示,cos(2πft)。
频域表示,1/2[δ(f-f0) + δ(f+f0)] 4. 矩形脉冲信号:
时域表示,rect(t/T)。
频域表示,T sinc(fT)。
5. 三角脉冲信号:
时域表示,tri(t/T)。
频域表示,T^2 sinc^2(fT)。
6. 高斯脉冲信号:
时域表示,exp(-πt^2/σ^2)。
频域表示,exp(-π^2f^2σ^2)。
7. 指数衰减信号:
时域表示,exp(-at)。
频域表示,1/(a+j2πf)。
8. 阶跃函数(单位阶跃函数):
时域表示,u(t)。
频域表示,1/(j2πf) + 1/2。
9. 周期方波信号:
时域表示,square(t/T)。
频域表示,(1/T)[δ(f-nf0) + δ(f+nf0)], n为整数。
以上仅列举了一些常见的信号及其傅里叶变换形式。
傅里叶变换对照表可以帮助我们在信号分析和系统设计中快速理解信号的频域特性,从而更好地理解信号与系统的行为和特性。
信号与系统(吴大正)--完整版答案--纠错修改后版本
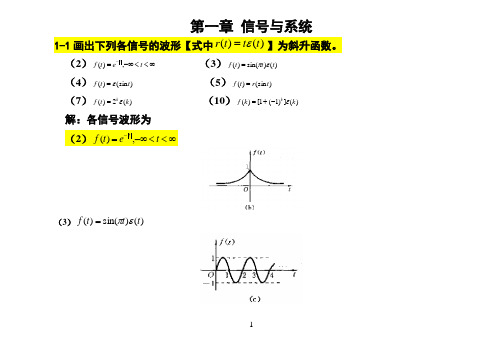
第一章 信号与系统1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为(3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与系统课件

■
信号与系统 电子教案 上述离散信号可简画为
f(k) 2 1 -1 2 1
1.2 信号的描述和分类
o 12 3 4 -1.5
或写为
k 1 用表达式可写为 1, 2, k 0 1.5, k 1 f ( k ) 2, k2 0, k 3 k 1, k 4 0, 其他k
f1(t) = sin(π t) 1 1 o -1
第1-7页
■
f2(t)
值域连 续
值域不 连续
o 1 2 t
1
2
t -1
信号与系统 电子教案
1.2 信号的描述和分类
离散时间信号: 仅在一些离散的瞬间才有定义的信号称为离散时间 信号,简称离散信号。实际中也常称为数字信号。 这里的“离散”指信号的定义域—时间是离散的, 它只在某些规定的离散瞬间给出函数值,其余时间无定 义。 如右图的f(t)仅在一些离散时刻 f(t) tk(k = 0,±1,±2,…)才有定义, 其余时间无定义。 2 2 1 相邻离散点的间隔Tk=tk+1-tk可 1 以相等也可不等。通常取等间隔T, o t1 t2 t3 t4 t-1 t 离散信号可表示为f(kT),简写为 f(k),这种等间隔的离散信号也常 -1.5 称为序列。其中k称为序号。
二、信号的时间变换运算
1. 反转
将 f (t) → f (– t) , f (k) → f (– k) 称为对信号f (· ) 的反转或反折。从图形上看是将f (· )以纵坐标为轴反 转180o。如
f (t) 1 o 1 t 反转 t → - t 1 -1 f (- t )
o
t
第1-18页
■
信号与系统 电子教案
《信号与系统》中冲激函数δ(t)的教学探讨

( p r n f l t ncIfr t nE g e r g S z o ct nl i r t, u h u 2 5 0 , hn ) De a me t e r i no ma o n i ei , u h uVo a o a Unv sy S z o 1 1 4 C i t oE co i n n i ei a
i f)(d=厂0 q3tt . ) ) (
# f)( td= ) I t —) l (8t o r ,
-
、, () 4
() 5
、。
; # 0
冲 激 函 数 的 采样 ( 选 ) 质 可 以 总结 为 4条 公 式 : 条 乘 积 , 条 积 分 。乘 积 公 式 在 使 用 时 要 与 卷 积 性 质 相 区别 , 例 题 2 积 筛 性 两 两 见 , 分 公 式 在 使 用 时 要 注 意 积 分 范 围是 否包 含 0或 t 下 面 举 例 说 明 。 o ,
若 函数 t tO连续 , 有 ) = 在 则 若 f】 tt连 续 , 有 (在 = t o 则 将 上 面两 式 分 别 取 积 分 , 得 可
f) (= o8t ( 8t )( t ) ) f)( t=( 8tt (8t o fo ( o t -) t —) )
() 2 () 3
Te c i g Dic s i n o r cDet u c i n i n o m a i n a d S se a h n s u so fDi a l F n t I f r to n y t m a o n
C HEN u ng— ong G a —h
Vo . , .5 e t mb r2 . 17 No2 ,S p e e 01 1
《 信号与系统》 中冲激 函数 6t的教学探讨 I )
信号与系统阶跃信号和冲激信号

O
2
2
sgn t
1
O
t
-1
1 sgn( t ) u ( t ) u ( t ) 2 u ( t ) 1 u ( t) [sgn( t) 1 ] 2
三.单位冲激δ(t)(难点)
概念引出 定义1 定义2 冲激函数的性质
冲激导数的抽样情况:利用分部积分运算
(t)f(t) d t
f ( t ) ( t ) ( t ) ( t ) d t f
f(0 )
3.冲激偶(冲激的导数)
s( t )
1
(t )
1
成为
(1)
O
o
求导
s( t )
集美大学信息工程学院201041414阶跃信号和冲激信号阶跃信号和冲激信号信号函数本身有不连续点跳变点或其导数与积分有不连续点的一类信号函数统称为奇异信号或奇异函数
§1.4 阶跃信号和冲激信号
集美大学信息工程学院 2010.4
本节介绍
信号(函数)本身有不连续点(跳变点)或其导 数与积分有不连续点的一类信号(函数)统称为 奇异信号或奇异函数。 主要内容: •单位斜变信号 •单位阶跃信号 •单位冲激信号 •冲激偶信号
0 u ( t t ) 0 1
t
u( t t 0 )
1
O
1
t t 0 , t 0 0 t t 0
0
t0 u(t t0 )
t
由宗量 t O t t 0 可 t 知 t , 即 时 0 0 ,函数有断点,跳变点 间为 t0 时 宗量>0 函数值为1 宗量<0 函数值为0
信号与系统名词解释

1 双端口网络:若网络有两个端口,则称为双口网络或二端口网络2 阶跃响应:当激励为单位阶跃函数时,系统的零状态响应3 冲激响应:当激励为单位冲激函数时,系统的零状态响应4 周期信号频谱的特点:①离散性》频谱是离散的②谐波性》频谱在频率轴上位置都是基波的整数倍③收敛性》谱线高度随着谐波次数的增高总趋势是减小的5 模拟离散系统的三种基本部件:数乘器·加法器·单位延迟器6 模拟连续系统的三种基本部件:数乘器·加法器·积分器7 线性系统:一个既具有分解特性,又具有零状态线性和零输入线性的系统8 通频带:我们把谐振曲线有最大值9 离散系统稳定的充分必要条件:∑︳h(n)︳〈∞(H(z)的极点在单位圆内时该系统必是稳定的因果系统)10网络函数:在正弦稳态电路中,常用响应向量与激励向量之比定义为网络函数,以H(jw)表示11 策动点函数:激励和响应在网络的同一端口的网络函数12 传输函数(转移函数):激励和响应在不同的端口的网络函数13 因果连续系统的充分必要条件:h(t)=0 t<0 (收敛域在S右半平面的系统均为因果系统)14 连续时间稳定系统的充分必要条件:∫︳h(t)︳dt≤M M:有界正实常数即h(t)满足绝对可积,则系统是稳定的15 傅里叶变换的时域卷积定理:若f1(t)↔F1(jw),f2(t)↔F2(jw)则f1(t)*f2(t)↔F1(jw)F2(jw)16 傅里叶变换的频域卷积定理:若f1(t)↔F1(jw),f2(t)↔F2(jw)则f1(t)·f2(t)↔(1/2π)F1(jw)*F2(jw)17 稳定系统:18 系统模拟:对被模拟系统的性能在实验室条件下模拟装置模仿19 因果系统:未加激励不会产生零状态响应的系统20 稳定的连续时间系统:一个连续时间系统,如果激励f(t)是有界的,其零状态响应y f(t)也是有界的,则称该系统是稳定的连续时间系统21 H(s)(h(t))求法:由微分方程、电路、时域模拟框图,考虑零状态条件下取拉氏变换、画运算电路、作S域模拟框图,应用Y f(s)/F(s)糗大H(s)。
北邮信号与系统复习: 典型例题 微分方程3种解法——含冲激函数匹配法

故:
(t>0)
7
例题3:零输入、零状态解法
描述某系统的微分方程为y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t),
已知y(0-)=2,y’(0-)=0,f(t)=u(t)。求该系统的全响应,零输 入响应和零状态响应。 解:(1.1)求零状态响应的起始点跳变 y”(t) + 3y’(t) + 2y(t) = 2δ(t) + 6u(t) 利用系数匹配法分析列式得: y’’(t)=aδ(t) +b Δu(t) y’(t)=aΔu(t)
10
2.5.4
各种响应之间的关系
P58页,理解问题核心,读一下
零输入响应
r (t ) rzi (t ) rzs (t )
n n
零状态响应
Azik e ak t Azsk e ak t B(t )
k 1 k 1
求和 齐次解 自由响应
Ak e ak t B (t )
所以
9
例题3:零输入、零状态解法
(2)零输入响应yzi (t), 激励为0 , yzi(0+)= yzi (0-)= y(0-)=2 yzi’(0+)= yzi’(0-)= y’(0-)=0 求特征根求,得齐次解的零输入响应: 代入,解得系数为:
所以: (3)全解为 零输入 + 零状态
瞬态分量 稳态分量
信号系统样写也没错, 和小时应用题一样。
1
例题1:线性、时移性质
2
例题2:经典法
,
,
求完全响应。
3
例题2:经典法
解:①由特征根写出齐次解形式 i)特征方程: 特征根: ii)齐次解形式: ②求特解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
4
4
2
1
f (t) (t 2 4)dt 0
1
第1章 信号与系统的基本概念
1.6 基本离散时间信号
单位阶跃序列 单位抽样序列 复指数序列
第1章 信号与系统的基本概念
单位阶跃序列
0 n 1,2,...... u[n] 1 n 0,1,2,......
f '(ti )
第1章 信号与系统的基本概念
例6 计算下列函数的值
f (t ) (t 2 4)dt
1
f (t ) (t 2 4)dt 1
解: (t 2 4) 0 t 2
f
' (t1 )
d dt
(t 2
4)
t 2
2t
4
f
' (t2 )
d dt
(t 2
4)
t 2
2t
4
(t第21章信4号)与系统的1基本概念(t 2) 1 (t 2)
4
4
1 [ (t 2) (t 2)]
4
(t 2 4)dt
[ 1 (t 2) 1 (t 2)]dt 1 2 1
f (t) ' (t)dt f ' (0)
t
'( )d (t)
第1章 信号与系统的基本概念
-
x(t )
(t
t0 )dt
x(t0 )
x(t) (t
例5:计算下列积-分(性质的应用)
t0
)dt
x(t0
)
1. (t 2 2)[ (t 1) (t 1)]dt -
-
4
2
1 (2t) 1 (t 2 2)
4
t2 2
t 3
4.5
第1章 信号与系统的基本概念
例6 计算下列函数的值
f (t) (t 2 4)dt 1
f (t) (t 2 4)dt 1
此题要注意应用冲激信号复合函数的性质(见郑君理教材 p77-p78,例2-12),我们知道冲激信号的含义是t≠0时 为零,t=0时有一个冲激信号,而其余全为零。这样就不 难理解如何求解函数的值了
c. (t ) (t ) [(t t0 )] (t t0 )
d . (at ) 1 (t )
a
e. du(t) (t)
t
( )d u(t)
dt
第1章 信号与系统的基本概念
•冲激偶的性质:
a. f (t) '(t) f (0) / (t) f / (0) (t)
[n] u[n] u[n 1]
性质2: [n]的求和函数是 u[n]
n
u[n] [m] m
性质3: [n]与任意函数的乘积
x[n][n] x[0][n]
第1章 信号与系统的基本概念
复指数序列
x[n] c n
实指数序列:此时 c 和 都是实数、如图1-35所示
2. 2[ ( t) ( t)]d 0
3. (t 2 2)[ (4-2t) (2t+6)]dt -
第1章 信号与系统的基本概念
1 (t 2 2)[ (t 1) (t 1)]dt -
(t 2 2) (t 1)dt (t 2 2) (t 1)dt
b. f (t) '(t)dt f / (0)
c. '[(t)] '(t)
d. ' (at) 1 1 ' (t)
aa
第1章 信号与系统的基本概念
函数名
冲激函数和冲激偶的对比
特性
(t)
‘ (t )
1.引出
2.奇偶
(t)dt 1
(t) 0(t 0)
-
-
(2t ) |t1 (t 2 2) |t1
2 3 5
2
2 0 [ ( t) ( t)]d
( t) |02 u( t) |02
(2 t) (t) u(2 t) u(t)
(t 2) (t) u(2 t) u(t)
(t) (t)
(t) d (t)
dt
(t)dt 0
' (t) ' (t)
3.抽样
f (t) (t) f (0) (t)
f (t) (t)dt f (0)
4.积分
t
( )d u(t)
f (t) (t) f (0) ' (t) f ' (0) (t)
第1章 信号与系统的基本概念
复指数序列: c c e j , e j0
x[n] c n cos(0n ) j c n sin(0n )
第1章 信号与系统的基本概念
虚指数序列: x[n] e j0n c 1, e j0
第1章 信号与系统的基本概念
第1章 信号与系统的基本概念
* δ(t)的复合函数δ[f(t)]性质
n
[ f (t)]
i 1
f
1 ' (ti
)
(t
ti
)
冲激发生在f(t) 0所解出的互不相同的实根
t ti上。
此式说明:δ[f(t)可 ] 以化简为t ti处一系列冲激 函数的迭加,每一冲激函数的强度等于 1 .
2 为有理数时,虚指数序列(或正弦序列)为 0 周期序列(周期为N 2m ),为无理数时,
0 虚指数序列(或正弦序列)为非周期序列
第1章 信号与系统的基本概念
作业: 1.11 1.18 1.21 (e-h)
第1章 信号与系统的基本概念
筛选特性
f (t) (t)dt f (0) (t)dt
第1章 信号与系统的基本概念
3. (t 2 2)[ (4-2t) (2t+6)]dt -
(t 2 2){ [2(t 2)] [2(t+3)]}dt -
(t 2 2)[ 1 (t 2) 1 [(t+3)]}dt
结论
1. 虚指数序列(或正弦序列)对频率0具有周 期性,周期为2π(图1-38)
e e e e j(0 2k)n
j0n j 2kn
j0n
2. 虚指数序列(或正弦序列)在奇数 的附近 频率最高,在偶数 的附近频率最低。
第1章 信号与系统的基本概念
虚指数序列的周期性
x[n] e j0n
第1章 信号与系统的基本概念
•冲激函数的性质
a. f (t) (t) f (0) (t) f (t) (t t0 ) f (t0 ) (t t0 )
b. f (t) (t)dt f (0)
f (t) (t t0 )dt f (t0 )
筛选特性
t0 )dt
- f (t0 ) (t t0 )dt f (t0 )
f (0)
0
t
f (t0 )
t
1
0 1 2 3 4..... n
第1章 信号与系统的基本概念
单位抽样序列
(n)
1 0
(n 0) (n 0)
1
(n n0 ) 0
(n n0 ) (n n0 )
(n)
0
n
(n n0 )
0
n0
n
第1章 信号与系统的基本概念
性质1: [n] 是 u[n] 的一次差分
