七年级数学平面直角坐标系PPT优质课件
合集下载
平面直角坐标系ppt优秀课件

益。──高尔基 • ● 生活就像海洋,只有意志坚强的人,才能到达彼岸。──马克思 • ● 浪费别人的时间是谋财害命,浪费自己的时间是慢性自杀。──列
宁
• ● 哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 • ● 完成工作的方法,是爱惜每一分钟。──达尔文 • ● 没有伟大的愿望,就没有伟大的天才。──巴尔扎克 • ● 读一切好的书,就是和许多高尚的人说话。──笛卡尔 • ● 成功=艰苦的劳动+正确的方法+少谈空话。 ──爱因斯坦
y
4
(4)单位长度一般
3 2
取相同的
1
-3 -2 -1-1 O1 2 3
x
-2
-3 -4
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
-2
(A)
(B)
3Y 2 1
-3 -2 -1-1 O1 2 3 X
-2 -3
3Y 2 1
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
· 纵轴 y 5
B(0,5)
4
3 2
·A(5,2)
1
-4 -3 (-2,-3)D
-3
-4
·C(2,-3)
例3.在下面直角坐标系中描出下列各组点,
并将各组的点用线段依次连接起来.
宁
• ● 哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 • ● 完成工作的方法,是爱惜每一分钟。──达尔文 • ● 没有伟大的愿望,就没有伟大的天才。──巴尔扎克 • ● 读一切好的书,就是和许多高尚的人说话。──笛卡尔 • ● 成功=艰苦的劳动+正确的方法+少谈空话。 ──爱因斯坦
y
4
(4)单位长度一般
3 2
取相同的
1
-3 -2 -1-1 O1 2 3
x
-2
-3 -4
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
-2
(A)
(B)
3Y 2 1
-3 -2 -1-1 O1 2 3 X
-2 -3
3Y 2 1
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
· 纵轴 y 5
B(0,5)
4
3 2
·A(5,2)
1
-4 -3 (-2,-3)D
-3
-4
·C(2,-3)
例3.在下面直角坐标系中描出下列各组点,
并将各组的点用线段依次连接起来.
人教初中数学七下 7.1.2 平面直角坐标系课件4 【经典初中数学课件 】

划计 T
正正T 正正正正正
正正 正
频数 2 12 25 13 8 3
由表可看出,153~164cm (含164cm)的人数是50人
三、研读课文
知
识 点
4、画频数分布直方图
一 为了更直观形象地看出频数分布
画 的情况,可以根据频数分布表画
直 方 图 的
出频数分布__直__方_图______.
(1)以横轴表示__身__高__,纵轴 表示__频_数___与__组__距___的比值,
三、研读课文
2、决定组距与组数
(1)把所有的数据分成若干组,每个小组的两__个__端点
知 之间的距离(组内数据的取值范围)称为组距.
识 (2)如果我们决定组距是3㎝
点 一 画
∵∴将最 数大 据值 分组 成-距 -最 小 8值 组 .( 这 些23 3 组) 为= _:7___23
直 149≤x< 15;2 15≤2x< 1;55
告诉大家
本节课你的学会了 什么!
第十章 直方图 10.2 直方图 第三课时 直方图(一)
一、新课引入
1、考试考生约2万名,从中抽取500名考生的 成绩进行分析,这个问题的样本是_________ _从__中__抽__取__的__5_0_0_名__考. 生的成绩 2、了解一批炮弹的杀伤半径,必须进行爆炸试 验,在这个问题中,只能进行___抽__样__调查.
图书馆
宿舍
食堂 中心广场
教学楼
门卫
平面直角坐标系 第二象限
y y轴或纵轴
6
5
4 第一象限
3
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2
七年级数学下册教学课件《平面直角坐标系 单元解读课件》

纵坐标为0 横坐标为0
知识结构
用坐标表示地理位置
坐
标 方
用方向和距离表示平面内点的位置
法
的
简
左减右加(横坐标)
单 应 用
用坐标表 示平移
点的平移
转化
上加下减(纵坐标)
图形的平移
课时安排
平面直角坐标系架起了数与形之间的桥梁,使得我们可以用几何方法研究 代数问题,又可以用代数的方法研究几何问题,是解决数学问题的一个强有力 的工具.
学习目标 教学内容
学习目标
7.2 坐标方法的
简单应用
1. 能建立适当的平面直角坐标系描述物体位置.
2. 能用方向和距离刻画两个物体的相对位置.
3. 掌握平面直角坐标系中图形的平移与图形对应点的坐标 的变化规律,感受数与形相互转化的过程,体会平面直 角坐标系的作用.
内容要点
7个概念:有序数对,平面直角坐标系,横轴,纵轴,原点,坐标, 象限
通过这一节内容的学习,可以帮助学生 更好的理解点与坐标的对应关系,顺利 实现由一维到二维的过渡.
教材内容
7.2 坐标方法的简单应用 联系实际,提出“地图上是怎样利用坐标表示一个地点的地理位置?”的问题,使学生联想 到坐标系再来学习如何建立直角坐标系,然后让同学们了解另一种描述物体位置的方法—— 用方向和距离表示平面内物体的位置.最后分析点及图形平移前后点的坐标的变化来归纳相关 规律.
2种确定点的位置方法:用坐标表示点的位置, 方向+距离表示点的位置
3类点的特征:不同象限点的坐标特征,坐标轴上点的坐标特征, 与坐标轴平行的直线上点的坐标特征
2个关系:点的坐标与位置之间的对应关系,点的平移与坐标的变 化规律之间的对应关系
人教版七年级数学下册课件 7.1.2 平面直角坐标系 (共22张PPT)

-3 -2 -1 0 1 2 3 4
A: -3; B: 2. 点C. 思考2 : 由(1)你发现数轴上的点与实数是什么关系?
一一对应. ①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标); ②反过来,知道一个数, 这个数在数轴上的位置就确定了.
新课导入
1596-1650
数学家笛卡儿潜心研究能否用代数中的 计算来代替几何中的证明. 有一天, 在梦中他 用金钥匙打开了数学宫殿的大门, 遍地的珠 子光彩夺目, 他看见窗框角上有一只蜘蛛正 忙着结网, 顺着吐出的丝在空中飘动, 一个念 头闪过脑际: 眼前这一条条的横线和竖线不 正是自己全力研究的直线和曲线吗?
5 N
A
平面内的点就可以用一个
4
x轴上的点的
(3, 4)
有序数对来表示了.
纵坐标为0; y 3
轴上的点的 2 C 例如, 由点 A 分别向 x 轴、横坐标为0. 1
原点O的坐标 为(0, 0)
y轴作垂线, 垂足M 在 x 轴 上的坐标3, 垂足 N 在 y 轴 -4 -3
-2
-1 O
M 1 2 3456
y
D (0, 6)
6
C(6, 6)
5
4
3
2
1
A(O) (0,10)2 3 4 5 B (6, 0)
x
新知探究
请另建立一个平面直角坐标系, 这时正方形的顶点A, B, C, D 的坐标又分别是什么?与同学们交流一下.
y
D (-3,3)
C (3,3)
A (-3,-3)
B (3,-3)
x
新知探究
由上得知, 建立的平面直角坐标系不同, 则各点的坐标也 不同. 你认为怎样建立直角坐标系才比较适当?
平面直角坐标系课件

y (2,3)
(-3,0)
(0,0)
(3,0)
x
(3,-3)
2、春天到了,初一某班组织同学到人民公园春游.张明、 王丽二位同学和其他同学走散了.同学们已经到了中心广
场,而他们仍在牡丹园赏花,他们对着景区示意图在电 话中向老师告知了他们的位置.
张明:“我这里的坐标是(300,300)”
王丽:“我这里的坐标是(200,30y0)”. y
图3-5
解 如图3-5,先在x 轴上找到表示5的点,再在y 轴 上找出表示4 的点,过这两个点分别作x 轴,y
轴的垂线,垂线的交点就是点A. 类似地,其他
各点的位置如图所示.点A 在第一象限,点B 在 第二象限,点C在第三象限,点D在第四象限.
图3-5
写出平面直角坐标系中的A、B、C、E、F、G、H、O、T
2叫做点A的纵坐B(标2,3) A点在平面内的坐标为(3, 2) 记作:A(3,2)
·
·A(3,2)
方法:先横后纵
-4 -3 -2 -1 0 -1
1 2 3 4 5 x 横轴
平面直角坐标系上-2的点和有序实数对一一对应
-3
D
-4
E
(-3,-3)
(5,-4)
笛卡尔,法国数学家、 科学家和哲学家.早在 1637年以前,他受到了 经纬度的启示.(地理上 的经纬度是以赤道和本 初子午线为标准的,这 两条线从局部上看可以 看成平面内互相垂直的 两条线.)发明了平面直 角坐标系,又称笛卡尔 坐标系.
我们把北偏西60°,南偏东60°这样的角称为方位角.
例4 如图3-10,12 时我渔政船在H 岛正南方向, 距H岛30海里的A 处,渔政船以每小时40 海 里的速度向东航行, 13 时到达B处,并测 得H 岛的方向是北偏西53°6′. 那么此时渔 政船相对于H岛的位置怎样描述呢?
(-3,0)
(0,0)
(3,0)
x
(3,-3)
2、春天到了,初一某班组织同学到人民公园春游.张明、 王丽二位同学和其他同学走散了.同学们已经到了中心广
场,而他们仍在牡丹园赏花,他们对着景区示意图在电 话中向老师告知了他们的位置.
张明:“我这里的坐标是(300,300)”
王丽:“我这里的坐标是(200,30y0)”. y
图3-5
解 如图3-5,先在x 轴上找到表示5的点,再在y 轴 上找出表示4 的点,过这两个点分别作x 轴,y
轴的垂线,垂线的交点就是点A. 类似地,其他
各点的位置如图所示.点A 在第一象限,点B 在 第二象限,点C在第三象限,点D在第四象限.
图3-5
写出平面直角坐标系中的A、B、C、E、F、G、H、O、T
2叫做点A的纵坐B(标2,3) A点在平面内的坐标为(3, 2) 记作:A(3,2)
·
·A(3,2)
方法:先横后纵
-4 -3 -2 -1 0 -1
1 2 3 4 5 x 横轴
平面直角坐标系上-2的点和有序实数对一一对应
-3
D
-4
E
(-3,-3)
(5,-4)
笛卡尔,法国数学家、 科学家和哲学家.早在 1637年以前,他受到了 经纬度的启示.(地理上 的经纬度是以赤道和本 初子午线为标准的,这 两条线从局部上看可以 看成平面内互相垂直的 两条线.)发明了平面直 角坐标系,又称笛卡尔 坐标系.
我们把北偏西60°,南偏东60°这样的角称为方位角.
例4 如图3-10,12 时我渔政船在H 岛正南方向, 距H岛30海里的A 处,渔政船以每小时40 海 里的速度向东航行, 13 时到达B处,并测 得H 岛的方向是北偏西53°6′. 那么此时渔 政船相对于H岛的位置怎样描述呢?
平面直角坐标系ppt
–3
–4
–5
–6 y(图1)
(–16, 5)
(5, 5)
5
D
C
4
3
1
x –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 7
(–3, –2) –1
(3, –2)
–2
A
B
–3
–4
–5
–6 y (图2) 6
5
4
(–3, 3)D3来自(3, 3) C2
2
1
–7 –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 7
A.平行于y轴 B.平行于x轴 C.与y轴相交 D.无法确定
4、P(-2,y)与Q(x,-3)关于x轴对称,则x-y的值为( B)
A.1 B.-5 C.5 D.-1 5、已知点P (x,y)在第四象限,它到x轴的距离为2,到y轴的距离为3,求P点的坐标。 6、若点P′ (m,-1)是点P(2,n)关于x轴的对称点,求m+n。
小结:
已知平面直角坐标系内一点M(4a+8,a+3),分别根据 下列条件求出点M的坐标。 (1)点M到x轴的距离为2 ; (2)点N的坐标为(3,-6),并且直线MN∥x轴。
学习需要团队的力量
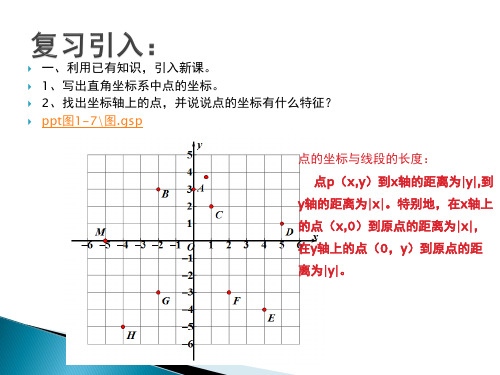
一、利用已有知识,引入新课。 1、写出直角坐标系中点的坐标。 2、找出坐标轴上的点,并说说点的坐标有什么特征? ppt图1-7\图.gsp
点的坐标与线段的长度: 点p(x,y)到x轴的距离为∣y∣,到
y轴的距离为∣x∣。特别地,在x轴上 的点(x,0)到原点的距离为∣x∣, 在y轴上的点(0,y)到原点的距 离为∣y∣。
1、学生通过不同的建系方式可得出多种建立平面直 角坐标系的方法,从而找到最优方法。同时知道对于 不同的建系方法,同一个点的坐标是不同的。
《平面直角坐标系》PPT优质课件

3Y 2 1
-3 -2 -1-1O1 2 3 X
-2 -3
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
概念2
平面直角坐标系的象限
y 4
第二象限
3
2
1
第一象限
–4 –3 –2 –1 O 1 2 3 4 x –1
–2
第三象限
–3
第四象限
–4
坐标平面被两条坐标轴分成四个部分,每个部分称为 象限 ,
(2)能在给定的平面直角坐标系中根据点的坐标描出点的位 置,由点的位置写出点的坐标。
(3)运用平面内的点的坐标特征解决问题时要注意数形结合, 不宜死记硬背.
知识回顾 问题探究 课堂小结 随堂检测 作业布置
课本第68页练习题1、2题。
向右为正方向;竖直的数轴称为纵轴或
1
y轴,一般取向上为正方向;两坐标轴 –4 –3 –2 –1 O 1 2 3 4 x
–1
的交点为平面直角坐标系的原点。
–2
–3
–4
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
如何正确画出平面直角坐标系?
y
1.选原点
4
2.作两轴
思考:已知点的坐标确定点的位置
y
5
A(3,4)
4
已知平面直角坐标系内一点的坐标,分别 3 以点的横坐标、纵坐标在数轴上表示点的垂足 2
,作x轴、y轴的垂线,两垂线的交点即为要找
1
的点。
-2 -1 0 -1
-2
· A(3,4)
1 2 3 4x
知识回顾 问题探究 课堂小结 随堂检测
-3 -2 -1-1O1 2 3 X
-2 -3
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
概念2
平面直角坐标系的象限
y 4
第二象限
3
2
1
第一象限
–4 –3 –2 –1 O 1 2 3 4 x –1
–2
第三象限
–3
第四象限
–4
坐标平面被两条坐标轴分成四个部分,每个部分称为 象限 ,
(2)能在给定的平面直角坐标系中根据点的坐标描出点的位 置,由点的位置写出点的坐标。
(3)运用平面内的点的坐标特征解决问题时要注意数形结合, 不宜死记硬背.
知识回顾 问题探究 课堂小结 随堂检测 作业布置
课本第68页练习题1、2题。
向右为正方向;竖直的数轴称为纵轴或
1
y轴,一般取向上为正方向;两坐标轴 –4 –3 –2 –1 O 1 2 3 4 x
–1
的交点为平面直角坐标系的原点。
–2
–3
–4
知识回顾 问题探究 课堂小结 随堂检测
探究一:平面直角坐标系的概念
重点、难点知识★
如何正确画出平面直角坐标系?
y
1.选原点
4
2.作两轴
思考:已知点的坐标确定点的位置
y
5
A(3,4)
4
已知平面直角坐标系内一点的坐标,分别 3 以点的横坐标、纵坐标在数轴上表示点的垂足 2
,作x轴、y轴的垂线,两垂线的交点即为要找
1
的点。
-2 -1 0 -1
-2
· A(3,4)
1 2 3 4x
知识回顾 问题探究 课堂小结 随堂检测
《平面直角坐标系》PPT课件

由CD长为6; CB长为4; 可得D ; B ; A的坐标分 别为D 6 ; 0 ; B 0 ; 4 ; A6;4
B 0;4
C 0;0
0
A 6;4
D 6;0
x
做一做
例2 如图;正三角形ABC的边长为 6 ; 建立适当的直角坐 标系 ;并写出各个顶点的坐标
y
解: 如图;以边AB所在 的直线为x 轴;以边AB 的中垂线y 轴建立直角 坐标系
布置作业
作业:
A类:课本习题5 5
B类:完成A类同时;补充:
1已知点A到x轴 y轴的距离均为4;求A点坐标;
2已知x轴上一点A3;0;B 3;b ;且AB=5;
求b的值
C类:建立坐标系表示右面图形各顶点的坐标
直角梯形上底3;下底5;底角60˚
y
o
x
练习提高
随堂练习:
课本 随堂练习
练习
1如图;某地为了发展城市群;在现有的四个中小城市A;B;C;D附近 新建机场E;试建立适当的直角坐标系;并写出各点的坐标
2点A1a;5;B3 ;b关于y轴对称;则 a + b =______
3在平面直角坐标系内;已知点P a ; b ; 且a b < 0 ; 则点P的位置 在________
在一次寻宝游戏中;寻宝人已
11 2
2
3
经找到了2和3;2的两个标志点;并
3
且知道藏宝地点的坐标为4;4;除4ຫໍສະໝຸດ 此外不知道其他信息 如何确定直
角坐标系找到宝藏 与同伴进行交
流
做一做
例1 如图; 矩形ABCD的长宽分别是6 ; 4 ; 建立适当的 坐标系;并写出各个顶点的坐标
y
解: 如图;以点C为坐标 原点; 分别以CD ; CB所 在的直线轴建 立直角坐标系 此时C点 坐标为 0 ; 0
B 0;4
C 0;0
0
A 6;4
D 6;0
x
做一做
例2 如图;正三角形ABC的边长为 6 ; 建立适当的直角坐 标系 ;并写出各个顶点的坐标
y
解: 如图;以边AB所在 的直线为x 轴;以边AB 的中垂线y 轴建立直角 坐标系
布置作业
作业:
A类:课本习题5 5
B类:完成A类同时;补充:
1已知点A到x轴 y轴的距离均为4;求A点坐标;
2已知x轴上一点A3;0;B 3;b ;且AB=5;
求b的值
C类:建立坐标系表示右面图形各顶点的坐标
直角梯形上底3;下底5;底角60˚
y
o
x
练习提高
随堂练习:
课本 随堂练习
练习
1如图;某地为了发展城市群;在现有的四个中小城市A;B;C;D附近 新建机场E;试建立适当的直角坐标系;并写出各点的坐标
2点A1a;5;B3 ;b关于y轴对称;则 a + b =______
3在平面直角坐标系内;已知点P a ; b ; 且a b < 0 ; 则点P的位置 在________
在一次寻宝游戏中;寻宝人已
11 2
2
3
经找到了2和3;2的两个标志点;并
3
且知道藏宝地点的坐标为4;4;除4ຫໍສະໝຸດ 此外不知道其他信息 如何确定直
角坐标系找到宝藏 与同伴进行交
流
做一做
例1 如图; 矩形ABCD的长宽分别是6 ; 4 ; 建立适当的 坐标系;并写出各个顶点的坐标
y
解: 如图;以点C为坐标 原点; 分别以CD ; CB所 在的直线轴建 立直角坐标系 此时C点 坐标为 0 ; 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)连接AB, BC, CD, DA, EF, HG.
(2)观察所得到的图形,你觉得它象什么?
作业:书本P65 2,3,6,9
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2021/02/25
2、在直角坐标中,A点的位置为(-3,2),B 点的位置是(3,2),连接A、B两点所成的线 段与 x轴 平行。
3、若点N(a+5,a-2)在x轴上,则点N的 坐标为(7,0)。
4、已知点M(2,-3),则M到x轴的距离为 3 , 到y轴的距离为 2 。
5、已知点P到x轴和y轴的距离分别是2和5, 求P点的坐标。
(2,5)或(-2,5)或(-2,-5)或(2,-5)
6、点M位于x轴下方,距x轴3个单位长,且位于y轴 左方,距y轴2个单位长,则M点坐标是(-2,-3) 。
7、若点P(x,y)的坐标满足xy=0,则点p在( D ) A 原点 B x轴上 C y轴上 D x轴上或y轴上
8、已知A(6,0),B(2,1),O(0,0),则
△ABO的面积是
。
9、已知A(-4,3),0(0,0),B(-2,-1), 求△ABO的面积。
10、已知A(-2,0),B(4,0),C(x,y); (1)若点C在第二象限,且|x|=4,|y|=4,求点C的 坐标,并求三角形ABC的面积; (2)若点C在第二、四象限的角平分线上,且三角 形ABC的面积=9,求点C的坐标。
10
11、说出已知坐标的点所在的象限或坐标 轴。
⑴A(-3,0); ⑵B(2,-4);⑶C(1,2); ⑷D(-1,-3);⑸E(0,2);⑹F(-1.2,+1)
12、点P在第二象限,它的横坐标与纵坐标的和为1,
点P的坐标上
(只要写出一个符合条件的坐
标即可)。
13、已知点P(1,b)在第四象限, 求点Q(-b,1)所在象限。
P3
坐标为__(_-2_,_-_5_)_;
(a,-b) (-a,-b)
P1(x1,y1),P2(x2,y2)
1、若P1与P2关于x轴对称,则x1=x2,y1+y2=0。
2、若P1与P2关于y轴对称,则x1+x2=0,y1=y2。
3、若P1与P2关于原点对称,则x1+x2=0,y1+y2=0。
巩固练习: 1、点A(0,-1)的位置在平面直角坐标系的 y轴上。
6.1.2平面直角坐标系(3)
特殊位置点的特殊坐标:
Байду номын сангаас
坐标轴上点 P(x,y)
连线平行于坐 标轴的点
点P(x,y)在各象 限的坐标特点
象限角平分 线上的点
x轴 y轴 原点 平行于 平行于 第一 第二 第三 第四 一三 二四象 x轴 y轴 象限 象限 象限 象限 象限 限
纵坐标 横坐标 (x,0) (0,y) (0,0) 相同 相同
x>0 x>0 x<0 x<0 (m,m) (m,-m) y>0 y<0 y>0 y<0
(a,b)y P
(-a,b) 点A的坐标为(2,5)
P2 • 点A关于x轴的对称点
的坐标是_(_2_,_-5_)__;
• 点A关于y轴的对称点
O
的坐标是_(_-2__,5_)__;
x
• 点A关于原点对称点的
P1
14、若点B(a,b)在第三象限,则点
C(-a+1,3b-5)在第
象限。
15、如果x·y>0,且x+y<0,则点P(x,y)在( )
A、第四象限 C、第二象限
B、第三象限 D、第一象限
16、在平面直角坐标系中,描出下列各点:
A(-1,5)
B(-1,1) C(5,1) D(5,5)
E(-1,3) F(5,3) G(2,5) H(2,-2)
