第十四章 固定资产更新决策模型
中级财务管理难点之固定资产更新决策

固定资产更新决策替换重置一共分寿命期相同和寿命期不同两种情况。
对于寿命期相同的,由于期限相同,则收入相同,因此只考虑成本的现值,选成本小,即现金净流量总和折现小的。
∑NCF折现后NPVmin而对于寿命期不同的,只能选年金净流量法,即:总成本折现/年金现值系数min解释:1.由于教材对于寿命期相同和寿命期不同的情况,寿命期相同的流入用+,流出用-,而寿命期不同的用成本法,流入用-,流出用+,导致看书理解上有所困惑。
因此,学习期间,将两种情况全部用第一种方法进行表示,比较直接。
即不管净现金流量总值和年金净流量法都用流入为+,流出为-2.整个设备无论新旧都要经过投资期、营运期和终结期。
对于新设备比较好理解,投资期和营运期为流出,为-,终结期为流入,为+其实对于旧设备也是这种思路。
理由:旧设备投资期,假设把旧设备变卖改为新设备,的确是现金流入,但现在只是假设,实际现在仍在使用,只是现在在决策中,并未真正变卖,这部分假设的变卖收入,真正的机会成本其实是丧失的,因而视为流出,为-;如果有所得税因素,若卖亏,出现的抵税收入,因为实际在使用中,因而实际也并未得到,从而抵税的流入实际视为流出,为-,卖赚则相反,纳税的流出实际为流入。
虽然旧设备的投资期难以理解,用简单的方法就是站在新设备的角度看旧设备,也就不用拐弯了。
而营运期和终结期,不管新旧设备,该流出的流出,流入的流入,正常理解即刻3.更新决策的收入有两类:残值收入(新旧设备均有)和现价收入(只有旧设备有),凡是遇到收入的,如果有所得税的,一定都会遇到卖亏抵税和卖赚纳税的情况,俗称拖小尾巴。
用实际的收入VS税法算的收入进行比较,无论赚亏都要乘以所得税税率T%,作为这个小尾巴哦4.费用、成本类的都要乘以(1-T%)解题具体步骤:1.分投资期、营运期和终结期分别计算其现金净流量NCF,然后予以折现2.营业期、终结期做正常思路的流入流出3.投资期旧设备变价收入流出流入做相反的处理或视同新设备的投资期对待4.旧设备的变价收入VS 税法角度使用N年后的价值,和正常卖亏抵税和卖赚纳税思路做相反处理5.将三期的折现NCF进行累加,求出NPV,选最小的数值更多知识点学习请加QQ群:3即将推出固定资产更新决策万能计算公式一步到位法,敬请期待!。
第十四章固定资产更新决策模型

第十四章固定资产更新决策模型固定资产更新决策模型是企业在决策是否更新固定资产时使用的一种分析工具。
固定资产更新决策涉及到多个因素,如资产的使用寿命、修理与更换的成本、资本回报率等,需要综合考虑以得出最佳的决策方案。
本文将介绍固定资产更新决策模型的基本原理和应用方法。
固定资产更新决策模型的基本原理是依据资产的使用寿命和修理与更换成本来进行分析。
当一项固定资产的使用寿命接近或超过了其经济寿命时,就需要进行更新决策。
更新固定资产可以提高生产效率,降低运营成本,并且有助于企业的可持续发展。
在进行固定资产更新决策时,首先需要对资产的使用寿命进行评估。
评估资产的使用寿命可以通过参考相关行业的经验数据以及实际运营情况来确定。
使用寿命的评估结果将为后续的决策提供依据。
其次,需要对修理与更换的成本进行评估。
修理成本包括维护费用、零部件更换费用等,而更换成本则包括购置新资产的费用以及老资产处置的费用等。
评估修理与更换的成本需要考虑到资产的残值以及折旧等因素。
基于使用寿命和修理与更换成本的评估结果,可以进一步计算资本回报率。
资本回报率可以通过将资产的净收益与资产的投资成本进行比较来计算。
净收益可以通过考虑资产的增值效应、降低成本效应等因素来计算。
最后,根据资本回报率的计算结果,可以得出固定资产更新的决策。
如果资本回报率大于预设的阈值,则说明固定资产的更新将产生正向的经济效益,应该进行更新。
反之,如果资本回报率小于预设的阈值,则说明固定资产的更新将产生负面的经济效益,不应该进行更新。
除了以上的基本原理,固定资产更新决策模型还可以考虑其他因素,如市场需求、竞争情况、技术进步等。
这些因素对于固定资产的使用寿命和经济效益都有一定的影响,需要进行综合考虑。
在应用固定资产更新决策模型时,需要收集和分析相关的数据。
这些数据包括资产的使用寿命、修理与更换的成本、资本回报率等。
通过对这些数据的分析,可以得出最佳的决策方案。
总之,固定资产更新决策模型是企业进行固定资产更新决策时的一种重要工具。
固定资产更新决策模型的设计_计算机财务管理——以Excel为分析工具_[共3页]
![固定资产更新决策模型的设计_计算机财务管理——以Excel为分析工具_[共3页]](https://img.taocdn.com/s3/m/00d43ef0a5e9856a571260c7.png)
179 投资决策的Excel 建模第7章从决策性质上看,固定资产更新决策属于互斥投资方案的决策类型。
因此,固定资产更新决策所采用的决策方法是净现值法和年金净流量法,一般不采用内含报酬率法。
通常,根据新旧设备的未来使用寿命是否相同,可以采用两种不同的方法来进行决策分析。
当新旧设备未来使用期限相等时,可采用净现值法来或差额分析法进行对比分析,净现值法是对比新旧设备的净现值,哪种方案的净现值大即采用哪种方案,而差额分析法是先进行差额对比,后用净现值法或内含报酬率法来进行分析,本书对该方法不做实际案例展示;当新旧设备的投资寿命期不相等时,以年成本较低的方案作为较优方案。
具体地,寿命期不同的设备重置方案,在决策时有如下特点。
(1)扩建重置的设备更新后会引起营业现金流入与流出的变动,应考虑年金净流量最大的方案。
替换重置的设备更新一般不改变生产能力,营业现金流入不会增加,只需比较各方案的年金流出量即可,年金流出量最小的方案最优。
(2)如果不考虑各方案营业现金流入量的变动,只比较各方案的现金流出量,我们把按年金净流量原理计算的等额年金流出量称为年金成本。
替换重置方案的决策标准,是要求年金成本最低。
扩建重置方案所增加或减少的营业现金流入也可以作为现金流出量的抵减,并据此比较各方案的年金成本。
(3)运用年金成本方式决策时,应考虑的现金流量主要有:①新旧设备目前的市场价值;②新旧设备残值变价收入,残值变价收入应作为现金流出的抵减。
残值变价收入与原始投资额的差额,称为投资净额;③新旧设备的年营运成本,即年付现成本,如果考虑每年的营业现金流入,应作为每年营运成本的抵减。
(4)年金成本可在特定条件下(无所得税因素、每年营运成本相等),按如下不同方式计算。
∑(各项目现金净流出现值)年金成本 = 年金现值系数投资额-残值收入×一般现值系数+∑(年营运成本现值)=年金现值系数投资额-残值收入∑(年营运成本现值)= 年金现值系数 +残值收入×贴现率+年金现值系数 7.7.2 固定资产更新决策模型的设计1.寿命期相同的固定资产更新决策在进行寿命期相同的固定资产更新决策时,常常使用净现值法或差额分析法。
第十四章 固定资产更新决策模型

SYD( cost , salvage ,life , per)
功能:
返回某项固定资产某期间的按年数总和法计
算的折旧数额。所有参数都应为正数,否则
将返回错误值#NUM!
年数总和法(sum-of-years’ digits)
参数:
Cost —— 固定资产的原始成本 Salvage—— 固定资产报废时预计净残值
双倍余额递减法函数DDB( )
双倍余额递减法(double_declining balance) 语法: DDB(cost,salvage,life,period,factor) 功能:
返回固定资产在某期间( period )的折旧 数额。折旧数额是根据资产的原始成本 ( cost )、预计使用年限( life )、预计净残 值( salvage )及递减速率( factor ),按倍率 递减法计算而得出的。DDB函数所有参数均需 为正。
固定资产更新决策模型设计
双倍余额递减法(double_declining balance) 参数:
Cost——指固定资产的原始成本 salvage——指固定资产使用期限结束时的预计 净残值。 life——指固定资产预计使用年数。 period——指所要计算折旧的期限。必须与life 参数采用相同的计量单位。 factor——参数为选择性参数,缺省值为2,即 为“双倍余额递减法”,但用户可改变此参数。
参数:
Cost——固定资产的原始成本。 Salvage—固定资产报废时的预计净残值 Life——固定资产可使用年数的估计数。
年数总和法(sum-of-years’ digits)
概念
年折旧额 尚可使用年限 =(原始成本—预计净残值)× 使用年限的各年年数之和
固定资产投资决策模型
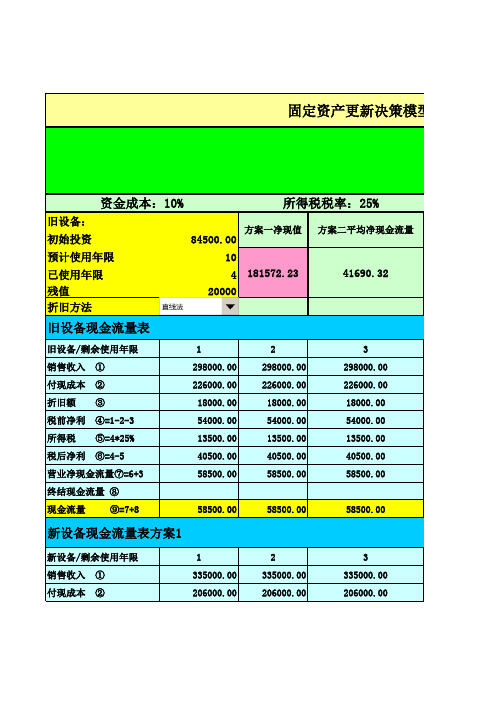
旧设备:初始投资84500.00预计使用年限10已使用年限4残值20000折旧方法旧设备/剩余使用年限123销售收入 ①298000.00298000.00298000.00付现成本 ②226000.00226000.00226000.00折旧额 ③18000.0018000.0018000.00税前净利 ④=1-2-354000.0054000.0054000.00所得税 ⑤=4*25%13500.0013500.0013500.00税后净利 ⑥=4-540500.0040500.0040500.00营业净现金流量⑦=6+358500.0058500.0058500.00终结现金流量 ⑧现金流量 ⑨=7+858500.0058500.0058500.00新设备/剩余使用年限123销售收入 ①335000.00335000.00335000.00付现成本 ②206000.00206000.00206000.00固定资产更新决策模型方方资金成本:10%所得税税率:25%旧设备现金流量表方案一净现值181572.23方案二平均净现金流量41690.32新设备现金流量表方案1折旧额 ③100000.0066666.6744444.44税前净利 ④=1-2-329000.0062333.33#N/A所得税 ⑤=4*25%7250.0015583.33#N/A税后净利 ⑥=4-521750.0046750.00#N/A营业净现金流量⑦=6+3121750.00113416.67#N/A终结现金流量 ⑧现金流量 ⑨=7+8121750.00113416.67#N/A 新设备现金流量表方案2新设备/剩余使用年限123销售收入 ①335000.00335000.00335000.00付现成本 ②206000.00206000.00206000.00折旧额 ③71250.0061071.4350892.86税前净利 ④=1-2-357750.0067928.57#N/A所得税 ⑤=4*25%14437.5016982.14#N/A税后净利 ⑥=4-543312.5050946.43#N/A营业净现金流量⑦=6+3114562.50112017.86#N/A终结现金流量 ⑧现金流量 ⑨=7+8114562.50112017.86#N/A1#N/A 新设备:初始投资300000预计使用年限6已使用年限0残值15000折旧方法45298000.00298000.00226000.00226000.0018000.0018000.0054000.0054000.0013500.0013500.0040500.0040500.0058500.0058500.0058500.0058500.0045335000.00335000.00206000.00206000.00模型方案一新设备使用6年结论#N/A 方案二新设备使用7年结论#N/A 设备净现值差:方案一净现值#N/A 54000.0013500.0040500.0058500.006298000.00226000.0018000.0020000.0078500.006335000.00方案二平均净现金流量#N/A 206000.0023。
固定资产更新决策

A方案PA=3000+60/14%+ =3752.76(万元)
B方案PB=(7000-2500)+70/14%+ =5226.71(万元)
显然,A方案PA<B方案PB,拓宽方案为优。
(二)寿命期不同的设备重置决策
年金成本=
资料二:相关货币时间价值系数如表7所示。
表7 货币时间价值系数
期限(n)
5
6
(P/F,12%,n)
0.5674
0.5066
(P/A,12%,n)
3.6048
4.1114
要求:
(1)计算与购置新设备相关的下列指标:①税后年营业收入;②税后年付现成本;③每年折旧抵税;④残值变价收入;⑤残值净收益纳税;⑥第1-5年现金净流量(NCF1-5)和第6年现金净流量(NCF6);⑦净现值(NPV)。
格力公司设备更换相关资料
A设备
B设备
C设备
购价(元)
年使用费(元)
最终残值(元)
可使用年限
3000
1200
0
5年
11270
900
0
10年
10000
1000
500
12年
根据上述资料,两个方案的年金成本分别为:
方案一的年金成本
=[3000+1200 (P/A,10%,5)+11270 (P/F,10%,5)
年金成本=4800-1280+[36000-4120×(P/F,15%,10)]/(P/A,15%,10)=10489.86(元)
旧设备原值35000元,年折旧3000元,4年累计折旧12000元,目前账面价值=23000元,变现价值10000元,ቤተ መጻሕፍቲ ባይዱ失减税=13000×40%=5200(元)
固定资产更新决策

预计还可使用6年,其年维修费用为4800元,若目前出售可作价8000元。现在市场上有一同类
性能优良的新机器,售价50000元,预计使用10年,估计残值3000元,年维修费用为2200元。
企业要求的设备投资报酬率至少要达到12%。要求做出现在是否更新旧设备的决策。
6
旧设备的平均年成本AC旧
= [8000 + 4800 × (P/A, 12%, 6) − 800 × (P/F, 12%, 6)]/(P/A, 12%, 6)
原来的年平均成本找到可代替的设备。
8
固定资产经济寿命的决策就是选择最佳淘汰旧设备的时间,即最优更新期。固定资产在使用初期,
运行成本比较低,但随着设备的逐渐陈旧,性能变差,各种费用(如保养费、修理费、能源消耗
等)会逐年增加。与此同时,固定资产的价值逐渐减少,占用资产上的资金所应计的利息也逐渐
减少,即固定资产的持有成本会逐年减少。因此,随着固定资产使用时间的增加,运行成本逐年
= 10878.58(元)
年均成本旧设备低于新设备,所以继续使用旧设备在经济上较有利。
7
▪ 注意运用年平均成本法时应注意以下两个问题:一是,年平均成本法是将继续使用旧设备和
更新设备看成是两个互斥的方案。因为两个可供选择的方案使用年限不同 ,因此不能将
NPV和IRR作为方案抉择标准。二是,年平均成本法的假设条件是将来设备再更换时,可以按
= (8000 + 4800 × 4.111 − 800 × 0.507)/4.111
= 6647.34(元)
新设备的平均年年成本AC新
= [50000 + 2200 × (P/A, 12%, 10) − 3000 × (P/F, 12%, 10)]/(P/A, 12%, 10)
固定资产更新决策

新烤炉 70000 10 0 10
目前变现价值(元Βιβλιοθήκη 2000070000能耗费用(元/年) 10000
5000
人工成本(元/年) 10000
5000
旧烤炉: 0时点投资:20000(元) 折旧抵税:50000/10*25%=1250(元/年) 1~4时点现金流量:-1250+(10000+10000)*75%=13750(元/年) 现金流出总现值:20000+13750*(P/A,10%,4)=63585.65(元) 平均年成本:63585.65/(P/A,10%,4)=20059.42(元/年)
结论: 新烤炉平均年成本17142.18元/年<旧烤炉平均年成本20059.42元/年, 所以应该用新烤炉替换旧烤炉。
70000元;新旧烤炉的使用年限都是10年。
原值(元)
旧烤炉 50000
②新烤炉:是全自动化先进设备,人工可降低 预计使用年限(年) 10
为旧烤炉的1/2,能耗费降低到原来的1/2。新旧 烤 炉 均 不 考虑 残 值 , 所得 税 率 25%, 资 本 成 本 已使用年限(年) 6
10%。
尚可使用年限(年) 4
新烤炉: 0时点投资:70000(元) 折旧抵税:70000/10*25%=1750(元/年) 1~10时点现金流量:-1750+(5000+5000)*75%=5750(元/年) 现金流出总现值:70000+5750*(P/A,10%,10)=105331.26(元) 平均年成本:105331.26/(P/A,10%,10)=17142.18(元/年)
2023
固定资产更新决策
案例资料:
B公司是一家地处华东地区某地级市,成立时间已超过5年,目前有80多个连锁店的老牌烘焙企业 。现准备更新生产车间的1台烤炉,相关资料如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cost——指固定资产的原始成本 salvage——指固定资产使用期限结束时的预计
净残值。 life——指固定资产预计使用年数。 period——指所要计算折旧的期限。必须与life
参数采用相同的计量单位。 factor——参数为选择性参数,缺省值为2,即
为“双倍余额递减法”,但用户可改变此参数。
应小于或等于 life。
双倍余额递减法(double_declining balance)
概念
年折旧额 = 期初固定计使用年限 ×100%
双倍余额递减法函数DDB( )
双倍余额递减法(double_declining balance)
语法: DDB(cost,salvage,life,period,factor)
参数:
Cost——固定资产的原始成本。 Salvage—固定资产报废时的预计净残值 Life——固定资产可使用年数的估计数。
年数总和法(sum-of-years’ digits)
概念
年折旧额 尚可使用年限
=(原始成本—预计净残值)× 使用年限的各年年数之和
年数总和法函数SYD( )
年数总和法(sum-of-years’ digits)
倍率(factor)余额递减法函数
概念
倍率( factor )余额递减法是指以不同倍率的 余额递减法计算某个时期内折旧额的方法。双 倍余额递减法是倍率等于2的倍率余额递减法 函数,是倍率余额递减法的特例。
倍率余额递减法函数 VDB( )
倍率(factor)余额递减法函数
语法:
VDB( cost ,salvage ,life ,start_period ,end_period , factor ,no_switch)
功能:
返回某项固定资产某个时期内(start_period与 end_period之间)的折旧数额。如果factor被省略, 此函数将根据该资产的原始成本(cost)及使用年限 (life)、预计净残值(salvage),采用“双倍余额递减法” 来计算折旧数额。
折旧计算模型
固定资产更新决策模型设计
语法:
SYD( cost , salvage ,life , per)
功能:
返回某项固定资产某期间的按年数总和法计 算的折旧数额。所有参数都应为正数,否则 将返回错误值#NUM!
年数总和法(sum-of-years’ digits)
参数:
Cost —— 固定资产的原始成本 Salvage—— 固定资产报废时预计净残值 Life —— 固定资产可使用年数的估计数 Per —— 指定要计算第几期折旧数额 Life 与 per 参数应采用相同的单位,且 per
第十四章 固定资产更新决策模型
计算机财务管理
本章教学内容
折旧计算模型 固定资产更新决策模型
折旧方法及其函数简介
概念 年折旧额=(原始成本-预计净残值)÷使
用年限
直线折旧法函数SLN( )
直线折旧法(straight-line)
语法:SLN( cost , salvage , life)
功能:返回某项固定资产每期按直线折旧法计 算的折旧数额。所有的参数值必须是正数。否 则将返回错误值#NUM!
功能:
返回固定资产在某期间( period )的折旧数 额。折旧数额是根据资产的原始成本( cost )、 预计使用年限( life )、预计净残值( salvage ) 及递减速率( factor ),按倍率递减法计算而得 出的。DDB函数所有参数均需为正。
双倍余额递减法(double_declining balance)
