《计算方法》插值方法
合集下载
计算方法第四章 插值法
《 计 算 方 法 》
4
3
xi 4 yi 2
9 16 3 4
2
0
4
7
9
16
第4章 插值法
应用背景
造函数表：三角函数、对数 预测：鸡蛋价格、城市用水量
《 计 算 方 法 》
数控加工：造船、飞机机翼骨架、服装 样片、模具加工、刀具 计算机辅助设计：潜水艇、汽车造型
服装样片
第4章 插值法
实际问题中，f (x)多样，复杂，通常只能观测到一些离散 数据；或者f (x)过于复杂而难以运算。这时我们要用近似函数 φ(x)来逼近f (x)。
《 计 算 方 法 》
φ (x)= y0
第4章 插值法
§2 线性插值与二次插值
2.1 线性插值
线性插值是代数多项式插值的最简单的形式。假设
《 计 算 方 法 》
给定了函数f (x)在两个互异点x0，x1的值,即
x x0值）
y y0 x0
y1
x1
x
第4章 插值法
现要用一线性函数
满足插值条件：
y( xi ) = yi , i = 0,1, 2
22
第4章 插值法 例：已知函数 y=f (x)的观测数据为
x
《 计 算 方 法 》
1 0
2 -5
3 -6
4 3
y
试求拉格朗日插值多项式。
第4章 插值法
《 计 算 方 法 》
( x 2)( x 3)( x 4) 解 ：p3 ( x ) = 0 (1 2)(1 3)(1 4) ( x 1)( x 3)( x 4) ( 5) (2 1)(2 3)(2 4) ( x 1)( x 2)( x 4) ( 6) (3 1)(3 2)(3 4) ( x 1)( x 2)( x 3) 3 (4 1)(4 2)(4 3) = x3 4 x2 3
4
3
xi 4 yi 2
9 16 3 4
2
0
4
7
9
16
第4章 插值法
应用背景
造函数表：三角函数、对数 预测：鸡蛋价格、城市用水量
《 计 算 方 法 》
数控加工：造船、飞机机翼骨架、服装 样片、模具加工、刀具 计算机辅助设计：潜水艇、汽车造型
服装样片
第4章 插值法
实际问题中，f (x)多样，复杂，通常只能观测到一些离散 数据；或者f (x)过于复杂而难以运算。这时我们要用近似函数 φ(x)来逼近f (x)。
《 计 算 方 法 》
φ (x)= y0
第4章 插值法
§2 线性插值与二次插值
2.1 线性插值
线性插值是代数多项式插值的最简单的形式。假设
《 计 算 方 法 》
给定了函数f (x)在两个互异点x0，x1的值,即
x x0值）
y y0 x0
y1
x1
x
第4章 插值法
现要用一线性函数
满足插值条件：
y( xi ) = yi , i = 0,1, 2
22
第4章 插值法 例：已知函数 y=f (x)的观测数据为
x
《 计 算 方 法 》
1 0
2 -5
3 -6
4 3
y
试求拉格朗日插值多项式。
第4章 插值法
《 计 算 方 法 》
( x 2)( x 3)( x 4) 解 ：p3 ( x ) = 0 (1 2)(1 3)(1 4) ( x 1)( x 3)( x 4) ( 5) (2 1)(2 3)(2 4) ( x 1)( x 2)( x 4) ( 6) (3 1)(3 2)(3 4) ( x 1)( x 2)( x 3) 3 (4 1)(4 2)(4 3) = x3 4 x2 3
《计算方法》第四章 插值方法
满足插值条件
P n (x ) a 0 a 1 x a n x n
Pn(xi)yi
Return 13
§4.2 拉格朗日多项式 /* Lagrange Polynomial */
1. 构造线性插值基函数的方法:
n= 1
已知 x0 , x1 ; y0 , y1 ，求 L1(x)= a0 +a1x使得 L1( x0 ) y0 , L1( x1) y1
R n(x)f(x)L n(x)
24
➢ Lagrange插值法的插值余项
设节点 ax0x1xnb，且 f 满足条件 f Cn[a,b], f (n1)在[a , b]内存在 , 截断误差(或插值余项):
R n(x)f(x)L n(x)f(( n n 1)1 ()!) n 1(x) , (a,b)
计算方法
第四章 插值方法
计算方法课程组
华中科技大学数学与统计学院
1
§4 插值方法
§4.1多项式插值问题的一般提法 §4.2 拉格朗日(Lagrange)插值 §4.3 差商与差分及其性质 §4.4 牛顿插值公式 §4.5 分段插值法 §4.6曲线拟合的最小二乘法
2
§4.0 引言
插值法是广泛应用于理论研究和生产实践的重 要数值方法, 它是用简单函数(特别是多项式或分 段多项式)为各种离散数组建立连续模型；为各种 非有理函数提供好的逼近方法。众所周知，反映 自然规律的数量关系的函数有三种表示方法：
y0 = f (x0) , …, yn = f (xn)， 由此构造一个简单易算的近似函数
p(x) f(x)，满足条件: p(xi) = f(xi) (i = 0, … n)。 这里的 p(x) 称为f(x) 的插值函数。 最常用的插值函数是 …?
计算方法Chapter01 - 插值方法
若函数族
中的函数 ( x) 满足条件
( xi ) = f ( xi ),
i = 0,1,, n
（ 1）
n ( x ) x f ( x ) 则称 为 在 中关于节点 i i =0 的一个插值函数。
f ( x) ——被插值函数； [a, b] ——插值区间；
xi in=0 ——插值节点； 式（1）——插值条件.
x12 x1n
2 n x2 x2
范德蒙行列式
x
2 n
n n
V=
x
0 i j n
( x j xi )
10
插值多项式的存在唯一性（续）
V= ( x j xi ) 0 i j n
由于 x0 , x1 , x2 , ..., xn 是 n 1 个互异的节点，即：
求插值函数(x)的问题称为插值问题。
5
插值问题
于是人们希望建立一个简单的而便于计算的函数 (x) 使其近似的代替 f (x)。
y 被插值函数 f (x) 插值函数 (x)
插值节点 0 x0 x1 x2 x3
… …… xn x
6
插值区间
多项式插值问题
对于不同的函数族Φ 的选择，得到不同的插值问题
( x0 , y0 ) 0
p2(x)
x0
x1
x2
x
19
抛物线插值（续）
p2 ( x ) = y0l0 ( x ) y1l1 ( x ) y2l2 ( x )
( x x1 )( x x2 ) ( x0 x1 )( x0 x2 )
( x x0 )( x x2 ) ( x1 x0 )( x1 x2 ) ( x x0 )( x x1 ) ( x2 x0 )( x2 x1 )
计算方法(2)-插值法
2
2
yk1 2
f (xk
h
2
),
y
k
1 2
f (xk
h) 2
21
3.牛顿向后插值公式
Nn (xn
th)
yn
tyn
t(t 1) 2!
2
yn
t(t
1)
(t n!
n
1)
n
yn
(t 0)
插值余项
Rn
(xn
th)
t(t
1) (t (n 1)!
Nn (x0
th)
y0
ty0
t(t 1) 2!
2
y0Leabharlann 插值余项t(t
1)
(t n!
n
1)
n
y0
Rn (x0
th)
t(t
1) (t (n 1)!
n)
h n1
f
(n1) ( ),
(x0 , xn )
20
二.向后差分与牛顿向后插值公式
杂.
根据f(x)函数表或复杂的解析表达式构
造某个简单函数P(x)作为f(x)的近似.
2
2.问题的提法
1)已知条件 设函数y f (x)在区间[a,b]上
连 续, 且 在n 1个不 同点a x0 , x1, , xn b 上 分 别 取 值y0 , y1, , yn
计算方法 插值法
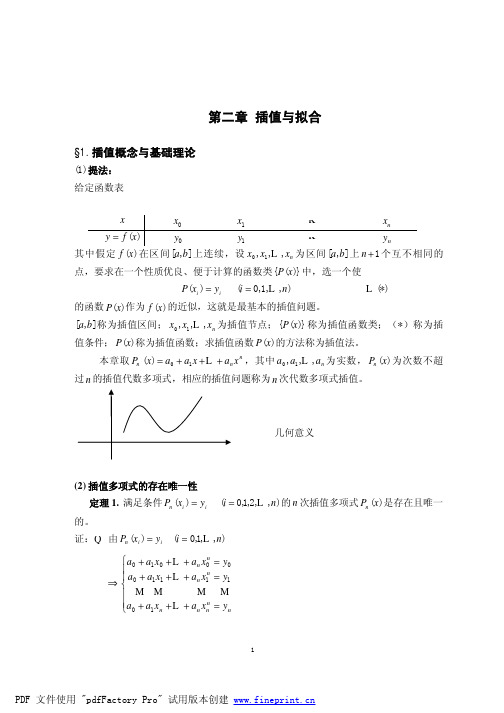
例见 P.74 例 1。 (2) 差商与牛顿基本插值多项式 考虑到拉格朗日插值的缺点：增加新的结点，需重新计算，工作量较大！ 改进的方向：选取形式： a 0 + a1 ( x − x0 ) + a 2 ( x − x0 )( x − x1 ) + L + a n ( x − x0 )( x − x1 ) L ( x − xn −1 ) ； （称之为 n 次牛顿插值多项式） 记 N n ( x) = a 0 + a1 ( x − x0 ) + a 2 ( x − x0 )( x − x1 ) + L + a n ( x − x0 )( x − x1 ) L ( x − x n −1 ) 为了给出 a i 简明计算表达式，引入差商（或均差）概念。 定义 1.
第二章 插值与拟合
§1.插值概念与基础理论
(1) 提法： 给定函数表 x y = f ( x) x0 y0 x1 y1
K K
xn yn
其中假定 f ( x) 在区间 [a, b] 上连续，设 x0 , x1 , L, x n 为区间 [a, b] 上 n + 1 个互不相同的 点，要求在一个性质优良、便于计算的函数类 {P ( x)} 中，选一个使 P ( xi ) = y i (i = 0,1,L, n) L (*) 的函数 P( x) 作为 f ( x) 的近似，这就是最基本的插值问题。 [a, b] 称为插值区间； x0 , x1 , L, x n 为插值节点； {P ( x)} 称为插值函数类；（*）称为插 值条件； P( x) 称为插值函数；求插值函数 P( x) 的方法称为插值法。 本章取 Pn ( x) = a 0 + a1 x + L + a n x n ，其中 a 0 , a1 , L, a n 为实数， Pn ( x) 为次数不超 过 n 的插值代数多项式，相应的插值问题称为 n 次代数多项式插值。
计算方法插值法(均差与牛顿插值公式)
为f ( x)关于节点 x0 , xk 一阶均差 (差商)
2018/11/7
5
2018/11/7
6
二、均差具有如下性质：
f [ x0 , x1 ,, xk 1 , xk ]
j 0
k
f (x j ) ( x j x0 )( x j x j 1 )(x j x j 1 )( x j xk )
2018/11/7
27
fk fk 1 fk 为f ( x)在 xk 处的二阶向前差分
2
依此类推
m f k m1 f k 1 m1 f k
为f ( x)在 xk 处的m阶向前差分
2018/11/7
28
差分表
xk f k 一阶差分 x0 f 0 x1 f 1 二阶差分 三阶差分 四阶差分
2018/11/7
31
等距节点插值公式
一、牛顿前插公式
2018/11/7
32
2018/11/7
33
二、牛顿插值公式与拉格朗日插值相比
牛顿插值法的优点是计算较简单,尤其是增加 节点时,计算只要增加一项,这是拉格朗日插值 无法比的. 但是牛顿插值仍然没有改变拉格朗日插值的 插值曲线在节点处有尖点，不光滑，插值多 项式在节点处不可导等缺点.
2018/11/7
25
2018/11/7
26
§
2.3.4 差分及其性质
一、差分
fk , 定义3. 设f ( x)在等距节点xk x0 kh 处的函数值为 k 0 ,1, , n , 称
f k f k 1 f k
k 0,1,, n 1
为f ( x)在 xk 处的一阶向前差分
计算方法-插值方法
这里
li(x)
n ji
(x xj) (xi x j )
j0
ai,bi ,ci,di为待定系数,分别由Li(xi)=1 和Li′(xi)=0
及hi′(xi)= 1 (i=0,1,2……,n)确定.
21
Li
x
1
2x
xi
n
k 0 k i
xi
1
xk
li2
x
hi x x xi li2 x
,
x
( 6
, ) 3
= 0.7660444…
外推 /* extrapolation */ 的实际误差 0.01001
利用
x1
4
,
x2
3
sin 50 0.76008,
0.00538
R~1
5
18
0.00660
内插 /* interpolation */ 的实际误差 0.00596
12
n= 2
L2 ( x)
注：若不将多项式次数限制为 n ，则插值多项式不唯一。
n
例如 P( x) Ln ( x) p( x) ( x xi ) 也是一个插值 i0
多项式，其中 p( x)可以是任意多项式。
7
拉格朗日多项式 /* Lagrange Polynomial */
求 n 次多项式 Pn ( x) a0 a1 x an xn 使得
0.00607001
15
Hermite插值简介
前述插值问题:要求被插函数与插值多项式在节点取
相同值,
Lagrange型插值条件
P
(
n
x
i
)
f (xi)
(i 0,1, ,n)
计算方法插值法
1)
Rn ( x ) K ( x) ( x - xi )
i 0
n
考察 j ( t ) Rn ( t ) - K ( x ) ( t - x i )
i0
n
j(t)有 n+2 个不同的根 x0 …
f (n ( x ) - L(nn
1)
xn x， j ( n1) ( x ) 0, x (a, b)
x - x0 y x1 - x 0 1
l ( x) y
i 0 i
1
i
l0(x)
l1(x)
n1
希望找到li(x)，i = 0, …, n 使得 li(xj)=ij ；然后令
Pn ( x )
l (x) y
i0 i
n
i
，则显然有Pn(xi) = yi 。
每个 li 有 n 个根 x0 … xi-1， xi+1 … xn li ( x) Ci ( x - x j )
插值法 比较古老, 常用的方法。 当未知函数 y = f(x) 非常复杂时，在一系列节 点 x0 … xn 处测得函数值： y0 = f(x0) … yn = f(xn) 由此构造一个简单易算的近似函数 P(x) f(x)， 满足条件P(xi) = f(xi) (i = 0, … n)，称P(x) 为f(x) 的插值函数。 最常用的插值函数是多项式
项式是唯一存在的。 证明：
i 0, ... , n 的 n 阶插值多
若除了Ln(x) 外还有另一 n 阶多项式 Pn(x) 满足 Pn(xi) = yi 。 考察 Qn ( x) Pn ( x) - Ln ( x) , 则 Qn 的阶数 n 而 Qn 有 n + 1 个不同的根 x0 … xn
Rn ( x ) K ( x) ( x - xi )
i 0
n
考察 j ( t ) Rn ( t ) - K ( x ) ( t - x i )
i0
n
j(t)有 n+2 个不同的根 x0 …
f (n ( x ) - L(nn
1)
xn x， j ( n1) ( x ) 0, x (a, b)
x - x0 y x1 - x 0 1
l ( x) y
i 0 i
1
i
l0(x)
l1(x)
n1
希望找到li(x)，i = 0, …, n 使得 li(xj)=ij ；然后令
Pn ( x )
l (x) y
i0 i
n
i
，则显然有Pn(xi) = yi 。
每个 li 有 n 个根 x0 … xi-1， xi+1 … xn li ( x) Ci ( x - x j )
插值法 比较古老, 常用的方法。 当未知函数 y = f(x) 非常复杂时，在一系列节 点 x0 … xn 处测得函数值： y0 = f(x0) … yn = f(xn) 由此构造一个简单易算的近似函数 P(x) f(x)， 满足条件P(xi) = f(xi) (i = 0, … n)，称P(x) 为f(x) 的插值函数。 最常用的插值函数是多项式
项式是唯一存在的。 证明：
i 0, ... , n 的 n 阶插值多
若除了Ln(x) 外还有另一 n 阶多项式 Pn(x) 满足 Pn(xi) = yi 。 考察 Qn ( x) Pn ( x) - Ln ( x) , 则 Qn 的阶数 n 而 Qn 有 n + 1 个不同的根 x0 … xn
计算方法课件_插值法
P( x) an x an1 x
n
n1
a1 x a0
满足
P( xi ) f ( xi )
(i 0,1,2,, n)
计 则称P(x)为f(x)的n次插值多项式。这种插值法通常 算 称为代数插值法。其几何意义如下图所示 方 法 课 件 y=p(x)
y=f(x)
2016/12/27
算 l0 ( x0 ) 1, l0 ( x1 ) 0 , l0 ( x2 ) 0 方 法 这个问题容易求解。由上式的后两个条件知 : 课 件 x1 , x 2 是 l0 ( x) 的两个零点。于是
1 再由另一条件 l0 ( x0 ) 1 确定系数 c ( x0 x1 )(x0 x2 ) ( x x1 )(x x2 ) 从而导出 l0 ( x) ( x0 x1 )(jkhh x0 x 2 ) 2016/12/27 14
直接由插值条件决定，
y
计 即 a0 , a1 , a 2 满足下面 y0 算 的代数方程组： 方 O x0 法 课 2 a a x a x 0 1 0 2 0 y0 件 该三元一
y=L2(x) y1 x1 y1 x2 y=f(x) x
2 a a x a x 0 1 1 2 1 y1 2 a a x a x 2 2 y2 0 1 2
(i=0,1,2,…,n )
的便于使用的插值多项式P(x),先考察几种简单情形,
线性插值是代数插值的最简单形式。假设给定了函数 近似地代替f(x)。选
x1 的值， f(x)在两个互异的点 x0 ， y0 f ( x0 ), y1 f ( x1 )
,现要求用线性函数 p( x) ax b 择参数a和b, 使 p( xi ) f ( xi )(i 0,1) P(x) 为f(x)的线性插值函数 2016/12/27 jkhh 。
计算方法第5章 插值法
N
7
5.2 拉格朗日插值
n次拉格郎日插值对应的程序（1/2）
#include <stdio.h> #include <math.h> #define MAXSIZE 50 void input(double x[MAXSIZE],double y[MAXSIZE],long n); void main(void) { double x[MAXSIZE],y[MAXSIZE],_x,_y,t; long n,i,j; printf("\n请输入插值节点的个数："); scanf("%ld",&n); input(x,y,n); printf("\n请输入插值点："); scanf("%lf",&_x); _y=0; for(i=0;i<=n-1;i++) { t=1; for(j=0;j<=n-1;j++) if(j!=i) t*=(_x-x[j])/(x[i]-x[j]); _y+=t*y[i];} printf("\n插值点(x,y)=(%lf,%lf)。",_x,_y);}
f ( n 1) ( ) 因此Rn(x)=f[x,x0,x1,…,xn]Wn(x)= Wn(x)，与差商的性质3吻合。 (n 1)!
13
5.3 差商与牛顿插值
五、n次牛顿插值的算法
输入插值节点的个数n。 输入插值节点(x[n],f[n][0])，插值点_x。 for(j=1;j<=n-1;j++) ① 构造差商表 for(i=j;i<=n-1;i++) f[i][j]=(f[i][j-1]-f[i-1][j-1])/(x[i]-x[i-j]); _y=f[n-1][n-1]; ② 牛顿插值 for(i=n-2;i>=0;i--) _y=f[i][i]+(_x-x[i])*_y; 输出插值点(_x,_y)。
计算方法-插值法报告
计算方法报告——插值1.原理简介插值法是利用函数f (x)在某区间中已知的若干点的函数值，作出适当的特定函数，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。
根据算法和插值要求的不同，有多种插值方法。
拉格朗日插值：有平面上点集{（x i,y i）}共n个点，现作函数f(x)图像使其过这n个点P i(x)=∏x−x j x i−x jnj=0 j≠i L n(x)=∑P i(x)×y ini=1则f(x)=L n(x)牛顿插值：同样点集，用不同方法构造插值多项式。
定义差商：f[x0，x1]=f(x0)−f(x1) x0−x1f[x0，x1……x k]=f[x0，x1……x k−1]−f[x1，x2……x k]x0−x k则有：N(x)=f[x0]+∑f[x0，x1……x k](x−x0)(x−x1)…（x−x k−1）nk=1理论上牛顿插值与拉格朗日插值所得插值多项式完全相同，只是不同写法。
2.算法描述分析函数：homework1.C 画图函数：DrawPlot.cpp为简化程序，将Lagrange插值与Newton插值算法作为子函数调用。
子函数Lagrange()中，输入插值点个数n，插值点集x[n]，y[n]，即可得到x点的Lagrange插值函数值L(x)。
同样，Newton()中输入相同信息可得到x点Newton插值函数值N(x)。
主函数main()中，先根据设定选择样点为等距分割还是Chebyshev分割，取得点集point_x[n+1]和point_y[n+1]，取点范围（-1，1）。
再调用子函数分别计算各x[i]点下的真实函数值，牛顿插值函数值，拉格朗日插值函数值及各种误差，在循环结束后将需要的误差L_inf 和L1输出到屏幕。
最后利用root TGraph把计算得到的数组画出函数图像，并存到rootfile 中。
在误差计算中只用了-1~0上的点，画图时扩大范围画到-1~1全部点DrawPlot函数中读取了homework1.C中画的函数图像，将其整合到一起，设置线条颜色及宽度，加上一个图例，重新生成一张图像。
计算方法 第四章 插值方法
§4.2.2 插值多项式的构造
现在考虑一般情况。已知节点 (xi, yi), i=0,1,…,n, x0<x1<…<xn, 则
Ln ( x ) yi li ( x )
i 0 n
( x x0 )...( x xi 1 )( x xi 1 )...( x xn ) yi i 0 ( xi x0 )...( xi xi 1 )( xi xi 1 )...( xi xn )
计算方法 (力学系本科生)
第四章 插值方法
(interpolation methods)
第四章插值方法
§4.1 问题的提出
§4.1 问题的提出
实际背景 • 实验和观察得到的一些离散数据点 ( xi , yi ), yi f ( xi ), i 0,1, 2,..., n, 需要 用这些离散数据点给出简单的函数表达 式 ( x)来近似原来函数 f ( x) 。
§4.2.2 插值多项式的构造
一般情形的拉格朗日插值多项式
设离散数据为(xk,δik), k=0,1,2,…,n, i 是固 定的非零整数 0 i n ,且 x0 x1 ... , n x δik是Kronecher记号
1, i k ik 0, i k
( n 1)
成立。
§4.2.3 拉格朗日插值余项
罗尔(Rolle)定理：若f(x)在[a,b]上连续,在 (a,b)上可导, 且f(a)=f(b), 则存在 (a, b) 满足 f ( ) 0 。
§4.2.3 拉格朗日插值余项
证明：∵ Rn(xi)=f(xi)-Ln(xi)=0, i=0,1,…,n
证明：由插值条件知
c x c x
计算方法(8) 第五章 插值法
得 a2abb10
a 1, b 2
(2)2( x)为四次多项式,且满足
2
(0)
0,
2
(1)
0,2
(2)
1,2'
(0)
0,
' 2
(1)
0
设
2
(
x
)
l22
(
x)
(
(x (2
0)( x 0)(2
1) 1)
)2
由2(2) 1, l2(2) 1得 1,2( x)
H 2n1 H '2n1
( (
xi xi
) )
yi y 'i
i 0，1，2，L n
一、一般情形的 Hermite插值问题
用Lagrange型插值基函数法
设Hermite插值多项式为
n
n
H2n1( x) i ( x) yi i ( x) y 'i
i0
i0
1( x) （1 （ 2 x x1）l（1 x1））l 2（1 x ）
0 ( x) （x x0）l 2（0 x ）
1( x) （x x1）l 2（1 x ）
其中
l0( x)
x x1 ， x0 x1
l
' 0
(
x
)
x0
1
x1
l1( x)
x x0 ， x1 x0
' i
(
xi
)
n j0
1
计算方法第5章插值
计算方法第5章插值插值与拟合5.1插值的基本概念设y = f (x)在某些离散点上的函数值, 或函数y = f (x)以表格形式给出:x yx0 y0x1 y1x2 xn y2 yn(5.1)插值问题：根据已知数据,构造函数y = f (x)的一种简单的近似表达式P(x),以便于计算点x xi 的函数值 f ( x ) , 或计算函数的导数值。
用简单的函数y=P(x)来近似地表示y=f(x), 使得:p( xi ) = f ( xi ) (i=0,1,2,。
,n)(5.1)称P(x)为插值函数，称f(x)为被插值函数, 称xi为插值节点, 称式(5.1)为插值条件.选P(x)为n次多项式Pn(x)作为f (x) 的近似,且使得Pn ( xi ) yi ,设x0 x1 。
xni 0, 1, 2, , n(5.2)满足关系(5.2)的函数Pn(x)为f (x)的n次插值多项式.记a = x0, b = xn,则[a, b] 为插值区间。
5.1.2插值多项式的存在唯一性三个问题: (1)满足插值条件的多项式是否存在? 是否唯一?(2)用pn ( x) 表示f(x)的误差是多少? (3)怎样求出pn ( x) ?定理1: 插值多项式Pn(x)存在且唯一. 证:设所要构造的插值多项式为：Pn ( x) a0 a1 x a2 x 2 an x n由插值条件Pn ( xi ) yii 0, 1, , n得到如下线性代数方程组：n 1 a0 x0 a1 x0 an y0 n 1 a0 x1a1 x1 an y1 1 a x a x n a y n 1 n n n 0此方程组的系数行列式为1 x0 D 1 x1 1 xn(范得蒙行列式！当2 n x0 x0 2 n x1 x10 j i n2 n xn xn( xix j ) 0,xi x ji 1,2, n;j 1,2, n时，0) D因此，Pn(x) 中的a0, a1,。