弧齿锥齿轮加工参数的全局优化设计
等顶隙弧齿锥齿轮的优化设计

0 引言
表1
锥齿轮传动齿轮箱在各行业的应用非 扭矩方向 旋向
轴向力
径向力
常普遍,主要以格里森锥齿轮和克林贝格制 逆时针右旋 顺时针左旋 (tan琢sin啄1-sin茁cos啄1)*Kp/cos茁 (tan琢cos啄1+sin茁sin啄1)*Kp/cos茁
等高齿锥齿轮为主。由于格里森弧齿锥齿轮 可以磨削齿面,加工效率较高,其具有承载
轴向力 合成方向
轴向力合成
597
12622
12025
1.26 -
597
12622
部分
524
12238
抵消
12025 11714
1.39
+
+
82.6
11798
+
11880
1.62
1.78
+
1008 1528
12174 11728
叠加
13182 13256
2.05
2164
12275
14439
表8
工作机功率 /4 级
根据图 2 可以得出大锥齿轮的轴向力大小相对二级 轴齿轮的轴向力大小要小,合成后的轴向力 在速比为 20:1~28:1 的范围内部分抵消,在 速比为 31.5:1~40:1 的范围内两者叠加。 2.3.2 扭矩方向 从输入锥齿轮轴小端 来看为逆时针旋转,来分别计算大锥齿轮产 生的轴向力,二级轴齿轮产生的轴向力和合 力大小及方向。(表 8) 根据表 8 可以得出在速比为 20:1~40:1 的范围内大锥齿轮和二级轴齿轮的轴向力 大部分进行抵消,具体如图 3。 根据图 3 可以得出大锥齿轮的轴向力 大小相对二级轴齿轮的轴向力大小接近,方 向相反,合成后的轴向力在全速比范围内进 行大部分抵消,其合成后的轴向力大大减 小,减低了对轴承寿命的影响。 3 结语 通过以上的分析可以得出我们可以根 据工作机的运行特点来设计减速机的布置 形式及齿轮的旋向,使大锥齿轮的轴向力和 二级轴齿轮的轴向力进行大部分抵消,从而 可以大大降低了轴承所受的轴向力,提高轴 承的寿命。
弧齿锥齿轮的高重合度设计

文章编号:1004-132 (2002)09-0791-05弧齿锥齿轮的高重合度设计邓效忠 教授邓效忠 方宗德 张金良 任东锋 摘要:针对航空和汽车弧齿锥齿轮对强度、动态性能和可靠性的特殊要求,提出了高重合度弧齿锥齿轮的设计方法。
这种设计是通过增加工作齿高和调整齿面啮合路径方向以及优化加工参数实现的。
结合弧齿锥齿轮的实际工况,提出了在不同载荷和安装误差下,实际重合度的综合分析方法,达到了既提高重合度又控制齿面啮合质量的目的。
关键词:弧齿锥齿轮;重合度;设计;啮合性能中图分类号:TH 132.4 文献标识码:A 收稿日期:2001—10—16基金项目:国家自然科学基金资助项目(50175090) 航空、汽车弧齿锥齿轮用于高速、重载的工况,故对其强度、动态性能与可靠性要求很高。
对于这类齿轮,因为其几何上的复杂性,控制它的啮合质量是相当困难的,在实际应用中往往存在着需要与制造水平的尖锐矛盾,提出了进一步开发高性能弧齿锥齿轮传动的要求。
传统的弧齿锥齿轮在设计与制造中,要求齿面接触路径接近与根锥垂直[1],齿向重合度没有发挥其应有的作用,其啮合性能近似于平行轴传动中的直齿轮,因而重合度小、强度较低、振动噪声大。
如何借鉴斜齿轮传动中端面重合度与轴向重合度的关系,以增大弧齿锥齿轮的实际重合度,提高其强度与动态性能,自然引起了众多学者的兴趣[2]。
笔者曾通过调整齿面接触路径方向使之倾斜以延长接触路径,提出重合度达到210的设计[3];在此基础上又提出重合度为3.0的设计,此时接触路径贯穿整个齿长方向。
此类设计在理论上对提高强度与动态性能有显著效果,但啮合质量对误差和变形的敏感性增大,尤其是齿面印痕移至齿宽一端时,易造成载荷与应力集中,这有可能导致轮齿断裂,引发事故。
本文以局部综合法的加工参数设计、啮合仿真和承载啮合仿真为主要工具,研究了齿面接触路径方向、齿面印痕位置和传动误差的综合设计方法,获得了既可控制齿面啮合质量,又能提高重合度的高性能弧齿锥齿轮设计。
汽车主减速器弧齿锥齿轮参数化设计与有限元分析

实验设计方面,首先需要准备相应的材料和设备,包括优质合金钢、数控机 床、滚齿机、测量仪器等。在具体步骤和方法上,首先需要根据图纸要求制定螺 旋锥齿轮的基本参数,如模数、齿数、压力角等,然后利用三维软件进行建模, 并通过有限元分析软件进行静态和动态性能分析。
在进行参数化建模与有限元分析后,我们可以得到一些有关螺旋锥齿轮性能 的关键数据。例如,通过静态分析,可以获得齿轮的应力分布、变形和接触应力 的数值;通过动态分析,可以了解齿轮在各种工况下的振动、噪音和疲劳寿命等 情况。对于这些数据,我们可以通过对比不同参数或不同设计方案的结果,进行 性能评估和优化建议。
参考内容二
基本内容
汽车主减速器是汽车传动系统中的关键部件,其主要功能是减速并增加扭矩, 以提高车辆的驱动力和行驶稳定性。而螺旋锥齿轮作为一种高效率、高承载的齿 轮形式,在汽车主减速器中得到广泛应用。为了优化其设计和性能,本次演示将 探讨汽车主减速器螺旋锥齿轮的参数化建模与有限元分析。
在汽车主减速器螺旋锥齿轮的参数化建模中,首先需要明确建模的目的和方 法。通过借助三维软件,如SolidWorks、CATIA等,可以对螺旋锥齿轮进行几何 建模,并利用有限元分析软件,如ANSYS、Abaqus等,进行性能分析和优化。此 外,参数化建模还可以为后续的优化设计和制造提供方便,缩短产品开发周期。
未来研究方向可以从以下几个方面展开:1)深入研究弧齿锥齿轮的啮合原 理和动力学特性,建立更加精确的数学模型;2)拓展材料库和网格划分方法, 提高分析的精度和效率;3)考虑多学科耦合因素,如热力学、流体动力学等, 以更加全面地评估弧齿锥齿轮的性能;4)开展实验研究,将有限元分析结果与 实验数据进行对比,以验证分析的准确性和有效性。
5、参数化设计流程
弧齿锥齿轮传动的多目标优化设计

那么相应于
fi ( X )的转化函数
fri ( X )的自变量
X
为
ri
:
X ri = ( fi ( X ) - pi ) 2π / ( qi - pi ) ,于是规格化目标函数
fri ( X )为 :
fri ( X )
=
X ri 2π
-
sinX ri
= fi (X ) qi -
- pi pi
-
sin ( fi ( X ) qi -
g3 ( X ) = 23 - x2 ≤0
g4 ( X ) = x2 - 40≤0
g5 ( X ) = 0. 24R e - x3 ≤0
g6 ( X ) = x3 - 0. 32R e ≤0
g7 ( X ) = 1. 5 - x4 ≤0
(6)
g8 ( X ) = x4 - 10≤0
g9 ( X ) = 1. 25 - 0. 5x4 x1 ( 0. 5x4 x1
- pi 2π) pi
( i = 1, 2, 3)
·加权因子 w i 选择采用目标函数的容限法求解 , 由于 目标函数变动范围为 : pi ≤fi ( X ) ≤qi ( i = 1, 2, 3)
那么各项目标的容限 :
Δfi = ( qi - pi ) /2 ( i = 1, 2, 3) 加权因子 w i = 1 / (Δfi ) 2 ( i = 1, 2, 3) ·统一多目标函数 ( 4)式可改写成 :
性能的发挥 。对其设计方法的研究 ,在改善其工作性能和提 高经济效益都具有重要的意义 。以往弧齿锥齿轮传动的优
化设计是以体积最小为基础 ,将设计中的应力 、强度等变量 视为确定型变量 ,这不符合实际运行情况 。本文在充分考虑 体积最小 、接触强度计算的许用传递功率最大和弯曲强度计
弧齿锥齿轮齿面优化修正及计算机仿真

( . rh se n P l tc nc l 1 No t we t r o y e h ia i r i Xi n 7 0 7 . i a; Un v st e y, ’ 1 0 2 Ch n a
i g p te n a d k n ma i lb h v o f c u l p r l b v lg a rv s a e u u l ifr n r m n a tr n i e t a e a i r o r a i e e e rd ie r s a l d fe e t fo c a s a y t e a a y i lr s l f t e o i ia e i n o t i e y To t o t c h n l t a e u t o h rgn ld s b an d b o h C n a t An lss ( c s g ay i TCA )t c — e h
正 过 程 带 来 了 困 难 , 易 获 得 良好 的 效 果 。 不
u i g Le s q a e M  ̄h d i r s n e . n me ia x mp e b a s o o p t r e i l— s a tS u r n o sp e e t d A u r l a l y me n f m u e i d smu a c e c z t n s o e a r e n fTCA e u sb t e o r c e o t u f c n h rg n l e i n, i h wst g e me t o h o r s R e we n c r e t d t o h s r a ea d t eo i a s i d g ic u i g t e b a i g p te n a d k n ma i l e a ir n l dn h e rn a tr n ie t a h vo . c b Ke r s p r l e e e r o t l n s o r c in y wo d :s i v l a ;t o h f k ;c re t a b g a o
弧齿锥齿轮动态啮合质量的优化设计

本思想为 :
束条件 ,采 用非 线性 规 划 的方 法求解 承 载接触 问题 ,获得 齿
1)在 大轮齿面上 预设 一个参 考 点 ,在 参 考点 处预 置 三 面载荷分布、承载啮合印痕和承载传动误差。
个齿面二阶接触参 数 :参考 点处 接触 迹线 与大轮 根锥 夹角 、
参考点处传动 比函数 的一 阶导数值 、参 考点处 瞬时接触椭 圆 3 动态 啮合 质量 的优 化设 计模 型
局 最优 解 。 为了克服上述设 计方法的局限性与反 复性 ,进一步提 高
优化质 量 ,本文基于改进粒子群优化算 法提 出了一种全局 优 化 思路 ,以局部综合 法 中的预设 啮合 参数 为优化 设计 变量 , 以设计 最大重合度不小于 2、无载传 动误差 曲线满 足一定 对 称性 、承载传动误差 曲线不低于无载传 动误差 曲线的下 限为 约束条件 ,以无载传 动误 差 曲线 的对 称度 、承 载传 动误差 的 下限与无载传动误差下 限之 间 的距 离及 承载 传动 误差 的均 方差为优化 目标函数 ,对弧齿锥齿轮 的动态 啮合质量进行 了 全局优化设计 。在对预 设 啮合参 数进行 优化 的 同时也获 得 了齿轮副最优加工参数 ,最终从设计 和加工环 节有效地 改善 了弧齿锥齿轮 的动态啮合质量 。
e(X)≥2,妒z≥
~ 37l 一
4 优化 算 法介绍
式 中: 、I13 i 分别 是惯 性权 重因 子 的最大 、最小 取值 ;N、n 分别是最大迭代次数 和 当前 迭代 次数 。通 常 在 0.9—0.2
由于本文 的设计变量 与 目标 函数之 间没有 直接 的关 系 , 之间取值 。
L壳 = 壳 ( ,0 , f)
(1) 0。。为了得 到大轮滞后 的抛 物线形状传 动误差 ,参考点处 传 动 比函数 的一 阶导数 值 m 取 为负 值。参考 点 的位 置坐 标
弧齿锥齿轮几何全参数设计分解
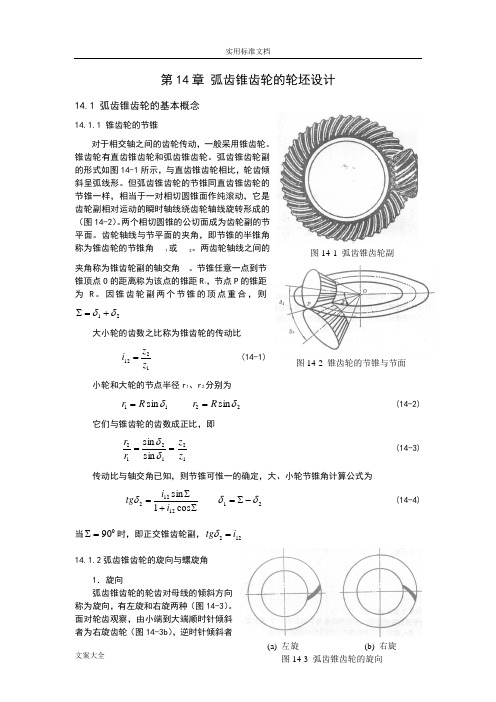
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角1或2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比,即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时,即正交锥齿轮副,122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b ),逆时针倾斜者图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-1 弧齿锥齿轮副旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。
这样可保证大小轮在传动时具有相互推开的轴向力,从而使主被动轮互相推开以避免齿轮承载过热而咬合。
2.螺旋角弧齿锥齿轮轮齿的倾斜程度由螺旋角i 来衡量。
弧齿锥齿轮几何参数设计.doc

弧齿锥齿轮几何参数设计..第14章弧齿锥齿轮的轮坯设计图14-1 弧齿锥齿轮副14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥图14-2 锥齿轮的节锥与节面对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角d1或d2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角S。
节锥任意一点到节锥顶点O的距离称为该点的锥距Ri,节点P的锥距为R。
因锥齿轮副两个节锥的顶点重合,则大小轮的齿数之比称为锥齿轮的传动比(14-1)小轮和大轮的节点半径r1、r2分别为(14-2)它们与锥齿轮的齿数成正比,即(14-3)传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为(14-4)(a) 左旋(b) 右旋图14-3 弧齿锥齿轮的旋向当时,即正交锥齿轮副,14.1.2弧齿锥齿轮的旋向与螺旋角1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b),逆时针倾斜者则为左旋齿(图14-3a)。
大小轮的旋向相反时,才能啮合。
一般情况下,工作面为顺时针旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。
这样可保证大小轮在传动时具有相互推开的轴向力,从而使主被动轮互相推开以避免齿轮承载过热而咬合。
2.螺旋角图14-4 弧齿锥齿轮的齿线与螺旋角弧齿锥齿轮轮齿的倾斜程度由螺旋角bi来衡量。
弧齿锥齿轮纵向齿形为节平面与轮齿面相交的弧线,该弧线称为节线,平面齿轮的节线称为齿线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:1999-02-08;修订日期:1999-04-26基金项目:航空科学基金资助项目(96C53037)作者简介:田行斌(1972-),男,西北工业大学,博士研究生第15卷 第1期2000年1月航空动力学报Journa l of Aerospace PowerV o l 115N o 11Jan . 2000文章编号:100028055(2000)0120075203弧齿锥齿轮加工参数的全局优化设计田行斌 方宗德(西北工业大学十系,陕西西安 710072)摘要:本文通过局部综合法对齿面一阶和二阶接触参数进行预控,在此基础上,全面考虑了齿轮副在小端、中部、大端啮合时的接触印痕和传动误差,通过对可选加工参数的优化设计,消除了齿轮副的三阶接触缺陷,从而实现了弧齿锥齿轮副啮合质量的全局控制。
关 键 词:弧齿锥齿轮;优化;加工参数中图分类号:TH 1321416 文献标识码:A1 前 言 航空用弧齿锥齿轮副的啮合质量至关重要。
弧齿锥齿轮副的啮合质量通常用接触印痕和传动误差来衡量。
鉴于高可靠性的要求,在实际生产中,对齿轮副在小端、中部、大端啮合时的接触印痕一般都有一定的要求。
为此,常常需要操作人员多次进行机床调整、试切、滚检等步骤,费时费力,且依赖于操作人员的经验。
然而即便如此,由于实际生产中缺乏对传动误差的检测手段,仅满足接触印痕要求的齿轮副在实际使用中仍未必能达到预定的要求。
因此,全面控制接触印痕和传动误差是提高弧齿锥齿轮副可靠性的关键。
本文采用局部综合法进行弧齿锥齿轮加工参数设计。
该方法能严格保证预定的齿面一阶和二阶接触参数。
在此基础上,本文全面考虑了齿轮副在小端、中部、大端啮合时的接触印痕和传动误差,并通过对可选加工参数的优化设计,有效消除了齿轮副的三阶接触缺陷,从而实现了弧齿锥齿轮副啮合质量的全局控制。
2 局部综合法 局部综合法是由L itvin 教授提出并完善的[1]。
本文简述此处应用基本步骤[2]:(1)按切齿调整卡确定大轮的加工参数,并在大轮齿面上指定参考点的位置,即预定齿面的一阶接触参数。
(2)根据产形轮和被加工大轮啮合时的线接触条件,由大轮加工参数和产形轮与被加工大轮间的相对运动关系求得大轮齿面上参考点处的主曲率和主方向。
(3)根据小轮和大轮啮合时的点接触条件,预定参考点处接触迹线的方向角、瞬时接触椭圆长轴长度和大轮相对于小轮的角加速度的值,即预定齿面的二阶接触参数,求得小轮齿面上参考点处的主曲率和主方向。
(4)根据产形轮和被加工小轮啮合时的线接触条件,由小轮参考点处的主曲率和主方向的值,确定小轮的加工参数。
3 弧齿锥齿轮加工参数的优化设计 按该法所得加工参数加工成弧齿锥齿轮副的齿面一阶和二阶接触参数能够被严格保证。
但是,齿轮副的三阶接触参数(参考点处的二阶接触参数在齿面相对滚动过程中及V H 检验时的变化率)并没有得到控制,因此,齿轮副仍有可能出现诸如菱形接触、鱼尾接触、S 形传动等三阶接触缺陷,还应通过优化设计加工参数来避免。
3.1 优化变量 在局部综合过程中,保证齿面的一阶和二阶接触参数所需的加工参数少于加工设备所能提供的调整参数,这才能通过对剩余参数的调整来实现优化过程。
对于采用磨齿工艺加工的弧齿锥齿轮副,可选的加工参数为小轮刀具齿形角、展成参考点时小轮滚比的一阶导数。
3.2 目标函数 通常认为理想的齿面接触情况是:接触迹线是一根直线并近似与根锥垂直,每一个瞬时接触椭圆的长轴大致相等,并有相同的方向,运动曲线呈中凸的抛物线形而且能够相交。
为达到这个目标,可通过三阶接触分析来进行优化方法设计[3]。
但该方法在齿面接触斑点较大时,可能达不到理想的效果。
本文采用如下方法来构造目标函数:(a )求参考点啮合时大、小轮的接触信息:在固定坐标系中,设:大轮的齿面方程为r ο2(Ηg ,Υg ,Ω2),法线方程为n ο2(Ηg ,Υg ,Ω2),其中Ηg 和Υg 为大轮齿面曲面坐标,Ω2为大轮转角。
小轮的齿面方程为r ο1(Ηp ,Υp ,Ω1),法线方程为r ο1(Ηp ,Υp ,Ω1),其中Ηp 和Υp 为小轮齿面曲面坐标,Ω1为小轮转角。
大、小轮连续接触应满足如下条件:r ο1(Ηp ,Υp ,Ω1)=r ο1(Ηg ,Υg ,Ω2)n ο1(Ηp ,Υp ,Ω1)=n ο1(Ηg ,Υg ,Ω2)(1) 参考点啮合时,两齿面满足啮合方程:n ο v ο(12)=0(2)且此时传动比等于理论值,即有:Ξ(2) Ξ(1)=N 1N 2。
其中N 1和N 2分别为小、大轮齿数。
(1)式中两个矢量方程包含了6个标量方程,由于n ο1和n ο2是单位矢量,故独立的方程数为5个。
(2)式为一标量方程。
将(1)式与(2)式联立,可解得所有6个未知数:Ηp 0,Υp 0,Ω10,Ηg 0,Υg 0和Ω20。
进而可由大轮齿面上的点r ο2(Ηg 0,Υg 0,Ω20)经锥面展开法变换得到大轮齿面二维旋转投影图上的点的位置(X 0,Y 0),并求得该点处瞬时接触椭圆长轴的长度A 0,而该点处的传动误差为0。
(b )求有效边界内大、小轮的接触迹线终点处的接触信息:在两相配齿面的有效边界内,接触迹线分别起止于两齿轮的齿顶处。
当两齿轮在大轮的齿顶处接触时,仍有(1)式成立。
此外,还有下列方程成立:∆a 2=tan -1y 22+z 22(x 2+f 2)(3)式中∆a 2为大轮面锥角,(x 2,y 2,z 2)为在与大轮固连的坐标系中的大轮齿面上点的三维坐标值,f 2为大轮节锥顶点到面锥顶点的距离。
将(1)式与(3)式联立,又可解得6个未知数:Ηp 1,Υp 1,Ω11,Ηg 1,g 121ο2(Ηg 1,Υg 1,Ω21)经锥面展开法变换得到大轮齿面二维旋转投影图上的点的位置(X 1,Y 1),并求得该点处瞬时接触椭圆长轴的长度A 1,而该点处的传动误差为:Ε1=(Ω21-Ω20)-(N 1 N 2)(Ω11-Ω10)。
同理,两齿轮在小轮的齿顶处接触时,有下列方程成立:∆a 1=tan -1y 21+z 21(x 1+f 1)(4)式中∆a 1为小轮面锥角,(x 1,y 1,z 1)为在与小轮固连的坐标系中的小轮齿面上点的三维坐标值,f 1为小轮节锥顶点到面锥顶点的距离。
将(1)式与(4)式联立,也可解得6个未知数:Ηp 2,Υp 2,Ω12,Ηg 2,Υg 2和Ω22。
在此基础上,由大轮齿面上的点r ο2(Ηg 2,Υg 2,Ω22)经锥面展开法变换得到大轮齿面二维旋转投影图上的点的位置(X 2,Y 2),并求得该点处瞬时接触椭圆长轴的长度A 2,而该点处的传动误差为:Ε2=(Ω22-Ω20)-(N 1 N 2)(Ω12-Ω10)。
(c )求出大、小轮在V H 检验时的接触信息:V H 检验是生产实践中常用的检验齿轮副啮合质量的一种方法。
当调整V H 值使齿轮副在大轮齿面小端中点共轭接触时,设小端中点在旋转投影图上的位置为(X t 0,Y t 0),则有:x 2=X t 0 , y 22+z 22=Y t 0(5) 可由(5)式解得大轮齿面上小端中点处的曲面坐标Ηg t 0,Υg t 0。
又有:r ο1-r ο2=f (Ηp ,Υp ,Ω1,Ω2,V ,H )n ο1-n ο2=f (Ηp ,Υp ,Ω1,Ω2)n ο v ο(12)=f (Ηp ,Υp ,Ω1,Ω2,V ,H )(6)(6)式中共有6个方程,可解得:Ηp t 0,Υp t 0,Ω1t 0,Ω2t 0,V t 0和H t 0六个未知数,在此基础上,可求得小端中点处瞬时接触椭圆长轴的长度A t 0,而该点处的传动误差为0。
在此条件下,重复(b )中的过程,可求得齿轮副在小端啮合时,接触迹线终点处的接触信息。
计有:在大轮齿顶接触时齿面旋转投影图上点的位置(X t 1,Y t 1)、该点处瞬时接触椭圆长轴长度A t 1及传动误差Εt 1;在小轮齿顶接触时齿面旋转投影图上点的位置(X t 2,Y t 2)、该点处瞬时接触椭圆长轴长度A t 2及传动误差Εt 2。
同理,求得齿轮副在大端啮合时的接触信息,计有:(X h 0,Y h 0),A h 0;(X h 1,Y h 1),A h 1,Εh 1;(X h 2,Y h 2),A h 2,Εh 2。
至此,求得了齿面上共9点处的接触信息,据此可形成目标函数进行优化,以消除三阶接触缺陷。
如:取 A 1-A 0 + A 2-A 0 最小,可避免菱形接触;取 X 1-X 0 + X 2-X 0 最小,可避免鱼尾接触;对于航空齿轮,为了尽可能地减少在载荷作用下产生边缘接触的可能性,可取 Ε1-Ε2 + Εt 167航空动力学报第 15 卷-Εt 2 + Εh 1-Εh 2 最小为目标函数等等。
实际应用中,可将多个目标加权求和后得到目标函数。
本文图1 齿轮副在不同安装误差下的接触印痕与传动误差算例中,为简明起见,取目标函数如下:m in: A 1-A 0 + A 2-A 0 + X 1-X 0 +X 2-X 0 + Ε1-Ε2 + Εt 1-Εt 2 + Εh 1-Εh 2 3.3 优化方法及结果 根据优化变量和目标函数的性质,采用轮流坐标搜索法[4]进行优化。
计算实例显示,小轮刀具齿形角的改变,主要对接触椭圆长轴长度影响较大,即该优化变量对避免菱形接触作用较大,而展成参考点时小轮滚比的一阶导数改变,主要对接触路径及传动误差曲线的形状影响较大,即该优化变量对避免鱼尾接触及S 形传动作用较大。
图1所示为采用本优化过程对某航空齿轮进行设计得到的TCA 结果。
上边依次为小端、中点、大端处的接触印痕图,下边为相应的传动曲线图。
由图中可以看出,优化结果是较为满意的。
4 结 论 本文采用局部综合法进行弧齿锥齿轮加工参数设计,在保证预定的齿面一阶和二阶接触参数的前提下,通过对可选加工参数优化设计,来消除齿轮副的三阶接触缺陷,使弧齿锥齿轮副试切调整过程大为简化,并可靠地保证了其啮合质量。
参 考 文 献1 L itvin F L .Gears Geom etry and A pp lied T heo ry [M ].Engle 2wood C liffs ,N J .P rentice H all ,19942 方宗德,杨宏斌.准双曲面齿轮的优化切齿设计[J ].汽车工程,1998,20(5):302-3073 王小椿,吴序堂.弧齿锥齿轮和双曲线齿轮的三阶接触分析和优化切齿计算[J ].齿轮,1989,13(2):1-104 王庆凯,王肇明.优化与最优控制中的计算方法[M ].北京:科学出版社,1986(责任编辑 王震华)Overa ll Opti m iza tion on M ach i ne -Tool Setti ngs of Sp ira l Bevel GearsT ian X ingb in , Fang Zongde(10th D ep t .N o rthw est Po lytechn ic U n iversity ,X i’an 710072,Ch ina )Abstract : T he first and second o rder con tact p aram eters of a sp iral bevel gear drive are p recon 2tro lled by u sing the local syn thesis m ethod .Con sidering the con tact p attern and tran s m issi on erro rs on toe ,m iddle ,heel con tacts ,the th ird o rder con tact sho rtcom ings are eli m inated by op ti m izing the m a 2ch ine -too l settings.T he overall con tro l of engagem en t quality is realized .Key words : sp iral bevel gear ;op ti m izati on ;m ach ine -too l settings77第 1 期田行斌等:弧齿锥齿轮加工参数的全局优化设计。
