二维方腔环流计算
雷诺数为22000的二维方柱绕流仿真计算

图 15-1-3 网格划分结果
图 15-1-3 给出了网格划分结果,在划分网格时,约束整个面的网格尺寸为 10mm, 并且定义入口、 出口、 上下边界、 方柱表面的名称集 (Named Selections) , 以方便在 Fluent 中定义边界条件。
图 15-1-4 局部网格示意
图 15-1-4 给出了局部网格示意图,从图中可以看出,在方柱表面的网格高 度是较高的, 使用尺度化近壁面函数法时并没有划分很细的边界层网格。最后共 得到 48900 个网格,网格最大长宽比为 1.0069,满足仿真计算的网格要求。
(3)对于存在较高导热率的共轭传热问题; (4)对于流场网格长宽比较大的问题。 在本算例中,虽然不存在以上问题,但仍采用双精度 4 核并行计算求解。 在进行计算时, 先进行稳态计算,然后将稳态计算的结果作为瞬态计算的初 场,再进行瞬态计算。 求解器采用压力基求解器,并进行湍流模型的设置。
图 15-1-6 湍流模型的选择
关于雷诺数 22000 方柱绕流 (关于壁面函数法、湍流粘度比的计算等概念可以参考 文献十六)
15.1.1 RNG 模型与尺度化壁面函数在方柱绕流中的应用
图 15-1-1 分析流程
图 15-1-1 给出了二维方柱绕流问题的分析流程, 在 Workbench 中建立模型, 然后使用 Mesh 模块进行分网,最后提交到 Fluent 中进行计算。
图 15-1-15 方柱表面的 Y+值分布范围
仿真后可以知道,近壁面 Y+值的分布范围为 7.07-68.6,在 Fluent 的官方 文献中推荐壁面函数法的 Y+值适用范围为 30-500,对于尺度化壁面函数,由于 在近壁面使用了预防 Y+值过小导致结果恶化的技术,其 Y+值范围下限可以适当 放宽, 但仍应尽量取在 11.25 以上。 过大或过小的 Y+值都可能引起结果的恶化。
4.2 顶盖驱动流(8)

4.2顶盖驱动流4.2.1物理模型在一个正方形的二维空腔中充满等密度的空气,方腔每边长为0.1m,其顶板以0.1m/s 的速度向右移动,同时带动方腔内流体的流动,流场内的流体为层流。
计算区域示意图如图4-2-1所示。
图4-2-1 计算区域示意图4.2.2在Gambit中建立模型Step1:启动Gambit并选择求解器为Fluent5/6。
Step2:创建面操作:→→打开对话框如图4-2-2所示。
输入长度和宽度10,在Direction中选择XY Centered。
图4-2-2 创建面设置对话框Step3:划分面网格操作:→→打开对话框如图4-2-3所示,Shift+鼠标左键选择正方形面,Internal size=0.5,其它保留默认,点击Apply确认。
划分后的网格如图4-2-4所示。
图4-2-3 网格划分设置对话框图4-2-4 计算区域网格图Step4:设置边界类型操作:→●在Name栏输入边界名称wall-1,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔顶部边线。
●在Name栏输入边界名称wall-2,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔其它三条边线。
Step5:输出网格文件操作:Fil m→export→mesh打开对话框如图4-2-5所示,选中Export 2-D mesh 前面的复选框,输出网格文件。
图4-2-5 网格文件输出对话框4.2.3求解计算Step1:启动Fluent选择2d单精度求解器,点击Run,如图4-2-6所示。
图4-2-6 启动求解器图4-2-7 网格尺寸设置对话框Step2:导入并检查网格1.读入网格文件操作:Fil e→Read→Case...找到文件后,单击OK按键确认。
2.检查网格操作:Grid→Check网格读入后,一定要进行网格检查,注意最小体积不能为负值。
3.网格比例设置操作:Grid→Scale...在Gambit中,生成网格使用的单位是cm,在Grid Was Created In下拉菜单中,选取cm,如图4-2-7所示,然后单击Scale,关闭对话框。
方腔环流

sn1 0 ,在四边
n 1 s
2 sn sn ,在两侧和底边 h2 2 sn sn h ,在顶面 h2
sn1
3.计算步骤 求解过程,可按照下列步骤进行,
1) 给定 , 的初值。可取 i,0j 0, i,0j 0
4h 2 4h 2 1 i 1, j 2 i , j i 1, j i , j 1 2 i , j i , j 1 2 2 Re h h
引进松弛因子 方程可化为下列的迭代格式
i 1, j i , j 1 i , j 1
3 n 1 1 n n 其中, R1 max in, ~ 10 4 j i , j , R2 max i , j i , j ,C 为给定精度,可取 C r 10
7) 4.计算结果 随着雷诺数的增加, 减少,对于一个 25 25 的网格,当 Re 10 时,可取 1 ,而当
0 ,在腔体四边
v 0 ,在 AB 和 CD 上 x
u 0 ,在 AD 和 BC 上 y
其中,Re 为雷诺数
图 1 方腔环流
2.取正方形网格(如图所示) ,网格数视情况可取 25、50、100 等,一般不建议超过 200,雷诺 数 Re 一般不超过 5000,因为超过 5000 流场已经呈现出非线性,开始出现偏差,雷诺数超过 10000 甚至根本不能算出结果,这是因为强非线性情况下描述流场行为的方程已经不能做如上简化。
图 2 方腔 1, j
2 i , j i 1, j h2
i , j 1
计算流体-二维

和式 (2) 在图3所示的网格上的离散形式如下 [ pi+1, j − pi, j ] 1 1 n ( C + D ) − uin,+ = u + dt − A − B + i, j j Re ∆x [ p i , j +1 − p i , j ] 1 1 n vin, + ( G + H ) − = v + dt − E − F + i, j j Re ∆y 其中 A = ui, j B= ui+1, j − ui−1, j 2∆ x
对于式样 (4) 的迭代方式非常简单. 每一步迭代, 本文都对每一个压强点用上式计算迭代后的 值, 一步迭代完成后, 检查一下同一压强点上的迭代前后值相差的最大值是否为 ε = 0(实际计算 过程中,ε 取一个非常小的值, 当迭代前后的 p′ 相差的最大值小于 ε 即认为迭代完成)
3.3
பைடு நூலகம்
边界条件
在交错网格中, 边界处理相对于非交错网格较为复杂, 一些量的节点恰好在边界上, 而另一些 节点则分布在边界两侧, 因此在施加边界条件时要非常小心, 本文对速度应用狄利克雷边界条件 (Dirichlet boundary condition), 压强施加诺伊曼边界条件 (Neumann boundary condition). 对 于速度恰好在边界上的情况, 应用边界条件时真接将这些速度设为边界上的速度 Ub (对于固壁 边界条件, Ub = 0), 比如在左右边界上的 u 及上下边界上的 v. 而对于速度点分布在边界两边的 情况, 比如在上下边界的 v 和左右边界的 v, 其边界条件为 u i , j + u i , j +1 = Ub ⇐= ui, j = 2Ub − ui, j+1 或 ui, j+1 = 2Ub − ui, j 2 对于边界上的压力的边界条件, 压力在边界法向上的导数 ∂ p/∂n 由边界两边对应的两个压 强点定义. 比如对于左边界, 诺伊曼边界条件为 p i , j +1 − p i , j = 0 =⇒ pi, j+1 = pi, j dy 实际上, 在本文的交错网格中, 固壁边界外的压力点并不参与到边界内速度的计算中, 因此在固 壁上并不需要对压强施加边界条件. 只在最后结果的后处理中将压强平均到网格节点上时需要.
水泥3D打印喷头内浆体流动的MRT-LBM分析

水泥3D打印喷头内浆体流动的MRT-LBM分析吴伟伟;黄筱调;方成刚;李媛媛【摘要】水泥3D打印时,水泥浆体在喷头内的流动性对挤出成型有重要影响.以水泥、水、聚羧酸减水剂、改性棒土和纤维素醚作为原始打印材料,根据流变特性测试,采用Herschel-Bulkley模型作为水泥浆体的流变模型,并利用多松弛时间的格子Boltzmann方法(MRT-LBM)对浆体在喷头中的流动进行了分析,引入矩函数来描述松弛过程中的碰撞步,并利用泊肃叶流的理论解对MRT模型进行了验证.在进行实际仿真时,以雷诺数作为准则进行物理单位和格子单位之间的转换,获得相关的流线图和速度场分布图.结果表明:水泥浆体在螺槽截面的流动呈现环流形状,环流的中心在(0. 5W,0. 7h)位置处;根据速度场的分布,在螺槽横截面的左下角和右下角不存在流体流动,适当增大螺杆速度或螺槽宽度有助于水泥浆体在螺槽内的有效输送.【期刊名称】《南京工业大学学报(自然科学版)》【年(卷),期】2018(040)005【总页数】6页(P79-84)【关键词】水泥3D打印;Herschel-Bulkley流体;多松弛时间的LBM;数值模拟;流线;速度分布【作者】吴伟伟;黄筱调;方成刚;李媛媛【作者单位】南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800【正文语种】中文【中图分类】TH12对浆体在喷头内部的流动进行分析,可以很好揭示其流动规律,流线图可以描述浆体在腔体中的主要流动区域和环流的形成,速度场分布图可以描述各速度分量沿不同方向的分布情况,速度较大的区域更有利于浆体的输送,速度较小的区域往往受黏性系数和机械结构的影响,因此合理的机械结构有助于浆体在喷头内部的流动。
方腔顶盖驱动流动
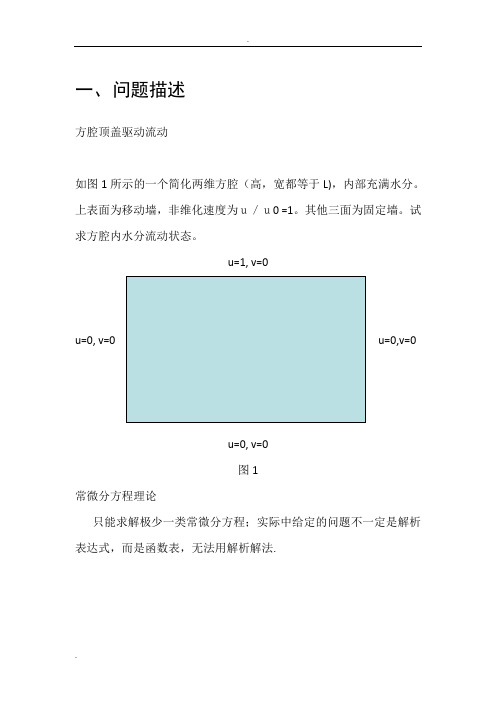
一、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0 u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1) y n +1 , 称为局部截断误差.截断误差: 实际上,y (x n ) ? y n , y n 也有误差,它对y n +1的误差也有影响,见下图。
但这里不考虑此误差的影响,仅考虑方法或公式本身带来的误差,因此称为方法误差或截断误差。
局部截断误差的分析:由于假设y n = y (x n ) ,即y n 准确,因此分析局部截断误差时将y (x n +1) 和 y n +1都用点x n 上的信息来表示,工具:Taylor 展开。
显式欧拉公式一阶向前差商近似一阶导数推导如下:223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+隐式欧拉公式xn +1点向后差商近似导数 推导如下:几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
流函数-涡量法的二维方腔流数值模拟

流函数- 涡量法的二维方腔流数值模拟基本方程:22v tξγξψξ∂=∇-∇∂-∇=⎧⎨⎩t ———时间步长, s;γ———流体的运动粘度, m2 /s;ξ———涡量, s- 1;ψ———流函数, m2 /s;v ———速度矢量, m/s;差分格式:采用FTCS 格式,对于ξ有:1,,1,1,,1,11,,1,,1,,1,2222()22()()n n n nn nn n nn n ni j i ji j i ji j i j i j i j i ji j i j i j nni ji juvtxyx y ξξξξξξξξξξξξυ++-+-+-+-+----+-+=--++∆∆∆∆∆采用FTCS 格式,对于ξ有:1,,1,,1,,1,,1,2222)()()n nn n n n n n i j i ji j i j i j i j i j i j i j tx y ψψψψψψψψξ++-+---+-+=++∆∆∆边界条件:速度的边界条件:固体壁面处设置无滑移边界条件, 即u=0, v=0; 流函数的边界条件:在固体壁面及平板驱动处的流函数ξ=0; 涡量的边界条件: 平板驱动处:2uxξ=∆ 左右壁面上:;,1,,22()()i j i j i j y ξξξ+-=∆网格划分:采用等距结构化网格划分(40*40)编程计算:本算例采用MATLAB进行编译,其主要优势是语言简单,可以方便地描绘出方腔环流的等值线图等。
主要语句:while norm(c1)>1e-4|norm(c2)>1e-4n=n+1;O1=O;E1=E;t=t+dt;for i=2:Ifor j=2:JO(i,j)=O(i,j)-dt*(u(i,j)*(O(i+1,j)-O(i-1,j))/(2*dx)+v(i,j)*(O(i,j+1)-O(i,j-1))/ (2*dy))+dt/re*((O(i+1,j)-2*O(i,j)+O(i-1,j))/dx^2+(O(i,j+1)-2*O(i,j)+O(i,j-1))/d y^2);endendfor i=2:Ifor j=2:JE(i,j)=E(i,j)+0.25*(E(i+1,j)+E(i-1,j)+E(i,j+1)+E(i,j-1)-4*E(i,j)+dx^2*O(i,j)); endend% 0为涡量,E流函数%计算效果图:分别设置雷诺数为200,500,1000雷诺数Re=200时的流函数图及速度矢量图雷诺数Re=500时的流函数图及速度矢量图雷诺数Re=1000时的流函数图及速度矢量图。
方腔环流的流场计算

中山大学工学院、理论与应用力学刘广编制
实验编号及题目:实验六
方腔环流
《计算流体力学试验》课程实验报告纸
院系:工学院 姓名:刘广 学号:11309018 日期:2014 年 05 月 23 号
方腔环流示意图
我们取网格做如下说明,取正方形网格,网格数量由用户输入,但是建议不超过 200,因 为超过 200 计算量会急剧增大,雷诺数也是由用户输入,建议不超过 5000,因为超过 5000 流 场已经呈现出非线性,开始出现偏差,雷诺数超过 10000 甚至根本不能算出结果,这是因为强 非线性情况下描述流场行为的方程已经不能做如上简化, 同样的, 在计算过程中我们采用超松 弛迭代法,下面对离散形式做一下说明: 我们用二阶精度的差商代替微商做以下说明,得
姓名:刘广
学号:11309018
日期:2014 年 05 月 23 号
程序执行时,我输入的是10E-3作为计算精度,对于程序的说明程序注释已经说的很清楚, 这里不再赘述。最终会在目录下生成OUTPUT.txt 。 四:实验结果 最终会在目录下生成OUTPUT.txt 。然后我们可以用Matlab软件对计算出来的数据进一步整 理,画成云图和画出流线,我们做一下说明。
Re n n [( in, j 1 in, j 1 )( in in1, j in1, j )( in 1, j i 1, j ) ( , j 1 i , j 1 )]} 4 (1 ) in ,j
边界值的点需要特殊处理,然后由内点差分格式顺序扫描,一次次迭代直到满足用户输入的 精度为止。边界条件如下:
( i 1, j 2 i , j i 1, j ) / h 2 ( i , j 1 2 i , j i , j 1 ) / h 2 i , j ( i , j 1 i , j 1 )(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
���������������,������+���+11
=
���������������������������,���������
−
������������∆������ 4ℎ2
(���������������,���������+1
−
���������������,���������−1)
(���������������+��� 1,������
cos(���⃗���,
���̂���)
4.用 fortran 编程(附件 1)进行计算,求出不同雷诺数(400,,1000,3200 等)下流场、
1
涡量场和压力场的数值解(调整ρ控制收敛速度);再用 matlab 程序进行绘图(附件 3),进行分析和比较。 (三)使用 ADI 方法和亚松弛迭代法对非定常问题进行求解
+
���������������−���+11,������
+
���������������,������+���−11
+
������������ 4
[(���������������,���������+1
−
���������������,������+���−11)(���������������+��� 1,������
二维方腔环流计算
一、实验目的
二维方形腔体,腔体内部充满了流体。当顶板沿着水平方向被匀速(u=1)拉动时,腔体内 部的流体被带动而作环状运动。这种环流导致了腔体底边的二次涡。 方程与边界条件
用流函数涡量法求解方腔环流, 和 满足下列无量纲定常方程与边界条件
������2������ ������2������ ������������2 + ������������2 = −������
+
2������������ ( ℎ2
+
������������)
���������������,������+��� 1
+
[−
������������∆������(���������������+��� 1,������ − 4ℎ2
���������������−��� 1,������)
−
������������ ℎ2]
3.边界条件 流函数边界条件:���������������,��������� = 0 ,在四边 涡量边界条件:
(1)左边(AD):ζ������������,���+��� 1
=
−
2(������������+1,������−������������,������) ℎ2
(2)右边(BC):ζ������������,���+��� 1
−
(������������+1,������+1
−
������������+1,������−1 − ������������−1,������+1 4∆������∆������
+
������������−1,������−1)2]
其中 k 为迭代次数,������1为亚松弛因子,������2为超松弛因子。一般亚松弛因子������1为 0<������1<1, 超松弛因子������2为 1<������2<2。当松弛因子选择恰当,会大大加快迭代收敛的 速度。
+
���������������,���������−1)
②校正:
[������������∆������(���������������+���41ℎ,������2−
���������������−��� 1,������)
−
������������ ℎ2]
���������������,������+���−11
(2)右边(BC):ζ������������,���+��� 1
=
−
2(���������������−��� 1,������−���������������,���������) ℎ2
(3)底边(CD):ζ������������,���+��� 1
−
������
������������ ������������)
cos(���⃗���,
���̂���)
+
������
(������∇2������
−
������������ ������������
−
������
������������ ������������
−
������
������������ ������������)
−
���������������−��� 1,������)
+
������������∆������ ℎ2
(���������������+��� 1,������
−
2���������������,���������
+
���������������−��� 1,������)
(2)流函数(FTCS 格式):
���������������,���������−1)
−
������������ ℎ2]
���������������+���+11,������
=
���������������������������,���������
+
������������∆������ 4ℎ2
(���������������+��� 1,������
2.差分方程:
���������������,������+��� 1
=
������1 4
(���������������,��������� ℎ2
+
���������������−���+11,������
+
���������������,������+���−11
+
���������������+��� 1,������
(���������������,������+��� 1)������+1
=
������1 4
(���������������,������+��� 1ℎ2
+
(���������������−���+11,������ )���������������,������+���−11)������+1
1.概述:每个时间步长内,使用 ADI 方法对涡量进行求解,再用亚松弛迭代法对流 函数进行求解;
2.差分方程
(1)涡量(D-R 格式):
①预报:
[−
������������∆������(���������������,���������+1 − 4ℎ2
���������������,���������−1)
=
−
2(������������,������−1−������������,������+ℎ) ℎ2
压强边界条件:
������������ ������������
=
������
(������∇2������
−
������������ ������������
−
������
������������ ������������
+
���������������,���������+1)
+
(1
−
������1)���������������,���������
���������������,������+��� 1
=
������1 4
{���������������+��� 1,������
+
���������������,���������+1
Figure 1.1 方腔环流示意图
二、实验要求
1. 用流函数涡量法计算定常情况下方腔环流的流场、涡量场和压力场,包括雷诺数为 400,1000,3200 等几种情况的解;
2. 用流函数涡量法计算非定常情况下方腔环流的流场、涡量场,包括雷诺数为 400,1000,3200,5000,10000 等几种情况的解;
[(������������+1,������
− 2������������,������ + (∆������)2
������������−1,������) (������������,������+1
− 2������������,������ + (∆������)2
������������,������−1)
−
���������������−��� 1,������)(���������������,���������+1
−
���������������,���������−1)
+
������������∆������ ℎ2
(���������������,���������+1
−
2���������������,���������
+
(���������������+���+11,������ )������
+
(���������������,������+���+11)������)
